文章编号: 2096-3203(2024)04-0067-10 中图分类号: TM61
2. 清华大学能源与动力工程系, 北京 100084
随着能源转型进程加快,我国大力发展风电[1]、光伏[2]等新能源发电技术,未来电力系统将朝大规模、高比例新能源电力系统方向发展[3-4]。新能源出力具有互补性,利用新能源总出力与系统总负荷之间的匹配效应可以凸显新能源出力间的互补效果,平抑新能源出力波动性,减小常规机组调峰压力[5]。
风电、光伏的出力波动性强[6-7],其大规模接入会对系统造成冲击,给电网调峰带来挑战[8-9]。实际上,风电和光伏出力具有互补特性[10-12],主要表现在两方面:一是新能源资源的广域平滑效应,二是风光出力具有时间上的互补性。
充分挖掘新能源出力互补特性是开展新能源协调规划的重要基础。文献[13]分析了各类能源的互补效应,讨论了配置不同容量电源的经济性和可行性;文献[14]分析了风、光、水资源之间的互补特性,提出了一种包含风、光、水、储的互补性微电网容量优化配置方法;文献[15]研究了新能源出力互补优化方法,定量计算了各类资源容量。上述文献研究了系统电源出力互补性,但对于新能源出力互补性的分析多是和常规电源一同考虑,未有研究单独考虑新能源出力自身互补性。
研究新能源出力自身互补特性,通常需要提出互补性评价指标[16],如文献[17]采用新能源总出力的标准差作为评价指标来刻画新能源出力互补性;文献[18]定义了由时间互补、能量互补和振幅互补组成的可再生能源互补性指标;文献[19]采用互补系数等指标描述多能互补系统中电源出力的互补性。以上关于新能源互补性的研究多注重新能源出力间的负相关性,即假定新能源场站的总出力恒定不变,则认为新能源互补效果最好。
由于负荷具有波动性,上述基于负相关性的研究中,负荷波动部分会由常规可控电源负担。但若新能源总出力与负荷波动规律保持一致,即新能源出力与负荷间存在匹配效应,那么新能源发电就能够承担一部分变化的负荷,火电机组则更多承担基荷并运行在较低的水平,从而大幅减小由新能源接入系统带来的常规电源调峰压力。因此,从提高新能源消纳方面看,关注新能源出力与负荷间的匹配(源-荷匹配)关系才可更凸显新能源互补的效果[20],此时互补性表现为新能源总出力与负荷呈正相关性。
针对源-荷匹配效果的描述,已有学者进行了研究,如文献[21]定义了负荷追踪度指标用以评价不同电源互补效果;文献[22]采用负荷追踪系数描述系统出力跟随负荷变化的能力,并量化多能互补系统总发电量与负荷的匹配程度;文献[23]以新能源出力与负荷之差的平方和最小为目标,提出了新能源出力追踪控制算法。上述利用负荷追踪能力来描述系统源-荷匹配效果的评价方法主要用于新能源电力系统优化调度,文中将该方法应用于新能源系统优化规划中,可在规划阶段充分计及多类型新能源出力间的互补特性。
基于上述分析,文中针对计及源-荷匹配的多区域多类型新能源系统优化规划问题进行研究。首先,为了量化新能源出力与负荷之间有功功率的匹配能力,从均衡度和一致性两方面评价源-荷匹配特性。其次,基于源-荷匹配思想,建立多区域新能源系统优化规划模型。模型以电网新能源发电量最大和源-荷匹配偏差系数最小为目标函数,采用带权极小模理想点法[24]统一2个目标函数的量纲,综合考虑新能源发电功率、新能源限电率、新能源装机容量等约束,通过引入所提源-荷匹配均衡度约束来保证新能源出力与系统负荷需求变化特性一致。然后,以各区域新能源全年出力时间序列和负荷序列为模型输入,对规划模型进行优化求解,得到各区域最优新能源接入容量,并利用一致性指标来评价源-荷匹配效果。最后,以我国北方4个区域的电网为例进行算例分析,结果验证了由源-荷匹配定义新能源出力互补性的合理性。研究可为多区域新能源规划布局提供参考意见。
1 源-荷匹配特性评价文中从均衡度和一致性两方面对源-荷匹配特性进行评价,用以量化新能源出力与负荷之间有功功率的匹配能力。
1.1 均衡度评价指标文中提出一种新能源出力与负荷匹配均衡度评价方法,即源-荷匹配均衡度约束,使新能源总出力尽可能贴近匹配负荷,即限制新能源出力与匹配负荷的偏差值在一定范围内,其形式如下:
| $\sum\limits_{n=1}^{N} P_{n, d}^{\mathrm{re}}(t)-w_{d}^{+}(t)+w_{d}^{-}(t)=P_{d}^{\mathrm{d-l}}(t) $ | (1) |
| $ P_{d}^{\mathrm{d-l}}(t)=\lambda_{d} \sum\limits_{n=1}^{N} P_{n, d}^{\mathrm{1}}(t) $ | (2) |
| $ w_{d}^{+}(t)+w_{d}^{-}(t) \leqslant \varepsilon \sum\limits_{t=1}^{T} \sum\limits_{n=1}^{N} P_{n, d}^{\mathrm{l}}(t) $ | (3) |
式中:下标d为源-荷匹配周期序号;Pn, dre(t)为n区域d周期t时刻新能源总出力;N为区域总数;wd+(t)、wd-(t)分别为引入的d周期负荷匹配的正、负偏差;Pdd-l(t)为全网d周期t时刻匹配负荷序列;Pn, dl(t)为n区域d周期t时刻基准负荷序列;λd为d周期基准用电负荷调节系数优化变量,表示匹配负荷占基准负荷的比例,0≤λd≤1;ε为负荷匹配偏差系数,表示全优化时段的匹配偏差不超过目标负荷电量的比率;T为总时间断面。
需要注意的是,文中的源-荷匹配是逐周期进行的,因此Pdd-l(t)、wd+(t)和wd-(t)均与周期d有关,例如对于全年8 760 h计算周期来说,若匹配周期为1 d,则周期d的总个数为365,t的长度为24 h;若采用匹配周期为5 d,则周期d的总个数为73,t的长度为120 h。该约束可以理解为一定匹配周期(可为周、日或者几小时)内,新能源出力与匹配负荷的出力偏差在一定范围内。
考虑约束式(1)—式(3)可以使得在每个匹配周期d内,新能源总出力与匹配负荷的偏差值在一定范围内,控制偏差范围的大小,可使得新能源出力与匹配负荷曲线贴近程度更高,达到新能源出力与负荷变化趋势保持一致的效果。由式(3)可知,误差范围由基准负荷序列和匹配偏差系数ε共同决定。由于基准负荷序列为固定的输入边界,因此改变匹配偏差系数ε即可控制偏差范围。
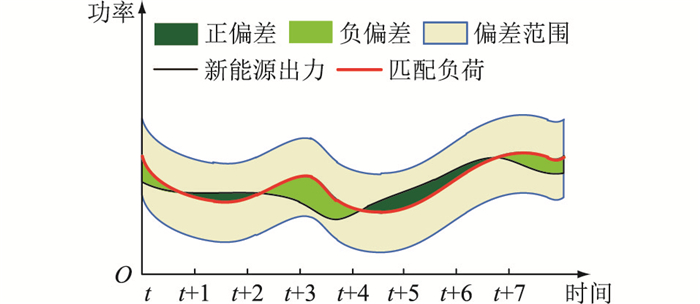
某个匹配偏差系数ε下的源-荷互补效果见图 1。可以看出,绿色区域总面积越小,新能源出力与匹配负荷贴近程度越高。匹配偏差范围受限于匹配偏差系数ε,因此控制ε即可保证源-荷匹配效果。然而,考虑源-荷匹配均衡度约束虽然可以保证新能源出力曲线与匹配负荷曲线尽可能地贴近,但无法保证两者变化趋势完全一致,正、负偏差交替现象的出现可能导致常规电源改变运行状态来弥补功率缺额或者压缩出力空间避免新能源弃电。
|
图 1 源-荷互补示意 Fig. 1 Schematic diagram of source-load complementarity |
1.1节中的分析指出,考虑源-荷匹配均衡度约束可以限制新能源出力与匹配负荷的偏差值在一定范围内,但难以评估新能源出力与基准负荷之间的正相关程度。因此,为评价新能源出力与基准负荷之间的一致性程度,文中定义了源-荷匹配一致性评价指标,具体形式如下:
| $ M^{\mathrm{s-l}}=\frac{\sum\limits_{d=1}^{D-1} \sum\limits_{t=1}^{T-1}\left|\chi_{d}^{s}(t)-\chi_{d}^{\mathrm{l}}(t)\right|}{(D-1)(T-1) \max \left(\left|\chi_{d}^{s}(t)-\chi_{d}^{\mathrm{l}}(t)\right|\right)} $ | (4) |
| $ \chi_{d}^{s}(t+1)=\sum\limits_{n=1}^{N} \frac{P_{n, d}^{\mathrm{re}}(t+1)-P_{n, d}^{\mathrm{re}}(t)}{\Delta t} $ | (5) |
| $ \begin{equation*} \chi_{d}^\mathrm{l}(t+1)=\sum\limits_{n=1}^{N} \frac{P_{n, d}^\mathrm{l}(t+1)-P_{n, d}^\mathrm{l}(t)}{\Delta t} \end{equation*} $ | (6) |
式中:D为源-荷匹配总周期数;Ms-l为源-荷匹配一致性评价指标,用来描述一段时间内源-荷匹配程度的平均效应,0≤Ms-l≤1,Ms-l越小,说明在该时段内新能源出力与匹配负荷变化趋势越接近,源-荷一致性程度越高;χds(t)为d周期t时刻新能源出力变化率;χdl(t)为d周期t时刻负荷的变化率;Δt为时间间隔,通常取1 h。当|χds(t)-χdl(t)|=0时,新能源出力与负荷的一阶变化量完全一致,即数值相等、方向相同,两者变化量正好抵消,此时一致性效果最好,新能源总出力与负荷呈显著正相关性;当|χds(t)-χdl(t)|>0时,源、荷出力的一阶变化量尚存在未抵消部分,两者未完全匹配。
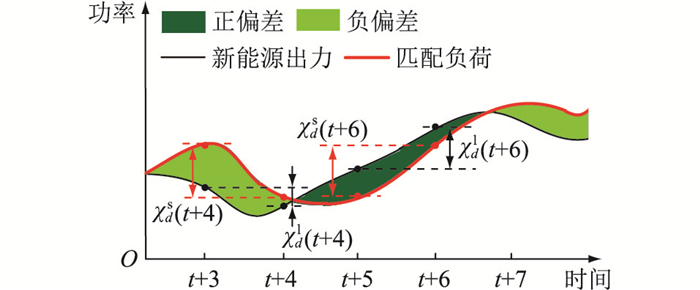
以图 1为例解释源-荷匹配一致性指标的意义,如图 2所示。可以看出,在t+3—t+4时间段内,新能源出力变化率χsd(t+4)和负荷变化率χld(t+4)均为负值;在t+5—t+6时间段内,χsd(t+6)和χld(t+6)均为正值。当源、荷一阶变化量同号时,源-荷出力变化率之差的绝对值较小,表明源-荷匹配效果更优,新能源互补性更强。可见,当χsd(t)和χld(t)同号时,|χds(t)- χdl(t)|≤max{|χds(t)|, |χdl(t)|};当χsd(t)和χld(t)异号时,|χds(t)- χdl(t)|≥max{|χds(t)|, |χdl(t)|},因此,源-荷匹配一致性评价指标可以描述新能源出力与负荷的变化趋势。
|
图 2 源-荷匹配一致性指标示意 Fig. 2 Schematic diagram of source-load matching consistency index |
不同于常规电源规划计及成本因素,文中将提升新能源消纳能力作为规划目标。计及新能源出力的互补效应,一方面是为了缓减由新能源接入系统带来的调峰压力,另一方面是为了减少新能源弃电,提升新能源的消纳能力。因此计及源-荷匹配的新能源优化规划数学模型为多目标优化问题,一是以全网各区域的新能源发电量最大为优化目标,具体形式如下:
| $ \begin{equation*} g_{1}=\max \sum\limits_{n=1}^{N} \sum\limits_{d=1}^{D} \sum\limits_{t=1}^{T} P_{n, d}^{\mathrm{re}}(t) \end{equation*} $ | (7) |
此外,由1.1节中的源-荷匹配均衡度约束可以看出,源-荷匹配程度受匹配偏差系数ε影响很大。对某一给定ε,可能会出现多组符合约束边界的最优解。而文中期望得到最优的互补效果,因此根据源-荷匹配思想,另一个目标为最小化匹配偏差系数ε。对多目标优化问题进行合并,将其转为最大化问题,具体形式如下:
| $\begin{equation*} g_{2}=\max (-\varepsilon) \end{equation*} $ | (8) |
采用带权极小模理想点法统一2个子目标函数的量纲,并反映其重要程度。模型综合目标函数为:
| $\begin{equation*} \max (G)=\rho_{1}\left|\frac{g_{1}-g_{1}^{\prime}}{g_{1}^{\prime}}\right|+\rho_{2}\left|\frac{g_{2}-g_{2}^{\prime}}{g_{2}^{\prime}}\right| \end{equation*} $ | (9) |
式中:ρ1、ρ2分别为子目标函数g1、g2的权重系数,且ρ1+ρ2=1;g′ 1、g′ 2为理想点目标值。该带权极小模函数可理解为计算解的各目标值与理想点的偏差,反映计算解的质量,其以计算解与理想点的相对距离统一为量纲,通过对应的权重系数反映各子目标的重要程度。
对于综合目标函数中的最优权重ρ1和ρ2,可采用层次分析法[25-26]进行综合评估。该方法的主要思想是将子目标两两对比,目标的重要性由与目标重要程度成正比的比率标度值决定,通过计算比率标度矩阵最终确定权重系数。确定权重的综合目标函数为:
| $\begin{equation*} \max (G)=\rho_{\mathrm{AHP}_{1}}\left|\frac{g_{1}-g_{1}^{\prime}}{g_{1}^{\prime}}\right|+\rho_{\mathrm{AHP}_{2}}\left|\frac{g_{2}-g_{2}^{\prime}}{g_{2}^{\prime}}\right| \end{equation*} $ | (10) |
式中:ρAHP1、ρAHP2分别为子目标函数g1、g2的层次分析权重值,根据比率标度法确定ρAHP1=0.75、ρAHP2=0.25。
2.1.2 约束条件(1) 时序电力平衡约束。
| $ \begin{gather*} \sum\limits_{n=1}^{N_{\mathrm{re}}} P_{n}^{\mathrm{re}}(t)+\sum\limits_{n=1}^{N_{\mathrm{g}}} P_{n}^{\mathrm{g}}(t)+\sum\limits_{n=1}^{N_{\mathrm{r}}} P_{n}^{\mathrm{r}}(t)+ \\ \sum\limits_{n=1}^{N_{\mathrm{L}}} P_{n}^{\mathrm{L}}(t)=\sum\limits_{n=1}^{N_{1}} P_{n}^\mathrm{l}(t) \end{gather*} $ | (11) |
式中:Pnre(t)为n区域t时刻新能源出力;Png(t)为n区域t时刻火电机组出力;Pnr(t)为n区域t时刻水电机组出力;PnL(t)为n区域t时刻联络线出力;Pnl(t)为n区域t时刻负荷;Nre为新能源总数量;Ng为火电机组总数量;Nr为水电机组总数量;NL为联络线总数量;Nl为负荷总数量。
文中从新能源出力与负荷匹配的角度进行规划,因此在考虑源-荷匹配均衡度约束的基础上,考虑功率平衡约束式(11),即新能源出力、常规电源出力以及外网通过联络线功率平衡系统负荷出力。
(2) 新能源电量约束。
| $ \begin{equation*} \sum\limits_{d=1}^{D} \sum\limits_{t=1}^{T} \sum\limits_{n=1}^{N} P_{n, d}^{\mathrm{re}}(t) \geqslant \lambda_{\mathrm{q}} \sum\limits_{d=1}^{D} \sum\limits_{t=1}^{T} \sum\limits_{n=1}^{N} P_{n, d}^\mathrm{l}(t) \end{equation*} $ | (12) |
式中:λq为新能源电量最小占比。该约束表示新能源年发电量不低于年负荷总量的一定比例。
(3) 灵活性新能源电源容量占比约束。
| $ \begin{equation*} \sum\limits_{n=1}^{N} \sum\limits_{i=1}^{N_{\text{c}}} C_{n, i} \geqslant \lambda_{\mathrm{c}} \sum\limits_{n=1}^{N} \sum\limits_{i=1}^{N_{\text{x}}} C_{n, i} \end{equation*} $ | (13) |
式中:Cn, i为n区域电源i容量;Nc为灵活性新能源电源总数量;Nx为电源总数量;λc为灵活性新能源电源占电源总装机容量的最小比例。该约束表示灵活性新能源电源容量不低于系统电源总装机容量的一定比例。接入的灵活性新能源电源比例越高,新能源电源总出力灵活性越高,源-荷匹配效果越优,能够进一步挖掘新能源出力的互补空间。
(4) 电源约束。
① 新能源出力约束。
| $ \left\{\begin{array}{l} 0 \leqslant P_{n}^{\mathrm{w}}(t) \leqslant p_{n}^{\mathrm{w}}(t) C_{n}^{\mathrm{w}} \\ 0 \leqslant P_{n}^{\mathrm{pv}}(t) \leqslant p_{n}^{\mathrm{pv}}(t) C_{n}^{\mathrm{pv}} \end{array}\right. $ | (14) |
式中:Pnw(t)、Pnpv(t)分别为n区域t时刻风电和光伏出力;pnw(t)、pnpv(t)分别为n区域t时刻风电和光伏归一化理论发电出力时间序列;Cnw、Cnpv分别为n区域风电和光伏场站装机容量。式(14)表示新能源实际出力在0和最大出力限值之间。通过新能源归一化理论发电出力时间序列,可以将新能源场站容量与发电功率联系起来。
② 光热电站运行约束,包括热电转换约束、发电功率约束、爬坡约束、储热容量约束、热功率关系约束、运行状态约束等。
| $ \left\{\begin{array}{l} P_n^{\mathrm{cs}}(t)=\eta^{\mathrm{cs}} P_n^{\mathrm{th}}(t) \\ \underline{P}_n^{\mathrm{cs}} \leqslant Z_n^{\mathrm{cs}}(t) P_n^{\mathrm{cs}}(t) \leqslant \bar{P}_n^{\mathrm{cs}} \\ P_n^{\mathrm{cs}}(t+\Delta t)-P_n^{\mathrm{cs}}(t) \leqslant P_{n, \mathrm{up}}^{\mathrm{cs}} \\ P_n^{\mathrm{cs}}(t)-P_n^{\mathrm{cs}}(t+\Delta t) \leqslant P_{n, \mathrm{down}}^{\mathrm{cs}} \\ E_n^{\mathrm{th}}(t+1)=(1-\gamma) E_n^{\mathrm{th}}(t)+\eta^{\mathrm{T}} P_n^{\mathrm{th},+}(t) \Delta t- \\ \quad P_n^{\mathrm{th},-}(t) \Delta t / \eta^{\mathrm{T}} \\ P_n^{\mathrm{th}}(t)+\beta^{+}(t) P_n^{\mathrm{th},+}(t)-\beta^{-}(t) P_n^{\mathrm{th},-}(t)+ \\ \quad Z_n^{\mathrm{cs}}(t) P^{\mathrm{su}}(t)=P_n^{\mathrm{th}, \mathrm{ss}}(t)-P_n^{\mathrm{th}, \mathrm{cur}}(t) \\ 0 \leqslant \beta^{+}(t)+\beta^{-}(t) \leqslant 1 \end{array}\right. $ | (15) |
式中:Pncs(t)、Pnth(t)分别为n区域t时刻光热电站发电功率和热功率;ηcs为热电转换效率;
③ 火电运行约束,包括发电功率约束、爬坡约束、最小启/停机时间约束、运行状态约束等。
| $\left\{\begin{array}{l} \underline{P}_n^{\mathrm{g}} \leqslant Z_n^{\mathrm{g}}(t) P_n^{\mathrm{g}}(t) \leqslant \bar{P}_n^{\mathrm{g}} \\ P_n^{\mathrm{g}}(t+\Delta t)-P_n^{\mathrm{g}}(t) \leqslant P_{n, \text { up }}^{\mathrm{g}} \\ P_n^{\mathrm{g}}(t)-P_n^{\mathrm{g}}(t+\Delta t) \leqslant P_{n, \text { down }}^{\mathrm{g}} \\ u_n^{\mathrm{g}}(t)+\sum\limits_{h=1}^{H_{\text {on }}} v_n^{\mathrm{g}}(t+h) \leqslant 1 \\ v_n^{\mathrm{g}}(t)+\sum\limits_{h=1}^{H_{\text {off }}} u_n^{\mathrm{g}}(t+h) \leqslant 1 \\ Z_n^{\mathrm{g}}(t)-Z_n^{\mathrm{g}}(t-\Delta t)+v_n^{\mathrm{g}}(t)-u_n^{\mathrm{g}}(t)=0 \end{array}\right. $ | (16) |
式中:
④ 水电运行约束,包括发电功率约束、流量约束、水库约束、水库蓄能值约束、水位水头关系约束等。
| $ \left\{\begin{array}{l} \underline{P}_n^{\mathrm{r}} \leqslant P_n^{\mathrm{r}}(t) \leqslant \bar{P}_n^{\mathrm{r}} \\ P_n^{\mathrm{r}}(t)=f_{\mathrm{NHQ}}\left(R_n^{\mathrm{r}}(t), H_n^{\mathrm{r}}(t)\right) \\ C_n^{\mathrm{r}}(t)=C_n^{\mathrm{r}}(t-1)+R_n^{\mathrm{in}}(t) \Delta t-R_n^{\text {out }}(t) \Delta t \\ C_{n, \min }(t) \leqslant C_n^{\mathrm{r}}(t) \leqslant C_{n, \max }(t) \\ E_n^{\mathrm{r}}(t)=E_n^{\mathrm{r}}(t-1)+f_{\mathrm{NHQ}}\left(R_n^{\mathrm{in}}(t), H_n^{\mathrm{r}}(t)\right) \Delta t- \\ \quad f_{\mathrm{NHQ}}\left(R_n^{\text {out }}(t), H_n^{\mathrm{r}}(t)\right) \Delta t \\ H(t)=f_{\mathrm{h}}\left(C_n^{\mathrm{r}}(t)\right) \\ H_n^{\mathrm{r}}(t)=f_{\mathrm{g}}(H(t)) \\ E_{n, T_t, \min } \leqslant \sum\limits_{t=1}^{T_t} P_n^{\mathrm{r}}(t) \Delta t \leqslant E_{n, T_t, \text { max }} \end{array}\right. $ | (17) |
式中:
(5) 联络线约束。
| $ \begin{equation*} \underline{P}_{n}^{\mathrm{L}} \leqslant P_{n}^{\mathrm{L}}(t) \leqslant \bar{P}_{n}^{\mathrm{L}} \end{equation*} $ | (18) |
式中:
(6) 备用需求约束。
| $\begin{equation*} \bar{P}_{n}^{\mathrm{g}}+\bar{P}_{n}^{\mathrm{r}}+P_{n}^{\mathrm{w}}(t)+P_{n}^{\mathrm{pv}}(t)-P_{n}^{\mathrm{L}}(t) \geqslant \bar{P}_{n}^\mathrm{l}+p^{+} \end{equation*} $ | (19) |
式中:
(7) 新能源限电率约束。
| $ \begin{gather*} \left(1-\eta^{\mathrm{re}}\right) \sum\limits_{t=1}^{T}\left(\sum\limits_{n=1}^{N_{\mathrm{w}}} p_{n}^{\mathrm{w}}(t) C_{n}^{\mathrm{w}}+\right. \\ \left.\sum\limits_{n=1}^{N_{\mathrm{pv}}} p_{n}^{\mathrm{pv}}(t) C_{n}^{\mathrm{pv}}+\sum\limits_{n=1}^{N_{\mathrm{cs}}} \frac{P_{n}^{\mathrm{th}, \mathrm{sf}}(t)}{\eta^{\mathrm{cs}}}\right) \leqslant \\ \sum\limits_{t=1}^{T}\left(\sum\limits_{n=1}^{N_{\mathrm{w}}} P_{n}^{\mathrm{w}}(t)+\sum\limits_{n=1}^{N_{\mathrm{pv}}} P_{n}^{\mathrm{pv}}(t)+\sum\limits_{n=1}^{N_{\mathrm{cs}}} P_{n}^{\mathrm{cs}}(t)\right) \end{gather*} $ | (20) |
式中:ηre为新能源限电率;Nw为风电总数量;Npv为光伏总数量;Ncs为光热电站总数量。
2.2 规划模型求解方法文中研究的问题为新能源电源容量规划问题,其目标函数为多目标优化问题,是一个线性目标;其决策变量为新能源装机容量,仅能取正整数;其约束条件中包含机组运行状态、机组启/停机状态等整数变量和整数约束。这些正整数约束和决策变量的存在使得文中所研究的规划模型从线性规划模型转变为混合整数线性规划问题。因此,文中所提模型是一个典型的混合整数线性规划模型,可在GAMS[27]平台上调用商业求解器CPLEX[28]进行求解。
2.3 规划所需基础数据(1) 系统数据。规划所需系统数据为系统网架结构和各区域详细的电网运行特性数据,包括各类型机组运行主要参数、联络线功率限值、系统新能源限电率限值、源-荷匹配周期限值等。
(2) 时序数据。文中采用时序生产模拟进行规划模型的分析计算,因此规划所需时序数据包括系统各区域负荷年度逐小时序列以及各区域新能源年度逐小时出力序列。
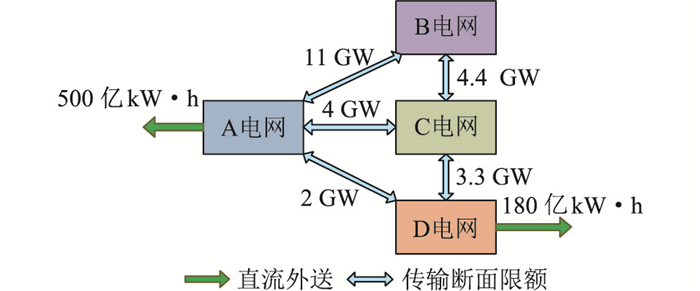
3 算例分析 3.1 算例介绍为验证所提计及源-荷匹配的新能源系统优化规划方法的正确性,以我国北方某相邻4个(省级)区域电网为测试系统,研究2030年的新能源规划布局问题。4个区域电网分布于总面积为125万平方公里的范围内,新能源渗透率超过30%。电网结构如图 3所示,A、C电网分别与其他电网相连,各区域间联络线功率限值分别为11 GW、4 GW、2 GW、4.4 GW、3.3 GW,A、D电网直流外送年电量分别为500亿kW ·h、180亿kW ·h。算例的计算步长为1 h,源-荷匹配周期设为1 d,即24 h,计算周期为8 760 h,其余算例参数见表 1。文中规划水平年的风电、光伏序列是基于这些区域历史出力序列进行新能源出力场景生成得到的,负荷序列是基于这些区域2021年的实际负荷需求序列,假设负荷年增长率为5%估计得到的。
|
图 3 测试系统等效结构 Fig. 3 Equivalent structure of the test system |
|
|
表 1 算例参数 Table 1 Simulation parameters |
为验证所提模型可深入挖掘新能源出力互补性,对比文中模型和传统模型的规划结果,其中传统模型不考虑源-荷匹配均衡度约束。设置2个仿真案例中光热接入容量均为3.35 GW,风电和光伏总装机为59.87 GW,所得结果见表 2、表 3。
|
|
表 2 文中模型的规划结果 Table 2 Planning results of the model in this paper |
|
|
表 3 传统模型的规划结果 Table 3 Planning results of the traditional model |
可以看出,对比传统模型,考虑源-荷匹配后,文中模型所得D区域风电和C区域光伏最优布局容量分别增长了35.81%和54.3%。从风电和光伏总装机方面看,文中模型所得风电总容量较传统模型高4.24%,这表明考虑源-荷匹配后,系统更倾向于配置互补性更好的风电,而光伏由于出力形状较为固定,容量越大越难以实现源-荷匹配。此外,在新能源总装机一致的情况下,文中模型得到的新能源年度总出力电量为1 117.10亿kW ·h,而传统模型所得新能源年度总出力电量为1 018.43亿kW ·h,前者相较后者提升9.69%,即考虑源-荷匹配可使新能源渗透率从28.51%增加至37.04%。从新能源限电方面看,考虑源-荷匹配可使新能源总限电率从传统模型的13.18%降低至文中模型的5.21%。可以看出,在同样的总装机容量下,考虑源-荷匹配可以充分提升新能源消纳能力,减少弃风、弃光情况。
图 4为求解2种模型所得的年度基准负荷调节系数,该参数描述的是每个匹配周期内新能源总出力占基准负荷的比例,其数值越高,说明新能源出力在系统总出力中占比越高。可以看出,文中模型中年度基准负荷调节系数变化范围为0~0.7,平均值为0.32;传统模型的年度基准负荷调节系数变化范围为0.1~0.3,平均值为0.2。文中模型所得基准负荷调节系数更高,有利于提升新能源消纳水平。

|
图 4 不同模型的年度基准负荷调节系数 Fig. 4 Annual reference load adjustment coefficient of different models |
综上可得,采用文中方法考虑源-荷匹配均衡度约束可以深入挖掘新能源出力互补性,有利于提升新能源消纳水平,促进新能源产业健康发展。
3.3 灵活性新能源电源接入对规划结果的影响为研究灵活性新能源电源接入系统对多区域新能源系统优化规划的影响,设置风/光组合和风/光/光热组合2类场景,分别计算2类场景下的多类型能源电力系统容量规划结果。令风/光组合的光伏装机容量与风/光/光热组合的光伏与光热总装机容量相等,其余约束条件和计算边界均一致,计算结果如表 4、表 5所示。
|
|
表 4 风/光组合场景下的规划结果 Table 4 Planning results under wind and photovoltatic scenarios |
|
|
表 5 风/光/光热组合场景下的规划结果 Table 5 Planning results under wind, photovoltatic and concentrating solar power scenarios |
可以看出,在新能源总装机容量一定的情况下,风/光/光热组合的源-荷匹配一致性指标为0.080,而风/光组合的源-荷匹配一致性指标为0.098。由该指标定义可知,Ms-l越小,说明在该时段内新能源出力与负荷的变化趋势越接近,源-荷匹配程度越高。此外,风/光/光热组合的新能源出力与负荷波动形状的年平均绝对偏差与风/光组合相比降低52.27%,新能源接入电网基本不增加电网调峰难度,同时风/光/光热组合的新能源总发电量比风/光组合高3.39%,因此可得出结论:灵活性新能源电源的接入对提高源-荷匹配具有积极作用。
图 5为2种场景下源-荷匹配效果对比。当新能源总装机容量一定时,从匹配效果方面看,4个区域的风/光组合和风/光/光热组合均可以在一定程度上实现新能源总出力与负荷形状的优化匹配,大幅度降低电网的调峰难度。风/光组合的匹配效果不及风/光/光热组合,这说明灵活新能源电源的接入有利于源-荷匹配互补。从匹配偏差方面看,风/光组合匹配偏差最小日的新能源出力非常低,说明仅靠风电和光伏很难完全匹配负荷波动。风/光/光热组合匹配偏差最小日的新能源出力有所提高,光热接入后,新能源出力与负荷匹配偏差减小,最优可达到匹配偏差为0的效果,即使是全年匹配偏差最大日,最大新能源功率缺额也未超过5 GW,验证了灵活性新能源电源光热电站可有效提升新能源出力互补能力。

|
图 5 不同场景下源-荷匹配效果 Fig. 5 Source-load matching effects under different scenarios |
为研究新能源限电率对多区域新能源系统优化规划和源-荷匹配效果的影响,给定光热电站发电容量为3.35 GW,系统最大新能源限电率由0增加至10%时,计算风、光最优接入容量和源-荷匹配一致性指标,结果如图 6所示。

|
图 6 不同新能源限电率下的优化结果 Fig. 6 Optimization results under different renewable energy curtailment rates |
可以看出,随着新能源限电率的增加,新能源总容量增加,相比于缓慢增加的光伏容量,风电容量增加趋势更大,系统优化配置的风电容量最大近乎于光伏容量的6.5倍,这主要有两方面原因:一方面,测试系统地区的风电资源利用小时数高于光伏资源,系统优先接纳风电;另一方面,由于光伏出力具有典型的“昼发夜停”特性,其出力形状一般较为固定,又由于源-荷匹配均衡度约束的限制,电网优先接纳出力形状更易匹配负荷的风电。此外,随着新能源限电率的增加,源-荷匹配一致性指标增加,由0.057近似线性增长至0.115。可见允许一定弃电可使新能源出力与负荷形状更容易匹配,能更好地利用新能源互补特性。
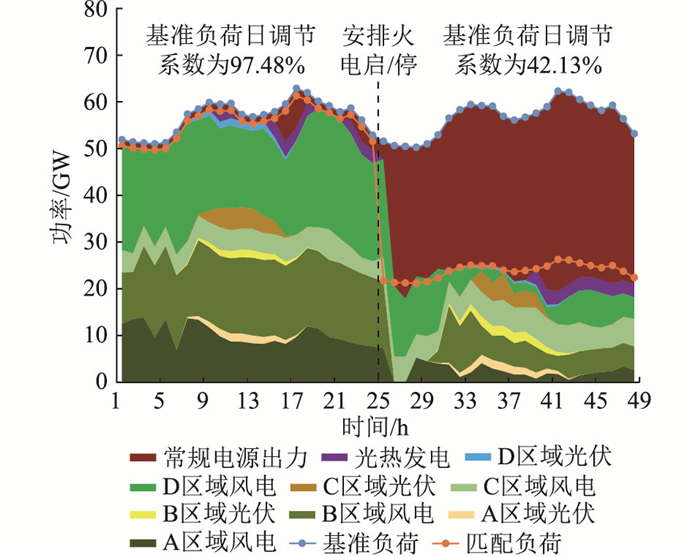
图 7为限电率10%的情况下各区域某两日电源出力运行情况,选取的这两日分别是新能源大发和小发场景。可以看出,在基准负荷日调节系数较高的情况下(97.48%),新能源出力几乎可以满足系统的总负荷需求,而在基准负荷日调节系数较低的情况下(42.13%),新能源出力也可以满足系统总负荷需求的40%以上。并且2种场景下均可以满足新能源出力与负荷变化形状相一致,需要提供支撑的常规电源出力变化量较小,因而常规电源可以更多地承担基荷发电任务。此外,可以看出,对应每日的基准负荷调节系数,需要的火电出力占负荷的比例也相对固定,因此可以在每日第一个时刻对火电机组启/停机状态变量进行限制,匹配周期内火电机组的运行状态变量即可固定下来,有效减少火电机组参与优化规划的0-1变量个数,提高模型的求解速度。
|
图 7 各区域某两日发电运行情况 Fig. 7 Two-day power generation operation in each region |
新能源出力随机性对新能源规划具有一定影响,由于文中从源-荷匹配角度量化新能源互补能力,模型中不包含经济性约束,因此着重分析新能源出力随机性对规划结果的影响。根据文献[29]采用的多场景法,文中以60组8 760 h的新能源出力场景为规划边界求解规划模型,所有场景下的风光规划结果如图 8所示。

|
图 8 60组新能源出力场景计算结果 Fig. 8 Calculation results of 60 renewable energy samples |
从图 8中可以看出,各区域风电装机容量波动范围分别为14.1~14.9 GW、7.9~8.7 GW、5.2~5.8 GW、17.3~20.8 GW,光伏装机容量波动范围分别为2.6~3.0 GW、2.3~2.5 GW、3.9~4.6 GW、2.5~2.8 GW。可以看出,单次规划结果具有一定随机性,多组规划结果的期望值可靠性更高,所得规划结果在60组场景下均收敛于期望值。
4 结论文中研究了计及源-荷匹配的多区域多类型新能源系统优化规划问题。首先,对源-荷匹配特性进行评价。其次,建立了计及源-荷匹配的多区域新能源系统优化规划模型。最后,经过算例分析验证所提模型和方法的有效性。主要研究结论如下:
(1) 从均衡度和一致性两方面评价源-荷匹配特性,可以量化新能源出力与负荷之间有功功率的匹配能力, 将其计入规划模型,可在规划过程中充分计及风光出力广域空间互补特性。
(2) 建立计及源-荷匹配的多区域新能源系统优化规划模型。模型以电网新能源发电量最大和源-荷匹配偏差系数最小为综合目标,适用于大规模区域电网规划,可得到在给定新能源利用率和源-荷匹配偏差约束下的新能源最优接入容量。
(3) 相比于光伏,风电的利用小时数更高,因此其在广域的互补特性更强。在规划阶段计及源-荷匹配后,系统更倾向于接纳风电。此外,灵活性新能源电源的接入对提高源-荷互补性具有积极作用,并在新能源总装机容量一定的情况下提升系统新能源发电量。
| [1] |
国家能源局. 2019风电并网运行情况[EB/OL]. (2020-02-28)[2024-02-13]. https://www.nea.gov.cn/2020-02/28/c_138827910.htm. National Energy Administration. Wind power grid-connected operation in 2019[EB/OL]. (2020-02-28)[2024-02-13]. https://www.nea.gov.cn/2020-02/28/c_138827910.htm. (  0) 0) |
| [2] |
国家能源局. 2019年光伏发电并网运行情况[EB/OL]. (2020-02-28)[2024-02-13]. https://www.nea.gov.cn/2020-02/28/c_138827923.htm. National Energy Administration. Grid connected operation of photovoltaic power in 2019[EB/OL]. (2020-02-28)[2024-02-13]. https://www.nea.gov.cn/2020-02/28/c_138827923.htm. (  0) 0) |
| [3] |
朱法华, 王玉山, 徐振, 等. 中国电力行业碳达峰、碳中和的发展路径研究[J]. 电力科技与环保, 2021, 37(3): 9-16. ZHU Fahua, WANG Yushan, XU Zhen, et al. Research on the development path of carbon peak and carbon neutrality in China's power industry[J]. Electric Power Technology and Environmental Protection, 2021, 37(3): 9-16. (  0) 0) |
| [4] |
文劲宇, 周博, 魏利屾. 中国未来电力系统储电网初探[J]. 电力系统保护与控制, 2022, 50(7): 1-10. WEN Jinyu, ZHOU Bo, WEI Lishen. Preliminary study on an energy storage grid for future power system in China[J]. Power System Protection and Control, 2022, 50(7): 1-10. (  0) 0) |
| [5] |
和萍, 宫智杰, 靳浩然, 等. 高比例可再生能源电力系统调峰问题综述[J]. 电力建设, 2022, 43(11): 108-121. HE Ping, GONG Zhijie, JIN Haoran, et al. Review of peak-shaving problem of electric power system with high proportion of renewable energy[J]. Electric Power Construction, 2022, 43(11): 108-121. (  0) 0) |
| [6] |
任冲, 柯贤波, 王吉利, 等. 高比例新能源电网新能源功率优化分配方法[J]. 电力工程技术, 2022, 41(3): 110-117. REN Chong, KE Xianbo, WANG Jili, et al. New energy power optimal distribution method for high proportion new energy power grid[J]. Electric Power Engineering Technology, 2022, 41(3): 110-117. (  0) 0) |
| [7] |
BILLINTON R, CHEN H, GHAJAR R. A sequential simulation technique for adequacy evaluation of generating systems including wind energy[J]. IEEE Transactions on Energy Conversion, 1996, 11(4): 728-734. DOI:10.1109/60.556371 (  0) 0) |
| [8] |
金梦, 朱鑫要, 周前. 新能源对电网调峰特性影响定量评估及应用[J]. 高压电器, 2023, 59(4): 70-76. JIN Meng, ZHU Xinyao, ZHOU Qian. Quantitative assessment of influence of renewable energy on peak regulation characteristics of power grid and its application[J]. High Voltage Apparatus, 2023, 59(4): 70-76. (  0) 0) |
| [9] |
郭力, 杨书强, 刘一欣, 等. 风光储微电网容量规划中的典型日选取方法[J]. 中国电机工程学报, 2020, 40(8): 2468-2479. GUO Li, YANG Shuqiang, LIU Yixin, et al. Typical day selection method for capacity planning of microgrid with wind turbine-photovoltaic and energy storage[J]. Proceedings of the CSEE, 2020, 40(8): 2468-2479. (  0) 0) |
| [10] |
万家豪, 苏浩, 冯冬涵, 等. 计及源荷匹配的风光互补特性分析与评价[J]. 电网技术, 2020, 44(9): 3219-3226. WAN Jiahao, SU Hao, FENG Donghan, et al. Analysis and evaluation of the complementarity characteristics of wind and photovoltaic considering source-load matching[J]. Power System Technology, 2020, 44(9): 3219-3226. (  0) 0) |
| [11] |
刘泽洪, 周原冰, 李隽, 等. 西南跨流域水风光协同开发研究[J]. 全球能源互联网, 2023, 6(3): 225-237. LIU Zehong, ZHOU Yuanbing, LI Jun, et al. Trans-basin complementary planning of hydro-wind-photovoltaic systems in southwest China[J]. Journal of Global Energy Interconnection, 2023, 6(3): 225-237. (  0) 0) |
| [12] |
吉祥, 谢敏, 曾东, 等. 考虑风光互补特征的多微网系统自治经济调度模型[J]. 浙江电力, 2022, 41(10): 97-105. JI Xiang, XIE Min, ZENG Dong, et al. Autonomous economic dispatch of multi-microgrid systems considering complementarity between wind and solar power[J]. Zhejiang Electric Power, 2022, 41(10): 97-105. (  0) 0) |
| [13] |
熊文, 刘育权, 苏万煌, 等. 考虑多能互补的区域综合能源系统多种储能优化配置[J]. 电力自动化设备, 2019, 39(1): 118-126. XIONG Wen, LIU Yuquan, SU Wanhuang, et al. Optimal configuration of multi-energy storage in regional integrated energy system considering multi-energy complementation[J]. Electric Power Automation Equipment, 2019, 39(1): 118-126. (  0) 0) |
| [14] |
夏永洪, 吴虹剑, 辛建波, 等. 考虑风/光/水/储多源互补特性的微网经济运行评价方法[J]. 电力自动化设备, 2017, 37(7): 63-69. XIA Yonghong, WU Hongjian, XIN Jianbo, et al. Evaluation of economic operation for microgrid with complementary DGs and energy storage[J]. Electric Power Automation Equipment, 2017, 37(7): 63-69. (  0) 0) |
| [15] |
晋宏杨, 孙宏斌, 郭庆来, 等. 含大规模储热的光热电站—风电联合系统多日自调度方法[J]. 电力系统自动化, 2016, 40(11): 17-23. JIN Hongyang, SUN Hongbin, GUO Qinglai, et al. Multi-day self-scheduling method for combined system of CSP plants and wind power with large-scale thermal energy storage contained[J]. Automation of Electric Power Systems, 2016, 40(11): 17-23. (  0) 0) |
| [16] |
CHEN Y Z, WANG Y S, KIRSCHEN D, et al. Model-free renewable scenario generation using generative adversarial networks[J]. IEEE Transactions on Power Systems, 2018, 33(3): 3265-3275. (  0) 0) |
| [17] |
朱燕梅, 陈仕军, 马光文, 等. 计及发电量和出力波动的水光互补短期调度[J]. 电工技术学报, 2020, 35(13): 2769-2779. ZHU Yanmei, CHEN Shijun, MA Guangwen, et al. Short-term complementary operation of hydro-photovoltaic integrated system considering power generation and output fluctuation[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2769-2779. (  0) 0) |
| [18] |
BELUCO A, DE SOUZA P K, KRENZINGER A. A dimensionless index evaluating the time complementarity between solar and hydraulic energies[J]. Renewable Energy, 2008, 33(10): 2157-2165. (  0) 0) |
| [19] |
叶林, 屈晓旭, 么艳香, 等. 风光水多能互补发电系统日内时间尺度运行特性分析[J]. 电力系统自动化, 2018, 42(4): 158-164. YE Lin, QU Xiaoxu, YAO Yanxiang, et al. Analysis on intraday operation characteristics of hybrid wind-solar-hydro power generation system[J]. Automation of Electric Power Systems, 2018, 42(4): 158-164. (  0) 0) |
| [20] |
李湃, 方保民, 祁太元, 等. 基于源-荷匹配的区域电网风/光/储容量配比优化方法[J]. 中国电力, 2022, 55(1): 46-54. LI Pai, FANG Baomin, QI Taiyuan, et al. Capacity proportion optimization of wind, solar power and battery energy storage system for regional power grid based on source-load matching[J]. Electric Power, 2022, 55(1): 46-54. (  0) 0) |
| [21] |
曾雪婷, 刘天琪, 李茜, 等. 基于虚拟电源配置策略的风光水火多源互补短期优化调度[J]. 电网技术, 2016, 40(5): 1379-1386. ZENG Xueting, LIU Tianqi, LI Qian, et al. Short-term complementary optimal dispatch model of multi-source hybrid power system based on virtual power configuration strategy[J]. Power System Technology, 2016, 40(5): 1379-1386. (  0) 0) |
| [22] |
温正楠, 刘继春. 风光水互补发电系统与需求侧数据中心联动的优化调度方法[J]. 电网技术, 2019, 43(7): 2449-2460. WEN Zhengnan, LIU Jichun. A optimal scheduling method for hybrid wind-solar-hydro power generation system with data center in demand side[J]. Power System Technology, 2019, 43(7): 2449-2460. (  0) 0) |
| [23] |
WU X, LIANG K X, HAN X. Renewable energy output tracking control algorithm based on the temperature control load state-queuing model[J]. Applied Sciences, 2018, 8(7): 1099. (  0) 0) |
| [24] |
隋鑫, 卢盛阳, 苏安龙, 等. 计及风电和柔性负荷的核电多目标优化调度研究[J]. 中国电机工程学报, 2019, 39(24): 7232-7241, 7496. SUI Xin, LU Shengyang, SU Anlong, et al. Research on multi-objective optimal scheduling of nuclear power considering wind power and flexible load[J]. Proceedings of the CSEE, 2019, 39(24): 7232-7241, 7496. (  0) 0) |
| [25] |
沙熠, 邱晓燕, 宁雪姣, 等. 协调储能与柔性负荷的主动配电网多目标优化调度[J]. 电网技术, 2016, 40(5): 1394-1399. SHA Yi, QIU Xiaoyan, NING Xuejiao, et al. Multi-objective optimization of active distribution network by coordinating energy storage system and flexible load[J]. Power System Technology, 2016, 40(5): 1394-1399. (  0) 0) |
| [26] |
汪湘晋, 黄滢, 蒋金琦, 等. 基于层次分析法的储能综合评估及类型选择[J]. 浙江电力, 2022, 41(11): 1-8. WANG Xiangjin, HUANG Ying, JIANG Jinqi, et al. Comprehensive evaluation and type selection of energy storage based on analytic hierarchy process[J]. Zhejiang Electric Power, 2022, 41(11): 1-8. (  0) 0) |
| [27] |
GAMS Development Corp. GAMS[EB/OL]. (2017-10-01)[2024-01-22]. http://www.gams.com.
(  0) 0) |
| [28] |
IBM ILOG. CPLEX[EB/OL]. (2017-12-01)[2024-01-22]. https://www.gams.com/latest/docs/S_CPLEX.html.
(  0) 0) |
| [29] |
史昭娣, 王伟胜, 黄越辉, 等. 考虑决策相关随机规划的光热电站容量配置[J]. 中国电机工程学报, 2020, 40(23): 7511-7522. SHI Zhaodi, WANG Weisheng, HUANG Yuehui, et al. Capacity optimization of concentrating solar power plant based on decision-dependent stochastic programming[J]. Proceedings of the CSEE, 2020, 40(23): 7511-7522. (  0) 0) |
2. Department of Energy and Power Engineering, Tsinghua University, Beijing 100084, China
 2024, Vol. 43
2024, Vol. 43


 史昭娣(1991),女,博士,助理研究员,从事新型电力系统源网荷储协同规划技术工作(E-mail:
史昭娣(1991),女,博士,助理研究员,从事新型电力系统源网荷储协同规划技术工作(E-mail: