文章编号: 2096-3203(2024)02-0002-09 中图分类号: TM73
2. 杭州电子科技大学信息工程学院, 浙江 杭州 311305;
3. 国网青海省电力公司电力科学研究院, 青海 西宁 810003
风电、光伏等新能源发电具有不确定性,是阻碍消纳的主要原因。氢能作为一种绿色能源,是国家未来重要的战略能源。新能源制氢系统是提升新能源发电消纳、优化氢能战略部署的最优方法之一[1-4]。新能源制氢技术以电解水为核心,包括碱性电解槽、质子交换膜电解槽和固体氧化物电解槽制氢[5-7],其中碱性电解槽是当前唯一能满足大规模制氢需求的电解水制氢设备[8]。
当前,国内外关于电解槽能量管理的研究可分为单电解槽和多电解槽。针对单电解槽,文献[9-11]从电解槽模型角度,通过电解槽和风力发电机的耦合运行,以多个电解槽为整体对比分析,比较了风能系统制氢的多种电解槽模型的明确优缺点。文献[12-13]从系统组成角度,将电解槽、燃料电池组合使用以代替储能单元,实现不同应用场景的最优运行,功率分配结果中电解槽制氢功率均为制氢总量,未归算至每台设备。文献[14-17]从能量管理优化角度提出不同优化模型,包括分段优化模型、小时能源监督模型、综合能源系统模型,其中电解槽能量管理均是当作整体处理。文献[18-20]从系统优化目标切入,提出技术、经济等多个目标,但未考虑制氢设备运行特性的影响。单电解槽能量管理是在管理过程中将多组电解槽当作整体,未考虑电解槽非线性的工作特性,采用总制氢功率分配至单台电解槽的方式,难以兼顾不同电解槽制氢效率,影响系统经济性。
多电解槽能量管理是将每组电解槽作为个体管理,现有研究主要集中在能量管理优化模型,涉及能量管理目标、设备寿命延长。文献[21]提出一种基于电解槽启停特性的日前出力优化模型,系统包括风光电源、外接电网、蓄电池、蓄氢系统、电解槽和氢负荷,以系统运行成本最低为目标,采用CPLEX求解计算,可提供日前出力计划,以多电解槽为对象,实现协调运行,减少电解槽的启停次数。文献[22]提出碱性电解槽阵列轮值协调控制策略,系统包括风电、超级电容、碱性电解槽,分3种工况计算,从电解槽阵列各个单体出发,充分挖掘电解槽装置的特性,有效提升电解槽阵列寿命和运行安全性并降低投资。文献[23]设计风氢一体化能源系统,系统包括风电、超级电容器、电解槽、外接电网,分多种工况计算,从风电频繁波动导致碱性电解槽频繁启停角度切入,以多电解槽为管理对象,通过减少电解槽切换次数,实现制氢产量提高和电解槽安全性提升。
多电解槽能量管理策略以单台电解槽制氢曲线为对象,以累加制氢产量最大为目标,能够有效提高制氢效率。现有的多电解槽制氢系统能量管理通过减少电解槽启停次数实现设备寿命和制氢产量提高,但未深入研究电解槽非线性制氢特性。与线性制氢相比,非线性制氢的制氢效率非定值,不同制氢功率下制氢效率不同。同时现有多电解槽能量管理目标均为单目标,须总结单电解槽现有研究成果并补充完善。文中以小时为时间尺度,分析电解槽运行特性和制氢函数,针对电解槽磨损管理优化问题,提出一种基于多电解槽的新能源制氢系统能量管理优化模型,并通过算例验证该模型的有效性。
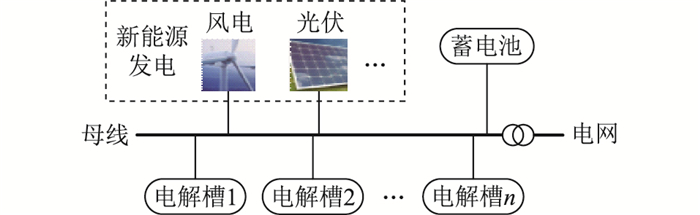
1 新能源制氢系统结构 1.1 系统组成新能源制氢系统结构如图 1所示,包括风电、光伏、蓄电池、电解槽等,与电网连接具备双向输电能力。
|
图 1 新能源制氢系统结构 Fig. 1 Structure of new energy hydrogen production system |
制氢系统优先消纳风电、光伏出力,提高系统新能源发电消纳率,其次利用电网支撑系统功率平衡。当出力超过电解槽额定功率总和时,通过电网售卖多余电量,当出力小于电解槽额定功率总和时,综合考虑制氢量、制氢成本后确定电网供电量。为方便理解,售氢单价定价略高于实际售电单价,实现系统优先制氢。
1.2 风电模型风电模块由风轮、转体、机头、机尾和叶片组成。风能驱动叶片转动,叶片驱动导体切割电机电场中的磁感应线,从而产生电能。风电出力计算[24]如式(1)所示。
| $ P_{\mathrm{wi}}=\frac{1}{2} \rho R^2 v^3 C_{\mathrm{p}} $ | (1) |
其中:
| $ C_{\mathrm{p}}=0.5176\left(\frac{116}{\lambda_{\mathrm{i}}}-0.4 \theta-5\right) \mathrm{e}^{-21 / \lambda_{\mathrm{i}}}+0.0068 \lambda $ | (2) |
| $ \lambda_{\mathrm{i}}=1 /\left(\frac{1}{\lambda+0.08 \theta}-\frac{0.035}{\theta^3+1}\right) $ | (3) |
式中:Pwi为风电出力;ρ为空气密度;R为风叶半径;v为实际风速;Cp为系统的风能利用系数;λi为中间变量;θ为桨矩角;λ为叶尖速比。
1.3 光伏模型光伏发电主要利用半导体的光电效应将太阳能转化为电能,通过外接电路实现光电压转换为光电流。光伏出力计算[25]如式(4)所示。
| $ P_{\mathrm{pv}}=U I $ | (4) |
其中:
| $ I=I_{\mathrm{s}}\left\{1-C_{1}\left[\mathrm{e}^{U /\left(C_{2} V_{\mathrm{oc}}\right)}-1\right]\right\} $ | (5) |
| $ C_{1}=\left(1-\frac{I_{\mathrm{m}}}{I_{\mathrm{s}}}\right) \mathrm{e}^{-U_{\mathrm{m}} /\left(C_{2} V_{\mathrm{oc}}\right)} $ | (6) |
| $ C_{2}=\left(\frac{U_{\mathrm{m}}}{V_{\mathrm{oc}}}-1\right) / \ln \left(1-\frac{I_{\mathrm{m}}}{I_{\mathrm{s}}}\right) $ | (7) |
式中:Ppv为光伏出力;U为光伏阵列输出电压;I为光伏阵列输出电流;Is为二极管饱和电流;Voc为端电压;C1、C2为中间变量;Um、Im分别为取得最大功率时对应的电压和电流。
1.4 蓄电池模型蓄电池通过充放电实现电能和化学能的相互转换,又称二次电池。荷电状态是表征电池运行状态的重要参数,其与充放电功率的关系[26]如下:
| $ R_{\mathrm{SOC}}(t+1)=R_{\mathrm{SOC}}(t)+\frac{P_{\mathrm{ac}}}{C_{\mathrm{ac}} V_{\mathrm{ac}}} \quad t=1, 2, \cdots, T $ | (8) |
式中:RSOC(t)为蓄电池在时刻t的荷电状态;T为时刻数;Pac为充放电功率,Pac≥0时充电,Pac<0时放电;Cac为储能电池容量;Vac为充放电电压,Vac≥0时充电,Vac<0时放电。
1.5 电解槽模型碱性电解槽的状态可以分为工作状态、冷备用状态、热备用状态和停机状态[21]。
(1) 工作状态。电解槽运行存在功率下限,低于下限则电解槽存在危险不制氢,目前技术允许的最小负载通常为额定负荷的10%[27]。依据实验数据拟合,碱性电解槽制氢功率与制氢量关系[28]如下:
| $ V_{\mathrm{el}}=205.31 P_{\mathrm{el}}+17.85 $ | (9) |
| $ V_{\mathrm{el}}=-11.24 P_{\mathrm{el}}^{2}+232.7 P_{\mathrm{el}}+8.89 $ | (10) |
式中:Vel为制氢量;Pel为制氢装置运行功率。
(2) 冷备用状态。电解槽只维持控制单元、防冻系统部件的供电,处于低功耗状态,该状态不制氢,转换至工作状态时间大约需要20 min[29]。
(3) 热备用状态。电解槽除维持控制单元、防冻系统部件的供电以外,还须保持槽温和压力,处于高功耗状态,该状态不制氢,转换至工作状态所需时间很短,可忽略不计。
(4) 停机状态。电解槽停机后不消耗功率,启动需要30~60 min,能量管理优化模型以电解槽运行状态、备用状态的功率分配为对象,不考虑电解槽停机状态下制氢系统的功率分配问题。
2 能量管理模型 2.1 目标函数新能源制氢系统主要以新能源发电消纳率、经济收益、制氢产量为目标。其中制氢产量与经济收益存在矛盾,当电网电价处于尖峰或高峰时段,风光出力不能满足电解槽额定功率时,满足最大制氢产量则需要降低系统经济收益,满足经济收益最大则需要降低制氢产量。
(1) 新能源消纳率。系统以实现新能源100%消纳为主要目标,新能源消纳率计算如下:
| $ R_{\mathrm{xnl}}=\left(\sum\limits_{i=1}^{n} P_{\mathrm{el}}(i)+P_{\mathrm{ac}}-P_{\mathrm{pg}}\right) /\left(P_{\mathrm{wi}}^{\max }+P_{\mathrm{pv}}^{\max }\right) $ | (11) |
式中:Rxnl为新能源消纳率;Pel(i)为第i台电解槽的制氢装置运行功率;n为电解槽数量;Ppg为电网交换功率,Ppg≥0时系统取电,Ppg<0时系统售电;Pwimax为实际天气条件下可达到的最大风电出力;Ppvmax为实际天气条件下可达到的最大光伏出力。
(2) 经济收益比。同等条件下系统收益越大则制氢成本越低。经济收益比计算如下:
| $ \left\{\begin{array}{l} G=\sum\limits_{i=1}^{n} V_{\mathrm{el}}^{\max }(i) C_{\mathrm{hy}}+C_{\mathrm{se}}\left(P_{\mathrm{wi}}+P_{\mathrm{pv}}-P_{\mathrm{el}}^{\max }\right)\\ E=\frac{G-\left(\sum\limits_{i=1}^{n} V_{\mathrm{el}}(i) C_{\mathrm{hy}}-P_{\mathrm{pg}} C\right)}{C_{\mathrm{se}}\left(P_{\mathrm{wi}}+P_{\mathrm{pv}}-P_{\mathrm{el}}^{\max }\right)+C_{\mathrm{pg}}^{\max } P_{\mathrm{el}}^{\max }} \end{array}\right. $ | (12) |
式中:G为系统最大售电、售氢收益;E为经济收益比;Velmax(i)为第i台电解槽最大制氢量;Chy为售氢单价;Pelmax为制氢装置最大运行功率;C为电网实时电价或售电电价;Cse为电网售电电价;Cpg为电网实时电价;Cpgmax为电网最大实时电价。
(3) 制氢率。制氢率越高则制氢量越高,同等条件下制氢系统效率越高。制氢率计算如下:
| $ \begin{equation*} R_{\mathrm{zql}}=\sum\limits_{i=1}^{n} V_{\mathrm{el}}(i) / \sum\limits_{i=1}^{n} V_{\mathrm{el}}^{\max }(i) \end{equation*} $ | (13) |
式中:Rzql为制氢率。
2.2 约束条件(1) 功率平衡约束。系统功率依据实际运行,电解槽功率总和不超过其他模块出力总和,即:
| $ \begin{equation*} P_{\mathrm{wi}}+P_{\mathrm{pv}}+P_{\mathrm{pg}}-P_{\mathrm{ac}} \geqslant \sum\limits_{i=1}^{n} P_{\mathrm{el}}(i) \end{equation*} $ | (14) |
(2) 风电出力约束。风电模块依据容量配置,存在最大出力,即:
| $ 0 \leqslant P_{\mathrm{wi}} \leqslant P_{\mathrm{wi}}^{\max } $ | (15) |
(3) 光伏出力约束。光伏模块依据容量配置,存在最大出力,即:
| $ 0 \leqslant P_{\mathrm{pv}} \leqslant P_{\mathrm{pv}}^{\max } $ | (16) |
(4) 电解槽功率约束。电解槽依据运行特性,存在安全功率限制[30-31],即:
| $ 0.1 P_{\mathrm{el}}^{\max } \leqslant P_{\mathrm{el}} \leqslant P_{\mathrm{el}}^{\max } $ | (17) |
(5) 蓄电池功率约束。蓄电池依据容量配置,充放电均存在功率限制,即:
| $ -P_{\mathrm{ac}}^{\max } \leqslant P_{\mathrm{ac}} \leqslant P_{\mathrm{ac}}^{\max } $ | (18) |
式中:Pacmax为蓄电池最大出力。
(6) 电网交换功率约束。电网依据系统各模块容量配置,取电、售电均存在功率限制,即:
| $ P_{\mathrm{pg}}^{\mathrm{se}} \leqslant P_{\mathrm{pg}} \leqslant P_{\mathrm{pg}}^{\mathrm{ta}} $ | (19) |
式中:Ppgse、Ppgta分别为电网最大售电量和用电量。
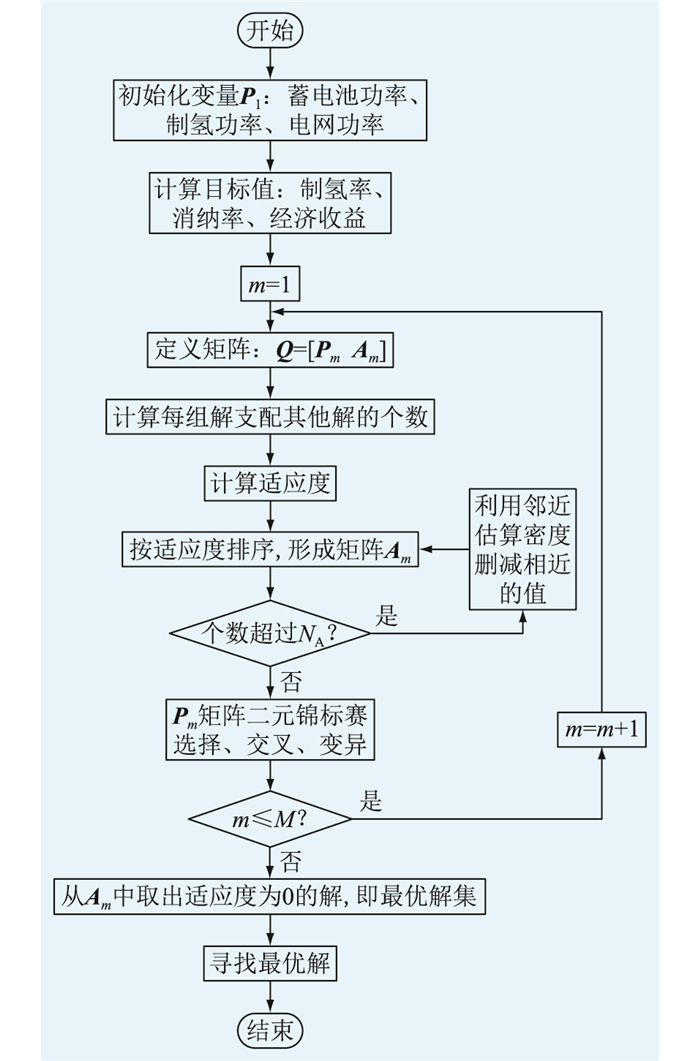
2.3 强度Pareto进化算法2(SPEA2)强度Pareto进化算法2(strength Pareto evolutionary algorithm 2, SPEA2)为多目标优化算法,可同时计算多个目标变量、决策变量。新能源制氢系统中包含新能源消纳率、经济收益、制氢率3个目标,以及Pac、Ppg及Pel(i)等多个决策变量。粒子群算法、遗传算法等仅适用于单目标求解,对比SPEA2可发现,新能源系统能量管理求解匹配SPEA2特点。SPEA2求解流程见图 2,具体步骤[32]如下。
|
图 2 SPEA2流程 Fig. 2 Flow chart of SPEA2 |
步骤1:数据初始化。确定最大迭代次数M,种群个数Np,档案大小NA。定义初始种群P1=[Pac Ppg Pel],外部空档案A1,组合形成矩阵Q=[P1 A1]用于计算。
步骤2:计算适应度。种群Pm中各组解依据新能源消纳率、经济收益、制氢量目标函数计算,形成目标矩阵Cm。目标矩阵相互比较统计小于各组解的目标个数,形成受支配解个数矩阵Sm。依次累加各组解受支配个数,计算解集适应度形成矩阵Bm。
| $ \boldsymbol{B}_{m}(k)=\sum \boldsymbol{S}_{m}(j) \quad j<N_{\mathrm{p}}+N_{\mathrm{A}} ; \boldsymbol{C}_{m}(j)<\boldsymbol{C}_{m}(k) $ | (20) |
式中: Bm(k)为第k组解的适应度;j为小于k组解目标矩阵的组号;Cm(j)、Cm(k)分别为Cm中第j行数据和第k行数据。
步骤3:确定最优解集。在矩阵Q中选出适应度为0的解形成解集即外部档案Am。若Am的解的个数超过NA,则利用近邻估算密度删减相近的值。
步骤4:更新种群。对种群Pm采用二元锦标赛方法选择个体进入种群。对更新后的种群进行交叉、变异。若迭代次数达到M,则进行下一步,否则,返回步骤2。
步骤5:寻找最优解。将新能源消纳率、经济收益、制氢量目标转换为标幺值,依据制氢系统期望选出最优解。
| $ R_{\mathrm{xnl}}^{\mathrm{pu}} =\frac{R_{\mathrm{xnl}}^{\max }-R_{\mathrm{xnl}}}{R_{\mathrm{xnl}}^{\max }-R_{\mathrm{xnl}}^{\min }} $ | (21) |
| $ E^{\mathrm{pu}} =\frac{E^{\max }-E}{E^{\max }-E^{\min }} $ | (22) |
| $ V_{\mathrm{el}}^{\mathrm{pu}} =\frac{V_{\mathrm{el}}^{\max }-V_{\mathrm{el}}}{V_{\mathrm{el}}^{\max }-V_{\mathrm{el}}^{\min }} $ | (23) |
式中:Rxnlpu、Rxnlmax、Rxnlmin分别为新能源消纳率标幺值、最大值、最小值;Epu、Emin分别为经济收益比标幺值、最小值;Velpu、Velmin分别为制氢量标幺值、最小值。
3 含多电解槽的能量管理策略新能源制氢系统中风电、光伏模块功率单相流动,仅出力;蓄电池、电网具备功率双向流动功能;电解槽模块只取电。所有模块均服从能量调度。
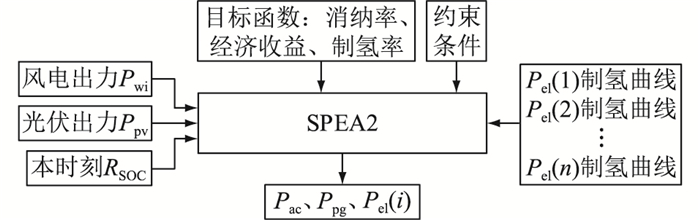
在下一小时调度计划制定过程中,首先结合天气预测(风速、光照、温度),依据式(1)—式(7)预测风电、光伏出力,结合当前时刻蓄电池荷电状态(式(8))确定蓄电池能否出力。其次明确目标函数(式(11)—式(13))、约束条件(式(14)—式(19))及单台制氢装置制氢函数(式(9)、式(10)),其中制氢函数可根据电解槽磨损情况及时更新、更换,制氢函数可由供应商提供或采集设备运行数据获得。最后采用SPEA2计算出Pac、Ppg及Pel(i)。能量管理框图如图 3所示。
|
图 3 新能源制氢系统能量管理框图 Fig. 3 Energy management diagram of new energy hydrogen production system |
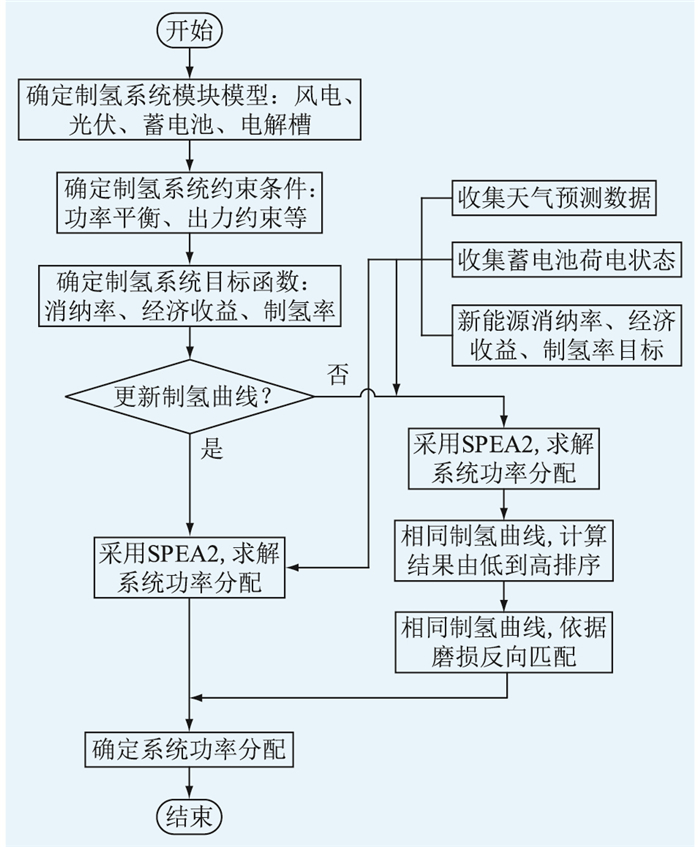
多电解槽策略的制氢函数为多种制氢函数叠加计算,每个制氢函数匹配1台电解槽。随着设备的运行磨损,制氢效率降低,依据设备实际运行制氢功率、制氢产量数据,可根据期望值或固定时间设定制氢函数更新周期。多个电解槽之间的功率分配主要呈此消彼长模式,须按照经济收益、制氢产量实现最优分配。与单电解槽策略制氢函数采用线性函数计算后均分至每一台电解槽不同,多电解槽策略的具体流程如图 4所示。
|
图 4 新能源制氢系统能量管理流程 Fig. 4 Energy management flow chart of new energy hydrogen production system |
两者相比,多电解槽策略更具优势:(1) 多电解槽策略可依据电解槽实际磨损情况,灵活更换电解槽或更新制氢函数,不受限制,而单电解槽策略无法任意更换,制氢函数须保持一致。(2) 实际运行中各台电解槽磨损情况不一,电解槽可依据磨损情况做降序排列,能量管理模型中电解槽功率采用升序排列,两者反向匹配可有效延长设备寿命周期。
4 算例分析新能源制氢系统风电模块配置容量25 MW,光伏模块配置容量10 MW,配置4台单台功率2.5 MW的电解槽,安全工作功率下限为0.25 MW,蓄电池初始荷电状态为20%。1号、2号电解槽功率与制氢量采用线性函数,3号、4号电解槽功率与制氢量采用非线性函数。1号电解槽磨损程度比2号电解槽严重,3号电解槽磨损程度比4号电解槽严重。SPEA2种群数量设置为200,档案数量设置为200,迭代次数设置为400。天气数据选取白天光照充足、夜间风力充足的24 h实际气象信息,包括风力、光照、温度数据。
依据天气数据,结合式(1)—式(7)计算新能源制氢系统风光出力,如图 5所示。由图可见,光伏出力集中在09:00—17:00,且光伏出力在10:00、11:00、13:00、15:00和16:00达到最大。风电出力集中在21:00—24:00,且风电出力在23:00最大,风电出力波动较光伏出力更大。白天为光伏出力,夜间为风电出力。

|
图 5 光伏和风电出力 Fig. 5 Photovoltaic and wind power output |
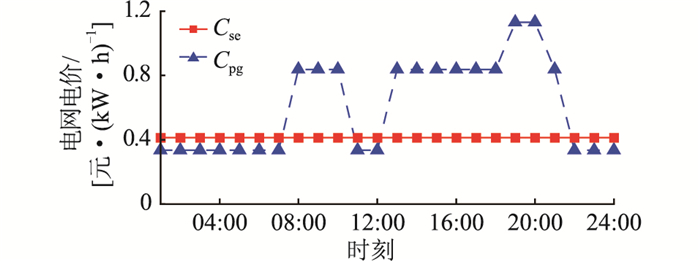
电网电价依据某地电网销售电价表编制,尖峰电价为1.130 3元/(kW ·h),高峰电价为0.837 3元/(kW ·h),低谷电价为0.334 3元/(kW ·h),售电电价为0.413 0元/(kW ·h)。峰谷平时段划分及电价如图 6所示。
|
图 6 电网售电和购电电价 Fig. 6 Electricity sale and purchase price of power grid |
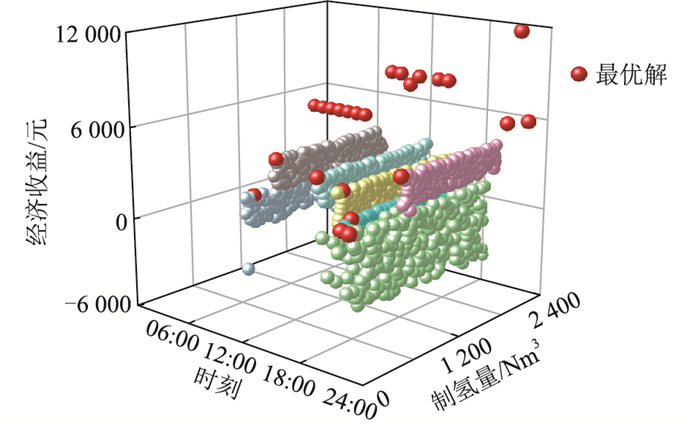
结合实际气象数据及电网电价,利用SPEA2求解新能源制氢系统,最优解集如图 7所示。在00:00—07:00,风光资源匮乏,系统无风光发电输出,系统解唯一,以市电满功率制氢。在10:00—11:00,光资源充沛,光伏最大功率输入系统使电解槽满功率运行,最优解也唯一。在21:00—24:00,风力资源较为充沛,同时处于低谷电价,系统中电解槽满功率运行为最优方案。若风光资源不够充沛,系统具有多组解,以系统经济收益为主制氢量为辅选取最优解,系统最优功率分配见图 8—图 10。
|
图 7 能量管理策略最优解集 Fig. 7 Optimal solution set of energy management strategy |
|
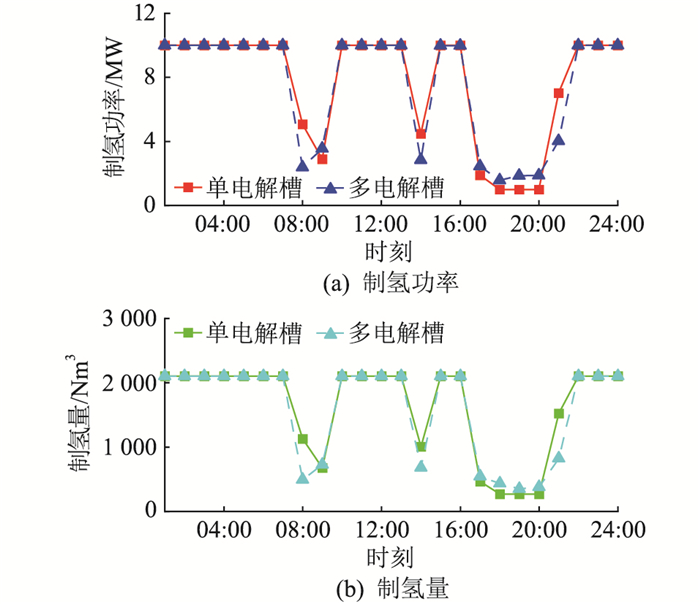
图 8 单、多电解槽制氢功率与制氢量 Fig. 8 Hydrogen production power and hydrogen production capacity of single-electrolyzer and multi-electrolyzers |
|
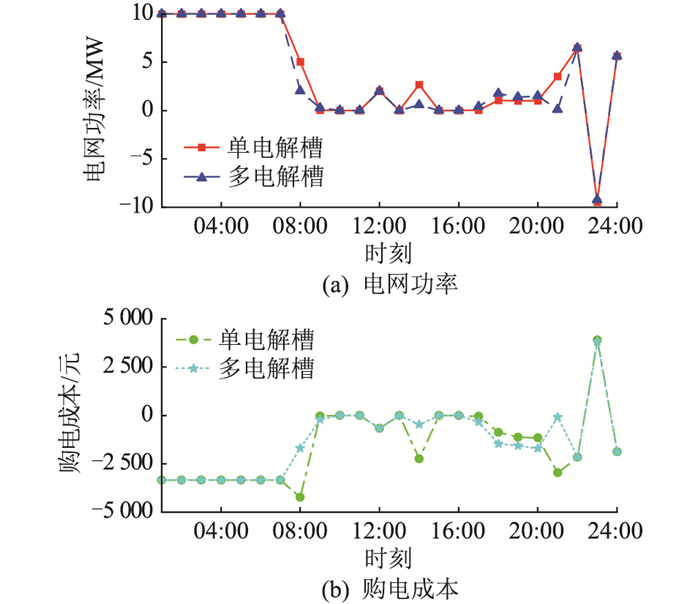
图 9 单、多电解槽电网功率与购电成本 Fig. 9 Grid power and purchasing cost of single-electrolyzer and multi-electrolyzers |
|
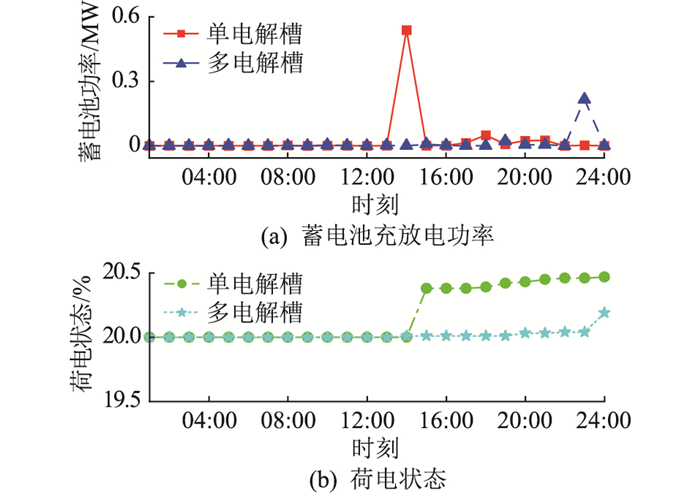
图 10 单、多电解槽蓄电池充放电功率与荷电状态 Fig. 10 Charge-discharge power and charge state of batteries in single-electrolyzer and multi-electrolyzers |
电解槽在风力充足时段、光照充足时段、电价谷值时段均工作在额定功率,可实现最大制氢量,符合能量管理策略,如图 8所示。单电解槽策略、多电解槽策略在电解槽满功率运行时段保持一致,在其余时段功率分配不一致,是因为能量管理策略不同。
电网在电价谷值时段给予新能源制氢系统充分的功率支撑,如图 9中01:00—07:00,风电、光伏模块均无电能产出,由电网取电实现电解槽最大制氢量。电网在电价谷值以外时段少量参与系统制氢,主要以风电、光伏模块为主,实现经济效益最大化。当风电、光伏出力超过系统需求时,向电网售电,提升系统经济效益,实现新能源发电100%消纳。
蓄电池在新能源制氢系统中始终处于充电状态,几乎不参与系统功率平衡,蓄电池荷电状态始终保持在初始值附近,如图 10所示。系统功率由电网实现支撑、消纳,蓄电池可作为备用电源、负荷。
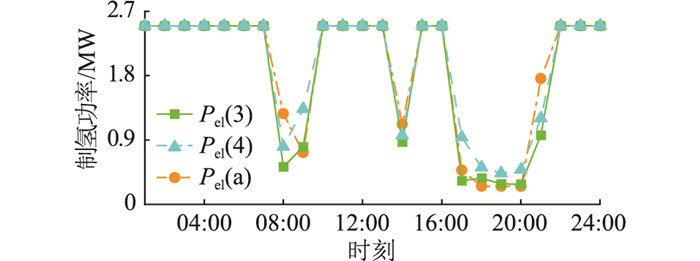
Pel(1)≤Pel(2),Pel(3)≤Pel(4),均呈上升排列,符合能量管理策略,如图 11、图 12所示,旨在匹配电解槽磨损情况。1号、2号电解槽功率与制氢量采用线性曲线,3号、4号采用非线性曲线,与均分功率曲线Pel(a)均存在交叉,功率分配存在差异,进而导致系统经济收益、制氢量不同。

|
图 11 1号和2号电解槽制氢功率 Fig. 11 Hydrogen production power of No.1 and No.2 electrolyzer |
|
图 12 3号和4号电解槽制氢功率 Fig. 12 Hydrogen production power of No.3 and No.4 electrolyzer |
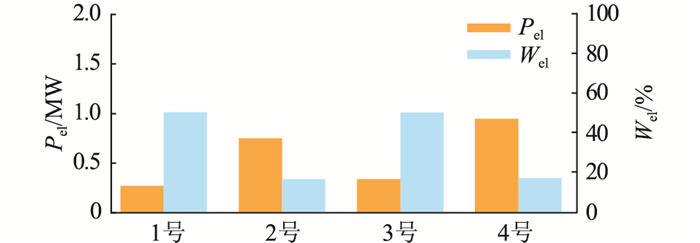
电解槽功率分配与磨损情况Wel反向匹配,磨损情况严重的设备采用小功率制氢,延长设备寿命周期,如图 13所示。不同制氢曲线的电解槽功率不采用升序排列,设备磨损情况也不采用降序排列,仅排列相同制氢曲线设备,保证系统目标实现最优。
|
图 13 电解槽17:00制氢功率 Fig. 13 Hydrogen production power of electrolyzer at 17:00 |
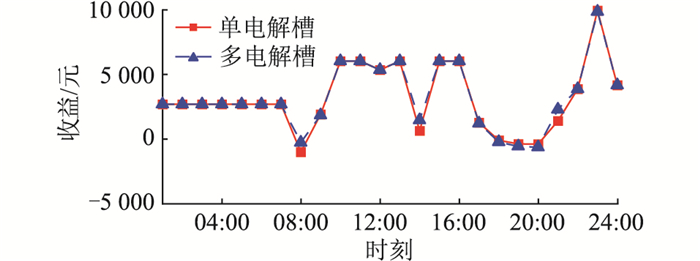
新能源制氢系统采用单电解槽、多电解槽策略均可实现新能源100%消纳,满足系统期望,如表 1所示。多电解槽策略较单电解槽策略经济收益提升2.18%,经济收益曲线如图 14所示。其中单电解槽策略单位制氢收益1.94元/Nm3,多电解槽策略单位制氢收益2.04元/Nm3,虽然制氢量有所下降,但单位制氢收益提升5.15%。根据4台电解槽功率的不同分配方案,从结果可以看出,多电解槽策略针对新能源制氢系统功率分配更合理,相较于均分功率误差更少。
|
|
表 1 24小时新能源消纳率、经济收益、制氢量统计 Table 1 Statistics of new energy consumption rate, economic benefits and hydrogen production in 24 hours |
|
图 14 新能源制氢系统经济收益 Fig. 14 Economic yield of new energy hydrogen production system |
针对包含多组电解槽的新能源制氢系统运行优化问题,提出多电解槽能量管理优化模型。多电解槽策略采用线性和非线性函数作为制氢函数,新能源消纳率、经济收益、制氢率计算结果较单电解槽策略综合更优。在保证新能源发电完全消纳的情况下,经济收益有较大提升,制氢函数越接近电解槽实际运行,系统能量管理效果越优。多电解槽策略具体有以下优势:
(1) 以单台制氢函数为基础系统,可根据电解槽磨损情况灵活更换设备或更新制氢函数,具有较好的灵活性。
(2) 可依据实际设备磨损情况反向匹配制氢功率,延长设备运行周期,提升实际运行经济性。
(3) 对制氢系统功率分配更为合理,相较于均分功率误差更少,从单位制氢收益可以看出经济收益更高。
文中优化方法同样适用于电解槽不规则制氢函数,也将进一步展开多电解槽策略理论及复杂系统等方面研究。
致谢
本文得到浙江省教育厅一般科研项目(Y202044527、Y202250621),国网青海省电力公司科技项目(522807220002)资助,谨此致谢!
| [1] |
杨馥源, 田雪沁, 徐彤, 等. 面向碳中和电力系统转型的电氢枢纽灵活性应用[J]. 电力建设, 2021, 42(8): 110-117. YANG Fuyuan, TIAN Xueqin, XU Tong, et al. Flexibility of electro-hydrogen hub for power system transformation under the goal of carbon neutrality[J]. Electric Power Construction, 2021, 42(8): 110-117. (  0) 0) |
| [2] |
滕越, 赵骞, 袁铁江, 等. 绿电-氢能-多域应用耦合网络关键技术现状及展望[J]. 发电技术, 2023, 44(3): 318-330. TENG Yue, ZHAO Qian, YUAN Tiejiang, et al. Key technology status and outlook for green electricity-hydrogen energy-multi-domain applications coupled network[J]. Power Generation Technology, 2023, 44(3): 318-330. (  0) 0) |
| [3] |
张春雁, 窦真兰, 王俊, 等. 电解水制氢-储氢-供氢在电力系统中的发展路线[J]. 发电技术, 2023, 44(3): 305-317. ZHANG Chunyan, DOU Zhenlan, WANG Jun, et al. Development route of hydrogen production by water electrolysis, hydrogen storage and hydrogen supply in power system[J]. Power Generation Technology, 2023, 44(3): 305-317. (  0) 0) |
| [4] |
李雪临, 袁凌. 海上风电制氢技术发展现状与建议[J]. 发电技术, 2022, 43(2): 198-206. LI Xuelin, YUAN Ling. Development status and suggestions of hydrogen production technology by offshore wind power[J]. Power Generation Technology, 2022, 43(2): 198-206. (  0) 0) |
| [5] |
CHI J, YU H M. Water electrolysis based on renewable energy for hydrogen production[J]. Chinese Journal of Catalysis, 2018, 39(3): 390-394. DOI:10.1016/S1872-2067(17)62949-8 (  0) 0) |
| [6] |
章寒冰, 叶吉超, 胡鑫威, 等. 碱液制氢电解槽动态阻抗建模[J]. 浙江电力, 2023, 42(5): 49-58. ZHANG Hanbing, YE Jichao, HU Xinwei, et al. Dynamic impedance modeling of an alkaline electrolyzer for hydrogen production[J]. Zhejiang Electric Power, 2023, 42(5): 49-58. (  0) 0) |
| [7] |
胡轶坤, 曹军文, 张文强, 等. 高温固体氧化物电解池应用研究进展[J]. 发电技术, 2023, 44(3): 361-372. HU Yikun, CAO Junwen, ZHANG Wenqiang, et al. Application research progress of high temperature solid oxide electrolysis cell[J]. Power Generation Technology, 2023, 44(3): 361-372. (  0) 0) |
| [8] |
HOSSEINI S E, WAHID M A. Hydrogen from solar energy, a clean energy carrier from a sustainable source of energy[J]. International Journal of Energy Research, 2020, 44(6): 4110-4131. DOI:10.1002/er.4930 (  0) 0) |
| [9] |
SARRIAS-MENA R, FERNÁNDEZ-RAMÍREZ L M, GARCÍA-VÁZQUEZ C A, et al. Electrolyzer models for hydrogen production from wind energy systems[J]. International Journal of Hydrogen Energy, 2015, 40(7): 2927-2938. DOI:10.1016/j.ijhydene.2014.12.125 (  0) 0) |
| [10] |
张焱, 郝振波, 朱振涛, 等. 海上风能岸上制氢的经济可行性分析[J]. 电力建设, 2023, 44(3): 148-154. ZHANG Yan, HAO Zhenbo, ZHU Zhentao, et al. Economic feasibility analysis of onshore hydrogen production using offshore wind power[J]. Electric Power Construction, 2023, 44(3): 148-154. (  0) 0) |
| [11] |
牛萌, 肖宇, 刘锋, 等. 可再生能源接入对氢储能系统的影响及控制策略[J]. 电力建设, 2018, 39(4): 28-34. NIU Meng, XIAO Yu, LIU Feng, et al. Influences of renewable energy on hydrogen storage system and its control strategy[J]. Electric Power Construction, 2018, 39(4): 28-34. (  0) 0) |
| [12] |
刘雨佳, 樊艳芳, 郝俊伟, 等. 基于碱性电解槽宽功率适应模型的风光氢热虚拟电厂容量配置与调度优化[J]. 电力系统保护与控制, 2022, 50(10): 48-60. LIU Yujia, FAN Yanfang, HAO Junwei, et al. Capacity configuration and optimal scheduling of a wind-photovoltaic-hydrogen-thermal virtual power plant based on a wide range power adaptation strategy for an alkaline electrolyzer[J]. Power System Protection and Control, 2022, 50(10): 48-60. (  0) 0) |
| [13] |
陈锦洲, 林飞, 何洪文, 等. 质子交换膜燃料电池/电解槽系统建模及负荷追踪策略[J]. 电工技术学报, 2020, 35(S2): 636-643. CHEN Jinzhou, LIN Fei, HE Hongwen, et al. Proton exchange membrane fuel cell/electrolyzer hybrid power system modeling and load tracking strategy[J]. Transactions of China Electrotechnical Society, 2020, 35(S2): 636-643. (  0) 0) |
| [14] |
FANG R M. Multi-objective optimized operation of integrated energy system with hydrogen storage[J]. International Journal of Hydrogen Energy, 2019, 44(56): 29409-29417. (  0) 0) |
| [15] |
GARCÍA P, TORREGLOSA J P, FERNÁNDEZ L M, et al. Improving long-term operation of power sources in off-grid hybrid systems based on renewable energy, hydrogen and battery[J]. Journal of Power Sources, 2014, 265: 149-159. (  0) 0) |
| [16] |
CASTAÑEDA M, CANO A, JURADO F, et al. Sizing optimization, dynamic modeling and energy management strategies of a stand-alone PV/hydrogen/battery-based hybrid system[J]. International Journal of Hydrogen Energy, 2013, 38(10): 3830-3845. (  0) 0) |
| [17] |
刘海涛, 朱海南, 李丰硕, 等. 计及碳成本的电-气-热-氢综合能源系统经济运行策略[J]. 电力建设, 2021, 42(12): 21-29. LIU Haitao, ZHU Hainan, LI Fengshuo, et al. Economic operation strategy of electric-gas-heat-hydrogen integrated energy system considering carbon cost[J]. Electric Power Construction, 2021, 42(12): 21-29. (  0) 0) |
| [18] |
VIVAS F J, DE LAS HERAS A, SEGURA F, et al. A review of energy management strategies for renewable hybrid energy systems with hydrogen backup[J]. Renewable and Sustainable Energy Reviews, 2018, 82: 126-155. (  0) 0) |
| [19] |
魏繁荣, 随权, 林湘宁, 等. 考虑制氢设备效率特性的煤风氢能源网调度优化策略[J]. 中国电机工程学报, 2018, 38(5): 1428-1439. WEI Fanrong, SUI Quan, LIN Xiangning, et al. Energy control scheduling optimization strategy for coal-wind-hydrogen energy grid under consideration of the efficiency features of hydrogen production equipment[J]. Proceedings of the CSEE, 2018, 38(5): 1428-1439. (  0) 0) |
| [20] |
GARCÍA-TRIVIÑO P, FERNÁNDEZ-RAMÍREZ L M, GIL-MENA A J, et al. Optimized operation combining costs, efficiency and lifetime of a hybrid renewable energy system with energy storage by battery and hydrogen in grid-connected applications[J]. International Journal of Hydrogen Energy, 2016, 41(48): 23132-23144. (  0) 0) |
| [21] |
袁铁江, 万志, 王进君, 等. 考虑电解槽启停特性的制氢系统日前出力计划[J]. 中国电力, 2022, 55(1): 101-109. YUAN Tiejiang, WAN Zhi, WANG Jinjun, et al. The day-ahead output plan of hydrogen production system considering the start-stop characteristics of electrolytic cell[J]. Electric Power, 2022, 55(1): 101-109. (  0) 0) |
| [22] |
沈小军, 聂聪颖, 吕洪. 计及电热特性的离网型风电制氢碱性电解槽阵列优化控制策略[J]. 电工技术学报, 2021, 36(3): 463-472. SHEN Xiaojun, NIE Congying, LÜ Hong. Coordination control strategy of wind power-hydrogen alkaline electrolyzer bank considering electrothermal characteristics[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 463-472. (  0) 0) |
| [23] |
FANG R M, LIANG Y. Control strategy of electrolyzer in a wind-hydrogen system considering the constraints of switching times[J]. International Journal of Hydrogen Energy, 2019, 44(46): 25104-25111. (  0) 0) |
| [24] |
许建明, 王蔚, 陈廷彧, 等. 直流微网用风力发电机建模[J]. 长春工业大学学报, 2020, 41(6): 581-586. XU Jianming, WANG Wei, CHEN Tingyu, et al. DC-microgrid wind turbine modeling[J]. Journal of Changchun University of Technology, 2020, 41(6): 581-586. (  0) 0) |
| [25] |
林洪, 袁红波. 光伏电池工作原理与物理建模方法分析[J]. 机电信息, 2020(36): 3-4. LIN Hong, YUAN Hongbo. Analysis of working principle and physical modeling method of photovoltaic cells[J]. Mechanical and Electrical Information, 2020(36): 3-4. (  0) 0) |
| [26] |
陈兵, 徐瑞, 徐春雷, 等. 规模化储能分区聚合有功调度控制技术研究[J]. 电力工程技术, 2021, 40(3): 35-41. CHEN Bing, XU Rui, XU Chunlei, et al. Large-scale energy storage aggregation active power dispatching and control in subarea division of power grid[J]. Electric Power Engineering Technology, 2021, 40(3): 35-41. (  0) 0) |
| [27] |
EICHMAN J, HARRISON K, PETERS M. Novel electrolyzer applications: providing more than just hydrogen[R]. Office of Scientific and Technical Information (OSTI), 2014.
(  0) 0) |
| [28] |
VARELA C, MOSTAFA M, ZONDERVAN E. Modeling alkaline water electrolysis for power-to-x applications: a scheduling approach[J]. International Journal of Hydrogen Energy, 2021, 46(14): 9303-9313. (  0) 0) |
| [29] |
ZHENG Y, YOU S, BINDNER H W, et al. Optimal day-ahead dispatch of an alkaline electrolyser system concerning thermal-electric properties and state-transitional dynamics[J]. Applied Energy, 2022, 307: 118091. (  0) 0) |
| [30] |
江叶峰, 周海强, 罗建裕, 等. 计及源荷区间不确定性的电力系统日前优化调度[J]. 电力工程技术, 2022, 41(4): 58-66. JIANG Yefeng, ZHOU Haiqiang, LUO Jianyu, et al. Day-ahead optimal dispatch of power system considering source and load interval uncertainties[J]. Electric Power Engineering Technology, 2022, 41(4): 58-66. (  0) 0) |
| [31] |
刘雨佳, 樊艳芳, 郝俊伟, 等. 基于碱性电解槽宽功率适应模型的风光氢热虚拟电厂容量配置与调度优化[J]. 电力系统保护与控制, 2022, 50(10): 48-60. LIU Yujia, FAN Yanfang, HAO Junwei, et al. Capacity configuration and optimal scheduling of a wind-photovoltaic-hydrogen-thermal virtual power plant based on a wide range power adaptation strategy for an alkaline electrolyzer[J]. Power System Protection and Control, 2022, 50(10): 48-60. (  0) 0) |
| [32] |
MOSTAPHA K H. Strength Pareto evolutionary algorithm 2 (SPEA2) in MATLAB[CP/OL]. Yarpiz, 2015. https://yarpiz.com/74/ypea122-spea2.
(  0) 0) |
2. College of Information Engineering, Hangzhou Dianzi University, Hangzhou 311305, China;
3. State Grid Qinghai Electric Power Company Research Institute, Xining 810003, China
 2024, Vol. 43
2024, Vol. 43


 陈磊磊(1992), 男, 硕士在读, 工程师, 研究方向为新能源制氢系统能量管理技术(E-mail:
陈磊磊(1992), 男, 硕士在读, 工程师, 研究方向为新能源制氢系统能量管理技术(E-mail: