文章编号: 2096-3203(2023)02-0119-11 中图分类号: TM76;TM73
物联网技术的快速发展有利于实现电力系统各环节设备以及客户状态的全面感知,达到高度信息交互和数据共享的目的,进而推进实现以信息数据为基础的高度自动化的智能电网建设进程[1-3]。在未来电力系统中,业务开展需要大量的数据作为支撑,而短时高并发信息内容的筛选、清理和处理工作将会大幅增加数据传输、计算和运维成本,尤其是信息冗余度高的需求侧,大量非必要数据汇入电力通信网将会带来巨大的经济和管理负担[4-7]。而边缘计算的发展可以解决上述问题,在用户侧部署具有计算和业务控制能力的边缘设备,仅将经过处理的信息汇入电力通信网,可大幅减轻需求侧冗余数据带来的压力[8-9]。
目前,已有诸多学者对边缘计算在电力系统中的应用进行了研究。文献[10]探讨了在广域发电控制、站域保护控制与负荷建模评估等场景下边缘计算的部署方式和应用前景;文献[11]提出借助边缘计算实现自动需求响应,并针对接口服务等问题给出相应的解决思路;文献[12]分析了边缘计算技术与主动配电网和信息物理系统(cyber physical system,CPS)的相似之处,提出基于边缘计算的主动配电网的分组传输网(packet transport network,PTN)物理架构模型,进一步构建了基于边缘计算的分层自治协同的主动配电网CPS管控模型;文献[13] 提出一种以能耗最小为优化目标来确定边缘计算任务的分配策略;文献[14]考虑网络中节点的介数大小配置边缘节点,实现计算业务的分配;文献[15]设计一种考虑计算资源和存储资源约束的边缘节点重配置方式,将计算业务分配到指定的边缘节点。
上述研究侧重于边缘计算在电力系统中的业务能力优化,对于边缘节点的部署大都基于电网拓扑,可选择特定的网络拓扑节点作为边缘计算设备的部署地点,进而以网格化的方法确定节点的服务范围。文献[16]提出一种考虑业务可靠性的需求响应边缘节点部署方法,通过对地级市的通信骨干网络拓扑进行可靠性分析,确定边缘节点的部署策略;文献[17]提出的边缘计算架构要求在台区内部署边缘节点为整个台区内的用户提供负荷监测服务;文献[18]用边缘云概念指代边缘节点,面向需求侧提出基于微电网运行需求的双层云部署方案。但上述方法受限于拓扑节点数量,边缘节点的部署灵活性较低;边缘节点与用户之间的距离较大,原始数据传输成本较高,延时较大;边缘节点间的距离较远,建设高速数据传输链路的成本较高,因此各节点的工作过程相互独立,可能造成计算资源的浪费。
为此,文中提出一种考虑计算任务迁移的配电网边缘计算节点部署方法。该方法考虑边缘计算设备特点和居民区特征,提出一种考虑任务迁移的边缘计算框架;然后分析特定区域内居民节点空间信息和用电规律,形成特征数据,进而利用改进的密度峰值分析算法确定该区域内边缘节点部署的数据、位置和服务对象;最后,为均衡利用各边缘节点的计算资源,提高系统的运行效率和稳定性,设计了任务迁移算法。
1 考虑任务迁移的边缘计算框架大力推进融合终端等配电网边缘设备可以满足中长期台区管控需求[19-20],但是面对复杂的城市住宅状况[21]可能造成资源利用不充分等问题,且配电侧数据分析业务日益多元化、复杂化,现有融合终端的安装形式必然造成维修和升级成本过高。随着计算机技术的大力发展,高密度计算资源的边缘终端设备快速发展,这种边缘设备体积小,安装灵活性较高,且计算能力较强,结合容器技术、微服务技术等多种新兴技术则可以满足形态多样的业务需求[22-23]。选择合适的部署地点,将上述设备充分下放到居民侧可将数据的处理和计算过程部署到数据源头,进而大幅减轻通信数据带来的压力,提高数据通信的安全性,在保证服务质量的条件下降低设备部署和维修成本。
传统的电力网络边缘计算框架一般采用集中式的通信调度方式,电力用户的边缘设备由需求侧管理平台控制,其计算数据可通过网络接入云端,在计算高峰时将计算任务卸载至云端。集中式调度的优势在于需求侧平台能同时掌握大规模的电力用户信息,同时利用云平台强大的计算能力实现电力数据的快速分析[24]。但出现大规模的负荷数据要分析时,需求侧管理平台以及数据传输线路的负担将会大幅加重,难以满足实时性要求较高的业务的需求,同时边缘计算设备在处理各自任务时相互独立,其计算资源潜力难以被完全挖掘。
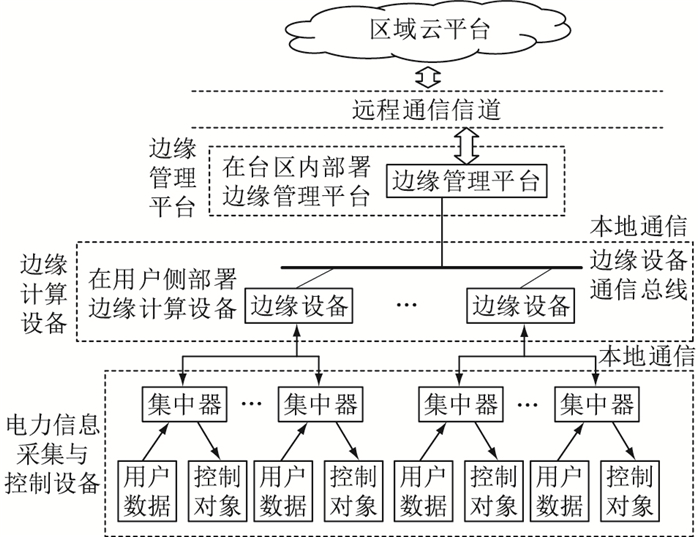
为充分提高边缘智能设备计算资源的利用率,降低计算负荷较高时需求侧管理平台的运行压力,减轻数据传输负担,文中提出一种考虑计算任务迁移的边缘计算框架。该框架由区域云平台、边缘管理平台、边缘计算设备、电力信息采集与控制设备以及通信信道构成,其结构如图 1所示。
|
图 1 边缘计算框架 Fig. 1 Architecture of edge calculation |
其中,电力信息采集与控制设备由数据采集模块和控制单元组成,数据采集模块包括智能电表等多种监测设备,采集用户用电信息,通过多种方式以报文的形式传输至集中器;控制单元包括多种控制器,执行边缘计算设备下达的指令。集中器由网关等设备构成,对多用户数据和指令进行集中收集管理。边缘计算设备指部署在居民侧的边缘计算服务器,每个边缘设备服务于多个用户,文中将其视为边缘计算节点,边缘计算节点之间通过高速通信总线实现组网进行数据传输。边缘管理平台指部署在台区内的边缘计算设备管理服务器,通过制定任务迁移策略实现边缘节点间计算任务的合理调度和分配。区域级云平台和边缘管理平台之间通过远程通信信道进行通信,根据边缘节点的计算结果对区域内配电网的运行状态进行全面评估。
2 基于改进密度峰值分析算法的边缘设备选址定容策略边缘设备的选址须充分考虑区域内居民节点的空间分布和用电特性,将边缘设备部署在计算需求密度较大的节点,从而大大降低线路建造成本,减轻数据通信压力,提升边缘节点服务水平。
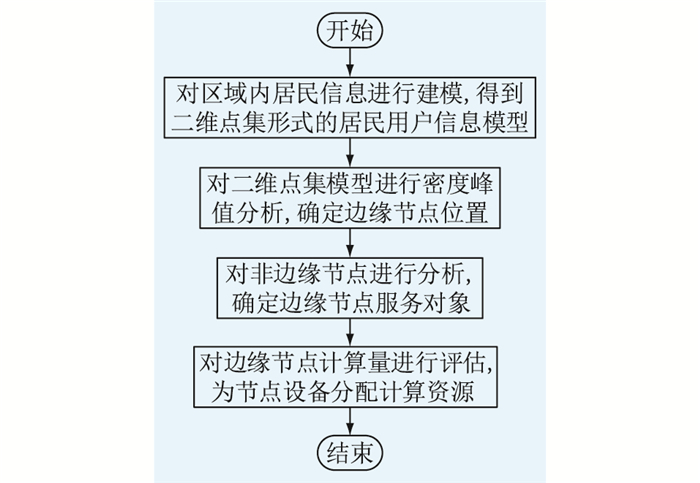
对区域内居民节点的多维度信息进行抽象融合,得到以平面点集表示的居民节点信息融合图;利用文献[25]中密度峰值分析的改进算法得到点集的密度峰值中心,确定边缘设备的部署地址;依次确定各边缘设备服务对象,为边缘设备分配合理的计算资源。边缘设备选址定容流程如图 2所示。
|
图 2 边缘设备选址定容流程 Fig. 2 Flow chart of location and capacity determination of edge equipment |
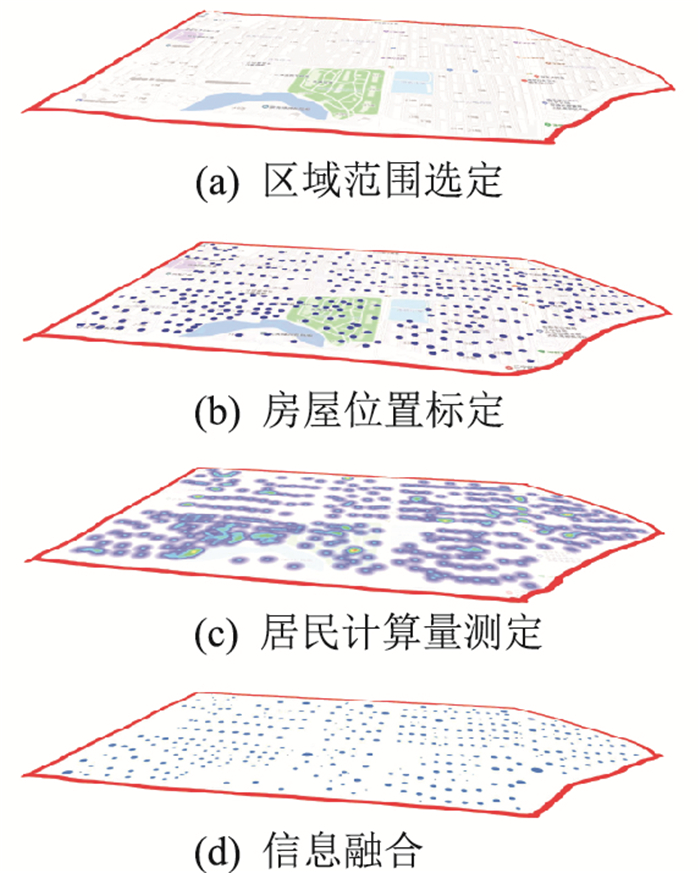
居民节点信息建模须考虑区域内节点的空间分布,各节点的居民入住情况、用电规律,以及各节点之间的线路建设成本。文中以南京市某大型居民区为研究对象,给出区域内居民节点信息挖掘和融合案例,其架构如图 3所示。
|
图 3 信息挖掘与融合架构 Fig. 3 Architecture of information mining and fusion |
首先对居民节点的空间信息进行评估,用户用电数据通过智能电表等监测设备获取,而这些设备多以较为集中的方式直接安装在居民楼内,利用RS485等通信方式向集中器传输数据[26]。因此,以整个居民楼作为居民节点,对居民用户空间位置进行刻画。结合地理信息系统(geographic information system,GIS)技术,利用高德地图提供的应用程序编程接口(application programming interface,API)获取划定居民区的俯视图和各居民楼的空间位置,如图 3(a)所示。假设居民楼的中心位置为居民数据采集设备的安装位置,以此为依据确定居民节点空间信息,图 3(b)中蓝色圆点表示各居民节点位置坐标,进而以节点间距离表示节点间线路建设成本。
其次,对居民节点计算需求进行评估,文献[27-28]提出了基于微服务架构的边缘计算资源建模方法,从中央处理器和内存的角度对配电网台区电价型负荷响应服务、光伏并网管控聚合服务、电动汽车充电聚合服务、配电网台区断线故障分析服务等作出详细的建模方法,而计算资源的大小往往和相应的配电网输出功率有关,为简化计算资源建模过程,假设计算资源的需求量和用户用电功率成正比。图 3(c)中用热力图的方式表示各居民楼用电功率的大小。
最后,将上述信息进行融合,用二维平面上不同大小的点描述各居民节点的信息,圆点的中心即为用户实际位置,圆点大小表示用户计算资源的需求量,如图 3(d)所示。
2.2 基于改进密度峰值分析的边缘节点选址策略假设居民区内包含的居民节点由集合X= {xi}i∈IS表示,其中IS={1, 2, …, N},N为居民节点总数;di, j=dist(xi, xj),为居民节点xi和xj之间的建设距离;S= {si}i∈IS,为各居民节点计算量。
根据密度峰值分析原理[27],边缘节点的选址主要考虑实现以下目标:(1) 为减轻原始数据的传输压力,选择计算需求密度最大的点作为边缘节点部署地址;(2) 为使各边缘节点的服务范围均匀覆盖整个区域,选定的边缘节点间的距离应尽可能大。
为此,对于任意居民节点xi,通过定义局部密度ρi和节点覆盖距离δi来刻画其成为边缘节点的可能性。
对于局部密度ρi,文中同时考虑各节点计算量和周围节点分布密度,计算如下:
| $ \rho_i=s_i+\sum\limits_{j \in I_{\mathrm{S}}} \chi\left(d_{i, j}-d_{\mathrm{c}}\right) s_j $ | (1) |
其中:
| $ \chi(x)= \begin{cases}1 & x<0 \\ 0 & x \geqslant 0\end{cases} $ | (2) |
式中:dc为截断距离,用来确定算法中各节点的区分度。dc选取过大会导致各节点区分度较低,极端情况下居民区内只存在一个边缘节点;而dc选取过小会导致各节点区分度较大,极端情况下居民区内每个节点都是边缘节点。在应用中根据计算需求量和边缘设备计算能力共同决定dc取值。
节点覆盖距离δi的计算如下:
| $ \delta_i= \begin{cases}\min\limits _{j \in I_{\mathrm{S}, i}}\left\{d_{i, j}\right\} & I_{\mathrm{S}, i} \neq \varnothing \\ \max\limits _{j \in I_{\mathrm{S}, i}}\left\{d_{i, j}\right\} & I_{\mathrm{S}, i}=\varnothing\end{cases} $ | (3) |
其中,IS, i满足如下条件:
| $ I_{\mathrm{S}, i}=\left\{k \in I_{\mathrm{S}} \mid \rho_k>\rho_i\right\} $ | (4) |
局部密度ρi刻画了各节点周围计算量的大小,计算量越大表明该节点成为边缘节点的可能性越大;节点覆盖距离δi刻画了各节点与其他潜在边缘节点的距离,其值越大则该节点受到其他边缘节点辐射的可能性越小,成为边缘节点的可能性越大。当节点的ρ值和δ值同时满足阈值要求时,判定该节点为边缘节点。
2.3 边缘节点计算容量和服务对象确定假设根据上述方法,共nc个用户节点被确定为边缘节点,集合M= {mk}(k=1, 2, …, nc)为对应的边缘节点编号,xmk为第k个边缘节点对应的居民节点;集合C={ci}为居民节点归属的边缘节点编号,即ci=mk为节点xi由节点xmk提供服务。集合Y={yi},yi为所有节点中局部密度ρ比ρi大的节点中与xi距离最近的节点编号;向量Q为各节点按照局部密度降序排列得到的序号向量。
基于上述变量,确定边缘节点服务对象,步骤如下:
(1) 初始化各节点的归属类型,如式(5)所示。对于边缘节点,其类型为自身编号;对于非边缘节点,为其赋值为-1。
| $ c_i= \begin{cases}m_k & i \in M \\ -1 & i \notin M\end{cases} $ | (5) |
(2) 对非边缘节点,按照向量Q中的顺序依次更新各节点类型,节点xi的类型同节点yi所代表的节点类型一致,即如式(6)所示。
| $ c_i=y_i \quad i \notin M $ | (6) |
根据边缘节点服务对象中各节点计算量的大小,确定各边缘节点所需计算容量的大小,以此作为边缘设备计算容量的选择依据,其计算如下:
| $ R_k=\sum\limits_{c_i=m_k} s_i $ | (7) |
考虑到边缘设备的规格化生产,假设备选边缘设备的标称容量为集合P,第k个边缘节点分配的计算容量pk从P中选择。定义边缘设备计算饱和度f表示所选边缘设备计算容量的利用率,计算如下:
| $ f_k=\frac{R_k}{p_k} $ | (8) |
在一定范围内,f越大表明计算资源的利用率越高,经济性越好,考虑到为每个边缘节点留有一定的计算余量,各边缘节点的计算饱和度应保持在0.75~0.95。同时用所有边缘设备计算饱和度的方差表示系统中各节点计算能力的均衡程度,方差越小表示各节点设备容量的选取越均衡,系统越稳定,计算饱和度方差的计算如下:
| $ s^2(f)=\frac{1}{n_{\mathrm{c}}}\left[\sum\limits_{k=1}^{n_{\mathrm{e}}} f_k^2-n_{\mathrm{c}}\left(\frac{1}{n_{\mathrm{c}}} \sum\limits_{k=1}^{n_{\mathrm{c}}} f_k\right)^2\right] $ | (9) |
如2.2节所述,dc值的大小直接影响到边缘节点的选取结果,dc值选取基本思路如下:
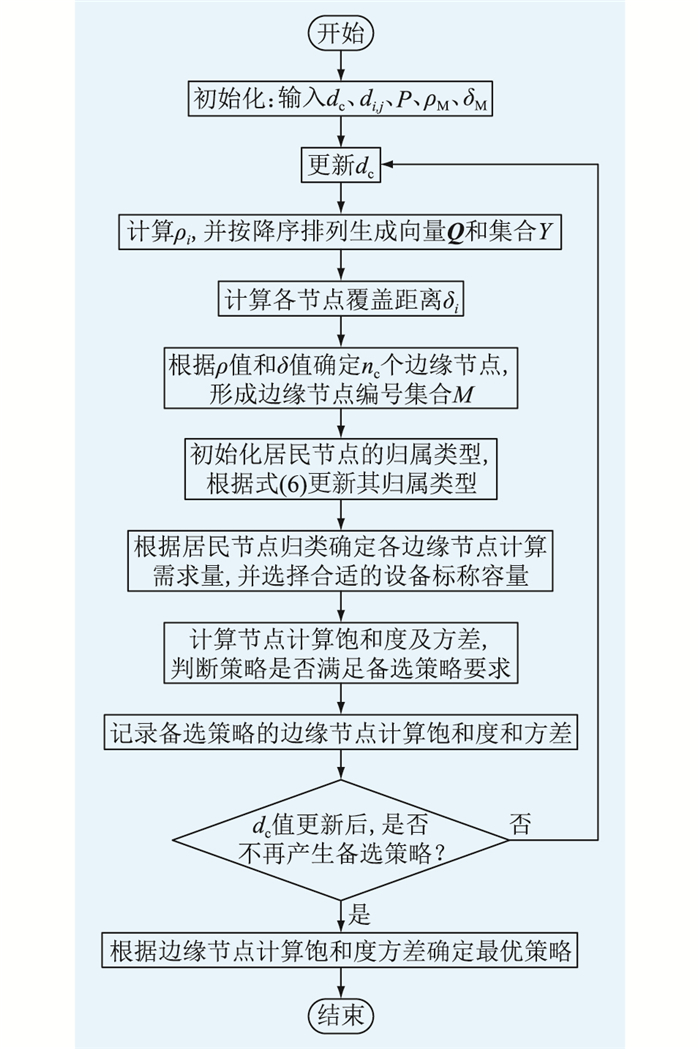
给定足够大的dc初始值,并逐步减小,每次减小后,按照前述方法更新边缘节点部署策略并确定边缘节点计算需求量,从集合P中选择合适的边缘节点标称容量,同时记录该策略下各节点的计算饱和度,将节点计算饱和度均在0.75~0.95内的策略作为备选策略,从所有备选策略中选择计算饱和度方差最小的方案。整个边缘节点选址定容流程如图 4所示,其中ρM、δM分别为局部密度阈值和节点覆盖距离阈值。
|
图 4 边缘节点选址定容流程 Fig. 4 Flow chart of location and capacity determination of edge nodes |
如图 1所示,为均衡各边缘节点计算资源,提升系统的运行效率和稳定性,边缘节点之间通过高速总线连接,当某些节点运行负荷较重时可在边缘管理平台的控制下将部分任务通过总线迁移到其他节点。
3.1 边缘节点模型假设边缘管理平台下的各边缘节点组成一个系统,边缘节点之间已经建立高速通信总线。每个用户节点实时收集计算任务和数据,通过有线或无线的方式将任务传输给边缘节点,在边缘节点内部形成计算队列。
考虑在时间段ξ1~ξ2实现边缘节点间的任务迁移,将时间段划分为时间窗口处理。假定时间窗口t内,边缘节点k接收各用户节点任务生成任务队列为Lk, t={lk, j}(j=1, 2, …, M′),其中,lk, j为第k个边缘节点任务队列中的第j个任务量的大小。则边缘节点在时间窗口t内接收到的用户节点的任务总量Jk, t为:
| $ J_{k, t}=\sum\limits_{j=1}^{M^{\prime}} l_{k, j} $ | (10) |
当前时间窗口结束时第k个边缘节点中剩余的计算量用Tk, t表示,则有如下关系:
| $ T_{k, t}=T_{k, t-1}+J_{k, t}+\alpha_{k, t}-r_{k, t}-\beta_{k, t} $ | (11) |
式中:αk, t为时间窗口t内由其他节点迁移至该节点的任务量;rk, t为该节点处理的任务总量;βk, t为由该节点迁移至其他节点的任务量。各变量一般满足如下约束:
| $ \left\{\begin{array}{l} T_{k, t} \geqslant 0 \\ p_k t_{\rm{ \mathsf{ ω}}} \geqslant r_{k, t} \geqslant 0 \\ \alpha_{k, t} \beta_{k, t}=0 \quad \alpha_{k, t} \geqslant 0 ; \beta_{k, t} \geqslant 0 \end{array}\right. $ | (12) |
设每个时间窗口内,除去各种初始化步骤后,可用于任务计算的最大时间为tω。在时间窗口开始时刻通过式(13)估算该时间窗口内节点处理完任务队列所需的实际时间。
| $ t_{k, t}=\frac{T_{k, t-1}+U_{k, t}}{p_k} $ | (13) |
式中:Uk, t为时间窗口t内,节点产生任务量的估算值,文中取前10个时间窗口该节点产生的计算量的平均值。
| $ U_{k, t}=\frac{1}{10} \sum\limits_{i=t-11}^{t-1} J_{k, i} $ | (14) |
同时,为考虑任务量估算带来的误差,定义值域为(0, 1)的负载系数ε,为各节点保留一定计算裕量。根据以上参数,将节点类型分为3种:
(1) tk, t < εtω,表示该节点目前处于轻载状态,在时间窗口内接收由其他节点迁移来的任务;
(2) εtω≤tk, t < tω,表示该节点处于正常工作状态,不接收其他节点迁移的任务,也不向其他节点迁移任务;
(3) tω≤tk, t,表示该节点处于重载状态,在该时间窗口内产生的计算任务将通过相应算法迁移至其他节点。
在实际应用中可根据用户对系统的要求,选择不同的负载系数:ε越大表示越注重计算资源的利用率,系统中的节点更易被判断为轻载节点,系统发生任务迁移的可能性较小;ε越小表示越注重服务的实时性,系统中节点更易被判断为重载节点,系统更容易发生任务迁移。
3.2 数据传输模型实现任务迁移依赖于各节点的稳定通信,在图 1中,边缘节点之间由高速有线链路连接。而链路距离和链路质量都可能影响整个系统的数据传输延时,将其抽象融合为一个复合量,定义为链路代价,表示网络中节点之间的传输成本。
用矩阵E表示系统中所有节点之间的链路代价大小。其中矩阵元素euv表示单位数量的任务数据由节点u传输到节点v须付出的链路代价,当数据量为d的任务参与任务迁移时,链路传输代价c的计算公式如式(15)所示。
| $ c(d)=d e_{u v} $ | (15) |
对于各节点产生的任务,在本地执行时,链路传输代价为0,当任务迁移到其他节点时,须考虑迁移过程产生的迁移成本。假设在时间窗口内,系统中存在重载节点m个,其节点编号由集合Xw表示;存在轻载节点n个,其节点编号由集合XI表示;系统采用的迁移策略由矩阵K表示,K为m×n阶,矩阵中的元素kuv表示由节点u向节点v迁移任务量的大小。则整个系统的数据传输成本由C表示,其计算公式如下:
| $ C=\sum\limits_{u \in X_{\mathrm{w}}} \sum\limits_{v \in X_{\mathrm{I}}} k_{u v} e_{u v} $ | (16) |
对于处在重载状态的节点,通过合理算法选择合适的轻载状态节点进行任务迁移,以充分利用系统计算能力。算法流程如图 5所示。
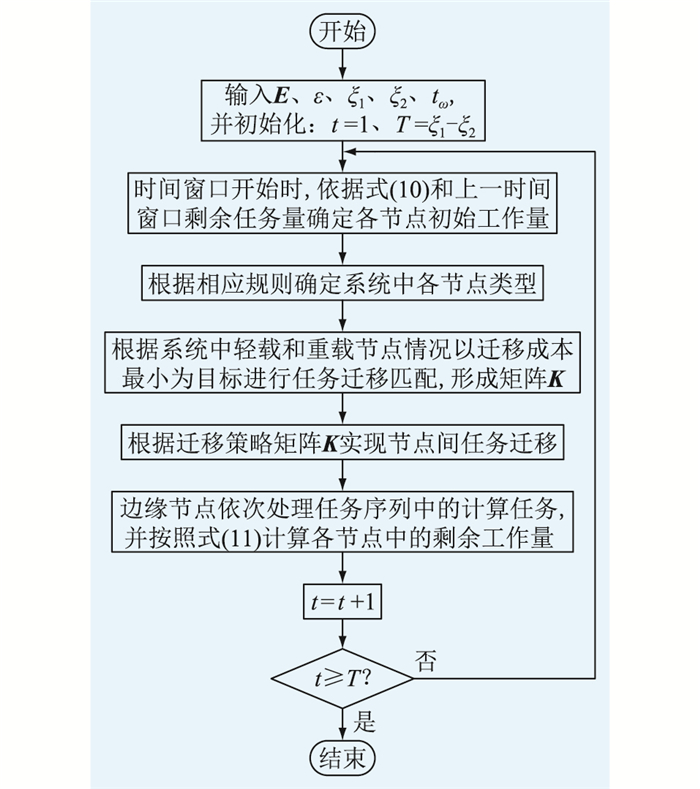
|
图 5 边缘节点任务迁移流程 Fig. 5 Flow chart of task migration of edge nodes |
算法的核心步骤为任务量匹配,对重载节点,任务队列应首先包含上一时间窗口结束时该节点剩余任务,对于本时间窗口内收集到的任务适当保留,超过自身处理能力的部分经过优化策略迁移至轻载节点。任务迁移量的确定须满足以下原则:
(1) 迁移完成后,系统中的各节点尽量在时间窗口内完成各自的任务量;
(2) 迁移完成后,原本的轻载节点不能变为重载节点;
(3) 在满足延时约束的条件下,使整个系统的数据传输成本最小。
任务量匹配的过程如下:首先,判断系统工作状态,若系统中轻载节点所能提供的计算资源足够满足重载节点的需要,则系统为轻载系统,否则为重载系统。计算公式如式(17)所示,其中F=0表示系统为轻载状态,F=1表示系统为重载状态。
| $ F= \begin{cases}0 & \sum\limits_{k \in X_{\mathrm{w}} \cup X_1}\left(T_{k, t-1}+J_{k, t}\right)<\sum\limits_{k \in X_{\mathrm{W}} \cup X_1} p_k t_{\rm{ \mathsf{ ω}}} \\ 1 & \sum\limits_{k \in X_{\mathrm{w}} \cup X_1}\left(T_{k, t-1}+J_{k, t}\right) \geqslant \sum\limits_{k \in X_{\mathrm{w}} \cup X_1} p_k t_{\rm{ \mathsf{ ω}}}\end{cases} $ | (17) |
其次,根据系统类型依次确定各节点系统的任务迁移策略。对于轻载系统,要求在任务迁移完成后,系统中不存在重载节点。且系统数据传输成本最小。则任务迁移策略矩阵K的确定过程如下:
(1) 确定各重载节点须分担的任务量,形成迁移量向量H1=[h1 h2 … hu … hm],其中,元素hu计算公式如下:
| $ h_u=T_{u, t-1}+J_{u, t}-p_u t_{\rm{ \mathsf{ ω}}} $ | (18) |
(2) 确定各轻载节点所能承担的最大任务量,形成约束量向量G1=[g1 g2 … gv … gn],其中,元素gv计算公式如下:
| $ g_v=p_v t_{\rm{ \mathsf{ ω}}}-T_{v, t-1}+J_{v, t} $ | (19) |
(3) 根据系统迁移量,确定任务迁移策略K使得系统的总传输成本最小。如此,原问题可简化为线性规划问题,形如:
| $ \begin{cases}\min\limits_{\boldsymbol{K}} C & \left(\boldsymbol{K}, \boldsymbol{H}_1, X_{\mathrm{w}}, X_{\mathrm{I}}, \boldsymbol{E}\right) \\ \text { s.t. } & \sum\limits_{v \in X_{\mathrm{I}}} k_{u v}=h_u \\ & 0 \leqslant \sum\limits_{u \in X_{\mathrm{w}}} k_{u v} \leqslant g_v\end{cases} $ | (20) |
对于重载系统,要求在任务迁移完成之后,系统轻载节点提供的计算资源被全部利用。数据传输成本最小。任务迁移策略K的确定过程如下:
(1) 确定各轻载节点所能承担的最大任务量,形成迁移量向量G2=[g1 g2 … gv … gn],其中,元素gv计算公式如下:
| $ g_v=p_v t_{\rm{ \mathsf{ ω}}}-T_{v, t-1}+J_{v, t} $ | (21) |
(2) 确定各重载节点须分担的任务量,形成约束量向量H2=[h1 h2 … hu … hm],其中,元素hu计算公式如下:
| $ h_u=T_{u, t-1}+J_{u, t}-p_u t_{\rm{ \mathsf{ ω}}} $ | (22) |
(3) 根据系统迁移量,确定任务迁移策略K使得系统的总传输成本最小。如此,原问题可简化为线性规划问题,形如:
| $ \begin{cases}\min\limits_{\boldsymbol{K}} C & \left(\boldsymbol{K}, \boldsymbol{H}_2, X_{\mathrm{w}}, X_{\mathrm{I}}, \boldsymbol{E}\right) \\ \text { s.t. } & \sum\limits_{u \in X_{\mathrm{w}}} k_{u v}=g_v \\ & 0 \leqslant \sum\limits_{v \in X_{\mathrm{I}}} k_{u v} \leqslant h_u\end{cases} $ | (23) |
上述问题属于运筹学中经典的“运输问题”,可利用启发式最小元素法进行求解[29],得到满足延时约束条件下的最优迁移策略K。
4 算例分析以南京市某大型居民区为研究对象,首先对该居民区内边缘节点进行选址定容分析,确定区域边缘节点的分布位置及服务对象;然后对边缘节点的运行状态进行分析,对比任务迁移前后各节点的工作状态和系统延时情况。
4.1 边缘节点选址定容分析为重点突出选址定容算法步骤,对居民区空间信息的建模进行简化:
(1) 简化居民入住和用电情况的统计过程,设居民节点的用电功率为100~400 kW内的随机数;
(2) 用户用电功率和产生计算数据量的比例系数为10 kW/(MB ·min-1),即用户用电功率为10 kW时将会以1 MB ·min-1的速度产生计算数据;
(3) 边缘计算设备的数据处理速度可通过选择不同型号的设备进行匹配,可供选择型号的处理数据速度为100~1 500 MB ·min-1且以100 MB ·min-1为阶梯,即P= 100, 200, 300, …, 1 500。
在上述假设条件下,图 3(d)信息融合图中包含的信息总结如下:居民节点305个,节点计算需求量以用电量大小表示,节点在二维平面上的坐标表示其位置信息,不同节点间通信距离由2点间的直线距离近似表示。
给定δM和ρM分别为90和150,初始截断距离dc为500,以1为步进距离减小dc进行迭代更新。每次更新后,统计边缘节点个数及每个边缘节点所需的计算资源大小,同时对于满足备选条件的dc值,进一步统计各节点的计算饱和度均值和方差,从而反映系统资源的利用情况,结果见表 1。
|
|
表 1 不同dc值下各节点计算资源分配情况 Table 1 Calculation resource allocation of nodes with different dc |
从表 1可以看出,当dc过高时,边缘节点个数较少,边缘设备最大计算资源需求量超过备选设备的最大标称容量,不符合选取要求;当dc下降到228时边缘节点的个数达到15,最大计算资源需求量下降到1 493.2 MB ·min-1,可以满足选取要求;当dc下降到20以下时,需要部署的边缘节点数量较多,边缘设备计算资源利用率较低。
当dc取值在173到205之间时,系统中所有节点的计算饱和度均值在0.85到0.93之间,说明系统资源被充分利用,节点的计算饱和度方差最小,此方案系统计算资源分配最均衡。文中选择dc取值为185,此时f=0.91、s2(f)=0.092。当dc=185时,各点的δ值和ρ值如图 6所示,图中满足阈值条件的16个居民节点被选为边缘节点。
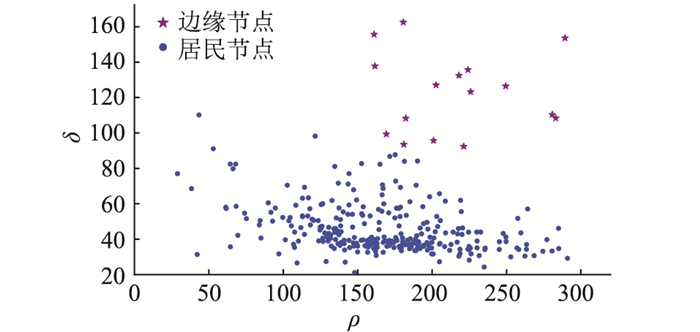
|
图 6 节点δ-ρ分布 Fig. 6 Node distribution diagram of δ-ρ |
采用2.3节所述方法确定边缘节点服务对象。得到区域内选取的边缘节点及其他居民节点之间的关系,如图 7所示,各边缘节点计算需求量及边缘设备选取容量如表 2所示。
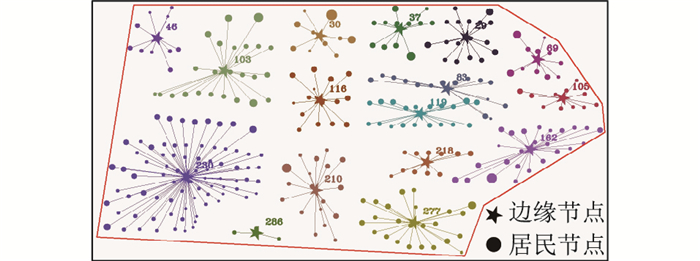
|
图 7 边缘节点分布结果 Fig. 7 Distribution of edge nodes |
|
|
表 2 边缘节点容量分配 Table 2 Edge node computing capacity allocation |
传统边缘节点部署方法往往忽略边缘节点的选址定容优化过程,对每个边缘节点分配相同计算容量,各边缘节点的服务对象主要以地理位置为依据进行均匀划分。为进一步说明选址定容策略的有效性,从居民原始数据传输的角度设计对比实验。
假设传统方法下居民区的用电量及边缘节点数量与文中结果一致,即部署16个边缘节点,所有边缘节点的计算资源总和为9 400 MB ·min-1,平均每个节点分配的计算资源为587.5 MB ·min-1,取标称值600 MB ·min-1。
采用1 200 min的仿真时长,每个居民节点随机产生以该节点表 2中的节点计算需求量为均值的符合正态分布的计算数据[30],并以该节点到对应边缘节点的距离代表原始数据单位传输成本,统计每个时间窗口内由居民节点向边缘节点传输数据的总成本,如图 8所示。
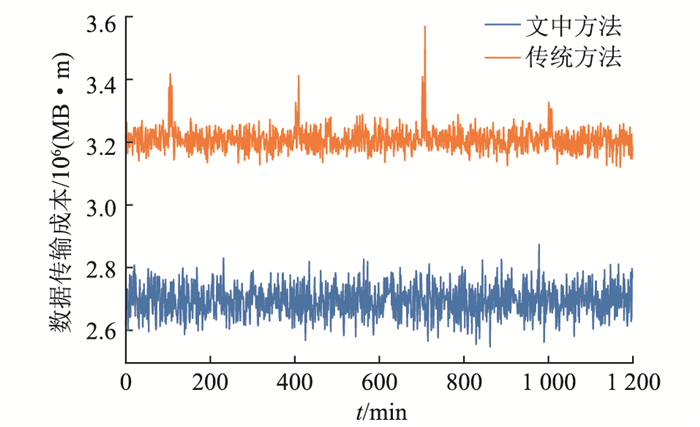
|
图 8 不同部署方法的数据迁移成本 Fig. 8 Data migration costs of different deployment methods |
从图中可以看出传统方法的传输成本明显高于文中方法。进一步计算2种方法的成本平均值可得,采用文中方法成本为2.68×106 MB ·m,相对于传统方法的3.25×106 MB ·m,降低了17.54%,说明文中提出的边缘计算节点选址定容策略降低了原始数据传输压力。
4.2 边缘节点任务迁移结果分析以16边缘节点系统为研究对象,验证边缘节点任务迁移算法的有效性。
正常情况下,以表 2中节点计算需求量为均值产生符合正态分布的随机数据作为各边缘节点接收到的任务量,在一些节点上叠加较大的随机变量模拟突发状况。用电高峰下,正态分布随机数据的均值变为原来的1.1倍。用长度为1 200的时间段模拟上述2种情况,突发状况设置在时间节点100、400、700、1 000处,长度为10。
设立2组对照实验,说明迁移算法的优越性,对照组1为系统采用不迁移运行策略时系统运行情况,对应于实验结果中“不迁移”;对照组2为系统不考虑迁移代价时各节点的运行状态,反映了系统可达到的最佳迁移效果,对应于实验结果中“迁移策略1”;文中算法对应于实验结果中“迁移策略2”。实验中涉及到的其他变量数值选取如下:负载系数ε为0.95,时间窗口内最大任务时间tω为1 min,各边缘节点单位时间内的计算能力pk按表 2中的边缘设备容量选取。
4.2.1 边缘节点任务迁移过程分析统计系统中各节点在各时间窗口内的计算量,将其换算为节点工作时间长度来表现边缘节点的任务迁移过程,图 9为某时间窗口内轻载系统和重载系统中边缘节点在任务迁移前后的任务量大小对比。
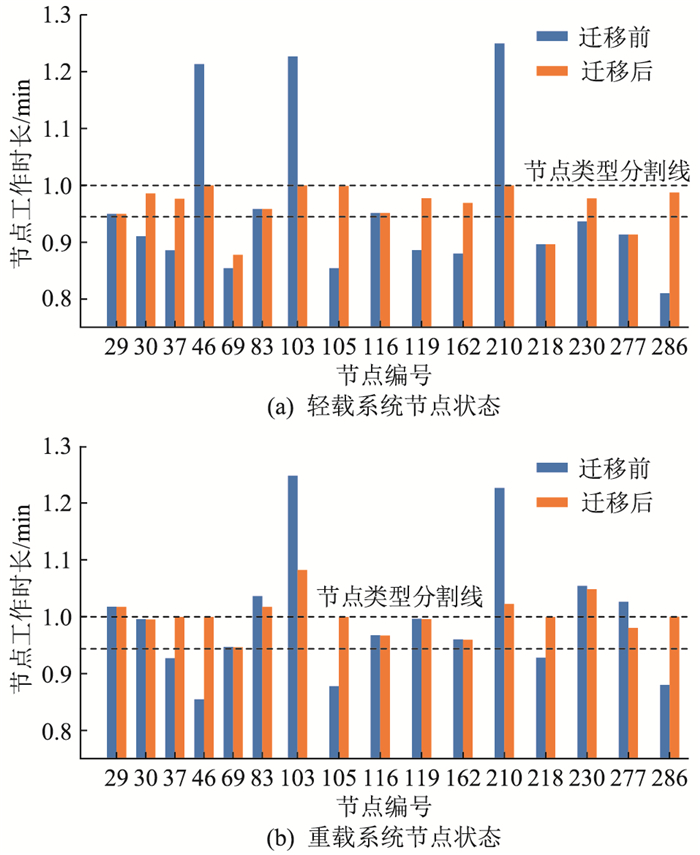
|
图 9 任务迁移前后节点状态 Fig. 9 Node status before and after task migration |
系统处于轻载状态时,各轻载节点富余的计算资源完全能覆盖重载节点的需要,在该时间窗口内迁移前节点46、103、210为重载节点,任务迁移后,这3个节点上任务量被迁移到其他轻载节点,整个系统不再存在重载节点;系统处于重载状态时,各轻载节点富余的计算资源不能完全满足重载节点的需求,迁移前节点29、83、103、210、230、277为重载节点,迁移后,虽然各重载节点的工作量均有不同程度的下降,但仅节点277转换为正常节点,而各轻载节点接收的任务量已达到最大正常节点的限制。
4.2.2 系统实时性分析用时间窗口内所有边缘节点最大工作时间表示系统工作时长。将实验结果反应在图 10中,其中图 10(a)为正常工作状态下工作时长,可以看出,无论采取哪种迁移策略都能将系统工作时长控制在tω内,但在出现突发状况时,迁移策略1和迁移策略2相对于不迁移运行策略能较好地限制系统运行时间突增。
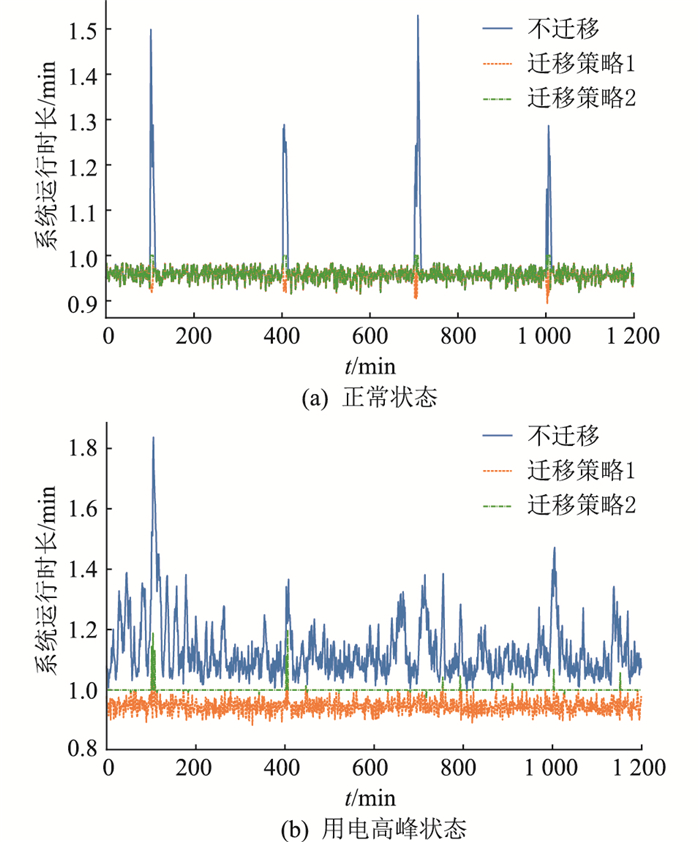
|
图 10 系统工作时长 Fig. 10 Working time of system |
图 10(b)反映了用电高峰时的系统延时状况,可以看出采取不迁移策略将导致在整个仿真时间段内的系统工作时间都大幅超过tω;采用迁移策略1时,系统工作时长会被限制在远低于tω的水平,这说明系统整体上还未达到算力上限;采用迁移策略2时,系统工作时长将基本稳定在tω,这是由于算法从降低系统数据迁移代价的角度考虑限制了重载节点迁移量。
4.2.3 系统计算资源均衡分析图 11为系统在仿真时间段内各边缘节点的平均计算饱和度,反映了各节点计算资源的使用情况。图 11(a)为系统正常状态时的情况,图中各节点的平均计算饱和度受迁移策略的影响不大,这是由于系统计算资源充足,系统内基本未发生任务迁移。图 11(b)为用电高峰时的情况,系统不发生迁移时,某些节点的平均计算饱和度较高,比如节点29、116、230等,而节点46、105、286的平均计算饱和度又较低,所有边缘节点的计算饱和度方差为0.532,系统中某些节点运算负荷过高而某些节点计算资源未充分利用。采用迁移策略1时,各节点的计算饱和度基本相等,其方差值为0.002,最大程度均衡了各节点的计算资源。采用迁移策略2时,节点的饱和度方差为0.131,相对于采用不迁移运行策略有很大的改善。
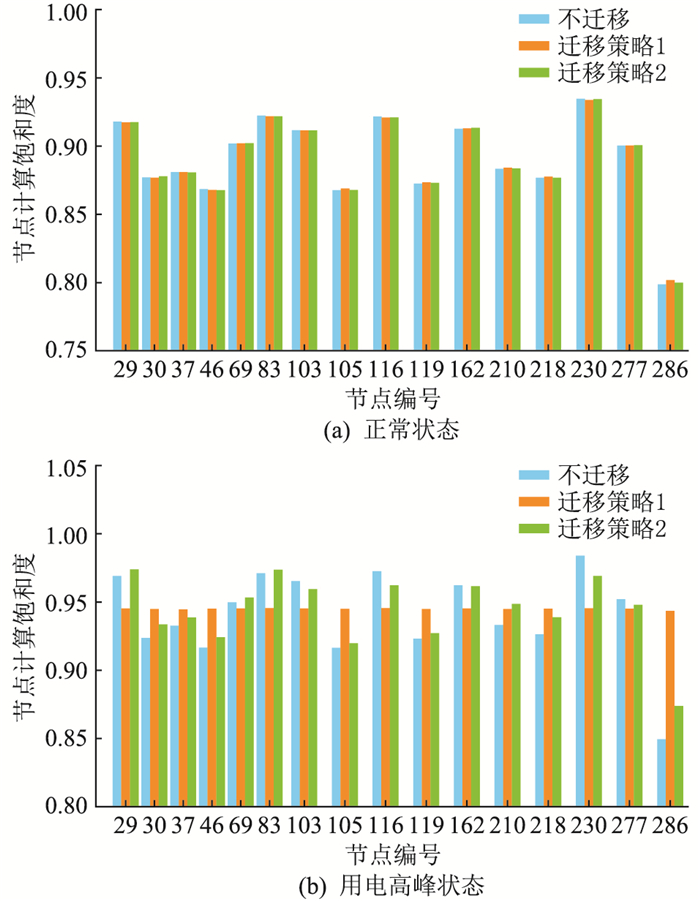
|
图 11 节点平均计算饱和度 Fig. 11 Node average calculated saturation |
图 12为采用不同迁移策略时系统总迁移成本对比。从图 12(a)中可以,看出系统正常工作情况下迁移成本只在突发状况时产生,通过计算得到迁移策略1每分钟内的数据传输成本均值为4.335 MB ·m,迁移策略2为3.695 MB ·m,两者较为接近。图 12(b)反映了用电高峰时2种迁移策略的迁移成本,采用迁移策略2的成本均值为93.602 MB ·m,相对于策略1的151.306 MB ·m,降低了38.1%。
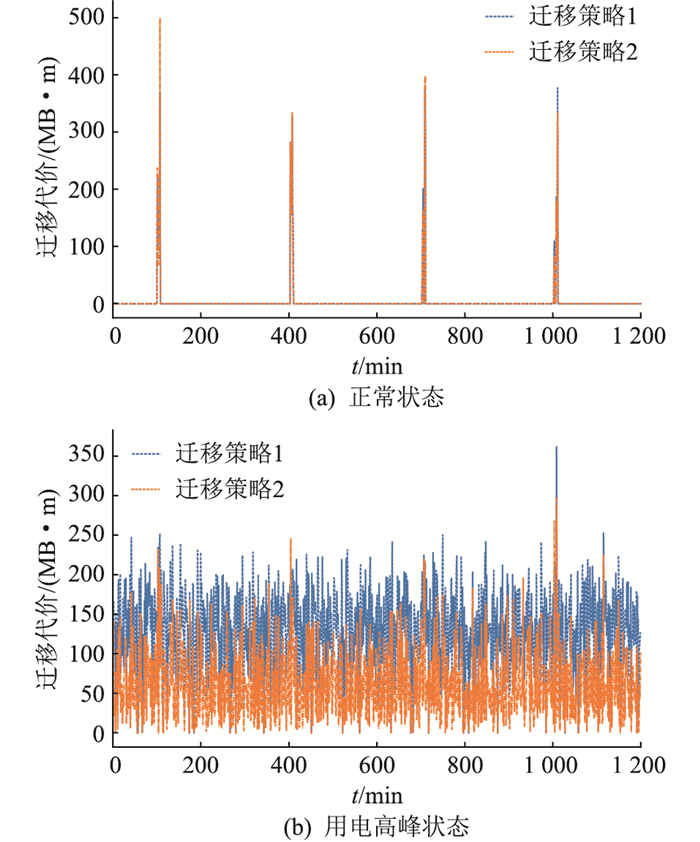
|
图 12 不同迁移策略迁移成本 Fig. 12 Migration costs of different migration strategies |
如3.2节所述,实际情况中系统的迁移成本包含了数据传输过程中各种因素比如时间成本、传输耗能、数据传输过程中的不稳定因素。因此,迁移策略2的系统稳定性相对迁移策略1会有一定程度的提高。
综上,文中迁移策略在降低系统延时、减少重载节点个数、节点计算资源均衡等方面的效果均接近于不考虑成本的迁移策略,但在降低迁移成本方面具有较大优势,考虑到迁移成本代表的各种问题,文中迁移策略更适合文中涉及的应用场景。
上述实验说明文中边缘计算节点部署方法在降低原始数据传输成本、减小系统计算延时、提高系统运行稳定性等方面都有较好的效果。
5 结语在新型电力系统建设过程中,边缘计算广泛应用将大大提高电网运行的灵活性和可靠性。文中从居民住宅特点的角度出发,结合边缘计算设备小型化,计算资源高密度的发展趋势提出一种考虑任务迁移的配电网边缘节点部署方法。该方法确定的边缘节点选址定容策略能尽量使边缘节点的部署地址选择在区域内计算需求的峰值地点,使原本应部署在台区边缘计算服务器上的服务程序充分下沉到用户侧,大大降低原始数据传输距离,大幅度提高需要大量数据支持的用户定制化用电服务的响应速度;同时任务迁移算法依赖边缘节点间的高速通信总线,并以特定的策略实现过载节点向其他节点进行任务转移的工作,充分利用边缘管理平台下所有节点的计算资源,更好地应对由于节点设备故障或者负荷高峰带来的负面影响,大幅提高边缘节点提供服务的可靠性和稳定性。
| [1] |
谢小瑜, 周俊煌, 张勇军. 深度学习在泛在电力物联网中的应用与挑战[J]. 电力自动化设备, 2020, 40(4): 77-87. XIE Xiaoyu, ZHOU Junhuang, ZHANG Yongjun. Application and challenge of deep learning in ubiquitous power Internet of Things[J]. Electric Power Automation Equipment, 2020, 40(4): 77-87. (  0) 0) |
| [2] |
谢可, 王剑锋, 金尧, 等. 电力物联网关键技术研究综述[J]. 电力信息与通信技术, 2022, 20(1): 1-12. XIE Ke, WANG Jianfeng, JIN Yao, et al. Review of key technologies for power Internet of Things[J]. Electric Power Information and Communication Technology, 2022, 20(1): 1-12. (  0) 0) |
| [3] |
苏华权, 周昉昉, 易仕敏, 等. 基于电力物联网的数据智能检测模型研究[J]. 电力信息与通信技术, 2022, 20(3): 34-39. SU Huaquan, ZHOU Fangfang, YI Shimin, et al. Research on intelligent data detection model based on power Internet of Things[J]. Electric Power Information and Communication Technology, 2022, 20(3): 34-39. (  0) 0) |
| [4] |
司羽飞, 谭阳红, 汪沨, 等. 面向电力物联网的云边协同结构模型[J]. 中国电机工程学报, 2020, 40(24): 7973-7979, 8234. SI Yufei, TAN Yanghong, WANG Feng, et al. Cloud-edge collaborative structure model for power Internet of Things[J]. Proceedings of the CSEE, 2020, 40(24): 7973-7979, 8234. (  0) 0) |
| [5] |
黄杰, 肖志清, 毛冬. 面向电力物联网的云边数据协同方法[J]. 电力信息与通信技术, 2022, 20(1): 35-42. HUANG Jie, XIAO Zhiqing, MAO Dong. Cloud-edge data collaboration method for power IoTs[J]. Electric Power Information and Communication Technology, 2022, 20(1): 35-42. (  0) 0) |
| [6] |
谢可, 郭文静, 祝文军, 等. 面向电力物联网海量终端接入技术研究综述[J]. 电力信息与通信技术, 2021, 19(9): 57-69. XIE Ke, GUO Wenjing, ZHU Wenjun, et al. Review on access technology of massive terminals of power Internet of Things[J]. Electric Power Information and Communication Technology, 2021, 19(9): 57-69. (  0) 0) |
| [7] |
KULKARNI S, GU Q C, MYERS E, et al. Enabling a decentralized smart grid using autonomous edge control devices[J]. IEEE Internet of Things Journal, 2019, 6(5): 7406-7419. DOI:10.1109/JIOT.2019.2898837 (  0) 0) |
| [8] |
祁兵, 夏琰, 李彬, 等. 基于边缘计算的家庭能源管理系统: 架构、关键技术及实现方式[J]. 电力建设, 2018, 39(3): 33-41. QI Bing, XIA Yan, LI Bin, et al. Family energy management system based on edge computing: architecture, key technology and implementation[J]. Electric Power Construction, 2018, 39(3): 33-41. (  0) 0) |
| [9] |
刘耀先, 孙毅, 李彬, 等. 基于边缘嵌入深度学习的非侵入式负荷分解方法[J]. 电网技术, 2019, 43(12): 4329-4337. LIU Yaoxian, SUN Yi, LI Bin, et al. Non-intrusive load disaggregation method based on edge embedded deep learning[J]. Power System Technology, 2019, 43(12): 4329-4337. (  0) 0) |
| [10] |
李彬, 贾滨诚, 曹望璋, 等. 边缘计算在电力需求响应业务中的应用展望[J]. 电网技术, 2018, 42(1): 79-87. LI Bin, JIA Bincheng, CAO Wangzhang, et al. Application prospect of edge computing in power demand response business[J]. Power System Technology, 2018, 42(1): 79-87. (  0) 0) |
| [11] |
白昱阳, 黄彦浩, 陈思远, 等. 云边智能: 电力系统运行控制的边缘计算方法及其应用现状与展望[J]. 自动化学报, 2020, 46(3): 397-410. BAI Yuyang, HUANG Yanhao, CHEN Siyuan, et al. Cloud-edge intelligence: status quo and future prospective of edge computing approaches and applications in power system operation and control[J]. Acta Automatica Sinica, 2020, 46(3): 397-410. (  0) 0) |
| [12] |
龚钢军, 罗安琴, 陈志敏, 等. 基于边缘计算的主动配电网信息物理系统[J]. 电网技术, 2018, 42(10): 3128-3135. GONG Gangjun, LUO Anqin, CHEN Zhimin, et al. Cyber physical system of active distribution network based on edge computing[J]. Power System Technology, 2018, 42(10): 3128-3135. (  0) 0) |
| [13] |
ZHANG G W, SHEN F, LIU Z N, et al. FEMTO: fair and energy-minimized task offloading for fog-enabled IoT networks[J]. IEEE Internet of Things Journal, 2019, 6(3): 4388-4400. (  0) 0) |
| [14] |
SUN H Y, YU H Q, FAN G S. Contract-based resource sharing for time effective task scheduling in fog-cloud environment[J]. IEEE Transactions on Network and Service Management, 2020, 17(2): 1040-1053. (  0) 0) |
| [15] |
RAHMAN T, YAO X X, TAO G, et al. Efficient edge nodes reconfiguration and selection for the Internet of Things[J]. IEEE Sensors Journal, 2019, 19(12): 4672-4679. (  0) 0) |
| [16] |
曹望璋, 李彬, 祁兵, 等. 一种考虑业务可靠性的需求响应边缘云部署方法[J]. 中国电机工程学报, 2021, 41(3): 846-857. CAO Wangzhang, LI Bin, QI Bing, et al. A deployment method of demand response edge cloud considering services reliability[J]. Proceedings of the CSEE, 2021, 41(3): 846-857. (  0) 0) |
| [17] |
陈中, 方国权, 赵奇, 等. 面向区域级用户的非侵入式负荷监测技术应用方法[J]. 电力自动化设备, 2020, 40(8): 126-132. CHEN Zhong, FANG Guoquan, ZHAO Qi, et al. Application method of non-intrusive load monitoring technology for region-level users[J]. Electric Power Automation Equipment, 2020, 40(8): 126-132. (  0) 0) |
| [18] |
YAGHMAEE M H, LEON-GARCIA A, MOGHADDASSIAN M. On the performance of distributed and cloud-based demand response in smart grid[J]. IEEE Transactions on Smart Grid, 2018, 9(5): 5403-5417. (  0) 0) |
| [19] |
刘浩, 赵伟, 温克欢, 等. 低压配电台区模组化智能融合终端构建方案与实现[J]. 电测与仪表, 2022, 59(1): 168-175. LIU Hao, ZHAO Wei, WEN Kehuan, et al. Construction scheme and realization of modularized intelligent fusion terminal in low-voltage distribution station areas[J]. Electrical Measurement & Instrumentation, 2022, 59(1): 168-175. (  0) 0) |
| [20] |
武超飞, 付义豪, 孙冲, 等. 基于模组电能表的居民侧智慧能源网关设计[J]. 电测与仪表, 2020, 57(21): 140-146. WU Chaofei, FU Yihao, SUN Chong, et al. Design of the smart energy gateway on residential side based on modular energy meter[J]. Electrical Measurement & Instrumentation, 2020, 57(21): 140-146. (  0) 0) |
| [21] |
胡晓青. 中国城市住区居住密度特征[J]. 住宅科技, 2015, 35(6): 14-18. HU Xiaoqing. Living density features of urban residential areas of China[J]. Housing Science, 2015, 35(6): 14-18. (  0) 0) |
| [22] |
杨清波, 陈振宇, 刘东, 等. 基于容器的调控云PaaS平台的设计与实现[J]. 电网技术, 2020, 44(6): 2030-2037. YANG Qingbo, CHEN Zhenyu, LIU Dong, et al. Design and implementation of dispatching and control cloud PaaS platform based on container[J]. Power System Technology, 2020, 44(6): 2030-2037. (  0) 0) |
| [23] |
杨漾, 敖知琪, 刘佳, 等. 面向数字电网的基于容器技术的边缘计算数据处理机制[J]. 南方电网技术, 2021, 15(5): 98-103. YANG Yang, AO Zhiqi, LIU Jia, et al. Edge computing data processing mechanism of digital power grid based on container technology[J]. Southern Power System Technology, 2021, 15(5): 98-103. (  0) 0) |
| [24] |
徐晓, 陈中, 丁宏恩, 等. 面向区域售电公司的边缘计算架构设计探讨[J]. 电力建设, 2019, 40(7): 41-47. XU Xiao, CHEN Zhong, DING Hongen, et al. Discussion on the design of edge computing architecture for regional electricity retailer[J]. Electric Power Construction, 2019, 40(7): 41-47. (  0) 0) |
| [25] |
RODRIGUEZ A, LAIO A. Clustering by fast search and find of density peaks[J]. Science, 2014, 344(6191): 1492-1496. (  0) 0) |
| [26] |
周峰, 周晖, 刁赢龙. 泛在电力物联网智能感知关键技术发展思路[J]. 中国电机工程学报, 2020, 40(1): 70-82, 375. ZHOU Feng, ZHOU Hui, DIAO Yinglong. Development of intelligent perception key technology in the ubiquitous Internet of Things in electricity[J]. Proceedings of the CSEE, 2020, 40(1): 70-82, 375. (  0) 0) |
| [27] |
岑伯维, 蔡泽祥, 胡凯强, 等. 电力物联网边缘计算终端业务时序逻辑与计算负荷建模方法[J]. 电力系统自动化, 2021, 45(9): 107-114. CEN Bowei, CAI Zexiang, HU Kaiqiang, et al. Modeling method for bussiness sequential logic and workload of edge computing terminal in electric Internet of Things[J]. Automation of Electric Power Systems, 2021, 45(9): 107-114. (  0) 0) |
| [28] |
岑伯维, 蔡泽祥, 武志刚, 等. 电力物联网边缘计算终端的微服务建模与计算资源配置方法[J]. 电力系统自动化, 2022, 46(5): 78-91. CEN Bowei, CAI Zexiang, WU Zhigang, et al. Microservice modeling and computing resource configuration method for edge computing terminal in electric Internet of Things[J]. Automation of Electric Power Systems, 2022, 46(5): 78-91. (  0) 0) |
| [29] |
刁在筠, 刘桂真, 戎晓霞. 运筹学[M]. 4版. 北京: 高等教育出版社, 2016: 326. DIAO Zaijun, LIU Guizhen, RONG Xiaoxia. Operational research[M]. 4th ed. Beijing: Higher Education Press, 2016: 326. (  0) 0) |
| [30] |
TRAN T X, POMPILI D. Joint task offloading and resource allocation for multi-server mobile-edge computing networks[J]. IEEE Transactions on Vehicular Technology, 2019, 68(1): 856-868. (  0) 0) |
 2023, Vol. 42
2023, Vol. 42


 杨凯(1996), 男, 硕士在读, 研究方向为人工智能在电力系统中的应用(E-mail:
杨凯(1996), 男, 硕士在读, 研究方向为人工智能在电力系统中的应用(E-mail: