文章编号: 2096-3203(2023)02-0130-09 中图分类号: TM712
2. 合肥综合性国家科学中心能源研究院(安徽省能源实验室), 安徽 合肥 230031;
3. 国网安徽省电力有限公司芜湖供电分公司, 安徽 芜湖 241000
谐振接地系统在中低压配电网中被广泛应用[1]。在该方式下发生单相接地故障时,故障特征提取困难[2],而分布式电源(distributed generator,DG)的接入使得配电网络更加复杂。因此,有必要针对谐振接地系统单相接地故障定位展开深入研究。
目前已存在多种故障定位方法,大致可分为稳态法[3-6]、暂态法[7-15]、注入法[16-18]以及人工智能法[19-21]。稳态法原理简单,但当系统运行工况变化时,稳态分量会有较大波动,局限性在所难免。注入法须增设信号注入设备,成本较高。人工智能算法虽具有一定的容错性能,但建模往往过于复杂,算法的收敛速度有待提升。
发生单相接地故障时,由于故障信号中包含丰富的暂态信息且不受消弧线圈的影响,因此暂态法在故障定位中得到广泛应用。文献[11]利用暂态电压导数与暂态电流的相关性定位故障区段,但该方法在高阻接地时存在定位盲区。文献[12]通过计算故障相电压与故障点上、下游暂态零序电流间的波形相似程度来实现故障定位,对高阻适应性好,但计算量大且对采样频率要求较高。文献[13]结合小波分解与Hausdorff距离算法,基于暂态零序电流的幅值差异进行定位,但仅利用小波分解后的幅值信息,未分析DG接入的影响。
现有的谐振接地系统单相接地故障的故障定位方法存在对不同过渡电阻适应性差、故障信息利用不充分和对采样频率要求高等问题。文中对故障馈线各区段两端的暂态零序电流进行db10小波包分解,利用频段能量构造幅值判据,并提取了波形层面的特征量,结合曼哈顿平均距离和余弦相似度算法,构造多维故障定位判据,充分利用故障信息,提高了故障定位的可靠性。文中所提方法在不同故障条件下均能准确定位,适应性好、灵敏度高,具有较好的工程应用前景。
1 谐振接地系统单相接地故障分析 1.1 DG接入的影响为保证系统稳定,主网的中性点接地方式应不受DG投切的影响。因此,当主网侧经消弧线圈接地时,DG高压侧宜采用中性点非有效接地方式[22]。DG并网时,若对地电容电流较大,可通过主网侧进行补偿,因此DG无须加装消弧线圈,且采用中性点不接地方式进一步降低了系统成本和调谐复杂度[9]。
当DG并网侧变压器采用△/Y绕组接线方式时,系统的零序网络不会发生改变。发生故障后,DG与主网侧的电流流通路径被切断,暂态零序电流在网络中的分布也不受影响,故利用暂态零序信号的故障定位方法仍能适用[23]。
逆变型DG在配电网中的应用更为广泛,选用DIgSILENT PowerFactory对其进行建模仿真。逆变器采用Detailed模型,控制如图 1所示。
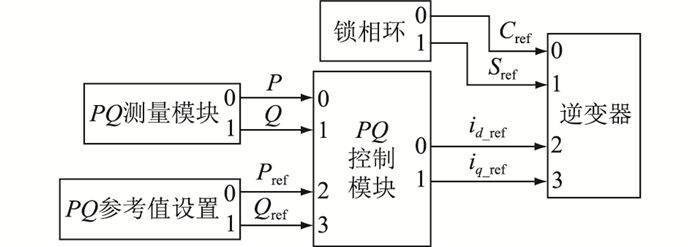
|
图 1 并网逆变器控制框图 Fig. 1 Control frame of inverter |
图 1中,P、Q分别为逆变器的有功功率和无功功率;Pref、Qref分别为有功功率、无功功率参考值;id_ref、iq_ref分别为电流d轴、q轴分量参考值;Sref、Cref分别为电压相角正弦值、余弦值的参考值。外环为恒功率控制,其中PQ测量模块用于计算逆变器的输出功率;有功和无功功率参考值由PQ参考值设置模块给定;PQ控制模块是外环控制的核心。内环控制器使用软件自带模块。
1.2 暂态零序电流故障特征单相接地系统的零序等效网络如图 2所示。图 2中,i0x(x=1, 2, …, n, n为馈线总数)为线路x的零序电容电流;C0x为线路x的等效对地电容;Lp为等效的3倍消弧线圈电感;iL为电感电流;ig为流经接地点的零序电流;u0为故障点虚拟电源。
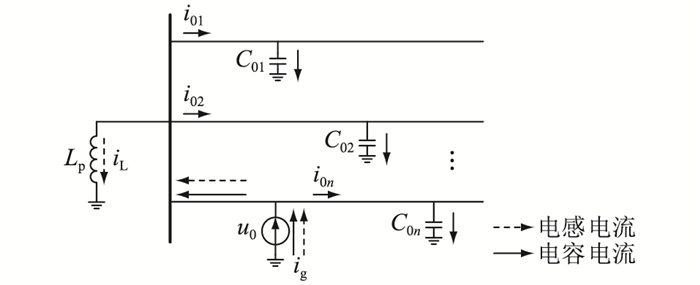
|
图 2 单相接地系统零序等效网络 Fig. 2 Zero-sequence equivalent network of single-phase grounded system |
接地电流主要由电容电流iC和电感电流iL组成,如式(1)所示。
| $ \begin{gathered} i_{\mathrm{g}}=i_{\mathrm{C}}+i_{\mathrm{L}}= \\ \left(I_{\mathrm{Cm}}-I_{\mathrm{Lm}}\right) \cos (\omega t+\varphi)+I_{\mathrm{Lm}} \mathrm{e}^{-t / \tau_{\mathrm{L}}} \cos \varphi+ \\ I_{\mathrm{Cm}}\left(\frac{\omega_{\mathrm{f}}}{\omega} \sin \varphi \times \sin \omega t-\cos \varphi \times \cos \omega_{\mathrm{f}} t\right) \mathrm{e}^{-t / \tau_{\mathrm{C}}} \end{gathered} $ | (1) |
式中:ICm、ILm分别为电容和电感电流的幅值;ωf为暂态自由振荡分量的角频率;τC、τL分别为电容和电感电流时间常数;ω为角频率;φ为初相角;t为时间。
由式(1)可知,故障零序电流的稳态分量经补偿后被大幅削减,利用稳态分量难以确定故障所在区段;而消弧线圈的接入有可能会使暂态接地电流的幅值增大。流向故障点上游的暂态零序电流为所有健全线路对地电容电流、消弧线圈电感电流以及故障点到母线处该线路的对地电容电流;流向下游的暂态零序电流仅为故障点至该线路末端这一区段的对地电容电流。故障初始时刻,电感电流不突变,消弧线圈补偿作用小,因此故障点上游暂态零序电流的幅值远大于下游,且极性相反,相似度低。简化的零序等值电路如图 3所示。
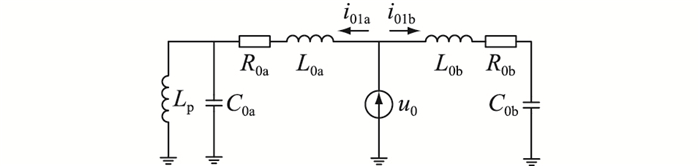
|
图 3 简化零序等值电路 Fig. 3 Simplified zero-sequence equivalent circuit |
图 3中,i01a、i01b分别为流向故障点上、下游的暂态零序电流;R0a、C0a、L0a分别为故障点上游线路的零序等值电阻、电容和电感;下游线路的等值参数分别用R0b、C0b、L0b表示。根据文献[13]可推导出i01a、i01b,如式(2)—式(5)所示。
| $ \begin{gathered} i_{01 \mathrm{a}}=\frac{U_{\mathrm{m}}\left(\omega C_{0 \mathrm{a}}+1 / \omega L_{\mathrm{p}}\right)}{\sqrt{\left(L_{\mathrm{p}}+L_{0 \mathrm{a}}\right) \sin ^2 \varphi /\left(\omega^2 L_{\mathrm{p}} L_{0 \mathrm{a}} C_{0 \mathrm{a}}\right)+\cos ^2 \varphi}} \times \\ \quad \sin \left(\sqrt{\left(L_{\mathrm{p}}+L_{0 \mathrm{a}}\right) /\left(L_{\mathrm{p}} L_{0 \mathrm{a}} C_{0 \mathrm{a}}\right) t} t+\alpha_{\mathrm{a}}\right) \mathrm{e}^{-R_{0 \mathrm{a}} t / 2 L_{0 \mathrm{a}}} \end{gathered} $ | (2) |
| $ \begin{aligned} i_{01 \mathrm{~b}}=& \frac{U_{\mathrm{m}} \omega C_{0 \mathrm{~b}}}{\sqrt{\sin ^2 \varphi /\left(\omega^2 L_{0 \mathrm{~b}} C_{0 \mathrm{~b}}\right)+\cos ^2 \varphi}} \times \\ & \sin \left(\frac{t}{\sqrt{L_{0 \mathrm{~b}} C_{0 \mathrm{~b}}}}+\alpha_{\mathrm{b}}\right) \mathrm{e}^{-R_{0 \mathrm{~b}} t / 2 L_{0 \mathrm{~b}}} \end{aligned} $ | (3) |
| $ \alpha_{\mathrm{a}}=\arctan \left(\omega \sqrt{\frac{L_{\mathrm{p}} L_{0 \mathrm{a}} C_{0 \mathrm{a}}}{L_{\mathrm{p}}+L_{0 \mathrm{a}}}} \tan \varphi\right) $ | (4) |
| $ \alpha_{\mathrm{b}}=\arctan \left(\omega \sqrt{L_{0 \mathrm{~b}} C_{0 \mathrm{~b}}} \tan \varphi\right) $ | (5) |
式中:Um为相电压峰值;αa、αb分别为故障点上、下游零序电流暂态分量初相位。
故障点上游线路的长度通常远大于下游线路[7],故有C0a>C0b,L0a>L0b。对式(2)—式(5)进行定量分析可知,上游暂态零序电流的幅值大于下游。又因两者极性相反,可通过比较故障点上、下游暂态零序电流的相似性进行故障定位。
2 故障定位算法 2.1 小波包分解提取故障特征 2.1.1 数据采集文中定位算法的实现基于对暂态零序电流的高精度同步测量,否则将会出现误判的情形。微型同步相量测量装置(micro-phasor measurement unit,μPMU)基于全球定位系统时钟信号,能够对配电网进行实时监控,因此将其作为采样设备。考虑谐波干扰和噪声的信号模型如式(6)所示。
| $ \left\{\begin{array}{l} x_{\mathrm{s}}(k)=\sqrt{2} A \cos \left(2 \pi\left(f_0+\Delta f\right) k T+\varphi\right)+ \\ \quad \sum\limits_{b=1}^{N_{\mathrm{ih}}} \sqrt{2} A_b \cos \left(2 \pi f_b k T+\varphi_b\right)+w_{\text {Noise }}(k)= \\ \quad \frac{\sqrt{2}}{2}\left(\lambda+\lambda^*\right)+\frac{\sqrt{2}}{2} \sum\limits_{b=1}^{N_{\mathrm{ih}}}\left(\lambda_b+\lambda_b^*\right)+w_{\text {Noise }}(k) \\ \lambda=A \mathrm{e}^{\mathrm{j}\left[2 \pi\left(f_0+\Delta f\right) k T+\varphi\right]} \\ \lambda_b=A_b \mathrm{e}^{\mathrm{j}\left(2 \pi f_b k T+\varphi_b\right)} \end{array}\right. $ | (6) |
式中:xs(k)为信号采样值;b为谐波次数;A、Ab分别为基波、谐波信号幅值;f0、fb分别为50 Hz基频、谐波频率;Δf为频率偏差;φ、φb分别为基波、谐波相位;Nih为谐波干扰数;T为采样间隔;k为采样值标号;wNoise(k)为白噪声;λ*、λb*分别为λ、λb的共轭。
电流信号经μPMU高频采样后被置于缓存区,再通过频率分析、滤波以及补偿矫正等环节,最终可在本地显示或被上传至配电网主站。
2.1.2 数据处理暂态零序电流中包含有丰富的故障信息,对故障信息的有效、精确提取是进行故障定位的前提。小波包能同时分解低频和高频分量,对信号的暂态突变和微弱变化的特征量进行提取分析,克服了小波分解在高频段分辨率低的缺点。其递归公式如式(7)所示。
| $ \left\{\begin{array}{l} \mu_{2 o}(t)=\sqrt{2} \sum\limits_{q \in \bf{N}} h_q \mu_o(2 t-q) \\ \mu_{2 o+1}(t)=\sqrt{2} \sum\limits_{q \in \bf{N}} g_q \mu_o(2 t-q) \end{array}\right. $ | (7) |
式中:hq、gq均为滤波器系数;q为平移变量且q∈N(非负整数);o为递归数。
分解后第k个频段的能量可用式(8)计算。
| $ \varepsilon_k=\sum\left(\mu_{k, j}(v)\right)^2 $ | (8) |
式中:j为小波包分解层数;μk,j(v)为第j层第k个频段下的分解系数,每个频段下共有v个系数。
第k个频段下的能量可用概率形式表示,如式(9)所示。
| $ p_k=\varepsilon_k / \sum\limits_{i=1}^m \varepsilon_i $ | (9) |
式中:m=2j为分解后的频段数量;εi为第i个频段的能量,i=1, 2, …, m。
由式(9)可得频段能量概率序列:P=[p1 p2 … pm],通过比较2个信号的频段能量概率序列可进行幅值相似度分析。文中选用db10小波包5层分解。
2.2 基于曼哈顿距离的幅值相似度分析文献[13]中基于Hausdorff距离构造幅值判据识别故障,其表示2个集合元素差值最小值中的最大值。曼哈顿平均距离为两点在标准坐标系上绝对轴距之和的平均值。相较而言,后者更能体现频段的整体性。
若信号向量X、Y经由式(7)—式(9)计算,得到的频段能量概率序列向量分别为P1、P2,则其幅值相似度可用曼哈顿平均距离,如式(10)所示。
| $ d\left(\boldsymbol{P}_1, \boldsymbol{P}_2\right)=\left(\sum\limits_{i=1}^m\left|p_{1 i}-p_{2 i}\right|\right) / m $ | (10) |
式中:P1=[p11 p12 … p1m];P2=[p21 p22 … p2m]。
对幅值相似度进行归一化处理后,可以得到式(11)。
| $ r(\boldsymbol{X}, \boldsymbol{Y})=\frac{1}{1+d\left(\boldsymbol{P}_1, \boldsymbol{P}_2\right)}=\frac{1}{1+\left(\sum\limits_{i=1}^m\left|p_{1 i}-p_{2 i}\right|\right) / m} $ | (11) |
式(11)中r的区间为[0, 1],r值越大代表幅值相似度越高。
2.3 基于余弦相似度的波形相似度分析前文给出了利用幅值相似度判定故障区段的算法,但当故障合闸角过小或接地电阻过大时,依赖单一的幅值判据有可能发生误判,因此引入余弦相似度算法。
余弦相似度通过计算两向量夹角的余弦值来反映向量轨迹的变化趋势[24],只与方向有关,可用于比较两波形之间的相似度。
信号向量X、Y经小波包j层分解后分别产生m=2j个频段,则X、Y相对应的2个频段x=[x1 x2…xw]与y=[y1 y2 … yw]间的余弦相似度可用式(12)计算。
| $ \cos (\boldsymbol{x}, \boldsymbol{y})=\frac{\boldsymbol{x} \cdot \boldsymbol{y}}{\|\boldsymbol{x}\|\|\boldsymbol{y}\|}=\frac{\sum\limits_{i=1}^w x_i y_i}{\sqrt{\sum\limits_{i=1}^w x_i^2} \sqrt{\sum\limits_{i=1}^w y_i^2}} $ | (12) |
式中:w为采样点数。
cos(x, y)∈(-1, 1),值越大,表示两向量间的夹角越小,两向量越相似。由于信号向量X、Y分别有m个频段,利用式(12)将以上频段依次进行余弦相似度比较,从而得到m个余弦相似度。为使波形相似度的取值区间落在[0, 1]内,可作如下变形:
| $ c(\boldsymbol{X}, \boldsymbol{Y})=\frac{m+\sum\limits_{i=1}^m \cos \left(x_i, y_i\right)}{2 m} $ | (13) |
当c(X, Y)=0时,表示X、Y之间完全不同;当c(X, Y)=1时,表示X、Y之间的波形相似度极高。
2.4 综合相似度对幅值和波形相似度分别赋予权重系数,即可得到综合相似度,如式(14)所示。
| $ s(\boldsymbol{X}, \boldsymbol{Y})=\beta \times r(\boldsymbol{X}, \boldsymbol{Y})+(1-\beta) \times c(\boldsymbol{X}, \boldsymbol{Y}) $ | (14) |
式中:β为幅值相似度的权重系数,0≤β≤1。
为说明采用综合判据的原因,文中取图 4所示的理想情形进行分析。
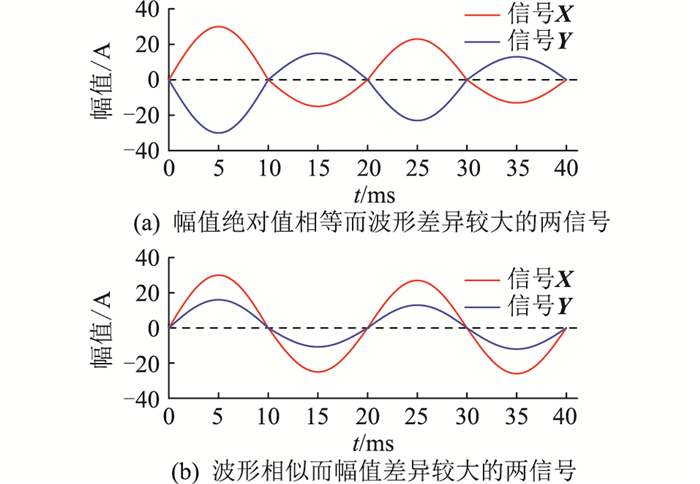
|
图 4 暂态零序电流信号 Fig. 4 Transient zero-sequence current signal |
幅值判据依赖于频段能量,当出现如图 4(a)所示的2个等值反向的电流信号时,幅值相似度为1,而波形完全相反。同理,在图 4(b)中,两信号的变化趋势一致,此时波形相似度很高而幅值相似度较低。出现上述情形时利用单一判据将有误判的可能。
设定相似度阈值sT.set,若某区段两端的综合相似度满足s < sT.set,即可判定为故障区段。
3 故障区段定位原理 3.1 故障选线发生单相接地故障时,故障线路与健全线路的暂态零序电流在幅值和波形等方面均存在着较大差异[15],因此可通过比较两两出线首个测量点间暂态电流的综合相似度来实现故障选线,与其余各条出线综合相似度最小的即为故障线路。而当故障馈线含有分支时还涉及到分支线路的选择问题。有分支馈线的简化拓扑如图 5所示。

|
图 5 含分支配电线路 Fig. 5 Distribution lines including branch |
当单相接地故障发生在f1处时,故障暂态电流大部分从故障点f1经点A流向母线,此时有s(A, B) < s(B, C),且s(A, B) < s(B, D)。其中,s(A, B)表示两测量点A、B之间暂态零序电流的综合相似度。若故障发生在f2处,电流大多经点B、点A流向母线,故有s(B, C) < s(C, E),且s(B, D) < s(D, F)。在故障点位于分支节点之前的情况下,选择任意一条支路计算均可定位出故障区段。
故障点f3位于分支线路,此时接地电流大部分由f3经点C、点B流向母线,故s(B, D) < s(B, C)。因此在确定分支线路时,应先计算分支节点前后测量点之间的零序电流综合相似度。当满足s(B, C)> s(B, D)时选择支路LG;反之,选择支路LH。
3.2 区段定位流程正确选择支路后,即可计算各个区段两端暂态零序电流的综合相似度,其值最小的判定为故障区段。若搜索到最末端检测点仍未确定故障区段,则判断故障位于该检测点下游区段。具体定位流程如图 6所示。
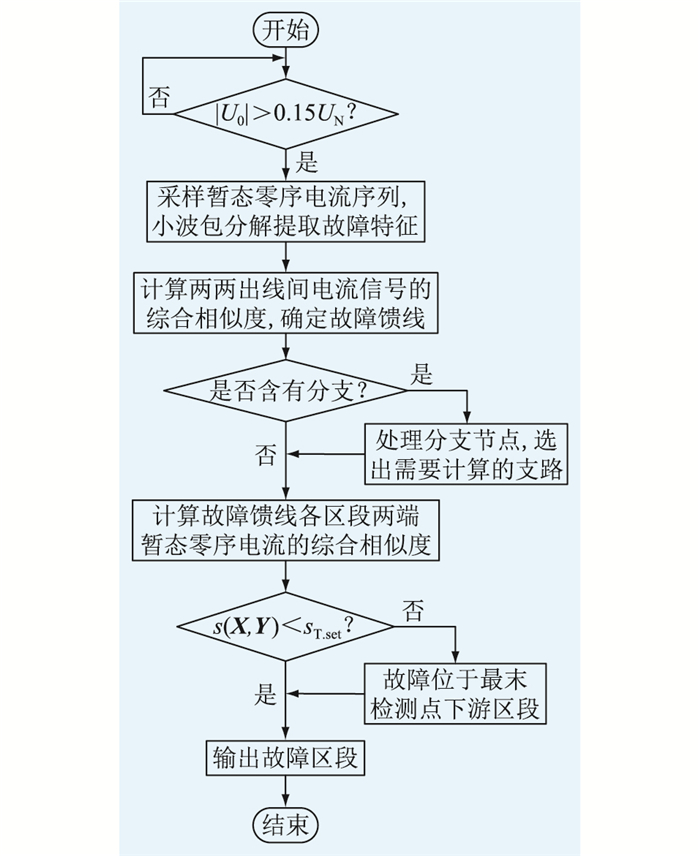
|
图 6 故障区段定位流程 Fig. 6 Flow chart of fault section location |
图 6中,监测终端的启动判据如式(15)所示。
| $ \left|U_0\right|>0.15 U_{\mathrm{N}} $ | (15) |
式中:U0为终端的零序电压;UN为额定电压。
sT.set的整定是依靠大量的仿真数据以及现场运行经验来确定的。文中通过大量的仿真数据得出:当故障发生在主线路时,健全区段的综合相似度均大于0.9,当涉及到分支线路的分流时,综合相似度均在0.8以上;而故障区段的综合相似度始终小于0.5。为保证文中算法在多分支线路也能准确定位,按式(16)进行整定。
| $ s_{\text {T.set }}=\frac{0.8}{K_{\mathrm{rel}}} $ | (16) |
式中:Krel取1.15(Krel的数值可由工程实际设定),可得sT.set=0.7。
4 仿真验证利用DIgSILENT PowerFactory仿真,搭建10 kV谐振接地系统,如图 7所示。系统共有4条出线,其中馈线L3含有分支线路。A1、A2、A、A3分别为各出线首端的电流测量点。同理,C、D为分支线路L31、L32首端的电流测量点。f1、f2、f3为文中算例设置的故障点。各出线的长度分别为:l1=8.5 km,l2=10 km,lAC=9.5 km,l31=11 km,l32=11 km,l4=11.5 km。线路采用NA2XSY 1×300 rm 6/10 kV ir模型,具体参数如表 1所示。消弧线圈过补偿,负荷采用三角形接法,各线路所接负荷均为2+j0.66 MV ·A。DG分别接在线路L1和L31上。配置有监测终端μPMU的节点为A、B、C、D、E和F,在图中用黑色节点表示。其中,A位于馈线出口,C、D位于分支线路出口,E为DG接入节点,B、F设为重要用户节点,均要配置监测终端。
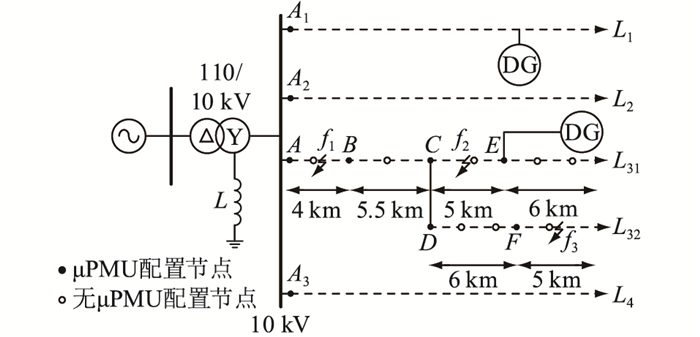
|
图 7 仿真系统模型 Fig. 7 Simulation system model |
|
|
表 1 单位长度线路参数 Table 1 Line parameters in unit length |
在馈线L3中,设置多种故障条件下的单相(A相)接地故障,采样频率取10 kHz。利用db10小波包对故障后1.5个周波的暂态零序电流进行分解,再经式(8)—式(14)计算可得到综合相似度。
4.1 主干线路故障算例1中,单相接地故障发生在区段(A, B)的中点f1处,过渡电阻Rg=2 kΩ,故障初相角φ=0°。
首先,进行故障选线;其次,采样各出线首个测量点的暂态零序电流,L1—L4对应的测量点分别为A1、A2、A和A3;最后,进行数据处理后输入Matlab计算综合相似度,结果如表 2所示。
|
|
表 2 两两线路间综合相似度 Table 2 Comprehensive similarity between two lines |
由表 2可知,L3的首个测量点A与其余各测量点的综合相似度明显小于其余测量点间的综合相似度,因此判定L3为故障馈线。
由于故障发生在主线路,因此选择任意一条支路计算均可定位出故障区段,选取支路L31。对L31各区段两端的暂态零序电流进行相似度计算,最终的定位结果如表 3所示。
|
|
表 3 算例1故障定位结果 Table 3 Fault location result under the first example |
表 3仅列出了β取0、0.6和1时的情况,进一步的,综合相似度随β变化的曲线如图 8所示。
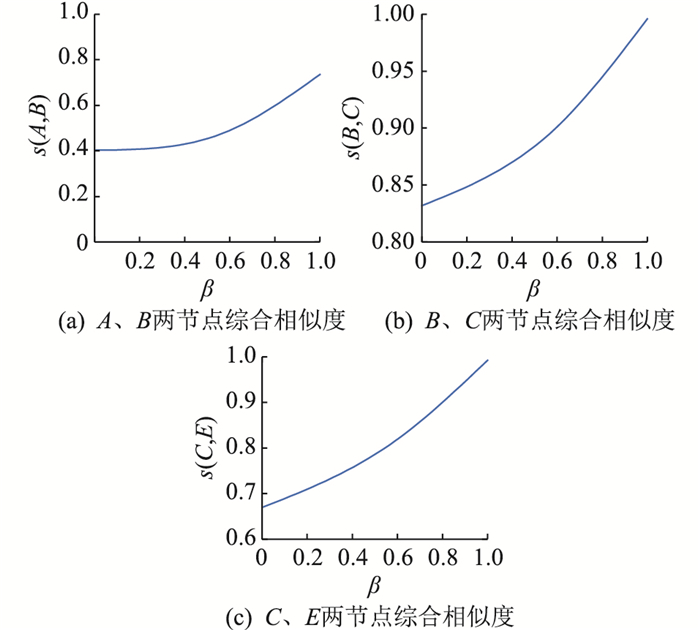
|
图 8 算例1综合相似度曲线 Fig. 8 Comprehensive similarity curves under the first example |
由表 3可知,当故障合闸角为0°且高阻接地时,利用单一的幅值或波形判据会导致误判。同时,故障区段两端暂态电流的极性关系易受外界因素的干扰而不一定呈负相关[25],相较而言,幅值关系的成立更加稳定,因此取β>0.5。结合图 8进一步分析,综合相似度随β增大而增大的速度逐渐变快,即使故障条件较为严苛,β=0.6时故障区段和健全区段的综合相似度就有较明显的区分,而β过大时有可能造成定位失败,因此文中选取β=0.6。
4.2 分支线路故障算例2中,故障f2位于区段(C, E)的中点,故障初相角为0°,过渡电阻为10 Ω。
按照与算例1相同的步骤,确定故障馈线为L3。接下来对分支节点进行处理,可通过计算得到s(B, C)=0.932>s(B, D)=0.403,L31为本算例选取的支路。计算L31各个区段两端暂态零序电流的综合相似度,定位结果如表 4所示。
|
|
表 4 算例2故障定位结果 Table 4 Fault location result under the second example |
表 4中,由于s(C, E)=0.422 < 0.7,而其余全部区段的综合相似度均大于设定阈值,因此可判定故障发生在(C, E)区段,与实际故障区段相符。
4.3 线路末端故障上述算例讨论主干、分支线路发生故障情况。算例3将故障点f3设置在线路L32末端区段(F-),过渡电阻为200 Ω,故障初相角为0°。
判断出故障发生在馈线L3后,可通过计算可得:s(B, D)=0.916>s(B, C)=0.404。支路选取L32,根据定位算法得到的结果如表 5所示。
|
|
表 5 算例3故障定位结果 Table 5 Fault location result under the third example |
由表 5可知,末端故障发生后,其线路各检测点的暂态零序电流相似度高,计算得到的综合相似度s均大于设定阈值,因此判定线路最末区段(F-)发生故障。算例3验证了文中方法对线路末端故障的适用性。
5 适用性分析 5.1 不同过渡电阻改变算例1发生单相接地故障时的过渡电阻,支路选择结果如表 6所示,故障定位结果如表 7和表 8所示。
|
|
表 6 不同过渡电阻下支路选择结果 Table 6 Branch selection results under different transition resistances |
|
|
表 7 过渡电阻为10 Ω、300 Ω及1 500 Ω下定位结果 Table 7 Location results under different transitionresistance values of 10 Ω, 300 Ω and 1 500 Ω |
|
|
表 8 过渡电阻为3 000 Ω下定位结果 Table 8 Location results under transition resistance value of 3 000 Ω |
由表 7和表 8可知,随着过渡电阻的增大,故障区段的综合相似度有所增大,而健全区段有所减小。当阻值大到一定程度后,s值基本保持不变,在高阻接地时也可实现准确定位。
5.2 不同故障初始角设置算例2在不同的故障初始角下发生单相接地故障,支路选择结果如表 9所示,故障定位结果如表 10所示。
|
|
表 9 不同故障初始角下支路选择结果 Table 9 Branch selection results at different initial fault angles |
|
|
表 10 不同故障初始角下定位结果 Table 10 Location results at different initial fault angles |
由表 10可知,在不同的故障初始角下,健全区段归一化后的综合相似度在0.9附近,明显高于故障区段的综合相似度(0.4附近)。根据综合相似度能准确区分出故障区段。
5.3 不同运行工况分析5.3节将在不同工况下进行仿真以验证文中方法的适用性,选取不同支路后的定位结果如表 11和表 12所示。
|
|
表 11 选取支路为L31下的定位结果 Table 11 Location results under the selected branch L31 |
|
|
表 12 选取支路为L32下的定位结果 Table 12 Location results under the selected branch L32 |
由表 11和表 12可知,在不同的故障条件下,故障区段两端的暂态电流信号均满足s < sT.set,健全区段均满足s>sT.set,且两者之间有较大差异。由此表明文中所提定位方法适应性好,灵敏度高。
6 现场数据验证图 9为南沙站10 kV沙32利民线示意。利用区段(5, 8)发生单相接地故障时的录波数据对文中方法进行验证,定位结果如表 13所示。
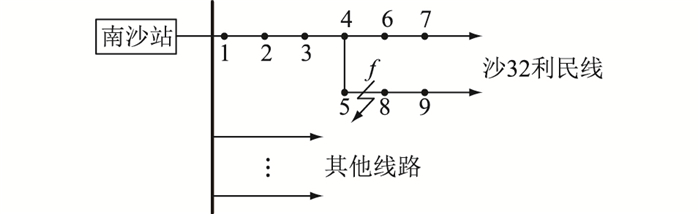
|
图 9 南沙站10 kV沙32利民线示意 Fig. 9 10 kV Sha32limin line of Nansha station |
|
|
表 13 现场故障区段定位结果 Table 13 Results of fault section location in field |
由表 13可知,故障区段为(5, 8),与实际故障位置一致,证明了文中方法在现场应用的有效性。
7 结语文中通过分析得出,当DG高压侧采用中性点不接地方式时,现有的利用暂态零序信号进行故障定位的方法仍然适用。在此基础上,提出了基于故障区段两端暂态零序电流相似度的单相接地故障定位方法。该方法利用μPMU采集故障后1.5个周波的暂态零序电流,随后进行小波包分解,分别利用曼哈顿平均距离、余弦相似度算法求得其幅值和波形相似度,最后计算综合相似度得到定位结果。
仿真数据表明,所提方法在故障初相角较小以及高阻接地时均有较好的适应性。同时该方法只对零序电流进行采样,且对采样频率要求不高。现场数据也验证了算法的可靠性。综上,文中所提方法的适用范围广,灵敏度高,具有较好的实用价值。
文中未涉及发生单相接地故障后逆变器的响应策略,其对故障定位的影响将在未来的研究中深入探讨。
致谢
本文得到合肥综合性国家科学中心能源研究院项目(21KZS211)资助,谨此致谢!
| [1] |
刘志文, 董旭柱, 邹林, 等. 基于零序电流衰减周期分量的高阻接地故障区段定位[J]. 电力系统自动化, 2020, 44(7): 161-168. LIU Zhiwen, DONG Xuzhu, ZOU Lin, et al. Section location method for high impedance grounding fault based on declining periodic component of zero sequence current[J]. Automation of Electric Power Systems, 2020, 44(7): 161-168. (  0) 0) |
| [2] |
刘斯琪, 喻锟, 曾祥君, 等. 基于零序电流幅值连调的小电流接地系统故障区段定位方法[J]. 电力系统保护与控制, 2021, 49(9): 48-56. LIU Siqi, YU Kun, ZENG Xiangjun, et al. Fault location method of a non-effective earthed system based on zero sequence current amplitude continuous regulation[J]. Power System Protection and Control, 2021, 49(9): 48-56. (  0) 0) |
| [3] |
杨涛, 金华锋, 曾兵元, 等. 能量法小电流接地方向判据的应用研究[J]. 电力系统保护与控制, 2022, 50(18): 116-122. YANG Tao, JIN Huafeng, ZENG Bingyuan, et al. Application of the criterion of small current grounding direction of the energy method[J]. Power System Protection and Control, 2022, 50(18): 116-122. (  0) 0) |
| [4] |
邵文权, 程畅, 卫晓辉, 等. 利用暂态电流Hausdorff距离的谐振配电网故障选线方案[J]. 电力系统保护与控制, 2022, 50(8): 33-42. SHAO Wenquan, CHENG Chang, WEI Xiaohui, et al. Fault line selection scheme using the Hausdorff distance of transient current in resonant distribution networks[J]. Power System Protection and Control, 2022, 50(8): 33-42. (  0) 0) |
| [5] |
魏科文, 张靖, 何宇, 等. 基于VMD和相关性聚类的谐振接地系统单相接地故障选线[J]. 电力系统保护与控制, 2021, 49(22): 105-113. WEI Kewen, ZHANG Jing, HE Yu, et al. Single-phase grounding fault line selection in a resonant grounding system based on VMD and correlation clustering[J]. Power System Protection and Control, 2021, 49(22): 105-113. (  0) 0) |
| [6] |
MIRSHEKALI H, DASHTI R, KESHAVARZ A, et al. A novel fault location methodology for smart distribution networks[J]. IEEE Transactions on Smart Grid, 2021, 12(2): 1277-1288. (  0) 0) |
| [7] |
张乃刚, 张加胜, 郑长明, 等. 基于零序电流幅值分布相似性的小电流接地故障定位方法[J]. 电力系统保护与控制, 2018, 46(13): 120-125. ZHANG Naigang, ZHANG Jiasheng, ZHENG Changming, et al. Fault section location based on similarity of zero sequence current amplitude distribution in non-solidly-earthed network[J]. Power System Protection and Control, 2018, 46(13): 120-125. (  0) 0) |
| [8] |
TASHAKKORI A, WOLFS P J, ISLAM S, et al. Fault location on radial distribution networks via distributed synchronized traveling wave detectors[J]. IEEE Transactions on Power Delivery, 2020, 35(3): 1553-1562. (  0) 0) |
| [9] |
陈洁羽, 左宝峰, 谈震, 等. 配电网单相接地快速处置装置运行情况研究[J]. 智慧电力, 2022, 50(2): 75-81. CHEN Jieyu, ZUO Baofeng, TAN Zhen, et al. Operation analysis of rapid disposal device for single-phase grounding fault in distribution network[J]. Smart Power, 2022, 50(2): 75-81. (  0) 0) |
| [10] |
XIE L W, LUO L F, LI Y, et al. A traveling wave-based fault location method employing VMD-TEO for distribution network[J]. IEEE Transactions on Power Delivery, 2020, 35(4): 1987-1998. (  0) 0) |
| [11] |
汤涛, 黄纯, 江亚群, 等. 基于高低频段暂态信号相关分析的谐振接地故障选线方法[J]. 电力系统自动化, 2016, 40(16): 105-111. TANG Tao, HUANG Chun, JIANG Yaqun, et al. Fault line selection method in resonant earthed system based on transient signal correlation analysis under high and low frequencies[J]. Automation of Electric Power Systems, 2016, 40(16): 105-111. (  0) 0) |
| [12] |
管廷龙, 薛永端, 徐丙垠. 基于故障相电压极化量的谐振接地系统高阻故障方向检测方法[J]. 电力系统保护与控制, 2020, 48(23): 73-81. GUAN Tinglong, XUE Yongduan, XU Bingyin. Method for detecting high-impedance fault direction in a resonant grounding system based on voltage polarization of the fault phase[J]. Power System Protection and Control, 2020, 48(23): 73-81. (  0) 0) |
| [13] |
李振兴, 王朋飞, 王新, 等. 基于幅值特征和Hausdorff距离的配电网故障定位方法[J]. 电力系统自动化, 2020, 44(7): 169-177. LI Zhenxing, WANG Pengfei, WANG Xin, et al. Fault location method of distribution network based on amplitude feature and Hausdorff distance[J]. Automation of Electric Power Systems, 2020, 44(7): 169-177. (  0) 0) |
| [14] |
WANG X W, ZHANG H X, SHI F, et al. Location of single phase to ground faults in distribution networks based on synchronous transients energy analysis[J]. IEEE Transactions on Smart Grid, 2020, 11(1): 774-785. (  0) 0) |
| [15] |
徐艳春, 赵彩彩, 孙思涵, 等. 基于改进LMD和能量相对熵的主动配电网故障定位方法[J]. 中国电力, 2021, 54(11): 133-143. XU Yanchun, ZHAO Caicai, SUN Sihan, et al. Fault location for active distribution network based on improved LMD and energy relative entropy[J]. Electric Power, 2021, 54(11): 133-143. (  0) 0) |
| [16] |
NIU L, WU G Q, XU Z S. Single-phase fault line selection in distribution network based on signal injection method[J]. IEEE Access, 2021, 9: 21567-21578. (  0) 0) |
| [17] |
CHEN B C, YU N, CHEN B, et al. Fault location for underground cables in ungrounded MV distribution networks based on ZSC signal injection[J]. IEEE Transactions on Power Delivery, 2021, 36(5): 2965-2977. (  0) 0) |
| [18] |
薛艳静, 徐岩, 程姝. 基于电流变化的环状直流配电网故障定位方法[J]. 智慧电力, 2021, 49(2): 76-82, 98. XUE Yanjing, XU Yan, CHENG Shu. Fault location method of ring DC distribution network based current variation[J]. Smart Power, 2021, 49(2): 76-82, 98. (  0) 0) |
| [19] |
KIAEI I, LOTFIFARD S. Fault section identification in smart distribution systems using multi-source data based on fuzzy petri nets[J]. IEEE Transactions on Smart Grid, 2020, 11(1): 74-83. (  0) 0) |
| [20] |
DU Y, LIU Y D, SHAO Q Z, et al. Single line-to-ground faulted line detection of distribution systems with resonant grounding based on feature fusion framework[J]. IEEE Transactions on Power Delivery, 2019, 34(4): 1766-1775. (  0) 0) |
| [21] |
PENG H, WANG J, MING J, et al. Fault diagnosis of power systems using intuitionistic fuzzy spiking neural P systems[J]. IEEE Transactions on Smart Grid, 2018, 9(5): 4777-4784. (  0) 0) |
| [22] |
叶雨晴, 马啸, 林湘宁, 等. 基于SOP的主动式谐振接地配电网单相接地故障区段定位方法[J]. 中国电机工程学报, 2020, 40(5): 1453-1465. YE Yuqing, MA Xiao, LIN Xiangning, et al. Active fault locating method based on SOP for single phase grounding faults in the resonant grounding distribution network[J]. Proceedings of the CSEE, 2020, 40(5): 1453-1465. (  0) 0) |
| [23] |
秦苏亚, 薛永端, 刘砾钲, 等. 有源配电网小电流接地故障暂态特征及其影响分析[J]. 电工技术学报, 2022, 37(3): 655-666. QIN Suya, XUE Yongduan, LIU Lizheng, et al. Transient characteristics and influence of small current grounding faults in active distribution network[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 655-666. (  0) 0) |
| [24] |
王聪博, 贾科, 毕天姝, 等. 基于暂态电流波形相似度识别的柔性直流配电线路保护[J]. 电网技术, 2019, 43(10): 3823-3832. WANG Congbo, JIA Ke, BI Tianshu, et al. Protection for flexible DC distribution system based on transient current waveform similarity identification[J]. Power System Technology, 2019, 43(10): 3823-3832. (  0) 0) |
| [25] |
刘渝根, 王建南, 马晋佩, 等. 结合小波包变换和5次谐波法的谐振接地系统综合故障选线方法[J]. 高电压技术, 2015, 41(5): 1519-1525. LIU Yugen, WANG Jiannan, MA Jinpei, et al. Comprehensive fault line selection method for resonant grounded system com-bining wavelet packet transform with fifth harmonic method[J]. High Voltage Engineering, 2015, 41(5): 1519-1525. (  0) 0) |
2. The Energy Research Institute of Hefei Comprehensive National Science Center, Hefei 230031, China;
3. State Grid Wuhu Power Supply Company of Anhui Electirc Power Co., Ltd., Wuhu 241000, China
 2023, Vol. 42
2023, Vol. 42


 陶维青(1964), 男, 硕士, 副教授, 研究方向为电力系统自动化(E-mail:
陶维青(1964), 男, 硕士, 副教授, 研究方向为电力系统自动化(E-mail: