文章编号: 2096-3203(2023)01-0169-09 中图分类号: TM726
交联聚乙烯(cross-linked polyethylene,XLPE)电力电缆因电气、理化性能优良,传输容量大,重量较轻,易于安装和维护等优点被广泛应用于交、直流输电系统[1-3]。XLPE绝缘可耐受的长时间工作温度为90 ℃,载流量大小对导体温度有较大影响,当电缆载流量较大时易造成导体温度过高,加快电缆绝缘结构和性能的劣化,缩短电缆的使用年限。当电缆载流量过低时导体材料得不到充分利用,将造成资源浪费和传输能力的下降[4-5]。因此在电缆实际敷设过程中,电缆载流量的正确计算有利于电缆安全、可靠地运行。
常见的电缆载流量计算手段主要包括试验、解析计算和数值计算[6-8]。文献[9]通过将直埋电缆本体钻孔,利用热电偶测量电缆本体各层温度,在实验室组建一套可监测电缆载流量及导体温度的实验系统,给电缆载流量计算提供较为准确的实验数据,但试验成本较高且试验过程复杂,在实际工程中应用较少。解析计算(基于IEC 60287标准制定的等效热路法)是在大地表面和电缆表面均为恒温面且叠加定理可用的假定基础上计算电缆载流量。因地下电缆敷设环境的复杂化,使得计算结果往往并不准确,文献[10]利用解析计算和数值计算2种方法对直埋敷设单芯电缆的温度场与载流量进行计算,得出解析计算结果误差较大,数值计算能构建较复杂且符合实际电缆敷设环境的模型被广泛使用。目前数值计算主要包括有限差分法[11-12]、有限容积法[13-14]、边界元法和有限元法[15]等,前3种方法很难处理复杂敷设条件下电缆的边界处网格剖分,有限元法综合有限差分法和变分法的优点,对于不同敷设环境的电缆边界处网格均可剖分,成为近年来计算和分析电缆温升与载流量的主要方法[16]。
土壤热阻及温度、空气温度、电缆埋设深度、相邻电缆间距离、热源等各种因素都会对直埋电缆载流量产生影响。改变电缆敷设环境以达到提升电缆载流量是输电线路工程的关键[17]。影响直埋敷设电缆散热的主要因素是土壤热阻,随土壤热阻系数的增大,载流量是非线性降低的,且变化速度越来越慢[18-21]。土壤温度的高低会对电缆散热产生影响,温度较低时电缆发散出的热量容易传递到土壤,土壤温度较高时则反之,载流量随土壤的温升呈线性下降的变化规律[18-21],相同材质的导体,电缆载流量随敷设回路的增多而降低,铜导体的载流能力要比铝导体强,且在土壤温度不变的条件下,敷设的回路数越少,载流量越高[22]。空气温度影响土壤与周围空气的对流换热能力,土壤与周围空气的对流换热能力随空气温度的升高而减弱,因而电缆载流量随空气温度升高呈线性下降趋势[18-21],相同材质的导体,回路数越多,载流量越低,在相同空气温度下,铜导体的载流能力比铝导体要高[22]。电缆埋设深度会影响电缆的载流量,埋设深度增加时,电缆的散热性变差,电缆载流量随埋设深度呈下降趋势,但埋设深度的增加对载流量的影响会越来越小[18-20];相同的埋设深度,单回路敷设时电缆的载流量远高于双回路和三回路敷设的情况[22]。电缆之间距离的增加有利于电缆散热,使导体温度降低来提升电缆载流量,随电缆之间距离的增加,电缆载流量也在增大,但电缆间距越大时对电缆载流量的影响越小[15, 19-20]。在电缆间距不变的条件下,电缆敷设的回路越多,载流量越小;相邻电缆的间距较小时,铝导体单回路敷设的电缆载流量要比铜导体三回路敷设时高,但随电缆间距的增大,铜导体电缆三回路敷设的载流量远大于铝导体电缆单回路敷设时情况[22]。当电缆周围存在外热源时,以热水管为例,设定热水管边界温度恒定不变,因热水管的存在,电缆载流量在降低,且热水管距离电缆越近时对电缆的散热影响越大,载流量越低[19]。直埋敷设时电缆的排列方式也会影响电缆的载流量,电缆水平排列时散热效果要强于三角形排列的情况,故水平排列时电缆的载流量较大[21]。
上述研究主要考虑土壤热阻、土壤温度、空气温度、电缆埋设深度、电缆间距、热源等因素对直埋电缆载流量的影响。在电力电缆的直埋敷设过程中,施工单位一般会在电缆周围回填沙土防止土壤水分流失对电缆载流量造成影响,加设混凝土盖板、加装套管等措施防止外界机械力对电缆造成损坏[4, 19]。电缆敷设规程对于直埋敷设仅提及回填沙土、加盖保护板、加设套管,但具体对回填的厚度及保护板厚度并未给出明确说明,对加设套管后的直埋电缆温度场与载流量分析仍鲜有研究。
文中以110 kV电力电缆作为研究对象,建立基于电磁场、热场和流体场的多物理场耦合仿真模型,重点研究回填沙土的干湿程度及回填厚度、加设保护盖板及其厚度、加装套管及填充套管内气隙对电缆温度场的变化情况,同时利用迭代法对上述3种情况的载流量数值进行计算和对比,分析不同敷设条件下载流量变化的原因,为运行部门在考虑提升电缆载流量时选择回填沙土干湿程度和厚度、加盖保护板厚度及套管内填充材料的选取提供一定参考。
1 电力电缆载流量数值计算原理实际电缆的运行环境较为复杂,因此在建立仿真模型时,考虑到敷设条件的不同,所选取的物理场就会有所不同,计算电缆载流量所需的耦合场也会不同。
当电力电缆直接埋于土壤时,其热量的传递主要是以热传导为主,即使考虑到在直埋电缆周围回填沙土、加盖保护板等情况,导热方式也是以热传导为主。此时,须耦合电磁场和热场对电缆温度场与载流量进行计算。
当电缆穿管埋地敷设时,由于电缆与套管内壁之间存在着空气流动,在进行电缆温度场与载流量计算时应考虑热传导、热对流和热辐射3种导热方式,其中电缆本体、套管与土壤之间以热传导方式导热,套管内空气与套管内壁、电缆表面与套管表面间主要以热对流和热辐射方式导热。此时,须耦合电磁场、热场和流体场。若在套管内填充固体填充物时,则不用考虑热对流,只须进行电磁场和热场的耦合。
1.1 电力电缆电磁场模型电缆正常运行时周边电磁场视为稳定的电磁场,电缆导体表面i电导率γi随温度的变化规律[23]如式(1)所示。
| $ \gamma_i=\frac{1}{\rho_{20}\left[1+\alpha_{20}\left(T-T_{20}\right)\right]} $ | (1) |
式中:ρ20为20 ℃时导体的电阻率;α20为导体电阻温度系数;T为温度;T20取20 ℃。
1.2 电力电缆温度场模型相对于电缆截面而言,电缆长度近似无穷大,地下直埋电缆温度场可简化为二维稳态温度场模型进行计算和分析[24-25]。电缆含有内热源(如电缆导体、电缆金属屏蔽、电缆铠装)区域的导热微分方程[24]如式(2)所示,不含内热源(如电缆绝缘层、半导电层、外护套层、土壤层)区域的导热微分方程[24]如式(3)所示。
| $ \frac{\partial^2 T}{\partial x^2}+\frac{\partial^2 T}{\partial y^2}+q_v=0 $ | (2) |
| $ \frac{\partial^2 T}{\partial x^2}+\frac{\partial^2 T}{\partial y^2}=0 $ | (3) |
式中:qv为内热源。
对于穿管敷设情况,电缆表面与套管表面间存在热辐射的传热微分方程[23]如式(4)所示。
| $ Q_i=\delta \varepsilon_i F_{i j} A_i\left(T_i^2+T_j^2\right)\left(T_i+T_j\right)\left(T_i-T_j\right) $ | (4) |
式中:Qi为表面i的传热率;δ为Stefan-Bolzman常数;εi为表面i的有效热辐射率;Fij为表面i表面j的角系数;Ai为表面i的面积;Ti、Tj分别为表面i、表面j的绝对温度值。
1.3 电力电缆流体场模型穿管敷设的电力电缆,套管内部存在空气流动,根据流体力学理论,套管内空气的自然对流遵循质量、动量和能量守恒定律[25]。具体的控制方程如式(5)—式(7)所示[23]。
| $ \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0 $ | (5) |
| $ \left\{\begin{array}{c} \rho\left(u \frac{\partial u}{\partial x}+v \frac{\partial u}{\partial y}\right)=-\frac{\partial p}{\partial x}+\eta\left(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}\right)+ \\ \rho g \beta\left(T-T_{\mathrm{r}}\right) \cos \theta \\ \rho\left(u \frac{\partial v}{\partial x}+v \frac{\partial v}{\partial y}\right)=-\frac{\partial p}{\partial y}+\eta\left(\frac{\partial^2 v}{\partial x^2}+\frac{\partial^2 v}{\partial y^2}\right)+ \\ \rho g \beta\left(T-T_{\mathrm{r}}\right) \sin \theta \end{array}\right. $ | (6) |
| $ u \frac{\partial T}{\partial x}+v \frac{\partial T}{\partial y}-\lambda\left(\frac{\partial^2 T}{\partial x^2}+\frac{\partial^2 T}{\partial y^2}\right)=0 $ | (7) |
式中:u、v分别为空气在x、y轴上的流速;ρ为电缆空气密度;θ为重力加速度与x轴方向的夹角;β为空气膨胀系数;η为空气动力黏度;p为空气的压力标量;Tr为空气初始温度;λ为空气的导热系数;g为重力加速度。
1.4 边界条件的设定求解直埋敷设电力电缆及周围土壤温度场的分布,实则是对导热微分方程的求解,要确定对应的边界条件,在求解固体导热微分方程时包含多类边界条件,第一类边界条件已知边界上的温度场恒定,如式(8)所示;第二类边界条件已知边界上的热流密度,如式(9)所示;第三类边界条件已知边界上物体与周围环境流体间的对流换热系数h以及周围环境流体的温度Tf[10],如式(10)所示。
| $ \left.T(x, y)\right|_{\Gamma}=\left.f(x, y)\right|_{\Gamma} $ | (8) |
| $ -\left.\lambda \frac{\partial T}{\partial n}\right|_{\Gamma}=q $ | (9) |
| $ -\left.\lambda \frac{\partial T}{\partial n}\right|_{\Gamma}=h\left(T-T_{\mathrm{f}}\right) $ | (10) |
式中:f(x, y) Γ为物体边界Γ的壁面温度;q为热流密度。
文中研究的对象为单回路直埋敷设XLPE电缆,电缆型号为64/110 kV-YJLW-02-630 mm2,电缆导体间距为250 mm,电缆的敷设深度为1 m。现有研究表明,电缆发热对距离其2 m以外的土壤影响就很微弱,为不影响电缆周围的传热,应当将求解区域范围设置得足够大,当远离电缆20 m后土壤的温度不再受电缆发热的影响[12]。现为保证模型计算的准确性,选定距离电缆下方20 m处为土壤深层,认为该边界离电缆足够远,不再受电缆温度的影响,温度恒定不变,属于第一类边界条件;距电缆左右20 m处为土壤的左右边界,认为该边界离电缆足够远,热流密度无变化,属于第二类边界条件;土壤上边界与空气存在对流换热,属于第三类边界条件。
2 直埋电缆不同敷设条件下温度场与载流量计算结果 2.1 电力电缆模型的建立图 1为电缆模型结构示意图。

|
图 1 64/110 kV-YJLW-02-630 mm2结构示意 Fig. 1 Schematic diagram of the 64/110 kV-YJLW-02-630 mm2 laying structure |
在电缆载流量计算中,通常采用土壤导热系数1 W·m-1·K-1作为基准计算参数[6]。电缆各部分结构的几何尺寸和导热系数如表 1所示,电特性参数[23]如表 2所示。
|
|
表 1 电缆结构、尺寸及导热系数 Table 1 Cable structure, size and thermal conductivity |
|
|
表 2 磁-热耦合模型电特性参数 Table 2 Electrical characteristics of magnetic-thermal coupling model |
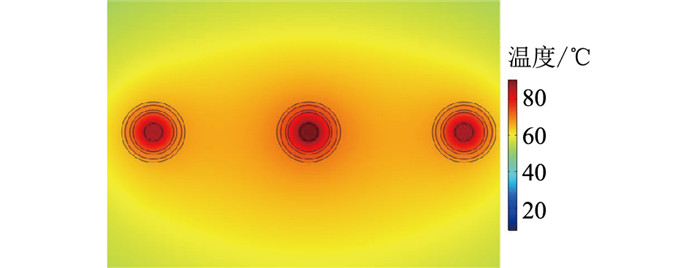
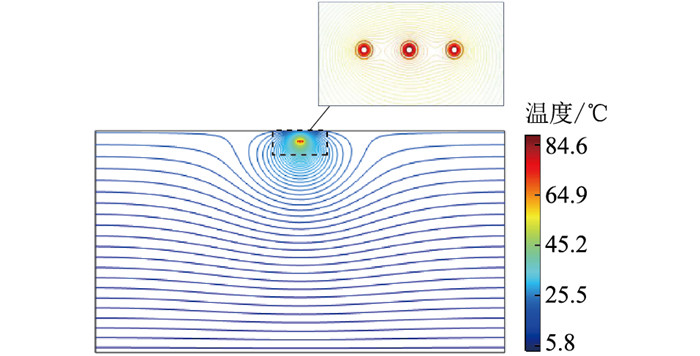
在实际电缆直埋敷设时为节约成本通常回填原状土壤,单回路电力电缆直埋于土壤,边界条件的设置如1.4节所示。当中间电缆导体的温度最高为90 ℃时,通过迭代法可得电缆载流量为938 A,其他两相电缆最高温度分别为85.87 ℃、86.16 ℃,电力电缆温度场分布如图 2所示,等温线分布如图 3所示。
|
图 2 直埋敷设电缆温度场分布 Fig. 2 Temperature field distribution for direct buried cables |
|
图 3 直埋敷设电缆等温线 Fig. 3 Isotherm diagram for direct buried cables |
由图 3可知,土壤深处的温度基本处于稳定,已不受电缆本体发热的影响,而在电缆本体及周围等温线分布较密集,受电缆发热的影响比较明显。左右两相电缆周边等温线分布比较对称,故温度相差不大。通过计算得知,在回填原状土壤时电缆载流量计算结果为938 A。
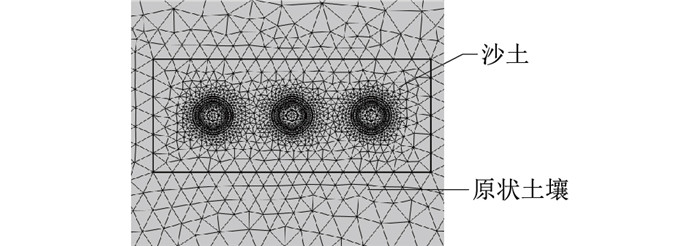
2.3 回填沙土时电缆的载流量计算根据电力工程电缆设计标准[4],电缆直埋敷设时会在电缆周围回填一层沙土以防止土壤自身水分迁移变化对载流量造成较大影响,但对于回填沙土的厚度及干湿程度并未给出明确说明。现为研究回填沙土及回填厚度对直埋电缆敷设时载流量的影响,沿电缆轴向上、下紧邻侧铺设厚度为100 mm的沙土,取潮湿沙土和干燥沙土的导热系数分别为2 W·m-1·K-1(含湿量15%)和1.5 W·m-1·K-1(含湿量9%)[26]。电缆的网格剖分如图 4所示。
|
图 4 添加回填土敷设电缆网格剖分 Fig. 4 Adding backfill to lay the cable grid profile |
除电缆本体超细化剖分之外,其他区域细化剖分,在不增加单元条件下更有利于精确计算电力电缆在电流作用下温度场的分布。
不改变其他敷设条件,回填沙土敷设时仍给电缆导体施加相同载流量938 A,得到三相电缆导体温度、载流量的计算如表 3所示。
|
|
表 3 回填沙土时三相电缆导体温度及载流量 Table 3 Three-phase cable conductor tempe-rature and current carrying capacity duringbackfilling with sandy soil |
由表 3可知,与回填原状土壤相比,回填潮湿沙土和干燥沙土时,电缆的载流量可分别提升4.48%、2.77%,三相电缆导体温度均有所下降,导体温度最高下降约为6.47 ℃和4.24 ℃。分析上述在不同回填情况下温度差异的原因在于:直埋敷设不管是否回填沙土,主要是固体间的热传导,电缆产生的热量通过土壤/沙土导热传递到周围环境,沙土的回填更有利于电缆散热,潮湿沙土的导热能力强于干燥沙土的导热能力,故在负荷保持不变的情况下,回填潮湿沙土敷设时的三相电缆产生的热量散热能力更强,更容易传递到周围环境,三相电缆导体温度相对较低,载流量最大。
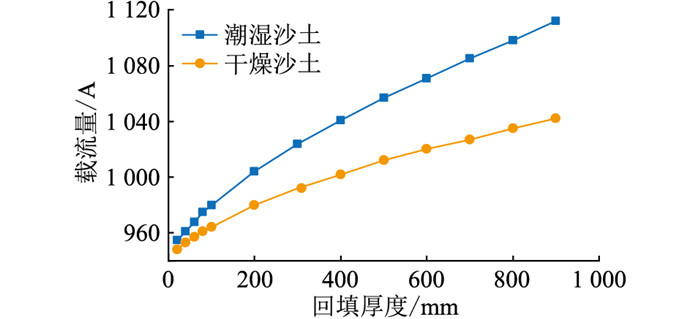
改变回填沙土的厚度,电缆载流量随沙土厚度的变化关系如图 5所示。
|
图 5 回填沙土时电缆载流量随沙土厚度的变化曲线 Fig. 5 Variation curve of cable carrying capacity with sand thickness when backfilling with sand |
由图 5可知,当回填沙土厚度在增加时,回填潮湿和干燥沙土时电缆载流量均在增加,回填厚度在100 mm范围内时,回填潮湿与干燥沙土的载流量差距较小,回填厚度超出100 mm之后差距逐渐变大。相比回填干燥沙土,回填潮湿沙土时电缆的载流量提升幅度更大,由955 A提升到1 112 A,回填干燥沙土时电缆载流量提升幅度不大,由948 A提升到1 024 A,呈非线性增长趋势,但均随着回填沙土厚度的增加对电缆载流量的影响变弱。
2.4 加盖保护板时电缆载流量计算结果分析在挖土施工过程中直埋电缆外护套可能会受到机械力的损坏,为保护电缆不受外力破坏会在回填沙土上方沿电缆全长覆盖宽度不小于电缆两侧各50 mm的保护板[4]。为研究加盖保护板及厚度的选取对电缆载流量的影响,文中选取混凝土材质保护板,其覆盖宽度超过电缆两侧各50 mm,保护板厚度为50 mm,导热系数为1.28 W·m-1·K-1,密度取2 400 kg·m-3,热容取970 J·kg-1·K-1,具体边界条件的选取与2.2节相同。当回填潮湿或干燥沙土时,通过迭代法计算可得加盖混凝土保护板后的电缆载流量分别为982 A、967 A,与不添加盖板时相比电缆载流量分别提升0.20%、0.31%。以回填干燥沙土为例,电缆温度场分布如图 6所示。
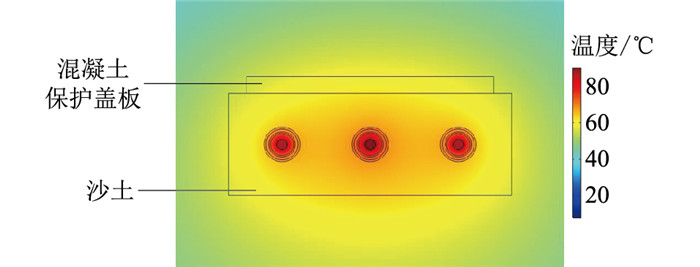
|
图 6 加盖混凝土盖板时电力电缆温度分布 Fig. 6 Temperature distribution of power cables when concrete cover is added |
采用迭代法计算选用不同厚度保护板时的电缆载流量,保护板厚度由50 mm增加到200 mm时,电缆载流量仅提升5 A,保护板厚度对电缆载流量的影响不大,因此在满足保护板自身强度且不影响电缆载流量大小的同时,从经济性方面考虑,合理选择混凝土保护板以保护电缆不受外力破坏。
2.5 穿管时电缆载流量计算结果分析对于35 kV及110 kV电压等级较高的电力电缆,为防止在挖掘地面时受到外部机械损伤,出于对电缆安全性、耐久度及防腐蚀性等方面考虑,要将电缆穿管后埋地敷设。电缆导体间距取300 mm,套管材料为聚氯乙烯材料,边界条件设置同2.2节。利用迭代法计算电缆载流量,当通入电流为813 A时,电缆及周围温度场分布如图 7所示,此时中间电缆导体的温度最高为90.1 ℃,左右两相电缆导体温度分别为87.10 ℃、87.64 ℃。与直埋于原状土壤时相比,左右两相导体温度略有上升(约1.39 ℃),电缆载流量下降约13.32%。
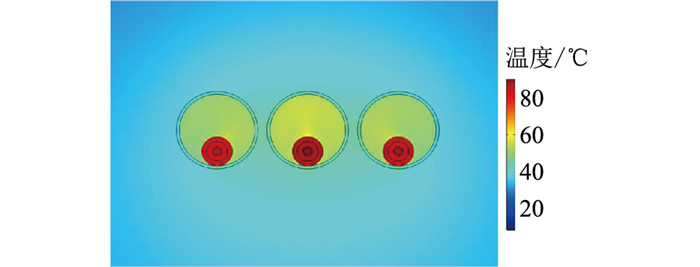
|
图 7 含有套管电缆直埋敷设温度分布 Fig. 7 Temperature distribution for direct burial of cables containing sleeves |
电缆载流量为813 A时套管内的空气流速见图 8。由图 8可知,套管中空气流速并不均匀,最高达到0.09 m/s,电缆本体周围空气流速较大,其原因为电缆导体与金属屏蔽作为主要热源产生的热量通过电缆表面与排管内空气进行对流换热,但由于排管内空气区域相对狭小,对流换热效率很低,且空气热阻远大于土壤热阻,这也是穿管敷设时载流量降低的原因。所以考虑通过填充电缆本体与套管之间的空隙以利于电缆的散热,提升电缆载流量。套管内的散热效果与填充的材料、填充方式密切相关,故2.5节研究三相电缆填充同一材料,仅中间相填充、三相不同填充时电缆载流量的变化,选择填充物提高载流量的同时,还要考虑填充物的经济性。
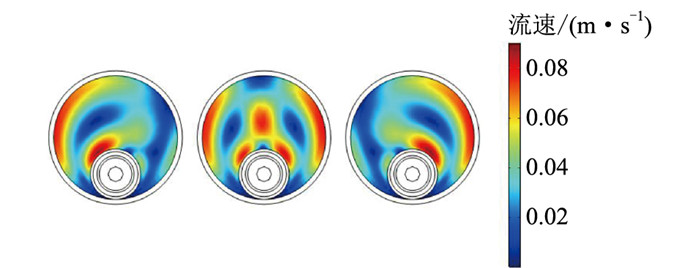
|
图 8 套管内空气流速 Fig. 8 Air flow rate in the casing |
在三相套管内填充同一材料,当电缆导体最高温度达到90 ℃时,电缆载流量随填充物导热系数变化关系见图 9。由图 9可知,填充物的导热系数在不超过1.5 W·m-1·K-1时电缆载流量随导热系数的增大而增长的速度较快,在超过1.5 W·m-1·K-1以后电缆载流量变化趋势相对较平缓。
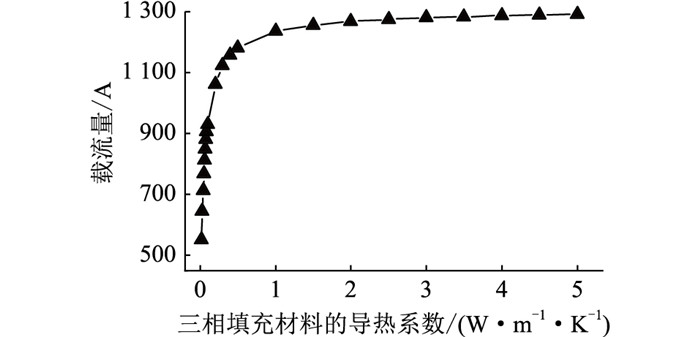
|
图 9 电缆载流量随三相填充物导热系数的变化关系 Fig. 9 Variation of cable current carrying capacity as a function of thermal conductivity of the three-phase filler |
以填充导热系数为1.5 W·m-1·K-1的干燥沙土为例,其电缆温度场分布如图 10所示,与无填充时的温度分布图 7对比可知,填充干燥沙土后电缆热量扩散更容易,而无填充时温度分布集中在电缆周围,热量很难扩散,使电缆载流量受到影响。当电缆导体最高温度达到90 ℃时,填充干燥沙土的载流量(1 255 A)相对于无填充时提高54.37%。
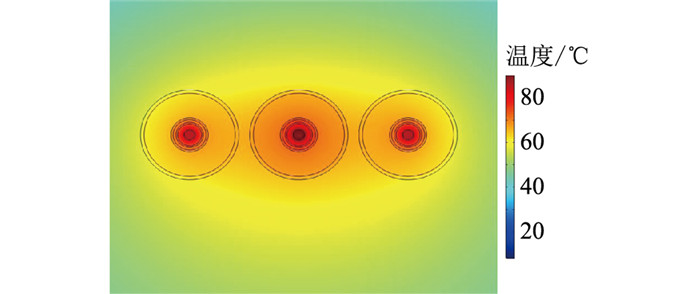
|
图 10 1.5 W·m-1·K-1干燥沙土填充三相电缆时的温度场分布 Fig. 10 Temperature field distribution for a 1.5 W·m-1·K-1dry sand filled three-phase cable |
电缆套管内无填充或填充相同材料时均为中间相电缆导体温度最高,所以考虑只在中间相填充高导热性材料而其他两相无填充的情况,通过迭代法计算得到电缆载流量随中间相填充物导热系数变化关系如图 11所示。
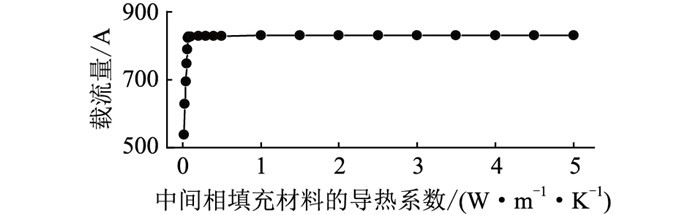
|
图 11 电缆载流量随中间相填充物导热系数的变化关系 Fig. 11 Variation of the cable current carrying capacity with the thermal conductivity of the intermediate phase filler |
由图 11可知,仅中间相填充与三相均填充时载流量的变化趋势相似,但中间相填充时的载流量提升幅度相对较小,随填充物导热系数的增加,电缆载流量由537 A提升到831 A。以1.5 W·m-1·K-1的干燥沙土填充物为例,计算得到电缆载流量为830 A,电缆的温度场分布如图 12所示。对比无填充、三相相同填充和中间相填充这3种情况的温度场分布图 7、图 10和图 12可知,仅中间相填充的散热效果优于无填充情况,但要比三相均填充时的散热效果差,且中间相填充时右侧电缆导体温度最先达到最高温度90 ℃,中间相电缆温度较低,载流量相比于无填充情况提升2.09%,明显低于三相相同填充情况。
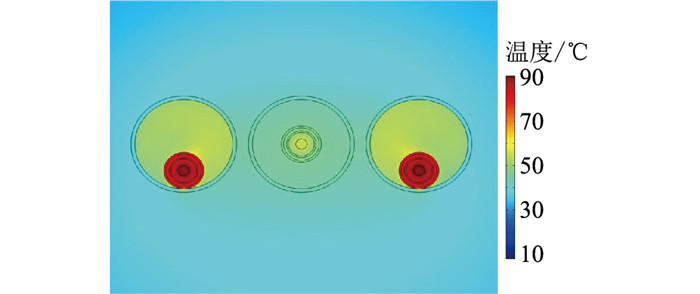
|
图 12 1.5 W·m-1·K-1干燥沙土填充中间相电缆时的温度场分布 Fig. 12 Temperature field distribution for 1.5 W·m-1·K-1dry sand filled intermediate phase cable |
由2.5.2节可知,仅中间相填充时载流量提升相对较低,所以考虑中间相填充高导热材料,左右两相电缆填充较廉价的土壤。
土壤导热系数取1 W·m-1·K-1,填充物导热系数取1.5 W·m-1·K-1时各情况载流量如表 4所示。
|
|
表 4 1.5 W·m-1·K-1时不同填充条件的载流量计算结果 Table 4 Calculation of the load capacity fordifferent filling conditions at 1.5 W·m-1·K-1 |
土壤导热系数取1 W·m-1·K-1,填充物的导热系数取3 W·m-1·K-1时各情况载流量如表 5所示。
|
|
表 5 3 W·m-1·K-1时不同填充条件的载流量计算结果 Table 5 Calculation of the load capacity fordifferent filling conditions at 3 W·m-1·K-1 |
由表 4可知,当填充物的导热系数取值为1.5 W·m-1·K-1时三相不同填充相比于无填充情况载流量提升53.75%,与三相相同填充情况的载流量提升54.37%差距很小。由表 5可知,当填充物的导热系数取值为3 W·m-1·K-1时三相不同填充的载流量提升55.84%,相比于三相相同填充载流量提升57.32%相差也很小。
由上述分析可知,三相不同填充可大幅度提升电缆载流量,且载流量的提升率与三相均填充高导热材料相差很小。所以可以在套管内填充导热性能较好的填充物来提升电缆的载流量,正如上述分析所采用导热系数为1.5 W·m-1·K-1的沙土就可以大幅度提升载流量。若选用沙土作为填充材料,其缺点也比较突出,当沙土凝结在套管中时会导致在电缆故障排查及检修时不易将电缆抽离,给维修人员带来不便。所以在选取高导热性能填充物提升电缆载流量时,还应该考虑该填充物应选取方便填入,容易抽离及可以多次回收利用的高导热性能材料。出于对经济性方面的考虑,可选择仅在中间相电缆填充高导热性能材料,其他两相填充较廉价的填充物以节约成本。
2.6 多种因素共同影响下的电缆载流量分析在实际工程中电缆穿管敷设可能会考虑在周围回填沙土及加盖保护板3种因素共同存在的情况,沙土及保护板的相关参数取值同2.4节。套管内无填充情况下电缆载流量随周围回填沙土及混凝土盖板厚度的变化规律如图 13所示。
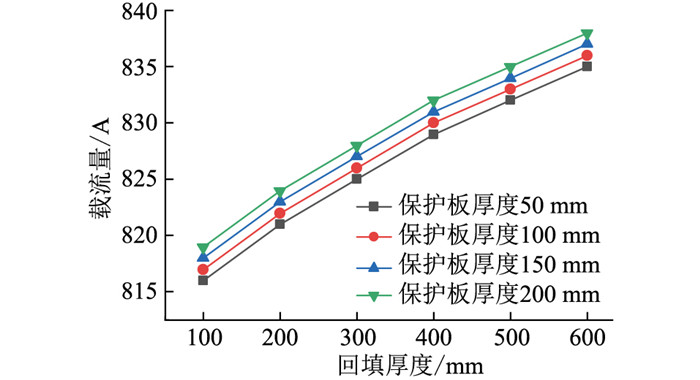
|
图 13 穿管电缆载流量随回填厚度及保护板厚度的变化关系 Fig. 13 Variation of cable load capacity withbackfill thickness and protection platethickness through the pipe |
由图 13可知,随着回填沙土厚度的增加,电缆载流量逐渐增大,回填厚度在100 mm~400 mm之间时,电缆载流量呈现近似线性的变化趋势,回填厚度大于400 mm后载流量提升幅度相对平缓,混凝土保护板厚度由50 mm增加到200 mm时,在相同回填厚度时电缆载流量仅提升约3 A,但与仅穿管敷设(813 A)时相比,回填沙土及加盖保护板有利于提升电缆载流量。
在考虑3种因素共同存在时,套管中不同填充方式下电缆载流量变化如图 14所示,保护板厚度取50 mm,回填干燥沙土厚度取100 mm,相关参数的选取同2.4节,套管中填充材料的选取同2.5节。
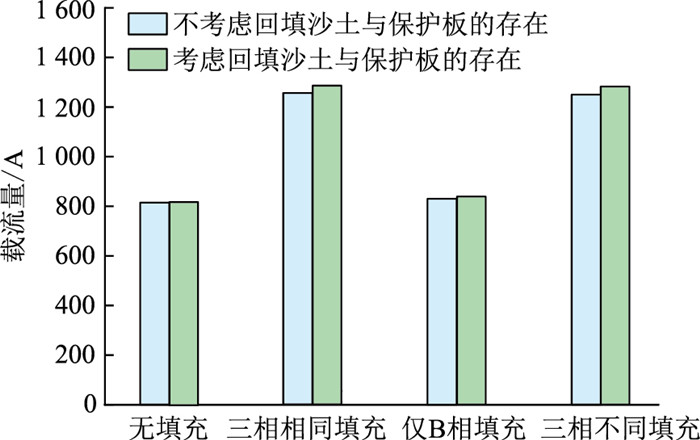
|
图 14 套管中不同填充方式下电缆载流量对比 Fig. 14 Comparison of cable load capacity under different filling methods in the casing |
由图 14可知,考虑3种因素共同作用时,套管中不同填充方式电缆载流量均有所提升,与不考虑上述因素时相比,三相相同填充和三相不同填充方式下电缆的载流量提升幅度最明显,分别为2.47%、2.56%,故填充方式的改变和回填沙土、加盖混凝土保护板都会提升电缆载流量。
3 结论文中采用Comsol有限元仿真软件构建110 kV电缆直埋敷设模型,在此基础上仿真计算单回路直埋电缆周围回填沙土、加盖混凝土保护板、装设电缆套管这3种情况的温度场与载流量,为提高直埋敷设电缆载流量提供思路和建议,得出以下结论:
(1) 电缆直埋于原状土壤时载流量为938 A,在电缆周围回填沙土时,电缆载流量随沙土厚度的增加而提升,但对载流量的影响减弱,因此在直埋敷设时可回填合适厚度的沙土以提升电缆载流量。
(2) 加盖混凝土保护板会提升电缆载流量,但提升的幅度不大(小于0.5%),保护板的厚度对电缆载流量的影响很小,因此在满足保护板自身强度且不影响电缆载流量大小的同时,从经济性方面考虑,合理选择混凝土保护板以保护电缆不受外力破坏。
(3) 穿管敷设时电缆的载流量为813 A,相比于直埋敷设下降约13.3%,因此可在套管内填充高导热材料以提升电缆载流量,填充方式及填充物导热系数的选取可为今后寻找和应用合适的填充材料提供参考。
(4) 在实际电缆敷设中提高电缆载流量的同时,出于经济性方面的考虑,可选择在中间相电缆套管中填充高导热材料,其余两相电缆填充廉价填充物以节约成本。
致谢
本文得到陕西省教育厅一般专项项目“不同敷设方式下XLPE电力电缆温度场与载流量仿真研究”(22JK0322),陕西理工大学研究生创新基金(SLGYCX2236)资助,谨此致谢!
| [1] |
李欢, 徐磊, 刘涛, 等. 直流XLPE电缆绝缘中空间电荷的抑制方法综述[J]. 电力工程技术, 2021, 40(5): 54-62. LI Huan, XU Lei, LIU Tao, et al. Summarization of space charge suppression methods in DC XLPE cable insulation[J]. Electric Power Engineering Technology, 2021, 40(5): 54-62. (  0) 0) |
| [2] |
黄之明, 傅明利, 郝艳捧, 等. 高压直流电缆热循环试验控温水槽三维仿真研究[J]. 中国电机工程学报, 2016, 36(11): 3133-3140. HUANG Zhiming, FU Mingli, HAO Yanpeng, et al. 3D simulation study on the water channel for temperature controlling of HVDC cable heat cycle test[J]. Proceedings of the CSEE, 2016, 36(11): 3133-3140. (  0) 0) |
| [3] |
LI J Y, LI H, WANG Q M, et al. Accelerated inhomogeneous degradation of XLPE insulation caused by copper-rich impurities at elevated temperature[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2016, 23(3): 1789-1797. DOI:10.1109/TDEI.2016.005142 (  0) 0) |
| [4] |
中华人民共和国住房和城乡建设部. 电力工程电缆设计标准: GB 50217—2018[S]. 北京: 中国计划出版社, 2018. Ministry of Housing and Urban-Rural Development of the People's Republic of China. Standard for design of cables of electric power engineering: GB 50217-2018[S]. Beijing: China Planning Press, 2018. (  0) 0) |
| [5] |
许志锋. 局部穿管电缆载流量评估与提升方法研究[D]. 广州: 华南理工大学, 2021. XU Zhifeng. Research on calculation and improvement methods for ampacity of cable installed in short-conduit[D]. Guangzhou: South China University of Technology, 2021. (  0) 0) |
| [6] |
王启隆, 王国海, 于竞哲, 等. 多种敷设方式下集群电缆的直流载流量仿真研究[J]. 高压电器, 2022, 58(6): 157-164. WANG Qilong, WANG Guohai, YU Jingzhe, et al. Research on simulation of DC current-carrying capacity of clustered cables laying under various laying modes[J]. High Voltage Apparatus, 2022, 58(6): 157-164. (  0) 0) |
| [7] |
徐涛, 王鹏宇, 徐研, 等. 110 kV电缆线路中间接头载流量实验研究及分析[J]. 绝缘材料, 2017, 50(1): 72-77, 83. XU Tao, WANG Pengyu, XU Yan, et al. Experiment and analysis on current-carrying capacity of 110 kV cable joint[J]. Insulating Materials, 2017, 50(1): 72-77, 83. (  0) 0) |
| [8] |
MALYSZKO O, ZENCZAK M. Current-carrying capacity of overhead power transmission lines in different weather conditions[C]//VXV International Symposium on Theoretical Engineering. Lübeck, Germany. VDE, 2009: 1-4.
(  0) 0) |
| [9] |
雷鸣. 依据表皮温度准确计算单芯高压电缆线芯温度的理论及实验研究[D]. 广州: 华南理工大学, 2011. LEI Ming. Theoretical and experimental study on accurate calculation of single-core high-voltage cable core temperature based on skin temperature[D]. Guangzhou: South China University of Technology, 2011. (  0) 0) |
| [10] |
黄诗雅, 吴勇, 李磊. 土壤直埋敷设单芯电力电缆温度场与载流量计算[J]. 武汉大学学报(工学版), 2014, 47(4): 502-505, 526. HUANG Shiya, WU Yong, LI Lei. Calculation of thermal field and ampacity of soil buried single-core power cable[J]. Engineering Journal of Wuhan University, 2014, 47(4): 502-505, 526. (  0) 0) |
| [11] |
HANNA M A, CHIKHANI A Y, SALAMA M M A. Thermal analysis of power cables in multi-layered soil. I. Theoretical model[J]. IEEE Transactions on Power Delivery, 1993, 8(3): 761-771. DOI:10.1109/61.252604 (  0) 0) |
| [12] |
GARRIDO C, OTERO A F, CIDRAS J. Theoretical model to calculate steady-state and transient ampacity and temperature in buried cables[J]. IEEE Transactions on Power Delivery, 2003, 18(3): 667-678. DOI:10.1109/TPWRD.2002.801429 (  0) 0) |
| [13] |
VAUCHERET P, HARTLEIN R A, BLACK W Z. Ampacity derating factors for cables buried in short segments of conduit[J]. IEEE Transactions on Power Delivery, 2005, 20(2): 560-565. (  0) 0) |
| [14] |
刘恒. 岸电电缆多物理场耦合模型研究及复杂环境实时载流量计算[D]. 重庆: 重庆大学, 2020. LIU Heng. Research on multiphysics coupling model of shore power cable and calculation method of real-time ampacity in complex environment[D]. Chongqing: Chongqing University, 2020. (  0) 0) |
| [15] |
范明明. 长距离三芯高压海底电缆的无功补偿和载流量计算研究[D]. 广州: 华南理工大学, 2021. FAN Mingming. Study on reactive power compensation and ampacity calculation of long distance three-cores high voltage submarine cable[D]. Guangzhou: South China University of Technology, 2021. (  0) 0) |
| [16] |
刘畅. 电力电缆载流量与温度场计算软件设计[D]. 杭州: 浙江大学, 2015. LIU Chang. Calculation software design on ampacity and temperature field of power cables[D]. Hangzhou: Zhejiang University, 2015. (  0) 0) |
| [17] |
周远翔, 赵健康, 刘睿, 等. 高压/超高压电力电缆关键技术分析及展望[J]. 高电压技术, 2014, 40(9): 2593-2612. ZHOU Yuanxiang, ZHAO Jiankang, LIU Rui, et al. Key technical analysis and prospect of high voltage and extra-high voltage power cable[J]. High Voltage Engineering, 2014, 40(9): 2593-2612. (  0) 0) |
| [18] |
朱攀勇, 文舒. 直埋电缆载流量影响因素的试验分析[J]. 电力科学与工程, 2017, 33(1): 67-72. ZHU Panyong, WEN Shu. Test and analysis of the influence on ampacity of buried cable[J]. Electric Power Science and Engineering, 2017, 33(1): 67-72. (  0) 0) |
| [19] |
张洪麟, 唐军, 陈伟根, 等. 基于有限元法的地下电缆群温度场及载流量的仿真计算[J]. 高压电器, 2010, 46(2): 42-45, 51. ZHANG Honglin, TANG Jun, CHEN Weigen, et al. Simulation of temperature field and ampacity of underground cable system based on finite element method[J]. High Voltage Apparatus, 2010, 46(2): 42-45, 51. (  0) 0) |
| [20] |
吴文克. 直埋电力电缆载流量的有限元数值计算[D]. 吉林: 东北电力大学, 2017. WU Wenke. Numeral calculations of ampacity for buried power cable based on the finite element method[D]. Jilin: Northeast Electric Power University, 2017. (  0) 0) |
| [21] |
戚建萍. 直埋方式下电缆载流量与温度场分析[D]. 济南: 山东大学, 2018. QI Jianping. Analysis of cable ampacity and temperature field in direct burial condition[D]. Jinan: Shandong University, 2018. (  0) 0) |
| [22] |
孟凡凤, 张兵, 方晓明, 等. 影响直埋电缆载流量的因素的研究[J]. 绝缘材料, 2007, 40(3): 64-66. MENG Fanfeng, ZHANG Bing, FANG Xiaoming, et al. Study of ampacity reduction factors for buried cables[J]. Insulating Materials, 2007, 40(3): 64-66. (  0) 0) |
| [23] |
胡明丽. 基于多物理场耦合模型的高压电力电缆温度场与载流量计算[D]. 广州: 华南理工大学, 2015. HU Mingli. Calculation of thermal distribution and ampacity for high-voltage power cables by using multi-physics coupled model[D]. Guangzhou: South China University of Technology, 2015. (  0) 0) |
| [24] |
黄涛, 文珊, 王庭华, 等. 不同材质电缆支架对电缆运行适用性研究[J]. 电力工程技术, 2017, 36(2): 104-109. HUANG Tao, WEN Shan, WANG Tinghua, et al. Research on applicability of different material cable brackets to cable operation[J]. Electric Power Engineering Technology, 2017, 36(2): 104-109. (  0) 0) |
| [25] |
肖冬萍, 包杨, 杨帆, 等. 计及沉积物渗透性的捆绑式高压直流海底电缆载流量评估模型[J]. 中国电机工程学报, 2021, 41(14): 5066-5076. XIAO Dongping, BAO Yang, YANG Fan, et al. A model for estimating the ampacity of bundled HVDC submarine cables considering sediment permeability[J]. Proceedings of the CSEE, 2021, 41(14): 5066-5076. (  0) 0) |
| [26] |
周桐. 沙土/石墨回填土中内置扭带地埋管换热性能实验研究[D]. 北京: 北京交通大学, 2018. ZHOU Tong. Experimental study on heat transfer performance of buried pipe heat exchanger with twisted tape inserts in the backfill materials of sand/graphite[D]. Beijing: Beijing Jiaotong University, 2018. (  0) 0) |
 2023, Vol. 42
2023, Vol. 42


 李欢(1988), 男, 博士, 副教授, 研究方向为电介质物理、聚合物的老化及失效机制(E-mail:
李欢(1988), 男, 博士, 副教授, 研究方向为电介质物理、聚合物的老化及失效机制(E-mail: