文章编号: 2096-3203(2023)01-0251-09 中图分类号: TM744
2. 南京理工大学自动化学院, 江苏 南京 210094
交直流混合配电网通过直流配电线路实现多区域交流配电网的互联以及分布式电源和直流负荷的直接接入,正成为世界范围内的研究热点[1-3]。目前,国内外的直流配电网开始逐步应用于实践,但其故障检测研究较为滞后,限制了直流配电网的进一步发展[4]。
当前直流配电网的故障检测方法基本是2种思路,第一种是分析故障电气量的暂态特征,第二种是利用智能算法对故障进行检测。借鉴柔性直流输电线路保护方法,文献[5-7]采用行波法、主动注入法和故障分析法研究直流配电网的线路保护。由于短数据窗暂态信号容易受到量测误差和控制切换的影响,文献[8]提出一种基于端口的本地保护与系统中各变换器协调控制配合的控保协同保护方案,其采样频率要求低且无须增加额外设备,但容易受到线路分布电容的影响。利用故障过程中的电容放电特征,文献[9]提出一种单端电气量的线路保护方案,并采用过电流判据及动作延时的后备保护方案。基于故障暂态特征的直流配电网故障分析[10-11]均能正确识别故障区域,但存在过渡电阻和噪声干扰时,准确度会受到一定的影响。
智能算法的发展给故障区域识别提供了新的解决思路。专家系统是发展较早且较为成熟的人工智能算法,文献[12]将模糊概念引入专家系统,提出基于模糊专家系统的电力系统故障诊断方法。近年来,以神经网络为基础的深度学习发展迅速,被广泛应用于配电网的故障检测中。文献[13]使用Tensorflow构建基于全连接网络的深度神经网络模型,挖掘故障数据向量与故障支路之间的联系,形成故障定位模型,但该方法在不同优化函数下的准确率差异较大。文献[14]搭建基于迁移学习的卷积神经网络模型,在小样本情况下能迅速实现故障区域识别,但该方法过于追求小样本学习,未考虑故障位置和不同故障类型对识别结果的影响。
交直流配电网的故障电流信号微弱,且换流设备中大量电力电子设备对电流信号产生了噪声干扰,致使现有检测方法不能提取丰富且有效的故障特征,无法建立故障特征与故障类型之间的联系,因此无法实现准确可靠的故障检测。为此,文中提出一种时域和频域双特征提取的基于深度置信网络(deep belief network,DBN)的交直流配电网直流故障检测方法。该方法采用傅里叶变换提取故障电流的高频量,利用相模变换提取解耦后的正负极故障电压变化量,构造故障特征数据集训练DBN,利用DBN强大的学习泛化能力来完成故障检测,并正确识别故障区域和故障极性。最后,基于PSCAD/EMTDC的大量仿真验证了算法在不同故障情况下仍具有较高的检测准确率,并通过对比实验说明了所提算法的有效性和可靠性。
1 多源交直流配电网直流线路故障分析基于模块化多电平换流器(modular multilevel converter,MMC)的直流配电网发生故障时,主要是由子模块电容放电通过故障点形成故障回路,故障电流会对绝缘栅双极型晶体管产生极大的冲击。因此,须在故障发生后的极短时间内准确识别故障区域和极性,从而及时排除故障,恢复配电系统的正常运行。
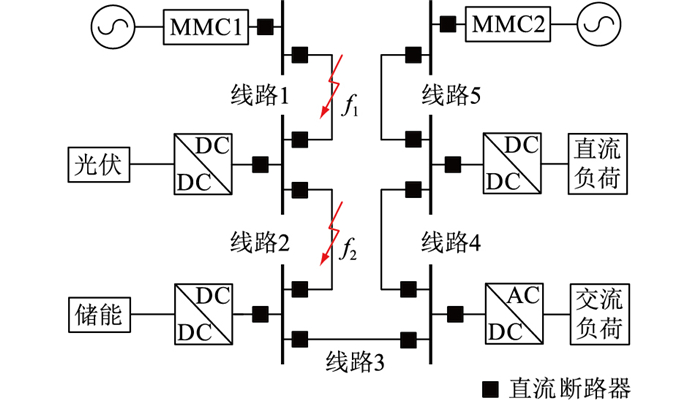
为对故障进行有效检测和识别,首先分析MMC直流配电网的故障特性。文中所研究的交直流配电网的拓扑结构为双端四分支,两端是MMC,配电线路上依次接入储能系统、分布式光伏、交流负荷和直流负荷,如图 1所示。
|
图 1 多源交直流配电网拓扑 Fig. 1 Topology of multi-source AC/DC distribution network |
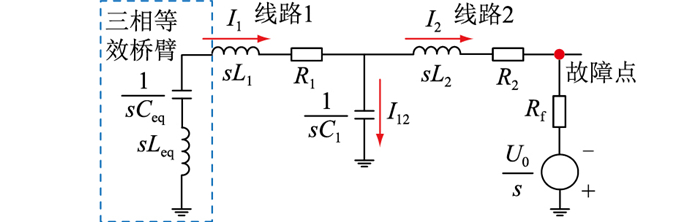
假设在线路2上发生单极接地故障f2,其拉普拉斯电路如图 2所示。其中,Leq=2Larm/3(Larm为一相桥臂电感)为三相等效桥臂电感;Ceq=3C0/N(C0为一相桥臂子模块电容,N为子模块数量)为三相等效子模块电容[15];L1、L2分别为线路1和2的线路电感;R1、R2分别为线路1和2的电阻;I1、I2分别为线路1和2的故障电流;C1为光伏的并联电容;I12为光伏并联电容的电流;Rf为过渡电阻;U0为故障电压源。由等效电路可知,线路2的故障电流I2为:
| $ I_2=\frac{U_0/s}{\left(R_2+R_{\mathrm{f}}\right)+s L_2+\frac{Z_1}{s C_1 Z_1+1}} $ | (1) |
| $ Z_1=s\left(L_1+L_{\text {eq }}\right)+1 /\left(s C_{\text {eq }}\right)+R_1 $ | (2) |
|
图 2 线路2单极故障时的拉普拉斯电路 Fig. 2 Laplace circuit for line 2 single pole fault |
式中:Z1为线路1与MMC的阻抗。
根据基尔霍夫电流定律,此时有:
| $ \begin{gathered} I_1=I_2 \frac{1 /\left(s C_1\right)}{1 /\left(s C_1\right)+Z_1}= \\ I_2 \frac{1}{s^2\left(C_1 L_1+C_1 L_{\text {eq }}\right)+s R_1 C_1+C_1/C_{\text {eq }}+1}= \\ I_2 H(s) \end{gathered} $ | (3) |
此时的区外(假定发生故障的线路2为区内)故障电流I1相当于I2与传递函数H(s)相乘。从形式上可以看出,H(s)是一个二阶低通滤波器,因此区内故障时,故障电流进入区外的高频分量大大减少,即线路2发生故障时,区外只能检测到幅值很小的高频电流。随着频率逐渐增大,区外高频电流几乎可以忽略。因此,文中通过区内外故障电流高频分量的差异来实现故障识别。需要说明的是,由于线路并联电容的存在,基于电压源换流器(voltage source converter,VSC)的直流配电网区内外故障电流间的传递函数也具有二阶低通滤波性质[16]。
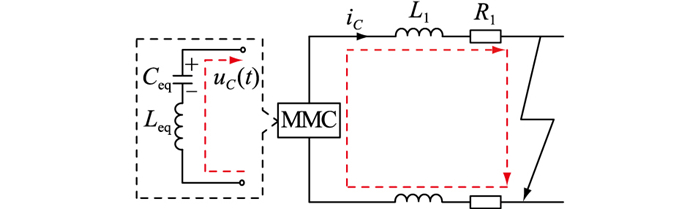
1.2 故障极性分析根据MMC故障时子模块电容放电等效电路[17],得到双极短路时的放电等效回路,如图 3所示。其中,uC(t)为子模块电容电压;iC为故障电流。
|
图 3 双极短路放电等效回路 Fig. 3 Bipolar short circuit discharge equivalent circuit |
由双极短路放电等效回路列写故障方程如下:
| $ \left\{\begin{array}{l} \left(2 L_1+L_{\text {eq }}\right) C_{\text {eq }} \frac{\mathrm{d}^2 u_C}{\mathrm{~d} t^2}+2 R_1 C_{\text {eq }} \frac{\mathrm{d} u_C}{\mathrm{~d} t}+u_C=0 \\ i_C=-C_{\text {eq }} \frac{\mathrm{d} u_C}{\mathrm{~d} t} \end{array}\right. $ | (4) |
假设故障发生时子模块电压和电流初值均为额定值V0和I0。根据直流配电网的特点,有R1<
| $ \left\{\begin{array}{l} u_C=\frac{V_0 \omega_0}{\omega} \mathrm{e}^{-\delta t} \sin (\omega t+\beta)-\frac{I_0}{\omega C_{\mathrm{eq}}} \mathrm{e}^{-\delta t} \sin (\omega t) \\ i_C=-\frac{I_0 \omega_0}{\omega} \mathrm{e}^{-\delta t} \sin (\omega t-\beta)+\frac{V_0}{\omega L_{\mathrm{eq}}} \mathrm{e}^{-\delta t} \sin (\omega t) \\ u_{\mathrm{dc}}=u_C+L_{\mathrm{eq}} C_{\mathrm{eq}} \frac{\mathrm{d}^2 u_C}{\mathrm{~d} t^2} \end{array}\right. $ | (5) |
其中:
| $ \left\{\begin{array}{l} \delta=R_1 /\left(2 L_{\text {eq }}\right) \\ \omega_0=\sqrt{\delta^2+\omega^2} \\ \beta=\arctan (\omega/\delta) \\ \omega^2=1 /\left(L_{\text {eq }} C_{\text {eq }}\right)-\left[R_1 /\left(2 L_{\text {eq }}\right)\right]^2 \end{array}\right. $ | (6) |
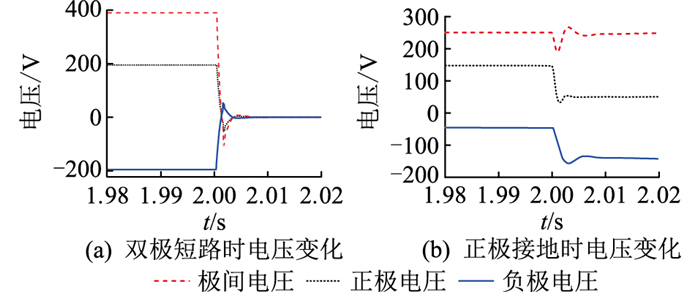
由式(5)可知,此阶段为二阶欠阻尼振荡。当双极短路时,极间直流电压udc经过振荡后降到0,正负极电压也降到0。单极接地时的等效电路相当于双极短路时等效电路的上(下)部分,因此,其动态求解过程与双极短路故障一致,区别只在于故障极线路参数计入故障回路。由此可知,单极接地时,故障极电压下降到0,非故障极电压上升为原来的2倍,以此来维持极间电压的稳定。根据以上分析,图 4分别给出了双极短路和正极接地时正负极和极间电压的变化示意。
|
图 4 双极短路和正极接地时的电压变化示意 Fig. 4 Schematic diagram of voltage variation during bipolar short circuit and positive ground |
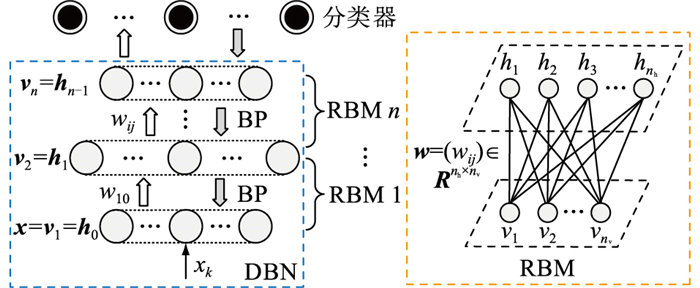
DBN是由多个受限玻尔兹曼机(restricted boltzmann machine,RBM)堆叠,并结合反向传播(back propagation,BP)神经网络构成的深度神经网络。RBM由可见层和隐藏层通过无向权值连接而成,且层内无连接,层间全连接,其结构见图 5。其中,xk为输入特征x的第k个特征量,k=1, 2, ⋯, Q;vr(r=1, 2, ⋯, n)为第r层可见层;hl(l=0, 1, ⋯, n-1)为第l层隐藏层;wrl为可见层和隐藏层之间的连接权重。在RBM中,vi(i=1, 2, ⋯, nv)为构成1个RBM的可见层第i个神经元的状态;hj(j=1, 2, ⋯, nh)为该RBM的隐藏层第j个神经元的状态;wij为连接权值。
|
图 5 RBM和DBN结构 Fig. 5 The structure of RBM and DBN |
从DBN的结构中可以看出,前一个RBM单元的隐藏层作为下一个RBM单元的可见层,从而利用多个RBM可见层和隐藏层全连接的无向权值的关系,求解复杂的输入和输出的非线性关系。同时,多层RBM堆叠可以更准确地提取输入向量的特征,更高效地完成数据分类等工作。
2.2 DBN训练过程神经网络的训练目的是找到合适的映射关系,包括各层之间的权值矩阵、偏置和激活函数,以满足输入向量和输出向量之间的非线性关系。DBN的训练过程由RBM的无监督训练和有监督反向调参两部分构成。
对每层RBM,采取贪婪学习的方式,展开自下向上的无监督训练。此过程中,为最大程度地保留原始数据的特征信息,利用无标签样本进行无监督训练,充分提取数据内部的特征,并抽象为高层的数据特征。当可见层神经元v或隐藏层神经元h状态分别确定时,隐藏层第j个神经元或可见层第i个神经元的激活概率分别为:
| $ \left\{\begin{array}{l} P\left(h_j=1 \mid \boldsymbol{v}\right)=\sigma\left(b_j+\sum\limits_{i=1}^{n_{\mathrm{v}}} v_i w_{i j}\right) \\ P\left(v_i=1 \mid \boldsymbol{h}\right)=\sigma\left(a_i+\sum\limits_{j=1}^{n_{\mathrm{h}}} h_j w_{i j}\right) \end{array}\right. $ | (7) |
式中:bj为隐藏层第j个神经元的偏置;σ(x)=1/(1+e-x)为激活函数,用来提高网络的非线性映射能力;ai为可见层第i个神经元的偏置。然后利用BP神经网络结构,根据给定的数据标签,自上向下对训练得到的模型进行有监督调参,最终完成最优网络的建立。调整网络参数时,对于1个RBM,隐藏层、可见层神经元h和v的偏置、可见层与隐藏层之间的权值矩阵w按照式(8)进行调节。
| $ \left\{\begin{array}{l} \boldsymbol{w}^{\prime}=\boldsymbol{w}+\lambda\left[\boldsymbol{P}(\boldsymbol{h}=1 \mid \boldsymbol{v}) \boldsymbol{v}^{\mathrm{T}}-\boldsymbol{P}\left(\boldsymbol{h}^*=1 \mid \boldsymbol{v}^*\right)\left(\boldsymbol{v}^*\right)^{\mathrm{T}}\right] \\ \boldsymbol{b}^{\prime}=\boldsymbol{b}+\lambda\left(\boldsymbol{P}(\boldsymbol{h}=1 \mid \boldsymbol{v})-\boldsymbol{P}\left(\boldsymbol{h}^*=1 \mid \boldsymbol{v}^*\right)\right) \\ \boldsymbol{a}^{\prime}=\boldsymbol{a}+\lambda\left(\boldsymbol{v}-\boldsymbol{v}^*\right) \end{array}\right. $ | (8) |
式中:w、w′分别为调整前、后的权值矩阵;λ为学习率;P(h=1丨v)为隐藏层神经元激活概率向量;v*为可见层v的重构,根据v*所得的隐藏层为h*;b、b′分别为调整前、后隐藏层的偏置向量;a、a′分别为调整前、后可见层的偏置向量。
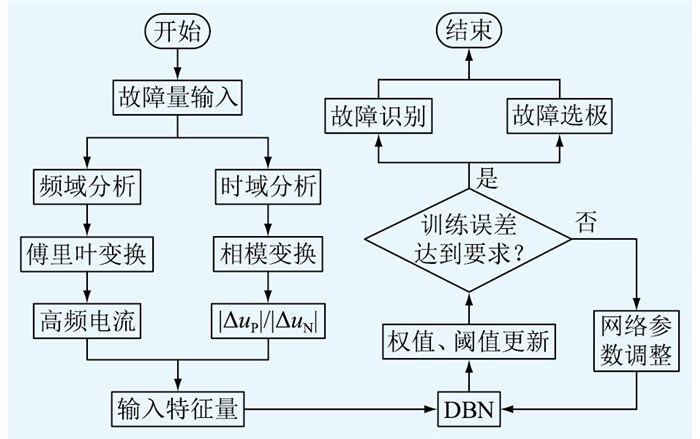
3 基于DBN的故障检测方法为能准确识别故障区域和故障极性,须建立故障特征与故障类型之间的映射关系,除了利用DBN自身的特征提取和求解分类问题的能力,文中还通过对故障特征分析,从时域和频域上提取有效且充分的故障特征,构造故障特征数据集作为DBN的输入,更加保证了故障检测结果的准确性和鲁棒性。具体的检测流程见图 6,ΔuP/ΔuN为输入量经相模变换后得到的正负极电压变化量比值。
|
图 6 故障检测流程 Fig. 6 Flow chart of fault detection |
由1.1节分析可知,故障电流的高频分量在不同区域故障时差异很大,因此可通过提取故障电流的高频部分作为故障特征数据集的一部分。文中利用傅里叶变换获取故障电流信号在不同频段的信息,并截取部分高频段作为输入特征量。采样频率为10 kHz,取故障前后各一个工频周期内的故障电流,采样点数为400。经过频率换算和幅值修正后,得到各信号的频谱图。MMC采用阶梯波逼近正弦波的调制方式,因此MMC的开关频率很低,通常在150 Hz左右[18]。同时,若截取的频率段的上限频率过高,则会导致输入数据中含有大量的无用特征量;若截取的频率段的下限频率过低,则检测结果会受MMC的开关频率影响。因此,为保证不同区域故障时的故障特征差异明显,同时减少换流器的调制策略和子模块电容投切对故障识别的影响,截取的故障电流的高频段在0.5~1.0 kHz。
直流配电网采用双极运行方式,故障时正负极之间的耦合作用会给时域分析造成一定影响。因此,采用相模变换法消除耦合作用,将正负极电压分解成零模分量和一模分量,再转换为正负极电压的变化量。以正极接地短路为例,故障点产生的零模分量和一模分量转换到正负极上。
| $ \left\{\begin{array}{l} \left|\Delta u_{\mathrm{P}}\right|=\frac{Z_{\mathrm{L} 0}+Z_{\mathrm{L} 1}}{Z_{\mathrm{L} 0}+Z_{\mathrm{L} 1}+2 R_{\mathrm{g}}} E \\ \left|\Delta u_{\mathrm{N}}\right|=\frac{Z_{\mathrm{L} 0}-Z_{\mathrm{L} 1}}{Z_{\mathrm{L} 0}+Z_{\mathrm{L} 1}+2 R_{\mathrm{g}}} E \end{array}\right. $ | (9) |
式中:ZL0为零模波阻抗;ZL1为一模波阻抗,且ZL1<ZL0;Rg为过渡电阻;E为对地电压。
当正极发生接地故障时,ΔuP/ΔuN >1;负极接地故障时,ΔuP/ΔuN<1;双极短路时,二者比值接近于1[19]。因此,可利用ΔuP/ΔuN作为输入特征集。为避免测量误差和过渡电阻的干扰,对一定数据窗内的故障电压变化量进行积分,选取数据窗为1.5 ms。
通过上述频域和时域的故障信息处理,获得故障电流高频分量和正负极电压变化量比值,从而完成故障特征数据集的构造。
3.2 建立并训练DBN由于构造的故障特征数据集量纲不同,在神经网络的训练过程中可能会出现梯度爆炸,因此要对输入特征量进行标准化处理。假设xk为待输入的特征量,则标准化处理后的特征量为:
| $ x_k^{\prime}=\left(x_k-x_{\min }\right) /\left(x_{\max }-x_{\min }\right) $ | (10) |
式中:xk′为处理后的特征量;xmin、xmax分别为xk中的最小值和最大值。
在DBN的权值训练过程中,考虑到样本数较多,为兼顾训练速度和权值更新的稳定性,文中采取随机梯度下降(stochastic gradient descent,SGD)算法和Mini Batch批量训练方法,首先选择训练数据中的一部分,用来批量计算权值更新,并利用平均权值更新来训练神经网络[20]。DBN中RBM的层数和隐藏层神经元的个数须根据每次训练产生的误差不断进行调整。经过多次试验后发现,网络层数增加虽会减少训练误差,但也会导致训练时间过长,而较少的网络层数会使得神经网络的分类效果不佳,因此最终确定最优DBN结构参数为5层RBM网络,每层隐藏层神经元个数为200。最终的输出结果采用Softmax分类器,输出最大值置为1,其余置为0,输出为1的对应的索引号即为分类最终结果。对输出的故障类型进行标签定义,文中以线路1和线路2为例进行训练,网络输出的分类标签定义见表 1。
|
|
表 1 不同故障类型的标签定义 Table 1 Label definitions for different faults types |
为保证时域和频域特征提取的广泛性和充分利用DBN处理非线性映射关系的能力,要对不同情况的故障进行遍历。交直流配电网中可能需要考虑的情况有故障区域、故障极、故障位置、过渡电阻和线路长度,因此,文中设定的样本参数遍历表如表 2所示。其中,故障位置中的l为故障所在线路长度,线路1和2的长度分别设置2种和3种,所以参数数量为2×3=6。由表 2可知,样本数据是3 600组,其中设定80%(2 880组)为训练样本,剩余20%(720组)为测试样本。
|
|
表 2 样本参数遍历表 Table 2 The traversal list of sample parameters |
在PSCAD/EMTDC平台中搭建如图 1所示的基于MMC的±0.4 kV交直流配电网模型,其中MMC1采用定直流电压和定无功功率控制,MMC2采用定有功功率控制,交流电网电压等级为10 kV。模型参数如下:线路单位电阻为0.12 Ω/km,线路单位电感为1.6 mH/km,线路3长度为5 km,线路4长度为3.5 km,线路5长度为3.5 km。
为准确描述网络性能,评价模型的有效性,从而调整DBN的模型参数,须设定模型评价指标来具体量化模型的正确性。3.2节中对不同网络输出结果定义了不同的标签,每个标签对应的是由多个0和1组成的向量,因此定义训练过程中的误差e为实际输出与期望输出之间的差距,差距越小,误差就越小,网络模型越准确。误差e的计算公式为:
| $ e=\frac{1}{n_{\mathrm{e}}} \sum\limits_{x=1}^{n_{\mathrm{e}}} \frac{y_{\mathrm{e}}(x)-Y_{\mathrm{e}}(x)}{Y_{\mathrm{e}}(x)} $ | (11) |
式中:ye(x)为训练样本的实际输出;Ye(x)为训练样本的期望输出;ne为训练样本数。
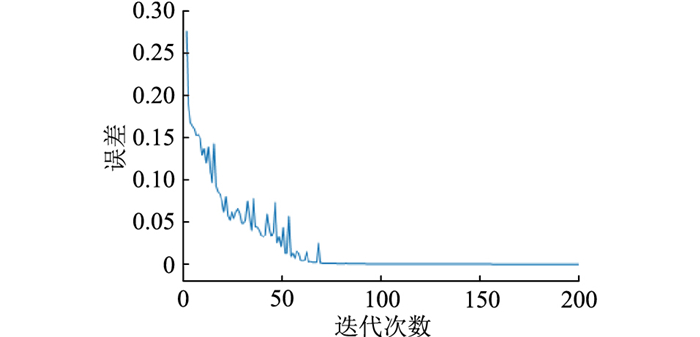
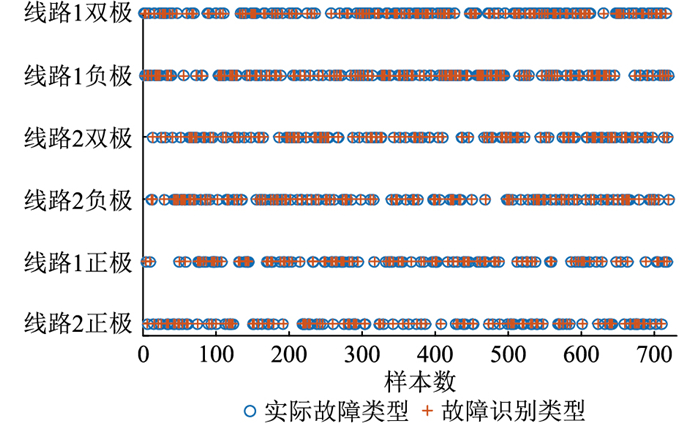
图 7为最优DBN结构训练误差的变化曲线,在经过70次迭代后,训练误差接近0,此后保持不变,说明此时根据构造的故障特征数据集,已经建立起故障类型与故障特征之间的强映射关系。通过建立DBN检验测试集的数据,得到的输出结果如图 8所示。文中所提故障检测算法在构造数据集时已对故障信息的时域和频域特征进行了一次提取,之后在DBN训练过程中通过大量的故障类型遍历,充分发挥DBN的泛化能力,完成更进一步的故障特征提取,充分保证其故障检测能力。测试集故障检测的准确率达到了100%,说明文中所提算法在交直流配电网故障检测方面具有相当高的准确性。
|
图 7 迭代次数与误差关系 Fig. 7 Relationship between training times and error |
|
图 8 测试集输出 Fig. 8 The output of test set |
交直流电网中含有很多电力电子元件,在电网运行时会产生大量的噪声。这些服从正态分布的高斯白噪声由于随机性较强,无法预测和消除,这也是很多故障检测理论无法应用于实际工程的原因。为测试文中算法对噪声的抗干扰能力,在故障信号提取过程中设定5组不同的信噪比来进行抗噪试验,测试结果如表 3所示。
|
|
表 3 噪声干扰测试结果 Table 3 Noise interference test results |
信噪比反应的是正常信号和噪声的比例,信噪比越大,说明正常信号所占比例越大,反之,信噪比越小,说明噪声在整个信号中的占比越大。由表 3可以看出,当输入信号正常且信噪比大于40 dB时,检测算法具有很强的抗干扰能力。在提取频域故障特征时,算法通过截取频带范围消除了部分频带噪声的干扰;时域分析时,利用相模变换也在信号处理过程中消除了部分噪声;同时DBN在梯度下降更新权值的过程中,因噪声与分类结果的相关性极小,通过不断的迭代更新,噪声影响也几乎被忽略。因此,在有噪声影响的情况下,文中所提检测算法仍然不失准确性,相较于现有算法,大大提高了工程应用价值。为模拟最恶劣的实际条件,设定信噪比为20 dB的噪声干扰(信号已接近失真),此时由于采集信号中噪声干扰太大,算法难以寻得最优解,出现了比较大的检测误差。此处模拟的是现场应用中的实际情况,若配电网系统中的信号监测采集系统或者控制管理系统被严重干扰或者出现病毒入侵的情况,所有算法均会失效,只能通过人工巡线进行排查。
4.3 线路分布电容对算法的影响测试直流配电线路较短,线路分布电容很小,但在故障时,其暂态特性会造成直流暂态电流波动[21],可能对算法的识别效果产生一定影响。为测试算法在线路分布电容影响下的可靠性,设置分布电容C为0.012 7 μF/km,并分别在线路1和线路2上设置正极接地、负极接地和双极短路故障,测试故障检测的准确率,测试结果如表 4所示。
|
|
表 4 线路分布电容影响下的测试结果 Table 4 Test results under the influence of line distribution capacitance |
由表 4可知,虽然线路分布电容的存在使线路故障电流产生了一定的波动性,但其值较小,且只有部分频带的故障电流特征被提取,因此线路分布电容对检测结果的影响较小,甚至可以忽略。文中利用故障电流高频量进行故障区域识别,线路分布电容的阻抗值-1/(ωC)(其中ω=2πf)远小于线路上感抗值ωL(L为线路电感值),因此线路上含2倍甚至3倍电容时,检测结果依然准确可靠。
4.4 换流器控制策略对算法的影响测试由3.1节分析可知,利用傅里叶变换提取故障电流中的高频分量可以忽略MMC控制策略的影响,现改变两端MMC的控制策略来进行影响测试。MMC的外环控制策略分为定直流电压控制和定功率控制,当MMC1采用定直流电压控制时,MMC2采用定功率控制,反之亦然。测试结果如表 5所示。为能有效区分不同区域的故障,文中利用故障电流的高频差异作为输入特征量,因此提取的高频量都在0.5 kHz以上,远远大于MMC的开关频率(由于MMC采用多电平换流器,相比于传统的VSC,大大降低了开关频率),因此文中提出的基于高频量的故障检测算法不会被换流器的控制策略影响。
|
|
表 5 控制策略影响下的测试结果 Table 5 Test results under the influence of control strategies |
以深度学习为代表的智能算法发展迅速,在电力行业,如负荷预测,故障诊断和稳定性评估等[22]中的应用也成为研究热点,但大部分工作仍停留在理论分析阶段,能够实际落地的较少。部分原因在于电力系统作为一个高维时变非线性电力信息物理系统,本身特征就极为复杂,且实际工程中环境因素和传感器量测误差等都会对算法的应用产生影响。另一个原因在于深度学习需要足够多的数据支撑模型的训练,而电力系统产生的大量数据并不意味着都具有价值,有些数据不能反映系统的特征,因此对于问题的研究并无意义。也就是说,深度学习的本质是数据加算法,现阶段的大部分研究仅仅热衷于算法层面,而忽略了有价值的数据挖掘和处理,导致深度学习的应用受到了限制。
文中所提的基于DBN的故障检测算法,不仅发挥了深度学习强大的学习泛化能力,还对故障信息进行了频域和时域上的数据处理,在物理层面提取了故障特征,因此能完成有价值数据挖掘和深度学习算法开发两部分工作,从而准确高效地完成配电网故障检测的目标。为说明所提算法的优越性,将设置另外2组对比实验,来验证特征提取和算法模型训练的有效性。表 6中列出了3种用于故障检测的方法,方法1为文中所提出的基于DBN的故障检测算法;方法2为根据文献[23]中的故障检测算法,利用小波包分解对电流、电压信号进行处理,并用遗传算法(genetic algorithm,GA)优化的BP神经网络(简称GA-BP)故障检测方法;方法3为无数据处理过程的GA-BP故障检测方法[24]。
|
|
表 6 对比实验测试结果 Table 6 Test results of comparison experiments |
由表 6中的对比实验结果可以看出,DBN相较于GA-BP,含有多个隐藏层,能完成向复杂函数的逼近,实现复杂特征下的分类问题。且时域和频域的故障特征分析有效规避了直流配电网中相关因素(正负极线路的耦合作用、换流器控制策略和子模块电容投切等)的干扰,在不同的故障条件下有极高的检测准确率。
5 结论文中首先根据直流配电网的故障等效电路分析了故障特征,并分别对故障极性和故障位置的检测原理进行分析;然后结合DBN,提出了利用傅里叶变换提取故障电流高频量进行故障区域判断、利用相模变换进行故障选极的算法;最后使用Softmax分类器输出故障选极和故障区域识别的结果。经过多种情况的仿真验证,该故障检测方法具有如下优点:
(1) 不受过渡电阻、故障位置和线路长度等的影响,具有很高的可靠性。
(2) 利用高频量进行故障位置判断,可以有效避免换流器的控制策略对检测结果的影响。
(3) 算法稳定性好,具有很强的耐受噪声、分布电容的能力。
仿真实验表明,文中所提基于DBN的交直流配电网故障检测技术结合了故障特征提取和深度学习算法,因此具有较高的可靠性和准确性,且在情况复杂的故障条件下均能正确检测故障,具有较高的实践应用价值,能推广到更加复杂的配电网中去。
| [1] |
曹文远, 韩民晓, 谢文强, 等. 交直流配电网逆变器并联控制技术研究现状分析[J]. 电工技术学报, 2019, 34(20): 4226-4241. CAO Wenyuan, HAN Minxiao, XIE Wenqiang, et al. Analysis on research status of parallel inverters control technologies for AC/DC distribution network[J]. Transactions of China Electrotechnical Society, 2019, 34(20): 4226-4241. (  0) 0) |
| [2] |
金国彬, 刘玉龙, 李国庆, 等. 考虑可靠性的交直流混合配电网网架与分布式电源协同优化规划[J]. 电力系统保护与控制, 2022, 50(22): 59-70. JIN Guobin, LIU Yulong, LI Guoqing, et al. Collaborative optimization planning of an AC/DC hybrid distribution network frame and distributed power generation considering reliability[J]. Power System Protection and Control, 2022, 50(22): 59-70. (  0) 0) |
| [3] |
ZHANG Y S, MENG X K, SHOTORBANI A M, et al. Minimization of AC-DC grid transmission loss and DC voltage deviation using adaptive droop control and improved AC-DC power flow algorithm[J]. IEEE Transactions on Power Systems, 2021, 36(1): 744-756. DOI:10.1109/TPWRS.2020.3020039 (  0) 0) |
| [4] |
余佶成, 岳长喜, 熊魁, 等. 基于量热法的LVDC配电系统用户侧逆变器能效测量方法[J]. 电测与仪表, 2020, 57(17): 147-152. YU Jicheng, YUE Changxi, XIONG Kui, et al. Energy efficiency measurements method of customer-end inverter in LVDC distribution system based on calorimetry[J]. Electrical Measurement & Instrumentation, 2020, 57(17): 147-152. (  0) 0) |
| [5] |
张益伟. 最小二乘滤波法在直流保护信号采样中的应用[J]. 电工技术, 2021(3): 14-15, 19. ZHANG Yiwei. Application of least square filtering method in DC protection signal sampling[J]. Electric Engineering, 2021(3): 14-15, 19. (  0) 0) |
| [6] |
贾科, 李论, 宣振文, 等. 基于扰动注入的柔性直流配电网主动故障定位及其仿真研究[J]. 电力系统保护与控制, 2019, 47(4): 99-106. JIA Ke, LI Lun, XUAN Zhenwen, et al. Study on fault location method and simulation for VSC-DC distribution network based on disturbance injection[J]. Power System Protection and Control, 2019, 47(4): 99-106. (  0) 0) |
| [7] |
戴志辉, 葛红波, 严思齐, 等. 柔性直流配电网故障分析[J]. 电工技术学报, 2018, 33(8): 1863-1874. DAI Zhihui, GE Hongbo, YAN Siqi, et al. Fault analysis of flexible DC distribution system[J]. Transactions of China Electrotechnical Society, 2018, 33(8): 1863-1874. (  0) 0) |
| [8] |
王聪博, 贾科, 毕天姝, 等. 基于控保协同的多端柔性直流配电系统线路保护[J]. 中国电机工程学报, 2020, 40(8): 2559-2568. WANG Congbo, JIA Ke, BI Tianshu, et al. Line protection for multi-terminal flexible DC distribution system based on control and protection coordination[J]. Proceedings of the CSEE, 2020, 40(8): 2559-2568. (  0) 0) |
| [9] |
周嘉阳, 李凤婷, 陈伟伟, 等. 基于电容放电特征的柔性直流配电网线路保护方案[J]. 电力系统保护与控制, 2019, 47(8): 42-48. ZHOU Jiayang, LI Fengting, CHEN Weiwei, et al. Line protection schemes for flexible DC distribution network based on capacitor discharge[J]. Power System Protection and Control, 2019, 47(8): 42-48. (  0) 0) |
| [10] |
张林, 邰能灵, 刘剑, 等. 直流微电网方向纵联保护方法研究[J]. 电测与仪表, 2018, 55(20): 1-7. ZHANG Lin, TAI Nengling, LIU Jian, et al. Analysis of directional pilot protection method for DC microgrid[J]. Electrical Measurement & Instrumentation, 2018, 55(20): 1-7. (  0) 0) |
| [11] |
YUAN Y L, KANG X N, LI X Y. A fault location algorithm for DC distribution network based on transient fault components[C]//5th Asia Conference on Power and Electrical Engineering (ACPEE). Chengdu, China. IEEE, 2020: 1316-1320.
(  0) 0) |
| [12] |
LEE H J, PARK D Y, AHN B S, et al. A fuzzy expert system for the integrated fault diagnosis[J]. IEEE Transactions on Power Delivery, 2000, 15(2): 833-838. (  0) 0) |
| [13] |
刘成民, 戴中坚, 陈轩. 基于TensorFlow框架的有源配电网深度学习故障定位方法[J]. 电力工程技术, 2019, 38(5): 8-15. LIU Chengmin, DAI Zhongjian, CHEN Xuan. A fault location method for active distribution network based on TensorFlow deep learning[J]. Electric Power Engineering Technology, 2019, 38(5): 8-15. (  0) 0) |
| [14] |
孟子超, 杜文娟, 王海风. 基于迁移学习深度卷积神经网络的配电网故障区域定位[J]. 南方电网技术, 2019, 13(7): 25-33. MENG Zichao, DU Wenjuan, WANG Haifeng. Distribution network fault area location based on deep convolution neural network with transfer learning[J]. Southern Power System Technology, 2019, 13(7): 25-33. (  0) 0) |
| [15] |
冯智博. 柔性直流电网直流侧短路故障分析及短路电流计算方法研究[D]. 吉林: 东北电力大学, 2020. FENG Zhibo. Research on short circuit fault analysis and short circuit current calculation method of flexible DC grid[D]. Jilin: Northeast Electric Power University, 2020. (  0) 0) |
| [16] |
周德生, 李佳朋, 李宇骏, 等. 基于暂态高频能量的多端直流系统故障检测方法[J]. 智慧电力, 2019, 47(5): 71-77. ZHOU Desheng, LI Jiapeng, LI Yujun, et al. DC fault detection in MTDC systems based on transient highfrequency current[J]. Smart Power, 2019, 47(5): 71-77. (  0) 0) |
| [17] |
杨赛昭, 向往, 张峻榤, 等. 基于人工神经网络的架空柔性直流电网故障检测方法[J]. 中国电机工程学报, 2019, 39(15): 4416-4430. YANG Saizhao, XIANG Wang, ZHANG Junjie, et al. The artificial neural network based fault detection method for the overhead MMC based DC grid[J]. Proceedings of the CSEE, 2019, 39(15): 4416-4430. (  0) 0) |
| [18] |
徐政, 肖晃庆, 张哲任. 柔性直流输电系统[M]. 2版. 北京: 机械工业出版社, 2017. XU Zheng, XIAO Huangqing, ZHANG Zheren. Flexible DC transmission system[M]. 2nd ed. Beijing: China Machine Press, 2017. (  0) 0) |
| [19] |
王艳婷, 张保会, 范新凯. 柔性直流电网架空线路快速保护方案[J]. 电力系统自动化, 2016, 40(21): 13-19. WANG Yanting, ZHANG Baohui, FAN Xinkai. Fastprotection scheme for overhead transmission lines of VSC-based HVDC grid[J]. Automation of Electric Power Systems, 2016, 40(21): 13-19. (  0) 0) |
| [20] |
Phil Kim. MATLAB深度学习机器学习、神经网络与人工智能[M]. 敖富江, 杜静, 周浩, 译. 北京: 清华大学出版社, 2018. KIM P. MATLAB deep learning: with machine learning, neural networks and artificial intelligence[M]. AO Fujiang, DU Jing, ZHOU Hao, Trans. Beijing: Tsinghua University Press, 2018. (  0) 0) |
| [21] |
王聪博, 贾科, 毕天姝, 等. 基于暂态电流波形相似度识别的柔性直流配电线路保护[J]. 电网技术, 2019, 43(10): 3823-3832. WANG Congbo, JIA Ke, BI Tianshu, et al. Protection for flexible DC distribution system based on transient current waveform similarity identification[J]. Power System Technology, 2019, 43(10): 3823-3832. (  0) 0) |
| [22] |
赵晋泉, 夏雪, 徐春雷, 等. 新一代人工智能技术在电力系统调度运行中的应用评述[J]. 电力系统自动化, 2020, 44(24): 1-10. ZHAO Jinquan, XIA Xue, XU Chunlei, et al. Review on application of new generation artificial intelligence technology in power system dispatching and operation[J]. Automation of Electric Power Systems, 2020, 44(24): 1-10. (  0) 0) |
| [23] |
CHEN Y P, ZHANG C, ZHANG Q Y, et al. UAV fault detection based on GA-BP neural network[C]//32nd Youth Academic Annual Conference of Chinese Association of Automation (YAC). Hefei, China. IEEE, 2017: 806-811.
(  0) 0) |
| [24] |
刘东, 李田泽, 刘开石, 等. GA-BP神经网络在光伏阵列故障检测中的应用研究[J]. 电源技术, 2021, 45(3): 370-373. LIU Dong, LI Tianze, LIU Kaishi, et al. Research on GA-BP neural network in photovoltaic array fault detection[J]. Chinese Journal of Power Sources, 2021, 45(3): 370-373. (  0) 0) |
2. School of Automation, Nanjing University of Science and Technology, Nanjing 210094, China
 2023, Vol. 42
2023, Vol. 42


 汪洋(1979),男,学士,高级工程师,从事配电运检、配网保护相关工作(E-mail:
汪洋(1979),男,学士,高级工程师,从事配电运检、配网保护相关工作(E-mail: