文章编号: 2096-3203(2022)04-0075-08 中图分类号: TM73
2. 东南大学电气工程学院, 江苏 南京 210096
随着我国“双碳”目标的提出,减少煤炭消费、提高新型清洁能源占比成为实现这一目标的重要途径。然而,风电、光伏等新能源发电存在波动性、间歇性等特点,一旦大规模接入电网将给电网安全稳定运行带来挑战[1-3]。采用包括温控负荷(thermostatically controlled loads,TCLs)在内的可调负荷作为需求响应参与电网的调控运行以实现源-网-荷的灵活互动,可作为平抑新能源波动的有效途径之一[4-5]。相比于其他可调负荷,TCLs不仅可平抑新能源并网带来的功率波动,且能依靠其储能(储热/储冷)特性,维持用户在一段时间内对热量或冷量的需求,避免功率波动给用户带来的瞬时体验不佳[6-7]。针对TCLs的控制策略主要包括分散式[8-9]、集中式[10-12]和分布式[13-17]。
文献[8]针对分散式TCLs采用随机控制方法实现精确调节大规模TCLs的总功耗;文献[9]考虑TCLs作为需求响应参与电力系统调频,提出了单向通信分散式TCLs的响应方案,并验证了TCLs参与电力系统一次调频的有效性。文献[10]针对聚合空调提出了一种基于状态队列模型的温度控制方法,并完成了负荷削减任务;文献[11]提出基于系统多样性的聚合空调负荷控制策略,通过广播温度设定值调整聚合空调的功率;文献[12]为了实现集中式负荷控制器性能最优,提出了一种动态参数选择方法。
根据上述文献的研究,可以发现分散式控制的控制对象不需要与调度控制中心直接通信,控制存在一定随机性;而集中式控制依赖于控制中心的信息处理能力,存在通信堵塞、延时等问题。分布式控制策略采用相邻单元间的两两通信方式,通过局部信息的交互实现全局关键信息的共享,减少受控单元对控制中心的依赖,有利于提高系统的可靠性。此外,TCLs参与电网调度具有TCLs特性各异、集群拓扑结构灵活、系统控制目标多样等特点,将TCLs加入电网调度运行十分复杂且需要协调大量控制主体。考虑分布式控制框架下的TCLs控制能够将复杂问题分解到各设备中单独求解,易于保证系统的稳定性,降低控制难度,降低建设与维护成本。
考虑分布式控制框架下的TCLs控制,文献[13]提出了一种包含两级代理的分布式控制策略,针对负荷代理内部所有聚合商的控制,采用温度设定值作为聚合功率的控制信号,以达到对聚合功率较精确的控制;文献[14]提出了一种多层自发触发控制器,采用时间检测预测算法实现功率共享和舒适状态一致;文献[15]提出了一种分层分布式控制策略,保证负荷调整量在聚合商间平均分配。针对TCLs控制成本的问题,文献[16]提出了一种仅基于功率测量的多智能体控制体系结构,通过降低电力需求侧管理所需基础设施成本,降低用户的响应成本。在此基础上,文献[17]进一步提出了基于负荷响应增量成本的多智能体一致性算法,实现电力系统高峰时段削负荷总成本最低。
尽管文献[13-17]在TCLs的分布式控制策略方面作出了重要的理论贡献,但文献[13-15]在控制策略中未计及TCLs的控制成本,不利于控制实施的经济性;文献[16-17]将增量成本引入控制策略中,但所采用的成本模型忽略了TCLs的热力学特性,可能导致大量TCLs在短时间内频繁开关,带来开关损耗,从而缩短使用寿命;此外,实施控制不考虑TCLs热力学特性可能导致用户的舒适度降低。
综上所述,现有研究成果中,考虑了开关寿命损耗的TCLs控制策略研究较少。因此,文中在现有研究的基础上,提出了一种计及开关寿命损耗的TCLs分布式协同控制策略。首先,基于等效热参数(equivalent thermal parameter,ETP)模型建立考虑开关寿命损耗的TCLs控制成本函数模型;然后,以负荷跟踪的总控制成本最低为目标,将上述控制成本函数模型引入基于多智能体一致性的分布式协同控制方法;最后,进行算例分析,提供数值结果来评估所提方法的性能。结果表明,所提的计及开关寿命损耗的TCLs分布式协同控制策略能够显著降低TCLs高频率开关切换造成的寿命损耗。
1 基于ETP的TCLs优化模型 1.1 基于ETP的TCLs建模ETP模型常被用来描述建筑物室内温度与TCLs制冷(热)量的时变关系。ETP模型将室内环境、室外环境和TCLs制冷(热)量等参数等效成电路中的相关电气参数,来描述TCLs的热量在室内传递的过程。
ETP模型的一阶微分方程形式如式(1)所示。
| $ \frac{\mathrm{d} T_{\mathrm{in}}\left(t_{0}\right)}{\mathrm{d} t}=-\frac{1}{R C} T_{\mathrm{in}}\left(t_{0}\right)+\frac{T_{\mathrm{a}}\left(t_{0}\right)}{R C}+s\left(t_{0}\right) \frac{Q\left(t_{0}\right)}{C} $ | (1) |
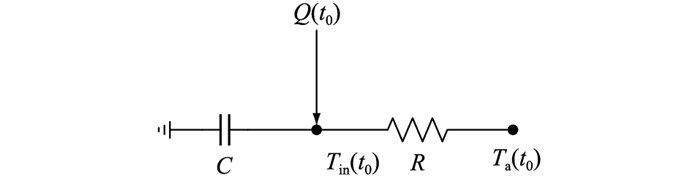
式中:Tin(t0)为t0时刻的室内温度;R为等效热阻值;C为等效热容;s(t0)为t0时刻TCLs的开关状态;Ta(t0)为t0时刻室外温度;Q(t0)为t0时刻的制冷(热)量。
|
图 1 一阶ETP模型 Fig. 1 First order ETP model |
假设室外温度在[t, t+Δt]内不变,以Tin(t)为初值求解式(1),可得ETP模型的递归计算形式如式(2)所示。
| $ \begin{gathered} T_{\mathrm{in}}(t+\Delta t)=T_{\mathrm{in}}(t) \mathrm{e}^{-\Delta t / R C)}+ \\ \left(1-\mathrm{e}^{-\Delta t / R C)}\right)\left(T_{\mathrm{a}}(t)-s(t) Q(t) R\right) \end{gathered} $ | (2) |
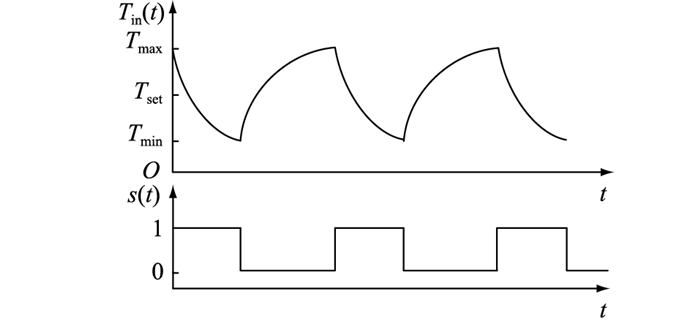
当TCLs设定温度在Tset,TCLs通过压缩机周期性运行来保持温度在设定区间内,如图 2所示。当TCLs处在制冷模式,室内温度上升至温度上限Tmax,TCLs压缩机工作,使得室内温度下降,下降至温度下限Tmin时,压缩机暂停工作,如此循环,保持室内温度在温度设定区间[Tmin, Tmax]内。
|
图 2 TCLs的工作周期(制冷模式) Fig. 2 TCLs operating cycle in refrigeration mode |
根据图 2可得出TCLs的开关状态与室内温度之间的关系如式(3)所示。
| $ s(t+1)= \begin{cases}0 & T_{\mathrm{in}}(t+1)<T_{\min } \\ 1 & T_{\mathrm{in}}(t+1)>T_{\max } \\ s(t) \quad \text { 其他 }\end{cases} $ | (3) |
式中:Tmax=Tset+Tdeadband/2;Tmin=Tset-Tdeadband/2,其中Tdeadband为TCL温度控制死区范围,反映TCLs控制温度的实际偏差,一般取0.25~1 ℃。
1.2 TCLs控制成本模型的建立文中将TCLs控制成本最小作为优化目标。考虑TCLs的异质性,基于单体TCL的控制成本进行分析。TCL参与控制的成本包括以下两方面:
(1) 温度改变对用户舒适性的影响,产生舒适性成本;
(2) 频繁的开关切换对TCL使用寿命的影响,产生开关损耗成本。
考虑这两方面的成本,文中引入矫正切换时间的概念,定义为τM。τM表征控制TCL开关的时刻距离下一次TCL自然切换开关状态时刻的时间间隔。τM越大,则表示此时实施控制对温度的改变越大,单体TCL开关切换的频率越高,从而导致舒适性成本和开关损耗成本同时增加。因此,通过τM能够反映TCL的控制成本。
基于控制成本的分析,目标函数如式(4)所示。
| $ {c_{{\rm{control }}}}(t) = {T_{\rm{M}}}(t){\tau _{\rm{M}}}(t) $ | (4) |
式中:ccontrol(t)为该TCL在t时刻切换状态的控制成本;τM(t)为t时刻该TCL距离下一次自然切换开关状态时刻的时间间隔;TM(t)为t时刻该TCL对应的室内温度与温度上/下限的温度差的绝对值。
当TCL在t时刻处于关闭状态,s(t)为0,下一次自然开启时该TCL对应的室内温度为Tmax,可得当TCL处于关闭状态,将TM, off(t)定义为该TCL对应的室内温度与Tmax的温度差,则TM, off(t)如式(5)所示。
| $ T_{\mathrm{M}, \text { off }}(t)=T_{\max }-T_{\text {in }}(t) $ | (5) |
将Tin(t+Δt)=Tmax,s(t)=0代入式(2),求解式(2),可得TCL关闭时式(2)中Δt, 即τM, off(t)的表达如式(6)所示。
| $\tau_{\mathrm{M}, \mathrm{off}}(t)=-R C \ln \frac{T_{\max }-T_{\mathrm{a}}(t)}{T_{\mathrm{in}}(t)-T_{\mathrm{a}}(t)} $ | (6) |
结合式(5)和式(6),当TCL处于关闭状态,需要将TCL开启时,目标函数式(4)的表达如式(7)所示。
| $ c_{\text {control, off }}(t)=-R C\left(T_{\max }-T_{\mathrm{in}}(t)\right) \ln \frac{T_{\max }-T_{\mathrm{a}}(t)}{T_{\mathrm{in}}(t)-T_{\mathrm{a}}(t)} $ | (7) |
当TCL在t时刻处于开启状态,s(t)为1,下一次自然关闭时该TCL对应的室内温度为Tmin,可得当TCL处于开启状态,将TM, on(t)定义为该TCL对应的室内温度与Tmin的温度差,则TM, on(t)的表达如式(8)所示。
| $ T_{\mathrm{M}, \text { on }}(t)=T_{\mathrm{in}}(t)-T_{\min } $ | (8) |
将Tin(t+Δt)=Tmin,s(t)=1代入式(2),求解式(2),可得TCL开启时式(2)中Δt,即τM, on(t)的表达如式(9)所示。
| $\tau_{\mathrm{M}, \text { on }}(t)=-R C \ln \frac{T_{\min }+Q(t) R-T_{\mathrm{a}}(t)}{T_{\mathrm{in}}(t)+Q(t) R-T_{\mathrm{a}}(t)} $ | (9) |
结合式(8)和式(9),当TCL处于开启状态,需要将TCL关闭时,目标函数式(4)的表达如式(10)所示。
| $ \begin{gathered} c_{\text {control, on }}(t)= \\ -R C\left(T_{\mathrm{in}}(t)-T_{\min }\right) \ln \frac{T_{\min }+Q(t) R-T_{\mathrm{a}}(t)}{T_{\mathrm{in}}(t)+Q(t) R-T_{\mathrm{a}}(t)} \end{gathered} $ | (10) |
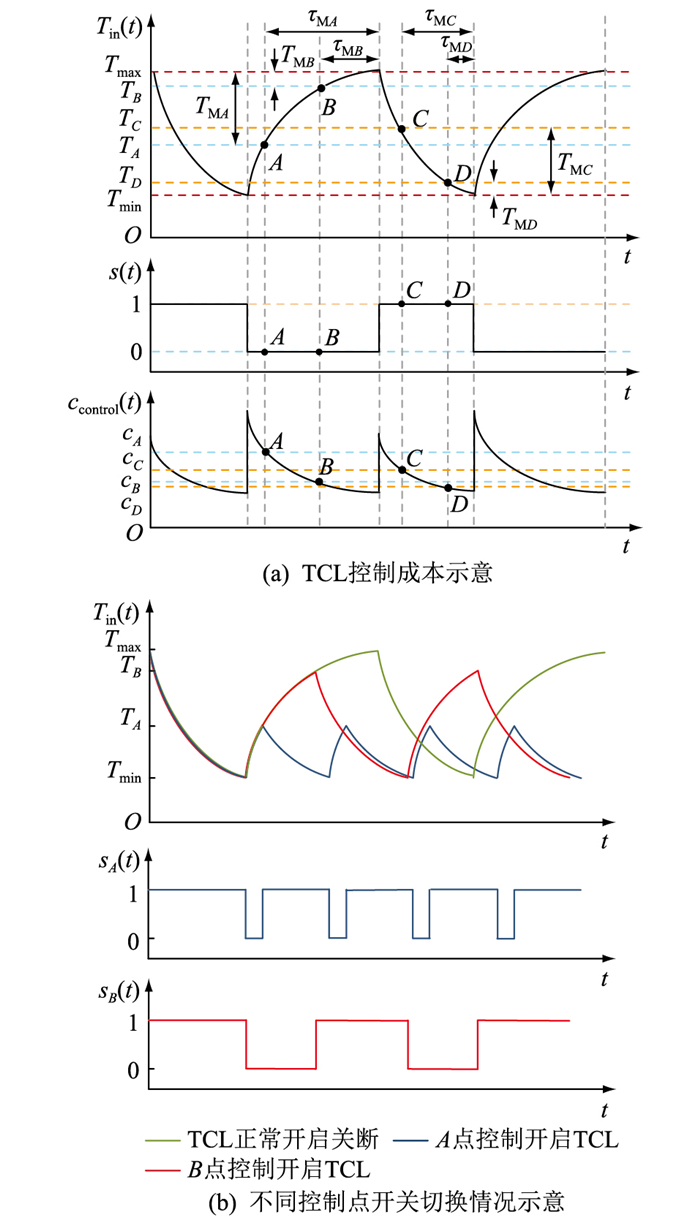
由式(7)、式(10)可得TCL工作状态与在该状态开启/关闭TCL相应的控制成本曲线如图 3(a)所示。
|
图 3 TCL的控制成本及工作周期 Fig. 3 TCL′s control cost and operating cycle |
由图 3(a)可知,当TCL工作于A、B点时,TCL处于关闭状态。不控制的情况下,如果在A、B点开启TCL,τMA,τMB分别为该TCL从A、B点到自然开启时刻的时间间隔,为A、B点的矫正切换时间;TA,TB分别为A、B点的室内温度,其差值为TM(t);cA,cB分别为该TCL在A、B点实施控制的成本。其中,τMA>τMB,则cA>cB,即矫正切换时间越大,控制成本越高。同样地,当TCL工作于C、D点时,TCL处于开启状态。如果在C、D点控制TCL关闭,则该TCL对应的控制成本为cC,cD,显然cC>cD。
为进一步说明矫正切换时间与开关损耗成本和舒适性成本之间的关系,考虑关闭状态下的TCL分别在A、B点被控制开启,TCL的室内温度变化情况与开关状态切换情况如图 3(b)所示。从图 3(b)可知,在A点控制开启TCL的开关切换频率高于在B点控制开启TCL,表明当τM较小时,实施控制的开关损耗成本较小。对比图 3(a)和图 3(b),B点控制开启TCL时,实施控制的时刻更加接近自然切换时刻,其工作周期与不控制TCL的工作周期相似,表明较小的τM能够使得控制TCL对用户的舒适性影响较小,即控制的舒适性成本较小。
2 基于多智能体一致性的TCLs分布式协同控制方法为了实现TCLs参与电力系统调度平抑电网功率波动的目标,第2章将一致性算法引入TCLs分布式控制,将控制任务确定为TCLs的实际总充放电功率能够跟踪功率需求,在满足功率平衡约束的前提下,实现控制过程中总控制成本最小化。
2.1 控制目标和约束条件控制目标为在完成控制任务的前提下最小化负载控制过程中用户的总成本,如式(11)所示。
| $\min c_{\mathrm{sum}}=\sum\limits_{t \in N_{\mathrm{t}}} \sum\limits_{i=1}^{N} c_{\text {control }, i}(t) $ | (11) |
式中:csum为控制时段总控制成本;N为TCLs总数;Nt为总时段数;ccontrol, i(t)为第i个TCL在t时刻切换状态的控制成本,TCL不进行开关状态切换时该TCL对应的ccontrol, i(t)取零值。
此外还需满足功率平衡约束条件。将ΔP(t)定义为t时刻供电系统总输入功率和用电系统总输出功率之间的偏差,即功率需求。功率平衡约束如式(12)、式(13)所示。
| $ \begin{gathered} \Delta P(t)-P_{\mathrm{DR}}(t)=0 \end{gathered} $ | (12) |
| $P_{\mathrm{c} i, \min } \leqslant P_{\mathrm{c} i}(t) \leqslant P_{\mathrm{c} i, \max } $ | (13) |
式中:PDR(t)为t时刻TCLs实际响应总功率;Pci(t)为t时刻第i个TCL充放电功率;Pci, max,Pci, min分别为第i个TCL的最大和最小输出功率。
基于TCLs等效储能模型,PDR(t)如式(14)所示。
| $ P_{\mathrm{DR}}(t)=\sum\limits_{i=1}^{N} P_{\mathrm{c} i}(t) $ | (14) |
| $P_{\mathrm{c} i}(t)=P_{\mathrm{TCL}, i}-P_{\mathrm{a} i}(t)=\frac{Q_{i}(t)}{\eta_{i}}-\frac{T_{\mathrm{a} i}(t)-T_{\mathrm{in}, i}(t)}{R_{i} \eta_{i}} $ | (15) |
式中:PTCL, i为第i个TCL电功率;Pai(t)为t时刻第i个TCL耗散功率;Tin, i(t)为t时刻第i个TCL对应的室内温度;Tai(t)为t时刻第i个TCL对应的室外温度;Qi(t)为t时刻第i个TCL的制冷/热量;ηi为第i个TCL能效比。
2.2 多智能体控制策略及更新规则将多智能体一致性引入控制策略。多智能体系统是解决分布式控制问题的基本形式,是一个由大量存在相互作用的节点(智能体)以及这些节点之间的相互连接线组成的复杂系统。多智能体系统中的信息和资源是局部的和分散分布的,各个智能体之间的相互协作解决复杂问题。因此,可利用多智能体系统在处理复杂问题时的优越性,实现复杂系统的最优运行。
图论是研究复杂网络一致性问题的有效手段,可以基于图论知识理解多智能体之间的信息传递关系。类比于图论中的相关概念,多智能体系统中的每个智能体都可看作一个节点,连接2个智能体的通信线路就相当于边。根据图论求出通讯拓扑对应的拉普拉斯矩阵L和稀疏迭代矩阵H,进而确定一致性变量更新的系数。
多单元系统的拉普拉斯矩阵L元素如式(16)所示。
| $ \begin{cases}l_{i i}=\sum\limits_{i \neq j} \alpha_{i j} & \text { 对角元素 } \\ l_{i j}=-\alpha_{i j} & \text { 非对角元素 }\end{cases} $ | (16) |
式中:αij为该多单元系统邻接矩阵中的对应元素。
稀疏迭代矩阵H元素hij如式(17)所示。
| $ h_{i j}=\left|l_{i j}\right| / \sum\limits_{j=1}^{N}\left|l_{i j}\right| \quad i=1, 2, \cdots, N $ | (17) |
选择控制成本作为信息状态,非主导节点的一致性变量更新规则如式(18)所示。
| $ u_{i, k+1}=\sum\limits_{j=1}^{N} h_{i j} u_{i, k}^{\prime} \quad i=1, 2, \cdots, N $ | (18) |
式中:ui为第i个TCL的信息状态;u′ i为与第i个TCL有通信连接的TCL的信息状态。
为了满足功率平衡约束(12),定义Pr(t)为t时刻ΔP(t)与TCLs实际响应功率PDR(t)的功率偏差,如式(19)所示。
| $ P_{\mathrm{r}}(t)=\Delta P(t)-P_{\mathrm{DR}}(t) $ | (19) |
将功率偏差量Pr(t)引入一致性变量,则主导节点的一致性变量更新规则如式(20)所示。
| $ u_{i, k+1}=\sum\limits_{i=1}^{N} h_{i j} u_{i, k}^{\prime}+\varepsilon P_{\mathrm{r}}(t) \quad i=1, 2, \cdots, N $ | (20) |
式中:ε为功率量转换为成本量的迭代系数。
需要注意的是,迭代得到的一致性变量不是各TCLs的实时控制成本,而是成本参考值,用于判断此刻是否控制该TCL。
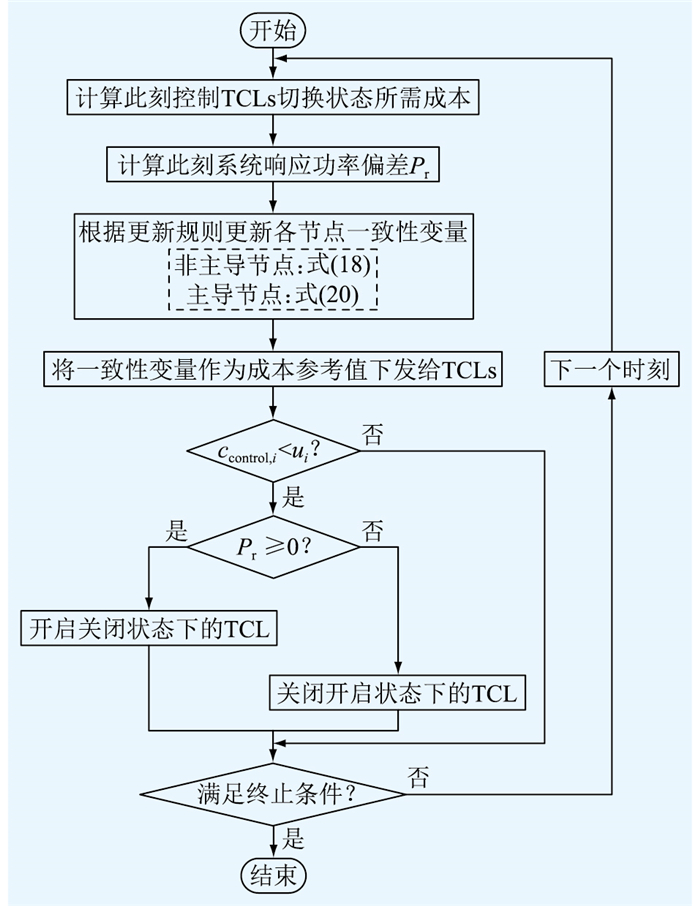
控制方法流程如图 4所示。在每一次迭代中,首先分别计算响应功率偏差Pr和此刻控制各TCLs会产生的控制成本。将Pr代入主导节点更新公式,各节点依照自身更新规则更新一致性变量,将各节点通过多智能体一致性算法迭代得到的一致性变量ui作为参考值下发给对应的TCLs。随后,由TCLs判断是否符合当前状态,即控制增加(减少)功率时,TCLs是否在对应的关闭(开启)状态,并对比控制成本与成本参考值,判断是否切换状态。如果控制成本小于成本参考值,则改变TCLs开关状态,否则保持原来的开关状态。重复以上步骤,直到满足终止条件。
|
图 4 控制方法流程 Fig. 4 Flow chart of the control method |
算例选择10栋楼共计360个用户作为控制对象。其中,每栋楼均为3个单元,每个单元12户(6层),共36户。结合实际考虑到窄带物联网(narrow band internet of things, NB-IoT)无线通信范围有限,每栋楼内的36个用户通信采用格子拓扑,即每个用户仅跟上下左右4个邻居用户通信。每栋楼间有3条通信线路相连,并且仅在相邻楼建立通信线路。每栋楼一楼的6个用户作为主导节点接收功率信号。
TCLs的参考控制信号曲线参考文献[18]的数据,选取其11:00-13:00之间的数据,经过线性插值得到有功功率不平衡数据,将其作为参考控制信号,如图 5所示。

|
图 5 参考控制信号 Fig. 5 Reference control signal |
假设所有TCLs都工作在制冷模式下,考虑到TCLs参数具有随机性,将各项参数设置为随机的正态分布[18],如表 1所示。同时,假设TCLs初始阶段已处于稳定状态。
|
|
表 1 TCLs的参数 Table 1 Parameters of the TCLs |
为了进行对比分析,采用3种负荷跟踪控制方法进行比较:
(1) 方案一:开关概率控制[19-20]。控制需求上传给控制中心,并由功率偏差量转换为接通/关闭概率后,将生成的概率下发给TCLs,各TCLs生成一个0~1的随机数,对比两者大小以判断是否应该切换TCL开关状态,即TCLs随机切换开关状态。
(2) 方案二:功率控制。基于多智能体一致性的分布式控制方法,功率偏差量转换为功率参考值,并作为一致性变量下发给TCLs,功率大的TCL优先切换状态。
(3) 方案三:成本控制。文中提出的计及开关寿命损耗的分布式控制方法,将功率偏差量转换为成本参考值,并作为一致性变量下发给TCLs,控制成本低的TCL优先切换状态。
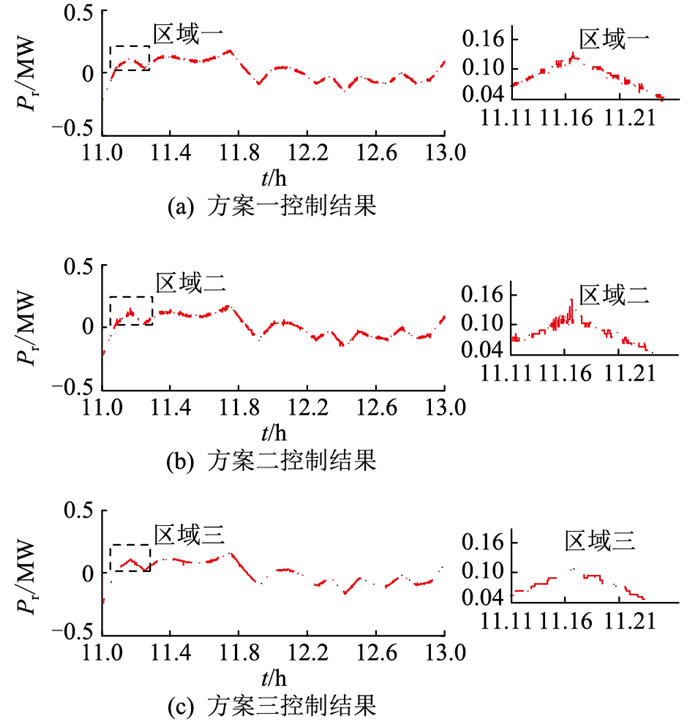
上述3种方案的负荷跟踪控制结果如图 6所示。由图 6可知,方案一、方案三都能够很好地跟踪参考功率控制信号,方案二在个别时段有小幅度的振荡,但整体达到了控制要求。从负荷跟踪控制角度来看,基于多智能体一致性的TCLs控制能够达到负荷跟踪控制要求,且控制效果更好。
|
图 6 各方案负荷跟踪控制结果 Fig. 6 Load tracking control results of different control schemes |
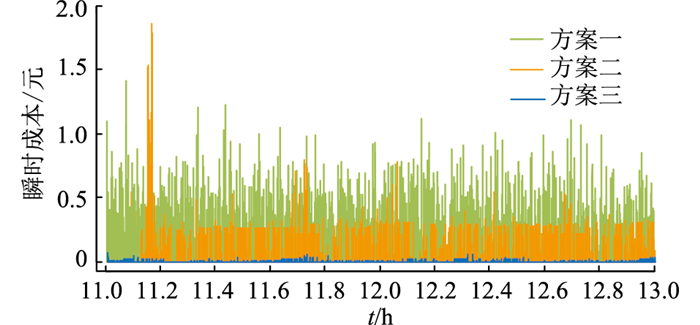
图 7给出了控制目标相同时不同控制方案的瞬时成本曲线。从图 7可以看出,方案一的瞬时成本曲线最为密集且数值最大,可见方案一的控制成本是3个方案中最高的。引入分布式控制方法的方案二瞬时成本曲线较方案一稀疏一些且数值有所降低,但由于个别时段有小幅度振荡,这些时刻瞬时控制成本相较其他时刻略有升高。方案三的瞬时成本曲线最为稀疏,且数值较方案一与方案二降低了90%以上,说明采用分布式控制方法并将成本引入TCLs控制很有必要,在保证控制效果的同时有效地减小控制成本。
|
图 7 不同方案的瞬时成本 Fig. 7 Instantaneous cost of different control schemes |
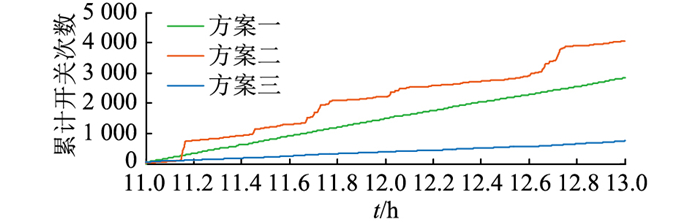
图 8为各方案的累计开关次数曲线。由图 8可知,在控制时段内方案三的TCLs总计开关次数相较方案一与方案二明显降低。用方案一进行负荷跟踪控制时TCLs根据下发的概率随机切换工作状态,因此存在多台TCLs在短时间内反复开关的情况;方案二不存在多台TCLs反复开启/关断的情况,但由于方案二将功率作为一致性变量下发给TCLs,功率最大的TCL总是被优先考虑切换工作状态,导致单台TCL状态切换频率很高;方案三则不存在多台或单台TCL高频率切换的情况。说明将成本引入TCLs控制,让接近自然切换状态时间点的TCL优先切换开关状态,能有效降低TCLs开关频率,避免TCLs因频繁开关切换减少使用寿命。
|
图 8 不同方案的累计开关次数 Fig. 8 Cumulative switching times of different control schemes |
为进一步分析各控制方案的控制成本及控制效果,计算每一时刻切换状态的TCL该时刻室内温度与设定值的差值,采用积分平方误差(integrated square error,ISE)表述优化效果,并计算控制成本总和以及TCLs累计开关次数。累计ISE值和TCLs累计开关次数表达式分别为:
| $ \begin{gathered} I_{\mathrm{sum}}=\int_{0}^{0} \sum\limits_{i=1}^{N} T_{\mathrm{M}}^{2}(t) \mathrm{d} t \end{gathered} $ | (21) |
| $S_{\mathrm{sum}}=\sum\limits_{t \in N_{\mathrm{t}}} \sum\limits_{i=1}^{N} S_{i}(t) $ | (22) |
式中:Isum为控制时段内TCL被控制时室内温度与设定值之间的ISE值总和,TCL不进行开关状态切换时,该TCL对应的TM(t)取零值;[0,O]为时段;Ssum为控制时段内TCLs的累计开关次数,Si(t)为t时刻第i个TCL的开关状态切换情况,Si(t)为1时该TCL切换了开关状态,Si(t)为0时该TCL保持当前状态。
结果如表 2所示,方案三的Isum值与总控制成本相较于方案一与方案二降低了90%以上,平均开关次数相较方案一与方案二减小了70%以上。说明文中的方法能够有效降低系统控制成本,同时避免同一台TCL反复开关切换造成故障。
|
|
表 2 不同方案的负荷跟踪控制结果数据 Table 2 Load tracking control result data of different schemes |
(1) 不同楼层数量比较。为了进一步评估文中方案的有效性,验证负荷数量对控制性能的影响,以每栋楼楼层数量为6~10层为例,比较在不同楼层数量情况下该方案的控制效果。
表 3给出了当楼层数量在6~10层,目标功率随楼层数增加,控制时段内各TCLs被控制时室内温度与设定值的ISE,控制产生的累计控制成本,以及累计开关次数这3项指标的数值。
|
|
表 3 楼层数量不同时方案三控制性能 Table 3 The control performance of scheme three under different number of floors |
由表 3可知,负荷数量越少,方案三的控制效果越好。负荷增加会导致系统控制成本及开关次数等指标数值的增加,但方案三的控制性能在不同楼层数量的情形下均优于方案一与方案二。相较方案一与方案二,方案三的Isum值与总控制成本均降低90%以上,累计开关次数降低50%以上。说明文中提出的方案能够适应不同体量的系统,且能够保持较好的控制效果。
(2) 不同通信延迟比较。为了评估通信延迟对控制性能的影响,比较在不同通信延迟情况下文中方案的控制效果,表 4给出了当通信延迟在0.5~2 s范围内变化时,控制时段内各TCLs被控制时各项指标的数值。从表 4可以看出,通信延迟会影响到方案三的控制性能,Isum值和累计控制成本都随着通信延迟时长的增加而接近同比例增长。相对而言,通信延迟对累计开关次数几乎没有影响。
|
|
表 4 通信延迟不同时方案三控制性能 Table 4 The control performance of scheme three under different communication delays |
TCLs在消纳可再生能源、平抑可再生能源方面具有重要的应用前景。为了更好地发挥TCLs在平抑新能源波动上的重要作用,主要开展了以下工作:
(1) 在ETP模型的基础上,建立了基于TCLs实时工作状态的控制成本模型。该模型能够反映TCLs的热力学特性和TCLs的开关(次数)损耗。
(2) 在上述控制成本模型的基础上,提出了一种基于多智能体一致的分布式协同控制方法。经仿真算例分析,计及TCL控制成本的分布式控制方法能够实现控制成本最低的控制目标。
本文得到江苏省研究生科研与实践创新计划项目“计及开关寿命损耗的温控负荷分层分布式协同控制策略研究”(1812000024572)资助,谨此致谢!
| [1] |
曾博, 杨雍琦, 段金辉, 等. 新能源电力系统中需求侧响应关键问题及未来研究展望[J]. 电力系统自动化, 2015, 39(17): 10-18. ZENG Bo, YANG Yongqi, DUAN Jinhui, et al. Key issues and research prospects for demand-side response in alternate electrical power systems with renewable energy sources[J]. Automation of Electric Power Systems, 2015, 39(17): 10-18. DOI:10.7500/AEPS20150408010 (  0) 0) |
| [2] |
LI J, LIU C, ZHANG P F, et al. Difference between grid connections of large-scale wind power and conventional synchronous generation[J]. Global Energy Interconnection, 2020, 3(5): 486-493. DOI:10.1016/j.gloei.2020.11.008 (  0) 0) |
| [3] |
XIE L J, YAO L Z, CHENG F, et al. Coordinate control strategy for stability operation of offshore wind farm integrated with Diode-rectifier HVDC[J]. Global Energy Interconnection, 2020, 3(3): 205-216. DOI:10.1016/j.gloei.2020.07.002 (  0) 0) |
| [4] |
王俐英, 曾鸣, 赵嘉欣, 等. 计及电力需求响应的多能源协同系统优化运行研究[J]. 电力工程技术, 2021, 40(1): 2-9. WANG Liying, ZENG Ming, ZHAO Jiaxin, et al. Optimal operation of multi-energy collaborative system considering electricity demand response[J]. Electric Power Engineering Technology, 2021, 40(1): 2-9. (  0) 0) |
| [5] |
高赐威, 梁甜甜, 李扬. 自动需求响应的理论与实践综述[J]. 电网技术, 2014, 38(2): 352-359. GAO Ciwei, LIANG Tiantian, LI Yang. A survey on theory and practice of automated demand response[J]. Power System Technology, 2014, 38(2): 352-359. (  0) 0) |
| [6] |
ZHAO H R, WU Q W, HUANG S J, et al. Hierarchical control of thermostatically controlled loads for primary frequency support[J]. IEEE Transactions on Smart Grid, 2018, 9(4): 2986-2998. DOI:10.1109/TSG.2016.2624509 (  0) 0) |
| [7] |
王东, 曾沅, 穆云飞, 等. 基于温控负荷控制技术的新能源优化利用方法[J]. 电网技术, 2015, 39(12): 3457-3462. WANG Dong, ZENG Yuan, MU Yunfei, et al. An optimization method for new energy utilization using thermostatically controlled appliances[J]. Power System Technology, 2015, 39(12): 3457-3462. (  0) 0) |
| [8] |
TINDEMANS S H, TROVATO V, STRBAC G. Decentralized control of thermostatic loads for flexible demand response[J]. IEEE Transactions on Control Systems Technology, 2015, 23(5): 1685-1700. DOI:10.1109/TCST.2014.2381163 (  0) 0) |
| [9] |
MOLINA-GARCÍA A, BOUFFARD F, KIRSCHEN D S. Decentralized demand-side contribution to primary frequency control[J]. IEEE Transactions on Power Systems, 2011, 26(1): 411-419. DOI:10.1109/TPWRS.2010.2048223 (  0) 0) |
| [10] |
周磊, 李扬, 高赐威. 聚合空调负荷的温度调节方法改进及控制策略[J]. 中国电机工程学报, 2014, 34(31): 5579-5589. ZHOU Lei, LI Yang, GAO Ciwei. Improvement of temperature adjusting method for aggregated air-conditioning loads and its control strategy[J]. Proceedings of the CSEE, 2014, 34(31): 5579-5589. (  0) 0) |
| [11] |
CALLAWAY D S. Tapping the energy storage potential in electric loads to deliver load following and regulation, with application to wind energy[J]. Energy Conversion and Management, 2009, 50(5): 1389-1400. DOI:10.1016/j.enconman.2008.12.012 (  0) 0) |
| [12] |
ZHANG Y, LU N. Parameter selection for a centralized thermostatically controlled appliances load controller used for intra-hour load balancing[J]. IEEE Transactions on Smart Grid, 2013, 4(4): 2100-2108. DOI:10.1109/TSG.2013.2258950 (  0) 0) |
| [13] |
张青. 温控负荷聚合建模及其功率控制[D]. 南京: 东南大学, 2016. ZHANG Qing. Aggregated modeling and control of thermostatically controlled loads[D]. Nanjing: Southeast University, 2016. (  0) 0) |
| [14] |
CHEN Z Y, YU X H, WEN G H, et al. Multilayered self-triggered control for thermostatically controlled loads[C]//IECON 2019-45th Annual Conference of the IEEE Industrial Electronics Society. Lisbon, Portugal. IEEE, 2019: 6532-6537.
(  0) 0) |
| [15] |
MENG K, WANG D X, DONG Z Y, et al. Distributed control of thermostatically controlled loads in distribution network with high penetration of solar PV[J]. CSEE Journal of Power and Energy Systems, 2017, 3(1): 53-62. DOI:10.17775/CSEEJPES.2017.0008 (  0) 0) |
| [16] |
FRANCESCHELLI M, PILLONI A, GASPARRI A. Multi-agent coordination of thermostatically controlled loads by smart power sockets for electric demand side management[J]. IEEE Transactions on Control Systems Technology, 2020, 29(2): 731-743. (  0) 0) |
| [17] |
王蓓蓓, 胡晓青, 顾伟扬, 等. 分层控制架构下大规模空调负荷参与调峰的分散式协同控制策略[J]. 中国电机工程学报, 2019, 39(12): 3514-3528. WANG Beibei, HU Xiaoqing, GU Weiyang, et al. Hierarchical control architecture and decentralized cooperative control strategy for large scale air conditioning load participating in peak load regulation[J]. Proceedings of the CSEE, 2019, 39(12): 3514-3528. (  0) 0) |
| [18] |
刘凤鸣, 杨秀媛, 陈麒宇. 一种平抑反弹效应的集群空调负荷控制方法[J]. 电网技术, 2021, 45(12): 4759-4767. LIU Fengming, YANG Xiuyuan, CHEN Qiyu. Control method for suppressing rebound effect of air conditioning loads[J]. Power System Technology, 2021, 45(12): 4759-4767. (  0) 0) |
| [19] |
DAS K, GHOSE D. Broadcast control mechanism for positional consensus in multiagent systems[J]. IEEE Transactions on Control Systems Technology, 2015, 23(5): 1807-1826. DOI:10.1109/TCST.2015.2388732 (  0) 0) |
| [20] |
BAO Y Q, CHEN P P, HU M Q, et al. Control parameter optimization of thermostatically controlled loads using a modified state-queuing model[J]. CSEE Journal of Power and Energy Systems, 2019, 6(2): 394-401. (  0) 0) |
2. School of Electrical Engineering, Southeast University, Nanjing 210096, China
 2022, Vol. 41
2022, Vol. 41


 李梓瑄(1998), 女, 硕士, 研究方向为电力系统的运行和调度、多智能体系统的共识控制(E-mail:
李梓瑄(1998), 女, 硕士, 研究方向为电力系统的运行和调度、多智能体系统的共识控制(E-mail: