0 引言

电力系统状态估计根据电网的实时量测信息估计出系统的运行状态，是能量管理系统(energy management systems，EMS)中其他高级软件应用的基础。随着电网规模的不断扩大和新能源渗透率的不断提高，传统集中式状态估计传输信息量大，难以避免坏数据、拓扑错误等不良数据，容易造成状态估计的不准确。而新能源自身的随机性、间歇性等特点，也会给不良数据辨识带来干扰^[1-2]。此外，相比于大电网，有源配电网信息通信系统的网络构成多元混杂，网络访问权限相对开放，安全防御措施欠缺。黑客易获取相关的系统量测配置以及实时量测信息，构建出恶意注入电网不良数据的攻击向量，系统数据安全受到严重威胁^[3-5]。

相比于传统的集中式状态估计，配电网多区域分布式计算方法复杂度低，数值稳定性好，能将坏数据造成的影响限制在子区域内，更具研究价值与现实意义^[6]。国内外学者针对分布式状态估计展开了一系列研究。文献[7-8]提出了基于一致性理论的输电网分布式状态估计算法，各子区域通过交换一致性变量和边界量测信息来得到全局信息变量。文献[9]提出了含分布式电源的中低压配电网状态估计方法，具有良好的估计精度和收敛性。文献[10]提出了多源量测数据融合的配电网状态估计方法，融合了同步相量测量单元(phasor measurement unit，PMU)量测、数据采集与监视控制系统(supervisory control and data acquisition，SCADA)量测以及高级量测系统(advanced metering infrastructure，AMI)量测进行状态估计，形式简单精度高，但应用于配电网时，因量测数据体量大导致计算量显著增加。文献[11]提出了含多类型分布式电源的主动配电网分布式三相状态估计，将分布式电源作为伪量测来满足可观性，需要的量测信息少。文献[12-13]提出了基于PMU量测的配电网状态估计，能消除不良数据的影响并满足估计精度以及计算速度的要求。上述文献主要研究正常量测情况下的分布式状态估计算法，尚未考虑网络攻击对状态估计的影响。

近年来，电力系统虚假数据攻击事件层出不穷，研究表明攻击者可以采用多种方法构建虚假数据攻击，严重危害电力系统的安全运行^[14-15]，业界开始研究考虑虚假数据注入攻击的状态估计方法。文献[16-18]设计了不同的检测器以及电网故障诊断方法来纠正错误信息，虽然可以有效应对随机虚假数据攻击，但难以准确辨识满足基尔霍夫定律的完美虚假数据攻击。

针对虚假数据注入攻击问题，文中以文献[7-8]所提分布式状态估计算法为基础，提出了基于PMU的有源配电网分布式状态估计方法，通过在关键节点配置PMU来抑制完美虚假数据攻击。为提高状态估计的抗差能力，文中提出在子区域状态估计中引入权函数来动态修正目标极值函数权重矩阵; 为提高虚假数据注入攻击辨识能力，文中提出在易受虚假数据攻击的节点和分区边界节点配置PMU。最后，通过对比试验证明了文中方法可有效减小有源配电网状态估计误差，提高虚假数据注入攻击辨识能力。

1 有源配电网状态估计模型

在电力系统状态估计中，量测数据主要包括节点注入有功和无功功率、支路有功和无功功率、节点电压幅值; 系统状态变量主要包括节点电压幅值和相角。两者的非线性关系可表示为：

$ \mathit{\boldsymbol{z}} = \mathit{\boldsymbol{h}}\left( \mathit{\boldsymbol{x}} \right) + \mathit{\boldsymbol{v}} $

(1)

式中：z=[z₁ z₂ … z_m]^T，为m维的量测向量; x=[x₁ x₂ … x_2n-1]^T，为2n-1维的状态向量，n为电力系统节点数; v=[v₁ v₂ … v_m]^T，为m维的量测噪声向量; h(·)为交流电网模型下量测量与状态变量之间的非线性映射函数向量。

假设配电网系统三相对称平衡，非线性映射函数向量h(·)与节点注入功率方程和支路功率方程相关。量测数据中不可避免地存在坏数据，使状态估计的精度降低，当电力系统中的坏数据较多时甚至会造成状态估计不收敛。因此，在状态估计后增加不良数据检测环节，一般采用目标函数极值检测或残差检测^[19]。

2 虚假数据攻击模型及检测方法 2.1 虚假数据攻击模型

虚假数据注入攻击利用配电网信息系统漏洞，恶意篡改量测终端数据，破坏状态估计结果的准确性和可靠性，危害配电网安全可靠运行。任一节点状态量改变将会导致其他节点和支路潮流发生变化。一般的随机虚假数据注入攻击情况下，攻击前后量测残差的差异较大，容易被不良数据检测环节发现而导致攻击失败。为成功实施虚假数据注入攻击，攻击者很可能采用完美虚假数据注入攻击，即：攻击者根据电力系统网络方程构建满足基尔霍夫定律的虚假数据注入攻击向量，使攻击前后的量测残差保持一致，从而躲过不良数据检测辨识。完美虚假数据注入攻击向量a可表示为：

$ \boldsymbol{a}=\boldsymbol{h}\left(\hat{\boldsymbol{x}}_{\mathrm{bad}}\right)-\boldsymbol{h}(\hat{\boldsymbol{x}}) $

(2)

式中：$ \hat{\boldsymbol{x}}_{\mathrm{bad}} $为系统遭受攻击后篡改的状态估计值; $\hat{\boldsymbol{x}} $为系统状态估计值。

假设攻击者通过篡改节点注入功率量测及支路功率量测的方式，间接篡改目标电压相角状态量来达到特定值。攻击者如果要向SCADA实施虚假数据注入攻击，通常会选择篡改量测数量较小而攻击结果影响较大的节点来进行攻击，以此降低自己的攻击成本，文中称这类节点为易受虚假数据注入攻击节点或脆弱节点。对于辐射状的配电网而言，如果要篡改某节点的状态值，则须篡改该节点与相邻节点的有功、无功功率量测，以及节点之间支路上的有功、无功量测。如果该节点与相邻节点以及支路间的量测数量越多，那么攻击该节点需要篡改的量测数量越多，攻击成本越大，该节点越不容易受到攻击，反之，如果该节点与相邻节点以及支路间的量测数量越少，那么攻击该节点需要篡改的量测数量越少，攻击成本越低，该节点就越容易受到攻击。

对于完美的虚假数据注入攻击行为，目前有效的检测方法较少^[20]。考虑到PMU量测数据中包含全球定位系统(global positioning system，GPS)时间戳，攻击者不易向PMU中注入虚假数据，文中提出在易受攻击的节点处配置PMU，利用PMU提供的可靠电压幅值和相角量测数据来抑制虚假数据注入攻击造成的影响。

2.2 虚假数据注入攻击检测原理

目标函数极值J($\hat{\boldsymbol{x}} $)检测实际上是统计样本的实际观测值与理论推断值之间的偏离程度，其服从卡方分布，卡方检测值χ²越大则实际观测值与理论推断值之间的偏离程度就越大，若实际观测值与理论推断值完全相等，则卡方检测值χ²为0。卡方检测具有可加性，可分为SCADA提供的节点、支路功率量测的卡方检测以及PMU提供的电压幅值、相角量测的卡方检测。当发生完美虚假数据注入攻击时，因为符合基尔霍夫定律，所以即使系统的状态量$\hat{\boldsymbol{x}} $发生改变，SCADA提供的节点、支路功率量测值与理论推断值也不会有较大差异，但PMU提供的电压幅值和相角量测值与理论推断值会有明显差异，远远大于0，卡方检测值即目标函数极值检测会发生显著增长。

在实际运用中，因为PMU提供的量测量权重较大，在推算过程中电压幅值、相角的实际观察值与理论推断值相比会减小，而节点、支路功率的实际观察值与理论推断值相比会增大，使得目标极值检测值发生显著增长。

3 多区域状态估计模型及其求解算法 3.1 多区域状态估计模型

不同应用场景下配电网的分区方法不同^[21-22]，具体的分区方法不再赘述。就文中所提状态估计方法而言，其分区主要考虑3个基本原则：(1) 各子区域内部量测应满足可观性，这是分布式状态估计算法收敛的必要条件; (2) 各子区域内节点数相对均衡，以期最大限度地提高分布式迭代计算效率; (3) 边界节点配置有PMU量测，为利用PMU的高精度量测来辨识和抑制虚假数据注入攻击提供条件。

配电网系统分区如图 1所示，其中子区域内不与相邻区域连接的节点称为内部节点，与相邻区域连接的节点称为边界节点。

为使状态估计全局收敛，在某一个子区域内设置全网的平衡节点，并在边界节点以及子区域内部的关键节点(易受到攻击节点)配置PMU，提供电压幅值以及相角量测，在保护内部关键节点的同时确保子区域内部不良数据的影响不会扩散到其他区域。

系统的状态估计量测方程可分为内部量测和边界量测，量测方程如下：

$ \left\{\begin{array}{l} \boldsymbol{z}_{i}=\boldsymbol{h}_{i}\left(\boldsymbol{x}_{i}\right)+\boldsymbol{v}_{i} \quad i=1,2, \cdots, l \\ \boldsymbol{z}_{\mathrm{c}}=\boldsymbol{h}_{\mathrm{c}}\left(\boldsymbol{x}_{\mathrm{c}}\right)+\boldsymbol{v}_{\mathrm{c}} \end{array}\right. $

(3)

式中：z_i为m_i维子区域S_i内部量测向量; x_i为子区域S_i内部状态变量向量; l为子区域个数; h_i(·)为交流模型下子区域S_i内部量测量和状态变量之间的非线性映射函数向量; v_i为子区域S_i内部量测误差向量; z_c为边界量测向量; x_c为边界状态变量向量; h_c(·)为交流模型下边界量测量和状态变量之间的非线性映射函数向量; v_c为边界量测误差向量。

分区后多区域状态估计模型如下：

$ \left\{\begin{array}{l} \min J(\boldsymbol{x})=\boldsymbol{r}_{\mathrm{c}}^{\mathrm{T}} \boldsymbol{R}_{\mathrm{c}}^{-1} \boldsymbol{r}_{\mathrm{c}}+\sum\limits_{i=1}^{l} \boldsymbol{r}_{i}^{\mathrm{T}} \boldsymbol{R}_{i}^{-1} \boldsymbol{r}_{i} \\ \boldsymbol{r}_{\mathrm{c}}=\boldsymbol{z}_{\mathrm{c}}-\boldsymbol{h}_{\mathrm{c}}(\boldsymbol{x}) \end{array}\right. $

(4)

式中：r_i=z_i-h_i(x_i)，为子区域S_i内部量测量所对应的残差向量; r_c为所有边界量测量所对应的残差向量; x=[x₁ x₂ … x_l]^T，为整个系统的状态向量; R_i=diag(σ₁², σ₂², …, σ_mi²)，为子区域S_i内部量测量所对应量测方差的方差对角阵; R_c=diag(σ_{c, 1}², σ_{c, 2}², …, σ_{c, mc}²)，为所有边界量测所对应量测误差的方差对角阵。

为了让分布式状态估计在迭代过程中消除粗差，避免粗差对分布式状态估计结果造成影响，在分布式状态估计模型中引入权函数。其原理为：在迭代过程中，残差向量e中某一量测值对应的残差$ e_{i}=z_{i}^{\prime}-\hat{z}_{i}^{\prime}$，其中z′ _i为实际量测值，$\hat{z}_{i}^{\prime} $为量测估计值，超过限定的门槛值K时，对该量测量对应的权值进行降权，不超过则权值保持不变^[23-24]。

首先引入一个稳健的尺度估计s来使残差标准化，s取值为绝对残差中位数除以一个常数C，则标准化残差u_i可表示为：

$ u_{i}=\frac{e_{i}}{s}=\frac{e_{i}}{\operatorname{med}(|\boldsymbol{e}|) / C} $

(5)

式中：med(|e|)为所有残差绝对值的中位数。

然后将标准化残差u_i与门槛值K进行比较求取权因子ω(u_i)，权因子ω(u_i)可表示为：

$ \omega\left(u_{i}\right)= \begin{cases}1 & \left|u_{i}\right| \leqslant K \\ K /\left|u_{i}\right| & \left|u_{i}\right|>K\end{cases} $

(6)

最后对权重进行更新：

$ P_{k+1}=\omega\left(u_{i}\right) P_{k} $

(7)

式中：P_k为变权前的初始权; P_k+1为变权后的等价权。

3.2 基于拉格朗日乘子法的整体模型求解

用拉格朗日乘子法求解多区域状态估计模型，构造拉格朗日函数如下：

$ \begin{aligned} L(\boldsymbol{x}, \boldsymbol{\lambda})=& \frac{1}{2} \boldsymbol{r}_{\mathrm{c}}^{\mathrm{T}} \boldsymbol{R}_{\mathrm{c}}^{-1} \boldsymbol{x}_{\mathrm{c}}+\frac{1}{2} \sum\limits_{i=1}^{l} \boldsymbol{x}_{i}^{\mathrm{T}} \boldsymbol{R}_{i}^{-1} \boldsymbol{x}_{i}+\\ & \boldsymbol{\lambda}^{\mathrm{T}}\left(\boldsymbol{r}_{\mathrm{c}}-\boldsymbol{z}_{\mathrm{c}}+\boldsymbol{h}_{\mathrm{c}}(\boldsymbol{x})\right) \end{aligned} $

(8)

式中：λ为拉格朗日乘子向量。

求解拉格朗日函数极值的迭代公式如下^[7-8]：

$ \Delta \boldsymbol{y}_{i, k}=\boldsymbol{G}_{i}^{-1}\left(\boldsymbol{x}_{i, k}\right) \boldsymbol{H}_{i}^{\mathrm{T}}\left(\boldsymbol{x}_{i, k}\right) \boldsymbol{R}_{i, k}^{-1} \Delta \boldsymbol{z}_{i, k} $

(9)

$ \boldsymbol{\lambda}_{k}=\boldsymbol{G}_{\bf{c}}^{-1}\left(\boldsymbol{x}_{k}\right)\left(\Delta \boldsymbol{z}_{\mathrm{c}, k}-\sum\limits_{i=1}^{l} \boldsymbol{H}_{\mathrm{c}, i}\left(\boldsymbol{x}_{i, k}\right) \Delta \boldsymbol{y}_{i, k}\right) $

(10)

$ \boldsymbol{u}_{i, k}=\boldsymbol{G}_{i}^{-1}\left(\boldsymbol{x}_{i, k}\right) \boldsymbol{H}_{\mathrm{c}, i}^{\mathrm{T}}\left(\boldsymbol{x}_{i, k}\right) \boldsymbol{\lambda}_{k} $

(11)

$ \Delta \boldsymbol{x}_{i, k}=\Delta \boldsymbol{y}_{i, k}+\boldsymbol{u}_{i, k} $

(12)

$ \boldsymbol{x}_{i, k+1}=\boldsymbol{x}_{i, k}+\Delta \boldsymbol{x}_{i, k} $

(13)

$ \boldsymbol{R}_{i, k+1}^{-1}=\omega \boldsymbol{R}_{i, k}^{-1} $

(14)

$ \boldsymbol{G}_{i}\left(\boldsymbol{x}_{i, k}\right)=\boldsymbol{H}_{i}^{\mathrm{T}}\left(\boldsymbol{x}_{i, k}\right) \boldsymbol{R}_{i}^{-1} \boldsymbol{H}_{i}\left(\boldsymbol{x}_{i, k}\right) $

(15)

$ \Delta \boldsymbol{z}_{i, k}=\boldsymbol{z}_{i}-\boldsymbol{h}_{i}\left(\boldsymbol{x}_{i, k}\right) \quad i=1,2, \cdots, l $

(16)

$ \Delta \boldsymbol{z}_{\mathrm{c}, k}=\boldsymbol{z}_{\mathrm{c}}-\boldsymbol{h}_{\mathrm{c}}\left(\boldsymbol{x}_{i, k}\right) $

(17)

$ \boldsymbol{G}_{\mathrm{c}}\left(\boldsymbol{x}_{k}\right)=\sum\limits_{i=1}^{l}\left(\boldsymbol{R}_{\mathrm{c}, i}+\boldsymbol{H}_{\mathrm{c}, i}\left(\boldsymbol{x}_{i, k}\right) \boldsymbol{G}_{i}^{-1}\left(\boldsymbol{x}_{i, k}\right) \boldsymbol{H}_{\mathrm{c}, i}^{\mathrm{T}}\left(\boldsymbol{x}_{i, k}\right)\right) $

(18)

式中：k为迭代次数; $ \boldsymbol{H}_{i}\left(\boldsymbol{x}_{i}\right)=\partial \boldsymbol{h}_{i}\left(\boldsymbol{x}_{i}\right) / \partial \boldsymbol{x}_{i}$，为与区域S_i内部量测相关的雅可比矩阵; $ \boldsymbol{H}_{\mathrm{c}, i}\left(\boldsymbol{x}_{i}\right)= \partial \boldsymbol{h}_{\mathrm{c}, i}\left(\boldsymbol{x}_{i}\right) / \partial \boldsymbol{x}_{i} $，为与子区域S_i边界量测相关的雅可比矩阵; u_{i, k}为各子区域相邻区域交互一致性变量后得到的状态量修正值。

因为是采取非重叠的分区方法，式(9)中G_i(x_{i, k})，H(x_{i, k})，Δz_{i, k}的计算只依赖子区域S_i内部的量测信息以及状态变量x_i，各子区域可通过式(9)独立求解出内部的估计值Δy_{i, k}。而式(10)中的$ \boldsymbol{G}_{\mathrm{c}}\left(\boldsymbol{x}_{k}\right), \Delta \boldsymbol{z}_{\mathrm{c}, k}, \sum\limits_{i=1}^{l} \boldsymbol{H}_{\mathrm{c}, i}\left(\boldsymbol{x}_{i, k}\right) \Delta \boldsymbol{y}_{i, k}$的计算则应依赖所有边界量测信息以及边界节点状态变量。为求取λ_k，这里采用平均一致性算法^[25]，通过分布式迭代方式进行求解。该算法只需要相邻子区域间交互量测信息，而无需控制中心统一量测信息，通过多次分布式迭代各子区域可获得全局变量λ_k。在获得全局变量λ_k之后，通过子区域S_i的内部以及边界的量测信息以及状态变量求解G_i(x_{i, k})以及H_{c, i}(x_{i, k})，获取内部估计值的修正量u_{i, k}。通过式(12)和式(13)获取全局最优解Δx_{i, k}以及x_{i, k+1}，并利用式(14)更新权重R_{i, k+1}^-1。

3.3 基于平均一致性算法的全局变量λ_k求解

为利用平均一致性算法通过分布式迭代求解λ_k，将式(10)改写为：

$ \begin{gathered} \boldsymbol{\lambda}_{k}=\left(\frac{1}{l} \boldsymbol{G}_{\mathrm{c}}\left(\boldsymbol{x}_{k}\right)\right)^{-1} \times \\ \frac{1}{l} \sum\limits_{i=1}^{l}\left(\Delta \boldsymbol{z}_{\mathrm{c}, i, k}-\boldsymbol{H}_{\mathrm{c}, i}\left(\boldsymbol{x}_{i, k}\right) \Delta \boldsymbol{y}_{i, k}\right) \end{gathered} $

(19)

用平均一致性算法分别对$\frac{1}{l} \boldsymbol{G}_{\mathrm{c}}\left(\boldsymbol{x}_{k}\right)$和$ \frac{1}{l} \sum\limits_{i=1}^{l}\left(\Delta z_{c, i, k}-\boldsymbol{H}_{\mathrm{c}, i}\left(\boldsymbol{x}_{i, k}\right) \Delta \boldsymbol{y}_{i, k}\right)$进行求解，迭代求解算法如下：

$ \begin{array}{c} \left[\begin{array}{c} \frac{1}{l} \boldsymbol{G}_{\mathrm{c}}\left(\boldsymbol{x}_{k}\right) \\ \frac{1}{l} \boldsymbol{G}_{\mathrm{c}}\left(\boldsymbol{x}_{k}\right) \\ \vdots \\ \frac{1}{l} \boldsymbol{G}_{\mathrm{c}}\left(\boldsymbol{x}_{k}\right) \end{array}\right]=\\ \lim \limits_{t \rightarrow \infty} \boldsymbol{D}^{t}\left[\begin{array}{c} \boldsymbol{R}_{\mathrm{c}, 1}+\boldsymbol{H}_{\mathrm{c}, 1}\left(\boldsymbol{x}_{1, k}\right) \boldsymbol{G}_{1}^{-1}\left(\boldsymbol{x}_{1, k}\right) \boldsymbol{H}_{\mathrm{c}, 1}^{\mathrm{T}}\left(\boldsymbol{x}_{1, k}\right) \\ \boldsymbol{R}_{\mathrm{c}, 2}+\boldsymbol{H}_{\mathrm{c}, 2}\left(\boldsymbol{x}_{2, k}\right) \boldsymbol{G}_{2}^{-1}\left(\boldsymbol{x}_{2, k}\right) \boldsymbol{H}_{\mathrm{c}, 2}^{\mathrm{T}}\left(\boldsymbol{x}_{2, k}\right) \\ \vdots \\ \boldsymbol{R}_{\mathrm{c}, l}+\boldsymbol{H}_{\mathrm{c}, l}\left(\boldsymbol{x}_{l, k}\right) \boldsymbol{G}_{r}^{-1}\left(\boldsymbol{x}_{l, k}\right) \boldsymbol{H}_{\mathrm{c}, l}^{\mathrm{T}}\left(\boldsymbol{x}_{l, k}\right) \end{array}\right]^{[0]} \end{array} $

(20)

$ \begin{gathered} {\left[\begin{array}{c} \frac{1}{l} \sum\limits_{i=1}^{l}\left(\Delta \boldsymbol{z}_{\mathrm{c}, i, k}-\boldsymbol{H}_{\mathrm{c}, i}\left(\boldsymbol{x}_{i, k}\right) \Delta \boldsymbol{y}_{i, k}\right) \\ \frac{1}{l} \sum\limits_{i=1}^{l}\left(\Delta \boldsymbol{z}_{\mathrm{c}, i, k}-\boldsymbol{H}_{\mathrm{c}, i}\left(\boldsymbol{x}_{i, k}\right) \Delta \boldsymbol{y}_{i, k}\right) \\ \vdots \\ \frac{1}{l} \sum\limits_{i=1}^{l}\left(\Delta \boldsymbol{z}_{\mathrm{c}, i, k}-\boldsymbol{H}_{\mathrm{c}, i}\left(\boldsymbol{x}_{i, k}\right) \Delta \boldsymbol{y}_{i, k}\right) \end{array}\right]=} \\ \lim \limits_{t \rightarrow \infty} \boldsymbol{D}^{t}\left[\begin{array}{c} \Delta \boldsymbol{z}_{\mathrm{c}, 1, k}-\boldsymbol{H}_{\mathrm{c}, 1}\left(\boldsymbol{x}_{1, k}\right) \Delta \boldsymbol{y}_{1, k} \\ \Delta \boldsymbol{z}_{\mathrm{c}, 2, k}-\boldsymbol{H}_{\mathrm{c}, 2}\left(\boldsymbol{x}_{2, k}\right) \Delta \boldsymbol{y}_{2, k} \\ \vdots \\ \Delta \boldsymbol{z}_{\mathrm{c}, l, k}-\boldsymbol{H}_{\mathrm{c}, l}\left(\boldsymbol{x}_{l, k}\right) \Delta \boldsymbol{y}_{l, k} \end{array}\right]^{[0]} \end{gathered} $

(21)

式中：t为一致性变量求解的迭代次数; D为行随机矩阵，与系统的通信拓扑有关^[7-8]; 上标[0]表示各子区域一致性变量初值。

根据式(20)和式(21)，子区域S_i独立计算本地一致性变量初值[R_{c, i}+H_{c, i}(x_{i, k})G_i^-1(x_{i, k})×H_{c, i}^T(x_{i, k})]^[0]和[Δz_{c, i, k}-H_{c, i}(x_{i, k})Δy_{i, k}]^[0]后，再通过行随机矩阵D与相邻子区域进行信息交换。行随机矩阵D各行元素和为1，实际起到了权重的作用，与子区域S_i相邻的区域的一致性变量权重非零，不相邻的区域的一致性变量权重为零，通过一次迭代即乘以行随机矩阵D，获取子区域S_i相邻区域的一致性变量信息，对子区域S_i本地一致性变量进行修正，得到[R_ci+H_{c, i}(x_{i, k})G_i^-1(x_{i, k})H_{c, i}^T(x_{i, k})]^[1]和[Δz_{c, i, k}-H_{c, i}(x_{i, k})Δy_{i, k}]^[1]。理论上，当t趋向于无穷大时，各子区域收敛于一致性变量均值，需要说明的是，在实际应用中只需经过有限次迭代求取满足一定精度的近似一致性变量均值。

3.4 多区域状态估计算法流程

图 2为各子区域的状态估计流程。首先，读入量测信息以及误差矩阵，并设置状态向量初值x_{i, 1}进行初始化，各子区域根据区域内部量测向量z_i和状态变量向量x_{i, k}进行区域内部状态估计得到内部状态估计值Δy_{i, k}，然后计算本地的一致性变量初值，并根据一致性协议与相邻子区域交互信息，经过有限次迭代后得到一致性变量均值，求解全局变量λ_k，结合子区域自身的边界量测求取内部状态修正量u_{i, k}，叠加得到全局最优解Δx_{i, k}以及x_{i, k+1}，并根据残差对子区域S_i内部量测权重R_i^-1进行更新，直到所有子区域全局最优解Δx_{i, k}(i=1, 2, …, l)都收敛至小于阈值τ时停止迭代。

4 IEEE 118节点配电网仿真 4.1 仿真系统介绍

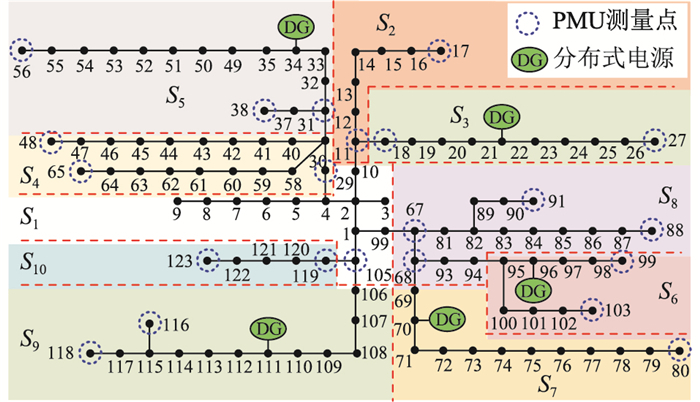
为验证所提分布式状态估计方法的有效性，选用IEEE 118节点配电网系统进行数值仿真。状态估计算法在Matlab 2017b软件平台上编程实现，并利用Matpower 7.0软件包计算配电网系统潮流，把潮流计算结果作为真实量测值，用于状态估计结果对比分析。仿真测试系统结构如图 3所示。

由图 3可以看出，将IEEE 118节点系统划分为S₁-S₁₀共10个子区域。将节点1设置为系统的平衡节点，除含平衡节点的子区域之外，在其余各子区域选取容易受到攻击的节点配置PMU量测，系统为全量测系统，SCADA量测量包括各支路功率和各节点注入功率。在仿真测试中，各变量的量测误差设置如下：电压幅值量测误差σ_v=1×10^-5，电压相角量测误差σ_θ=1×10^-5，节点i注入功率量测误差σ_i=1×10^-4，线路i-j输送功率量测误差σ_ij=8×10^-5。

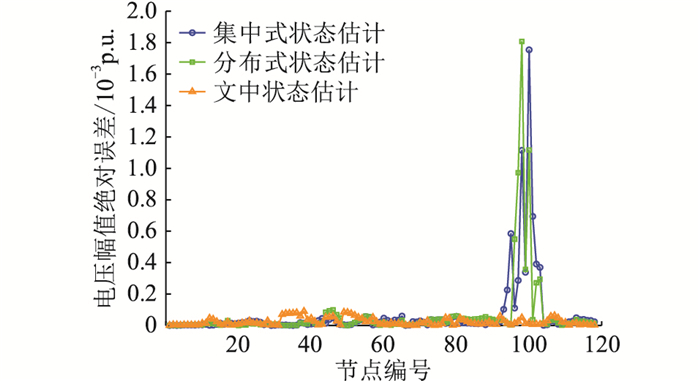
4.2 多区域状态估计结果分析

在正常运行的情况下，采用文中所提状态估计方法对IEEE 118节点测试系统进行仿真，利用仿真结果与真实值的绝对误差作为评估状态估计方法性能的指标，并将仿真结果与集中式状态估计和分布式状态估计^[7-8]进行比较，比较结果如图 4和图 5所示。

由图 4和图 5可以看出，在相同量测值的情况下，与集中式和分布式状态估计方法相比，文中所提状态估计方法得到的电压幅值与真实值相差不大，绝对误差都在0.000 1内，而电压相角与其他估计方法所得相角相比更接近真实值，具有更高的估计精度。

4.3 虚假数据检测与抑制效果分析 4.3.1 随机虚假数据攻击场景

在IEEE 118节点系统中的S₆区域随机注入攻击向量，攻击向量无须满足基尔霍夫定律。分别采用文中所提状态估计方法、集中式状态估计、分布式状态估计进行仿真，随机虚假数据攻击后电压幅值与相角绝对误差如图 6和图 7所示。

由图 6和图 7可以看出，随机虚假数据攻击后文中所提状态估计结果比起集中式和分布式状态估计结果要更加接近真实值，可以看出文中所提状态估计方法能够有效地抑制随机虚假数据攻击对状态估计造成的影响。

文中所提状态估计和现有的分布式状态估计在遭受随机虚假数据注入攻击后目标函数极值J($\hat{\boldsymbol{x}} $)的变化如表 1和表 2所示，残差r的变化如表 3和表 4所示。

在实验中，集中式状态估计在受随机虚假数据攻击后目标极值检测值J($\hat{\boldsymbol{x}} $)由250.380 1变为90 237，残差检测值r由0.015 0变为0.027 90，变化幅度较大，因此集中式状态估计可通过目标极值或残差检测来辨识攻击。由表 1-表 4可以看出，现有的分布式状态估计在随机虚假数据攻击后，区域S₆的目标极值检测值J($\hat{\boldsymbol{x}} $)由22.900 7变为88 121，残差检测值r由0.000 44变为0.027 60，变化幅度也较大，而其他子区域目标极值检测值J($\hat{\boldsymbol{x}} $)以及残差检测值r不发生改变，因此分布式状态估计也可以有效检测出随机虚假数据攻击。文中所提状态估计方法，由于权函数的存在，在迭代过程中消除了不良数据的影响，因此目标极值检测值J($\hat{\boldsymbol{x}} $)基本不发生变化，但残差检测值r由0.000 49变为0.041 20，变化幅度较大，可见文中状态估计不仅可以有效检测出随机虚假数据攻击，还能减小虚假数据注入攻击对估计结果的影响。

4.3.2 完美虚假数据攻击场景

在IEEE 118节点系统的节点103处注入攻击向量来篡改其相角+0.045°，如要构造符合基尔霍夫定律的完美虚假数据，则需要篡改节点102和103的有功和无功注入功率以及支路102-103的有功和无功潮流。文中构造攻击向量a，改变节点102的有功注入功率-0.003 14 p.u.，无功注入功率+0.000 76 p.u.，节点103的有功注入功率+0.003 15 p.u.，无功注入功率-0.000 71 p.u.，支路102-103的有功潮流-0.003 14 p.u.，无功潮流+0.000 76 p.u.。对于文中所提分布式状态估计，在节点103处配置PMU，将节点103的电压幅值和相角量测作为区域S₆的内部量测。当系统遭受到上文构建的虚假数据攻击时，PMU为状态估计提供了准确且高精度的量测，状态估计会强制拟合电压幅值和相角量测。

分别采用文中所提状态估计法、集中式状态估计法和分布式状态估计法进行仿真，完美虚假数据攻击后电压相角绝对误差如图 8所示。

由图 8可以看出，完美虚假数据攻击对于集中式和分布式状态估计的危害较大，攻击者可以随意篡改节点的状态值，而文中状态估计结果相对接近真实值，能够有效抑制完美虚假数据攻击对状态估计造成的影响。

文中状态估计和分布式状态估计在遭受完美虚假数据注入攻击后目标函数极值J($\hat{\boldsymbol{x}} $)如表 5和表 6所示，残差r的变化如表 7和表 8所示。

在实验中，集中式状态估计方法在受到完美虚假数据攻击后的目标极值检测值J($\hat{\boldsymbol{x}} $)由250.380 1变为259.036 5，残差检测值r由0.015 0变为0.014 0，可见目标极值和残差的变化幅度较小，难以准确辨识完美虚假数据注入攻击。由表 5-表 8可以看出，分布式状态估计在受到完美虚假数据攻击后目标极值检测值J($\hat{\boldsymbol{x}} $)以及残差检测值r基本保持不变，完美虚假数据攻击可以绕过不良数据检测环节。对于文中状态估计，子区域S₆的目标函数检测值J($\hat{\boldsymbol{x}} $)由11.556 9变为264.536 8，残差检测值r由0.000 49变为0.002 70，变化幅度较大，其他子区域的目标函数检测值J($\hat{\boldsymbol{x}} $)以及残差检测值r基本保持不变，可见文中状态估计方法可以有效识别子区域内是否发生完美虚假数据攻击。

从上述实验结果可以看出，无论是随机虚假数据注入攻击，还是完美虚假数据注入攻击，因攻击导致状态估计结果偏差较大的子区域都是S₆，即虚假数据注入攻击所在的子区域。主要原因为：(1) 采用了分布式计算方法，各子区域独立进行运算; (2) 在各子区域边界节点配置的PMU提供了高精度的电压幅值和相角量测，从而把强制拟合电压幅值和相角量测时对状态估计结果造成的影响限制在本子区域内，保证其他子区域的状态估计结果不受影响。

5 结论

针对有源配电网量测干扰多、易受虚假数据注入攻击而导致状态估计不可靠的问题，文中提出了基于PMU的多区域分布式状态估计方法。该方法具有3个特征：各子区域独立进行运算，并通过平均一致性协议实现子区域间的信息交互，实现了完全分布式状态估计; 在子区域内引入权函数，提高了状态估计的抗差能力; 在易受攻击的节点以及边界节点配置PMU，抑制了虚假数据攻击的不良影响。

基于IEEE 118节点系统的算例仿真对比试验，得到结论：(1) 与传统的集中式状态估计和现有的分布式状态估计相比，文中方法具有更高的估计精度; (2) 无论是随机虚假数据攻击还是完美虚假数据攻击，文中状态估计方法均可有效减小攻击造成的估计误差，同时可通过目标极值检测或残差检测准确辨识攻击。

需要说明的是，文中方法主要侧重于虚假数据注入攻击下有源配电网状态估计，尚未考虑拒绝服务攻击、重放攻击等其他攻击类型。另外，文中方法的计算过程需要各子区域分布式迭代实现，后续将研究算法的迭代计算效率问题。