文章编号: 2096-3203(2022)03-0216-08 中图分类号: TM85
2. 中国能源建设集团安徽省电力设计院有限公司,安徽 合肥 230601;
3. 国网安徽省电力有限公司合肥供电公司,安徽 合肥 230061
与传统架空线路、直埋式电缆和电缆沟敷设电缆相比,电缆隧道具有敷设不受外界条件影响、可靠性高、容纳回路数多等优势[1-4]。然而,电缆在带负荷运行过程中存在热损耗,这些热损耗使得电缆本体及隧道内部温度不断升高。尤其是电压等级高、回路数多时,温度问题将进一步加剧,常加装通风设备来改善空间散热问题。强制通风与自然通风相比,其好处在于能在相同时间内带走更多的热量,提高散热速率,从而大幅减小风口的高度差,降低建设成本。为了保证电缆线路安全稳定运行,亟须研究和掌握电缆温度场在风机流场作用下的变化规律及其对载流量的影响。
目前已提出的电缆温度计算方法包括热路法和数值法[5]。A.E.Kennelly最早提出了计算电缆温度的热路模型。随后,Neher与McGrath[6]利用电路模型与热路模型形式上的相似性,根据欧姆定律和基尔霍夫定律,提出了计算温度分布的NM法。NM法考虑外部环境因素的影响从而计算电缆温度和载流量。IEC对NM法进行了改进,制定了电缆载流量计算标准和周期载流量标准,但计算结果与实际测量值偏差较大。在一些敷设方式下,例如排管敷设、电缆沟敷设、电缆隧道敷设,电缆与壁面之间存在空气层。IEC给出的载流量计算标准尚未考虑空气层中的热传导、热对流及热辐射现象,因此载流量计算准确度不高。为弥补IEC标准的不足,诸多学者提出了改进的热路法[7-13]以提高精度。
随着计算机技术的发展,数值仿真已成为计算电缆温度的常用手段,尤其是有限元法已得到广泛的应用[14-18]。文献[14]结合有限元法和粒子群算法对电缆周围土壤的热特性参数进行估算;文献[15-16]针对排管敷设方式,采用有限元法进行数值计算;文献[17]建立了电缆接头电-热耦合模型,分析接头内部温度和电场分布规律。有限元法能够模拟计算耦合的多物理场,适用于计算复杂敷设时的电缆温度。
敷设于隧道中的运行电缆,其温度分布与空气流动息息相关,故须考虑热-流之间的耦合作用。文中采用有限元法,运用COMSOL Multiphysics仿真软件,根据实际电缆隧道尺寸结构及电缆排布情况,建立超高压电缆热-流耦合模型,全面考虑了空气温度、空气速率、隧道截面形状、电缆空间排布等因素,分析空气流动影响下电缆温度场的分布情况及电缆载流量。
1 电缆隧道敷设电缆温度场计算原理 1.1 电缆传热分析根据热力学基本定律,当某个系统存在温差时,系统内部就会产生方向为高温到低温的热量交换过程。热量交换方式分为热传导、热对流、热辐射3种类型[19]。
热传导的热量交换方式大多为热量从温度较高处传递到温度较低处。热传导的热量交换规律可由傅里叶定律来表述,如式(1)所示。
| $ q_{\mathrm{c}}=-k \frac{\partial T}{\partial x} $ | (1) |
式中:qc为传导热流密度;k为导热系数,是反映材料的导热能力的重要参数;∂T/∂x为单位面积温度梯度。
电缆在运行过程中,气流流过电缆表面,带走部分热量,这种传热方式为对流传热。根据产生的原因不同,对流传热可分为自然对流与强制对流。自然对流是由于流体内部温度不同而引起的,与外力无关。强制对流则是由风机等外力作用导致的流体流动。对于启动风机的电缆隧道,其对流传热方式为强制对流,热流密度如式(2)所示。
| $ q_{\mathrm{d}}=h\left(T_{1}-T_{2}\right) $ | (2) |
式中:h为对流换热系数;T1为流体温度;T2为物体表面温度。
热辐射是指物体具有温度而产生辐射电磁波的热量传递过程,且温度越高,热辐射越大。
电缆隧道内的传热方式包括热传导、对流传热和热辐射3种。热传导发生在电缆本体内部、隧道与周围土壤之间。由于电缆隧道内装有通风装置,空气与电缆表面之间的传热过程主要为强制对流。相较于对流传热,电缆表面与隧道壁之间的热辐射对温度影响较小[20-24]。
1.2 电缆发热计算在运行过程中电缆带负荷产生的热损耗,是导致电缆发热的主要原因。
1.2.1 导体损耗单位长度导体产生的损耗如式(3)所示。
| $ W_{\mathrm{c}}=I^{2} R $ | (3) |
式中:I为电缆负荷电流;R为单位长度导体交流电阻,其具体的计算方法如式(4)-式(9)所示。
| $ R=R^{\prime}\left(1+Y_{\mathrm{s}}+Y_{\mathrm{p}}\right) $ | (4) |
| $ R^{\prime}=[1+\alpha(\theta-20)] R_{0} $ | (5) |
| $ Y_{\mathrm{s}}=\frac{x_{\mathrm{s}}^{4}}{192+0.8 x_{\mathrm{s}}^{4}} $ | (6) |
| $ x_{\mathrm{s}}^{2}=\left(8 {\rm{ \mathsf{ π} }} f / R^{\prime}\right) \times 10^{-7} k_{\mathrm{s}} $ | (7) |
| $ \begin{gathered} Y_{\mathrm{p}}=\frac{x_{\mathrm{p}}^{4}}{192+0.8 x_{\mathrm{p}}^{4}}\left(\frac{D_{\mathrm{c}}}{s}\right)^{2} \times \\ {\left[0.312\left(\frac{D_{\mathrm{c}}}{s}\right)^{2}+\frac{1.18}{\frac{x_{\mathrm{p}}^{4}}{192+0.8 x_{\mathrm{p}}^{4}}+0.27}\right]} \end{gathered} $ | (8) |
| $ x_{\mathrm{p}}^{2}=\frac{8 {\rm{ \mathsf{ π} }} f}{R^{\prime}} \times 10^{-7} k_{\mathrm{p}} $ | (9) |
式中:R0为温度20 ℃时单位长度电缆的直流电阻值;α为电缆导体电阻温度系数,对于铜导体,α取0.003 93;θ为导体最高允许温度;Dc为电缆导体的直径;s为相邻电缆导体的轴心距;kp, ks为常数;f为电流频率,取电流工频50 Hz;Ys为趋肤效应系数;Yp为邻近效应系数;xs,xp分别为用于计算趋肤效应系数和邻近效应系数的参数。
1.2.2 绝缘损耗绝缘介质由于加载电压而产生损耗,每相电缆单位长度的绝缘损耗如式(10)所示。
| $ \left\{\begin{array}{l} W_{\mathrm{d}}=2 {\rm{ \mathsf{ π} }} f c U_{0}^{2} \tan \delta \\ c=\frac{\varepsilon}{18 \ln \left(D_{\mathrm{i}} / D_{\mathrm{c}}\right)} \times 10^{-9} \end{array}\right. $ | (10) |
式中:U0为额定相电压;tan δ为介质损耗角的正切值;c为单位长度电容;ε为绝缘的介电常数;Di,Dc分别为绝缘层和导体的直径。
1.2.3 金属护套损耗金属护套损耗包含两部分:涡流损耗和环流损耗。金属护套损耗可表示为:
| $ W_{\mathrm{e1}}=\lambda W_{\mathrm{c}} $ | (11) |
式中:λ为金属护套损耗因数,代表金属护套损耗与导体损耗的比值。
| $ \lambda=\lambda^{\prime}+\lambda^{\prime \prime} $ | (12) |
式中:λ′为环流损耗因数,如式(13)所示;λ″为涡流损耗因数。当3根单芯电缆两端交叉互联接地且电缆排布方式为三角形排列时,涡流损耗可忽略不计,即λ″为0。
| $ \left\{\begin{array}{l} \lambda^{\prime}=\frac{R_{\mathrm{s}}}{R} \frac{1}{1+\left(R_{\mathrm{s}} / X\right)^{2}} \\ X=4 {\rm{ \mathsf{ π} }} f \ln \left(\frac{2 s}{d}\right) \times 10^{-7} \end{array}\right. $ | (13) |
式中:Rs为在一定温度下单位长度电缆金属护套的电阻值;X为单位长度金属护套电抗;d为金属护套层的直径。
1.3 温度场数学模型在实际运行过程中,电缆各层的导热系数会随温度变化。由于电缆的温度须控制在一定的范围内,因此假设电缆各层导热系数保持不变。电缆隧道中配备有通风装置,隧道中的空气会沿着平行于电缆轴向方向快速流动,强制对流对电缆轴向温度的影响不可忽略,据此建立三维模型分析稳态温度分布情况。式(14)为稳态有内热源时对应的温度控制方程。
| $ k\left(\frac{\partial^{2} T}{\partial x^{2}}+\frac{\partial^{2} T}{\partial y^{2}}+\frac{\partial^{2} T}{\partial z^{2}}\right)+Q=0 $ | (14) |
式中:Q为热源;T为温度。
稳态无内热源时温度控制方程如式(15)所示。
| $ \frac{\partial^{2} T}{\partial x^{2}}+\frac{\partial^{2} T}{\partial y^{2}}+\frac{\partial^{2} T}{\partial z^{2}}=0 $ | (15) |
为了完整地描述一个热量传递过程,需要结合温度控制方程和边界条件。导热问题具有3类边界条件。
第1类边界条件给定了某边界上的温度值,如式(16)所示。
| $ \left\{\begin{array}{l} \left.T\right|_{\varGamma}=T_{w} \\ \left.T\right|_{\varGamma}=f(x, y, z, t) \end{array}\right. $ | (16) |
式中:f(x, y, z, t)为已知的边界温度函数,与位置和时间有关;Γ为该求解域的边界;Tw为已知的边界温度。
第2类边界条件给定了某边界上的热流密度大小,如式(17)所示。
| $ \left\{\begin{array}{l} \left.k \frac{\partial T}{\partial n}\right|_{\varGamma}+q_{\mathrm{w}}=0 \\ \left.k \frac{\partial T}{\partial n}\right|_{\varGamma}+g(x, y, z, t)=0 \end{array}\right. $ | (17) |
式中:qw为已知边界的热流密度;g(x, y, z, t)为已知边界的热流密度函数,同样与位置和时间相关。
第3类边界条件给定了某边界上物体表面与周围流体的对流换热系数以及流体的温度。
| $ -\left.k \frac{\partial T}{\partial n}\right|_{\varGamma}=\left.h\left(T-T_{\mathrm{f}}\right)\right|_{\varGamma} $ | (18) |
式中:Tf为流体的温度。
1.4 流体场数学模型假设流体在流动过程中密度的变化忽略不计,流体的特性参数为常数,忽略粘性耗散的影响。流体与物体表面间的对流传热可由流体运动微分方程描述。
由流体流动的质量守恒定律可知,流体流过某一微元体时,流体的总质量保持不变,由此得出流体运动连续性方程如式(19)所示。
| $ \frac{\partial v_{x}}{\partial x}+\frac{\partial v_{y}}{\partial y}=0 $ | (19) |
式中:vx,vy分别为x,y方向上的流速。流体运动问题也须给定边界条件,即设置流体的入口和出口,并给定入口和出口截面的速度和压强分布。
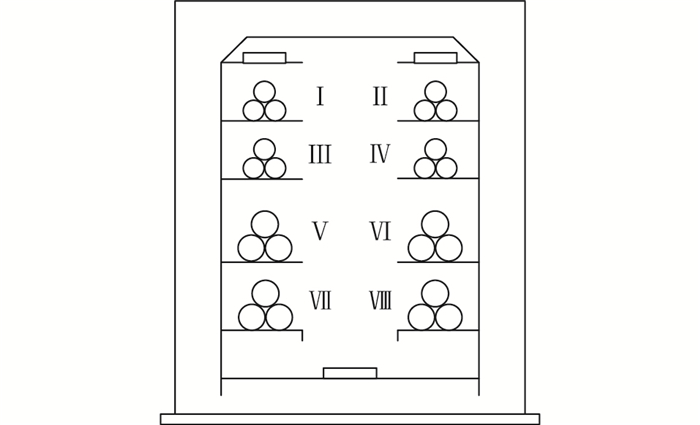
2 电缆热-流耦合场仿真模型建立文中主要依托“京张铁路张家口南牵引站双回外部供电”电缆工程,研究具有8回传输电缆的超高压电缆隧道。实际运行的电缆隧道基本情况如下:隧道尺寸宽为3 m,高为3.6 m;隧道内共敷设8回路单芯电缆,其中4回路为220 kV电缆,4回路为500 kV电缆;电缆三相布置方式为品字形。隧道尺寸及隧道内电缆排布位置如图 1所示。
|
图 1 隧道尺寸及内部电缆排布 Fig. 1 Tunnel dimensions and internal cable layout |
图 1所示的8回路中,隧道上部4回路为220 kV电缆,分别命名为Ⅰ、Ⅱ、Ⅲ、Ⅳ;隧道下部4回路为500 kV电缆,分别命名为Ⅴ、Ⅵ、Ⅶ、Ⅷ。高压电缆截面均为2 500 mm2,具体结构参数如表 1和表 2所示。
|
|
表 1 220 kV电缆各层尺寸参数 Table 1 Parameters of 220 kV cable |
|
|
表 2 500 kV电缆各层尺寸参数 Table 2 Parameters of 500 kV cable |
隧道电缆的实际长度很长且中间有弯曲,为减少计算的难度和复杂度,文中选取其中的一段建立模型,进行仿真研究。根据文献[23],当通风的距离大于5 m时,通风距离的增加对电缆温度的影响将逐渐减小,因此在构建几何模型时,选取5 m长的电缆隧道进行建模。距离隧道2 m以外的土壤,其温度不受电缆产生热量的影响[20],因此土壤厚度选取为2 m,即整个模型的上下左右边界为距离隧道外表面2 m处。
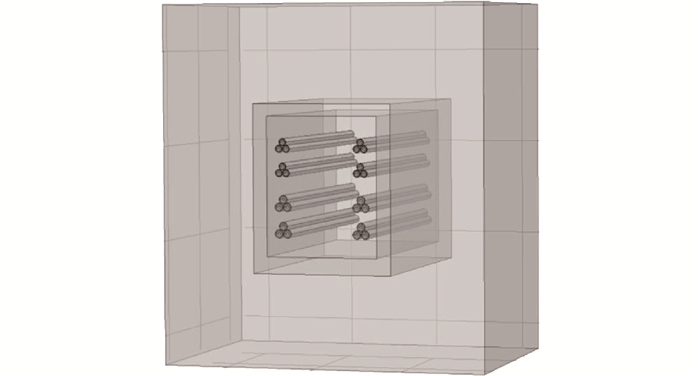
根据图 1所示的隧道尺寸及内部电缆排布在COMSOL Multiphysics仿真软件中建立有限元几何模型,如图 2所示。由于电缆本体层数多且厚度不一,内外屏蔽层等结构厚度极薄,对温度在各层的传导不会产生较大的影响。为了减小网格剖分的难度,减少有限元仿真的计算量,将内外屏蔽层归于绝缘层。
|
图 2 电缆隧道仿真几何模型 Fig. 2 Cable tunnel geometric model |
电缆隧道热-流耦合场仿真计算中用到的材料及参数如表 3所示。根据表 3中的数值对模型中的对应区域进行材料参数的设置。空气的比热容、密度以及土壤的比热容这3个参数与温度相关,在COMSOL内置材料中自动定义。
|
|
表 3 材料参数 Table 3 Material parameters |
考虑到风机作用时,隧道内的空气发生强制对流,因此在仿真中必须设置流体的入口和出口。在电缆隧道仿真模型中,定义隧道区域前端截面为入口,同时设置入口处空气的温度和流速;定义隧道区域后端截面处为出口。强制对流使得电缆表面与隧道壁之间的温差较小,与对流传热相比,热辐射的影响较小,所以在有限元仿真计算中暂不考虑电缆表面与隧道壁之间的热辐射传热作用。
对于整个仿真几何模型的下边界面,符合第1类边界条件,设置该边界温度为隧道下方2 m位置处土壤温度。对于整个几何模型的上边界面,即隧道上方2 m处土壤,同样符合第1类边界条件。几何模型上下边界温度的取值都依据此处最热月平均地温进行取值,上边界最热月平均地温为26.7 ℃,下边界最热月平均地温为18.3 ℃。几何模型左、右边界面则符合第2类边界条件,将其视为绝热面。
在COMSOL Multiphysics仿真软件中完成构建几何模型、添加材料、定义物理场之后,对几何模型进行网格剖分。采用自由四面体网格对仿真几何模型进行剖分,对导体、绝缘层、外护套等对温度影响较大的部分采用细化网格剖分,剩余部分采用常规网格尺寸剖分。网格统计结果如下:网格顶点数为55 803,四面体单元数325 524,三角形单元数68 224,边单元数21 168,顶点单元数888。
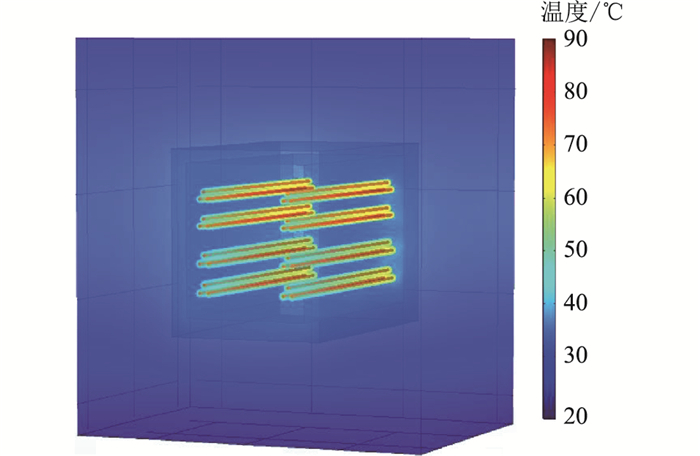
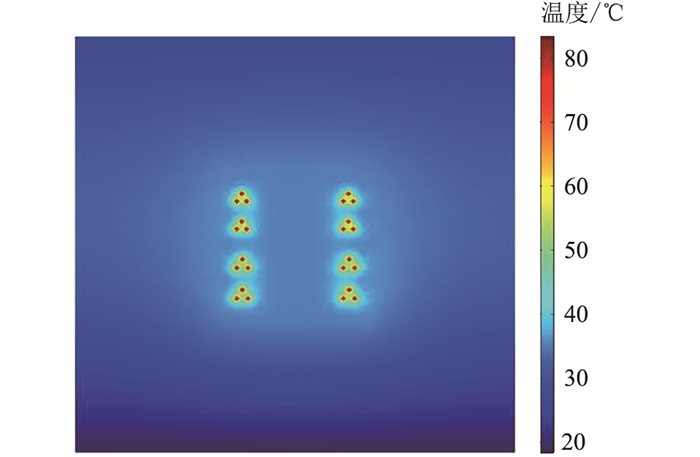
3 电缆隧道温度场与流场耦合仿真结果 3.1 温度分布仿真结果 3.1.1 温度场分布规律根据DL/T 5484-2013 《电力电缆隧道设计规程》可知,隧道内排风温度不应高于40 ℃,进、排风温差不宜大于10 ℃。机械通风隧道内风速不宜大于5 m/s。在实际工程中,为了留有一定的裕度,隧道温度通常控制在35 ℃以内。为了得到此8回电缆能够承载的最大载流量,应在最差工况下进行计算。此时,入口风机吸入空气温度应取最热月最高温度35 ℃。因此,载流量确定的依据是,当入口风机风速为0.8 m/s,隧道内环境温度达到35 ℃,电缆导体温度达到90 ℃时,电力电缆所能承载的最大电流值。在仿真计算中,设置入口处温度为35 ℃,入口风速为0.8 m/s,将出口截面设置为出口。根据损耗计算方法将相应的损耗值作为热源加载在相应的区域上,进行热-流耦合场仿真,采用割线法计算载流量,对电流加载值进行微调。取导体温度与最高工作温度之差小于0.1 ℃时的电流加载值,将之作为导体最大载流量。计算结果表明,220 kV电缆最大载流量为2 200 A,500 kV电缆最大载流量为2 260 A,电缆隧道中温度场的三维分布情况如图 3所示。为了能够更加直观地展示电缆隧道内部的温度分布情况,取隧道敷设电缆几何模型中部横截面,隧道内部的温度场分布如图 4所示。
|
图 3 温度场三维分布 Fig. 3 Three dimensional distribution of temperature |
|
图 4 中部截面温度分布 Fig. 4 Temperature profile of middle section |
结合图 3和图 4可知,电缆导体处的发热最为严重,温度沿着电缆径向递减。出口处的温度高于入口处的温度,最高温度出现在电缆的导体中心处,为90.08 ℃。引起温度差异的原因在于隧道内流体的强制对流作用。风机启动使得隧道内空气流速加快,空气经过电缆表面并带走热量,带走的热量会随着空气不断沿着电缆轴向累积从而导致出口温度升高。
3.1.2 不同电流负载下的温度场分布规律为了研究不同电流负载下电缆隧道温度场的分布规律,以8回超高压电缆隧道为例。在空气温度为35 ℃、入口风速为0.8 m/s的条件下,通过有限元仿真研究不同电流负载下的温度场分布。
分别取电流值为1 000 A,1 200 A,1 400 A,1 600 A,1 800 A,2 000 A,2 200 A,计算不同电流值对应的导体损耗、绝缘损耗和金属护套损耗,并作为热源加载于相应区域上。研究发现随着电流的增加,隧道及周围土壤的温度也随之升高。在不同电流作用下,通过有限元法得到的电缆最高温度如图 5所示。
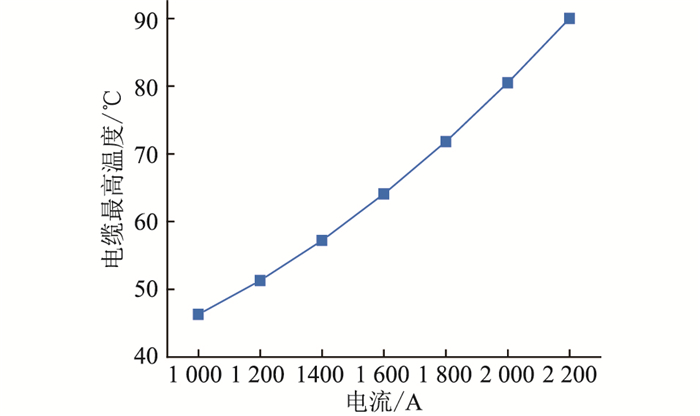
|
图 5 不同电流负载下电缆最高温度 Fig. 5 Maximum cable temperature under different currents |
为研究回路数对电缆载流量的影响,文中分别对双回路、4回路电缆进行仿真,并与之前分析的8回路进行了对比。双回路的设置包括:Ⅰ+Ⅱ、Ⅲ+Ⅳ、Ⅴ+Ⅵ、Ⅶ+Ⅷ;4回路的设置包括:Ⅰ+Ⅱ+Ⅲ+Ⅳ、Ⅴ+Ⅵ+Ⅶ+Ⅷ。通过计算得出,空气温度35 ℃、风速0.8 m/s时,双回路和4回路电缆的稳态载流量如表 4所示。由表 4中的稳态载流量数据可知,双回路和4回路敷设时,电缆的稳态载流量高于8回路敷设时的电缆稳态载流量,这是由于随着电缆回路数的增加,电缆回路间的热效应和电磁效应越来越强烈,导致电缆发热增加,载流量降低。
|
|
表 4 多回路敷设电缆稳态载流量 Table 4 Steady-state ampacity of multi-loop laying cables |
在空气温度35 ℃、风速0.8 m/s的初始条件下,进行温度场与流体场的耦合仿真,得到如图 6所示的流速切面分布。由图 6的切面图可以看出,空气经过隧道,热场与流场相互作用,流速增加。隧道内空气的最大流动速度为1.32 m/s,位于空气流动出口处。电缆表面和隧道壁的空气流速均为0 m/s,这是由于空气的粘性作用使得空气在电缆表面和隧道壁处无相对位移,导致流速为0 m/s。

|
图 6 流速分布切面 Fig. 6 Velocity distribution |
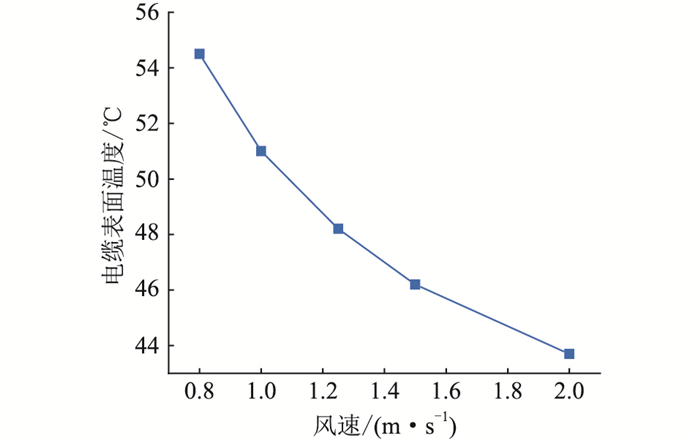
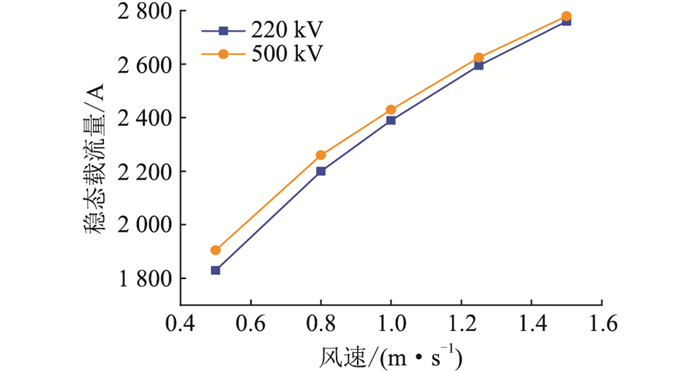
在隧道空气温度为35 ℃,负荷电流为2 000 A条件下,取风速分别为0.8 m/s,1 m/s,1.25 m/s,1.5 m/s,2 m/s进行热流场耦合仿真。不同通风速度下,电缆表面温度变化如图 7所示。进一步分析流速对电缆稳态载流量的影响,结果如图 8所示。
|
图 7 电缆表面温度随风速变化 Fig. 7 Cable surface temperature variation with wind speed |
|
图 8 稳态载流量随风速变化 Fig. 8 Cable ampacity variation with wind speed |
由图 7可知,随着风速的增加,电缆表面温度逐渐减小。因此,合适的通风量能够有效降低电缆表面温度。由图 8可知,增大通风速度能够增强电缆表面与空气的对流换热程度,有效降低电缆表面的温度,更有利于热量的扩散,从而增大电缆的稳态载流量。
4 结论依据实际电缆隧道结构和内部电缆排布方式,在COMSOL Multiphysics仿真软件中构建几何模型,进行温度场和流体场的耦合仿真计算,采用有限元法研究内部温度分布情况,确定电缆载流量,对不同运行方式和环境条件下的温度场和流体场分布规律进行分析。仿真计算结果表明:
(1) 在环境温度为35 ℃,风机风速为0.8 m/s的运行条件下,8回路电缆会全部投入使用时,220 kV电缆最大载流量为2 200 A;500 kV电缆最大载流量为2 260 A。电缆导体的发热最为严重,温度沿着电缆径向逐渐递减。出口处的温度比入口处的温度高。
(2) 随着负载电流的增大,电缆发热对周围环境温度的影响也随之增加。回路数设置的变化对载流量也存在影响。由仿真结果得,双回路和4回路敷设时电缆的稳态载流量高于8回路敷设时的电缆稳态载流量。
(3) 仿真结果表明,空气经过隧道后,流速增加,出口截面处风速最大。随着风速的增加,电缆表面温度逐渐减小。
本文得到中国能源建设股份有限公司科技项目“多回超高压电缆隧道中温度场与流场耦合分析”资助,谨此致谢!
| [1] |
周承科, 李明贞, 王航, 等. 电力电缆资产的状态评估与运维决策综述[J]. 高电压技术, 2016, 42(8): 2353-2362. ZHOU Chengke, LI Mingzhen, WANG Hang, et al. Review of condition assessment and maintenance strategy of power cable assets[J]. High Voltage Engineering, 2016, 42(8): 2353-2362. (  0) 0) |
| [2] |
王昭钦, 庞丹, 戴斌. 隧道电缆载流量计算与影响因素分析[J]. 东北电力大学学报, 2020, 40(4): 11-18. WANG Zhaoqin, PANG Dan, DAI Bin. Calculation of tunnel cable load and analysis of influencing factors[J]. Journal of Northeast Electric Power University, 2020, 40(4): 11-18. (  0) 0) |
| [3] |
刘云龙, 周大明, 周勇, 等. 基于物联网的110 kV电缆管井智能监测系统建设与应用[J]. 四川电力技术, 2020, 43(6): 75-80, 91. LIU Yunlong, ZHOU Daming, ZHOU Yong, et al. Construction and application of intelligent monitoring system for 110 kV cable bank well based on Internet of Things[J]. Sichuan Electric Power Technology, 2020, 43(6): 75-80, 91. (  0) 0) |
| [4] |
罗楚军, 梁家鸣, 李健, 等. 计及空气流场影响的电力电缆隧道温度场分布研究[J]. 电工技术, 2021(1): 28-31. LUO Chujun, LIANG Jiaming, LI Jian, et al. Study on temperature distribution of power cable tunnel considering air flow field[J]. Electric Engineering, 2021(1): 28-31. (  0) 0) |
| [5] |
江福章. 电力电缆载流量计算及提升的研究现状及展望[J]. 电线电缆, 2020(3): 6-9, 17. JIANG Fuzhang. Status and prospect on calculation and increase of cable ampacity[J]. Wire & Cable, 2020(3): 6-9, 17. DOI:10.3969/j.issn.1672-6901.2020.03.002 (  0) 0) |
| [6] |
NEHER J H, MCGRATH M H. The calculation of the temperature rise and load capability of cable systems[J]. Transactions of the American Institute of Electrical Engineers Part Ⅲ: Power Apparatus and Systems, 1957, 76(3): 752-764. (  0) 0) |
| [7] |
陈向荣, 王启隆, 于竞哲, 等. 10 kV交流XLPE电缆在不同直流拓扑结构和敷设方式下的直流载流量仿真研究[J]. 高电压技术, 2021, 47(11): 4044-4054. CHEN Xiangrong, WANG Qilong, YU Jingzhe, et al. Simulation research on DC ampacity of 10 kV AC XLPE cable under different DC operation topologies and laying modes[J]. High Voltage Engineering, 2021, 47(11): 4044-4054. (  0) 0) |
| [8] |
陆莹, 范明明, 郑明, 等. 基于电磁-热-流耦合场的非开挖敷设方案的海底电缆载流量计算[J]. 广东电力, 2020, 33(5): 117-124. LU Ying, FAN Mingming, ZHENG Ming, et al. Calculation of ampacity for submarine cables under trenchless laying method based on electromagnetic-thermal-flow coupled field[J]. Guang dong Electric Power, 2020, 33(5): 117-124. (  0) 0) |
| [9] |
张洪亮, 尹毅, 谢书鸿, 等. 不同金属屏蔽形式XLPE高压直流电缆载流量计算与试验验证[J]. 高电压技术, 2021, 47(6): 2117-2123. ZHANG Hongliang, YIN Yi, XIE Shuhong, et al. Calculation and testing research on current rating capacity of XLPE insulated HVDC cable with different metallic screen type[J]. High Voltage Engineering, 2021, 47(6): 2117-2123. (  0) 0) |
| [10] |
乐彦杰, 郑新龙, 张占奎, 等. 基于电磁-热-流耦合场的多回路排管敷设电缆载流量数值计算[J]. 科学技术与工程, 2017, 17(5): 197-202, 261. YUE Yanjie, ZHENG Xinlong, ZHANG Zhankui, et al. Numerical caculation of ampacity for multi-loop cable system in ducts based on electromagnetic-thermal-flow coupled field[J]. Science Technology and Engineering, 2017, 17(5): 197-202, 261. DOI:10.3969/j.issn.1671-1815.2017.05.034 (  0) 0) |
| [11] |
陈玉, 孙冠姝, 张靖雯, 等. 基于有限元分析的光纤复合低压电缆热场仿真和结构优化[J]. 智慧电力, 2021, 49(10): 1-7. CHEN Yu, SUN Guanshu, ZHANG Jingwen, et al. Thermal field simulation and structure optimization of optical fiber composite low voltage cable based on finite element analysis[J]. Smart Power, 2021, 49(10): 1-7. DOI:10.3969/j.issn.1673-7598.2021.10.002 (  0) 0) |
| [12] |
许鹏飞, 杨帆, 刘刚, 等. 110 kV插拔式GIS电缆终端轴向传热分析[J]. 电力工程技术, 2020, 39(5): 30-35. XU Pengfei, YANG Fan, LIU Gang, et al. Assessment on axial heat transfer of 110 kV plug-in GIS cable terminal[J]. Electric Power Engineering Technology, 2020, 39(5): 30-35. (  0) 0) |
| [13] |
SUN Q Q, LIN Z Q, WANG F, et al. Thermal network modeling of tunnel cable considering circumferential heat transfer and tunnel curvature[J]. Electric Power Systems Research, 2021, 196: 107190. DOI:10.1016/j.epsr.2021.107190 (  0) 0) |
| [14] |
牛海清, 郑文坚, 雷超平, 等. 基于有限元和粒子群算法的电缆周围土壤热特性参数估算方法[J]. 高电压技术, 2018, 44(5): 1557-1563. NIU Haiqing, ZHENG Wenjian, LEI Chaoping, et al. Estimation method for thermal parameters of soil around the cable based on finite element and particle swarm optimization[J]. High Voltage Engineering, 2018, 44(5): 1557-1563. (  0) 0) |
| [15] |
LIU G, XU Z F, MA H, et al. An improved analytical thermal rating method for cables installed in short-conduits[J]. International Journal of Electrical Power & Energy Systems, 2020, 123: 106223. (  0) 0) |
| [16] |
郭然, 牛海清, 吴炬卓. 基于有限元温度场仿真的排管敷设电缆及新增电缆的位置优化[J]. 中国电力, 2017, 50(7): 169-174. GUO Ran, NIU Haiqing, WU Juzhuo. Position optimization of existing and added cables based on finite element method[J]. Electric Power, 2017, 50(7): 169-174. (  0) 0) |
| [17] |
陈胤, 黄瑞梅. 基于电-热场耦合的35 kV电缆中间接头气隙缺陷仿真分析[J]. 电气技术, 2021, 22(10): 46-50. CHEN Yin, HUANG Ruimei. Simulation analysis of 35 kV cable joint with air gap defect based on electrothermal field coupling[J]. Electrical Engineering, 2021, 22(10): 46-50. (  0) 0) |
| [18] |
马悦, 张勇, 张思祥. 排管内部强制水冷对地下电缆载流温度场的影响[J]. 智慧电力, 2020, 48(10): 120-125. MA Yue, ZHANG Yong, ZHANG Sixiang. Influence of forced water cooling in duct on temperature field of underground power cables[J]. Smart Power, 2020, 48(10): 120-125. (  0) 0) |
| [19] |
杨世铭, 陶文铨. 传热学[M]. 4版. 北京: 高等教育出版社, 2006. YANG Shiming, TAO Wenquan. Heat transfer[M]. 4th ed. Beijing: Higher Education Press, 2006. (  0) 0) |
| [20] |
郑文坚. 空气敷设电缆热-流耦合场仿真及其参数研究[D]. 广州: 华南理工大学, 2018. ZHENG Wenjian. The study of thermal-fluid coupling field simulation and parameters of cable in air[D]. Guangzhou: South China University of Technology, 2018. (  0) 0) |
| [21] |
乐彦杰, 孙璐, 彭维龙, 等. 典型交流高压海缆工程载流量瓶颈分析与仿真研究[J]. 高压电器, 2022, 58(1): 70-78. YUE Yanjie, SUN Lu, PENG Weilong, et al. Analysis and simulation research on current carrying capacity bottleneck of typical AC high-voltage submarine cable project[J]. High Voltage Apparatus, 2022, 58(1): 70-78. (  0) 0) |
| [22] |
王启隆, 王国海, 陈向荣, 等. 10 kV交流XLPE电缆改为直流运行的热电耦合仿真[J]. 西南交通大学学报, 2022, 57(1): 46-54. WANG Qilong, WANG Guohai, CHEN Xiangrong, et al. Thermo-electric coupling simulation for 10 kV AC XLPE cable in DC operation[J]. Journal of Southwest Jiaotong University, 2022, 57(1): 46-54. (  0) 0) |
| [23] |
傅晨钊, 郝谦, 梁永春, 等. 复杂直埋电缆群缆芯温升快速算法研究[J]. 高压电器, 2021, 57(5): 130-136. FU Chenzhao, HAO Qian, LIANG Yongchun, et al. Study on fast calculation method for temperature rise of complex direct soil-buried cable group core[J]. High Voltage Apparatus, 2021, 57(5): 130-136. (  0) 0) |
| [24] |
马爱清, 张杨欢. 考虑互热效应的超高压电缆隧道敷设热路模型[J]. 高电压技术, 2022, 48(3): 1068-1076. MA Aiqing, ZHANG Yanghuan. Thermal circuit model of EHV cable laid in tunnel considering mutual thermal effect[J]. High Voltage Engineering, 2022, 48(3): 1068-1076. (  0) 0) |
| [25] |
杨永明, 程鹏, 陈俊, 等. 基于耦合场的通风电缆沟敷设电缆载流量计算及其影响因素分析[J]. 电力自动化设备, 2013, 33(7): 139-143, 154. YANG Yongming, CHENG Peng, CHEN Jun, et al. Current- carrying capacity calculation based on coupling fields for cable in ventilated trench and its influencing factors[J]. Electric Power Automation Equipment, 2013, 33(7): 139-143, 154. (  0) 0) |
2. Anhui Electric Power Design Institute Co., Ltd., China Energy Engineering Group, Hefei 230601, China;
3. State Grid Hefei Power Supply Company of Anhui Electric Power Co., Ltd., Hefei 230601, China
 2022, Vol. 41
2022, Vol. 41


 林梓圻(1996),女,硕士在读,研究方向为高电压与绝缘技术(E-mail:
林梓圻(1996),女,硕士在读,研究方向为高电压与绝缘技术(E-mail: