文章编号: 2096-3203(2022)02-0179-07 中图分类号: TM07
2. 国网江苏省电力有限公司电力科学研究院,江苏 南京 211103
智能变电站保护装置、合并单元、互感器以及通信网络等二次系统的运行状态直接影响了大电网运行的稳定性与安全性[1-3]。世界范围内多起电网连锁故障都与二次系统失效有关。有学者通过分析2003年8月14日美加大停电事故分析报告指出,电力监测与控制管理系统出现软件错误导致设备故障预警未及时通报和处理是此次大规模停电的原因之一[4]。2003年8月28日,由于英国国家电网公司保护继电器故障,致使保护设备误动切除了某变电所变压器,经过一连串连锁事故最终导致伦敦电力损失了五分之一的电力供应。
二次系统失效不仅无法及时遏制电力一次系统故障,还会导致电网发生故障连锁反应,严重威胁大电网的安全稳定运行。目前,二次系统失效对电力系统安全运行风险评估主要是由二次设备失效风险与系统失效风险两方面构成。二次设备失效风险评估方面,由于设备种类繁多、型号不一、影响运行因素复杂、互操作性不佳等因素,精确计算设备失效时刻十分困难。然而,在获得足够样本数据时,可以通过统计方法构建失效模型,并有效估计出模型参数。系统失效风险评估方面,系统内部相互影响机理复杂、难以描述[5-7],很难建立确定性模型以开展定量分析,即使采用诸如隐马尔可夫链等系统模型,也易因状态数量爆炸性增长导致分析计算复杂度指数上升[8-10]。
文献[11]提出了风险传递和网络理论相结合的方法量化二次设备运行风险;文献[12]针对应用层设备应用软件和应用层电网管理服务系统软件失效影响,提出了功能分解法进行建模,并计算智能变电站系统安全风险;文献[13]利用层次分析法考虑期望功能失效量、功能稳态不可用率和失效概率3个评价指标研究二次系统可靠性。上述文献多采用基于指数分布、正态分布等概率模型为二次系统设备、元器件建立失效概率模型从而开展评价分析。实际上采用威布尔分布刻画二次系统关键部件失效概率分布更加符合实际情况。威布尔分布是系统可靠性分析普遍使用的方法。整体系统内局部发生异常、故障的设备、部件统计分布特征可以通过威布尔分布精准刻画,并且该方法能更好地拟合设备在实际运行中的可靠性样本数据。此外,威布尔分布在改变其参数取值时可以简化为指数分布、对数正态分布及正态分布等常见分布,因此适应性较强,特别适用于刻画设备的全生命周期。
文中基于设备或部件失效行为特征采用威布尔概率分布建模,并利用平均秩次法、最小二乘拟合算法以及设备型式试验或运行可靠性数据拟合出各类二次设备失效分布模型,同时建立针对智能变电站二次系统的失效分析。
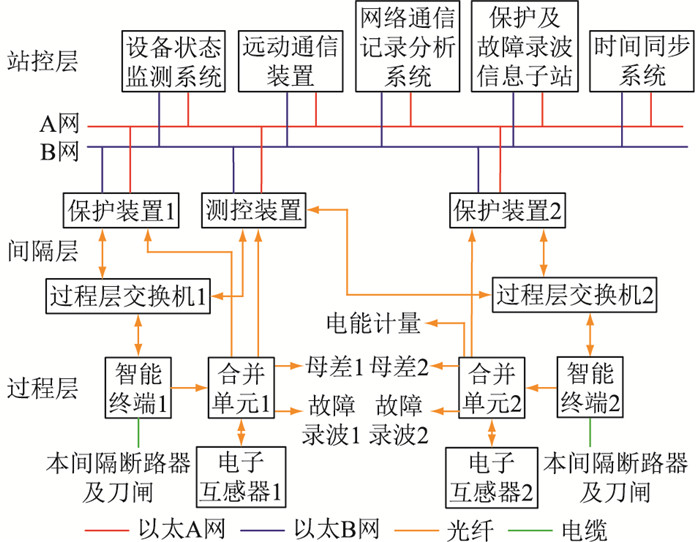
1 智能变电站二次系统失效建模 1.1 智能变电站二次系统二次系统自底向上分别为过程层、间隔层、站控层,网络层分为过程层网络和站控层网络[14],如图 1所示。二次系统内采用统一的数据模型交互,包括制造报文规范(manufacturing message specification, MMS)、面向对象的通用变电站事件(generic object oriented substation event, GOOSE)、采样值(sampled measured value, SMV)等。
|
图 1 智能变电站二次系统示意 Fig. 1 Schematic diagram of secondary system in intelligent substation |
MMS报文规定了智能终端、智能传感器、智能控制设备的通信规则与设备间互操作方法。GOOSE报文传输的是控制指令和状态信号,主要包含正常/异常,分/合闸,动作/复归,联锁/解锁,使能/闭锁,投入/退出,SF6压力降低等信号。SMV报文包含了电压、电流周期性SMV。
站控层网络通过MMS/GOOSE实现信息传递,负责间隔层与站控层设备之间的信息交互,面向运行和保护人员提供智能变电站内信息收集汇总和高级应用系统功能。过程层网络包含SMV链路和GOOSE链路,负责过程层及间隔层设备之间的信息交互。
过程层设备包括电子式互感器、合并单元、智能终端、过程层交换机等。其中电子式互感器、合并单元分别实现对一次交流模拟量采样值的数字处理和数据共享;智能终端实现对断路器、刀闸开入开出命令和信号的数字化;过程层交换机实现过程层网络组网,在过程层与间隔层设备间传递GOOSE报文及SMV报文。
间隔层设备主要有保护装置、测控装置、故障录波装置及计量装置等,主要功能是完成过程层设备采集信息的实时汇总、分析与计算,实现多种保护与控制功能。
站控层设备主要包括设备状态监测系统、远动通信装置、网络通信记录分析系统、保护及故障录波信息子站、时间同步系统等,为站内运维人员针对间隔层及过程层设备提供监控与操作界面,并提供同步时钟源以及维护与上级调度中心通信等功能。
1.2 故障树分析方法文中选择二次设备作为研究对象,重点考察二次设备失效风险评估。因此,选择二次测量回路(包括电子互感器和合并单元)、智能终端、过程层交换机、站内通信网、保护装置、测控装置及同步系统为研究对象,通过其失效模型,利用故障树分析方法开展二次系统失效评估。
故障树基本分析模型有顺序相关门、功能相关门、冷备件门和热备件门等逻辑模块。任何复杂系统内部部件(底部件)或子系统故障对系统故障(顶系统)的影响可以分解为有底部件构成的多层、嵌套逻辑关系。因此,通过计算底层部件失效即可求解此类随机变量函数的分布,进而通过故障树总体的失效分布得到顶系统的失效分布。
顺序相关门指顶系统及各部件故障是顺序发生关系,即“且”关系。定义部件i故障时间Ti(i=1, 2, …, m)的统计分布函数为Fi(t),则顶系统故障时间T的累计分布函数F(t)可表示为:
| $ \begin{gathered} F(t)=P\left\{T_{1} \leqslant T_{2} \leqslant \cdots \leqslant T_{m} \leqslant t\right\}= \\ \int_{0}^{t} \int_{x_{1}}^{t} \cdots \int_{x_{m-1}}^{t} \mathrm{~d} F_{m}\left(x_{m}\right) \cdots \mathrm{d} F_{2}\left(x_{2}\right) \mathrm{d} F_{1}\left(x_{1}\right) \end{gathered} $ | (1) |
式中:P{·}为事件概率。
功能相关门指的是顶系统故障与部件故障是“或”关系。考虑两底部件构成的功能相关门,假设底部件1发生时间T1的分布为F1(t),底部件2失效时间T2的分布为F2(t),顶系统故障时间T的累计分布函数可表示为:
| $ \begin{gathered} F(t)=P\left\{\min \left(T_{1}, T_{2}\right) \leqslant t\right\}= \\ 1-\left(1-F_{1}(t)\right)\left(1-F_{2}(t)\right) \end{gathered} $ | (2) |
冷备件门指在部件冷备时,只有当所有冷备部件接连失效,才引发顶系统故障,假设当前工作部件失效时间T1的累计分布函数为F1(t),冷备件失效时间T2的累计分布函数为F2(t),则顶系统故障时间T的累计分布函数可表示为:
| $ F(t)=P\left\{T_{1}+T_{2} \leqslant t\right\}=\int_{0}^{t} \int_{0}^{y} F_{1}(x) F_{2}(y-x) \mathrm{d} x \mathrm{d} y $ | (3) |
热备件门指部件热备时,当热备的多个部件均同时失效时,顶系统判为故障。定义2个热备部件失效时间T1,T2的累计分布函数为F1(t),F2(t),系统故障时间T的累计分布函数可表示为:
| $ F(t)=P\left\{\max \left(T_{1}, T_{2}\right) \leqslant t\right\}=F_{1}(t) F_{2}(t) $ | (4) |
设备从投入使用到运行过程中发送故障的概率分布情况是状态评价的基础[15],因此借助于统计学原理为电力系统二次设备建立失效概率分布函数显得十分关键。若设备失效前运行时间T为随机变量,则可定义多个函数以刻画设备失效的关系[16-17]。例如:设备的可靠度函数R(t)=P{T≥t},其含义为设备工作到t时刻还未失效的概率;而设备失效的累计分布函数F(t)=P{T≤t}则表示到t时刻设备失效的概率;自然地,可以定义设备失效的概率密度函数为f(t)=dF(t)/dt。为刻画设备失效概率随运行时间变化的特征,定义设备失效率函数:
| $ \begin{gathered} \lambda(t)=\lim \limits_{\Delta t \rightarrow 0} \frac{P(t<T \leqslant t+\Delta t \mid T>t)}{\Delta t}= \\ \frac{1}{R(t)}\left(-\frac{\mathrm{d} R(t)}{\mathrm{d} t}\right)=\frac{f(t)}{R(t)} \end{gathered} $ | (5) |
即设备正常工作到时刻t后,单位时间内发生失效的概率。威布尔分布概率密度函数为:
| $ f(t, \lambda, k)=\left\{\begin{array}{l} \frac{k}{\lambda}\left(\frac{t}{\lambda}\right)^{k-1} \mathrm{e}^{-(t / \lambda)^{k}}\quad t \geqslant 0 \\ 0 \quad t<0 \end{array}\right. $ | (6) |
式中:λ>0,为比例参数;k>0,为形状参数。基于威布尔分布概率密度函数,可列出设备运行可靠度累计分布函数、故障概率累计分布函数分别为:
| $ R(t)=\mathrm{e}^{-(t / \lambda)^{k}} $ | (7) |
| $ F(t)=1-\mathrm{e}^{-(t / \lambda)^{k}} $ | (8) |
因此,失效率函数可表示为:
| $ \lambda(t)=\frac{k}{\lambda}\left(\frac{t}{\lambda}\right)^{k-1} $ | (9) |
|
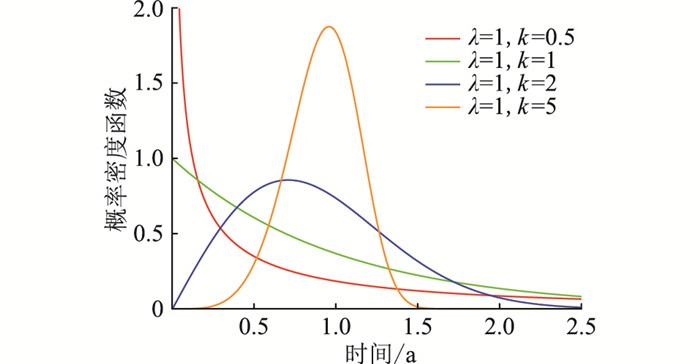
图 2 威布尔概率密度函数随形状参数变化示意 Fig. 2 Schematic diagram of Weibull probability density function curves as shape parameters changes |
改变形状参数k可更贴近实际地反映设备运行过程中失效率函数,从而客观地反映设备全生命周期使用寿命的变化特性。
当k < 1时,失效率函数λ(t)为单调递减函数,适用于针对设备运行早期失效进行建模。例如设备生产过程中采用元器件次品、早期误操作等原因导致的失效事件,可以在设备投运前通过试运行等方式剔除不良产品,从而降低失效率。
当k=1时,失效率函数λ(t)为常数,适用于针对设备运行过程中偶发性失效进行建模。例如电子互感器、合并单元、交换机在使用过程中超出额定使用调度导致的设备失效,可以通过降额设计、容差分析等手段提高设备的安全裕度,从而获得更低的失效率;
当k>1时,失效率函数λ(t)为单调递增函数,适用于针对设备运行后期退化失效进行建模。例如设备长期运行后发生的性能衰退、元器件磨损、老化及疲劳累积等导致的设备失效,可经优化生产流程,采用更加优质元器件延长设备退化时间。
在分析二次设备可靠性过程中,需要通过估计分布中的参数来获取与设备运行特性相符合的失效率函数、设备失效概率密度函数等,此类问题属于统计推断中的参数估计问题,通常可采用中位秩方法结合最小二乘估计求解。
对R(t)取2次对数可将指数函数转变为线性函数:
| $ \ln \left(\ln \frac{1}{R(t)}\right)=k \ln t-k \ln \lambda $ | (10) |
令
| $ y=A x+B $ | (11) |
利用最小二乘估计方法求解式(11)可以获得参数A和B的最优估计解
| $ \hat{A}=\frac{\sum\limits_{i=1}^{n}\left(x_{i} y_{i}\right)-n \bar{x} \bar{y}}{\sum\limits_{i=1}^{n} x_{i}^{2}-n \bar{x}^{2}} $ | (12) |
| $ \hat{B}=\bar{y}-\hat{A} \bar{x} $ | (13) |
式中:
通过对小规模设备样品进行可靠度试验,可记录下设备失效时间,估算可靠度函数R(t)的经验概率值,从而获得时间-概率试验数据,再通过最小二乘法求解线性回归参数获得设备失效概率分布函数的参数估计值。由于样品数量有限,且在试验过程中某些样品可能未发生故障即退出运行,可采用平均秩次法获得概率分布的经验值。依据统计学原理,对于不完整试验数据的平均秩次计算如式(14)所示[18]。
| $ \left\{\begin{array}{l} \Delta A_{i}=\frac{n+1-A_{i-1}}{n-m+2} \\ A_{i}=A_{i-1}+\Delta A_{i} \end{array}\right. $ | (14) |
式中:n为试验设备样本总数;m为所有设备按照故障时间或退出时间由小到大排序的顺序号;Ai为第i套故障设备的平均秩次;Ai-1为前一套故障设备的平均秩次。通过将新故障设备秩次Ai代入经验中位秩公式可得经验失效概率如式(15)所示。
| $ F_{n}\left(t_{i}\right)=\frac{A_{i}-0.3}{n+0.4} $ | (15) |
式中:ti为设备故障时刻。利用式(12)—式(15)拟合出设备失效概率曲线,进而获得针对设备失效的威布尔分布函数。
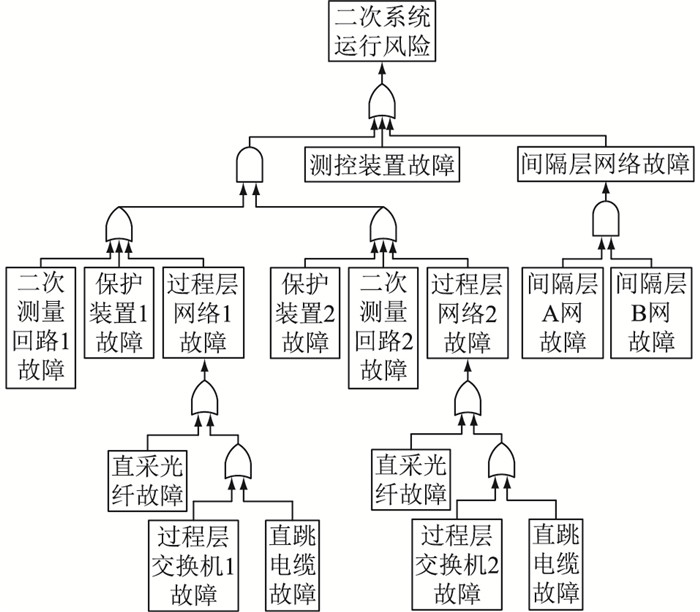
3 智能变电站二次设备失效故障树模型智能变电站二次系统“三层两网”结构涉及的二次设备状态量种类繁多,其可靠运行不同程度地影响了一次系统安全运行,如故障录波、电能计量等状态采集量影响一次系统运行控制,而保护装置功能闭锁、拒动或误动将导致故障设备无法有效切除,极可能造成电网故障大范围扩散,从而带来严重的系统性事故风险。二次设备失效风险评估故障树如图 3所示。
|
图 3 二次设备失效风险评估故障树 Fig. 3 The risk estimation fault tree for the secondary system failure |
文中针对二次设备开展失效建模,并建立故障树风险评估体系,分析计算二次设备失效风险。选择的二次设备研究对象包括过程层与间隔层设备及网络,如:保护设备、测控设备、间隔层网络、过程层网络以及由电子互感器、合并单元和智能终端构成的二次回路。
为保障二次系统的可靠性与安全性,间隔层通信网络采用A、B双网组网,过程层网络则采用光纤以太网方式将保护装置与智能终端互联,跳闸动作信号传输时延固定;采用光纤以太网将二次测量回路与保护装置、测控装置互联,交流采样信号同步通过精准时钟同步协议实现;采用2套保护装置、测量回路构成热备份,以上组网冗余、设备冗余方式可以在网络或设备发生故障时及时倒换,从而提高二次系统状态变量传输的可靠性[19-26]。
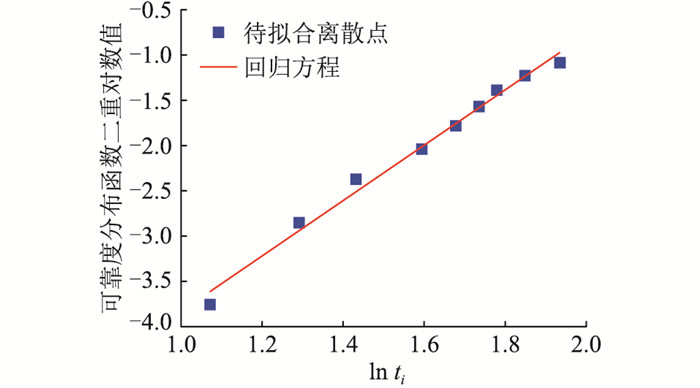
4 二次系统失效风险评估计算实例文中以变电站典型二次系统为例,根据文中提出的二次系统设备失效风险故障树模型,以某保护设备实际运行状态数据为例,演示二次设备失效概率模型建模计算过程。首先,剔除未失效而停止运行记录的设备状态数据,针对样本数据利用式(14)和式(15)计算设备失效概率,如表 1所示;通过式(12)、式(13)计算失效概率离散样本点的线性回归方程为y=3.059x-6.892,拟合如图 4所示。
|
|
表 1 利用平均秩次法求解失效分布概率示例 Table 1 An example of failure distribution probability calculation with average rank order method |
|
图 4 保护装置失效概率分布函数拟合效果 Fig. 4 Fitting effect of failure probability distribution function of protection device |
重复上述方法,拟合其他各类二次设备失效概率分布函数如表 2所示。
|
|
表 2 二次系统各类设备失效概率分布函数 Table 2 Failure probability distribution function of all kinds of equipment in secondary system |
故障树中A套与B套过程层、间隔层网络和设备互为热备份,根据热备件门(逻辑与门)逻辑计算可得单套过程层、间隔层网络和设备失效概率分布函数F1为:
| $ \begin{gathered} F_{1}= 1-\left(1-F_{\mathrm{J}}\right)\left(1-F_{\mathrm{E}}\right)\left(1-F_{\mathrm{P}}\right) \times \\ \left(1-F_{\mathrm{B}}\right)\left(1-F_{\mathrm{S}}-F_{\mathrm{C}}+F_{\mathrm{S}} F_{\mathrm{C}}\right) \end{gathered} $ | (16) |
同理,间隔层网络由A、B双网冗余组网,因此其失效概率分布函数Fnet(t)为:
| $ F_{\text {net }}(t)=F_{\mathrm{S}}(t)+F_{\mathrm{B}}(t)-F_{\mathrm{S}}(t) F_{\mathrm{B}}(t) $ | (17) |
则A、B双网同时失效概率F2为:
| $ F_{2}=F_{\text {net }}^{2} $ | (18) |
综上,结合故障树图中功能相关门(逻辑或门),由二次系统失效概率分布函数可以表示为:
| $ F=1-\left(1-F_{1}\right)^{2}\left(1-F_{2}\right)\left(1-F_{\mathrm{J}}\right) $ | (19) |
可靠度函数R可表示为:
| $ R=1-F=\left(1-F_{1}\right)\left(1-F_{2}\right)\left(1-F_{\mathrm{J}}\right) $ | (20) |
当可靠度R=0.99时,通过数值可计算出二次系统可靠工作时间可达1.731 a。
5 结语智能变电站二次系统的间隔层设备、过程层设备及对应通信网络失效分布符合威布尔分布模型。通过各类设备的型式试验、日常运行状态数据可收集得到足够的样本数据,再利用平均秩次法与最小二乘估计计算回归方程,可获得相应设备的失效概率分布函数。针对二次系统失效对电力系统安全风险的评估,可以通过故障树方法进行数据建模,较好地模拟出设备、网络故障之间的内在联系逻辑,有效计算出系统运行风险顶事件概率分布函数,从而为状态评估、状态检修、风险预警提供辅助决策。未来,可以进一步从设备层面深入到元件层面开展建模分析,例如将交换机失效分解为端口失效、板卡失效及连接光纤失效等,通过在二次系统中传递设备元件状态量从而更加精确地建立设备失效模型,有效获得设备运行状态的全貌,指导智能变电站二次系统状态检修向智能化、自动化、精准化方向发展。
| [1] |
罗超, 林芳, 李子, 等. 考虑连锁故障运行风险的机会约束最优潮流模型[J]. 智慧电力, 2018, 46(1): 57-62. LUO Chao, LIN Fang, LI Zi, et al. Optimal power flow model considering operation risk of cascading failure[J]. Smart Power, 2018, 46(1): 57-62. (  0) 0) |
| [2] |
易俊, 周孝信. 考虑系统频率特性以及保护隐藏故障的电网连锁故障模型[J]. 电力系统自动化, 2006, 30(14): 1-5. YI Jun, ZHOU Xiaoxin. Cascading failure model of power grids considering frequency response characteristics and hidden failures[J]. Automation of Electric Power Systems, 2006, 30(14): 1-5. DOI:10.3321/j.issn:1000-1026.2006.14.001 (  0) 0) |
| [3] |
胡斌, 郭亚飞, 杨彬, 等. 智能变电站技术的现状与发展趋势研究[J]. 智慧电力, 2018, 46(3): 87-90. HU Bin, GUO Yafei, YANG Bin, et al. Research on status and development trend of smart substation technology[J]. Smart Power, 2018, 46(3): 87-90. DOI:10.3969/j.issn.1673-7598.2018.03.015 (  0) 0) |
| [4] |
唐桃波, 夏云非, 鲁文, 等. 美国近年的停电事故及对我国电力系统安全稳定运行的启示[J]. 电力建设, 2003, 24(11): 2-4. TANG Taobo, XIA Yunfei, LU Wen, et al. Power failure of this year in USA and its inspiration to safe stable operation of power system in China[J]. Electric Power Construction, 2003, 24(11): 2-4. DOI:10.3969/j.issn.1000-7229.2003.11.002 (  0) 0) |
| [5] |
程松, 李欣, 刘扬, 等. 一种考虑业务关联的电力通信检修安全校核方法[J]. 电力信息与通信技术, 2021, 19(11): 140-145. CHENG Song, LI Xin, LIU Yang, et al. A security check method for power communication maintenance considering service association[J]. Electric Power Information and Communication Technology, 2021, 19(11): 140-145. (  0) 0) |
| [6] |
傅质馨, 孙宁新, 朱俊澎, 等. 基于输出功率预测的风电机组运行风险度评估[J]. 电力信息与通信技术, 2021, 19(5): 14-22. FU Zhixin, SUN Ningxin, ZHU Junpeng, et al. Risk assessment of wind turbine operation based on wind power output prediction[J]. Electric Power Information and Communication Technology, 2021, 19(5): 14-22. (  0) 0) |
| [7] |
苏海林, 龙翩翩. 基于负荷预测的0.4 kV配网低电压风险评估方法[J]. 电力信息与通信技术, 2020, 18(3): 53-58. SU Hailin, LONG Pianpian. A low voltage risk assessment method of 0.4 kV distribution network based on load forecasting[J]. Electric Power Information and Communication Technology, 2020, 18(3): 53-58. (  0) 0) |
| [8] |
刘兆君. 模糊马尔可夫链状态取值及其机会测度函数[J]. 统计与决策, 2021, 37(14): 29-32. LIU Zhaojun. State value of fuzzy Markov chain and its chance measure function[J]. Statistics & Decision, 2021, 37(14): 29-32. (  0) 0) |
| [9] |
陈雯, 吕王勇, 李思奇, 等. 两种马尔可夫链状态转移概率矩阵的估计与比较[J]. 重庆理工大学学报(自然科学), 2021, 35(8): 217-223. CHEN Wen, LYU Wangyong, LI Siqi, et al. Estimation and comparison of two Markov chain state transition probability matrices[J]. Journal of Chongqing University of Technology (Natural Science), 2021, 35(8): 217-223. (  0) 0) |
| [10] |
陈彦交, 罗晓庆. 基于故障树分析法的电力变压器故障诊断专家系统[J]. 陕西电力, 2012, 40(12): 55-59, 74. CHEN Yanjiao, LUO Xiaoqing. Probe into power transformer fault diagnosis expert system based on fault tree analysis[J]. Shaanxi Electric Power, 2012, 40(12): 55-59, 74. (  0) 0) |
| [11] |
王力军, 周凯, 吴迪, 等. 基于风险传递网络的智能变电站二次系统风险评估[J]. 电力系统保护与控制, 2018, 46(6): 97-105. WANG Lijun, ZHOU Kai, WU Di, et al. Risk assessment for smart substation secondary system using risk transfer network model[J]. Power System Protection and Control, 2018, 46(6): 97-105. (  0) 0) |
| [12] |
韩宇奇, 郭嘉, 郭创新, 等. 考虑软件失效的信息物理融合电力系统智能变电站安全风险评估[J]. 中国电机工程学报, 2016, 36(6): 1500-1508. HAN Yuqi, GUO Jia, GUO Chuangxin, et al. Intelligent substation security risk assessment of cyber physical power systems incorporating software failures[J]. Proceedings of the CSEE, 2016, 36(6): 1500-1508. (  0) 0) |
| [13] |
唐志军, 翟博龙, 晁武杰, 等. 智能变电站二次系统可靠性评估与分析研究[J]. 电网与清洁能源, 2017, 33(9): 84-88, 98. TANG Zhijun, ZHAI Bolong, CHAO Wujie, et al. Research on reliability evaluation and analysis of the secondary system in the intelligent substation[J]. Power System and Clean Energy, 2017, 33(9): 84-88, 98. DOI:10.3969/j.issn.1674-3814.2017.09.014 (  0) 0) |
| [14] |
国网江苏省电力有限公司电力科学研究院组. 智能变电站原理及测试技术[M]. 北京: 中国电力出版社, 2019. State Grid Jiangsu Electric Power Co., Ltd. Research Institute. Principle and test technology of intelligent substation[M]. Beijing: China Electric Power Press, 2019. (  0) 0) |
| [15] |
国家电力监管委员会电力可靠性管理中心. 电力可靠性技术与管理培训教材[M]. 北京: 中国电力出版社, 2007: 53-54. Power Reliability Management Center of the State Electricity Regulatory Commission. Power reliability technology and management training materials[M]. Beijing: China Electric Power Press, 2007: 53-54. (  0) 0) |
| [16] |
程宏波, 伦利, 康琛, 等. 一种基于多元统计分析的变压器状态评判方法[J]. 电网技术, 2018, 42(8): 2719-2724. CHENG Hongbo, LUN Li, KANG Chen, et al. A method for evaluating the state of a transformer based on multivariate statistical analysis[J]. Power System Technology, 2018, 42(8): 2719-2724. (  0) 0) |
| [17] |
陈莹, 王松岩, 陈彬, 等. 台风环境下考虑地理高程信息的输电通道结构失效故障概率评估方法[J]. 电网技术, 2018, 42(7): 2295-2302. CHEN Ying, WANG Songyan, CHEN Bin, et al. Evaluation of the failure probability of power transimmision corridors during typhoons using digital elevation information[J]. Power System Technology, 2018, 42(7): 2295-2302. (  0) 0) |
| [18] |
李博. 多类型地铁站环境数据相关性分析及趋势预测[D]. 北京: 北方工业大学, 2021. LI Bo. Correlation analysis and trend prediction of environmental data of multi type subway stations[D]. Beijing: North China University of Technology, 2021. (  0) 0) |
| [19] |
戴婷, 宋斌, 彭正洪. 基于灰色层次分析法的变电站通信网络状态评价[J]. 武汉大学学报(工学版), 2011, 44(4): 526-529. DAI Ting, SONG Bin, PENG Zhenghong. Substation communication network condition evaluation based on grey analytic hierarchy process[J]. Engineering Journal of Wuhan University, 2011, 44(4): 526-529. (  0) 0) |
| [20] |
王有元, 陈璧君. 基于层次分析结构的变压器健康状态与综合寿命评估模型[J]. 电网技术, 2014, 38(10): 2845-2850. WANG Youyuan, CHEN Bijun. An integrated life estimation model of power transformer based on hierarchical architecture and health index[J]. Power System Technology, 2014, 38(10): 2845-2850. (  0) 0) |
| [21] |
熊小伏, 杨雪东, 刘年. 基于站间信息的电子式互感器故障协同诊断方法[J]. 电力系统保护与控制, 2012, 40(21): 80-83, 89. XIONG Xiaofu, YANG Xuedong, LIU Nian. A collaborative diagnosis method of electronic transformer fault based on the inter-substation information[J]. Power System Protection and Control, 2012, 40(21): 80-83, 89. DOI:10.7667/j.issn.1674-3415.2012.21.014 (  0) 0) |
| [22] |
李嘉, 饶丹, 李耕, 等. 基于典型间隔模板的智能变电站虚端子自动连接方法[J]. 电力工程技术, 2020, 39(4): 157-163. LI Jia, RAO Dan, LI Geng, et al. Automatic connection method of virtual terminator in smart substation based on typical bay template[J]. Electric Power Engineering Technology, 2020, 39(4): 157-163. (  0) 0) |
| [23] |
唐志军, 李泽科, 陈建洪, 等. 考虑设备相关性的智能变电站二次系统可靠性分析[J]. 福州大学学报(自然科学版), 2021, 49(6): 782-789. TANG Zhijun, LI Zeke, CHEN Jianhong, et al. Reliability analysis for intelligent substation secondary system considering equipment correlation[J]. Journal of Fuzhou University (Natural Science Edition), 2021, 49(6): 782-789. (  0) 0) |
| [24] |
BILLINTON R, WANGDEE W. Predicting bulk electricity system reliability performance indices using sequential Monte Carlo simulation[J]. IEEE Transactions on Power Delivery, 2006, 21(2): 909-917. DOI:10.1109/TPWRD.2005.861237 (  0) 0) |
| [25] |
夏勇军, 肖繁. 考虑电力二次系统影响的智能配电网综合可靠性评估方法[J]. 电力系统自动化, 2020, 44(23): 165-172. XIA Yongjun, XIAO Fan. Comprehensive reliability evaluation method for smart distribution network considering influence of secondary power system[J]. Automation of Electric Power Systems, 2020, 44(23): 165-172. (  0) 0) |
| [26] |
赵武智, 邬小坤, 王宇恩, 等. 面向变电站安全隔离的一体化通信分析平台构建[J]. 电力系统保护与控制, 2020, 48(18): 123-129. ZHAO Wuzhi, WU Xiaokun, WANG Yuen, et al. Construction of integrated communication analysis platform for substation safety isolation[J]. Power System Protection and Control, 2020, 48(18): 123-129. (  0) 0) |
2. State Grid Jiangsu Electric Power Co., Ltd. Research Institute, Nanjing 211103, China
 2022, Vol. 41
2022, Vol. 41


 杨庆(1976),女,硕士,副教授,研究方向为工业物联网、人工智能、电力通信(E-mail:
杨庆(1976),女,硕士,副教授,研究方向为工业物联网、人工智能、电力通信(E-mail: