文章编号: 2096-3203(2022)02-0201-08 中图分类号: TM711
2. 清华大学电机工程与应用电子技术系,北京 100084;
3. 上海电力设计院有限公司,上海 200025
电力系统的惯量响应对频率调节有重要影响[1-4]。实时监测同步发电机惯量是电力系统频率安全稳定在线分析与控制的重要基础。一般采用甩负荷实验离线测量发电机惯量,但转子涡动和测量噪声会降低结果的可信度[5-6]。而在线辨识能更好地反映发电机在实际工况下的动态特性[7],因此采用在线辨识方法估计发电机惯量。同步相量测量装置(phasor measurement unit, PMU)可在电力系统正常运行中实时测量丰富的类噪声数据,反映电力系统动态特性[8],为在线监测发电机惯量提供数据条件[9]。使用系统辨识,以摇摆方程为基础,实时估计PMU功率和频率扰动信号的动态模型,并从中获取发电机惯量的方法已得到较多研究[10-12]。
这类辨识方法对于仿真系统中产生的数据有较好的效果[10, 12],但在实测数据中的适用性和可靠性一直难以保证[13-14]。其原因一是实际电网高度复杂,而现有模型完备性有所欠缺;二是数据质量存在问题[15],使用坏数据或精度较低的数据进行辨识会得到错误的结果;三是类噪声数据信噪比较低[16],导致部分数据信息不足而无法辨识。
处理实测数据是提升辨识效果的重要手段。数据的修复和筛选是处理实测数据的2种途径。现有基于类噪声的参数辨识工作多采用异常数据检测、恢复、降采样和去噪等方法[17-21],然而,在数据质量较低时,不能保证修复后数据的可靠性。数据的筛选多采用频域分析方法,其目的在于筛选出可以反映系统动态特性的数据段。文献[22]指出,输入信号频谱覆盖振荡频段时,才能较准确地辨识负荷参数。用类噪声信号辨识系统振荡模式时,文献[9, 23]基于类噪声信号的功率谱在关心频段的峰度指标进行数据筛选,但关心频段的选取主观性较强,且可解释性较差。惯量辨识领域尚无有关数据筛选的文献。
文中针对功频一阶模型,基于类噪声信号的谱分析和系统辨识理论,建立惯量估计的先验方差统计量作为可辨识指标,反映不同数据窗用于辨识的效果,实现对数据的评估和筛选。文中和现有数据筛选文献的思路均为类噪声信号的频域分析,但文中方法的理论性、可解释性与适应性较强,仿真和实测数据的算例验证了文中方法的有效性。
1 辨识模型和算法与评价指标针对发电机机端量测的类噪声数据,采用基于系统辨识的方法实现惯量监测。辨识的模型是发电机稳定工作点附近建立的小信号模型,其输入为离散时间的标幺有功扰动,记为u(n);输出为标幺频率扰动,记为y(n)。文中该模型结构固定为一阶的输出误差(output error, OE)模型,如式(1)所示,各项的具体形式如式(2)所示。
| $ y(n)=G(z, \boldsymbol{\theta}) u(n)+H(z, \boldsymbol{\theta}) e(n) $ | (1) |
| $ \left\{\begin{array}{l} \boldsymbol{\theta}=\left[\begin{array}{ll} A & B \end{array}\right]^{\mathrm{T}} \\ G(z, \boldsymbol{\theta})=\frac{B z^{-1}}{1+A z^{-1}} \\ H(z, \boldsymbol{\theta}) \equiv 1 \end{array}\right. $ | (2) |
式中:z-1为移位算子;A,B为2个模型参数,将其合并记为θ;e(n)为白噪声。对PMU量测的类噪声数据截取长度为N的数据窗。对于式(1)、式(2)所述OE模型,采用预报误差算法进行优化求解。
| $ y_{\text {pre }}(n)=-A y_{\text {pre }}(n-1)+B u(n-1) $ | (3) |
| $ \boldsymbol{\theta}_{N}=\arg \min {}_\boldsymbol{\theta} \sum\limits_{k=0}^{N-1}\left(y_{\text {pre }}(k)-y(k)\right)^{2} $ | (4) |
式中:ypre(n)为对输出的预报;θN为长度为N的数据窗辨识出的模型参数。忽略噪声,将系统传递函数G(z, θ)双线性变换连续化,得到连续系统传递函数,最终得到惯量M:
| $ M(\boldsymbol{\theta})=-\frac{1}{h\left(0^{+}\right)}=\frac{(A-1)(1-A) T_{\mathrm{S}}}{4 B} $ | (5) |
式中:h(0+)为连续系统冲激响应在0+时刻的值;TS为PMU中2帧数据的时间间隔;M(θ)为数据窗的惯量估计。尽管一阶OE模型可能不足以准确建模发电机的调速器特性,但该模型结构的辨识结果数值稳定性较高。而采用更高阶的模型较易出现数值问题,得到大量错误的辨识结果,导致整个数据集的辨识成功率降低。
定义数据窗的惯量辨识误差为ε,拟合度为η。2个量都描述一组数据窗的辨识效果,拟合度越高,模型预测输出和实际输出越接近。ε和η的计算如下:
| $ \varepsilon=\left(\left|M-M_{0}\right| / M_{0}\right) \times 100 \% $ | (6) |
| $ \eta=\left(1-\sqrt{\frac{\sum\limits_{k=0}^{N-1}\left(y_{\text {pre }}(k)-y(k)\right)^{2}}{\sum\limits_{k=0}^{N-1} y^{2}(k)-\frac{1}{N}\left(\sum\limits_{k=0}^{N-1} y(k)\right)^{2}}}\right) \times 100 \% $ | (7) |
式中:M0为惯量真值;M为该数据窗惯量辨识值。ypre(k)根据辨识出的θN使用式(3)进行递推得到。设某数据集中数据窗总数为NT。定义有效误差门限为εTH,并认为满足ε < εTH的数据窗为有效辨识。统计数据集有效辨识的数据窗个数NS,并定义辨识有效率ξ。ξ的计算如下:
| $ \xi=\left(N_{\mathrm{S}} / N_{\mathrm{T}}\right) \times 100 \% $ | (8) |
对数据集中各个数据窗的辨识误差和拟合度取平均,得到平均误差εav和平均拟合度ηav。平均误差、平均拟合度和辨识有效率可描述辨识方法对数据集总体的辨识效果。
2 先验方差与数据筛选系统辨识理论分析需要以一个理论上的“真实系统”为基础,该系统应反映物理上功率和频率的关系。调速器动作时,真实系统结构如图 1所示[12]。其中,Gp(s)为调速器的动态特性传递函数;Δpm(s)为发电机机械功率扰动;M为发电机惯量;D为发电机阻尼系数。

|
图 1 调速器-转子系统结构 Fig. 1 Structure of governor-rotor system |
该系统为闭环系统,考虑了调速器的动态特性,即频率对机械功率的影响,而摇摆方程反映了功率对频率的影响。电机正常运行时,频率波动较小,可认为调速器不动作,摇摆方程中机械功率不变,发电机的有功功率扰动和频率扰动满足一阶微分方程,因此假设离散化的真实系统结构为一阶OE模型是合理的。采用OE模型求解时,若辨识的模型结构和真实系统结构相同,则数据窗长度N趋于无穷时,按照式(3)和式(4)估计的模型参数θN依概率1收敛于真实系统的参数θ0;同时参数辨识θN服从渐近正态分布,其渐近期望为θ0,渐近方差记为cov(θN)[19]。cov(θN)的计算如下:
| $ \begin{gathered} \operatorname{cov}\left(\boldsymbol{\theta}_{N}\right)=\frac{2 {\rm{ \mathsf{ π} }}}{N} \times \\ \left(\int_{-{\rm{ \mathsf{ π} }}}^{{\rm{ \mathsf{ π} }}} \frac{T^{\prime}\left(\mathrm{e}^{\mathrm{j} \omega}, \boldsymbol{\theta}_{0}\right)\left[\begin{array}{cc} \varPhi_{\mathrm{u}}(\omega) & \varPhi_{\mathrm{ue}}(\omega) \\ \varPhi_{\mathrm{eu}}(\omega) & \lambda_{0} \end{array}\right]\left(T^{\prime}\left(\mathrm{e}^{-\mathrm{j} \omega}, \boldsymbol{\theta}_{0}\right)\right)^{\mathrm{T}}}{\left|H\left(\mathrm{e}^{\mathrm{j} \omega}, \boldsymbol{\theta}_{0}\right)\right|^{2} \lambda_{0}} \mathrm{~d} \omega\right)^{-1} \end{gathered} $ | (9) |
其中:
| $ T^{\prime}(z, \boldsymbol{\theta})=\left[\frac{\partial G(z, \boldsymbol{\theta})}{\partial \boldsymbol{\theta}} \quad \frac{\partial H(z, \boldsymbol{\theta})}{\partial \boldsymbol{\theta}}\right] $ | (10) |
式中:Φu(ω)为u(n)的功率谱;Φue(ω),Φeu(ω)为u(n)和e(n)的互功率谱;λ0为白噪声的方差[19]。
因此可认为所述的一阶模型辨识结果是依概率1收敛至真实系统参数的。而不同数据窗得到辨识结果误差的波动较大这一现象理解为相应数据得到的惯量估计量方差不同。产生较大方差的输入数据,其辨识结果偏差较大的可能性更高。
每个独立的数据窗的量测数据均可看作具有相应功率谱的随机过程的一个实现,进而估计该随机过程各个不同实现的数据用于辨识后得到的惯量估计的方差。该方差体现了辨识结果的分散性,分散性越大,随机过程的每个特定实现进行参数辨识得到误差较大的值的可能性越高。惯量估计的先验方差由估计参考系统的参数、估计模型参数的方差和估计惯量的方差3个步骤实现。
2.1 估计参考系统的参数由式(9)可知,求取模型参数的渐近方差时,需要已知真实系统的参数,因此可以通过预辨识估计一个参考系统参数θ1来代替真实系统,以估计方差。具体过程为:对一段数据集中的各个数据窗,进行惯量辨识并统计拟合度。一般认为,拟合度越高,辨识结果越准确。因此设置一个拟合度的门限值ηTH,对数据集中拟合度高于ηTH的数据窗的模型参数各取平均值。为实现ηTH选取的自适应性,ηTH可以选取为各数据窗辨识拟合度的某分位数。
| $ \boldsymbol{\theta}_{1}=\operatorname{mean}\left(\left\{\boldsymbol{\theta}_{N i} \mid \eta_{i}>\eta_{\mathrm{TH}}\right\}\right) $ | (11) |
式中:θNi,ηi分别为数据集中第i个数据窗所得模型参数和拟合度;mean(·)为对各向量取平均值。
2.2 模型参数的方差假设真实系统结构为一阶OE模型,则u(n)与e(n)是独立的随机变量,Φue(ω)≡Φeu(ω)≡0。数据窗长度N相同时,可不考虑N对参数估计方差的影响。由于OE模型的特殊噪声结构,T′(z, θ)第二列为0,式(9)化简得到R矩阵,可反映数据窗辨识得到的模型参数θN的方差。
| $ \boldsymbol{R}=\left(\int_{-{\rm{ \mathsf{ π} }}}^{{\rm{ \mathsf{ π} }}} K\left(\mathrm{e}^{\mathrm{j} \omega}, \boldsymbol{\theta}_{1}\right)\left(K\left(\mathrm{e}^{-\mathrm{j} \omega}, \boldsymbol{\theta}_{1}\right)\right)^{\mathrm{T}} \varPhi_{\mathrm{u}}(\omega) \mathrm{d} \omega\right)^{-1} $ | (12) |
其中:
| $ K(z, \boldsymbol{\theta})=\left[\frac{\partial G(z, \boldsymbol{\theta})}{\partial A} \quad \frac{\partial G(z, \boldsymbol{\theta})}{\partial B}\right]^{\mathrm{T}} $ | (13) |
各组数据中输入功率谱可用周期图估计:
| $ \varPhi_{\mathrm{u}}(\omega) \approx\left|\frac{1}{\sqrt{N}} \sum\limits_{k=0}^{N-1}\left(u(k) \mathrm{e}^{-\mathrm{j} \omega k}\right)\right|^{2} $ | (14) |
使用2.1节估计出的θ1,可估计出模型参数的方差。实际计算时,式(12)由数值积分得到。
2.3 惯量的方差由于模型参数θ和惯量估计M具有式(5)所述的函数关系,因此可以根据辨识得到的θN的方差,进一步估计惯量估计M的方差。假设辨识出的θN≈θ1,则根据高斯近似表达式可得到惯量先验方差的估计量σ[19]。
| $ \sigma \approx\left(\left.\frac{\partial M(\boldsymbol{\theta})}{\partial \boldsymbol{\theta}}\right|_{\boldsymbol{\theta}=\boldsymbol{\theta}_{1}}\right)^{\mathrm{T}} \boldsymbol{R}\left(\left.\frac{\partial M(\boldsymbol{\theta})}{\partial \boldsymbol{\theta}}\right|_{\boldsymbol{\theta}=\boldsymbol{\theta}_{1}}\right) \propto \operatorname{cov}(M) $ | (15) |
σ和惯量的方差成正比关系,在各数据窗长度N相同时,可直接用σ衡量一个数据窗惯量估计方差的大小。
2.4 筛选方法由于不同机组先验方差变化较大,因此采用自适应方法。对一段较长时间(例如15 min)的PMU数据集,先均匀取等长数据窗,计算各数据窗先验方差并排序,取出先验方差较小的那部分数据窗(经验上取前10%或25%),得到一个新数据集。一般而言,新数据集的总体辨识效果优于原数据集。
2.5 讨论事实上,2.1节中估计参考系统参数的步骤与2.2~2.3节中估计先验方差的步骤相独立,用于估计参考系统的数据集与筛选的数据集可以不一致。参考系统更新的频度低于求取惯量估计方差的频度。在参考系统固定且已经先验求出的条件下,式(12)和式(15)中带有θ1的项均已固定,不同组数据的先验方差σ只与其模型输入数据u的功率谱Φu(ω)相关。每个数据窗求先验方差时的主要运算为该数据窗功率谱的估计和数值积分的计算,算法实现时那些固定的值可事先算好并储存。Φu(ω)表征扰动的能量,一般而言,扰动的能量越大,辨识的方差越小,辨识结果越准确,这与式(12)相一致,即Φu(ω)的值越大,θN的方差越小。定义加权矩阵W(ω):
| $ \boldsymbol{W}(\omega)=K\left(\mathrm{e}^{\mathrm{j} \omega}, \boldsymbol{\theta}_{1}\right)\left(K\left(\mathrm{e}^{-\mathrm{j} \omega}, \boldsymbol{\theta}_{1}\right)\right)^{\mathrm{T}} $ | (16) |
式(12)可理解为采用W(ω)给Φu(ω)在不同频率加权并积分。经简易的推导可知,在频率较高时,W(ω)各项的值迅速衰减,因此先验方差对各个频段的敏感性不一致,对较低频段尤为敏感。而类噪声信号的能量也多集中于低频,因此只需要关心输入功率谱在较低频的幅值。文中方法是频域筛选方法的延续与规范化。与现有文献中的方法相比,通过估计参考系统与加权矩阵可自适应地确定关心频段的位置与不同频率的权值。文中方法的特点为:基于先验方差,在辨识前即可对数据进行筛选,从而不辨识那些被去除的数据窗,提升辨识的效率与准确度。
3 数据评估筛选算法的验证将上述数据筛选方法用于处理仿真和实测数据,以检验该方法的有效性。
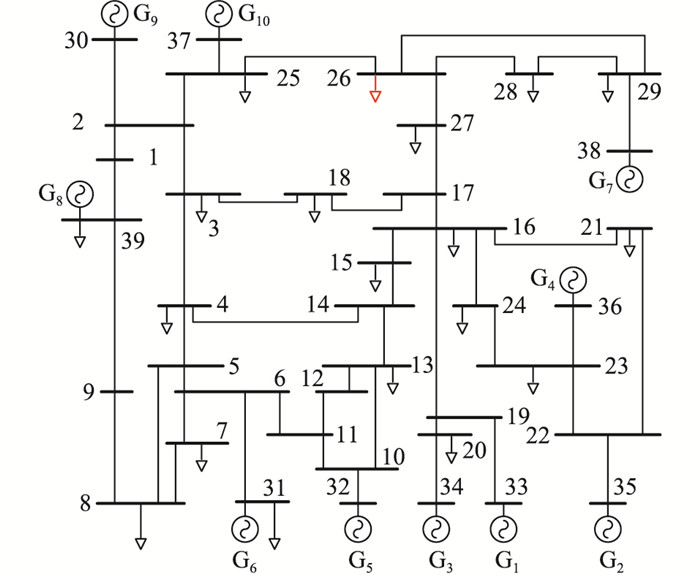
3.1 仿真数据算例使用基于Matlab的电力系统时域仿真软件PSAT得到电力系统类噪声工况的数据。仿真系统为标准的IEEE 10机39节点系统,系统结构如图 2所示,其中G1—G10为发电机[24-25]。对26号节点的有功功率施加标准差为0.05倍均值的典型类噪声扰动,该类噪声信号为电网中实测有功功率信号。
|
图 2 IEEE 39节点系统结构 Fig. 2 Structure of IEEE 39 node system |
测量有功扰动下各个发电机端的有功功率和频率,共进行6 min仿真。固定每个数据窗长1 min,实时传送速率为25次/s,即N为1 500。辨识前,对各数据窗进行标幺化、去均值等预处理得到u(n)与y(n)。为近似真实系统中PMU频率量测精度不高的情况,对频率数据进行了舍入,将频率的精度设为0.001 Hz(标幺值2×10-5),与实测数据情况相符。先取仿真数据中前80 s的数据集用于参考系统参数估计,之后使用该参考系统对后280 s的数据集进行筛选,对各数据集中每隔2 s取一个数据窗进行辨识。估算参考系统参数,其中ηTH取各组数据拟合度的95%分位数,事实上相当于取拟合度最高的一组数据窗模型参数为θ1。各机组的惯量设定值为M0,θ1,表 1为使用θ1经式(5)得到的惯量M1及其误差ε。
|
|
表 1 各机组参考系统参数及其惯量误差 Table 1 Reference system parameters of each generator and its inertia error |
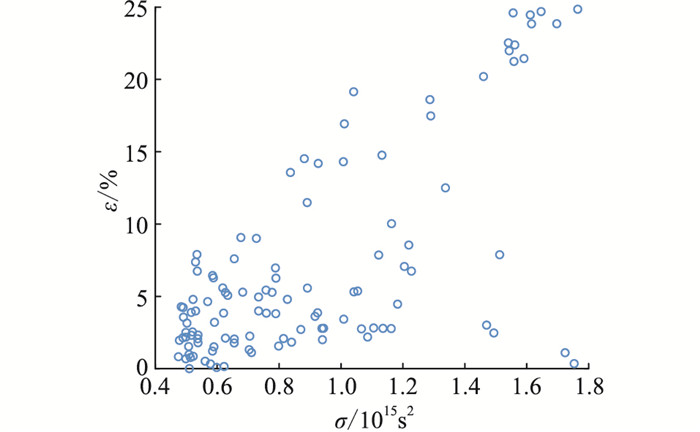
可见,估计的参考系统惯量与设定值较为接近,参考系统能够近似真实系统。之后对各机组后280 s的数据集各数据窗进行惯量辨识。统计每个数据窗的辨识误差ε,并进行先验方差σ的估计。G5的先验方差和辨识误差关系如图 3所示。可见先验方差和辨识误差有明显正相关关系,先验方差σ较小的数据组,辨识误差ε一般也较小。对G1,G5,G6,G9,筛选出先验方差较低的50%数据窗,得到新的数据集。仿真数据辨识误差较小,因此取有效误差门限εTH为5%。
|
图 3 G5各组惯量辨识误差和先验方差关系 Fig. 3 Relationship between inertia identification error and prior variance of G5 |
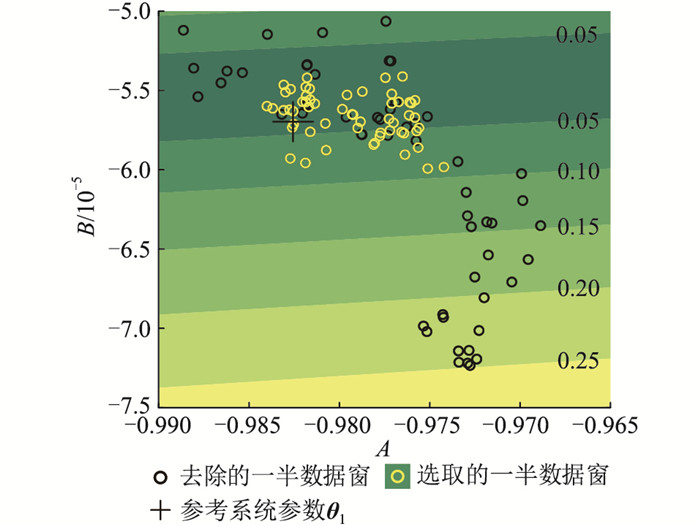
表 2为筛选前后数据集的数据窗数、平均拟合度、平均辨识误差和辨识有效率。以G5为例,图 4为筛选前后模型参数分布与相对应的误差,图中等高线为辨识误差。数据筛选前后,使用的辨识模型与算法相同。由表 2和图 4可得,筛选后,各机组平均误差、辨识有效率和平均拟合度都有所提升,辨识效果提高。
|
|
表 2 仿真数据筛选前后惯量辨识结果对比 Table 2 Comparison of inertia identification results before and after simulation data selection |
|
图 4 G5模型参数与辨识误差 Fig. 4 Relationship between inertia identification error and prior variance of G5 |
算例还展示了文中方法的先验性,估计参考系统的数据集和用于筛选检验的数据集相互分离。用文中方法筛选一个数据集时,参考系统可以根据先于该数据集的辨识经验求得。求取参考系统的辨识过程与筛选过程是独立的,筛选时完全不用对该数据集中的各数据窗进行辨识操作。
3.2 实测数据算例用文中方法处理电力系统中实测数据,选取实际电网中的5台发电机的数据用于处理,分别记作1号至5号。
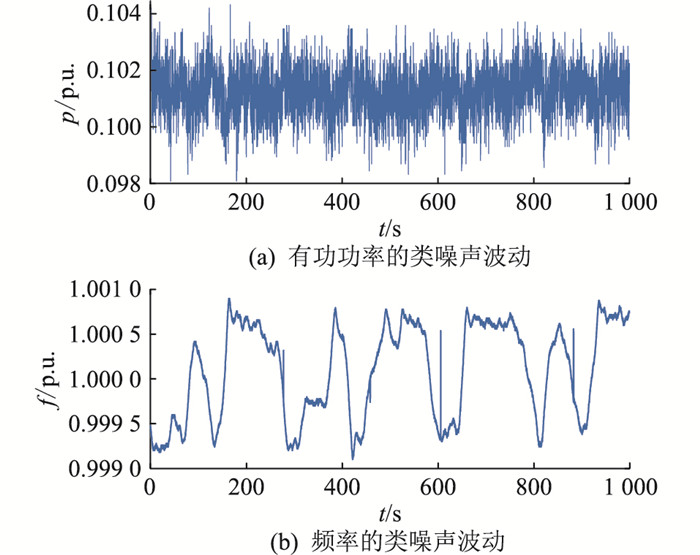
1号发电机典型的有功功率、频率类噪声信号波形如图 5所示,两图选取时间段相同,展示了功率和频率同步变化。可以观察到频率信号的毛刺缺陷。为解决这一缺陷,数据预处理时在标幺化、去均值前增加零相移低通滤波操作[20]。由于信号能量主要分布在较低的频段,滤波操作对频率信号有效成分的影响较弱,因此能有效地滤除波形中的毛刺与高频噪声。文中处理实测数据时,零相移低通滤波器的截止频率选为0.5 Hz。
|
图 5 1号发电机典型有功功率和频率波形 Fig. 5 Typicalactive power and frequency waveform of generator No.1 |
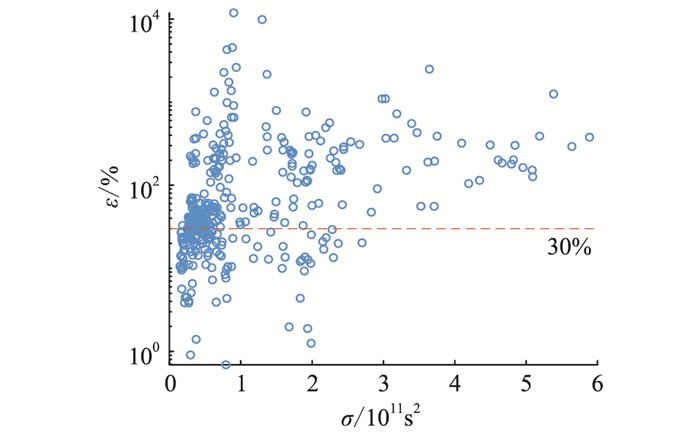
频率数据的精度、实时传送速率、数据窗长分别为0.001 Hz,25次/s,1 min。以2 s为间距均匀取数据窗。以1号发电机为例,总长为1 000 s的类噪声数据,取前200 s的数据估计参考系统。后800 s中各数据窗的先验方差和辨识误差如图 6所示。其中ηTH为各组辨识拟合度的90%分位数。根据图 6,先验方差σ和惯量辨识误差ε具有正相关性。且实测数据的辨识中较多辨识结果较差的数据组,辨识误差最大可以达到11 859.9%。在计算辨识误差时,采用实际调度系统使用的仿真模型中相应机组惯量作为真值。
|
图 6 1号发电机各组惯量辨识误差与先验方差关系 Fig. 6 Relationship between inertia identification error and prior variance of generator No.1 |
每个机组选取出先验方差较小的前10%的数据窗作为新数据集,表 3为筛选前后数据集的窗数、平均误差、辨识有效率和平均拟合度。
|
|
表 3 实测数据筛选前后惯量辨识结果 Table 3 Inertia identification results before and after selection of real world data |
由于实测数据辨识误差较大,因此εTH选取为30%。可以得到和仿真数据类似的结论。可见用文中方法先对各数据组进行筛选,再进行辨识可以有效提高辨识的质量,其中1号发电机和2号发电机筛选后辨识精度得到显著提升。
加权矩阵W(ω)是一个2×2的复矩阵,记其第i行第j列的元素为wij(ω)。图 7为W(ω)矩阵各个元素的虚实部值与ω的关系。

|
图 7 1号发电机先验加权矩阵W的各元素 Fig. 7 Each entry of prior weight matrix W of generator No.1 |
可见,对1号发电机,在辨识之前应该关注的是输入数据中非常低频的有功扰动,该频段有功扰动越大,数据窗辨识结果较好;ω大于0.01π rad/s以后,加权矩阵的值几乎为0,考虑实时传送速率为25次/s,该ω对应的频率为0.125 Hz。上述结果表明,对发电机,低于0.125 Hz的频段是频率扰动u的有效频段。为了节省计算时间,在计算式(12)时可以只在低频段积分(如[-0.02π, 0.02π]),而不用在[-π, π]整个区间积分。
实测数据的辨识效果较差,有辨识误差极大的组。在这种情况下,若不进行数据筛选,直接进行辨识,则第1章的辨识方法不能实际应用。但若采用第2章所述筛选方法,可在辨识之前,有效地筛选出辨识结果较好的数据窗。
4 结论文中在已有的类噪声数据辨识惯量方法的基础上,从概率的角度建立了先验方差统计量,并将其应用于数据筛选。在进行辨识运算之前,即可先验地从大量数据中选取出辨识效果较好的一些数据窗,为辨识算法的实施提供重要帮助。文中将所提方法应用于处理仿真和实测数据,检验了方法的有效性。但由于实测数据的复杂性及概率的不确定性等原因,筛选后辨识结果虽有所提升,但仍有不尽人意的地方,这也是下一步研究中亟需解决的问题。
本文得到国网上海市电力公司科技项目(SGSH0000DKJS1900681)资助,谨此致谢!
| [1] |
孙华东, 王宝财, 李文锋, 等. 高比例电力电子电力系统频率响应的惯量体系研究[J]. 中国电机工程学报, 2020, 40(16): 5179-5192. SUN Huadong, WANG Baocai, LI Wenfeng, et al. Research on inertia system of frequency response for power system with high penetration electronics[J]. Proceedings of the CSEE, 2020, 40(16): 5179-5192. (  0) 0) |
| [2] |
陈雪梅, 陆超, 韩英铎. 电力系统频率问题浅析与频率特性研究综述[J]. 电力工程技术, 2020, 39(1): 1-9. CHEN Xuemei, LU Chao, HAN Yingduo. Review of power system frequency problems and frequency dynamic characteristics[J]. Electric Power Engineering Technology, 2020, 39(1): 1-9. (  0) 0) |
| [3] |
文云峰, 杨伟峰, 林晓煌. 低惯量电力系统频率稳定分析与控制研究综述及展望[J]. 电力自动化设备, 2020, 40(9): 211-222. WEN Yunfeng, YANG Weifeng, LIN Xiaohuang. Review and prospect of frequency stability analysis and control of low-inertia power systems[J]. Electric Power Automation Equipment, 2020, 40(9): 211-222. (  0) 0) |
| [4] |
王博, 杨德友, 蔡国伟. 高比例新能源接入下电力系统惯量相关问题研究综述[J]. 电网技术, 2020, 44(8): 2998-3007. WANG Bo, YANG Deyou, CAI Guowei. Review of research on power system inertia related issues in the context of high penetration of renewable power generation[J]. Power System Technology, 2020, 44(8): 2998-3007. (  0) 0) |
| [5] |
段刚, 李海峰, 武二克, 等. 基于PMU和缓变功率的发电机组运动方程参数在线辨识[J]. 电力自动化设备, 2020, 40(6): 198-204. DUAN Gang, LI Haifeng, WU Erke, et al. Online parameter identification of generator motion equation based on PMU and slow-varying power[J]. Electric Power Automation Equipment, 2020, 40(6): 198-204. (  0) 0) |
| [6] |
田丰. 甩负荷试验转子转动惯量计算方法研究[J]. 中国电力, 2005, 38(7): 37-41. TIAN Feng. Calculation methods for inertia moment of steam turbogenerator rotor using load rejection test[J]. Electric Power, 2005, 38(7): 37-41. DOI:10.3969/j.issn.1004-9649.2005.07.009 (  0) 0) |
| [7] |
孙昊, 王茂海, 齐霞. 基于PMU实测数据的同步发电机参数在线辨识方法[J]. 电力系统保护与控制, 2014, 42(3): 31-36. SUN Hao, WANG Maohai, QI Xia. Synchronous generator parameters identification based on PMU data[J]. Power System Protection and Control, 2014, 42(3): 31-36. (  0) 0) |
| [8] |
PIERRE J W, TRUDNOWSKI D J, DONNELLY M K. Initial results in electromechanical mode identification from ambient data[J]. IEEE Transactions on Power Systems, 1997, 12(3): 1245-1251. DOI:10.1109/59.630467 (  0) 0) |
| [9] |
陆超, 张俊勃, 韩英铎. 电力系统广域动态稳定辨识与控制[M]. 北京: 科学出版社, 2015. LU Chao, ZHANG Junbo, HAN Yingduo. Wide area dynamic stability identification and control of power system[M]. Beijing: Science Press, 2015. (  0) 0) |
| [10] |
ZENG F H, ZHANG J B, CHEN G, et al. Online estimation of power system inertia constant under normal operating conditions[J]. IEEE Access, 2020, 8: 101426-101436. DOI:10.1109/ACCESS.2020.2997728 (  0) 0) |
| [11] |
TUTTELBERG K, KILTER J, WILSON D, et al. Estimation of power system inertia from ambient wide area measurements[J]. IEEE Transactions on Power Systems, 2018, 33(6): 7249-7257. DOI:10.1109/TPWRS.2018.2843381 (  0) 0) |
| [12] |
李世春, 夏智雄, 程绪长, 等. 基于类噪声扰动的电网惯量常态化连续估计方法[J]. 中国电机工程学报, 2020, 40(14): 4430-4439, 4723. LI Shichun, XIA Zhixiong, CHENG Xuchang, et al. Continuous estimation method of power system inertia based on ambient disturbance[J]. Proceedings of the CSEE, 2020, 40(14): 4430-4439, 4723. (  0) 0) |
| [13] |
TAMRAKAR U, GURUWACHARYA N, BHUJEL N, et al. Inertia estimation in power systems using energy storage and system identification techniques[C]//2020 International Symposium on Power Electronics, Electrical Drives, Automation and Motion(SPEEDAM). Sorrento, Italy. IEEE, 2020: 577- 582.
(  0) 0) |
| [14] |
JAKOBSEN S H, UHLEN K, BOMBOIS X. Identification of hydro turbine governors using PMU data[C]//2018 IEEE International Conference on Probabilistic Methods Applied to Power Systems. Boise, ID, USA. IEEE, 2018: 1-6.
(  0) 0) |
| [15] |
BROWN M, BISWAL M, BRAHMA S, et al. Characterizing and quantifying noise in PMU data[C]//2016 IEEE Power and Energy Society General Meeting. Boston, MA, USA. IEEE, 2016: 1-5.
(  0) 0) |
| [16] |
ZHANG X R, LU C, WANG Y. A two-stage framework for ambient signal based load model parameter identification[J]. International Journal of Electrical Power & Energy Systems, 2020, 121: 106064. (  0) 0) |
| [17] |
吴沛萱, 叶洪波, 崔勇, 等. 主导负荷参数类噪声辨识的数据处理方法[J]. 电网技术, 2021, 45(6): 2335-2341. WU Peixuan, YE Hongbo, CUI Yong, et al. Data processing method of ambient signal-based dominant load parameter identification[J]. Power System Technology, 2021, 45(6): 2335-2341. (  0) 0) |
| [18] |
熊传平, 曹军杰, 陈谦, 等. 基于小波分析的电力负荷模型辨识数据去噪[J]. 河海大学学报(自然科学版), 2011, 39(4): 470-474. XIONG Chuanping, CAO Junjie, CHEN Qian, et al. A wavelet-based method for de-noising data of electric load modeling[J]. Journal of Hohai University (Natural Sciences), 2011, 39(4): 470-474. DOI:10.3876/j.issn.1000-1980.2011.04.021 (  0) 0) |
| [19] |
LJUNG L. System identification: theory for the user[M]. Beijing: Tsinghua University Press, 2002.
(  0) 0) |
| [20] |
伍双喜, 吴文传, 张伯明, 等. 用PMU实测数据辨识同步发电机参数的关键问题[J]. 电力系统自动化, 2012, 36(17): 50-55. WU Shuangxi, WU Wenchuan, ZHANG Boming, et al. Key issues of synchronous generator parameter identification using PMU measurements[J]. Automation of Electric Power Systems, 2012, 36(17): 50-55. (  0) 0) |
| [21] |
万楚林, 陈皓勇, 郭曼兰, 等. 基于模式识别的WAMS有功功率错误数据处理[J]. 电网技术, 2017, 41(3): 922-930. WAN Chulin, CHEN Haoyong, GUO Manlan. Wrong active power data identification and correction for WAMS based on pattern recognition[J]. Power System Technology, 2017, 41(3): 922-930. (  0) 0) |
| [22] |
鞠平, 张正利, 潘学萍, 等. 参数可观测性分析及其在电力负荷模型中的应用[J]. 电力系统自动化, 2016, 40(5): 32-37. JU Ping, ZHANG Zhengli, PAN Xueping, et al. Parameter observability analysis and its application to power load model[J]. Automation of Electric Power Systems, 2016, 40(5): 32-37. (  0) 0) |
| [23] |
张俊勃. 基于广域信息的电力系统动态建模与应用[D]. 北京: 清华大学, 2013. ZHANG Junbo. Wide-area information based power system dynamic modeling and its applications[D]. Beijing: Tsinghua University, 2013. (  0) 0) |
| [24] |
王增平, 朱劭璇, 王彤, 等. 基于故障全景信息的电力系统暂态稳定分析方法[J]. 电力系统保护与控制, 2020, 48(15): 34-42. WANG Zengping, ZHU Shaoxuan, WANG Tong, et al. Transient stability analysis for a power system based on fault panoramic information[J]. Power System Protection and Control, 2020, 48(15): 34-42. (  0) 0) |
| [25] |
朱劭璇, 王彤, 王增平, 等. 考虑主导不稳定平衡点变化的电力系统暂态稳定切机控制策略[J]. 电力系统保护与控制, 2021, 49(5): 20-28. ZHU Shaoxuan, WANG Tong, WANG Zengping, et al. Generator tripping strategy in transient stability control of a power system considering the change of the controlling unstable equilibrium point[J]. Power System Protection and Control, 2021, 49(5): 20-28. (  0) 0) |
2. Department of Electrical Engineering, Tsinghua University, Beijing 100084, China;
3. Shanghai Electric Power Design Institute Co., Ltd., Shanghai 200025, China
 2022, Vol. 41
2022, Vol. 41


 叶洪波(1977), 男, 学士, 高级工程师, 从事电力系统分析与建模相关工作(E-mail:
叶洪波(1977), 男, 学士, 高级工程师, 从事电力系统分析与建模相关工作(E-mail: