文章编号: 2096-3203(2022)02-0163-08 中图分类号: TM732
微电网是由分布式能源、储能系统、电能转换装置等单元组成的系统[1-2],我国“十四五”规划及2035远景目标中提出的集中式与分布式能源建设纲要[3],将大力推动我国微电网工程的建设。随着分布式能源发电技术逐渐成熟及建设难度不断降低[4],在一定约束条件下降低发电成本与环境成本,提高发电利用水平,实现微电网优化调度是目前需要研究的方向[5-7]。
微电网优化调度是典型的非线性问题,目前的研究多应用智能算法进行寻优求解[8-10]。文献[11]利用鸟群算法对微电网的功率和能量进行多目标优化管理,具有较好的稳定性和精度,但鸟群算法搜索速度较慢、参数较多,影响寻优结果;文献[12]提出了改进遗传算法的微电网多目标最优调度方法,建立了包括环境成本、系统运行维护成本、起停成本和主电网电价的目标函数,但该算法存在局部收敛的情况,稳定性不高;文献[13]提出了基于改进人工鱼群算法的微电网优化调度方法,利用鱼群聚集和追尾行为改进粒子飞行方向和位置,优化结果的收敛速度与准确性有所提升;文献[14]提出了一种基于自适应权重和混沌搜索粒子群优化的多智能体微电网能量管理模型,可有效避免陷入早熟,但自适应权重因子缺乏约束,寻优效率较低;文献[15]通过引入纵横交叉算法、双向学习机制和转换调节机制改进蝙蝠算法,降低了微电网发电成本,但微电网模型中缺少环境效益建模。
麻雀搜索算法(sparrow search algorithm, SSA)是一种新型群优化算法[16],其收敛速度快、精准度较高,具有解决多个领域问题的潜力[17],但在某些条件下依然存在陷入局部最优,导致收敛速度下降的不足。为改善这一问题,增强SSA的全局搜索能力,文中利用反向学习策略和自适应t分布变异对SSA进行改进,提出一种反向变异麻雀搜索算法(reverse mutation sparrow search algorithm, RMSSA)。以某微电网系统为例,设定包含经济性和环境效益的目标函数与约束条件,建立微电网优化调度模型,应用RMSSA对其进行优化求解。对比仿真结果表明改进算法寻优能力有明显提高。
1 改进型SSA 1.1 基本SSA自然界中麻雀种群内部存在明显分工,根据其捕食与反捕食习性,SSA将麻雀种群中成员分为发现者、跟随者、预警者3类。发现者是具有最高适应度的成员,其搜索范围最广,可引导种群觅食。加入者根据其适应度的高低分为2组,适应度高的加入者向发现者位置移动,追求更高的适应度;适应度低的加入者由于距离发现者过远,会自行寻找食物,若寻找到食物,则转变为发现者,因此发现者与跟随者的身份是动态变化的,但发现者与跟随者占种群的比例不变。预警者是位于种群边缘的部分个体,若发生危险,会立即提醒种群进行反捕食行为,逃避危险。
设定在D维空间中,由M只麻雀组成的种群在觅食,第i只麻雀的位置为X=[xi1 xi2 … xiD],其中i=1, 2, …, M。根据SSA的运算规则,对麻雀个体位置更新规则进行设定。
发现者位置更新规则为:
| $ x_{i j, T+1}= \begin{cases}x_{i j, T} \mathrm{e}^{\frac{-i}{\alpha T_{\mathrm{iter}}}} \quad R<S_{\mathrm{T}} \\ x_{i j, T}+Q L_{j} \quad R \geqslant S_{\mathrm{T}}\end{cases} $ | (1) |
式中:T为当前迭代次数;j=1, 2, …, D;xij, T为当前个体i在j维空间位置,xij, T+1为下次迭代时个体i在j维空间位置;α为(0, 1]之间均匀分布的随机数;Titer为算法最大迭代次数;Q为服从正态分布的随机数;Lj为1行D维全1矩阵L的元素;R(R∈[0, 1])为预警值;ST(ST∈[0.5, 1])为安全值。当R < ST时,麻雀个体可在边界内广泛搜索;当R≥ST时,预警者发出警报,种群个体做出反捕食行为。
加入者位置更新规则为:
| $ \begin{gathered} x_{i j, T+1}= \\ \left\{\begin{array}{l} Q \mathrm{e}^{\left(x_{i j, T, \mathrm{w}} x_{i j, T}\right) / i^{2}} \quad i>M / 2 \\ x_{i j, T+1, \mathrm{~b}}+\left|x_{i j, T}-x_{i j, T+1, \mathrm{~b}}\right|\left(\boldsymbol{A}^{+} \boldsymbol{L}\right)_{j} \quad i \leqslant M / 2 \end{array}\right. \end{gathered} $ | (2) |
式中:A为1行D维矩阵,其元素随机为1或-1,A+= A T(AAT)-1。将式(2)简化,可得:
| $ \begin{gathered} x_{i j, T+1}= \\ \left\{\begin{array}{l} Q^{\left(x_{i j, T, \mathrm{w}}-x_{i j, T}\right) / i^{2}} \quad i>M / 2 \\ x_{i j, T, \mathrm{~b}}+\frac{1}{D} \sum\limits_{j=1}^{D}\left(\operatorname{rand}\{-1,1\}\left|x_{i j, T, \mathrm{~b}}-x_{i j, T}\right|\right) \\ \quad\quad\quad\quad\quad\quad\quad i \leqslant M / 2 \end{array}\right. \end{gathered} $ | (3) |
式中:xij, T, w为第T次迭代时麻雀种群在第j维空间的全局最差位置;xij, T, b为第T次迭代时麻雀种群在第j维空间的全局最优位置;rand{-1, 1}为-1至1间的随机数。当i>M/2时,表明加入者没有获得食物,适应度较差,会自行向其他位置移动寻找食物;当i≤M/2时,加入者适应度较高,向发现者位置移动进行觅食。
预警者位置更新规则为:
| $ x_{i j, T+1}= \begin{cases}x_{i j, T, \mathrm{~b}}+\beta\left(x_{i j, T}-x_{i j, T, \mathrm{~b}}\right) \quad f_{\mathrm{i}} \neq f_{\mathrm{g}} \\ x_{i j, T}+K \frac{x_{i j, T}-x_{i j, T, \mathrm{w}}}{\left|f_{\mathrm{i}}-f_{\mathrm{w}}\right|+\varepsilon} \quad f_{\mathrm{i}}=f_{\mathrm{g}}\end{cases} $ | (4) |
式中:β为均值为0、方差为1的正态分布随机数,用于控制每次迭代的步长;ε为极小的数,以防止分母为0;K为[-1, 1]间的均匀随机数;fi为当前麻雀个体的适应度值;fg,fw分别为第T次迭代时麻雀种群的全局最优适应度值和最差适应度值。当fi=fg时,预警者在种群最优位置发现危险,立即向种群中其他位置移动;当fi≠fg时,预警者在种群边缘发现危险,向当前种群最优位置移动逃避。
1.2 反向学习策略反向学习策略是一种可以提高群优化算法搜索能力的方法[18],主要思想是在当前个体所在区域产生反向个体,并在反向个体与当前个体中选取适应度高的个体进行算法迭代。
已知处于D维空间的麻雀个体位置为Xi=[xi1 xi2 … xiD],满足xij∈[ui, li]的边界条件,令其产生的反向个体为Xi*=[xi1* xi2* … xiD*],其中xij*=li+ui-xij。当初始麻雀种群个体数为W时,反向麻雀种群个体数同样为W。将初始麻雀种群与反向麻雀种群合并,按照适应度大小进行排序,选取适应度最高的W只麻雀个体进入下一轮迭代,以达到拓宽种群搜索面积,提高种群多样性的目的。
1.3 自适应t分布变异t分布也称学生分布,定义p(x)为t分布概率密度函数,如式(5)所示。
| $ \begin{gathered} p(x)=\frac{\Gamma\left(\frac{m+1}{2}\right)}{\sqrt{m {\rm{ \mathsf{ π} }}} \Gamma(m / 2)}\left(\frac{x^{2}}{m}+1\right)^{-\frac{m+1}{2}} \\ -\infty<x<+\infty \end{gathered} $ | (5) |
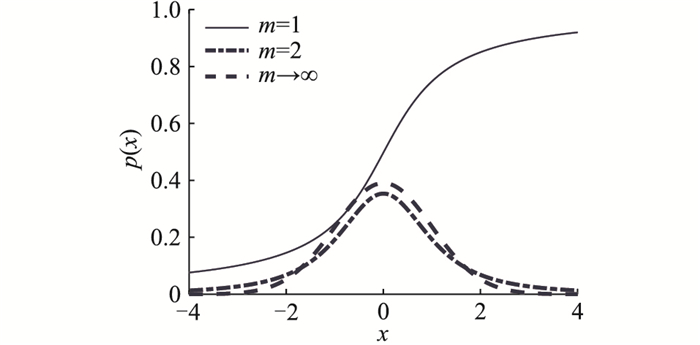
式中:Γ(·)为伽马函数。p(x)含有参数自由度m,函数曲线形态与自由度m的大小有关。m值越小,其曲线越平坦,中间越低,双侧尾部越上翘。m→∞时,p(x)→ N(0, 1);m=1时,p(x)=C(0, 1)。其中,N(0, 1)为高斯分布,期望为0,方差为1;C(0, 1)为柯西分布,期望不存在,方差无限大[19]。m=1,m=2,m→∞时的p(x)函数如图 1所示。
|
图 1 t分布概率密度函数 Fig. 1 Probability density function of t-distribution |
文中利用t分布对麻雀个体位置进行变异,提高种群搜索能力。但t分布作用于算法时,在迭代过程中也存在变异程度超出范围,导致局部收敛较弱的问题。文中定义自适应因子θ,利用θ对t分布的变异程度进行控制,定义如下:
| $ \boldsymbol{\theta}=p^{T}\left(1-\frac{T}{T_{\mathrm{iter}}+\mathrm{e}^{1 / T}}\right) $ | (6) |
式中: pT为限制因子,以迭代次数T作为其指数,用于控制迭代开始时的变异幅度,避免算法运行初期,变异幅度过大导致局部收敛失效,文中设定p=0.5。迭代过程中,θ值非线性减小,其发挥的作用也随之减弱。
根据定义,文中对麻雀个体位置Xi=[xi1 xi2 … xiD]进行自适应t分布变异:
| $ \boldsymbol{X}_{i}^{\prime}=\boldsymbol{X}_{i}+\theta \boldsymbol{X}_{i} t\left(T_{\mathrm{iter}}\right) $ | (7) |
式中:Xi为变异前第i只麻雀个体位置;X′i为变异后第i只麻雀个体位置;t(Titer)为以算法的最大迭代次数Titer为自由度的自适应t分布。式(7)在Xi的基础上增加了随机干扰项θXit(Titer),充分利用当前种群信息进行干扰。在算法运行初期,X′i具有较强的全局搜索能力,有助于算法脱离局部最优;在算法运行末期,X′i具有较强的局部搜索能力,收敛于全局极值点,同时也提高了收敛速度,从而增强了算法搜索能力。
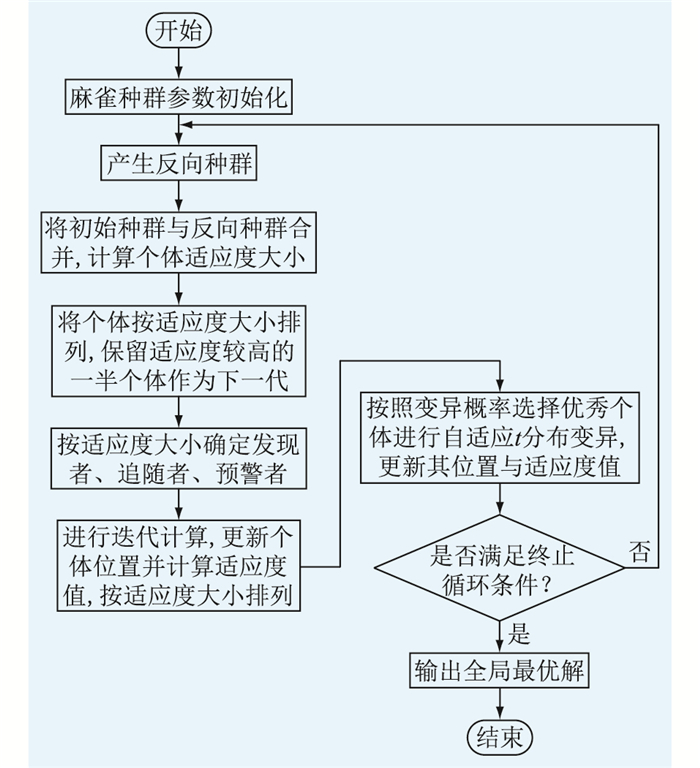
1.4 RMSSARMSSA弥补了SSA在应用中可能陷入局部收敛的不足,其核心思想为:建立初始麻雀种群时,产生反向种群,在2个种群中保留优秀个体进入迭代计算。本次迭代结束后,按照变异概率再次选择优秀个体,引入最大迭代次数Titer为参数自由度的随机干扰项θXit(Titer),对当前种群信息进行干扰,使优秀麻雀个体可以脱离局部极值点的限制,收敛于全局极值点,同时也提高了寻优搜索能力。RMSSA的求解流程如图 2所示。
|
图 2 RMSSA流程 Fig. 2 Flow chart of RMSSA |
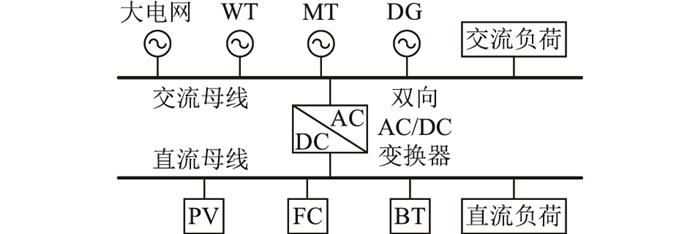
以某微电网为例,如图 3所示。分布式电源包括光伏(photovoltaic, PV)、风力发电机(wind turbine, WT)、燃料电池(fuel cell, FC)、柴油发电机(diesel generators, DG)、蓄电池(battery, BT)、微型燃气轮机(micro gas turbine, MT),输出部分包括交流负荷和直流负荷。
|
图 3 微电网系统基本结构 Fig. 3 Basic structure of microgrid system |
WT的输出功率与风速关系呈非线性,此处风速指风力机轮毂位置的平均风速[20],其输出功率为:
| $ P_{\mathrm{WT}}(t)=\left\{\begin{array}{l} 0 \quad v(t)<v_{\mathrm{i}}, v(t)>v_{\mathrm{c}} \\ \frac{P_{\mathrm{r}}\left(v^{w}(t)-v_{\mathrm{i}}^{w}\right)}{v_{\mathrm{r}}^{w}-v_{\mathrm{i}}^{w}} \quad v_{\mathrm{i}} \leqslant v(t) \leqslant v_{\mathrm{r}} \\ P_{\mathrm{r}} \quad v_{\mathrm{r}}<v(t) \leqslant v_{\mathrm{c}} \end{array}\right. $ | (8) |
式中:PWT(t)为WT的输出功率;Pr为机组的额定功率;vi,vr,vc分别为WT的启动风速、额定风速和截止风速。为体现设备磨损对输出影响,引入威布尔分布参数w。文中取vi=3 m/s,vr=12 m/s,vc=25 m/s,w=3。
2.2.2 PV发电模型PV发电的输出功率可由光照强度、环境温度等决定,文中设定PV电池工作时表面温度为Tc=25 ℃,光辐射量GAC=800 W/m2,其输出功率为:
| $ P_{\mathrm{PV}}(t)=P_{\mathrm{STC}} f\left[1+\alpha_{\mathrm{p}}\left(T_{\mathrm{c}}-T_{\mathrm{STC}}\right)\right] \frac{G_{\mathrm{AC}}}{G_{\mathrm{STC}}} $ | (9) |
式中:PPV(t)为PV电池板的输出功率;PSTC为PV电池板的额定容量;f为降额因子,表示电池衰减和尘土对PV电池的影响系数,文中取0.95;αp为功率温度系数, 其值为-0.47 %/K;TSTC,GSTC分别为标准测试条件下的温度与光照强度,文中分别取25 ℃和1 000 W/m2。
2.2.3 DG发电模型DG具有可靠性高,运行检修技术成熟等特点。当其他单元发电量不足时,DG在微电网中可以进行补充。在任意负载下,其发电所需的燃料消耗为二次函数形式[21]。DG的燃烧成本为:
| $ C_{\mathrm{DG}}(t)=\left(a+b P_{\mathrm{DG}}(t)+c P_{\mathrm{DG}}^{2}(t)\right) \Delta t $ | (10) |
式中:PDG为DG的输出功率;a,b,c为燃烧成本系数;Δt为间隔时间。
2.2.4 MT发电模型MT以天然气为燃料,具有体积小、排放低、噪音污染轻等特点。MT的燃烧成本为:
| $ C_{\mathrm{MT}}(t)=\frac{Q_{\mathrm{g}}}{L_{\mathrm{HVg}}} \frac{P_{\mathrm{MT}}(t)}{\eta_{\mathrm{MT}}} \Delta t $ | (11) |
式中:Qg为天然气的价格;LHVg为天然气的低位热值;PMT(t)为MT的输出功率;ηMT为MT的输出效率。
2.2.5 FC发电模型FC是一种把燃料所具有的化学能直接转换成电能的发电装置。FC用燃料和氧气作为原料,其启动时间短、功率密度高[22]。文中采用甲醇作为FC的燃料,运行成本为:
| $ C_{\mathrm{FC}}(t)=\frac{Q_{\mathrm{m}}}{L_{\mathrm{HVm}}} \frac{P_{\mathrm{FC}}(t)}{\eta_{\mathrm{FC}}} \Delta t $ | (12) |
式中:Qm为甲醇的价格;LHVm为甲醇的低位热值;PFC(t)为FC的输出功率;ηFC为FC的输出效率。
2.2.6 BT充放电模型微电网需要储能装置来平抑其输出功率的波动,以提高稳定性,因此BT作为储能装置得到了广泛应用。BT的性能指标主要为容量、充电功率、放电功率、荷电状态,在调度周期内分为充电阶段和放电阶段,由此建立BT充、放电模型:
| $ C_{\mathrm{SOC}}(t)=\left\{\begin{array}{c} C_{\mathrm{SOC}}(t-\Delta t)(1-\delta)-\frac{P_{\mathrm{BT}}(t) \Delta t}{\eta_{\mathrm{d}} E_{\mathrm{BT}}} \\ P_{\mathrm{BT}}(t) \geqslant 0 \\ C_{\mathrm{SOC}}(t-\Delta t)(1-\delta)-\frac{\eta_{\mathrm{c}} P_{\mathrm{BT}}(t) \Delta t}{E_{\mathrm{BT}}} \\ P_{\mathrm{BT}}(t)<0 \end{array}\right. $ | (13) |
式中:δ为能量自损率;CSOC(t)为BT在t时段的容量;EBT为BT的额定容量;PBT(t)为BT在t时段的瞬时功率,在BT放电时为正,充电时为负;ηc,ηd分别为其充、放电效率。
2.3 目标函数以每个自然日为一个优化周期,设定T=24,Δt=1 h。微电网优化调度的目标函数计及燃料成本、维护成本、环境成本、电网交互成本。
燃料成本CF包括MT、DG、FC运行过程中使用燃料的成本,计算如下:
| $ C_{\mathrm{F}}=\sum\limits_{t=1}^{T}\left(C_{\mathrm{FC}}(t)+C_{\mathrm{MT}}(t)+C_{\mathrm{DG}}(t)\right) $ | (14) |
微电网内各分布式电源设备均存在维护成本CM,计算如下:
| $ C_{\mathrm{M}}=\sum\limits_{t=1}^{T} \sum\limits_{n=1}^{N}\left(K_{n} P_{n}(t) \Delta t\right) $ | (15) |
式中:N为微电网内分布式电源设备种类数;Kn为第n种设备的维护成本系数;Pn(t)为第n种分布式电源设备t时段内的输出有功功率。
微电网需要承担污染物排放后的环境治理费用,以环境成本CE表示。PV、WT发电污染排放可忽略不计,污染物主要来源于DG、MT、FC工作产生的一氧化碳、一氧化氮、二氧化硫。环境成本的计算如下:
| $ C_{\mathrm{E}}=\sum\limits_{t=1}^{T} \sum\limits_{y=1}^{M} \sum\limits_{n=1}^{Y}\left(D_{n, y} H_{n, y} P_{n}(t) \Delta t\right) $ | (16) |
式中:M为污染物种类数;Y为产生污染物的设备数;Hn, y为第n种设备输出单位有功功率产生的第y种污染物重量;Dn, y为处理每单位重量此种污染物的成本。
微电网通过与大电网进行购电与售电,产生电网交互成本CI,计算如下:
| $ C_{\mathrm{I}}=\sum\limits_{t=1}^{T}\left(P_{\text {grid }}(t) C_{\text {grid }}(t) \Delta t\right) $ | (17) |
式中:Pgrid(t)为微电网与大电网之间的交互功率;Cgrid(t)为微电网向大电网购电或售电产生的动态电价。
以综合运行成本f最低为微电网优化调度的目标,可得目标函数为:
| $ f=\min \left(C_{\mathrm{F}}+C_{\mathrm{M}}+C_{\mathrm{E}}+C_{\mathrm{I}}\right) $ | (18) |
正常工作时,微电网内各电源提供的功率与负荷功率相等。
| $ P_{\text {load }}(t)=\sum\limits_{n=1}^{N} P_{n}(t)+P_{\text {grid }}(t) $ | (19) |
式中:Pload(t)为负荷功率。当Pgrid(t)>0时,微电网向大电网购电;当Pgrid(t)<0时,微电网向大电网售电。
2.4.2 交互功率约束由于大电网、输电线路等设备均存在功率上限,交互功率约束范围定义如下:
| $ P_{\text {grid, } \min } \leqslant P_{\text {grid }}(t) \leqslant P_{\text {grid, } \max } $ | (20) |
式中:Pgrid, min,Pgrid, max分别为交互功率约束最小值和最大值。
2.4.3 发电单元出力约束PV、WT、MT、FC、DG作为分布式电源,输出有功功率均有限,定义有功出力约束如下:
| $ P_{n, \min } \leqslant P_{n}(t) \leqslant P_{n, \max } $ | (21) |
式中:Pn, min,Pn, max分别为各分布式电源功率约束最小值和最大值。
2.4.4 BT充、放电约束BT在充电末期电压上升速率较快,在放电末期电压下降速率也较快,因此过充、过放均会导致正极不可逆反应及电解液分解,减少BT的工作寿命[23],因此BT一般不会充电至最满、放电至耗尽,定义BT充、放电约束如下:
| $ C_{\mathrm{SOC}, \min } \leqslant C_{\mathrm{SOC}}(t) \leqslant C_{\mathrm{SOC}, \max } $ | (22) |
式中:CSOC, max, CSOC, min分别为BT容量上、下限。
2.4.5 爬坡速率约束MT、DG与FC的输出功率变化率均有限,定义爬坡速率约束如下:
| $ \left\{\begin{array}{l} P_{\mathrm{MT}, \text { down }} \leqslant P_{\mathrm{MT}}(t+\Delta t)-P_{\mathrm{MT}}(t) \leqslant P_{\mathrm{MT}, \text { up }} \\ P_{\mathrm{DG}, \text { down }} \leqslant P_{\mathrm{DG}}(t+\Delta t)-P_{\mathrm{DG}}(t) \leqslant P_{\mathrm{DG}, \text { up }} \\ P_{\mathrm{FC}, \text { down }} \leqslant P_{\mathrm{FC}}(t+\Delta t)-P_{\mathrm{FC}}(t) \leqslant P_{\mathrm{FC}, \text { up }} \end{array}\right. $ | (23) |
式中:PMT(t),PMT(t+Δt)分别为t和t+Δt时段MT输出功率;PMT, down,PMT, up分别为MT爬坡速率最小、最大值;PDG(t),PDG(t+Δt)分别为t和t+Δt时段DG输出功率;PDG, down,PDG, up分别为DG爬坡速率最小、最大值;PFC(t),PFC(t+Δt)分别为t和t+Δt时段FC输出功率;PFC, down,PFC, up分别为FC爬坡速率最小、最大值。
3 算例仿真 3.1 微电网基本参数文中将微电网优化调度模型作为算例进行仿真分析。设定DG的燃烧成本系数a=6,b=0.12,c=0.000 85,其爬坡速率最大、最小值分别为12 kW/min,-12 kW/min;BT的CSOC(t)初始值为0.4,CSOC, min=0.2,CSOC, max=0.8;FC的爬坡速率最大、最小值分别为10 kW/min,-10 kW/min;MT的爬坡速率最大、最小值分别为15 kW/min,-15 kW/min;微电网与大电网之间的交互功率约束为100 kW。表 1、表 2分别为各分布式电源有关参数和其产生的污染物相关排放参数,表 3为微电网所在地的分时电价。
|
|
表 1 各分布式电源有关参数 Table 1 Related parameters of each distributed generation |
|
|
表 2 污染物排放相关系数 Table 2 Pollutant-related emission coefficient |
|
|
表 3 分时电价参数 Table 3 Time-of-use price parameters |
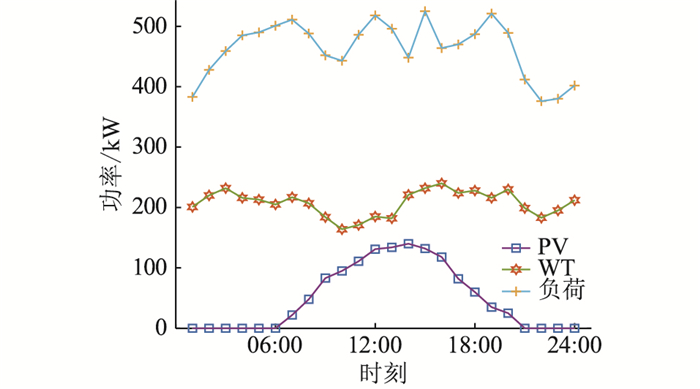
风力与PV作为可再生能源,不消耗化石燃料,对环境几乎无污染,并且输出具有随机性和不可控性,因此在微电网调度中应优先出力。微电网的日负荷曲线、WT出力曲线、PV出力曲线见图 4。
|
图 4 负荷、WT及PV出力曲线 Fig. 4 Load, WT and PV output curves |
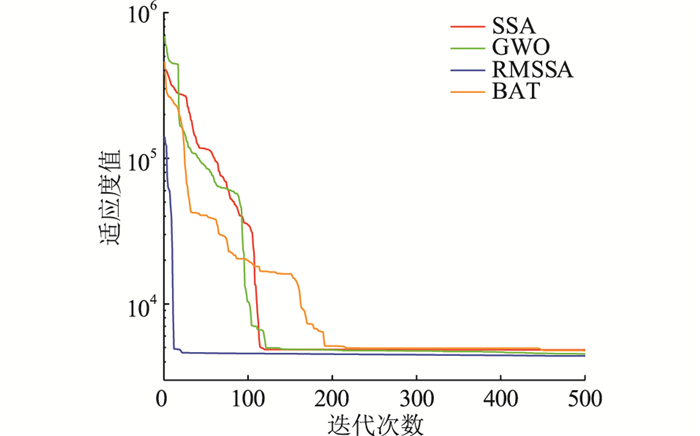
根据文中建立的微电网优化调度模型,设定麻雀种群初始参数,如表 4所示,采用RMSSA进行求解,并将寻优结果与SSA、蝙蝠算法(bat algorithm, BAT)、灰狼算法(grey wolf optimizer, GWO)进行对比分析。各算法设定相同的个体数与迭代次数,迭代所得适应度值即为优化所得的日综合运行成本,迭代寻优过程对比如图 5所示。
|
|
表 4 麻雀种群初始参数 Table 4 Initial parameters of sparrow population |
|
图 5 迭代过程对比 Fig. 5 Comparison of iterative processes |
由图 5可知,迭代寻优初期,SSA、GWO、BAT均陷入局部最优,收敛速度下降,其中BAT最为严重,SSA与GWO严重程度相似。RMSSA不易陷入局部最优,收敛速度更快,最早得到稳定的全局最优解;当所有算法均达到全局最优时,RMSSA所得适应度值最小,寻优精准度最高。因此,RMSSA较其他算法在收敛速度与寻优精度方面具有优势。
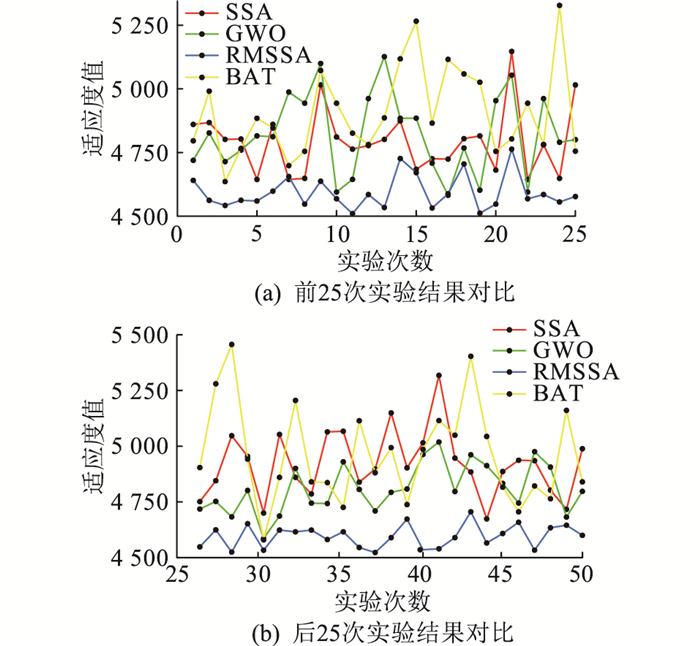
为比较几种算法求解结果的稳定性,将50次仿真实验结果绘制成曲线进行对比,如图 6所示。50次实验所得的均值、标准差、最小值、中位数的对比结果见表 5。
|
图 6 算法稳定性曲线 Fig. 6 Algorithm stability curves |
|
|
表 5 算法求解结果对比 Table 5 Comparison of algorithm solution results |
由图 6和表 5可知,BAT稳定性曲线波动最大,求解结果最差;SSA由于陷入局部收敛,寻优缺少随机性,求解结果稳定性较差,精度较低;GWO在求解过程中稳定性与精准度较BAT和SSA有所提高;RMSSA相比其他算法在均值、标准差、最小值、中位数方面均具有优势,稳定性曲线较平稳,求解稳定性最高。取RMSSA求解结果最小值,得微电网日综合运行成本为4 509.82元,其中,燃料成本为2 870.87元,维护成本为313.18元,环境成本为923.75元,交互成本为399.27元。
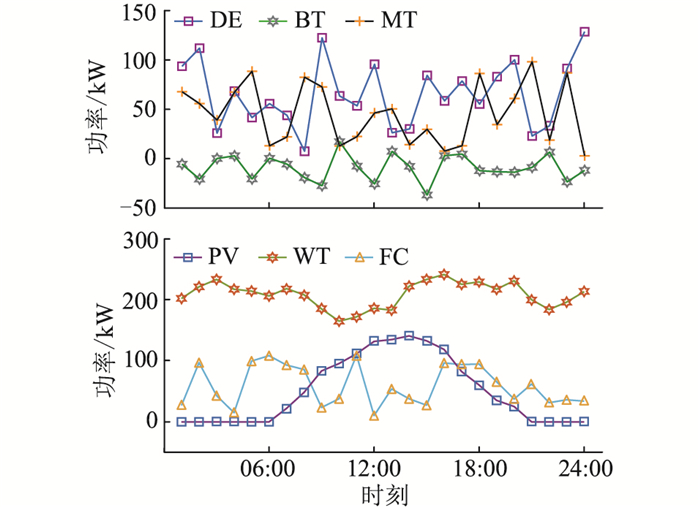
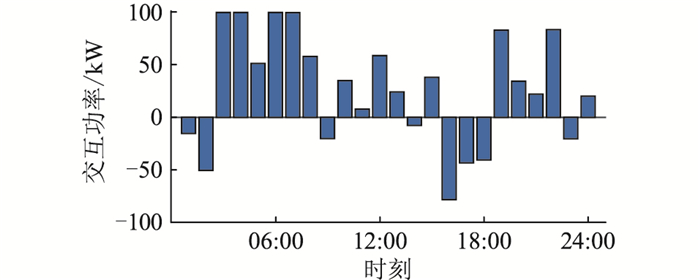
图 7和图 8分别为各分布式电源出力曲线和微电网与大电网之间的电能交互情况。
|
图 7 分布式电源出力曲线 Fig. 7 Distributed generation output curves |
|
图 8 电能交互情况 Fig. 8 Electric energy interaction |
由图 7、图 8可知,当负荷处于较低位,且风、光资源较为充足时,以13:00-14:00为例,微电网内部可再生能源发电和蓄电池放电可满足负荷大部分电能需求,存在污染的FC、DG、MT总体出力较多,向大电网购电的量处于低位,同时可将过剩的电能销售至大电网获利;夜间由于光照较弱,可再生能源发电量较少,以18:00-23:00为例,微电网内部FC、DG、MT出力增加,并向大电网采购一定电量满足负荷;在其余时间,综合分析燃料成本、维护成本、交互成本与环境成本,优化微电网内部的分布式电源出力,适时向大电网购电与售电,以实现效益最大化的调度方案。
4 结论针对传统优化算法存在的不足,在SSA的基础上提出了RMSSA,有效提升了原算法的寻优搜索能力。应用RMSSA对微电网优化调度模型进行求解,并与SSA、GWO、BAT进行性能对比,得出以下结论:
(1) 在收敛速度和求解精度方面,RMSSA的收敛速度更快、精度较其他算法有所提高;
(2) 在稳定性方面,根据对结果均值、标准差、中位数等参数的比较,RMSSA具有更高的稳定性;
(3) RMSSA的性能具有优势,可以有效降低微电网的综合运行成本。
| [1] |
LIU N, CHEN Q F, LIU J, et al. A heuristic operation strategy for commercial building microgrids containing EVs and PV system[J]. IEEE Transactions on Industrial Electronics, 2015, 62(4): 2560-2570. DOI:10.1109/TIE.2014.2364553 (  0) 0) |
| [2] |
ALOTAIBI I, ABIDO M A, KHALID M, et al. A comprehensive review of recent advances in smart grids: a sustainable future with renewable energy resources[J]. Energies, 2020, 13(23): 6269. DOI:10.3390/en13236269 (  0) 0) |
| [3] |
宁吉喆. "十四五"规划的重要意义及其与2035年远景目标的内在逻辑[J]. 人民论坛, 2020(34): 6-10. NING Jizhe. The significance of the ″14th Five-Year Plan″ and its internal logic with the long-term goal of 2035[J]. People′s Tribune, 2020(34): 6-10. DOI:10.3969/j.issn.1004-3381.2020.34.001 (  0) 0) |
| [4] |
徐晖. "十四五"进入新能源高质量发展新阶段[J]. 电器工业, 2021(3): 1. XU Hui. The ″4th Five-Year Plan″ has entered a new stage of high-quality development of new energy[J]. China Electrical Equipment Industry, 2021(3): 1. DOI:10.3969/j.issn.1009-5578.2021.03.001 (  0) 0) |
| [5] |
桑博, 张涛, 刘亚杰, 等. 多微电网能量管理系统研究综述[J]. 中国电机工程学报, 2020, 40(10): 3077-3093. SANG Bo, ZHANG Tao, LIU Yajie, et al. Energy management system research of multi-microgrid: a review[J]. Proceedings of the CSEE, 2020, 40(10): 3077-3093. (  0) 0) |
| [6] |
原亚宁, 李琳, 赵浩然. 基于主从博弈模型的交直流混合微电网源网协调优化运行方法[J]. 智慧电力, 2019, 47(3): 30-37. YUAN Yaning, LI Lin, ZHAO Haoran. Optimization operation method for AC/DC hybrid microgrid considering source network coordination based on master-slave game[J]. Smart Power, 2019, 47(3): 30-37. (  0) 0) |
| [7] |
王尧, 谭彩霞, 王佳伟, 等. 分时电价机制下计及用户需求响应的微网优化调度模型[J]. 智慧电力, 2020, 48(10): 9-15. WANG Yao, TAN Caixia, WANG Jiawei, et al. Micro-grid optimization scheduling model considering user demand response under time-of-use electricity price mechanism[J]. Smart Power, 2020, 48(10): 9-15. DOI:10.3969/j.issn.1673-7598.2020.10.003 (  0) 0) |
| [8] |
滕德云, 滕欢, 刘鑫, 等. 基于改进鲸鱼优化算法的多目标无功优化调度[J]. 电力电容器与无功补偿, 2019, 40(3): 123-128. TENG Deyun, TENG Huan, LIU Xin, et al. Multi-objective reactive power optimization dispatch based on improved whale optimization algorithm[J]. Power Capacitors & Reactive Power Compensation, 2019, 40(3): 123-128. (  0) 0) |
| [9] |
王亚东, 崔承刚, 钱申晟, 等. 基于深度强化学习的微电网储能调度策略研究[J]. 可再生能源, 2019, 37(8): 1220-1228. WANG Yadong, CUI Chenggang, QIAN Shensheng, et al. Study on micro-grid energy storage dispatching strategy based on deep Q-value reinforcement learning[J]. Renewable Energy Resources, 2019, 37(8): 1220-1228. DOI:10.3969/j.issn.1671-5292.2019.08.018 (  0) 0) |
| [10] |
颜宁, 潘霄, 张明理, 等. 基于复合储能的多互联微电网日内调度研究[J]. 电工技术学报, 2018, 33(S2): 577-585. YAN Ning, PAN Xiao, ZHANG Mingli, et al. Research on intra-day dispatch of multi-connected microgrids based on hybrid energy storage[J]. Transactions of China Electrotechnical Society, 2018, 33(S2): 577-585. (  0) 0) |
| [11] |
曾嶒, 彭春华, 王奎, 等. 基于鸟群算法的微电网多目标运行优化[J]. 电力系统保护与控制, 2016, 44(13): 117-122. ZENG Ceng, PENG Chunhua, WANG Kui, et al. Multi-objective operation optimization of micro grid based on bird swarm algorithm[J]. Power System Protection and Control, 2016, 44(13): 117-122. DOI:10.7667/PSPC151381 (  0) 0) |
| [12] |
CHEN H D, AN Y, MENG X C. Multi-objective optimal dispatching of microgrid based on improved genetic algorithm[J]. IOP Conference Series: Earth and Environmental Science, 2019, 295(3): 032013. DOI:10.1088/1755-1315/295/3/032013 (  0) 0) |
| [13] |
刘荣荣, 张靠社, 张刚, 等. 基于自适应人工鱼群算法的微电网优化运行[J]. 电网与清洁能源, 2017, 33(4): 71-76. LIU Rongrong, ZHANG Kaoshe, ZHANG Gang, et al. Micro grid optimal operation based on adaptive artificial fish algorithm[J]. Power System and Clean Energy, 2017, 33(4): 71-76. DOI:10.3969/j.issn.1674-3814.2017.04.011 (  0) 0) |
| [14] |
LI C B, JIA X F, ZHOU Y, et al. A microgrids energy management model based on multi-agent system using adaptive weight and chaotic search particle swarm optimization considering demand response[J]. Journal of Cleaner Production, 2020, 262: 121247. DOI:10.1016/j.jclepro.2020.121247 (  0) 0) |
| [15] |
沈艳军, 杨博. 需求响应的微电网优化调度及改进的蝙蝠算法[J]. 华中科技大学学报(自然科学版), 2020, 48(2): 120-125. SHEN Yanjun, YANG Bo. Optimal dispatch of microgrid with demand response and an improved bat algorithm[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2020, 48(2): 120-125. (  0) 0) |
| [16] |
XUE J K, SHEN B. A novel swarm intelligence optimization approach: sparrow search algorithm[J]. Systems Science & Control Engineering, 2020, 8(1): 22-34. (  0) 0) |
| [17] |
吕鑫, 慕晓冬, 张钧. 基于改进麻雀搜索算法的多阈值图像分割[J]. 系统工程与电子技术, 2021, 43(2): 318-327. LYU Xin, MU Xiaodong, ZHANG Jun. Multi-threshold image segmentation based on improved sparrow search algorithm[J]. Systems Engineering and Electronics, 2021, 43(2): 318-327. (  0) 0) |
| [18] |
周蓉, 李俊, 王浩. 基于灰狼优化的反向学习粒子群算法[J]. 计算机工程与应用, 2020, 56(7): 48-56. ZHOU Rong, LI Jun, WANG Hao. Reverse learning particle swarm optimization based on grey wolf optimization[J]. Computer Engineering and Applications, 2020, 56(7): 48-56. (  0) 0) |
| [19] |
徐鹏超, 李琰, 赵艳雷. 基于自适应变异蝙蝠优化BP神经网络的短期风电功率预测[J]. 电测与仪表, 2021, 58(4): 121-127. XU Pengchao, LI Yan, ZHAO Yanlei. Short-term wind power prediction based on BP neural network with adaptive mutation bat optimization algorithm[J]. Electrical Measurement & Instrumentation, 2021, 58(4): 121-127. (  0) 0) |
| [20] |
SMAOUI M, ABDELKAFI A, KRICHEN L. Optimal sizing of stand-alone photovoltaic/wind/hydrogen hybrid system supply- ing a desalination unit[J]. Solar Energy, 2015, 120: 263-276. DOI:10.1016/j.solener.2015.07.032 (  0) 0) |
| [21] |
PALIWAL N K, SINGH A K, SINGH N K. A day-ahead optimal energy scheduling in a remote microgrid alongwith battery storage system via global best guided ABC algorithm[J]. Journal of Energy Storage, 2019, 25: 100877. DOI:10.1016/j.est.2019.100877 (  0) 0) |
| [22] |
HONG L, CHEN J, LIU Z Y, et al. A nonlinear control strategy for fuel delivery in PEM fuel cells considering nitrogen permeation[J]. International Journal of Hydrogen Energy, 2017, 42(2): 1565-1576. (  0) 0) |
| [23] |
朱洋艳, 王致杰, 王鸿, 等. 基于分层控制的微电网混合储能协调优化策略研究[J]. 太阳能学报, 2021, 42(3): 235-242. ZHU Yangyan, WANG Zhijie, WANG Hong, et al. Research on hierarchical control of micro power grid hybrid energy storage coordination optimization strategy[J]. Acta Energiae Solaris Sinica, 2021, 42(3): 235-242. (  0) 0) |
 2022, Vol. 41
2022, Vol. 41


 宋扬(1996),男,硕士在读,研究方向为微电网智能化监控与调度(E-mail:
宋扬(1996),男,硕士在读,研究方向为微电网智能化监控与调度(E-mail: