文章编号: 2096-3203(2022)02-0110-09 中图分类号: TM743
为顺应国际能源转型大势,我国将在“十四五”期间加快建设风电、光伏等新能源产业,推动能源清洁低碳、安全高效利用,提升新能源消纳和存储能力。近些年随着风电、光伏的渗透率不断提高,推进其消纳和高效利用面临着巨大挑战[1-2]。而制氢-储氢-发电系统因其清洁高效的优势已经成为部分发达国家解决该问题的有效方案[3]。
氢能作为一种理想的清洁能源,具备大容量、高密度、低排放,对环境无污染等优点,且制氢设备使用寿命长,原料获取简单,氢气储存和运输都较为方便,为风电、光伏的大规模开发、利用和消纳提供了一种新的优选方案[4-5]。以风、光、氢等多能源互补发电的微电网系统容量配置和能量管理成为了研究热点。文献[6]针对风机联合制氢-储氢-发电系统的最优容量配置,建立了以风-氢互补系统的安装成本和负荷缺电率最低、输出功率波动率最小为目标的多目标优化模型; 文献[7]在风-光-氢耦合系统中加入了蓄电池,以减小波动功率对电解池效率和寿命的影响,同时考虑了动态电价对储能电池和制氢单元容量配置的影响; 文献[8]通过为风电场配置储氢系统和超级电容来平抑风电波动功率; 文献[9]通过引入电池-氢储混合储能系统解决了单一电池储能系统容量小的问题,实现了风电场的柔性并网。
上述文献对于多能源互补微电网系统容量优化配置的研究都只考虑微电网单一利益主体,但随着大量“增量配网”试点的投资运营,在进行微电网容量配置和能量管理时必须考虑各投资方的利益需求。博弈论作为一种解决此类问题的有效途径,通过寻找Nash均衡点来达到各博弈参与者的利益最大化[10-11]。文献[12]以各博弈参与者的日运行成本最低为优化目标,建立了多能量枢纽之间的非合作博弈模型,降低了各能量枢纽的运行成本,提高了系统调度的灵活性; 文献[13]为了减小系统故障时切负荷所造成的影响,以各负荷用户作为博弈参与者,建立了多负荷用户的非合作博弈模型,实现了系统功率缺额时切负荷策略的自动优化计算。总体而言,博弈论在风-光-氢混合微电网容量优化配置方面的文献和成果还较少,亟待深入研究。
基于此,文中分别以风电场、光伏电站和制氢-储氢-发电系统作为博弈参与者构建经济模型,以各博弈参与者的收益最大化为优化目标,提出了基于非合作博弈的风-光-氢微电网容量优化配置模型,并利用粒子群算法对模型进行求解。最后通过算例仿真验证了所提模型能够提高微电网运行的经济性和可靠性。
1 多能源微电网系统结构与传统化学电池储能相比,氢储在多个方面具有良好的性能:(1) 氢气的能量密度比常规蓄电池的平均能量密度高[14]; (2) 能量转换设备中质子交换膜的使用寿命要高于蓄电池的电解液[15]; (3) 蓄电池存在自放电的问题,只能作为短期储能的介质; (4) 氢气为清洁能源,对环境无污染,且其存储和运输十分方便。文中构建的风-光-氢微电网系统如图 1所示,由电解槽(electrolysis cell, EC)、储氢罐(hydrogen storage tank, HST)、燃料电池(fuel cell, FC)、风电场、光伏电站和微电网调度中心等组成。当风电、光伏出力大于负荷需求时,通过EC将多余的电能转换为氢气进行存储; 在风电、光伏出力不足或负荷处于高峰期时通过FC将氢气转换成电能进行补充。
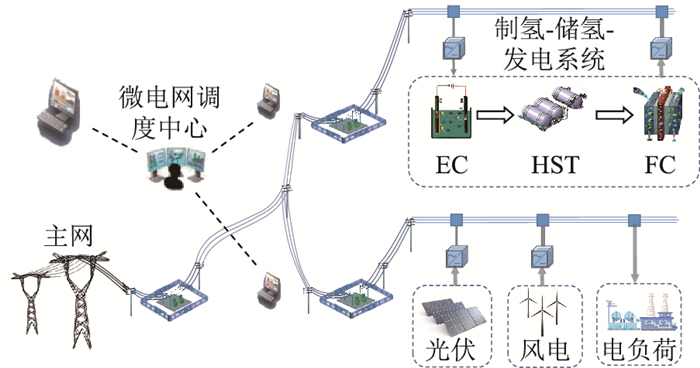
|
图 1 微电网能源架构 Fig. 1 Microgrid energy architecture |
风电的输出功率主要与风速相关,而风速的变化服从威布尔分布[16],其概率密度函数f(v)为:
| $ f(v)=(k / c)(v / c)^{k-1} \mathrm{e}^{-(v / c)^{k}} $ | (1) |
式中:v为风速; k为形状参数; c为比例参数。
由此可推出风电的输出功率模型为:
| $ P_{\mathrm{w}}=\left\{\begin{array}{l} 0 \quad v<v_{\mathrm{in}}, v>v_{\text {out }} \\ P_{\mathrm{r}} \frac{v-v_{\mathrm{in}}}{v_{\mathrm{r}}-v_{\mathrm{in}}} \quad v_{\mathrm{in}} \leqslant v \leqslant v_{\mathrm{r}} \\ P_{\mathrm{r}} \quad v_{\mathrm{r}}<v \leqslant v_{\text {out }} \end{array}\right. $ | (2) |
式中:Pr为风电机组的总装机容量; vin为切入风速; vout为切出风速; vr为额定风速。
2.2 光伏发电光照强度在一定时段内认为服从Beta分布[17],其概率密度函数f(r)为:
| $ f(r)=\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)+\Gamma(\beta)}\left(\frac{r}{r_{\max }}\right)^{\alpha-1}\left(1-\frac{r}{r_{\max }}\right)^{\beta-1} $ | (3) |
式中:Γ(·)为伽马函数; α,β分别为Beta分布的形状参数; r,rmax分别为太阳辐射强度和最大太阳辐射强度。
由此可推出光伏输出功率的概率模型为:
| $ f\left(P_{\mathrm{PV}}^{\text {real }}\right)=\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)+\Gamma(\beta)}\left(\frac{P_{\mathrm{PV}}^{\text {real }}}{P_{\mathrm{PV}}^{\max }}\right)^{\alpha-1}\left(1-\frac{P_{\mathrm{PV}}^{\text {real }}}{P_{\mathrm{PV}}^{\max }}\right)^{\beta-1} $ | (4) |
式中:PPVreal,PPVmax分别为某一时段光伏的输出功率和最大输出功率。
2.3 制氢-氢储-发电系统为了应对风电、光伏输出功率的随机性和波动性,文中以制氢-储氢-发电系统作为能量缓冲单元,平抑微电网波动功率。能量转换及储氢的数学模型如式(5)-式(7)所示。
| $ W_{\mathrm{EC}, t}=P_{\mathrm{EC}, t} \eta_{\mathrm{EC}} \lambda $ | (5) |
式中:WEC, t为t时段EC产生的氢气量; PEC, t为t时段EC的电解功率; ηEC为EC的电解效率; λ为每度电电解生成的氢气量。
| $ P_{\mathrm{FC}, t}=\frac{W_{\mathrm{FC}, t}}{\mu} \eta_{\mathrm{FC}} $ | (6) |
式中:PFC, t为t时段FC的输出电功率; WFC, t为t时段FC消耗的氢气量; ηFC为FC的效率; μ为生产每度电需要的氢气量。
| $ E_{\mathrm{HST}, t+1}=E_{\mathrm{HST}, t}+\left(\eta_{\mathrm{HST}}^{\mathrm{cha}} W_{\mathrm{HST}, t}^{\mathrm{cha}}-W_{\mathrm{HST}, t}^{\mathrm{dis}} / \eta_{\mathrm{HST}}^{\mathrm{dis}}\right) $ | (7) |
式中:EHST, t,EHST, t+1分别为t时刻和t+1时刻的HST储氢量; ηHSTcha,ηHSTdis分别为HST储氢、放氢的效率; WHST, tcha,WHST, tdis分别为t时刻的储氢量和释氢量。
3 基于非合作博弈的容量配置方法 3.1 系统运行成本 3.1.1 优化目标文中以各博弈参与者的收益最大化为优化目标,对风电场、光伏电站和制氢-储氢-发电系统进行容量配置。由于风电、光伏输出功率的随机性和不确定性,微电网系统会不可避免地出现功率不足或盈余的情况。功率不足时需要从主网购买相应的功率以补足缺额; 而功率盈余时则会出现弃风弃光现象。因此目标函数中考虑了各投资方的设备投资费用、购售电费用、运行维护成本、弃风弃光惩罚费用、负荷中断惩罚费用和政府补贴等因素,旨在寻求更合理的容量配置策略,降低容量配置成本,提高可再生能源的利用率。文中将系统的全周期成本转化为月平均成本进行分析计算,各博弈参与者的收益函数如式(8)所示。
| $ \begin{gathered} u_{x}=C_{x, \mathrm{SE}}+C_{x, \mathrm{SUB}}-C_{x, \mathrm{BUY}}-C_{x, \mathrm{WA}}- \\ C_{x, \mathrm{BRE}}-C_{x, \mathrm{INV}} / 12-C_{x, \mathrm{RUN}} / 12 \end{gathered} $ | (8) |
式中:ux为x博弈参与者的收益函数; Cx, SE为x博弈参与者典型月的售电收益; Cx, SUB为x博弈参与者典型月的政府补贴; Cx, BUY为x博弈参与者典型月的购电成本; Cx, WA为x博弈参与者典型月的弃风弃光惩罚费用; Cx, BRE为x博弈参与者典型月的负荷中断补偿费用; Cx, INV/12为x博弈参与者的月平均投资安装成本; Cx, RUN/12为x博弈参与者的月平均运行维护成本。
(1) 投资安装成本。
| $ C_{\mathrm{WT}, \mathrm{INV}}=N_{\mathrm{WT}} P_{\mathrm{WT}} e_{\mathrm{WT}} \frac{r(1+r)^{m}}{(1+r)^{m}-1} $ | (9) |
| $ C_{\mathrm{PV}, \mathrm{INV}}=N_{\mathrm{PV}} P_{\mathrm{PV}} e_{\mathrm{PV}} \frac{r(1+r)^{m}}{(1+r)^{m}-1} $ | (10) |
| $ C_{\mathrm{H}, \mathrm{INV}}=C_{\mathrm{FC}}+C_{\mathrm{HST}}+C_{\mathrm{EC}} $ | (11) |
| $ \left\{\begin{array}{l} C_{\mathrm{FC}}=N_{\mathrm{FC}} P_{\mathrm{FC}} e_{\mathrm{FC}} \frac{r(1+r)^{m}}{(1+r)^{m}-1} \\ C_{\mathrm{HST}}=N_{\mathrm{HST}} E_{\mathrm{HST}}^{\mathrm{cap}} e_{\mathrm{HST}} \frac{r(1+r)^{m}}{(1+r)^{m}-1} \\ C_{\mathrm{EC}}=N_{\mathrm{EC}} W_{\mathrm{EC}} e_{\mathrm{EC}} \frac{r(1+r)^{m}}{(1+r)^{m}-1} \end{array}\right. $ | (12) |
式中:CWT, INV,CPV, INV,CH, INV分别为风电场、光伏电站和制氢-储氢-发电系统的投资成本等年值,其中,制氢-储氢-发电系统的投资成本等年值由FC、HST和EC的投资成本等年值CFC,CHST,CEC组成; NWT,NPV,NFC,NHST,NEC分别为风电机组、光伏阵列、FC、HST和EC的数量; PWT,PPV,PFC分别为风电机组、光伏阵列、FC的装机容量; EHSTcap为HST的容量; WEC为EC能够产生氢气的最大量; eWT,ePV,eFC,eHST,eEC分别为风电机组、光伏阵列、FC、HST和EC的单位造价; r为折旧率,取6%;m为使用年限,取15 a。
(2) 运行维护成本。
| $ C_{\mathrm{WT}, \mathrm{RUN}} =N_{\mathrm{WT}} P_{\mathrm{WT}} y_{\mathrm{WT}} $ | (13) |
| $ C_{\mathrm{PV}, \mathrm{RUN}} =N_{\mathrm{PV}} P_{\mathrm{PV}} y_{\mathrm{PV}} $ | (14) |
| $ C_{\mathrm{H}, \mathrm{RUN}}=N_{\mathrm{FC}} P_{\mathrm{FC}} y_{\mathrm{FC}}+N_{\mathrm{HST}} E_{\mathrm{HST}}^{\text {cap }} y_{\mathrm{HST}}+N_{\mathrm{EC}} W_{\mathrm{EC}} y_{\mathrm{EC}} $ | (15) |
式中:CWT, RUN,CPV, RUN,CH, RUN分别为风电场、光伏电站和制氢-储氢-发电系统的年运行维护成本; yWT,yPV,yFC,yHST,yEC分别为风电机组、光伏阵列、FC、HST和EC单位功率的运行维护成本。
(3) 售电收益。售电收益是微电网内各博弈参与者的主要收益,不仅与博弈参与者自身出力相关,还受其他博弈参与者的出力影响。当博弈参与者典型月的总出力大于负荷需求时,在传输线允许的功率范围内微电网将盈余功率卖给大电网获得额外收益。微电网系统可消纳的最大功率PMAX(t)与t时段的负荷需求、EC的最大电解功率和传输线功率上限有关,如式(16)所示。
| $ P_{\mathrm{MAX}}(t)=P_{\mathrm{L}}(t)+P_{\mathrm{grid}, \max }+P_{\mathrm{EC}}(t) $ | (16) |
式中:PL(t)为t时段的负荷需求; Pgrid, max为传输线功率上限; PEC(t)为t时段EC的最大电解功率。
t时段微电网的过剩功率如式(17)所示。
| $ P_{\mathrm{EXC}}(t)=P_{\mathrm{WT}}(t)+P_{\mathrm{PV}}(t)-P_{\mathrm{MAX}}(t) $ | (17) |
| $ P_{x, \mathrm{SE}}(t)=\left\{\begin{array}{l} P_{x}(t) \quad P_{\mathrm{EXC}}(t) \leqslant 0 \\ \frac{P_{x}(t) P_{\mathrm{MAX}}(t)}{P_{\mathrm{WT}}(t)+P_{\mathrm{PV}}(t)} \quad P_{\mathrm{EXC}}(t)>0 \end{array}\right. $ | (18) |
| $ C_{x, \mathrm{SE}}=c_{\mathrm{SE}} \sum\limits_{t=1}^{T}\left(P_{x, \mathrm{SE}}(t) \Delta t\right) $ | (19) |
式中:T为调度周期,取720 h; Px(t)为t时段x博弈参与者的输出功率,文中特指t时段风电出力PWT(t)和光伏出力PPV(t); Px, SE(t)为t时段x博弈参与者的售电功率; cSE为售电电价。
制氢-储氢-发电系统的收益主要来自FC发电、售氢气和售氧气产生的附加收益,忽略外部条件对氢气和氧气产率的影响,文中将氢气的产率简化为氧气的2倍[18]。
| $ P_{\mathrm{H}, \mathrm{SE}}(t)=\left\{\begin{array}{l} P_{\mathrm{FC}}(t) \quad P_{\mathrm{WT}}(t)+P_{\mathrm{PV}}(t)<P_{\mathrm{L}}(t) \\ 0 \quad P_{\mathrm{WT}}(t)+P_{\mathrm{PV}}(t) \geqslant P_{\mathrm{L}}(t) \end{array}\right. $ | (20) |
| $ W_{\mathrm{O}_{2}}=\frac{1}{2} \sum\limits_{t=1}^{T} W_{\mathrm{EC}, t} $ | (21) |
| $ C_{\mathrm{H}, \mathrm{SE}}=c_{\mathrm{SE}, \mathrm{O}_{2}} W_{\mathrm{O}_{2}}+c_{\mathrm{SE}, \mathrm{H}_{2}} W_{\mathrm{H}_{2}}+c_{\mathrm{SE}} \sum\limits_{t=1}^{T} P_{\mathrm{H}, \mathrm{SE}}(t) $ | (22) |
式中:CH, SE,PH, SE(t)分别为制氢-储氢-发电系统的售电收益和售电功率; PFC(t)为t时段FC的出力; WO2为调度周期内电解水制氢时的产氧量; WH2为调度周期内的售氢量; cSE, O2,cSE, H2分别为当前的单位售氧、售氢价格,参考文献[19]分别取2.5元/Nm3,3元/Nm3。
(4) 购电费用。当各博弈参与者总出力难以满足负荷需求时,微电网则需要从大电网购电。为方便计算,用等效负荷(equivalent load,EL)来表征各博弈参与者总出力同负荷需求的匹配度,即:
| $ P_{\mathrm{EL}}(t)=P_{\mathrm{L}}(t)-\left(P_{\mathrm{WT}}(t)+P_{\mathrm{PV}}(t)+P_{\mathrm{FC}}(t)\right) $ | (23) |
| $ P_{\mathrm{BUY}}(t)= \begin{cases}0 \quad P_{\mathrm{EL}}(t) \leqslant 0 \\ P_{\mathrm{EL}}(t) \quad 0<P_{\mathrm{EL}}(t) \leqslant P_{\text {grid }, \max } \\ P_{\text {grid, } \max } \quad P_{\mathrm{EL}}(t)>P_{\text {grid }, \max }\end{cases} $ | (24) |
| $ C_{x, \mathrm{BUY}}=\frac{c_{\mathrm{BUY}} \sum\limits_{t=1}^{T}\left(P_{\mathrm{BUY}}(t) \Delta t\right)}{P_{\mathrm{WT}}+P_{\mathrm{PV}}+P_{\mathrm{FC}}} P_{x} $ | (25) |
式中:PEL(t)为t时段的EL功率; PBUY(t)为t时段微电网向主网的购电量; Px为x博弈参与者的装机容量; cBUY为购电电价。
(5) 弃风弃光惩罚费用。当微电网内分布式电源的出力大于微电网可消纳的最大功率时,会出现弃风弃光现象,此时引入弃风弃光惩罚费用,如式(26)和式(27)所示。
| $ P_{x, \mathrm{WA}}(t)=\left\{\begin{array}{l} 0 \quad P_{\mathrm{EXC}}(t) \leqslant 0 \\ P_{x}(t)-P_{x, \mathrm{SE}}(t) \quad P_{\mathrm{EXC}}(t)>0 \end{array}\right. $ | (26) |
| $ C_{x, \mathrm{WA}}=c_{\mathrm{WA}} \sum\limits_{t=1}^{T}\left(P_{x, \mathrm{WA}}(t) \Delta t\right) $ | (27) |
式中:Px, WA (t)为t时段x博弈参与者的弃风弃光量; Cx, WA为t时段x博弈参与者弃风弃光惩罚费用; cWA为弃风弃光的惩罚因子,取0.3元/(kW ·h)[20]。
(6) 负荷中断补偿费用。若从主网最大限度购电仍无法满足负荷需求,则系统需要切除部分负荷以维持微电网稳定运行,微电网要对切除的负荷给予一定的经济补偿,如式(28)和式(29)所示。
| $ P_{\mathrm{BRE}}(t)= \begin{cases}0 \quad P_{\mathrm{EL}}(t) \leqslant P_{\text {grid, } \max } \\ P_{\mathrm{EL}}(t)-P_{\text {grid, } \max } \quad P_{\mathrm{EL}}(t)>P_{\text {grid }, \max }\end{cases} $ | (28) |
| $ C_{x, \mathrm{BRE}}=\frac{c_{\mathrm{BRE}} \sum\limits_{t=1}^{T}\left(P_{\mathrm{BRE}}(t) \Delta t\right)}{P_{\mathrm{WT}}+P_{\mathrm{PV}}+P_{\mathrm{FC}}} P_{x} $ | (29) |
式中:PBRE(t)为t时段微电网系统总负荷中断量; Cx, BRE为t时段x博弈参与者的负荷中断补偿费用; cBRE为负荷中断补偿因子, 取0.9元/(kW ·h)[21]。
(7) 政府补贴。对于风电、光伏和氢能的开发利用,在发电成本上与传统能源相比并没有优势。国家提倡大力发展清洁能源,降低碳排放,就需要提供相关的政策支持鼓励其发展,因此引入如式(30)所示的发电补贴。
| $ C_{x, \mathrm{SUB}}=c_{x, \mathrm{SUB}} \sum\limits_{t=1}^{T}\left(P_{x, \mathrm{SE}}(t) \Delta t\right) $ | (30) |
式中:cx, SUB为x博弈参与者的发电补贴电价,取值参照文献[22]。
3.1.2 约束条件风-光-氢微电网容量优化配置模型的约束条件包括发电设备的最大安装数量约束、功率平衡约束、EC的电解功率约束、FC的发电功率约束以及HST的容量和充放氢约束[23]。
(1) 个数约束。
| $ \left\{\begin{array}{l} N_{\mathrm{WT}} \leqslant N_{\mathrm{WT}}^{\mathrm{max}} \\ N_{\mathrm{PV}} \leqslant N_{\mathrm{PV}}^{\max } \\ N_{\mathrm{FC}} \leqslant N_{\mathrm{FC}}^{\max } \\ N_{\mathrm{EC}} \leqslant N_{\mathrm{EC}}^{\max } \\ N_{\mathrm{HST}} \leqslant N_{\mathrm{HST}}^{\max } \end{array}\right. $ | (31) |
式中:NWTmax,NPVmax,NFCmax,NECmax,NHSTmax分别为所允许安装的风电机组、光伏阵列、FC、EC和HST的最大数量。
(2) 功率平衡约束。
| $ P_{\mathrm{WT}}(t)+P_{\mathrm{PV}}(t)+P_{\mathrm{H}}(t)+P_{\text {grid }}(t)=P_{\mathrm{L}}(t) $ | (32) |
式中:PH(t)为正表示FC在工作,为负表示EC在工作; Pgrid(t)为正表示微电网从主网购电,为负表示微电网向主网售电。
(3) EC功率约束。
| $ 0 \leqslant P_{\mathrm{EC}}(t) \leqslant P_{\mathrm{EC}}^{\max } $ | (33) |
式中:PECmax为EC的最大电解功率。
(4) FC功率约束。
| $ 0 \leqslant P_{\mathrm{FC}}(t) \leqslant P_{\mathrm{FC}}^{\max } $ | (34) |
式中:PFCmax为FC的最大输出功率。
(5) HST约束。
| $ \left\{\begin{array}{l} 0 \leqslant W_{\mathrm{HST}, t}^{\text {cha }} \leqslant \alpha_{\mathrm{HST}}^{\text {cha }} \lambda_{\mathrm{HST}}^{\text {cha }} E_{\mathrm{HST}}^{\text {cap }} \\ 0 \leqslant W_{\mathrm{HST}, t}^{\text {dis }} \leqslant \alpha_{\mathrm{HST}}^{\text {dis }} \lambda_{\mathrm{HST}}^{\text {dis }} E_{\mathrm{HST}}^{\text {cap }} \\ \alpha_{\mathrm{HST}}^{\text {cha }}+\alpha_{\mathrm{HST}}^{\text {dis }}=1 \quad \alpha_{\mathrm{HST}}^{\text {dis }}, \alpha_{\mathrm{HST}}^{\text {cha }} \in\{0,1\} \\ \varepsilon_{\mathrm{HST}}^{\text {min }} E_{\mathrm{HST}}^{\text {cap }} \leqslant E_{\mathrm{HST}, t} \leqslant \varepsilon_{\mathrm{HST}}^{\text {max }} E_{\mathrm{HST}}^{\text {cap }} \\ E_{\mathrm{HST}}^{\text {start }}=E_{\mathrm{HST}}^{\text {end }} \end{array}\right. $ | (35) |
式中:αHSTcha,αHSTdis分别为制氢和耗氢的状态变量; λHSTcha,λHSTdis分别为t时段HST储氢和耗氢的上限系数; εHSTmax,εHSTmin分别为HST容量的上、下限系数; EHSTstart,EHSTend分别为调度周期起始和终止时HST的容量。
3.2 非合作博弈模型在文中所述的微电网系统中,风电、光伏和制氢-储氢-发电系统的投资方都希望各自电厂配置的容量尽可能大,以增大己方收益,而微电网内总的负荷需求相对稳定,因此各投资方在微电网容量配置的过程中存在相互博弈、公平竞争的关系,这是一种典型的非合作博弈[24]。风电、光伏和制氢-储氢-发电系统的投资方之间的非合作博弈可以表述为:
| $ G=\left\{N ; P_{\mathrm{WT}}, P_{\mathrm{PV}}, P_{\mathrm{H}} ; u_{\mathrm{WT}}, u_{\mathrm{PV}}, u_{\mathrm{H}}\right\} $ | (36) |
具体描述如下:
(1) 博弈方。在博弈过程中,每一个具有决策权的参与者称之为博弈方。文中的博弈参与者分别风电场、光伏电站和制氢-储氢-发电系统,将各博弈参与者集合表示为N= WT,PV,H。
(2) 策略集。博弈方在相互博弈过程中所选择的实际可行的方案称为策略。文中博弈的策略分别为风电场、光伏电站和制氢-储氢-发电系统各自配置的容量,策略集可以表示为P= PWT, PPV, PH。
(3) 收益。收益函数用来评估博弈互动决策过程中的获利情况,并以此作为调整相邻下一轮决策的重要信息。各博弈参与者的收益函数不仅与己方的策略有关,还受其他博弈参与者的策略影响,是一种策略组合函数,如式(37)所示。
| $ \left\{\begin{array}{l} u_{\mathrm{WT}}\left(P_{\mathrm{WT}}, P_{\mathrm{PV}}, P_{\mathrm{H}}\right) \\ u_{\mathrm{PV}}\left(P_{\mathrm{WT}}, P_{\mathrm{PV}}, P_{\mathrm{H}}\right) \\ u_{\mathrm{H}}\left(P_{\mathrm{WT}}, P_{\mathrm{PV}}, P_{\mathrm{H}}\right) \end{array}\right. $ | (37) |
文中采用粒子群算法对非合作博弈模型进行求解,粒子群相关参数设置为:种群规模为500,迭代次数为100,个体学习因子和群体学习因子均取1.45,惯性权重采用线性递减方式,初始惯性因子取0.9,最终惯性因子取0.4。具体求解步骤如下。
步骤1:输入系统相关参数,获取负荷需求曲线,根据风速、光照和温度历史数据预测风电和光伏的出力。
步骤2:各博弈参与者策略初始化,即在容量允许范围内随机初始化容量配置。
步骤3:各博弈参与者容量单独优化。根据Nash均衡的定义,各博弈参与者依据其他2个博弈参与者第i-1轮的容量配置策略,以最大化自身效用函数为优化目标,优化得出自身第i轮的容量配置方案。各博弈参与者第i轮最优容量配置方案的数学表达式如式(38)所示。
| $ \left\{\begin{array}{l} P_{\mathrm{WT}, i}=\arg _{P_{\mathrm{WT}, i}}^{\max }\left(P_{\mathrm{WT}, i}, P_{\mathrm{PV}, i-1}, P_{\mathrm{H}, i-1}\right) \\ P_{\mathrm{PV}, i}=\arg _{P_{\mathrm{PV}, i}}^{\max }\left(P_{\mathrm{WT}, i-1}, P_{\mathrm{PV}, i}, P_{\mathrm{H}, i-1}\right) \\ P_{\mathrm{H}, i}=\arg _{P_{\mathrm{H}, i}}^{\max }\left(P_{\mathrm{WT}, i-1}, P_{\mathrm{PV}, i-1}, P_{\mathrm{H}, i}\right) \end{array}\right. $ | (38) |
步骤4:判断是否找到了Nash均衡点。如果相邻2次的策略完全一致,即满足式(39),则说明找到了Nash均衡点,各博弈参与者按照此时的策略配置容量,并计算自身的效用函数。否则,重新返回步骤3。
| $ \begin{gathered} \left(P_{\mathrm{WT}}^{*}, P_{\mathrm{PV}}^{*}, P_{\mathrm{H}}^{*}\right)=\left(P_{\mathrm{WT}, i}, P_{\mathrm{PV}, i}, P_{\mathrm{H}, i}\right)= \\ \left(P_{\mathrm{WT}, i-1}, P_{\mathrm{PV}, i-1}, P_{\mathrm{H}, i-1}\right) \end{gathered} $ | (39) |
步骤5:输出Nash均衡点(PWT*, PPV*, PH*)和收益函数uWT,uPV和uH。
4 算例分析 4.1 基础数据文中以新疆某地区的实际数据为例,对该地区进行风-光-氢微电网容量优化配置。选取风电机组的型号为WD-10,额定功率10 kW,切入、额定和切出风速分别为2.5 m/s,12 m/s,15 m/s; 光伏组件的型号为MSX-83,额定功率为0.083 kW; 单个EC的额定产氢量为1.941 Nm3/(kW ·h),效率为75%,每度电的制氢量为0.19 Nm3; 单个HST的容量为10 m3,额定压力为10 MPa,标准气压下的储氢量为1 000 Nm3,存储效率为95%;单台FC的额定功率为2 kW,效率为40%,生产每度电的耗氢量为0.8 Nm3。该地区典型月的小时级光照强度、风速数据如图 2、图 3所示,典型日的小时级负荷数据如图 4所示,各对象单位造价、运维成本占比投资成本和补贴数据如表 1所示。
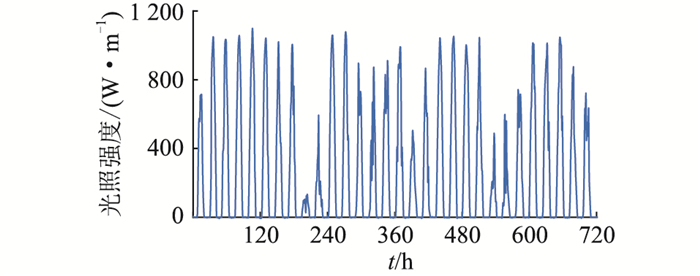
|
图 2 典型月小时级光照强度 Fig. 2 Hourly solar radiation in a typical month |
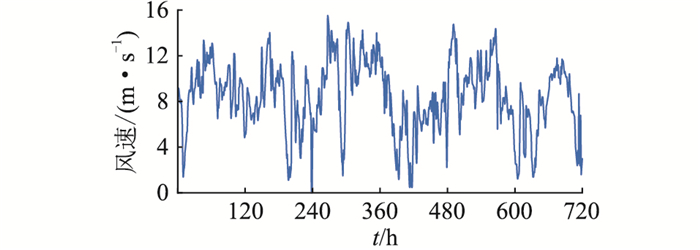
|
图 3 典型月小时级实际风速 Fig. 3 Actual hourly wind speed in a typical month |
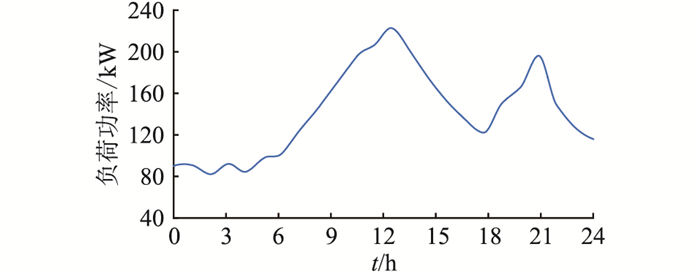
|
图 4 典型日小时级负荷功率 Fig. 4 Hourly load power in a typical day |
|
|
表 1 各对象单位造价、运维成本占比投资成本和补贴数据 Table 1 Unit cost, ratio of operation and maintenance cost to investment cost and subsidy cost of each object |
为了研究各博弈参与者不同组合下容量配置的经济性,设立以下3种组合场景进行对比分析。场景1中包含风电、光伏和制氢-储氢-发电3种分布式电源,而场景2中仅包含风电和光伏,场景3中包含风电和制氢-储氢-发电。
表 2和表 3分别为3种组合场景下各博弈参与者的容量配置结果和收益情况。
|
|
表 2 3种场景下的容量配置结果 Table 2 The results of capacity configuration in three scenarios |
|
|
表 3 3种场景下的收益对比 Table 3 Comparison of income in three scenarios |
场景1中各博弈参与者所配置的容量大于场景2,且收益也明显较高。这是由于场景1中有制氢-储氢-发电系统,能平抑风电、光伏的波动功率,起到能量缓冲的作用,同时减小弃风弃光量,在负荷高峰期通过FC将氢能转化成电能补充负荷缺额; 而场景2中无能量缓冲单元,因此会使得弃风弃光惩罚费用显著增大,且在负荷高峰期造成部分负荷缺电,增加负荷中断补偿费用,最终导致场景2中各博弈参与者的收益远低于场景1;场景3中各博弈参与者的容量略高于场景1,同时收益也明显更高。因此,增加风电机组和储氢系统容量配置可以提高系统收益,但净收益与配置容量之比是下降的。这是由于光伏和风电无论是在时间上还是地域上都存在天然的互补性,即白天光照充足,而夜间风多; 夏季日照好、风弱,而春冬季节风大、日照弱,使得同时包含风电和光伏的场景1整体功率波动较只含风电的场景3要小,场景3中若单靠增加风电机组容量来满足负荷需求,则会增加弃风成本。
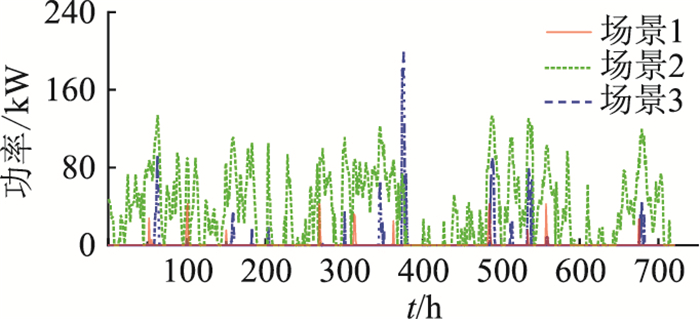
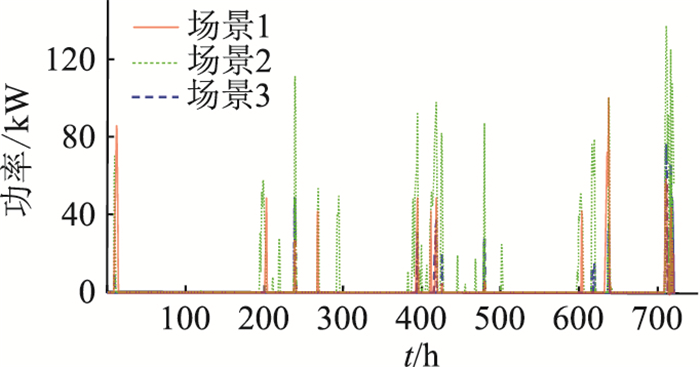
图 5和图 6分别为3种场景下的弃风弃光量和缺电量。弃风弃光量反映微电网系统的能源浪费情况,缺电量反映微电网系统的供电可靠性,二者均由系统的容量优化配置和运行策略控制。
|
图 5 3种场景下的弃风弃光量 Fig. 5 Wind and light abandonment in three scenarios |
|
图 6 3种场景下的缺电量 Fig. 6 Power shortage in three scenarios |
由图 5、图 6可知,场景2中的弃风弃光量和缺电量远高于场景1和场景3。当风电和光伏发电功率大于负荷需求且超过联络线最大功率时,由于场景2中无能量缓冲单元,不得不大量弃风弃光。而到了负荷高峰期,系统最大供电仍无法满足负荷需求时,若得不到制氢-储氢-发电系统的能量补充,则不得不切除部分负荷,导致弃风弃光量和缺电量的增加。场景1和场景3的累计弃风弃光量分别为233 kW和835 kW,累计缺电量分别为640 kW和782 kW。与场景3相比,场景1的弃风弃光量明显较小,但缺电量相近。这是由于场景3中无光伏参与,风电作为主要能源,存在着极大的随机性和不确定性; 而场景1中风电和光伏天然的互补特性使得二者在整体容量配置相对较低的情况下可以作为主要能源满足负荷需求。此外,制氢-储氢-发电系统在微电网系统中因其配置成本昂贵只能起到辅助作用。
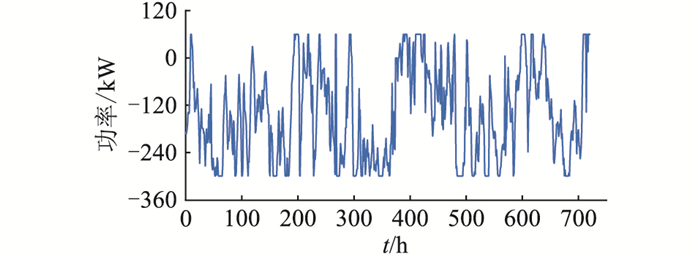
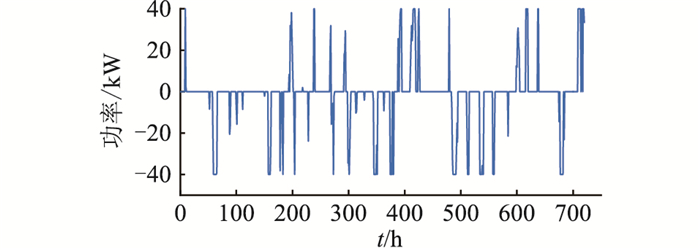
为进一步研究场景1中风-光-氢协调工作的过程,以图 7和图 8作具体说明,风电和光伏作为不可控、不可调度电源,主要由制氢-储氢-发电系统通过电解制氢、耗氢发电来维持功率平衡。
|
图 7 制氢-储氢-发电系统功率曲线 Fig. 7 Power curve of hydrogen production-storage- power generation system |
|
图 8 联络线功率曲线 Fig. 8 Power curve of contact line |
由图 7可知,制氢-储氢-发电系统多数时间处于电解制氢的状态,主要发挥了消纳风电、光伏多余功率的作用。为使HST在调度周期始末保持相同的储氢量以满足下个调度周期的需求,出售耗氢发电后多余的氢气,获取额外收益。由图 8可知,微电网只在少数时间从主网购售电。当FC以最大功率发电仍无法满足负荷需求时,则从主网购电补充缺额; 而当EC以最大功率电解制氢仍然无法消耗风电、光伏的多余功率时,则向电网售电。
综上分析,场景1对应的组合方式不但能使各博弈参与者得到较高的收益,还可以保障系统供电的可靠性,减小弃风弃光量,实现安全经济运行。
为验证文中所提基于风-光-氢多利益主体优化方法的有效性,将单一利益主体优化和多利益主体优化的仿真结果进行了对比,结果如表 4所示。
|
|
表 4 不同方法下微电网投资方的月收益 Table 4 Monthly returns of microgrid investors under different methods |
由表 4分析可知,单一利益主体优化方法只能保证微电网总收益最大,不能协调微电网内每一投资方的利益需求,其中风电场收益占微电网总收益比例较高,而其他投资方收益较低。文中所提基于多利益主体优化的非合作博弈模型能使微电网内各博弈参与者的利益均衡化,在保证微电网总收益相差不大的前提下使各投资方的收益最大化,光伏电站和制氢-储氢-发电系统收益分别增长了24.8%和6.4%,有利于微电网内各投资方的长期协调发展。
4.3 累积弃风弃光量和累积缺电量对月综合成本的影响累积缺电量与微电网系统的供电可靠性相关,而累积弃风弃光量与微电网系统运行的经济性相关。微电网系统容量配置的过程需要在可靠性和经济性之间取得平衡,在减小系统缺电量的同时避免能源浪费。图 9为一个月的累积弃风弃光量、累积缺电量与系统月综合成本的关系,月综合成本包括投资成本、运维成本、购电成本、负荷中断惩罚费用和弃风弃光惩罚费用。
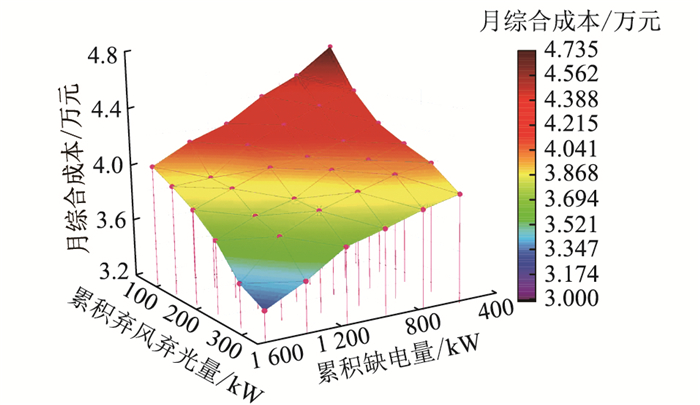
|
图 9 累积弃风弃光量、累积缺电量和月综合成本的关系 Fig. 9 Relationship between cumulative abandoned wind and light, cumulative power shortage and monthly comprehensive cost |
由图 9分析可知,随着累积弃风弃光量和累积缺电量的减小,微电网系统的月综合成本显著增大,特别是当累积弃风弃光量低于100 kW以下,累积缺电量低于500 kW以下时。这是因为当以风电和光伏作为主要能源对负荷进行供电时,减小缺电量就需要增大风电场和光伏电站的容量配置,此时弃风弃光量随之增加,而控制弃风弃光量则需要增加制氢-储氢-发电系统的容量,因此微电网系统月综合成本跳跃式增加。
目前我国制氢-储氢-发电系统的投资成本较高,相关技术还不成熟,因此并不能大规模地进行容量配置,其发电成本与传统电源相比明显较高,还需要政府以相关政策进行引导才能得到进一步的发展。与此同时,微电网系统需要根据负荷的重要程度,在极端条件下切除部分可中断负荷以满足一定缺电量的限制,从而优化计算出最佳的容量配置方案,使系统经济性和可靠性实现均衡。
5 结论针对风-光-氢多利益主体的微电网容量优化配置问题,文中以各博弈参与者的收益最大化为优化目标,建立了基于非合作博弈的微电网容量优化配置模型,根据典型月的风速和光照强度数据,考虑各博弈参与者的综合成本,通过粒子群算法对模型进行了求解。算例仿真研究得出以下结论:
(1) 通过引入非合作博弈理论对风-光-氢多利益主体的容量进行优化配置,与常规单一主体优化相比,同时保证了各博弈参与者的利益最大化和系统供电的可靠性。利用制氢-储氢-发电系统作为能量缓冲单元,减小了弃风弃光量,提高了资源的利用率。
(2) 累积弃风弃光量和累积缺电量是决定系统安全经济运行的主要指标,系统容量配置时须在两者之间进行平衡才能得到兼顾经济性和可靠性的容量配置方案。
文中未考虑氢运输、氧运输、系统设备安装人工费、传输损耗等成本,可能使得文中计算成本与实际运行成本之间存在一定偏差,然而这种偏差可以被有效控制在合理范围之内。文中的研究为今后针对区域供电问题建设风电-光伏-储氢一体化供电系统提供了理论参考。
| [1] |
胡迪, 丁明, 毕锐, 等. 光伏和风电互补性对高渗透率可再生能源集群接入规划影响分析[J]. 中国电机工程学报, 2020, 40(3): 821-836. HU Di, DING Ming, BI Rui, et al. Impact analysis of PV and WT complementarity on access planning of high penetrated renewable energy cluster[J]. Proceedings of the CSEE, 2020, 40(3): 821-836. (  0) 0) |
| [2] |
刘若河, 贾燕冰, 谢栋, 等. 考虑配电网消纳能力的分布式电源与储能优化配置[J]. 电力电容器与无功补偿, 2021, 42(1): 166-172. LIU Ruohe, JIA Yanbing, XIE Dong, et al. Optimal configuration of distributed generation and energy storage considering the consumption capacity in distribution network[J]. Power Capacitor & Reactive Power Compensation, 2021, 42(1): 166-172. (  0) 0) |
| [3] |
李争, 张蕊, 孙鹤旭, 等. 可再生能源多能互补制-储-运氢关键技术综述[J]. 电工技术学报, 2021, 36(3): 446-462. LI Zheng, ZHANG Rui, SUN Hexu, et al. Review on key technologies of hydrogen generation, storage and transportation based on multi-energy complementary renewable energy[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 446-462. (  0) 0) |
| [4] |
邵志芳, 吴继兰, 赵强. 城市电网耦合氢储能系统投资决策方法研究[J]. 电力工程技术, 2017, 36(5): 45-51. SHAO Zhifang, WU Jilan, ZHAO Qiang. Research on investment decision method of urban grid coupled hydrogen energy storage system[J]. Electric Power Engineering Technology, 2017, 36(5): 45-51. DOI:10.3969/j.issn.1009-0665.2017.05.008 (  0) 0) |
| [5] |
张红, 袁铁江, 谭捷, 等. 面向统一能源系统的氢能规划框架[J]. 中国电机工程学报, 2022, 42(1): 83-94. ZHANG Hong, YUAN Tiejiang, TAN Jie, et al. Hydrogen energy system planning framework for unified energy system[J]. Proceedings of the CSEE, 2022, 42(1): 83-94. (  0) 0) |
| [6] |
马榕谷, 陈洁, 赵军超, 等. 非并网风氢互补系统的容量多目标优化[J]. 太阳能学报, 2019, 40(2): 422-429. MA Ronggu, CHEN Jie, ZHAO Junchao, et al. Multi-objective optimization for capacity of non-grid-connected wind/hydrogen hybrid power system[J]. Acta Energiae Solaris Sinica, 2019, 40(2): 422-429. (  0) 0) |
| [7] |
邵志芳, 吴继兰. 基于动态电价风光电制氢容量配置优化[J]. 太阳能学报, 2020, 41(8): 227-235. SHAO Zhifang, WU Jilan. Capacity configuration optimization of hydrogen production from wind and PV power based on dynamic electricity price[J]. Acta Energiae Solaris Sinica, 2020, 41(8): 227-235. (  0) 0) |
| [8] |
赵军超, 陈洁, 马小晶, 等. 计及调度计划与经济性的风/氢系统储能容量优化[J]. 电测与仪表, 2018, 55(24): 94-99. ZHAO Junchao, CHEN Jie, MA Xiaojing, et al. Energy storage capacity optimization for wind power/hydrogen system considering dispatching program and economy[J]. Electrical Measurement & Instrumentation, 2018, 55(24): 94-99. (  0) 0) |
| [9] |
WEN T, ZHANG Z Y, LIN X N, et al. Research on modeling and the operation strategy of a hydrogen-battery hybrid energy storage system for flexible wind farm grid-connection[J]. IEEE Access, 2020, 8: 79347-79356. DOI:10.1109/ACCESS.2020.2990581 (  0) 0) |
| [10] |
李晨迪, 陈渊睿, 曾君, 等. 基于非合作博弈的微电网能量管理系统优化算法[J]. 电网技术, 2016, 40(2): 387-395. LI Chendi, CHEN Yuanrui, ZENG Jun, et al. Research on optimization algorithm of microgrid energy management system based on non-cooperative game theory[J]. Power System Technology, 2016, 40(2): 387-395. (  0) 0) |
| [11] |
付菁. 基于非合作博弈的风-水-气区域电网调度研究[D]. 西安: 西安理工大学, 2018. FU Jing. Study on non-cooperative game dispatching of regional power system with wind-water-gas power[D]. Xi'an: Xi'an University of Technology, 2018. (  0) 0) |
| [12] |
魏春, 徐向志, 王国烽, 等. 基于非合作博弈的多能量枢纽优化运行方法[J]. 电力自动化设备, 2020, 40(11): 48-53, 60, 54. WEI Chun, XU Xiangzhi, WANG Guofeng, et al. Non-cooperative game-based optimal operation method of multiple energy hubs[J]. Electric Power Automation Equipment, 2020, 40(11): 48-53, 60, 54. (  0) 0) |
| [13] |
张金锋, 崔晓丹, 许剑冰, 等. 基于多用户非合作博弈模型的切负荷策略优化方法[J]. 电力系统保护与控制, 2020, 48(22): 127-134. ZHANG Jinfeng, CUI Xiaodan, XU Jianbing, et al. An optimization method of load-shedding strategy based on a multi-user non-cooperative game model[J]. Power System Protection and Control, 2020, 48(22): 127-134. (  0) 0) |
| [14] |
丁苏阳, 林湘宁, 陈哲, 等. 资源富集岛蓄-氢-冷联合可再生能源消纳系统设计及调度策略研究[J]. 中国电机工程学报, 2019, 39(16): 4659-4673, 4969. DING Suyang, LIN Xiangning, CHEN Zhe, et al. A design and dispatch strategy of storage-hydrogen-cooling combined renewable energy absorption facility on rich resource island[J]. Proceedings of the CSEE, 2019, 39(16): 4659-4673, 4969. (  0) 0) |
| [15] |
YAN C Z, CHEN J, LIU H, et al. Health management for PEM fuel cells based on an active fault tolerant control strategy[J]. IEEE Transactions on Sustainable Energy, 2021, 12(2): 1311-1320. (  0) 0) |
| [16] |
LI Y, YANG Z, LI G Q, et al. Optimal scheduling of an isolated microgrid with battery storage considering load and renewable generation uncertainties[J]. IEEE Transactions on Industrial Electronics, 2019, 66(2): 1565-1575. (  0) 0) |
| [17] |
WAHBAH M, FENG S, EL-FOULY T H M, et al. Root-transformed local linear regression for solar irradiance probability density estimation[J]. IEEE Transactions on Power Systems, 2020, 35(1): 652-661. (  0) 0) |
| [18] |
WANG Z K, JIA Y, CAI C, et al. Study on the optimal configuration of a wind-solar-battery-fuel cell system based on a regional power supply[J]. IEEE Access, 2021, 9: 47056-47068. (  0) 0) |
| [19] |
黄大为, 齐德卿, 于娜, 等. 利用制氢系统消纳风电弃风的制氢容量配置方法[J]. 太阳能学报, 2017, 38(6): 1517-1525. HUANG Dawei, QI Deqing, YU Na, et al. Capacity allocation method of hydrogen production system consuming abandoned wind power[J]. Acta Energiae Solaris Sinica, 2017, 38(6): 1517-1525. (  0) 0) |
| [20] |
朱永胜, 杨俊林, 刘洲峰, 等. 基于博弈论的风-光-车容量配置研究[J]. 太阳能学报, 2020, 41(9): 95-103. ZHU Yongsheng, YANG Junlin, LIU Zhoufeng, et al. Research on capacity allocation of wind-PV-EV based on game theory[J]. Acta Energiae Solaris Sinica, 2020, 41(9): 95-103. (  0) 0) |
| [21] |
王晓毅, 唐忠. 考虑供需自平衡和独立运行能力的并网型微电网容量优化配置[J]. 太阳能学报, 2021, 42(5): 74-82. WANG Xiaoyi, TANG Zhong. Capacity optimization of grid-connected microgrid considering self-balance and independent operation capability[J]. Acta Energiae Solaris Sinica, 2021, 42(5): 74-82. (  0) 0) |
| [22] |
曹建伟, 穆川文, 孙可, 等. 考虑碳交易的区域电网风光储容量配置优化方法[J]. 武汉大学学报(工学版), 2020, 53(12): 1091-1096, 1105. CAO Jianwei, MU Chuanwen, SUN Ke, et al. Optimal configuration method of wind-photovoltaic-storage capacities for regional power grid considering carbon trading[J]. Engineering Journal of Wuhan University, 2020, 53(12): 1091-1096, 1105. (  0) 0) |
| [23] |
侯慧, 刘鹏, 刘志刚, 等. 电热氢多元储能系统优化调度方法[J]. 高电压技术, 2022, 48(2): 536-545. HOU Hui, LIU Peng, LIU Zhigang, et al. Optimal dispatch method for multi-energy storage system of electricity heat hydrogen[J]. High Voltage Engineering, 2022, 48(2): 536-545. (  0) 0) |
| [24] |
李咸善, 杨宇翔. 基于双向电价补偿的含氢储能风电和梯级水电联合优化调度[J]. 电网技术, 2020, 44(9): 3297-3306. LI Xianshan, YANG Yuxiang. Optimization dispatching for joint operation of hydrogen storage-wind power and cascade hydropower station based on bidirectional electricity price compensation[J]. Power System Technology, 2020, 44(9): 3297-3306. (  0) 0) |
 2022, Vol. 41
2022, Vol. 41


 希望·阿不都瓦依提(1967),男,博士,副教授,研究方向为电力电子技术及多种可再生能源互补发电(E-mail:
希望·阿不都瓦依提(1967),男,博士,副教授,研究方向为电力电子技术及多种可再生能源互补发电(E-mail: