文章编号: 2096-3203(2022)02-0002-08 中图分类号: TM712
换相失败是高压直流输电(high voltage direct current,HVDC)中常见的故障之一[1-4]。若在首次换相失败后的故障恢复期间,直流系统控制处理不当,则可能发生后续换相失败,对交流系统造成多次冲击,甚至会引发直流闭锁导致功率传输中断,由局部故障演变为连锁故障,严重威胁大规模交直流混联系统的安全稳定运行[5-6]。
目前针对后续换相失败的抑制方法,主要从改进直流系统的拓扑结构和控制策略两方面考虑。在拓扑结构方面,文献[7-9]通过在换流母线处配置动态无功补偿装置,增大故障恢复过程中的换相电压时间面积,实现对后续换相失败的抑制;文献[10-11]采用全控型器件改造逆变站, 在恢复期间提供辅助换相电压,有效抵御后续换相失败的发生。但改进拓扑结构会增加投资成本和控制系统的复杂度。在控制策略方面,文献[12]通过设计一种减小不对称故障后超前触发角波动的内环控制器达到抑制后续换相失败的目的,但对于对称性故障的适用性有待验证;文献[13-14]利用虚拟电阻、虚拟电感进行限流以抑制后续换相失败,但较难选取合适的虚拟元件参数;文献[15]在文献[13]的基础上采用精确变斜率曲线作为低压限流控制(voltage dependent current order limiter,VDCOL)的特性曲线,一定程度上弥补了虚拟电阻故障稳态时过度限流的不足;文献[16]指出故障后VDCOL启动电压的大幅度波动会引发后续换相失败,以换流母线线电压作为输入得到波动较小的启动电压,但直流故障时可能不起作用;文献[17]提出一种根据换流母线线电压动态调节的非线性VDCOL策略,降低了后续换相失败的发生概率;文献[18]采用虚拟换相面积缺乏量作为故障特征指标整定电流指令值,提高了VDCOL的灵敏度。以上方法均能有效抑制后续换相失败,但对抑制后的直流功率传输能力变化考虑较少,以致运行经济性略有降低。
文中首先分析首次换相失败后故障恢复期间电气量和控制量的变化特性, 得出影响后续换相失败的关键因素。然后利用瞬时电压实时检测换流母线线电压幅值,结合分析结果提出一种根据换流母线线电压动态调节最小电流指令值的VDCOL改进策略,实现对后续换相失败的抑制。最后基于CIGRE标准模型实现VDCOL改进策略,不同故障条件下的仿真测试结果表明该策略能够有效抑制后续换相失败。
1 直流系统后续换相失败机理分析 1.1 直流系统换相失败换相失败是由于关断角γ小于晶闸管的最小关断角γmin,导致换相过程未能完成[5]。逆变器换相过程中触发角α、超前触发角β、关断角γ以及换相角μ之间的关系为:
| $ \gamma={\rm{ \mathsf{ π} }}-\alpha-\mu=\beta-\mu $ | (1) |
当系统对称运行时,γ可计算为[7]:
| $ \gamma=\arccos \left(\cos \beta+\frac{\sqrt{2} X_{\mathrm{C}} I_{\mathrm{d}}}{U_{\mathrm{L}}}\right) $ | (2) |
式中:XC为等值换相电感;Id为直流电流;UL为换流母线线电压。
当逆变侧发生不对称故障时,电压过零点会偏移电角度φ[19],此时γ为:
| $ \gamma=\arccos \left(\cos \beta+\frac{\sqrt{2} X_{\mathrm{C}} I_{\mathrm{d}}}{U_{\mathrm{L}}}\right)-\varphi $ | (3) |
当逆变侧交流系统故障时,UL下降,Id增大,此时直流控制系统无法及时做出反应,β基本不变,γ大幅度下降且极易降低至最小关断角γmin以下,发生首次换相失败。
1.2 HVDC控制环节首次换相失败后HVDC控制环节迅速响应调节系统运行状态,因此后续换相失败是否发生与直流系统的控制特性密切相关。稳态时整流侧为定电流(constant current,CC)控制,逆变侧为定关断角(constant extinction angle,CEA)控制。CIGRE标准模型控制系统见图 1[20],Idr,Ior分别为整流侧直流电流实测值和指令值;αr,αi分别为两侧触发角指令值;Udi,Idi分别为逆变侧直流电压和电流;G1,G2,G3为一阶惯性环节增益;T1,T2,T3为惯性时间常数;Ides为主控制级传递的电流指令值;βCC,βCEA分别为逆变侧CC、CEA控制输出的超前触发角指令值;γ,γ0分别为CEA控制中关断角实测值和额定值。
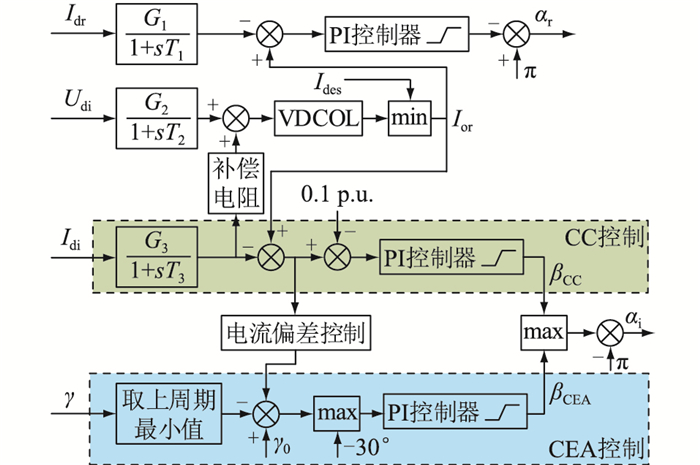
|
图 1 CIGRE标准模型控制系统 Fig. 1 CIGRE benchmark model control system |
VDCOL作为控制系统的重要环节,在直流电压Ud下降时减小直流电流指令值Ior,促进换相过程,其特性曲线见图 2。
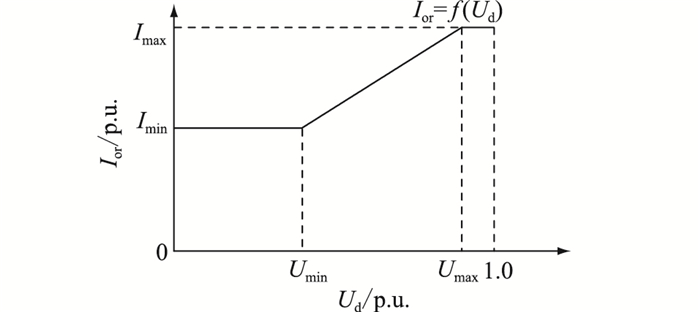
|
图 2 VDCOL特性曲线 Fig. 2 Characteristic curve of VDCOL |
图 2中,Imax,Imin分别为最大、最小电流指令值;Umax,Umin分别为取最高和最低电流的限流电压。对应的Ud与Ior的关系如式(4)所示。
| $ I_{\mathrm{or}}=f\left(U_{\mathrm{d}}\right)=\left\{\begin{array}{l} I_{\min } \quad U_{\mathrm{d}} \leqslant U_{\min } \\ I_{\min }+\frac{I_{\max }-I_{\min }}{U_{\max }-U_{\min }}\left(U_{\mathrm{d}}-U_{\min }\right) \\ \quad\quad\quad U_{\min }<U_{\mathrm{d}} \leqslant U_{\max } \\ I_{\max } \quad U_{\mathrm{d}}>U_{\max } \end{array}\right. $ | (4) |
以逆变侧控制器切换逻辑为依据,根据CIGRE标准模型稳态运行曲线将故障恢复过程划分为首次换相失败阶段(阶段1)、系统开始恢复阶段(阶段2)和电流偏差控制阶段(阶段3),见图 3[21-23]。
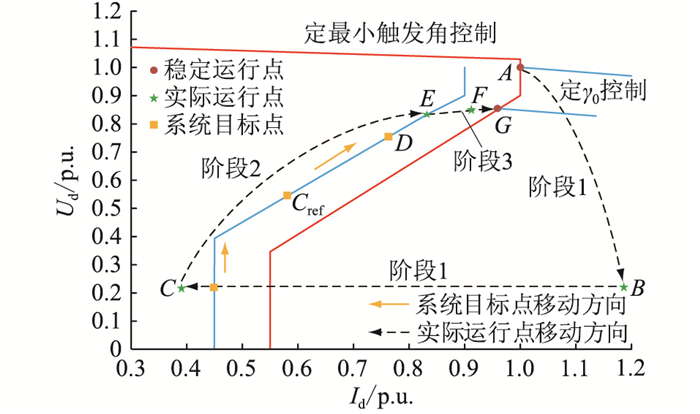
|
图 3 CIGRE标准模型稳态运行曲线 Fig. 3 Steady state operation curve of CIGRE benchmark model |
阶段1:首次换相失败后,换流阀短路导致Udi大幅度下降,Idi增大,逆变侧运行点由A点偏离至B点,此时VDCOL进入最小电流限制,逆变侧运行点由B点向C点移动。在控制系统作用下,Idi减小至低于整流侧CC控制的电流指令时,电流偏差控制启动,逆变侧由CEA控制切换为CC控制,运行至C点时进入阶段2。
阶段2:系统运行至C点换流阀恢复正常换相,Udi上升,VDCOL的电流指令值增大,此时系统目标点已到达Cref点。随着Udi进一步提高,在CC控制的作用下,Idi继续增大并向系统目标点靠近,系统目标点在VDCOL作用下沿Cref→D→E移动,运行至E点时进入阶段3。
阶段3:在控制系统作用下,实际运行点与系统目标点重合于E点,逆变侧的电流指令值与Idi相等,逆变器进入电流偏差控制。随着Udi和Idi的进一步恢复,系统实际运行点由E点移动至F点,逆变侧由CC控制切换为CEA控制,整流侧重获直流电流控制权,系统逐渐恢复至故障稳定运行点G。从A点移至G点的时间即为故障恢复时间。该阶段中,逆变侧控制器交互不当是造成后续换相失败的重要原因[24],电流偏差控制的设计初衷是通过提高CEA控制的整定值使逆变侧由CC控制平稳切换为CEA控制,但忽略了作用期间电流上升对关断角的不利影响。βinv_1,γinv_1,Iinv_d1,UL1分别为进入阶段3时逆变侧的超前触发角、关断角、直流电流和换流母线线电压,根据式(2)可得该阶段中的直流电流恢复量ΔId为:
| $ \begin{gathered} \Delta I_{\mathrm{d}}=\frac{\sqrt{2}\left(U_{\mathrm{L} 1}+\Delta U_{\mathrm{L}}\right)}{2 X_{\mathrm{C}}}\left(\cos \left(\gamma_{\mathrm{inv}\_1}+\Delta \gamma\right)-\right. \\ \left.\cos \left(\beta_{\mathrm{inv}\_1}+\Delta \beta\right)\right)-I_{\mathrm{inv}\_ \mathrm{d} 1} \end{gathered} $ | (5) |
式中:Δβ,Δγ,ΔUL分别为阶段3中逆变侧超前触发角、关断角和换流母线线电压的变化量。
将式(5)对Δγ偏导:
| $ \frac{\partial \Delta I_{\mathrm{d}}}{\partial \Delta \gamma}=-\frac{\sqrt{2}\left(U_{\mathrm{L} 1}+\Delta U_{\mathrm{L}}\right)}{2 X_{\mathrm{C}}} \sin \left(\gamma_{\mathrm{inv}\_1}+\Delta \gamma\right) $ | (6) |
由式(6)可知,ΔId与Δγ负相关,Δγ随ΔId的增大而减小。阶段3中直流电流恢复速度越快,ΔId越大,则电流偏差控制期间关断角的下降量越大。由式(2)可知,γ与Id负相关,与UL,β正相关。阶段3中Idi逐渐增加,逆变器无功消耗增大,会从交流系统吸收无功导致换流母线线电压略微下降,逆变侧交流系统越强,ΔUL越小。电流偏差控制的实际目标可近似为维持β恒定,通过仿真分析可知阶段3开始和结束时的β基本不变(见附录A图A1)。因此该阶段中,Δβ,ΔUL对Δγ影响较小,ΔId是影响Δγ的主要因素。综上所述,电流偏差控制期间(阶段3)的直流电流恢复量过大导致关断角大幅下降,使直流系统面临后续换相失败风险。
2 VDCOL改进策略提高VDCOL最小电流指令值可以加快故障前期直流电流的恢复速度,从而抑制电流偏差控制期间直流电流恢复量过大引起的后续换相失败。但提高最小电流指令值会增加故障前期逆变器的无功消耗,若换流母线线电压较低,则无功补偿装置发出的无功功率较小,直流系统会从交流系统吸收大量无功,造成换流母线线电压持续下降,逆变侧交流系统电压失稳。逆变侧交流系统故障导致换流母线线电压轻微跌落时,无功补偿装置仍能发出较多无功功率,此时适当提高VDCOL最小电流指令值不会引起换流母线线电压的进一步跌落。因此提出一种根据故障后换流母线线电压动态调整VDCOL最小电流指令值的VDCOL改进策略,函数特性见图 4,Imin1,Umin1分别为正常运行时VDCOL最小电流指令值和取最低电流时的限流电压。
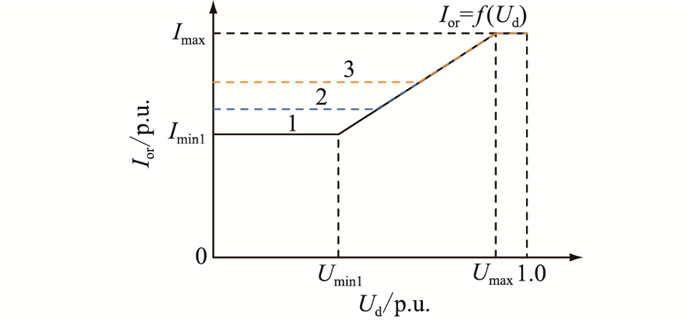
|
图 4 VDCOL改进策略函数特性 Fig. 4 Characteristic curve of VDCOL improvement strategy |
图 4中,曲线1为系统正常运行时的VDCOL特性曲线。当逆变侧交流系统故障引发换相失败时,VDCOL改进策略根据换流母线线电压跌落程度调整最小电流指令值,换流母线线电压跌落越小,最小电流指令值越大,即曲线2和曲线3。
文献[25]采用正余弦分量法实时检测换流母线线电压幅值,该方法响应速度较慢,且难以有效获得不对称运行状态下的换流母线线电压幅值。文中利用瞬时电压对换流母线线电压幅值进行快速检测。逆变侧交流系统三相电压瞬时值uai,ubi,uci可分别表示为:
| $ \left\{\begin{array}{l} u_{\mathrm{ai}}=\sqrt{2} U_{\mathrm{ai}} \cos \left(\omega t+\varphi_{\mathrm{a}}\right) \\ u_{\mathrm{bi}}=\sqrt{2} U_{\mathrm{bi}} \cos \left(\omega t+2 {\rm{ \mathsf{ π} }} / 3+\varphi_{\mathrm{b}}\right) \\ u_{\mathrm{ci}}=\sqrt{2} U_{\mathrm{ci}} \cos \left(\omega t-2 {\rm{ \mathsf{ π} }} / 3+\varphi_{\mathrm{c}}\right) \end{array}\right. $ | (7) |
式中:Uai,Ubi,Uci分别为三相电压有效值;φa,φb,φc分别为三相电压的初始相位;ω为交流系统角频率。
式(7)求导可得:
| $ \left\{\begin{array}{l} \frac{\mathrm{d} u_{\mathrm{ai}}}{\mathrm{d} t}=-\sqrt{2} \omega U_{\mathrm{ai}} \sin \left(\omega t+\varphi_{\mathrm{a}}\right) \\ \frac{\mathrm{d} u_{\mathrm{bi}}}{\mathrm{d} t}=-\sqrt{2} \omega U_{\mathrm{bi}} \sin \left(\omega t+2 {\rm{ \mathsf{ π} }} / 3+\varphi_{\mathrm{b}}\right) \\ \frac{\mathrm{d} u_{\mathrm{ci}}}{\mathrm{d} t}=-\sqrt{2} \omega U_{\mathrm{ci}} \sin \left(\omega t-2 {\rm{ \mathsf{ π} }} / 3+\varphi_{\mathrm{c}}\right) \end{array}\right. $ | (8) |
三角函数平方和公式可表示为:
| $ U^{2} \sin ^{2} \omega t+U^{2} \cos ^{2} \omega t=U^{2} $ | (9) |
将式(7)与式(8)代入式(9),可得交流系统故障后的三相电压幅值Ufa,Ufb,Ufc分别为:
| $ \left\{\begin{array}{l} U_{\mathrm{fa}}=\left[u_{\mathrm{ai}}^{2}+\left(\frac{\mathrm{d} u_{\mathrm{ai}}}{\omega \mathrm{d} t}\right)^{2}\right]^{1 / 2} / 2 \\ U_{\mathrm{fb}}=\left[u_{\mathrm{bi}}^{2}+\left(\frac{\mathrm{d} u_{\mathrm{bi}}}{\omega \mathrm{d} t}\right)^{2}\right]^{1 / 2} / 2 \\ U_{\mathrm{fc}}=\left[u_{\mathrm{ci}}^{2}+\left(\frac{\mathrm{d} u_{\mathrm{ci}}}{\omega \mathrm{d} t}\right)^{2}\right]^{1 / 2} / 2 \end{array}\right. $ | (10) |
实际工程中可采用基于离散数字量的差分法对三相电压求导[26]:
| $ \left[\begin{array}{c} \frac{\mathrm{d} u_{\mathrm{ai}}}{\mathrm{d} t} \\ \frac{\mathrm{d} u_{\mathrm{bi}}}{\mathrm{d} t} \\ \frac{\mathrm{d} u_{\mathrm{ci}}}{\mathrm{d} t} \end{array}\right]=-\frac{1}{\omega}\left[\begin{array}{l} \frac{u_{\mathrm{ai}}(t)-u_{\mathrm{ai}}(t-\Delta t)}{\Delta t} \\ \frac{u_{\mathrm{bi}}(t)-u_{\mathrm{bi}}(t-\Delta t)}{\Delta t} \\ \frac{u_{\mathrm{ci}}(t)-u_{\mathrm{ci}}(t-\Delta t)}{\Delta t} \end{array}\right] $ | (11) |
式中:Δt为步长;uai(t),ubi(t),uci(t)分别为三相电压当前步长的瞬时值;uai(t-Δt),ubi(t-Δt),uci(t-Δt)分别为三相电压前一步长的瞬时值。
基于瞬时电压,式(10)可实现交流系统故障运行状态下换流母线线电压幅值的实时快速检测。
定义关于UL的线性一次函数调节Imin:
| $ I_{\min }=a U_{\mathrm{L}}+b $ | (12) |
式中:a,b为待定常系数。
将式(12)代入式(4),得到改进VDCOL的启动电压Ud与电流指令值Ior的关系为:
| $ I_{\mathrm{or}}=\left\{\begin{array}{l} a U_{\mathrm{L}}+b \quad U_{\mathrm{d}} \leqslant U_{\min } \\ a U_{\mathrm{L}}+b+\frac{I_{\max }-a U_{\mathrm{L}}-b}{U_{\max }-U_{\min }}\left(U_{\mathrm{d}}-U_{\min }\right) \\ \quad\quad\quad\quad U_{\min }<U_{\mathrm{d}} \leqslant U_{\max } \\ I_{\max } \quad U_{\mathrm{d}}>U_{\max } \end{array}\right. $ | (13) |
其中,Umin为常数,具体计算公式为:
| $ U_{\min }=\frac{\left(I_{\max }-a U_{\mathrm{L}}-b\right) U_{\min 1}}{U_{\max }^{2}-U_{\max } U_{\min 1}} $ | (14) |
由式(13)可知,换流母线线电压跌落越小,则VDCOL改进策略的最小电流指令值越大,故障前期直流电流恢复速度越快,电流偏差控制期间直流电流的恢复量越小。当逆变侧换流母线发生金属性三相接地故障时,UL=0,直流系统基本不具有可控性,提高VDCOL最小电流指令值无意义,改进VDCOL器的最小电流指令值与原VDCOL相等,故b=Imin1,系数a根据系统的实际情况确定。
当直流线路故障时,暂态电流冲击时间较长,亟需VDCOL充分发挥限流作用抑制暂态电流。但换流母线线电压在交流系统的支撑作用下只有较低程度的跌落,此时提高VDCOL的最小电流指令值会大幅削弱其限流作用。因此所提策略只应在逆变侧交流系统故障导致换相失败时投入,系统运行于其他工况时应保持Imin=Imin1,VDCOL改进策略如图 5所示。
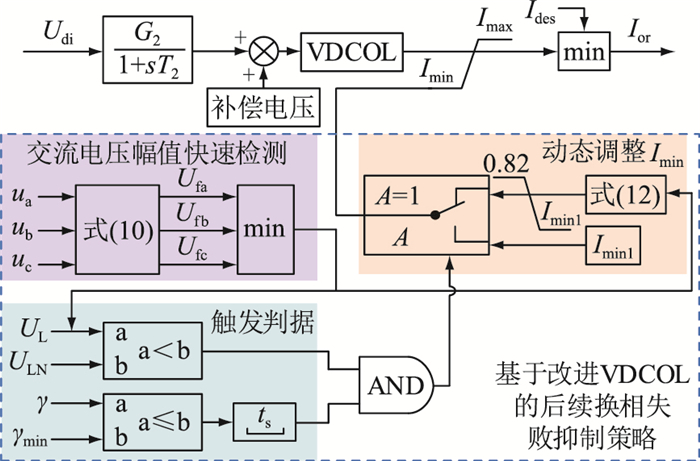
|
图 5 VDCOL改进策略 Fig. 5 Improved strategy of VDCOL |
图 5中,ULN为换流母线额定电压;A为切换信号;ts为信号保持时间。换相失败引起的功率波动通常可持续100~200 ms,为使换相失败期间切换信号A始终为1,将换相失败信号保持时间ts设置为200 ms。稳态时,VDCOL的最小电流指令值保持为Imin1。当逆变侧交流系统故障引发换相失败时换流母线线电压跌落,γ降至γmin以下。触发判据环节输出高电平使切换信号A=1,Imin计算模块投入,根据实时检测的交流电压动态调整Imin。当系统恢复正常时,触发判据环节输出低电平使A=0,最小电流指令值已保持为Imin1。该策略利用关断角γ和换流母线线电压UL相互配合,仅在交流系统故障引发换相失败时提高VDCOL的最小电流指令值,避免了系统运行于其他工况时控制器失效的问题。
3 仿真验证 3.1 仿真模型基于PSCAD仿真软件中的CIGRE标准模型搭建测试系统。晶闸管的关断时间约400 μs(对应电角度7.2°)[15],因此取γmin=7.2°。测试模型中的VDCOL参数为:Umin1=0.4 p.u.,Imin1=0.55 p.u.,Umax=0.9 p.u.,Imax=1 p.u.。为避免Imin设定过高恶化交流系统暂态性能,综合实验对比取上限为0.82 p.u.对Imin进行限幅。换流母线线电压大于标准模型的临界换相电压(0.94 p.u.)时[27],Imin达到输出上限。因此取a=0.29,b=0.55。
3.2 VDCOL改进策略抑制效果验证为验证文中提出的VDCOL改进策略对原系统控制效果的影响。设置逆变侧换流母线在2 s发生接地电感Lf分别为1.1 H(轻微故障)和0.1 H(严重故障)的三相接地故障,故障持续0.5 s。对比分析原策略与改进策略下直流系统的故障运行特性,仿真结果如图 6、图 7所示。
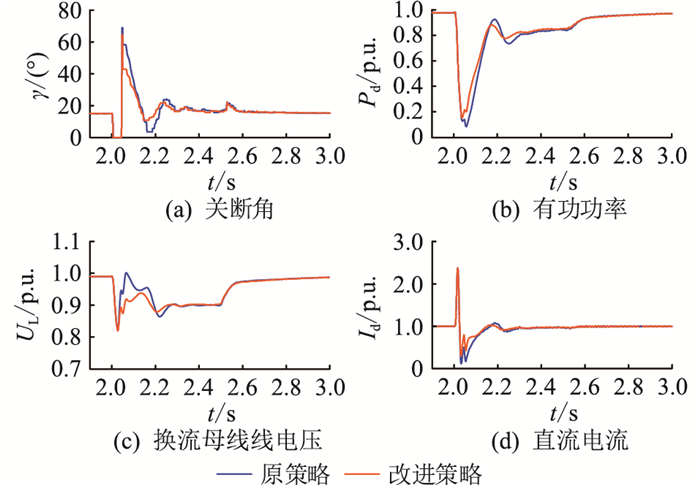
|
图 6 三相故障Lf=1.1 H时的逆变侧暂态运行特性 Fig. 6 Transient operation characteristics of inverter side under three-phase fault with Lf=1.1 H |
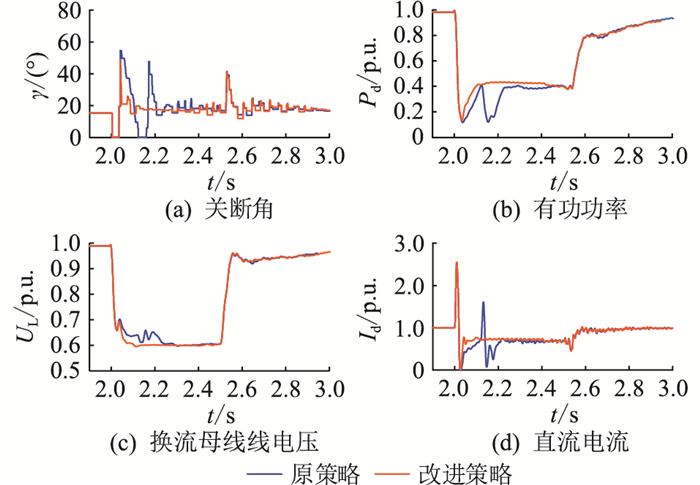
|
图 7 三相故障Lf=0.1 H时的逆变侧暂态运行特性 Fig. 7 Transient operation characteristics of inverter side under three-phase fault with Lf=0.1 H |
由图 6可知,改进策略和原策略均不发生后续换相失败。改进策略下的有功功率波动范围小,故障恢复时间较短,且故障稳态时的直流系统传输能力优于原策略。由图 6(c)和图 6(d)可见,故障恢复前期,改进策略下的直流电流恢复较快,换流母线线电压略低于原策略,但二者换流母线线电压跌落后的最低值相等,且系统达到故障稳态时的换流母线线电压未降低。因此,在故障较轻导致单次换相失败时,改进策略不会削弱原系统的控制效果。
由图 7可知,原策略发生后续换相失败,改进策略仅发生单次换相失败,系统较快达到故障稳态。对比图 7(c)和图 7(d)可见,与原策略相比,改进策略故障恢复前期直流电流上升较快,换流母线线电压持续下降,但2种策略下的换流母线线电压最低值相等。因此改进策略在故障较严重时仍能有效抑制后续换相失败,不会削弱原系统的控制效果。
为验证所提VDCOL改进策略对后续换相失败的抑制效果,采用以下3种控制策略,设置逆变侧换流母线在2 s发生经0.7 H电感的三相接地故障,故障持续0.5 s。仿真结果如图 8所示。
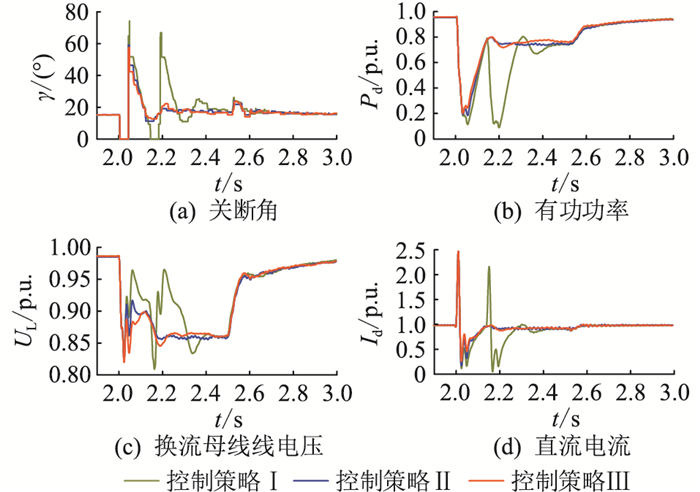
|
图 8 3种控制策略下系统暂态运行特性 Fig. 8 Transient operation characteristics of systems under three control strategies |
控制策略Ⅰ:使用CIGRE标准模型控制。
控制策略Ⅱ:使用文献[15]中所提的基于虚拟电阻限流的变斜率VDCOL策略,其余控制环节保持一致。
控制策略Ⅲ:在控制策略Ⅰ中使用文中提出的VDCOL改进策略,其余控制环节保持一致。
由图 8可知,控制策略Ⅰ在交流系统故障期间关断角2次下降至0,直流系统发生后续换相失败,功率波动2次,故障恢复时间约为420 ms。控制策略Ⅱ、Ⅲ仅发生单次换相失败,功率波动1次,故障恢复时间分别为222 ms和225 ms。由图 8(c)可知,在系统处于故障下的稳定运行点时,控制策略Ⅰ、Ⅲ的换流母线线电压跌落0.14 p.u.,控制策略Ⅱ的换流母线线电压跌落最大(约0.15 p.u.),不利于逆变侧交流系统的稳定。对比图 8(b)和图 8(d)中的控制策略Ⅱ、Ⅲ可知,二者均较快达到故障稳态,但控制策略Ⅲ能使故障稳态期间的直流系统输送功率提高0.06 p.u.,提高了直流系统的功率传输能力,为逆变侧交流系统提供更高的稳定裕度,且故障清除后直流系统的恢复速度较快。
为进一步验证所提策略的抑制效果,在逆变侧换流母线处设置不同程度的感性接地故障(0.2~1.1 H),故障发生时刻为2.000~2.009 s(覆盖半个周期0.01 s),故障持续时间为0.5 s,仿真统计结果见图 9和图 10。
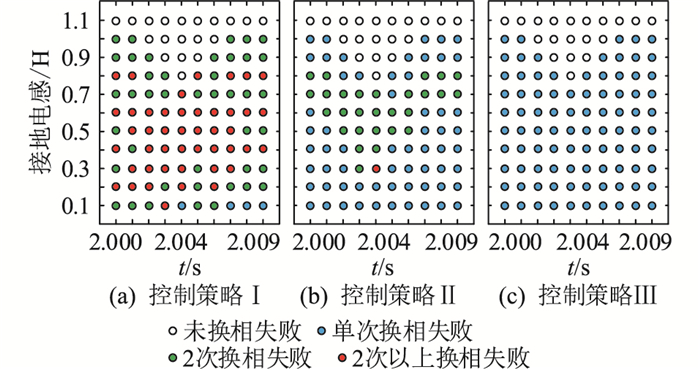
|
图 9 3种控制策略下的单相接地故障换相失败统计结果 Fig. 9 Statistical results of commutation failure for sin- gle-phase ground fault under three control strategies |
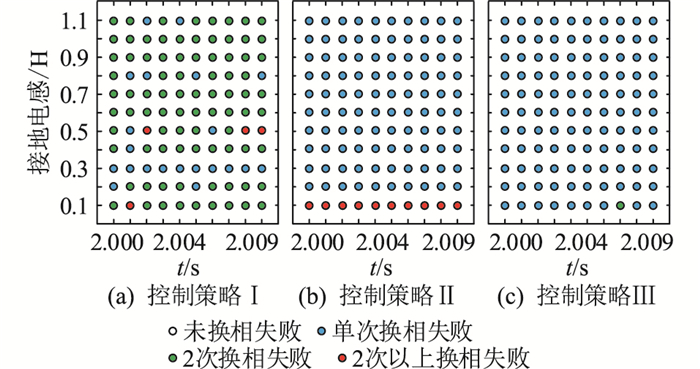
|
图 10 3种控制策略下的三相接地故障换相失败统计结果 Fig. 10 Statistical results of commutation failure for th- ree-phase ground fault under three control strategies |
由图 9可知,单相接地故障下控制策略Ⅱ、Ⅲ均能有效抑制后续换相失败。但不对称故障下产生的非特征谐波会影响直流电流,导致控制策略Ⅱ在部分工况下失效,直流系统仍发生2次及以上换相失败;而控制策略Ⅲ能够减小电流偏差控制期间的直流电流恢复量,在不同单相接地故障工况下均能较好抑制后续换相失败的发生。
由图 10可知,三相接地故障下控制策略Ⅱ、Ⅲ对后续换相失败均有较好的抑制效果。但在严重故障(Lf=0.1 H)下,控制策略Ⅱ会失去抑制效果,甚至恶化系统运行状态,直流系统发生2次以上换相失败;而控制策略Ⅲ(文中所提策略)仍能较好抑制后续换相失败,且故障稳态期间直流系统的功率输送能力和故障清除后的恢复速度均优于控制策略Ⅱ。
4 结语通过分析首次换相失败后的恢复过程中电气量和控制量的变化特性,得出电流偏差控制期间直流电流恢复量过大是引发后续换相失败的主要因素。为此,利用瞬时电压快速准确检测交流故障后的逆变侧换流母线线电压幅值,基于实时检测的电压动态计算直流电流最小指令值,减小电流偏差控制期间的直流电流恢复量,抑制后续换相失败。仿真结果表明所提策略能够有效抑制后续换相失败,改善直流系统的故障运行特性。
附录A设置逆变侧换流母线在2 s发生Lf=0.4 H的单相接地故障,故障持续0.5 s。仿真结果如图A1所示。图A1(a)中E点直流电流实测值等于逆变侧CC控制的电流指令值,此时逆变侧进入电流偏差控制,G点直流电流实测值等于整流侧CC控制的电流指令值,此时电流偏差控制退出运行。因此图A1中黄色阴影部分即为电流偏差控制过程(阶段3)。由图A1(a)和图A1(d)可以看出,EG段直流电流恢复量较大,换流母线线电压略微下降。由图A1(b)可以看出,EF段和FG段逆变侧超前触发角β变化幅度约5°,且进入和退出电流偏差控制时的β相差很小,仅1°左右。
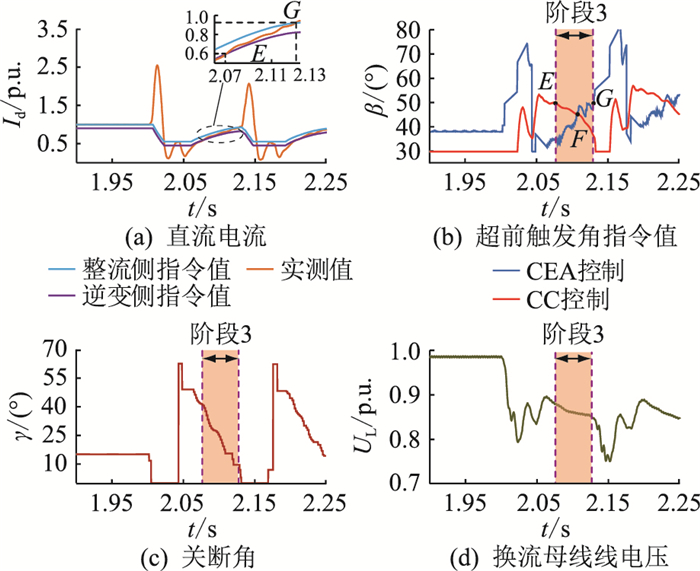
|
图 A1 逆变侧控制系统暂态运行特性 Fig. A1 Transient operation characteristics of inverter system |
| [1] |
李明节. 大规模特高压交直流混联电网特性分析与运行控制[J]. 电网技术, 2016, 40(4): 985-991. LI Mingjie. Characteristic analysis and operational control of large-scale hybrid UHV AC/DC power grids[J]. Power System Technology, 2016, 40(4): 985-991. (  0) 0) |
| [2] |
张国辉, 景柳铭, 王宾, 等. 谐波引起的高压直流输电连续换相失败抑制方法研究[J]. 电力系统保护与控制, 2020, 48(5): 33-41. ZHANG Guohui, JING Liuming, WANG Bin, et al. Study on HVDC consecutive commutation failures mitigation method caused by harmonics[J]. Power System Protection and Control, 2020, 48(5): 33-41. (  0) 0) |
| [3] |
尹纯亚, 李凤婷, 宋新甫, 等. 多馈出直流系统换相失败快速判别方法[J]. 电网技术, 2019, 43(10): 3459-3465. YIN Chunya, LI Fengting, SONG Xinfu, et al. A fast detection method of commutation failure in multi-outfeed DC system[J]. Power System Technology, 2019, 43(10): 3459-3465. (  0) 0) |
| [4] |
董新洲, 汤涌, 卜广全, 等. 大型交直流混联电网安全运行面临的问题与挑战[J]. 中国电机工程学报, 2019, 39(11): 3107-3119. DONG Xinzhou, TANG Yong, BU Guangquan, et al. Confronting problem and challenge of large scale AC-DC hybrid power grid operation[J]. Proceedings of the CSEE, 2019, 39(11): 3107-3119. (  0) 0) |
| [5] |
王增平, 刘席洋, 郑博文, 等. 基于电压波形拟合的换相失败快速预测与抑制措施[J]. 电工技术学报, 2020, 35(7): 1454-1463. WANG Zengping, LIU Xiyang, ZHENG Bowen, et al. The research on fast prediction and suppression measures of commutation failure based on voltage waveform fitting[J]. Transactions of China Electrotechnical Society, 2020, 35(7): 1454-1463. (  0) 0) |
| [6] |
尹纯亚, 李凤婷, 王丹东, 等. 风电高渗透率交直流外送系统直流闭锁稳控方案研究[J]. 电力系统保护与控制, 2019, 47(3): 95-102. YIN Chunya, LI Fengting, WANG Dandong, et al. Research on stability control scheme for AC/DC hybrid transmission system with wind power high permeability under DC blocking[J]. Power System Protection and Control, 2019, 47(3): 95-102. (  0) 0) |
| [7] |
王维, 赵梦阳, 唐小波, 等. 接地故障下的SVC优化设计及其对后续换相失败控制策略[J]. 电力系统自动化, 2019, 43(20): 123-129. WANG Wei, ZHAO Mengyang, TANG Xiaobo, et al. Optimization design of static var compensator and its control strategy for subsquent commutation failure with grounding fault[J]. Automation of Electric Power Systems, 2019, 43(20): 123-129. DOI:10.7500/AEPS20190117005 (  0) 0) |
| [8] |
邢超, 奚鑫泽, 李胜男, 等. 大容量STATCOM对于受端直流换流站运行与故障特性影响[J]. 电力系统保护与控制, 2019, 47(15): 78-85. XING Chao, XI Xinze, LI Shengnan, et al. Effect of large capacity STATCOM on operation and fault characteristics of receiving DC converter station[J]. Power System Protection and Control, 2019, 47(15): 78-85. DOI:10.7667/PSPC20191511 (  0) 0) |
| [9] |
沙江波, 杨硕, 郭春义, 等. 同步调相机对分层接入特高压直流输电系统的换相失败抑制作用研究[J]. 电网技术, 2019, 43(10): 3552-3561. SHA Jiangbo, YANG Shuo, GUO Chunyi, et al. Study on suppression effect of synchronous condenser on commutation failure of UHVDC system under hierarchical connection mode[J]. Power System Technology, 2019, 43(10): 3552-3561. (  0) 0) |
| [10] |
GUO C Y, LI C H, ZHAO C Y, et al. An evolutional line-commutated converter integrated with thyristor-based full-bridge module to mitigate the commutation failure[J]. IEEE Transactions on Power Electronics, 2017, 32(2): 967-976. DOI:10.1109/TPEL.2016.2544107 (  0) 0) |
| [11] |
XUE Y, ZHANG X P, YANG C H. Commutation failure elimination of LCC HVDC systems using thyristor-based controllable capacitors[J]. IEEE Transactions on Power Delivery, 2017, 33(3): 1448-1458. (  0) 0) |
| [12] |
曾亮, 李永丽, 张云柯, 等. 逆变侧交流系统不对称故障引发HVDC系统连续换相失败的机理及抑制策略研究[J]. 中国电机工程学报, 2019, 39(11): 3159-3168. ZENG Liang, LI Yongli, ZHANG Yunke, et al. Research on mechanism and control strategy of continuous commutation failures in HVDC system caused by asymmetrical fault in inverter-side AC system[J]. Proceedings of the CSEE, 2019, 39(11): 3159-3168. (  0) 0) |
| [13] |
郭春义, 李春华, 刘羽超, 等. 一种抑制传统直流输电连续换相失败的虚拟电阻电流限制控制方法[J]. 中国电机工程学报, 2016, 36(18): 4930-4937, 5117. GUO Chunyi, LI Chunhua, LIU Yuchao, et al. A DC current limitation control method based on virtual-resistance to mitigate the continuous commutation failure for conventional HVDC[J]. Proceedings of the CSEE, 2016, 36(18): 4930-4937, 5117. (  0) 0) |
| [14] |
陆翌, 童凯, 宁琳如, 等. 基于虚拟电感的双馈入直流输电系统连续换相失败的抑制方法[J]. 电网技术, 2017, 41(5): 1503-1509. LU Yi, TONG Kai, NING Linru, et al. A method mitigating continuous commutation failure for double-infeed HVDC system based on virtual inductor[J]. Power System Technology, 2017, 41(5): 1503-1509. (  0) 0) |
| [15] |
王立舒, 刘勃, 乔帅翔, 等. 改变获取补偿电压方法的精确变斜率VDCOL设计[J]. 高电压技术, 2020, 46(8): 2740-2750. WANG Lishu, LIU Bo, QIAO Shuaixiang, et al. Design of precise variable slope VDCOL for changing the method of obtaining compensation voltage[J]. High Voltage Engineering, 2020, 46(8): 2740-2750. (  0) 0) |
| [16] |
李瑞鹏, 李永丽, 陈晓龙. 一种抑制直流输电连续换相失败的控制方法[J]. 中国电机工程学报, 2018, 38(17): 5029-5042, 5300. LI Ruipeng, LI Yongli, CHEN Xiaolong. A control method for suppressing the continuous commutation failure of HVDC transmission[J]. Proceedings of the CSEE, 2018, 38(17): 5029-5042, 5300. (  0) 0) |
| [17] |
孟庆强, 刘泽洪, 洪乐荣, 等. 一种抑制连续换相失败的非线性VDCOL控制策略[J]. 电力系统保护与控制, 2019, 47(7): 119-127. MENG Qingqiang, LIU Zehong, HONG Lerong, et al. A suppression method based on nonlinear VDCOL to mitigate the continuous commutation failure[J]. Power System Protection and Control, 2019, 47(7): 119-127. (  0) 0) |
| [18] |
刘磊, 林圣, 何正友. 基于虚拟换相面积缺乏量的HVDC系统连续换相失败抑制策略[J]. 中国电机工程学报, 2018, 38(18): 5361-5368. LIU Lei, LIN Sheng, HE Zhengyou. A novel method based on virtual commutation area insufficient to mitigate the continuous commutation failure for HVDC[J]. Proceedings of the CSEE, 2018, 38(18): 5361-5368. (  0) 0) |
| [19] |
穆文凯, 王涛, 刘文轩, 等. 基于虚拟电容的高压直流后续换相失败抑制方法[J]. 华北电力大学学报(自然科学版), 2021, 48(5): 25-35. MU Wenkai, WANG Tao, LIU Wenxuan, et al. Virtual-capacitance-based method to suppress the subsequent commutation failure in HVDC system[J]. Journal of North China Electric Power University (Natural Science Edition), 2021, 48(5): 25-35. DOI:10.3969/j.ISSN.1007-2691.2021.05.03 (  0) 0) |
| [20] |
朱龙臻, 牛翀, 王志冰, 等. 一种抑制连续换相失败的关断角动态补偿控制方法[J]. 中国电机工程学报, 2021, 41(22): 7621-7631. ZHU Longzhen, NIU Chong, WANG Zhibing, et al. An extinction angle dynamic compensation control method for suppressing continuous commutation failure[J]. Proceedings of the CSEE, 2021, 41(22): 7621-7631. (  0) 0) |
| [21] |
刘席洋, 王增平, 郑博文, 等. LCC-HVDC故障恢复型连续换相失败机理分析与抑制措施[J]. 中国电机工程学报, 2020, 40(10): 3163-3172. LIU Xiyang, WANG Zengping, ZHENG Bowen, et al. Mechanism analysis and mitigation measures for continuous commutation failure during the restoration of LCC-HVDC[J]. Proceedings of the CSEE, 2020, 40(10): 3163-3172. (  0) 0) |
| [22] |
王璐, 李凤婷, 尹纯亚. 考虑直流电流变化的HVDC系统不对称故障换相失败分析[J]. 电力系统保护与控制, 2021, 49(1): 17-23. WANG Lu, LI Fengting, YIN Chunya. Analysis of asymmetric fault commutation failure in an HVDC system with DC current variation[J]. Power System Protection and Control, 2021, 49(1): 17-23. (  0) 0) |
| [23] |
张伟晨, 熊永新, 李程昊, 等. 基于改进VDCOL的多馈入直流系统连续换相失败抑制及协调恢复[J]. 电力系统保护与控制, 2020, 48(13): 63-72. ZHANG Weichen, XIONG Yongxin, LI Chenghao, et al. Continuous commutation failure suppression and coordinated recovery of multi-infeed DC system based on improved VDCOL[J]. Power System Protection and Control, 2020, 48(13): 63-72. (  0) 0) |
| [24] |
刘磊, 林圣, 刘健, 等. 控制器交互不当引发后续换相失败的机理分析[J]. 电网技术, 2019, 43(10): 3562-3568. LIU Lei, LIN Sheng, LIU Jian, et al. Mechanism analysis of subsequent commutation failures caused by improper interac tion of controllers[J]. Power System Technology, 2019, 43(10): 3562-3568. (  0) 0) |
| [25] |
夏海涛, 周小平, 洪乐荣, 等. 一种抑制后续换相失败的自适应电流偏差控制方法[J]. 中国电机工程学报, 2019, 39(15): 4345-4356. XIA Haitao, ZHOU Xiaoping, HONG Lerong, et al. An adaptive current deviation control method for suppressing following commutation failures[J]. Proceedings of the CSEE, 2019, 39(15): 4345-4356. (  0) 0) |
| [26] |
杨奇逊, 黄少锋. 微型机继电保护基础[M]. 4版. 北京: 中国电力出版社, 2013: 76-78. YANG Qixun, HUANG Shaofeng. Microcomputer relay protection foundation[M]. 4th ed. Beijing: China Electric Power Press, 2013: 76-78. (  0) 0) |
| [27] |
徐敬友, 谭海燕, 孙海顺, 等. 考虑直流电流变化及交流故障发生时刻影响的HVDC换相失败分析方法[J]. 电网技术, 2015, 39(5): 1261-1267. XU Jingyou, TAN Haiyan, SUN Haishun, et al. Research on method to analyze commutation failure in HVDC power transmission system considering the impact of DC current variation and occurrence moment of AC fault[J]. Power System Technology, 2015, 39(5): 1261-1267. (  0) 0) |
 2022, Vol. 41
2022, Vol. 41


 陈睿康(1997),男,硕士在读,研究方向为交直流混联系统运行与控制(E-mail:
陈睿康(1997),男,硕士在读,研究方向为交直流混联系统运行与控制(E-mail: