文章编号: 2096-3203(2022)02-0090-07 中图分类号: TM743
2. 四川大学电气工程学院,四川 成都 610065
随着半导体数字化等技术的发展,新型用电设备在各行各业发挥着越来越重要的作用[1]。电压暂降作为电能质量中最突出的问题,已经成为用电设备的主要威胁[2]。对暂降进行监测,有助于分析其产生原因、评估其扰动水平、为用户选取最佳接入点或电网改造等提供数据支撑[3],因此合理配置暂降监测装置具有重要的实际意义[4]。
目前,针对暂降监测装置的优化配置研究,最主要的模型是基于监测点可观测域(monitor reach area,MRA)法[5-6]。该模型以暂降监测装置数目最少为目标,以暂降全网可观为约束[7],可以使用遗传[7]、粒子群[8]、整数线性规划[9]等算法求解。然而该模型通常多解且难以确定最优解[10],一方面是因为缺乏新的优化目标,导致寻优条件不足; 另一方面是传统方法默认系统中所有节点同等重要,配置缺乏针对性。后续研究通过引入新的优化目标来确定配置方案的最优解,比如:暂降可观性指数最大[11]、暂降严重指数最大[12]、暂降权重系数最大[13]、不确定区域指数最小[14]、抗扰指数最大[15]等。这些研究都能唯一确定监测方案,但有的增加了监测装置数目,有的对暂降敏感区域的监测能力还可进一步提升[16]。此外,同步相量测量单元(phasor measurement unit,PMU)能高频采集电流、电压信息,在暂降等扰动下记录录波数据[17],理论上可以用于辅助监测电压暂降。
基于上述分析,文中认为系统中的暂降敏感区域更重要,并提出一种考虑暂降敏感区域监测可靠性和PMU布点的暂降监测装置联合优化配置模型。首先提出使用Zeroin迭代法提高暂降域计算的准确性; 然后在暂降域的基础上定义了风险域矩阵来细化系统中不同位置的暂降敏感程度; 接着分别以监测装置数目最少、覆盖暂降敏感区域范围最大为目标,以暂降全网可观为约束,引入优先因子,简化后形成多目标联合优化配置模型。在模型中考虑配置PMU用于辅助监测电压暂降,减少暂降监测装置数目,同时提高暂降敏感区域监测可靠性。由IEEE 30节点系统仿真结果可知,文中方法能唯一获得满足配置经济性同时兼顾敏感区域监测需求的方案,具有实际应用价值。
1 暂降域及监测装置可观测域计算 1.1 暂降域计算电力系统中发生短路故障能引起敏感负荷所处节点暂降幅值低于整定暂降阈值的区域,就是节点在该整定幅值下的暂降域。故障点在系统中某一线路上移动时,敏感负荷所在节点处的暂降幅值是一个开口向下的单峰函数,并且近似二次函数,可以直接使用线路上0,0.5,1这3个位置的暂降幅值进行二次插值,并与暂降阈值形成方程求解临界点[18]。为了提高临界值的计算准确性,文献[19]给出了一种分段二次插值的技巧。求解暂降域的关键过程如下。
1.1.1 负荷点残余电压计算系统中线路发生短路是导致敏感负荷节点产生暂降的主要原因,因此求解暂降域首先需要获取不同短路类型下的负荷点残余电压。电力系统短路计算模型见图 1。其中m为待求敏感节点; i,j为节点; f为故障点; p为故障点到节点i的归一化距离。

|
图 1 电力系统短路计算模型 Fig. 1 Model of power system short-circuit calculation |
首先进行潮流计算,然后形成各序阻抗,接着在不同故障类型下获取敏感节点m的三相电压幅值并取其中最小的作为暂降幅值,即|vmfault|=min(|vA, mfault|, |vB, mfault|, |vC, mfault|),计算公式可以参考文献[20]。
1.1.2 支路判别矩阵计算短路计算完成之后,需要根据短路计算结果形成判别矩阵Bsag和Lsag,分别用于判断不同节点和线路在敏感节点暂降域中的包含情况。首先计算节点m的暂降幅值向量Vsag为:
| $ \boldsymbol{V}_{\mathrm{sag}}=\left[\left|v_{m, 1}^{\text {fault }}\right| \quad \cdots\left| v_{m, u}^{\text {fault }}\right|\cdots \cdots\left| v_{m, n}^{\text {fault }} \right|\right]^{\mathrm{T}} $ | (1) |
式中:|vm, ufault|为节点u发生故障时节点m处的暂降幅值; n为系统中节点总数。接着形成判别矩阵Bsag和Lsag,从而确定Zeroin法所需计算线路。其中矩阵Bsag的元素bsag, u由节点m的暂降幅值向量Vsag和暂降阈值向量Vth的差值ΔVsag来决定。
| $ \begin{gathered} \Delta \boldsymbol{V}_{\mathrm{sag}}=\left[\Delta v_{\mathrm{sag}, 1} \cdots \Delta v_{\mathrm{sag}, u} \cdots \Delta v_{\mathrm{sag}, n}\right]^{\mathrm{T}}= \\ \boldsymbol{V}_{\mathrm{sag}}-\boldsymbol{V}_{\mathrm{th}} \end{gathered} $ | (2) |
| $ b_{\mathrm{sag}, u}= \begin{cases}1 & \Delta v_{\mathrm{sag}, u} \leqslant 0 \\ 0 & \Delta v_{\mathrm{sag}, u}>0\end{cases} $ | (3) |
若bsag, u=1,则u在暂降域内; 若bsag, u=0,则u在暂降域外。设线路条数为v,根据矩阵Bsag可进一步确定线路的参数矩阵Lsag如下:
| $ \boldsymbol{L}_{\mathrm{sag}}=\left[\begin{array}{c} l_{\mathrm{sag}, 1} \\ \vdots \\ l_{\mathrm{sag}, v} \end{array}\right]=\left[\begin{array}{c} \vdots \\ b_{\mathrm{sag}, i} \\ \vdots \end{array}\right]+\left[\begin{array}{c} \vdots \\ b_{\mathrm{sag}, j} \\ \vdots \end{array}\right] $ | (4) |
式中:bsag, i,bsag, j为矩阵Bsag的元素,其下标i,j分别为其所在行对应线路的两端节点编号。Lsag中元素为0表示对应线路ij不在m暂降域中,后续无须计算; 为1表示线路ij中包含1个临界点; 为2表示有2个临界点。确定线路临界点的个数之后,可以通过合适的区间及端点值拟合暂降幅值,计算线路中的临界点[19]。
1.2 监测装置可观测域计算短路导致的暂降是随机的,暂降监测装置配置的关键就是能否准确识别任意短路故障引起的暂降事件。系统的电压暂降可观性可以用电压暂降可观性矩阵,也称作MRA矩阵来反映。设系统中节点数为n,线路分段数为s,则任意短路故障类型下的MRA矩阵Mw可以表示如下:
| $ \boldsymbol{M}_{w}=\left[\begin{array}{cccc} m_{11, w} & m_{12, w} & \cdots & m_{1 s, w} \\ m_{21, w} & m_{22, w} & \cdots & m_{2 s, w} \\ \vdots & \vdots & & \vdots \\ m_{n 1, w} & m_{n 2, w} & \cdots & m_{n s, w} \end{array}\right] $ | (5) |
其中,w为故障类型,其取值0,1,2,3分别表示三相短路、单相接地短路、两相短路和两相接地短路。Mw是二进制矩阵,其元素mab, w(a=1, 2, …, n; b=1, 2, …, s)按照如下规则进行取值:
| $ m_{a b, w}= \begin{cases}1 & v_{a b} \leqslant v_{\mathrm{th}} \\ 0 & v_{a b}>v_{\mathrm{th}}\end{cases} $ | (6) |
式中:vab为线路段b发生短路时,节点a处的暂降幅值; vth为Vth中相应位置的元素,表示暂降监测装置整定的暂降阈值。若mab=1,则线路段b发生短路会导致节点a处暂降并被该处的监测装置监测到; 若mab=0,则表示不能被监测。由于Mw中的行代表了对应节点的暂降监测范围,所以如果能确定部分节点,并使其监测范围的并集能覆盖整个电力系统,则不用在所有节点配置监测装置,即可实现全网暂降可观。
2 电压暂降监测装置优化配置 2.1 基于Zeroin方法的暂降域计算由于电力系统的复杂性,暂降幅值与线路的关系并不能用拟合二次函数完全刻画,且拟合情况的好坏受初始选取值的直接影响。事实上,确定节点的暂降域本质是找到各条线路中的临界点,即求解方程vmfault-vth=0的根。将方程转化为如式(7)所示的目标函数,通过合适的迭代法保证暂降域计算的准确度与速度。
| $ \min f=\left|v_{m}^{\text {fault }}-v_{\mathrm{th}}\right| $ | (7) |
可以根据Lsag确定各线路上的临界点:当lsag, v=0时,线路v位于暂降域外,不需要计算临界点; 当lsag, v=1时,线路上只有1个临界点,可以通过对式(7)使用Zeroin迭代法求得; 当lsag, v=2时,线路上有2个临界点,这时先利用Zeroin法求解线路中使暂降幅值vmfault最大的点pmax,然后在[0, pmax]和[pmax, 1]区间内各自对式(7)使用Zeroin迭代法即可求出2个临界点。利用Zeroin算法求解线路临界点的具体步骤如下。
步骤1:选取初始值x, y,使得f(x),f(y)的符号相反,初始值取端点值即可。
步骤2:将x的值赋给z。
步骤3:若f(y),f(x)符号相同,将z赋值给x。
步骤4:若|f(x)| < |f(y)|,则将y的值赋给z,然后对调x,y的值。
步骤5:如果z≠x,利用x,y,z及其函数值作逆二次插值并赋值给z; 如果z=x,则用x,y及其函数值做割线迭代并赋值给z。
步骤6:如果步骤5中迭代的结果z∈[x, y],则将z赋值给y,否则取x,y的平均作为z值,并将z赋值给y。
步骤7:重复步骤3-6,直到f(y)=vth或y-x < ε|y|,其中ε为误差控制阈值。遍历系统中的线路,重复步骤1-7就可以获取节点m的暂降域。
2.2 考虑暂降敏感区域的监测装置经济配置设系统总共n个节点,配置暂降监测装置的决策向量可以表示为:
| $ \boldsymbol{X}=\left[\begin{array}{llll} x_{1} & x_{2} & \cdots & x_{n} \end{array}\right] $ | (8) |
X是二进制向量,其元素按照式(9)取值:
| $ x_{i}= \begin{cases}1 & \text { 配置监测装置 } \\ 0 & \text { 不配置监测装置 }\end{cases} $ | (9) |
按照配置原则,以暂降全网可观构造约束条件,即须满足任意故障所引发的暂降能够至少被1台监测装置记录这一基本原则,如式(10)所示。
| $ \sum\limits_{i=1}^{n}\left(x_{i} m_{i j}\right) \geqslant 1 $ | (10) |
考虑实际应用中,监测装置费用高昂,配置应该以监测点数目最少为目标,如式(11)所示。
| $ \min f_{1}=\sum\limits_{i=1}^{n} x_{i} $ | (11) |
上述配置方法默认所有节点同等重要,此外寻优条件不足也导致配置方案并不唯一。暂降敏感区域内发生故障,对系统和用户造成的危害巨大。从提高系统运行安全可靠性的角度出发,可以认为暂降敏感区域更为重要,在暂降可观的基础上着重提高对暂降敏感区域的监测冗余性,有助于在短路导致暂降时及时采取相关治理措施,尽可能降低暂降带来的危害,提高系统运行的可靠性,节点重要性的划分也避免了配置的盲目性。暂降域能呈现系统中的暂降敏感区域,但暂降域是针对一个节点而言的概念,在电力系统实际运行过程中,设备必然分布于多个节点。基于此,文中提出如式(12)所示的风险域矩阵来进一步刻画系统中不同区域的暂降敏感程度。
| $ \boldsymbol{R}=\left[\begin{array}{cccc} r_{11} & r_{12} & \cdots & r_{1 l} \\ r_{21} & r_{22} & \cdots & r_{2 l} \\ \vdots & \vdots & & \vdots \\ r_{n 1} & r_{n 2} & \cdots & r_{n l} \end{array}\right] $ | (12) |
式中:下标l为系统线路总数。当矩阵任意元素rcd≠0时,其值为线路d被包含在所有节点暂降域中的总次数,且只有线路d在节点c的暂降域中时,rcd才不为0。若rcd>1,则表明线路d处于不止一个节点的暂降域中,且rcd值越大,对暂降越敏感。式(12)是单一故障类型下的风险域矩阵,为了综合考虑4种故障类型,须作如下修正:
| $ \boldsymbol{R}=\lambda_{1} \boldsymbol{R}_{1}+\lambda_{2} \boldsymbol{R}_{2}+\lambda_{3} \boldsymbol{R}_{3}+\lambda_{4} \boldsymbol{R}_{4} $ | (13) |
式中:R1,R2,R3,R4分别为三相短路、单相短路、两相短路和两相接地短路时的风险域矩阵; λ1,λ2,λ3,λ4分别为4种故障发生的概率,取值为0.7,0.15,0.1,0.05[21]。以式(11)为一级目标,利用式(13)所示的风险域矩阵,以监测装置覆盖更广、更敏感的薄弱环节为二级目标,如式(14)所示。
| $ \max f_{2}=\sum\limits_{i=1}^{n}\left(x_{i} r_{i p}\right) \quad p=1,2, \cdots, l $ | (14) |
为了便于求解,需要根据2个目标函数的实际特性进行变形。对式(11)引入优先因子α,则可以将2个目标转化为式(15)。
| $ \min f=\alpha \sum\limits_{i=1}^{n} x_{i}-\sum\limits_{i=1}^{n}\left(x_{i} r_{i p}\right) \quad p=1,2, \cdots, l $ | (15) |
为了确定α的值,对式(14)作灵敏性分析。设暂降监测装置数目变动一个,即:
| $ \Delta \sum\limits_{i=1}^{n} x_{i}=1 $ | (16) |
则二级目标变化量为:
| $ \Delta f_{2}=\Delta \sum\limits_{i=1}^{n}\left(x_{i} r_{i p}\right) \in[0, n l] $ | (17) |
因此式(15)的改变量为:
| $ \Delta f=\alpha \Delta \sum\limits_{i=1}^{n} x_{i}-\Delta \sum\limits_{i=1}^{n}\left(x_{i} r_{i p}\right)=\alpha-\beta $ | (18) |
其中β∈[0, nl],要保证一级目标先于二级目标被满足,则须满足α> >β即α> >nl,将二级目标除以nl,则优化配置模型可以表示为:
| $ \left\{\begin{array}{l} \min f=\alpha \sum\limits_{i=1}^{n} x_{i}-\frac{\sum\limits_{i=1}^{n}\left(x_{i} r_{i p}\right)}{n l} \quad \alpha \gg 1 \\ \text { s.t. } \sum\limits_{i=1}^{n}\left(x_{i} m_{i j}\right) \geqslant 1 \end{array}\right. $ | (19) |
PMU可广泛应用于电力系统的状态估计、暂态稳定分析与预测、故障定位、系统保护等诸多专业领域,具有十分重要的地位[22],因此国内在统一规划部署PMU方面作了大量工作。一方面,PMU能高频率、高分辨率地对节点电压向量、流经节点的支路电流采样[23],完全满足监测电压暂降的要求[17]; 另一方面,电压暂降监测装置同PMU一样,由于造价较高,短期内难以全面铺设。PMU铺设必要性高,理论上也能监测电压暂降,将电网已经安装的PMU装置用于辅助监测电压暂降,可以进一步降低暂降监测装置的安装成本。
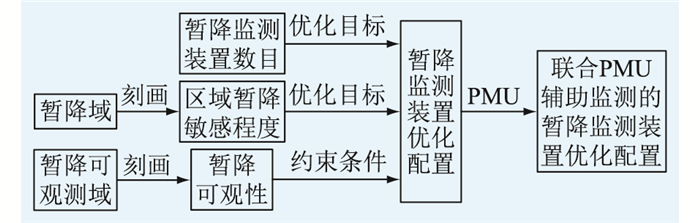
联合PMU的电压暂降监测装置优化配置的首要目标是保证安装的监测装置数目最少,其次是提高暂降敏感区域的监测冗余性。首先使用式(10)、式(11)所示的优化配置模型获取所有能保证暂降全网可观且监测装置数目最少的配置方案,然后判断现有PMU铺设节点是否出现在这些配置方案中。如果出现,则从包含PMU节点的配置方案中选出使式(14)最大的一组配置方案。如果没有出现,表明现有已安装的PMU用于辅助监测电压暂降时,由于暂降可观的约束将不能减少暂降监测装置的数目。但可通过改进式(19)所示的优化模型,并利用PMU辅助监测电压暂降得到对暂降敏感区域监测冗余性最高的暂降监测装置优化配置方案,改进后的优化配置模型如式(20)所示。
| $ \left\{\begin{array}{l} \min f=\alpha \sum\limits_{i=1, i \neq k}^{n} x_{i}-\frac{\sum\limits_{i=1, i \neq k}^{n}\left(x_{i} r_{i p}\right)}{n l}\ \ \alpha \gg 1 \\ \text { s.t. } x_{k} m_{k j}+\sum\limits_{i=1, i \neq k}^{n}\left(x_{i} m_{i j}\right) \geqslant 1 \end{array}\right. $ | (20) |
式中:xk为决策向量中的元素,k为安装了PMU的节点编号。模型构建逻辑如图 2所示。
|
图 2 配置模型构建逻辑 Fig. 2 Logic of optimization model construction |
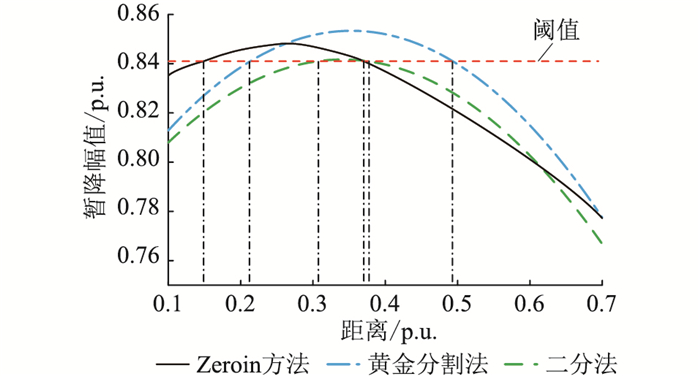
为了验证文中方法的可行性和有效性,在IEEE 30节点系统中进行测试,系统由37条线路连接30个节点组成。设20号节点处暂降阈值为0.841 p.u.,分别用黄金分割法[18]、二分法[19]及Zeroin方法获取线路l24的临界点,结果如图 3所示。
|
图 3 线路临界点计算结果对比 Fig. 3 Comparison of calculation results of line critical points |
图 3中2条虚线分别为黄金分割法和二分法使用二次插值拟合暂降幅值的结果,虚线与暂降阈值交点向横轴的投影代表线路中的临界点,图中实线为Zeroin方法计算得到的故障点随线路移动时的暂降幅值。线路中2个临界点的准确值为0.148 8和0.370 1,使用黄金分割法和二分法得到的解分别为0.213 2,0.493 4和0.305 6,0.376 1,文中使用Zeroin法迭代求解暂降幅值方程,由于没有拟合曲线,因此结果0.148 7,0.370 0与实际值的误差小,表明了该方法能够有效提高暂降域求解的准确性。
为了说明不同方法的计算效率,以节点2,4之间线路单相短路故障为例,计算临界点。设定收敛条件为ε=0.000 1,图 4为几种方法各自达到设定阈值所需要的迭代次数,其中的误差是不同方法迭代值与符合方法自身收敛条件的解的误差,不是如图 3所示的与真实值的误差。此外从图 4中可以看出,在计算速度上,Zeroin法也有较大优势。

|
图 4 不同方法迭代次数与误差的关系 Fig. 4 Comparison of the relationship between error and the number of iterations |
首先求解式(10)、式(11)所示的传统配置模型,得到实现0.9 p.u.暂降全网可观的配置方案,如表 1所示。在暂降全网可观的约束下,仅满足监测装置数目最少这一目标的方案并不唯一。为了利用文中所提多目标优化模型并获得最优配置方案,首先获取系统中所有节点的暂降域,然后统计线路出现在不同节点暂降域中的总次数,次数越高说明该线路越需要被重点监测。相关统计结果见表 2。此外,不同暂降域中线路包含情况见表 3。
|
|
表 1 传统方法得到的配置方案 Table 1 Combination plan obtained by traditional method |
|
|
表 2 线路在不同暂降域中出现的总次数 Table 2 Total times of lines appearing in different exposed areas |
|
|
表 3 不同暂降域中线路分布情况 Table 3 Distribution of lines in different exposed areas |
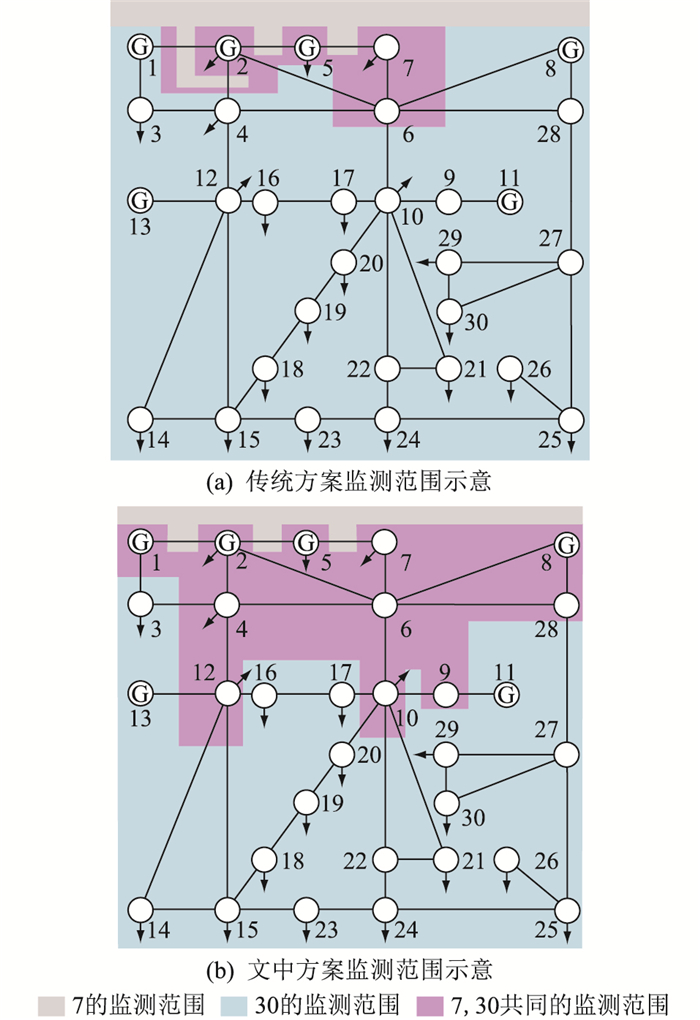
基于统计结果,利用式(12)形成风险域矩阵,进而利用式(19)所示的多目标优化模型解得最优方案为:在节点7,30各配置1台暂降监测装置。最后从传统方法解得的配置方案中随机选取1组方案,如5,26与文中方法所得方案7,30进行对比。基于表 2和表 3,统计得2种监测方案被监测装置覆盖的线路出现在系统各个暂降域内的总次数分别为573次和804次,说明文中方法能更多地监测到系统中对暂降敏感的线路。为了直观呈现出2种监测方案对暂降敏感区域的监测冗余性,通过暂降域计算结果绘制2种方案监测范围,如图 5所示。
|
图 5 2种方案监测范围对比示意 Fig. 5 Schematic diagram of comparison of the monitoring scope of the two programs |
图 5只列举了单相短路故障时的情形,其余故障下结果类似。由图 5可得,2种监测方案中不同监测装置监测范围的并集均能覆盖整个系统,表明2种方案均能实现暂降的全网可观,但从对敏感区域的监测能力来看,由于传统方案中2个监测装置共同覆盖的敏感区域范围更小,当单一监测装置故障时,剩余监测装置对敏感区域的监测能力与文中方案相比不足,表明文中方法能提高对暂降风险高的区域的监测可靠性。
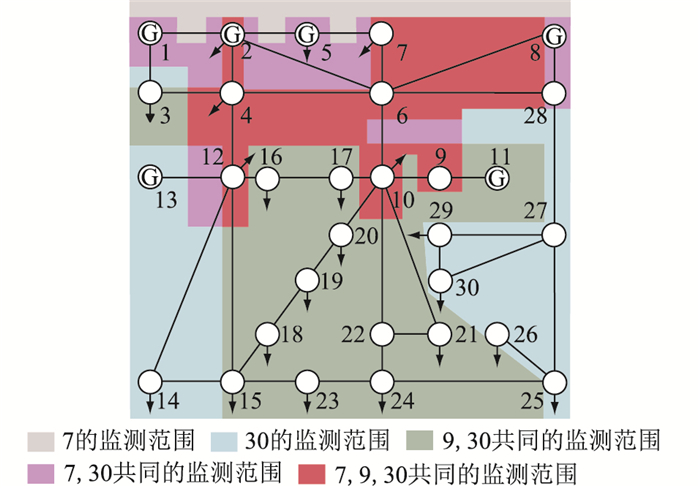
3.3 考虑PMU的暂降敏感区域监测冗余性分析假设9号节点安装了PMU,由于表 1所示的方案中不含该节点,因此暂降监测装置数目仍为2台。求解式(20)所示优化配置模型,得到监测装置铺设节点为7,30号。此时9号节点处的PMU辅助监测暂降联合监测下的监测范围如图 6所示。
|
图 6 PMU辅助监测暂降时的监测范围 Fig. 6 Monitoring of PMU auxiliary monitoring range during sag |
PMU辅助监测电压暂降时监测装置能覆盖的线路出现在系统不同暂降域中的总次数为1 188次,该方案对暂降敏感区域监测可靠性有进一步提高但并未增加暂降监测装置的数目。
4 结语文中基于暂降域的概念构建风险域矩阵,刻画出不同线路故障产生暂降对系统造成的危害程度,从而为不同区域划分重要性等级。这一划分原则也契合电力系统运行要保证安全可靠优质供电的基本要求,避免了传统方法在暂降监测装置的安装过程中认为所有节点同等重要导致的配置盲目性。求解系统暂降域时,利用Zeroin迭代将二分法的稳定性和抛物线法、割线法的快速收敛性相结合的优势,提高了求解速度,与拟合方法相比准确性有大幅提高。文中提出一种以提高暂降敏感区域监测冗余性为目标的满足暂降可观性和配置经济性的优化模型,解决了传统优化配置模型因多解难以唯一确定符合工程需求的方案这一问题。在此基础上提出将PMU与暂降监测装置联合优化配置,尽可能保证暂降监测装置数目最少,同时对系统中的暂降敏感区域的监测能力最大。
| [1] |
XU W, HUANG Z Y, XIE X R, et al. Synchronized waveforms- a frontier of data-based power system and apparatus monitoring, protection, and control[J]. IEEE Transactions on Power Delivery, 2021, 37(1): 3-17. (  0) 0) |
| [2] |
ANSAL V. ALO-optimized artificial neural network-controlled dynamic voltage restorer for compensation of voltage issues in distribution system[J]. Soft Computing, 2020, 24(2): 1171-1184. DOI:10.1007/s00500-019-03952-1 (  0) 0) |
| [3] |
ZHENG Z C, QI L H, WANG H, et al. Recognition method of voltage sag causes based on Bi-LSTM[J]. IEEE Transactions on Electrical and Electronic Engineering, 2020, 15(3): 418-425. DOI:10.1002/tee.23070 (  0) 0) |
| [4] |
WANG Y, LUO H, XIAO X Y. Joint optimal planning of distributed generations and sensitive users considering voltage sag[J]. IEEE Transactions on Power Delivery, 2022, 37(1): 93-104. DOI:10.1109/TPWRD.2021.3053996 (  0) 0) |
| [5] |
HU W X, XIAO X Y, ZHENG Z X. Voltage sag/swell waveform analysis method based on multi-dimension characterisation[J]. IET Generation, Transmission & Distribution, 2020, 14(3): 486-493. (  0) 0) |
| [6] |
LIAO H, LIU Z, MILANOVIC J V, et al. Optimisation framework for development of cost-effective monitoring in distribution networks[J]. IET Generation, Transmission & Distribution, 2016, 10(1): 240-246. (  0) 0) |
| [7] |
ZHANG Y, LIN Y, SHAO Z. Multi-objective optimal placement of positioning monitoring points under the constraints of considerable voltage sag[J]. Transactions of the Chinese Society of Electrical Engineering, 2019, 34(11): 2375-2383. (  0) 0) |
| [8] |
ALMEIDA C, KAGAN N. Using genetic algorithms and fuzzy programming to monitor voltage sags and swells[J]. IEEE Intelligent Systems, 2011, 26(2): 46-53. DOI:10.1109/MIS.2011.2 (  0) 0) |
| [9] |
周超, 田立军. 基于粒子群优化算法的电压暂降监测点优化配置[J]. 电工技术学报, 2014, 29(4): 181-187. ZHOU Chao, TIAN Lijun. An optimum allocation method of voltage sag monitoring nodes based on particle swarm optimization algorithm[J]. Transactions of China Electrotechnical Society, 2014, 29(4): 181-187. DOI:10.3969/j.issn.1000-6753.2014.04.024 (  0) 0) |
| [10] |
WANG Y, HE H S, FU Q, et al. Optimized placement of voltage sag monitors considering distributed generation dominated grids and customer demands[J]. Frontiers in Energy Research, 2021, 9(1): 1-13. (  0) 0) |
| [11] |
JIANG H W, XU Y H, LIU Z T, et al. A BPSO-based method for optimal voltage sag monitor placement considering uncertainties of transition resistance[J]. IEEE Access, 2020, 8: 80382-80394. DOI:10.1109/ACCESS.2020.2990634 (  0) 0) |
| [12] |
IBRAHIM A A, MOHAMED A, SHAREEF H, et al. Optimal placement of voltage sag monitors based on monitor reach area and sag severity index[C]//2010 IEEE Student Conference on Research and Development. Kuala Lumpur, Malaysia. IEEE, 2010: 467-470.
(  0) 0) |
| [13] |
SIPOS M, KLAI Z, NYARKO E K, et al. Determining the optimal location and number of voltage dip monitoring devices using the binary bat algorithm[J]. Energies, 2021, 14(1): 255. DOI:10.3390/en14010255 (  0) 0) |
| [14] |
张嫣, 林涌艺, 邵振国. 电压暂降可观约束下的定位监测点多目标优化配置[J]. 电工技术学报, 2019, 34(11): 2375-2383. ZHANG Yan, LIN Yongyi, SHAO Zhenguo. Multi-objective optimal allocation of monitors for voltage sag location under observability constraint[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2375-2383. (  0) 0) |
| [15] |
罗珊珊, 孙浩天, 杜晓彤, 等. 考虑暂降定位及抗扰指数的监测点优化配置方法研究[J]. 电力电容器与无功补偿, 2019, 40(4): 119-125. LUO Shanshan, SUN Haotian, DU Xiaotong, et al. Study on optimal allocation method of monitoring point considering voltage-sag location and interference resistance index[J]. Power Capacitor & Reactive Power Compensation, 2019, 40(4): 119-125. (  0) 0) |
| [16] |
LIAO H L, MILANOVI J V, RODRIGUES M, et al. Voltage sag estimation in sparsely monitored power systems based on deep learning and system area mapping[J]. IEEE Transactions on Power Delivery, 2018, 33(6): 3162-3172. DOI:10.1109/TPWRD.2018.2865906 (  0) 0) |
| [17] |
田书欣, 李昆鹏, 魏书荣, 等. 基于同步相量测量装置的配电网安全态势感知方法[J]. 中国电机工程学报, 2021, 41(2): 617-632. TIAN Shuxin, LI Kunpeng, WEI Shurong, et al. Security situation awareness approach for distribution network based on synchronous phasor measurement unit[J]. Proceedings of the CSEE, 2021, 41(2): 617-632. (  0) 0) |
| [18] |
PARK C H, JANG G. Stochastic estimation of voltage sags in a large meshed network[J]. IEEE Transactions on Power Delivery, 2007, 22(3): 1655-1664. DOI:10.1109/TPWRD.2006.886795 (  0) 0) |
| [19] |
马明, 徐柏榆, 汪颖, 等. 一种基于临界点法的电压暂降域混合识别方法[J]. 供用电, 2019, 36(4): 50-55. MA Ming, XU Boyu, WANG Ying, et al. A voltage sag domain hybrid identification method based on critical-point method[J]. Distribution & Utilization, 2019, 36(4): 50-55. (  0) 0) |
| [20] |
KHALILI R, ABUR A. PMU-based decoupled state estimation for unsymmetrical power systems[J]. IEEE Transactions on Power Systems, 2021, 36(6): 5359-5368. DOI:10.1109/TPWRS.2021.3069738 (  0) 0) |
| [21] |
BUZO R F, BARRADAS H M, LEÃO F B. A new method for fault location in distribution networks based on voltage sag measurements[J]. IEEE Transactions on Power Delivery, 2021, 36(2): 651-662. DOI:10.1109/TPWRD.2020.2987892 (  0) 0) |
| [22] |
MOHAMMADI P, MEHRAEEN S, NAZARIPOUYA H. Sensitivity analysis-based optimal PMU placement for fault observ ability[J]. IET Generation, Transmission & Distribution, 2021, 15(4): 737-750. (  0) 0) |
| [23] |
MOHD Z, MOHD R. Identification of low-frequency oscillation modes using PMU based data-driven dynamic mode decomposition algorithm[J]. Ieee Access, 2021, 9: 49434-49447. DOI:10.1109/ACCESS.2021.3068227 (  0) 0) |
2. School of Electrical Engineering, Sichuan University, Chengdu 610065, China
 2022, Vol. 41
2022, Vol. 41


 刘海泳(1969),男,学士,高级工程师,从事输变配电运行技术管理相关工作(E-mail:
刘海泳(1969),男,学士,高级工程师,从事输变配电运行技术管理相关工作(E-mail: