文章编号: 2096-3203(2022)02-0224-10 中图分类号: TM614
2. 国网青海省电力公司经济技术研究院,青海 西宁 810008;
3. 国网青海省电力公司清洁能源发展研究院,青海 西宁 810008;
4. 南京工业大学电气工程与控制科学学院,江苏 南京 211816
随着全球能源的短缺、环境问题的日益凸显,可再生能源技术受到越来越多国家重视与青睐。预计到2030年,非化石能源占一次能源消费比重将达到25%左右,其中,风电、光伏发电总装机容量将超过12亿kW[1]。间歇和波动的风电、光伏出力通常难以匹配净负荷需求,会造成切负荷或弃风弃光等损失,甚至引发电网故障。因此,根据各地风光资源特点合理规划风电、光伏发电的装机配比容量以匹配负荷需求,对新能源的开发利用具有重要意义[2-4]。
风光新能源电站的理论功率数据可以明确反应电站对当地风光资源的利用能力,因此电站理论功率的准确计算至关重要。目前,风光新能源电站所采用的理论功率计算方法为气象数据外推法和样板机法[5-8]。气象数据外推法通常基于历史数据建立新能源电站出力与自然资源特征(风速、辐照度等)的关联模型,但往往会因忽略风向、光伏板积灰等因素而出现较大误差;样板机法为各类型机组(风电机组/光伏逆变器)选取一定数量不参与电站限电的样板机,利用其实测出力线性外推同类型非样板机的出力,从而求得新能源电站的理论输出功率。样板机法较气象数据外推法计算更简单方便,但未考虑样板机在运行期间出现异常的情况以及非样板机与样板机之间的实际发电差异,算得的理论功率尚有改进空间。
针对风光容量配比优化问题,文献[9]建立了等效负荷峰谷差指标,通过风电、光伏出力模拟研究了不同风光容量配比对该指标的影响,并得到了使等效负荷峰谷差变化最小的风光容量配比;文献[10]基于新能源出力数据分析某地区电网风电、光伏出力特性,并用Spearman秩相关系数研究2种波动性能源出力的互补特性及其合理容量配比;文献[11]基于天气预报数据,构建了基于核主成分分析和自组织特征映射神经网络的天气类型划分模型,从波动性和爬坡性2个角度定量分析了不同天气类型下风光出力互补程度,确定了风光最佳并网容量比例。相关文献较少考虑理论功率计算的改进问题,且未考虑新能源电站出力与净负荷需求不匹配所带来的风险。
为了准确计算风光新能源电站的理论功率,文中对样板机法进行改进,通过样板机和非样板机的实测出力值动态评估二者间的发电性能差异,进而计算新能源电站的理论功率。同时为了得到地区合理的风光容量配比,文中利用改进样板机法得到更准确的新能源电站历史理论功率,挖掘风光电站出力特性,提出了面向降低源荷不匹配风险的风光容量配比优化方法,从而可为地区电网风光发电容量配置提供参照。
1 异常数据的识别及重构为保证文中所用数据的准确可靠,须进行数据预处理[12-16],包括对新能源电站的实测功率进行异常数据识别及剔除,并对缺失的数据进行重构。
1.1 异常数据识别数据异常主要由数据采集或通信设备发生故障造成,体现为数据缺失、数据越限、数值不刷新、数据畸变。数据缺失、越限和不刷新,可根据数据特征直接进行识别及剔除,而对于数据在正常范围内与实际值偏差较大的畸变数据,由于位置邻近的同类机组的实测功率具有空间相关性[17],可利用与待校验机组邻近的同类机组的实测功率来识别。
对所有机组的实测功率进行归一化处理:
| $ P_{m}^{*}=\frac{P_{m}-P_{\min }}{P_{\max }-P_{\min }} $ | (1) |
式中:Pm,Pm*分别为第m个采样点的实测功率值和归一化值;Pmax,Pmin分别为统计时段内实测功率最大、最小值。
在统计时段内,假设待校验的第i个机组Ti归一化后的实测功率为Pi*={Pi, 1*, Pi, 2*, …, Pi, n*}(n为该时段内采样点个数),与Ti邻近的第j(j≤N, N为与Ti邻近的同类机组总个数)个同类机组Tj归一化后的实测功率为Pj*={Pj, 1*, Pj, 2*, …, Pj, n*},则Pi*和Pj*的差值序列Ei-j为{|Pi, 1*-Pj, 1*|, |Pi, 2*-Pj, 2*|, …, |Pi, n*-Pj, n*|},计算可得Ti与所有位置邻近的同类机组归一化后实测功率的差值序列集{Ei-j|j=1, 2, …, N}。由式(2)可得差值序列集在每个采样点的平均值em,记平均值序列{e1, e2, …, en}中所有元素的均值为e,由式(3)可得平均值序列的标准差σ。
| $ \bar{e}_{m}=\frac{1}{N} \sum\limits_{j=1}^{N}\left|P_{i, m}^{*}-P_{j, m}^{*}\right| \quad m=1,2, \cdots, n $ | (2) |
| $ \sigma=\sqrt{\sum\limits_{m=1}^{n}\left(\bar{e}_{m}-\bar{e}\right)^{2} /(n-1)} $ | (3) |
式中:Pi, m*,Pj, m*分别为Ti和Tj在第m个采样点归一化后的实测功率值。
根据莱以特准则[18],若em-e>3σ成立,则认为Ti在第m个采样点的实测功率为畸变数据。特别说明的是,文中因限电和故障检修等异常工况产生的数据不属于上述异常数据类型,需要根据电站限电和故障检修记录予以识别并对其相应时间段的实测出力数据进行标定及保留。
1.2 缺失数据重构对剔除异常数据引起的单点数据缺失,利用缺失部分前后数据的均值对其进行重构。
对剔除异常数据所引起的多点数据缺失,采用自回归滑动平均(auto regressive moving average, ARMA)模型进行重构。采用ARMA对新能源电站/机组完好的历史实测功率数据进行预测,若第p步预测误差Ep小于预设阈值ε0,则预测结果可信。对大量历史实测功率数据进行A次预测,根据式(4)可计算第p步预测结果的平均可接受率γp。
| $ \gamma_{p}=\frac{C\left(\left|E_{p}\right|<\varepsilon_{0}\right)}{A} $ | (4) |
式中:C(·)为次数统计;A为ARMA模型预测的总次数。
对新能源电站/机组实测功率缺失数据时段[c, d],利用ARMA进行双向预测,预测结果为
| $ P_{l}=\frac{\gamma_{l-c+1} \vec{P}_{l}+\gamma_{d-l+1} \vec{P}_{l}}{\gamma_{l-c+1}+\gamma_{d-l+1}} $ | (5) |
按照此方法,可完成新能源电站/机组实测功率缺失数据时段[c, d]的数据重构。
2 基于改进样板机法的理论功率计算 2.1 基于气象特征的气象信息相似时段识别建立风电场天气特征向量:
| $ \boldsymbol{W}_{\mathrm{w}}=\left[\begin{array}{llll} w_{\mathrm{w} 1} & w_{\mathrm{w} 2} & w_{\mathrm{w} 3} & w_{\mathrm{w} 4} \end{array}\right] $ | (6) |
式中:ww1为风电场测风塔迎风面在所选时段内的平均风速;ww2,ww3,ww4分别为风电场在所选时段内的最高、最低、平均空气密度。
建立光伏电站天气特征向量:
| $ \boldsymbol{W}_{\mathrm{pv}}=\left[w_{\mathrm{pv} 1}\ w_{\mathrm{pv} 2}\ w_{\mathrm{pv} 3}\ w_{\mathrm{pv} 4}\right] $ | (7) |
式中:wpv1为光伏电站在所选时段内的天气类型,取1~4,含义参见文献[19];wpv2,wpv3,wpv4分别为光伏电站在所选时段内的最高、最低和平均温度。
根据新能源电站的气象特征识别运行过程中的气象信息相似时段。设新能源电站第x,y个时段的天气特征向量分别为Wx与Wy,根据式(8)计算两者的Pearson相关系数R(Wx, Wy)。若R(Wx, Wy)大于预设阈值α,则第x,y个时段互为气象信息相似时段。用相同方法分别找出统计时间内气象信息相似的所有时段。
| $ \begin{aligned} &R\left(\boldsymbol{W}_{x}, \boldsymbol{W}_{y}\right)=\\ &\frac{\sum\limits_{z=1}^{4}\left[\left(w_{x, z}-w_{x, \text { ave }}\right)\left(w_{y, z}-w_{y, \mathrm{ave}}\right)\right]}{\sqrt{\sum\limits_{z=1}^{4}\left(w_{x, z}-w_{x, \text { ave }}\right)^{2} \sum\limits_{z=1}^{4}\left(w_{y, z}-w_{y, \mathrm{ave}}\right)^{2}}} \end{aligned} $ | (8) |
式中:wx, ave,wy, ave分别为Wx和Wy中元素的算术平均;wx, z,wy, z分别为Wx和Wy中的第z个元素。
2.2 基于时空相关性的样板机异常识别及处理实际运行中,新能源电站中的样板机会因为恶劣天气、自身老化等发生运行故障,继而影响后续的理论功率计算精度,所以需要对发生异常的样板机及时进行识别及更换。由于在气象信息相似的时段内,新能源电站中机组自身出力往往具有相同趋势,呈现时间相关性;而同一电站中机组间的地理位置较近,其风光资源特性较为一致,机组间出力通常也具有相同趋势,呈现空间相关性。因此文中基于站内样板机出力的时空相关性来识别异常样板机,步骤如下。
步骤1:根据2.1节所提方法识别得到评估时间内新能源电站共I个气象信息相似时段(若未搜索到相似时段,则I=1),设新能源电站内k型号机组的样板机数量为Mk,第b台样板机在第v个气象信息相似时段的实测功率序列为Pbvs={Pbvs, 1, Pbvs, 2, …, Pbvs, n},n为该时段的采样点个数。
步骤2:对Mk×I个实测功率序列进行K-means聚类[20],得到K个实测功率序列簇类,并由式(9)可得每个簇类的聚类中心Ch。
| $ C_{h}=\frac{1}{N\left(\varphi_{h}\right)} \sum\limits_{X_{\tau} \in \varphi_{h}} X_{\tau} $ | (9) |
式中:φh为第h个实测功率序列簇类(h=1, 2, …, K);N(φh)为φh中实测功率序列的个数;Xτ为φh中的第τ个实测功率序列。
步骤3:计算Pbvs与其所属聚类中心Ch的欧式距离,若距离大于预设阈值δ,则判断第b台样板机的第v个气象信息相似时段发生异常,将该时段定义为异常时段,否则判断其为正常时段。按此方法依次遍历新能源电站每台样板机各时段,得到各样板机的异常时段。
步骤4:针对各样板机的异常时段,依次将异常样板机剔除,并将其归为非样板机。判断样板机数量是否满足要求,若满足则更新样板机数量;若样板机数量不满足理论功率计算需求,则从非样板机中选择机组实测功率离聚类中心最近的若干机组作为候选样板机,增补进样板机集合。
2.3 非样板机出力系数的动态识别 2.3.1 动态信息窗的设置为实时跟踪非样板机与样板机出力的关系,需要设置动态信息窗以获取同型号下每台非样板机的出力情况。当非样板机在计算时刻t之前的时段[t-φ, t]发生限电、故障或检修等情况时,需要调整t时刻信息窗的选取位置,以避免按照异常情况获取非样板机出力信息而使理论功率计算不准。
设新能源电站内k型号机组共有B台非样板机,其中第q台非样板机为Tq(q=1, 2, …, B)。选取新能源电站理论功率计算时刻t之前的时段[t-φ, t],根据该时段内Tq实际运行情况来确定动态信息窗的选取。
(1) 当Tq在[t-φ, t]内正常运行时,则选取[t-φ, t)作为Tq在t时刻的信息窗,并随理论功率的计算时刻动态调整。
(2) 当Tq在[t-φ, t]内为限电、故障或检修状态时,选择该时段内新能源电站的天气特征向量W0作为t时刻理论功率计算的基准天气特征向量。根据新能源电站限电、故障检修记录寻找距离t时刻前D天(如取30 d)内Tq正常运行的时段集合,剔除长度小于φ的时段,并将满足条件的时间段划分成Q个长度为φ的时段。然后,提取新能源电站第g个时段的天气特征向量Wg(g=1, 2, …, Q),根据式(8)计算相关系数R(W0, Wg),依次计算形成相关系数集{R(W0, W1), R(W0, W2), …, R(W0, WQ)},取其中最大元素对应的正常运行时段作为Tq在t时刻的信息窗,并随理论功率计算时刻的变化而动态调整。在机组长期退出运行的特殊情况下,可适当放宽历史气象特征的时间搜索范围。
2.3.2 非样板机分组及出力系数的动态识别设k型号机组下第q台非样板机Tq在信息窗内经过数据预处理后的实测功率为Pqk={Pqk, 1, Pqk, 2, …, Pqk, n},所有样板机的平均实测功率为Pks={Pks,1, Pks,2, …, Pks, n},则Pqk和Pks在信息窗内功率差率的平均值为:
| $ \begin{gathered} \bar{R}_{k q \mathrm{s}}= \\ \frac{\left(P_{q k, 1}-\bar{P}_{k \mathrm{s}, 1}\right)+\left(P_{q k, 2}-\bar{P}_{k \mathrm{s}, 2}\right)+\cdots+\left(P_{q k, n}-\bar{P}_{k \mathrm{s}, n}\right)}{n P_{k \mathrm{N}}} \end{gathered} $ | (10) |
式中:n为信息窗内的采样点个数;PkN为k型号机组的额定功率;Rkqs∈[-1, 1]。
根据计算得到的Rkqs对非样板机Tq进行分组,设单位区间长度为u,当u=0.05时,若Rkqs∈[0.05×(a-21), 0.05(a-20)),则非样板机Tq被划分到第a组(a=1, 2, …, 40)。按照上述方法对k型号机组的每台非样板机进行分组,可得t时刻第a组内的非样板机数量Hak(t)。
k型号第a组内所有非样板机组相对于样板机组出力的比例系数可取λak=0.05a-0.05。理想情况下,当新能源电站内所有机组理论出力都相等时,Rkqs=0,此时a=21,非样板机组相对于样板机出力的比例系数均为1,该电站的理论功率计算公式与目前所采用的较为理想的计算公式相同。
2.4 新能源电站理论功率计算利用样板机的实测功率,可得到新能源电站在t时刻改进后的理论功率计算模型:
| $ P_{k \mathrm{th}}(t)=\bar{P}_{k \mathrm{s}}(t) M_{k}+\sum\limits_{a=1}^{40}\left(\bar{P}_{k \mathrm{s}}(t) \lambda_{a k} H_{a k}(t)\right) $ | (11) |
| $ P_{\mathrm{th}}(t)=\sum\limits_{k=1}^{M} P_{k \mathrm{th}}(t) $ | (12) |
式中:Pks(t)为t时刻k型号机组所有样板机的平均实测功率;Pkth(t)为t时刻新能源电站所有k型号机组的理论功率之和;Pth(t)为t时刻新能源电站所有机组的理论功率之和;M为机组型号数量。
3 考虑源荷不匹配风险的风光容量配比优化不合理的风光容量配比会导致风光出力与负荷不匹配,从而产生弃风弃光或切负荷等现象,造成经济损失,甚至引发电网故障。风光电站发电能力评估的不准确性、出力的不确定性均会使风光不合理匹配的损失评估存在较大误差,从而在面向风光容量配比这一长周期规划问题时分配不合理。文中在第2章的基础上,利用蒙特卡洛法对风光电站出力进行长周期模拟抽样,并计算每一确定的抽样场景下因产生弃风弃光或切负荷现象造成的经济损失。某场景的源荷不匹配风险即为风光电站出力场景发生概率与该场景下经济损失的积。
3.1 风光容量配比优化模型风光容量配比优化目标为最小化长周期源荷不匹配风险R:
| $ \min R=\sum\limits_{f=1}^{F} \sum\limits_{t=1}^{T}\left(p_{f}\left|P_{f}(t)-P_{\mathrm{L}}(t)\right| C_{\mathrm{epun}}(t)\right) $ | (13) |
| $ P_{f}(t)=P_{\mathrm{N}}\left[\lambda P_{f \mathrm{w}}^{*}(t)+(1-\lambda) P_{f \mathrm{pv}}^{*}(t)\right] $ | (14) |
式中:pf为第f个风光电站出力场景发生的概率;F为风光电站出力场景个数;T为时间周期;Pf(t)为t时刻第f个风光电站出力场景下的理论功率之和;PL(t)为t时刻的负荷;Cepun(t)为t时刻弃风弃光或切负荷对应的单位功率经济损失;PN
为风光电站总装机容量;λ为风电站装机容量占风光电站总装机容量的比例(0<λ<1);Pfw*(t),Pfpv*(t)分别为t时刻第f个风电站、光伏电站出力场景下的理论功率归一化值。
3.2 基于理论功率的新能源电站随机出力场景生成在进行新能源电站随机出力场景生成时,若不考虑新能源电站自身出力的时间相关性,则会导致模拟的出力波动特性与实际情况不符。为生成风光电站随机出力场景,文中建立了新能源电站长周期出力场景生成方法,具体过程如下:
(1) 生成平均波动序列。在确定的时间颗粒度(5 min)下,计算多年理论功率波动量并取各时刻平均值,得到平均波动序列{μt|t=1, 2, …, T-1}。
(2) 生成新能源电站初始出力场景集。通过对新能源电站多年理论功率的统计可得新能源电站在各时刻出力区间的概率分布,并利用蒙特卡洛法模拟得到新能源电站初始出力场景集Ω:
| $ \boldsymbol{\varOmega}=\left[\begin{array}{ccccc} P_{1,1} & \cdots & P_{1, t} & \cdots & P_{1, T} \\ P_{2,1} & \cdots & P_{2, t} & \cdots & P_{2, T} \\ P_{3,1} & \cdots & P_{3, t} & \cdots & P_{3, T} \\ \vdots & & \vdots & & \vdots \\ P_{f, 1} & \cdots & P_{f, t} & \cdots & P_{f, T} \end{array}\right] $ | (15) |
式中:Pf, t为t时刻第f个出力场景下的新能源电站出力值。行向量表示新能源电站在时间周期T内随机抽样生成的一个出力场景;列向量表示同一时刻不同场景下新能源电站的出力。Ω反映了新能源电站在各时刻出力区间的概率分布,但无法满足新能源电站自身出力的时间相关性,因此需要对Ω中各行向量的数据进行重构。
(3) 重构初始出力场景集的数据。结合平均波动序列中该时刻的平均波动量μt,从t+1时刻新能源电站出力集[P1, t+1 P2, t+1 … Pf, t+1]T中选出最接近Pf, t+μt的数值Pk, t+1(k≤f),作为该出力场景下t+1时刻的出力值,按上述方法依次确定各时刻的出力值。遍历初始出力场景集Ω,得到重构后的新能源电站出力场景集Ω′。重构后的Ω′既满足新能源电站在各时刻出力区间的概率分布,也能较为准确地反映新能源电站出力的时间相关性。分别对风光电站按此方法模拟生成出力场景,从而得到风光电站出力场景集。
3.3 极端场景筛选为避免小概率高风险场景对风光容量配比规划的影响,需要对极端场景进行筛选,再进行风光容量最优配比的计算,具体步骤如下。
步骤1:根据风光电站出力场景集,结合式(13)和式(14)计算得到使源荷不匹配风险最小的风电装机占比λ。
步骤2:根据步骤1得到的λ值依次计算各个出力场景对应的源荷不匹配风险。若所有场景对应的源荷不匹配风险值均小于给定的风险阈值ξ,则将风电装机占比λ确定为风电最优装机占比,进而得到风光容量最优配比;若存在某些出力场景的源荷不匹配风险值大于ξ,则将这些场景识别为极端场景并进行剔除,更新风光电站出力场景集,并返回步骤1。
为了提高计算效率,可对模拟生成的场景进行聚类,以较小数目的场景代替原始繁多的场景,每种聚类场景中场景个数之和与模拟生成的场景总数的比值即为该聚类场景的概率。
4 算例与分析为验证文中方法的有效性,以含100台风电机组的风电场为例进行分析,单台容量为1.5 MW,总装机容量为150 MW。设风电机组共有3个型号,各型号机组沿风向排列,其信息见表 1。
|
|
表 1 机组参数信息 Table 1 Parameter information of wind turbines |
根据中国西北地区春季的风速及空气密度变化规律,同时计及风电场内风速分布的空间相关性[21]和风速变化的时间相关性[22](忽略风向变化的影响),模拟得到各风电机组轮毂处风速、测风塔迎风面风速和风电场空气密度(三者皆为5 min一个值)[23-29],并根据风速-功率关系计算得到各型号风电机组的模拟理论功率[26, 30],全场叠加可得风电场的模拟理论功率。为得到较为符合风电场实际运行特性的风电机组模拟出力,须进一步构造计及风电数据通信故障和局部运行等情况的异常数据场景,并人工设定一定比例的带限电和故障检修标签位的风电机组运行数据,最终构造出风电机组的实测功率数据。
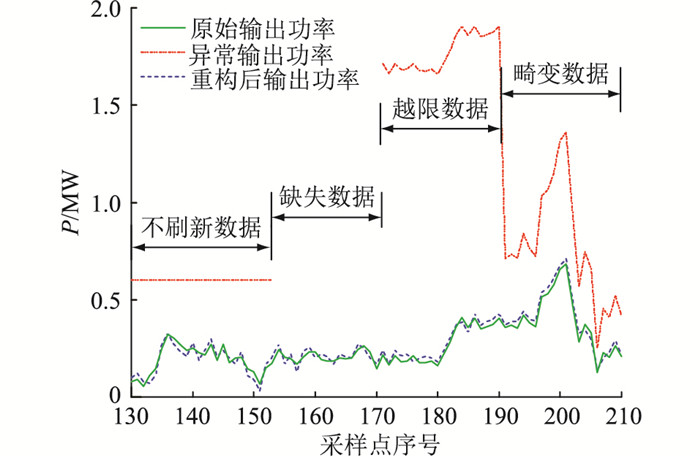
实测功率数据的可靠与完整是后续理论功率计算的基础,因此有必要对上述风电场中所有机组的实测功率数据进行异常识别及重构。分别构造风电机组在某日原始输出功率中出现缺失、越限、不刷新和畸变的异常数据情况,并采用文中所提方法对上述异常数据进行识别及重构,结果如图 1所示。经计算,异常输出功率和重构后输出功率相对于原始输出功率的均方根误差(root mean square error, RMSE)ERMSE分别为0.45 MW, 0.27 MW,异常数据情况得到了较好处理。
|
图 1 风电机组出力的异常识别及重构结果 Fig. 1 Abnormal identification and reconstruction result of wind turbine output |
在对上述风电场中所有机组的实测功率数据采用1.1节和1.2节所提方法进行异常数据识别、剔除及缺失数据重构后,通过2.2节所提方法识别异常样板机,将其从样板机集合中剔除,并用其他性能好的机组替补,进一步根据所提出的改进样板机法对风电场的理论功率进行计算并讨论了相关参数设置对理论功率计算精度的影响。
4.1 理论功率计算方法对比及讨论算例 4.1.1 改进样板机法和样板机法对比文中选取西北地区春季某3 d不同风速(风速1~3)下风电场经数据预处理后的实测功率数据(5 min一个采样点,1 d共288个点),风速1~3的平均风速分别为9.06 m/s, 11.17 m/s和15.07 m/s。采用改进样板机法和样板机法分别计算风电场在风速1~3下当日的理论功率。改进样板机法在计算理论功率时已对出现异常的样板机进行处理并选取长度为50 min的动态信息窗,即在计算t时刻的理论功率时会选取[t-50, t)时段作为信息窗,且信息窗随t时刻变化而动态变化,单位区间长度u取0.05,结果见图 2。风速1~3理论功率计算的误差统计见表 2,所涉及指标为平均绝对百分比误差(mean absolute percentage error, MAPE)EMAPE、ERMSE和最大绝对误差(mean absolute error, MAE)EMAE。
|
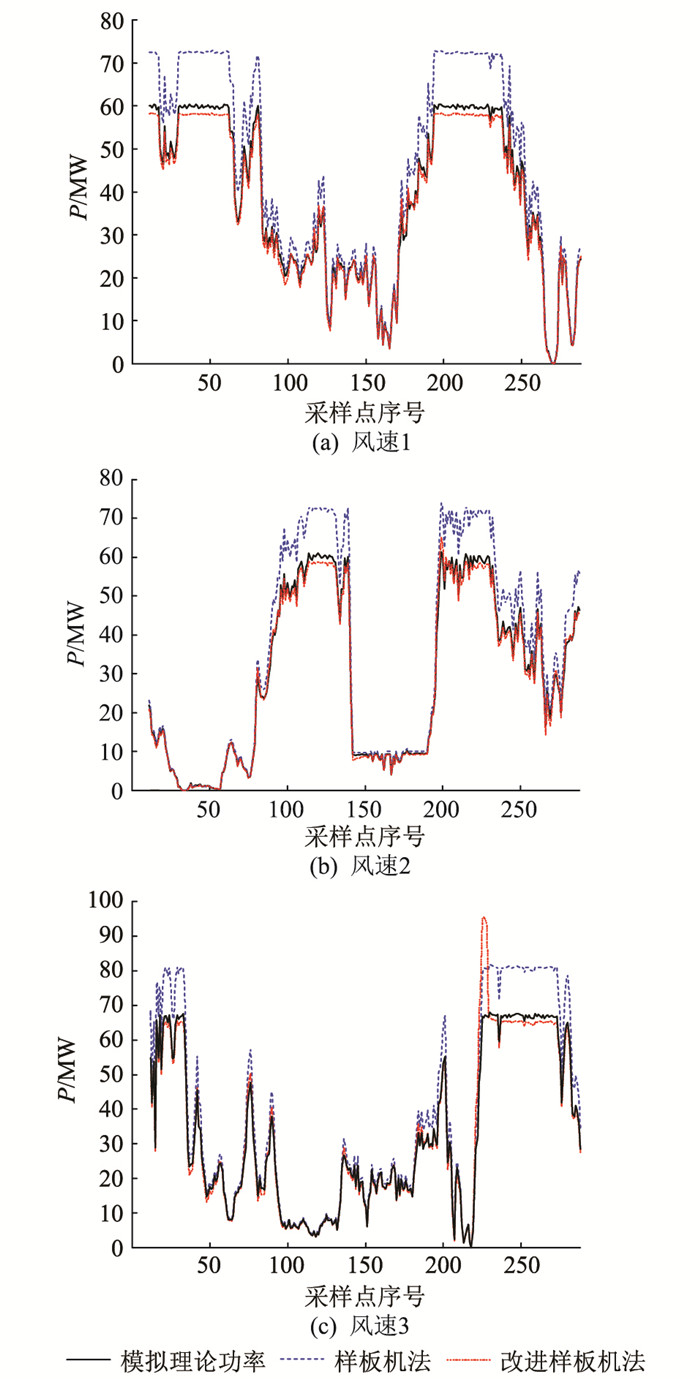
图 2 不同风速下理论功率的计算 Fig. 2 Calculation of theoretical power under different wind speeds |
|
|
表 2 不同风速下理论功率计算误差统计 Table 2 Calculation error statistics of theoretical power under different wind speeds |
结合图 2和表 2可知,在风速1~3下采用改进样板机法得到的各项误差统计指标整体上优于样板机法,理论功率曲线与模拟理论功率曲线较贴近。尤其是在大风时段,由改进样板机法计算得到的理论功率较样板机法更准确,但会在某些时刻与模拟理论功率偏差较大,如风速3第226个采样点时刻。对于此类问题,文中在4.1.2节进行分析。
4.1.2 不同动态信息窗长度的对比分析以4.1.1节中风速1当日为观察日,在采样频率相同的情况下,研究动态信息窗长度对改进样板机法理论功率计算精度的影响。分别选取长度为5 min, 25 min, 50 min, 100 min和250 min的动态信息窗计算风电场观察日全天的理论功率,并进行对比分析。其中,单位区间长度u均为0.05。根据不同动态信息窗长度计算得到风电场观察日全天的理论功率及误差,结果如图 3、表 3所示。
|
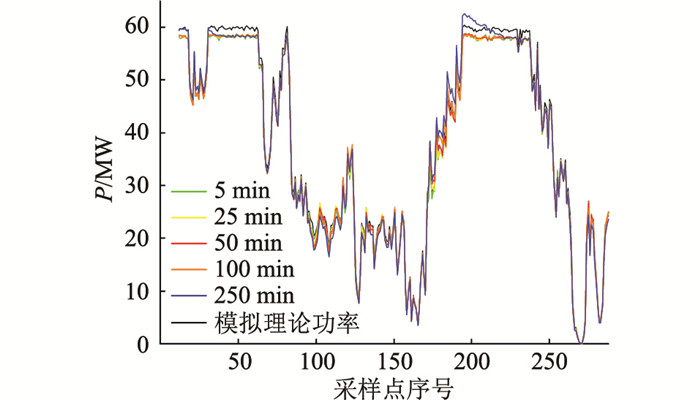
图 3 动态信息窗长度对理论功率计算的影响 Fig. 3 The influence of the length of dynamic infor-mation window on theoretical power calculation |
|
|
表 3 动态信息窗长度对理论功率计算误差的影响 Table 3 The influence of the length of dynamic information window on the calculation error of theoretical power |
结合图 3和表 3可以看出,随着动态信息窗长度缩短,得到的各项误差统计指标越优,计算的理论功率曲线也更贴近模拟理论功率曲线。这说明风电机组发电效率在不同风速下表现不同,而短时间内风速变化幅度较大时,若动态信息窗长度较大,则会将风速较宽范围下的风速-功率特征纳入统计,从而难以准确捕捉计算时刻风速下的风电机组效率特点,出现较大的理论功率计算误差。
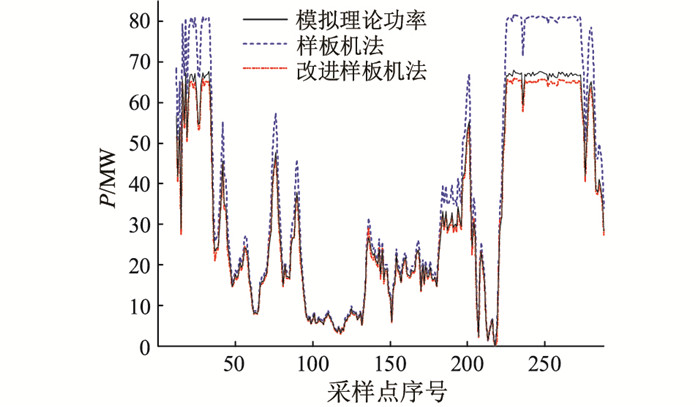
考虑到4.1.1节中某些时刻点理论功率与模拟理论功率偏差较大可能是由上述原因所致,因此设置改进样板机法的动态信息窗为5 min以及单位区间长度u为0.05,重新计算得到风速3当日全天的理论功率,结果如图 4所示。可以看出,当动态信息窗长度由50 min缩小为5 min时,风速3第226个采样点时刻的理论功率得到了改善。
|
图 4 风速3修改动态信息窗长度后理论功率的计算 Fig. 4 Calculation of theoretical power after modified the length of dynamic information window at wind speed 3 |
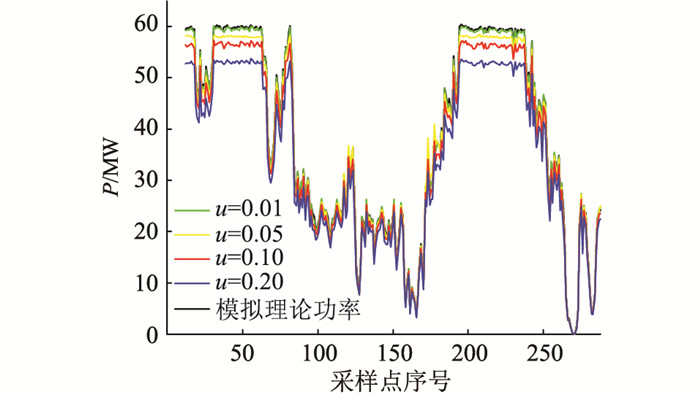
以4.1.1节中的风速1当日为观察日,选取动态信息窗长度为5 min,u分别为0.01, 0.05, 0.10和0.20,计算风电场观察日全天的理论功率,并进行对比分析。根据不同单位区间长度u计算得到风电场观察日全天的理论功率及误差,结果如图 5、表 4所示。
|
图 5 不同u对理论功率计算的影响 Fig. 5 The influence of different u on theoretical power calculation |
|
|
表 4 不同u对理论功率计算误差的影响 Table 4 The influence of different u on the calculation error of theoretical power |
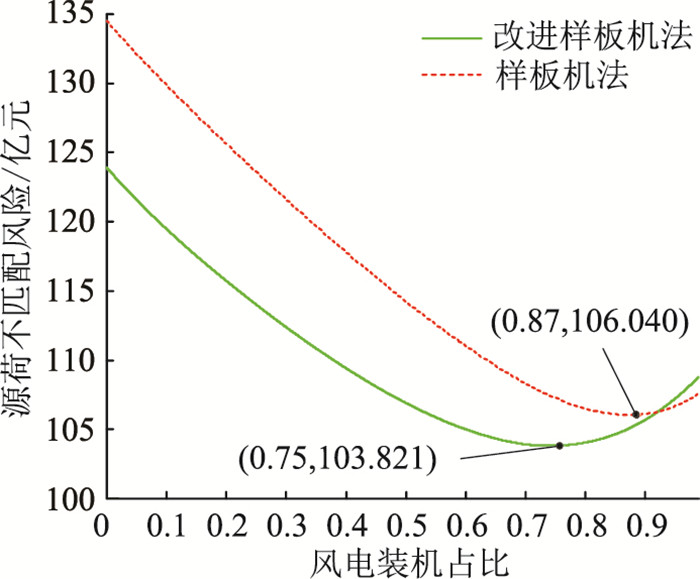
结合图 5和表 4可知,各项误差统计指标随着单位区间长度u的减小而不断改善,计算得到的理论功率曲线也更贴近模拟理论功率曲线。4.2风光容量优化配置文中分别通过样板机法和改进样板机法计算得到中国某地区电网风电场、光伏电站多年的理论功率数据,为了计及新能源电站装机容量的不断变化,对理论功率数据进行归一化处理,并根据第4章所提的场景生成方法生成若干个风光电站出力场景,此处显示其中1 000个。采用该地区2020年全年的负荷数据,截止2020年底该地区电网风光电站总装机容量为35 590.5 MW,Cepun(t)可根据当地不同时刻的上网电价以及切负荷代价综合考虑得到。根据风光容量配比优化模型,分析不同风电装机占比对全年源荷不匹配风险的影响,结果如图 6所示。由图 6可知,理论功率计算的精度会影响到风光最优配比的结果,通过计算样板机法得到的理论功率可得该地区风光容量最优配比为1 ∶0.15,此时全年源荷不匹配风险最小,为106.040亿元;而通过计算改进样板机法得到的理论功率可得该地区风光容量最优配比为1 ∶0.33,此时全年源荷不匹配风险最小,为103.821亿元。
|
图 6 不同风光容量配比对源荷不匹配风险的影响 Fig. 6 The influence of different wind-solar capacity ratio on the risk of source-load mismatching |
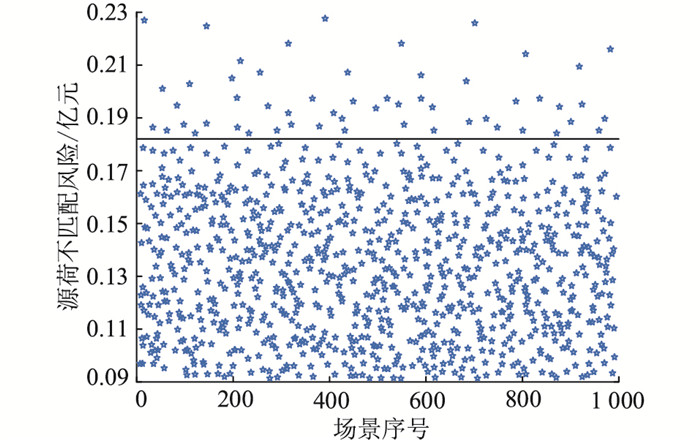
依次计算各出力场景对应的源荷不匹配风险,并依据风险阈值ξ迭代剔除极端场景,从生成的1 000个场景中得到54个源荷不匹配风险超出风险度阈值(如黑线所示)的场景,如图 7所示。
|
图 7 基于源荷不匹配风险的场景筛 Fig. 7 Scene screening based on the risk of source-load mismatching |
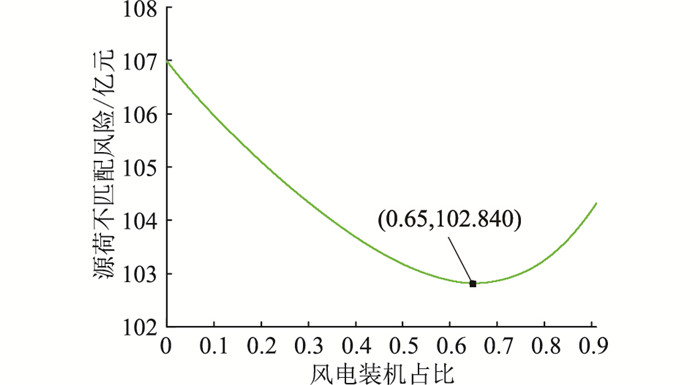
再使用风光容量配比优化方法对剩余的出力场景进行计算,最终得到剔除极端出力场景后R最小时的风光容量最优配比,其对源荷不匹配风险的影响如图 8所示。
|
图 8 剔除极端场景后不同风光容量配比对源荷不匹配风险的影响 Fig. 8 The influence of different wind-solar capacity ratioon the risk of source-load mismatching after excluding extreme scenes |
由图 8分析可知,剔除极端出力场景后,当风光容量最优配比为1 ∶0.54时,源荷不匹配风险最小为102.840亿元。结合图 6和图 8可知,在剔除极端出力场景后,风电最优装机占比减小,考虑其原因为该地区风资源较光资源好,更多风电容量的配置可以减少极端场景对源荷不匹配风险的影响。此结论受制于地区风光资源特性,不同地区的风光配置需要具体研究。
5 结语文中针对新能源电站理论功率计算问题展开研究,提出了基于改进样板机法的理论功率计算新方法。相较于传统的样板机法,由改进样板机法计算所得到的新能源电站的理论功率精度更高,且具有较强的工程适用性。文中利用改进样板机法得到更为准确的新能源电站理论功率,提出了面向降低源荷不匹配风险的风光容量配比优化方法,可为规划区域中风光装机容量的比例提供参考。
文中提出的源荷不匹配风险仅考虑了弃风弃光以及切负荷所带来的风险,如何将其他因素所带来的风险纳入评估模型,从而得到更加合理可信的风光容量最优配比,是下一步有待深入研究的重要问题。
本文得到国网青海省电力公司科技项目“基于清洁能源泛在调度控制的新能源发电性能精细化评估方法研究及应用”(522830190018),江苏省配电网智能技术与装备协同创新中心开放基金项目(No.XTCX202001)资助,谨此致谢!
| [1] |
习近平. 继往开来, 开启全球应对气候变化新征程[N]. 人民日报, 2020-12-13(2). XI Jinping. Building on past achievements and launching a new journey for global climate actions[N]. People's Daily, 2020-12-13(2). (  0) 0) |
| [2] |
姚天亮, 吴兴全, 李志伟, 等. 计及多约束条件的风光互补容量配比研究[J]. 电力系统保护与控制, 2017, 45(9): 126-132. YAO Tianliang, WU Xingquan, LI Zhiwei, et al. Research on complementary capacity ratio of wind power and photovoltaic considering multiple constraints[J]. Power System Protection and Control, 2017, 45(9): 126-132. (  0) 0) |
| [3] |
刘新苗, 卢洵, 娄源媛, 等. 基于时序运行模拟的风火打捆最优容量配比整定[J]. 电力系统保护与控制, 2021, 49(21): 53-62. LIU Xinmiao, LU Xun, LOU Yuanyuan, et al. Optimal setting of wind-thermal-bundled capacity ratio based on chronological operation simulation[J]. Power System Protection and Control, 2021, 49(21): 53-62. (  0) 0) |
| [4] |
王子琳, 鲁玺, 庄明浩, 等. 中国三北地区风—光互补发电系统空间优化研究[J]. 全球能源互联网, 2020, 3(1): 97-104. WANG Zilin, LU Xi, ZHUANG Minghao, et al. Spatial optimization of wind-PV hybrid energy systems for the three-north region in China[J]. Journal of Global Energy Interconnection, 2020, 3(1): 97-104. (  0) 0) |
| [5] |
刘永前, 邵振州, 王铮, 等. 基于分段支持向量机的风电机组理论功率计算研究[J]. 太阳能学报, 2019, 40(3): 673-680. LIU Yongqian, SHAO Zhenzhou, WANG Zheng, et al. Piecewise support vector machine model for theoretical wind-power calculation[J]. Acta Energiae Solaris Sinica, 2019, 40(3): 673-680. (  0) 0) |
| [6] |
郭海思, 何慧, 包大恩. 风电机组理论发电功率计算及对比优化[J]. 电力与能源, 2019, 40(3): 339-343. GUO Haisi, HE Hui, BAO Daen. Theoretical power calculation and comparative optimization of wind turbines[J]. Power & Energy, 2019, 40(3): 339-343. (  0) 0) |
| [7] |
丁坤, 吕清泉, 蔡旭, 等. 采用样板机法计算风电场弃风电量的实测数据统计分析[J]. 可再生能源, 2016, 34(1): 56-63. DING Kun, LYU Qingquan, CAI Xu, et al. Statistical analysis of measured data for calculation of curtailed wind power using modal machine method[J]. Renewable Energy Resources, 2016, 34(1): 56-63. (  0) 0) |
| [8] |
ZOU P, CHEN Q X, YU Y, et al. Electricity markets evolution with the changing generation mix: an empirical analysis based on China 2050 high renewable energy penetration roadmap[J]. Applied Energy, 2017, 185: 56-67. DOI:10.1016/j.apenergy.2016.10.061 (  0) 0) |
| [9] |
孙川永, 魏磊, 贾宏刚, 等. 新能源开发中风电、光伏理论装机比例的探讨[J]. 电网与清洁能源, 2014, 30(6): 24-27, 32. SUN Chuanyong, WEI Lei, JIA Honggang, et al. Discussions on the theoretical installed proportion of wind power and photovoltaic power in new energy development[J]. Power System and Clean Energy, 2014, 30(6): 24-27, 32. DOI:10.3969/j.issn.1674-3814.2014.06.006 (  0) 0) |
| [10] |
吕盼, 徐龙秀, 周专, 等. 基于风光出力相关性的新能源容量配比研究[J]. 通信电源技术, 2016, 33(2): 1-3. LYU Pan, XU Longxiu, ZHOU Zhuan, et al. Study on the proportion of new energy capacity based on wind power and photovoltaic power correlation analysis[J]. Telecom Power Technology, 2016, 33(2): 1-3. (  0) 0) |
| [11] |
乔延辉, 韩爽, 许彦平, 等. 基于天气分型的风光出力互补性分析方法[J]. 电力系统自动化, 2021, 45(2): 82-88. QIAO Yanhui, HAN Shuang, XU Yanping, et al. Analysis method for complementarity between wind and photovoltaic power outputs based on weather classification[J]. Automation of Electric Power Systems, 2021, 45(2): 82-88. (  0) 0) |
| [12] |
龚莺飞, 鲁宗相, 乔颖, 等. 基于Copula理论的光伏功率高比例异常数据机器识别算法[J]. 电力系统自动化, 2016, 40(9): 16-22, 55. GONG Yingfei, LU Zongxiang, QIAO Ying, et al. Copula theory based machine identification algorithm of high proportion of outliers in photovoltaic power data[J]. Automation of Electric Power Systems, 2016, 40(9): 16-22, 55. (  0) 0) |
| [13] |
左松林, 陈伟, 付真斌, 等. 基于EKF算法的分布式光伏发电异常数据排查技术[J]. 电力工程技术, 2020, 39(5): 120-125. ZUO Songlin, CHEN Wei, FU Zhenbin, et al. Abnormal data inspection technology of photovoltaic power generation based on EKF algorithm[J]. Electric Power Engineering Technology, 2020, 39(5): 120-125. (  0) 0) |
| [14] |
WANG J Z, WANG Y, LI Z W, et al. A combined framework based on data preprocessing, neural networks and multi-tracker optimizer for wind speed prediction[J]. Sustainable Energy Technologies and Assessments, 2020, 40: 100757. DOI:10.1016/j.seta.2020.100757 (  0) 0) |
| [15] |
BO H, NIE Y, WANG J Z. Electric load forecasting use a novelty hybrid model on the basic of data preprocessing technique and multi-objective optimization algorithm[J]. IEEE Access, 2020, 8: 13858-13874. DOI:10.1109/ACCESS.2020.2966641 (  0) 0) |
| [16] |
时珉, 尹瑞, 胡傲宇, 等. 基于滑动标准差计算的光伏阵列异常数据清洗办法[J]. 电力系统保护与控制, 2020, 48(6): 108-114. SHI Min, YIN Rui, HU Aoyu, et al. A novel photovoltaic array outlier cleaning algorithm based on moving standard deviation[J]. Power System Protection and Control, 2020, 48(6): 108-114. (  0) 0) |
| [17] |
LUKASSEN L J, STEVENS R J A M, MENEVEAU C, et al. Modeling space-time correlations of velocity fluctuations in wind farms[J]. Wind Energy, 2018, 21(7): 474-487. DOI:10.1002/we.2172 (  0) 0) |
| [18] |
徐海翔, 王靖然, 吴林林, 等. 新能源机组运行数据多维度校验研究及应用[J]. 华北电力技术, 2017(10): 7-12, 18. XU Haixiang, WANG Jingran, WU Linlin, et al. Research on multi-dimensional data verification of renewable power equipment information and its application[J]. North China Electric Power, 2017(10): 7-12, 18. (  0) 0) |
| [19] |
于若英, 陈宁, 苗淼, 等. 考虑天气和空间相关性的光伏电站输出功率修复方法[J]. 电网技术, 2017, 41(7): 2229-2236. YU Ruoying, CHEN Ning, MIAO Miao, et al. A repair method for PV power station output data considering weather and spatial correlations[J]. Power System Technology, 2017, 41(7): 2229-2236. (  0) 0) |
| [20] |
TALASBEK A, SEREK A, ZHAPAROV M, et al. Personality classification experiment by applying k-means clustering[J]. International Journal of Emerging Technologies in Learning (IJET), 2020, 15(16): 162. DOI:10.3991/ijet.v15i16.15049 (  0) 0) |
| [21] |
杨正瓴, 王如雪, 乔健, 等. 大气压的差值对风速空间相关性预测的影响分析[J]. 发电技术, 2020, 41(6): 617-624. YANG Zhengling, WAGN Ruxue, QIAO Jian, et al. Analysis of the influence of atmospheric pressure difference on spatial correlation prediction of wind speed[J]. Power Generation Technology, 2020, 41(6): 617-624. (  0) 0) |
| [22] |
王果毅, 牟金磊, 李润祥. 基于时间相关性的风速威布尔分布优化方法[J]. 中国电业, 2020(5): 92-95. WANG Guoyi, MU Jinlei, LI Runxiang. A Weibull distribution optimization method for wind speed based on time correlation[J]. China Electric Power, 2020(5): 92-95. (  0) 0) |
| [23] |
HUANG N T, WU Y Y, CAI G W, et al. Short-term wind speed forecast with low loss of information based on feature generation of OSVD[J]. IEEE Access, 2019, 7: 81027-81046. DOI:10.1109/ACCESS.2019.2922662 (  0) 0) |
| [24] |
WANG J Z, WANG S Q, YANG W D. A novel non-linear combination system for short-term wind speed forecast[J]. Renewable Energy, 2019, 143: 1172-1192. DOI:10.1016/j.renene.2019.04.154 (  0) 0) |
| [25] |
齐霞, 安磊, 张妍, 等. 风电机组功率曲线建模方法对比研究[J]. 可再生能源, 2018, 36(4): 580-585. QI Xia, AN Lei, ZHANG Yan, et al. Comparative study of multiple power curve modelling methods[J]. Renewable Energy Resources, 2018, 36(4): 580-585. (  0) 0) |
| [26] |
DINDAR A, ARDEHALI M M, VAKILIAN M. Integration of wind turbines in distribution systems and development of an adaptive overcurrent relay coordination scheme with considerations for wind speed forecast uncertainty[J]. IET Renewable Power Generation, 2020, 14(15): 2983-2992. (  0) 0) |
| [27] |
韩松, 王兴龙. 弱一致性风速分布山区风电场机电暂态建模及适用性研究[J]. 电力系统保护与控制, 2017, 45(15): 1-7. HAN Song, WANG Xinglong. Modeling of DFIG based wind farm considering temporal and spatial non-uniformity of wind speed in mountainous region and its applicability analysis[J]. Power System Protection and Control, 2017, 45(15): 1-7. (  0) 0) |
| [28] |
李永刚, 王月, 刘丰瑞, 等. 基于Stacking融合的短期风速预测组合模型[J]. 电网技术, 2020, 44(8): 2875-2882. LI Yonggang, WANG Yue, LIU Fengrui, et al. Combination model of short-term wind speed prediction based on stacking fusion[J]. Power System Technology, 2020, 44(8): 2875-2882. (  0) 0) |
| [29] |
陈金富, 朱乔木, 石东源, 等. 利用时空相关性的多位置多步风速预测模型[J]. 中国电机工程学报, 2019, 39(7): 2093-2106. CHEN Jinfu, ZHU Qiaomu, SHI Dongyuan, et al. A multi-step wind speed prediction model for multiple sites leveraging spatio-temporal correlation[J]. Proceedings of the CSEE, 2019, 39(7): 2093-2106. (  0) 0) |
| [30] |
张旭, 张宏立, 王聪. 基于PSOGSA全参数连分式的风速预测模型[J]. 电力系统保护与控制, 2020, 48(23): 100-107. ZHANG Xu, ZHANG Hongli, WANG Cong. Wind speed prediction model based on PSOGSA full-parameter continuous fractions[J]. Power System Protection and Control, 2020, 48(23): 100-107. (  0) 0) |
2. State Grid Qinghai Electric Power Company Economic Research Institute, Xining 810008, China;
3. State Grid Qinghai Electric Power Company Clean Energy Development Research Institute, Xining 810008, China;
4. College of Electrical Engineering and Control Science, Nanjing Tech University, Nanjing 211816, China
 2022, Vol. 41
2022, Vol. 41


 李延和(1983), 男, 硕士, 高级工程师, 从事新能源接入电力系统运行控制相关工作(E-mail:
李延和(1983), 男, 硕士, 高级工程师, 从事新能源接入电力系统运行控制相关工作(E-mail: