文章编号: 2096-3203(2022)02-0119-09 中图分类号: TM732
2. 南京工程学院经济与管理学院,江苏 南京 211167;
3. 南京理工大学自动化学院,江苏 南京 210094
现阶段由于碳排放引起的全球气候变化问题已受到各国政府重视[1-2]。2019年全球能源碳排放量达历史高位,亟待积极采取措施实现“碳中和”[3-6]。目前,全球有30个国家或地区通过正式渠道明确提出“碳中和”目标,欧盟和日本已发布碳排放路线,其他国家则在进一步制定路线中[7-11]。随着双碳政策的提出,我国碳排放交易市场也已启动,研究碳排放配额对我国综合微能源网系统的影响具有重要意义[12-17]。
国内外学者针对能源网中的碳排放问题开展了广泛研究。针对微电网中能源调度的经济效益、充电效率优化以及碳排放问题,文献将强化学习运用到微电网调度中,使其在不断迭代的过程中得到最优策略,实现经济效益最大化收敛和碳排放量最小化收敛。文献提出一种同时考虑碳价以及风电出力不确定性的经济排放调度模型,在经济和环境两方面考虑了消除风电不确定性的不利因素。文献以发电成本和碳排放量最小为优化目标建立了多目标的含低负荷场景的低碳多源协调调度模型,可降低系统碳排放量。文献从促进能源综合利用效率与可再生能源消纳两方面出发,提出了多能源系统的规划与运行,并设计了面向低碳的能源市场机制。文献提出了一种基于可再生能源配额制的综合能源系统优化调度模型,可保证系统经济性,减少系统碳排放。然而,现有模型大多仅对微电网进行碳排放成本分析,对综合微能源网系统考虑碳排放成本的最优运行,特别是引入碳排放免费配额后的综合微能源网系统优化运行策略研究较少。
文中考虑环境效益,结合碳排放交易政策,构建了含混和储能装置的综合微能源网系统,并建立了考虑碳排放配额的最优经济运行模型,结合某地区数据对模型进行求解,并对所制定的考虑碳排放免费配额的综合微能源网系统运行优化策略进行了验证,为当地经济投资与进一步开展综合微能源网能源结构研究提供了理论基础。
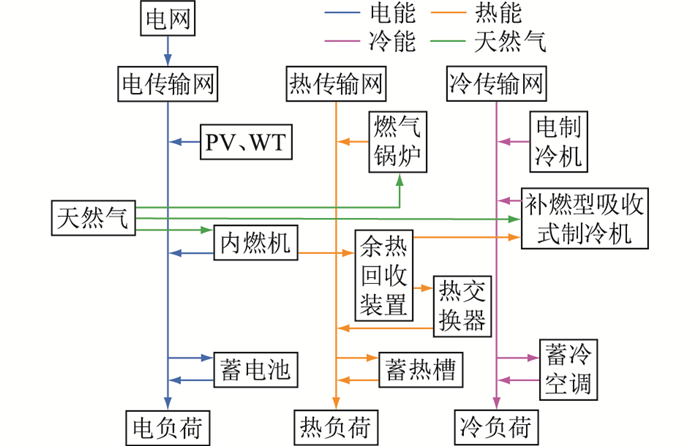
1 综合微能源网系统结构与建模 1.1 模型架构文中所建立的综合微能源网系统涵盖了多种供能与能量转换设备,包括光伏(photovoltaic, PV)、风力发电机(wind turbine, WT)、内燃机、余热回收装置、热交换器、燃气锅炉、电制冷机、补燃型吸收式制冷机,并加入了蓄电池、蓄热槽及蓄冷空调等混合储能装置。此外,该系统与大电网联接,当系统本身电能短缺时,采用分时电价向大电网购电。所构建的含混合储能装置的综合微能源网系统模型架构如图 1所示。
|
图 1 混合储能综合微能源网架构 Fig. 1 Hybrid energy storage integrated micro-energy network architecture |
PV作为微能源网的重要组成部分,出力受太阳辐射强度和温度的影响,其数学模型为[23-24]:
| $ P_{\mathrm{pv}, t}=\left[1-\gamma_{\mathrm{T}}\left(T_{\mathrm{air}}+\frac{T_{\mathrm{n}}-20}{800} R-T_{\mathrm{ref}}\right)\right] \eta_{\mathrm{ref}} N_{\mathrm{pv}} A_{\mathrm{pv}} R $ | (1) |
式中:Ppv, t为PV出力, 下标t表示处于t时段, 下文不再赘述;γT为PV板转换效率的温度参数;Tair为环境温度;Tn为正常工作温度;Tref为参考温度;ηref为参考效率;Npv为PV面板数量;Apv为单个PV面板面积;R为太阳辐射强度。
1.2.2 WT在WT中配置相应的环境预报装置,提供日前风速预测值和实时风速预测值。风电作为微能源网中一个出力可预测的电源,其主要影响因素为风速[25]。分布式风电出力的数学模型为:
| $ P_{\mathrm{wt}, t}=\left\{\begin{array}{l} 0 \quad v \leqslant v_{\mathrm{ci}} \\ k_{1} v+k_{2} \quad v_{\mathrm{ci}}<v \leqslant v_{\mathrm{co}} \\ P_{\mathrm{wtr}} \quad v_{\mathrm{r}}<v \leqslant v_{\mathrm{co}} \\ 0 \quad v>v_{\mathrm{co}} \end{array}\right. $ | (2) |
| $ k_{1}=\frac{P_{\mathrm{wtr}}}{v_{\mathrm{r}}-v_{\mathrm{ci}}} $ | (3) |
| $ k_{2}=-k_{1} v_{\mathrm{ci}} $ | (4) |
式中:Pwt, t为WT的输出功率;Pwtr为WT的额定功率;v为风速;vci,vco,vr分别为切入、切出和额定风速;k1,k2为切入功率系数。
1.2.3 内燃机内燃机内部产生电能,并将高温气体进行二次利用。内燃机发电效率与发电功率的拟合函数[26]为:
| $ P_{\mathrm{ce}, t}=f_{t} F_{\mathrm{g}, t} $ | (5) |
| $ f_{t}=\frac{P_{\mathrm{ce}, t}}{E_{\mathrm{ce}}} \times 100 \% $ | (6) |
| $ \eta_{\mathrm{e}}=-0.07 f_{t}{}^{2}+0.19 f_{t}+0.26 $ | (7) |
式中:Pce, t为内燃机的实际发电功率;Ece为内燃机的额定发电功率;ft为内燃机的部分负荷率;ηe为发电效率;Fg, t为内燃机消耗的燃气热值。
内燃机包含余热回收装置,可将其做功后排出的热量回收进行二次利用,实现能量梯级利用。内燃机余热回收的数学模型为:
| $ Q_{\mathrm{Re}}=\eta_{\mathrm{Re}}\left(1-f_{t}\right) F_{\mathrm{g}, t} $ | (8) |
式中:QRe为内燃机回收的余热值;ηRe为内燃机的热回收效率,参考热交换器的平均换热效率,文中取0.8。余热回收装置所回收的余热一部分用于热交换器制热,一部分用于补燃型吸收式制冷机制冷。
1.2.4 热交换器热交换器回收内燃机发电的余热进行制热,满足用户的一部分热需求。其数学模型为:
| $ H_{\mathrm{he}, t}=Q_{\mathrm{hre}, t} \eta_{\mathrm{he}} $ | (9) |
式中:Hhe, t为热交换器的制热功率;Qhre, t为热交换器所利用的余热值;ηhe为热交换器的制热效率。
1.2.5 燃气锅炉燃气锅炉消耗天然气进行产热,以满足用户需求。燃气锅炉的燃气耗量与产热功率和锅炉效率有关,其数学模型为:
| $ Q_{\mathrm{gb}, t}=F_{\mathrm{gb}, t} \eta_{\mathrm{gb}} $ | (10) |
式中:Fgb, t为天然气的耗量;Qgb, t为燃气锅炉产生的热功率;ηgb为燃气锅炉的转换效率。
1.2.6 电制冷机电制冷机将电能转换成冷能来满足冷负荷需求。电制冷机的制冷循环为:压缩-液化-吸热-蒸发,其数学模型如式(11)所示[27-28]。
| $ C_{\mathrm{el}, t}=P_{\mathrm{el}, t} \gamma_{\mathrm{ec}} $ | (11) |
式中:Cel, t为电制冷机输出的冷功率;Pel, t为电制冷机消耗的电功率;γec为电制冷机的制冷性能系数。
1.2.7 补燃型吸收式制冷机为了充分利用内燃机产生的余热(包括高温烟气和缸套冷却水),文中选用补燃型吸收式制冷机,利用天然气补燃以满足制冷机做功需求,其数学模型为:
| $ \left\{\begin{array}{l} \beta_{\mathrm{c}, t}=\frac{C_{\mathrm{ac}, t}}{C_{\mathrm{Nc}}} \times 100 \% \\ \gamma_{\mathrm{c}, t}=\frac{\gamma_{\mathrm{rc}} \beta_{\mathrm{c}, t}}{0.75 \beta_{\mathrm{c}, t}^{2}+0.019\ 5 \beta_{\mathrm{c}, t}+0.213} \\ Q_{\mathrm{ah}, t}=Q_{\mathrm{rac}}+Q_{\mathrm{ac}} \\ C_{\mathrm{ac}, t}=Q_{\mathrm{ah}, t} \gamma_{\mathrm{c}, t} \end{array}\right. $ | (12) |
式中:βc, t为制冷机的负荷率;γc, t为制冷机的性能系数;Cac, t为制冷机的实际制冷功率;CNC为制冷机的额定制冷功率;γrc为制冷机的额定制冷性能系数;Qac为制冷机补燃产生的功率;Qrac为进入制冷机的余热值;Qah, t为进入制冷机的总热值。
1.2.8 储能装置储能装置主要包含蓄电池、蓄热槽及蓄冷空调。对于蓄电池而言,主要考虑充电、放电功率,其荷电状态(state of charge, SOC)数学模型为:
| $ S_{\mathrm{SOC}, t+1}=\left(1-\delta_{\mathrm{i}}\right) S_{\mathrm{SOC}, t}+\left(\eta_{\mathrm{ic}} P_{\mathrm{ic}, t} \Delta t-\frac{P_{\mathrm{id}, t} \Delta t}{\eta_{\mathrm{id}}}\right) / S_{\mathrm{is}} $ | (13) |
式中:δi为蓄电池的自放电率;Pic, t,Pid, t分别为蓄电池在t时段的充电、放电功率;ηic,ηid分别为蓄电池的充电、放电效率;Sis为蓄电池的容量。
使用蓄热、蓄冷装置,其目的是使其在系统热负荷、冷负荷较低的情况下进行蓄能,在系统热负荷、冷负荷较高或合适时放热、放冷,起到削峰填谷的作用。储能状态值SSOH,SSOI表达式分别为:
| $ S_{\mathrm{SOH}, t+1}=\left(1-\delta_{\mathrm{h}}\right) S_{\mathrm{SOH}, t}+\left(\eta_{\mathrm{hc}} P_{\mathrm{hc}, t} \Delta t-\frac{P_{\mathrm{hd}, t} \Delta t}{\eta_{\mathrm{hd}}}\right) / S_{\mathrm{hs}} $ | (14) |
| $ S_{\mathrm{SOI}, t+1}=\left(1-\delta_{\mathrm{c}}\right) S_{\mathrm{SOI}, t}+\left(\eta_{\mathrm{cc}} P_{\mathrm{cc}, t} \Delta t-\frac{P_{\mathrm{cd}, t} \Delta t}{\eta_{\mathrm{cd}}}\right) / S_{\mathrm{cs}} $ | (15) |
式中:Phc, t,Phd, t分别为t时段蓄热槽的蓄热、放热功率;Pcc, t,Pcd, t分别为t时段蓄冷空调的蓄冷、放冷功率;ηhc,ηhd分别为蓄热、放热效率;ηcc,ηcd分别为蓄冷、放冷效率;Shs,Scs分别为蓄热、蓄冷装置的额定容量;δh,δc分别为装置的蓄热、蓄冷损失率。
2 综合微能源网系统日前运行优化 2.1 优化目标函数为了兼顾系统碳排放和经济性,该综合能源系统优化模型考虑了碳排放免费配额,以系统运行成本最小为优化目标。系统运行成本C包括电网购电成本Cbe,内燃机、燃气锅炉和补燃型吸收式制冷机运行消耗的燃气成本Cfu,所有设备的日运行维护成本Com,系统碳排放成本Cenv。文中根据《2019年发电行业重点排放单位二氧化碳排放配额分配实施方案(试算版)》,在系统碳排放成本中引入碳排放配额进行建模。采用基准法核算机组配额总量为:
| $ A=B_{\mathrm{e}} Q_{\mathrm{e}} F_{\mathrm{de}}+B_{\mathrm{h}} Q_{\mathrm{h}} $ | (16) |
式中:A为机组配额总量;Be为供电基准值;Qe为实际供电量;Fde为修正系数;Bh为供热基准值;Qh为实际供热量,各类机组的CO2排放配额(A)皆由供电配额(Ae)和供热配额(Ah)两部分构成。
各成本数学模型描述如下:
| $ \left\{\begin{array}{l} \min C=C_{\mathrm{be}}+C_{\mathrm{fu}}+C_{\mathrm{om}}+C_{\mathrm{env}} \\ C_{\mathrm{be}}=\sum\limits_{t=1}^{T}\left(c_{\mathrm{e}, t} P_{\mathrm{gr}, t}\right) \Delta t \\ C_{\mathrm{fu}}=\sum\limits_{t=1}^{T}\left(c_{\mathrm{fu}, t} Q_{\mathrm{Fgas}, t}\right) \Delta t\\ C_{\mathrm{om}}=\sum\limits_{t=1}^{T}\left[\begin{array}{l} R_{\mathrm{pv}} \\ R_{\mathrm{wt}} \\ R_{\mathrm{ce}} \\ R_{\mathrm{he}} \\ R_{\mathrm{gb}} \\ R_{\mathrm{l}} \\ R_{\mathrm{ac}} \\ R_{\mathrm{is}} \\ R_{\mathrm{hs}} \\ R_{\mathrm{cs}} \end{array}\right]^{\mathrm{T}}\left[\begin{array}{c} P_{\mathrm{pv}, t} \\ P_{\mathrm{wt}, t} \\ P_{\mathrm{ce}, t} \\ H_{\mathrm{he}, t} \\ Q_{\mathrm{gb}, t} \\ C_{\mathrm{el}, t} \\ C_{\mathrm{ac}, t} \\ P_{\mathrm{ic}, t}+P_{\mathrm{id}, t} \\ P_{\mathrm{hc}, t}+P_{\mathrm{hd}, t} \\ P_{\mathrm{cc}, t}+P_{\mathrm{cd}, t} \end{array}\right]^{2}\\ C_{\mathrm{env}}=\sum\limits_{t=1}^{T}\left[\alpha\left(\beta_{\mathrm{gr}} P_{\mathrm{gr}, t}+\beta_{\mathrm{gas}} Q_{\mathrm{Fgas}, t}\right)\right] \Delta t \\ C_{\mathrm{env}}^{\prime}=c_{\mathrm{bs}}\left[\sum\limits_{t=1}^{T}\left(\beta_{\mathrm{gr}} P_{\mathrm{gr}, t}+\beta_{\mathrm{gas}} Q_{\mathrm{gas}, t}\right) \Delta t-\right. \\ \ \ \ \ \ \ \ \ \ \ \ \ \left.\sum\limits_{t=1}^{T}\left(B_{\mathrm{e}} F_{\mathrm{de}} P_{\mathrm{ce}, t}\right) \Delta t\right] \end{array}\right. $ | (17) |
式中:ce, t为t时段的电价;cfu, t为t时段的天然气价格;QFgas, t为t时段系统消耗的总燃气热值;Rpv,Rwt,Rce,Rhe,Rgb,Rl,Rac,Ris,Rhs,Rcs分别为PV、WT、内燃机、热交换器、燃气锅炉、电制冷机、补燃型吸收式制冷机、蓄电池、蓄热槽和蓄冷空调的运行维护系数;Pgr, t为向电网购电量;α为碳排放价格,取0.22元/kg;βgr为电网购电碳排放转换系数;βgas为天然气碳排放转换系数;Qgas, t为t时段系统消耗天然气量;Cenv为考虑碳排放免费配额前的环境成本;C′env为考虑碳排放免费配额后的环境成本。碳排放免费配额政策带来的收益分为2种情况:(1) 碳排放免费配额小于系统碳排放总量,此时只需要考虑碳排放免费配额对成本带来的收益;(2) 碳排放免费配额大于系统碳排放总量,此时可进行碳交易,将碳排放免费配额多余部分进行售卖,此时成本须同时考虑碳排放免费配额对环境成本方面的收益及售卖配额所带来的收益。当碳排放免费配额小于碳排放总量时,cbs为碳排放价格,取0.22元/kg;当配额大于碳排放总量时,该系统碳排放成本为负,即为收益,此时cbs为碳交易市场售卖价格,取-0.49元/kg。
2.2 优化约束条件式(18)-式(35)为综合微能源网系统的约束。
| $ P_{\mathrm{grmin}} \leqslant P_{\mathrm{gr}, t} \leqslant P_{\mathrm{grmax}} $ | (18) |
| $ P_{\text {cemin }} \leqslant P_{\text {ce }, t} \leqslant P_{\text {cemax }} $ | (19) |
| $ H_{\text {hemin }} \leqslant H_{\text {he }, t} \leqslant H_{\text {hemax }} $ | (20) |
| $ Q_{\mathrm{gbmin}} \leqslant Q_{\mathrm{gb}, t} \leqslant Q_{\mathrm{gbmax}} $ | (21) |
| $ C_{\text {elmin }} \leqslant C_{\mathrm{el}, t} \leqslant C_{\mathrm{elmax}} $ | (22) |
| $ C_{\text {acmin }} \leqslant C_{\mathrm{ac}, t} \leqslant C_{\text {acmax }} $ | (23) |
| $ P_{\text {icmin }} \leqslant P_{\text {ic }, t} \leqslant P_{\text {icmax }} $ | (24) |
| $ P_{\mathrm{idmin}} \leqslant P_{\mathrm{id}, t} \leqslant P_{\mathrm{idmax}} $ | (25) |
| $ P_{\mathrm{hcmin}} \leqslant P_{\mathrm{hc}, t} \leqslant P_{\mathrm{hcmax}} $ | (26) |
| $ P_{\text {hdmin }} \leqslant P_{\mathrm{hd}, t} \leqslant P_{\text {hdmax }} $ | (27) |
| $ P_{\mathrm{ccmin}} \leqslant P_{\mathrm{cc}, t} \leqslant P_{\mathrm{ccmax}} $ | (28) |
| $ P_{\mathrm{cdmin}} \leqslant P_{\mathrm{cd}, t} \leqslant P_{\mathrm{cdmax}} $ | (29) |
| $ S_{\text {SOC } \min } \leqslant S_{\text {SOC }, t} \leqslant S_{\text {SOC } \max } $ | (30) |
| $ S_{\mathrm{SOH \operatorname {min }}} \leqslant S_{\mathrm{SOH}, t} \leqslant S_{\mathrm{SOH \operatorname {max }}} $ | (31) |
| $ S_{\text {SOImin }} \leqslant S_{\text {SOI }, t} \leqslant S_{\text {SOImax }} $ | (32) |
| $ \begin{gathered} P_{\mathrm{gr}, t}+P_{\mathrm{pv}, t}+P_{\mathrm{wt}, t}+P_{\mathrm{ce}, t}+P_{\mathrm{id}, t}= \\ P_{\mathrm{eload}, t}+P_{\mathrm{el}, t}+P_{\mathrm{ic}, t} \end{gathered} $ | (33) |
| $ Q_{\mathrm{gb}, t}+H_{\mathrm{he}, t}+P_{\mathrm{hd}, t}=H_{\mathrm{hload}, t}+P_{\mathrm{hc}, t} $ | (34) |
| $ C_{\mathrm{ac}, t}+C_{\mathrm{el}, t}+P_{\mathrm{cd}, t}=C_{\mathrm{cload}, t} $ | (35) |
式中:Peload, t为系统用电负荷;Hhload, t为系统用热负荷;Ccload, t为系统用冷负荷。式(18)表示从电网购电的功率上、下限约束;式(19)-式(23)分别表示内燃机、热交换器、燃气锅炉、电制冷机、补燃型吸收式制冷机各机组的出力上、下限约束;式(24)-式(29)分别表示蓄电池、蓄热槽和蓄冷空调的储、放能功率约束;式(30)-式(32)分别表示蓄电池、蓄热槽和蓄冷空调的储能状态值约束;式(33)表示电力平衡约束;式(34)表示热平衡约束;式(35)表示冷平衡约束。
2.3 优化解法Gurobi是美国Gurobi公司研发的一种成熟的全局优化器,其支持的优化模型类型包括:连续和混合整数线性问题,凸目标或约束连续和混合整数二次问题,非凸目标或约束连续和混合整数二次问题,含有对数、指数、三角函数、高阶多项式目标或约束以及任何形式的分段约束的非线性问题。文中模型是混合整数二次型规划模型,故采用Gurobi进行优化求解。主要包括以下5个步骤:
(1) 创建决策变量。将需要优化的决策变量存放于创建的决策变量矩阵中。
(2) 设定目标函数。指定所需求解的最优化问题,当求解的最优化问题为最小化问题时,目标函数为f,当为最大化问题时,目标函数为-f。
(3) 设置约束条件。创建以constraints指定的约束,当约束条件为多个时,约束条件可进行累加。
(4) 进行参数配置。在参数配置中设置求解器及冗余度等参数,冗余度越大,求解过程越详细。一般参数用ops进行指定。
(5) 优化求解。设置好前面所有步骤以后可进行模型优化求解,求解结果存储在result结构体中。
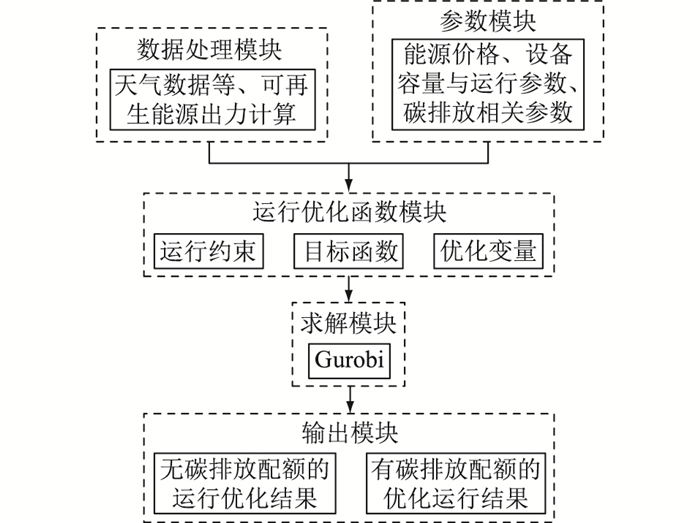
3 算例分析 3.1 日前优化运行模型模型的求解主要包括5个模块。模型的输入包括用户的负荷数据,光照强度和风速等天气数据,电网分时售电价格,天然气价格以及供能设备的容量与运行参数,通过Gurobi对模型进行求解,实现综合微能源网系统的经济运行。该系统日前优化运行模型框架如图 2所示。
|
图 2 日前优化运行模型框架 Fig. 2 Framework of optimized day-ahead operation model |
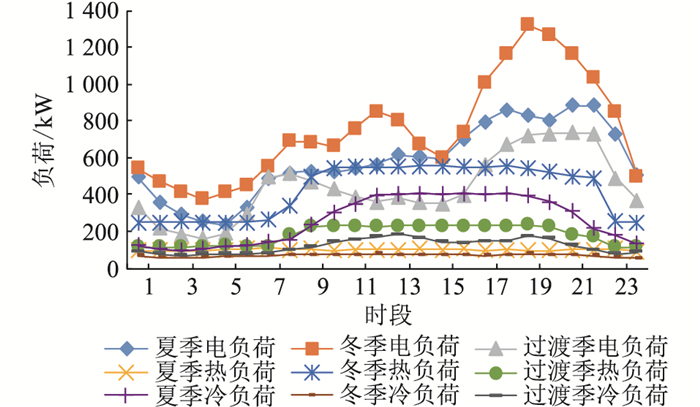
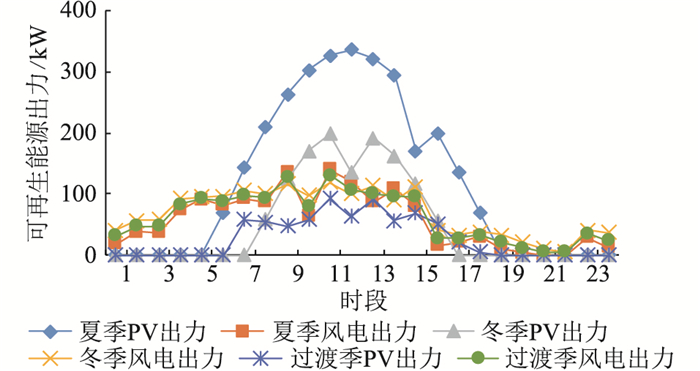
为了验证文中所提优化运行模型的有效性,以我国某地区的日前运行方案作为研究对象,选取该地区用户的电、热、冷负荷数据及天气数据作为算例基础数据进行仿真。为兼顾模型计算精度与复杂度,探究碳排放免费配额对所提系统运行方式与经济性的影响,文中基于负荷的季节性差异,将全年分为夏季(6月-9月)、冬季(12月、1月-2月)和春秋过渡季(3月-5月、10月-11月)3类典型日场景,持续时间分别为122 d,90 d,153 d,对该系统进行全年优化计算。该区域3类典型日负荷如图 3所示,根据当地天气数据对可再生能源出力进行仿真,得到典型日PV与风电出力数据,见图 4。
|
图 3 综合微能源网系统典型日负荷 Fig. 3 Typical daily load of integrated energy microgrid |
|
图 4 典型日可再生能源出力 Fig. 4 Typical daily renewable energy output |
该综合能源系统中所有能源转换设备参数见表 1,储能设备参数见表 2。各典型日负荷情况见表 3。电网购电采用分时电价,分平段(07:00-10:00,15:00-18:00,21:00-23:00)、峰段(10:00-15:00,18:00-21:00)、谷段(23:00-次日07:00)3个时段,其电价依次分别为0.84元/(kW ·h),1.38元/(kW ·h),0.28元/(kW ·h)。其中,峰段中时间段11:00-13:00,20:00-21:00的电价为1.5元/(kW ·h)。微能源网的谷段电价较电网电价稍低,峰段电价较电网电价稍高,平段电价与电网相同[26]。天然气价格为2.3元/m3。文中通过调用Gurobi求解器进行优化求解,考虑碳排放免费配额后的系统优化运行结果见图 5-图 7,经济优化结果见表 4。
|
|
表 1 能源转换设备模型参数 Table 1 Model parameters of energy conversion equipment |
|
|
表 2 储能设备模型参数 Table 2 Model parameters of energy storage equipment |
|
|
表 3 典型日负荷情况 Table 3 Typical daily loads |

|
图 5 有配额夏季优化运行结果 Fig. 5 Results of optimized operation with quota in summer |
|
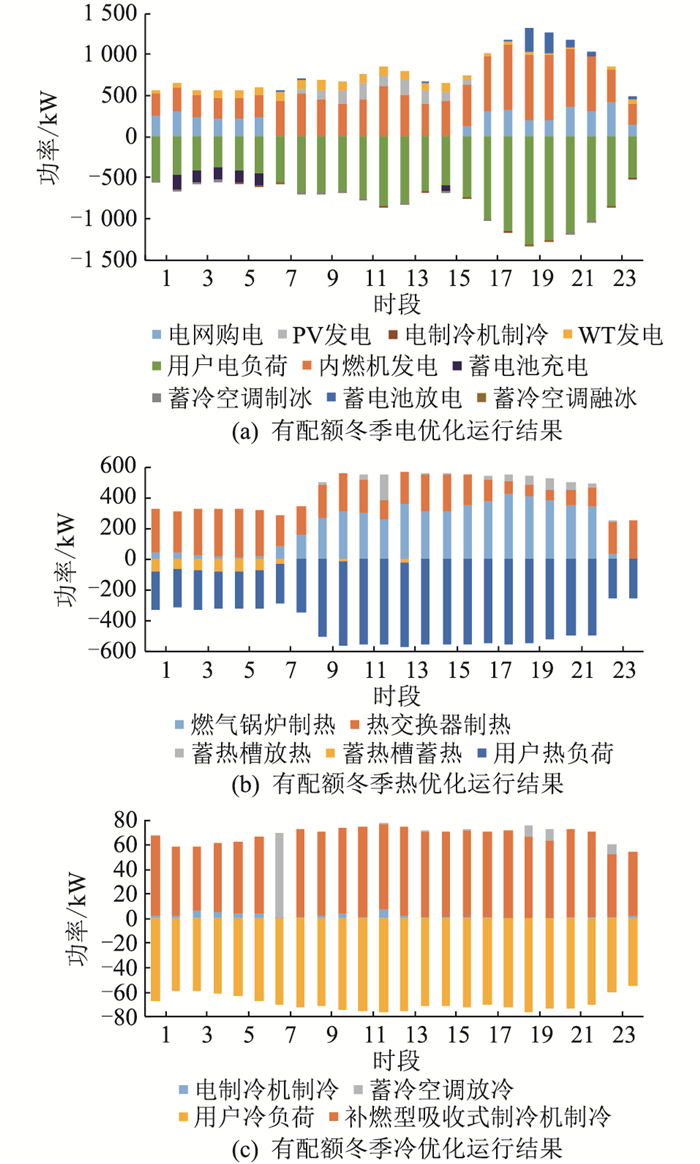
图 6 有配额冬季优化运行结果 Fig. 6 Results of optimized operation with quota in winter |
|
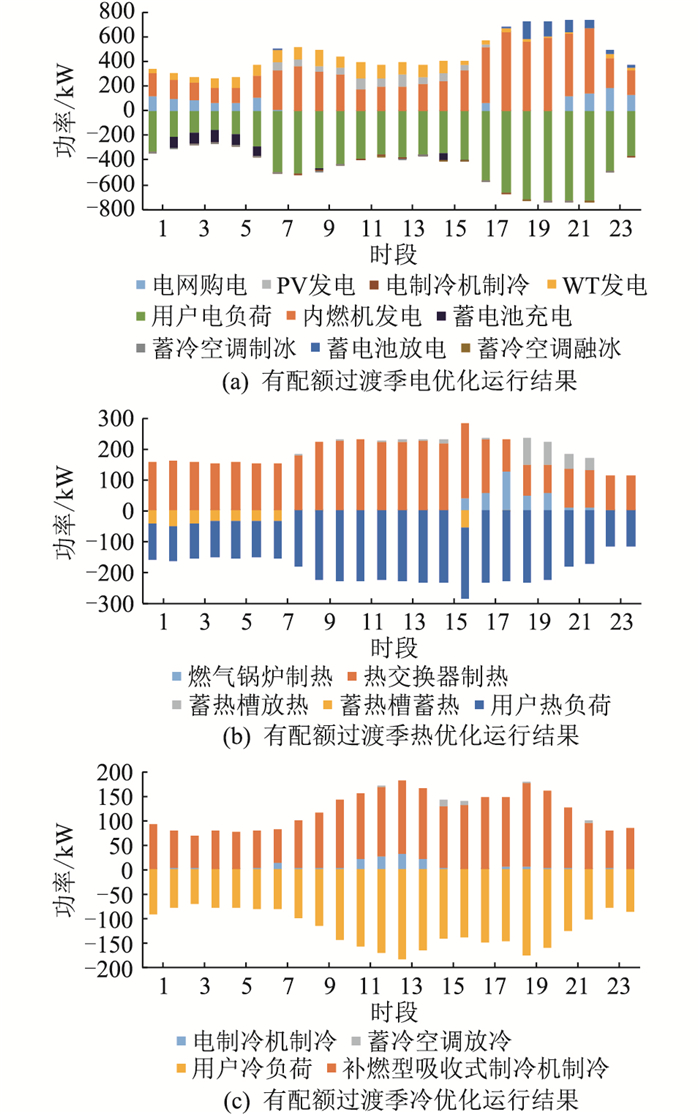
图 7 有配额过渡季优化运行结果 Fig. 7 Results of optimized operation with quota in transition season |
|
|
表 4 优化结果对比 Table 4 Comparison of optimization results |
分析综合微能源网系统在该场景中的日前优化运行结果可知:
(1) 该综合微能源网系统对分时电价的敏感度较高,可通过比较不同时段的购电价格与燃气价格灵活调整购电量,使系统运行更加经济。凌晨为电价谷段,此时段用电、用冷量小,系统更倾向于向电网购电并进行蓄能,并在用电、用冷高峰进行放能;电价峰段即用能高峰期,系统衡量电负荷与热负荷比例,进行电热交互,通过内燃机发电、补燃型吸收式制冷机制冷,降低购电比例或不购电,减少购电费用;电价平段则通过比较电价与燃气的价格,以更经济的方式进行电能与冷能的产出。
(2) 有碳排放免费配额时,该综合能源系统在比较不同时段的购电价格与燃气价格的基础上,综合考虑燃气机组发电时的经济效益。利用燃气进行发电可增加系统碳免费配额,除高峰期不购电外,当电价不高于燃气价格时,若向电网购电比购买燃气进行发电更经济,则系统选择购电,反之,系统通过购买燃气进行发电,通过比较2种运行方式制定优化运行策略。从运行结果可看出,电价谷段的电网购电量有所降低,内燃机发电增多,余热产生更多,热交换器制热、补燃型吸收式制冷机制冷量增多,一定程度上减少不具配额的燃气锅炉制热与电制冷机制冷,进而减少系统燃料成本和碳排放成本,系统选择更具经济性的方式进行能源的购入和产出。
(3) 混合储能设备在电价谷段、可再生能源出力盈余及电、热、冷负荷需求量低的时段进行能量的储存,电价峰段与负荷需求大的时段进行放能,起到了削峰填谷的作用,同时促进可再生能源的消纳,提高系统的经济性、安全性和可靠性。
(4) 由表 4分析可知,计入碳排放免费配额后,系统年运行成本由177.09万元降低至172.55万元,降低了2.6%;碳排放成本由3.63万元降低至1.09万元,降低了69.97%,结果表明系统的经济性与环保性均得到提高。但文中所建模型仅燃气发电机组享有碳排放免费配额,不具备发电能力的纯供热设施不在实施方案范围内,因此后续的投资可在该模型的基础上,引进热电联产机组,提高综合微能源网系统的经济性与投资回报率。
4 结语文中在分布式综合能源系统的基础上,加入电、热、冷负荷储能设备,结合碳排放配额分配实施方案,提出一种计及碳排放成本的含混合储能装置的综合微能源网系统的优化运行模型,并对所提模型优化运行结果进行求解。算例结果表明,模型中的混合储能装置可在能源价格低时或用能谷期储存能量,在能源价格高时或用能高峰期释放能量,调节系统出力方式并提高综合能源网系统的经济性;并且算例结果能够反映碳排放成本因素对能源消费结构的影响,碳排放免费配额可降低综合能源网系统的运行投资成本,可为进一步探索碳排放及相关交易政策对综合能源网系统能源结构的影响以及地区相关设备的投资提供理论基础。
本文得到江苏省高校哲学社会科学研究基金项目(2021SJA0438),南京工程学院创新基金面上项目Ⅰ(CKJB201908),南京工程学院产业经济与创新管理研究院开放基金项目(JGKB202103)资助,谨此致谢!
| [1] |
潘栋, 李楠, 李锋, 等. 基于能源碳排放预测的中国东部地区达峰策略制定[J]. 环境科学学报, 2021, 41(3): 1142-1152. PAN Dong, LI Nan, LI Feng, et al. Mitigation strategy of eastern China based on energy-source carbon emission estimation[J]. Acta Scientiae Circumstantiae, 2021, 41(3): 1142-1152. (  0) 0) |
| [2] |
聂海宁, 黄小琳, 曾智勇. 中国清洁能源供热现状及发展前景[J]. 能源与节能, 2018(12): 87-89. NIE Haining, HUANG Xiaolin, ZENG Zhiyong. Present situation and development prospect of clean energy heating in China[J]. Energy and Energy Conservation, 2018(12): 87-89. DOI:10.3969/j.issn.2095-0802.2018.12.036 (  0) 0) |
| [3] |
袁晓玲, 郗继宏, 李朝鹏, 等. 中国工业部门碳排放峰值预测及减排潜力研究[J]. 统计与信息论坛, 2020, 35(9): 72-82. YUAN Xiaoling, XI Jihong, LI Zhaopeng, et al. A study on carbon emission peak forecast and emission reduction potential of China′s industrial sector[J]. Statistics & Information Forum, 2020, 35(9): 72-82. DOI:10.3969/j.issn.1007-3116.2020.09.009 (  0) 0) |
| [4] |
SALVIA M, RECKIEN D, PIETRAPERTOSA F, et al. Will climate mitigation ambitions lead to carbon neutrality?An analysis of the local-level plans of 327 cities in the EU[J]. Renewable and Sustainable Energy Reviews, 2021, 135: 110253. DOI:10.1016/j.rser.2020.110253 (  0) 0) |
| [5] |
邓旭, 谢俊, 滕飞. 何谓"碳中和"?[J]. 气候变化研究进展, 2021, 17(1): 107-113. DENG Xu, XIE Jun, TENG Fei. What is carbon neutrality?[J]. Climate Change Research, 2021, 17(1): 107-113. (  0) 0) |
| [6] |
陈浮, 于昊辰, 卞正富, 等. 碳中和愿景下煤炭行业发展的危机与应对[J]. 煤炭学报, 2021, 46(6): 1808-1820. CHEN Fu, YU Haochen, BIAN Zhengfu, et al. How to handle the crisis of coal industry in China under the vision of carbon neutrality[J]. Journal of China Coal Society, 2021, 46(6): 1808-1820. (  0) 0) |
| [7] |
ROGELJ J, HUPPMANN D, KREY V, et al. A new scenario logic for the Paris agreement long-term temperature goal[J]. Nature, 2019, 573: 357-363. DOI:10.1038/s41586-019-1541-4 (  0) 0) |
| [8] |
周淑慧, 王军, 梁严. 碳中和背景下中国"十四五"天然气行业发展[J]. 天然气工业, 2021, 41(2): 171-182. ZHOU Shuhui, WANG Jun, LIANG Yan. Development of China′s natural gas industry during the 14th Five-Year Plan in the background of carbon neutrality[J]. Natural Gas Industry, 2021, 41(2): 171-182. DOI:10.3787/j.issn.1000-0976.2021.02.02( (  0) 0) |
| [9] |
邹才能, 熊波, 薛华庆, 等. 新能源在碳中和中的地位与作用[J]. 石油勘探与开发, 2021, 48(2): 411-420. ZOU Caineng, XIONG Bo, XUE Huaqing, et al. The role of new energy in carbon neutral[J]. Petroleum Exploration and Development, 2021, 48(2): 411-420. (  0) 0) |
| [10] |
申洪, 周勤勇, 刘耀, 等. 碳中和背景下全球能源互联网构建的关键技术及展望[J]. 发电技术, 2021, 42(1): 8-19. SHEN Hong, ZHOU Qinyong, LIU Yao, et al. Key technologies and prospects for the construction of global energy internet under the background of carbon neutral[J]. Power Generation Technology, 2021, 42(1): 8-19. (  0) 0) |
| [11] |
王汝英, 魏伟, 闫松, 等. 面向"碳中和"能源互联网的风光储联动配置算法[J]. 电力电容器与无功补偿, 2021, 42(4): 73-81. WANG Ruying, WEI Wei, YAN Song, et al. Wind-solar-storage linkage configuration algorithm on carbon neutral energy internet[J]. Power Capacitor & Reactive Power Compensation, 2021, 42(4): 73-81. (  0) 0) |
| [12] |
童光毅. 基于双碳目标的智慧能源体系构建[J]. 智慧电力, 2021, 49(5): 1-6. TONG Guangyi. Construction of smart energy system based on dual carbon goal[J]. Smart Power, 2021, 49(5): 1-6. DOI:10.3969/j.issn.1673-7598.2021.05.002 (  0) 0) |
| [13] |
宋阳, 张静页, 王磊, 等. 计及预测偏差的光伏消纳多时间尺度调度研究[J]. 电力工程技术, 2018, 37(1): 58-64. SONG Yang, ZHANG Jingye, WANG Lei, et al. Research on multi-time scheduling of accommodating photovoltaic considering the error of photovoltaic prediction[J]. Electric Power Engineering Technology, 2018, 37(1): 58-64. DOI:10.3969/j.issn.1009-0665.2018.01.010 (  0) 0) |
| [14] |
VAHIDINASAB V. Optimal distributed energy resources planning in a competitive electricity market: multiobjective optimization and probabilistic design[J]. Renewable Energy, 2014, 66: 354-363. DOI:10.1016/j.renene.2013.12.042 (  0) 0) |
| [15] |
滕云, 孙鹏, 罗桓桓, 等. 计及电热混合储能的多源微网自治优化运行模型[J]. 中国电机工程学报, 2019, 39(18): 5316-5324, 5578. TENG Yun, SUN Peng, LUO Huanhuan, et al. Autonomous optimization operation model for multi-source microgrid considering electrothermal hybrid energy storage[J]. Proceedings of the CSEE, 2019, 39(18): 5316-5324, 5578. (  0) 0) |
| [16] |
尚敬福, 马克睿, 花志浩, 等. 计及碳排放的综合能源系统优化调度及仿真实现[J]. 供用电, 2021, 38(11): 77-84. SHANG Jingfu, MA Kerui, HUA Zhihao, et al. Optimal scheduling and simulation of integrated energy system considering carbon emission[J]. Distribution & Utilization, 2021, 38(11): 77-84. (  0) 0) |
| [17] |
冯奕, 应展烽, 颜建虎. 考虑碳排放成本的多能互补微能源网储能装置优化运行[J]. 电力系统保护与控制, 2021, 49(8): 92-99. FENG Yi, YING Zhanfeng, YAN Jianhu. Optimized operation of energy storage in a multi-energy complementary micro-energy network considering carbon emission cost[J]. Power System Protection and Control, 2021, 49(8): 92-99. (  0) 0) |
| [18] |
刘金华, 柯钟鸣, 周文辉. 基于强化学习的微电网能源调度策略及优化[J]. 北京邮电大学学报, 2020, 43(1): 28-34. LIU Jinhua, KE Zhongming, ZHOU Wenhui. Reinforcement learning based energy dispatch strategy and control optimization of microgrid[J]. Journal of Beijing University of Posts and Telecommunications, 2020, 43(1): 28-34. (  0) 0) |
| [19] |
JIN J L, ZHOU P, ZHANG M M, et al. Balancing low-carbon power dispatching strategy for wind power integrated system[J]. Energy, 2018, 149: 914-924. DOI:10.1016/j.energy.2018.02.103 (  0) 0) |
| [20] |
崔岱, 葛维春, 赵文广, 等. 含低负荷场景低碳多源协调调度[J]. 仪器仪表学报, 2019, 40(11): 155-164. CUI Dai, GE Weichun, ZHAO Wenguang, et al. Low-carbon multi-source coordinated dispatch in the low-load scenario[J]. Chinese Journal of Scientific Instrument, 2019, 40(11): 155-164. (  0) 0) |
| [21] |
程耀华, 张宁, 康重庆, 等. 低碳多能源系统的研究框架及展望[J]. 中国电机工程学报, 2017, 37(14): 4060-4069, 4285. CHENG Yaohua, ZHANG Ning, KANG Chongqing, et al. Research framework and prospects of low-carbon multiple energy systems[J]. Proceedings of the CSEE, 2017, 37(14): 4060-4069, 4285. (  0) 0) |
| [22] |
骆钊, 卢涛, 马瑞, 等. 可再生能源配额制下多园区综合能源系统优化调度[J]. 电力自动化设备, 2021, 41(4): 8-14. LUO Zhao, LU Tao, MA Rui, et al. Optimal scheduling of multi-park integrated energy system under renewable portfolio standard[J]. Electric Power Automation Equipment, 2021, 41(4): 8-14. (  0) 0) |
| [23] |
刘维康, 王丹, 余晓丹, 等. 考虑电气转换储能和可再生能源集成的微能源网多目标规划[J]. 电力系统自动化, 2018, 42(16): 11-20, 72. LIU Weikang, WANG Dan, YU Xiaodan, et al. Multi-objective planning of micro energy network considering P2G-based storage system and renewable energy integration[J]. Automation of Electric Power Systems, 2018, 42(16): 11-20, 72. (  0) 0) |
| [24] |
郭博文, 罗聃, 周红军. 可再生能源电解制氢技术及催化剂的研究进展[J]. 化工进展, 2021, 40(6): 2933-2951. GUO Bowen, LUO Dan, ZHOU Hongjun. Recent advances in renewable energy electrolysis hydrogen production technology and related electrocatalysts[J]. Chemical Industry and Engineering Progress, 2021, 40(6): 2933-2951. (  0) 0) |
| [25] |
万灿, 宋永华. 新能源电力系统概率预测理论与方法及其应用[J]. 电力系统自动化, 2021, 45(1): 2-16. WAN Can, SONG Yonghua. Theories, methodologies and applications of probabilistic forecasting for power systems with renewable energy sources[J]. Automation of Electric Power Systems, 2021, 45(1): 2-16. (  0) 0) |
| [26] |
MA T F, WU J Y, HAO L L, et al. Energy flow matrix modeling and optimal operation analysis of multi energy systems based on graph theory[J]. Applied Thermal Engineering, 2019, 146: 648-663. DOI:10.1016/j.applthermaleng.2018.10.022 (  0) 0) |
| [27] |
刘俊峰, 陈剑龙, 王晓生, 等. 基于深度强化学习的微能源网能量管理与优化策略研究[J]. 电网技术, 2020, 44(10): 3794-3803. LIU Junfeng, CHEN Jianlong, WANG Xiaosheng, et al. Energy management and optimization of multi-energy grid based on deep reinforcement learning[J]. Power System Technology, 2020, 44(10): 3794-3803. (  0) 0) |
| [28] |
LIN K J, WU J Y, LIU D, et al. Energy management of combined cooling, heating and power micro energy grid based on leader-follower game theory[J]. Energies, 2018, 11(3): 647. (  0) 0) |
2. College of Economics and Management, Nanjing Institute of Technology, Nanjing 211167, China;
3. School of Automation, Nanjing University of Science and Technology, Nanjing 210094, China
 2022, Vol. 41
2022, Vol. 41


 邱纯(1997),女,硕士在读,研究方向为综合能源管理与优化运行(E-mail:
邱纯(1997),女,硕士在读,研究方向为综合能源管理与优化运行(E-mail: