文章编号: 2096-3203(2022)02-0186-07 中图分类号: TM352
2. 南京航空航天大学自动化学院,江苏 南京 211106
随着工业应用需求的不断提升,直线电机在智能电梯[1]、伺服生产线[2]、轨道交通[3-5]等工业领域以及航空军事领域应用越来越广泛[6-8]。
新型直线初级永磁式电机,如直线永磁磁通切换(linear flux-switching permanent magnet, LFSPM)电机的出现与研究,为提高直线驱动系统的整体性能提供了新的思路[9-10]。该类型电机结合了直线永磁同步电机高功率密度和直线开关磁阻电机定子结构简单的优点,在应用于如轨道交通等长定子应用场合时,定子侧仅由结构简单的硅钢片组成,因此可靠性高,易于维护[11-12]。然而由于定、动子的双凸极结构,LFSPM电机往往具有较大推力脉动[10-12]。因此研究LFSPM电机推力脉动的产生机理以及抑制方法具有重要的学术及工程价值。
一般来说,从本体结构角度造成直线永磁电机(永磁同步和初级永磁式)推力脉动主要有以下3个原因:(1) 定、动子齿槽效应产生的齿槽力[13-14];(2) 端部效应产生的端部力[10-12];(3) 空载磁链/反电势谐波[15-18]。
可见,端部效应产生的端部力是直线电机所特有的。由于LFSPM电机的端部力仅与电机端部结构和端部磁场分布有关,目前抑制端部力的方法主要是削弱和抵消端部力,一般采用优化端部结构,目前采用较多的是结构简单的辅助齿结构[19-20]。
齿槽力(转矩)和反电势谐波在旋转电机中也存在,是引起旋转电机转矩脉动的主要原因。因此,旋转电机中减小齿槽转矩和反电势谐波的方法可以移植到直线电机上来减小其齿槽力和反电势谐波。LFSPM电机齿槽力的减小可以直接移植其旋转结构齿槽转矩的减小方法,如转子步进斜槽结构[21]以及转子齿开槽[22],也可以借鉴永磁同步电机(直线结构和旋转结构)齿槽力(转矩)的减小方法,如斜槽结构[23]、优化转子齿尺寸[23]、齿槽极数配合[24-25]以及虚槽[23]等方法。
文中针对LFSPM电机,对抑制不同成因推力脉动的方法以及这些方法的组合效果进行仿真比较,比较过程中,提出一种的步进(错齿)位移选择方法。基于该方法,各组合结构在减小推力脉动的同时可以有效兼顾电机输出推力平均值。
1 辅助齿结构的比较根据引言中对推力脉动产生原因的分析,图 1给出了各种推力脉动抑制方法的分类。
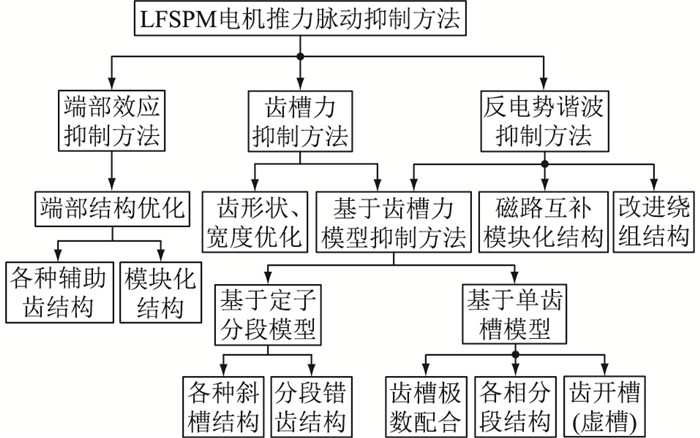
|
图 1 LFSPM电机推力脉动抑制方法分类 Fig. 1 Classification of the thrust ripple reduction methods for LFSPM machines |
以传统的12/14极LFSPM(12/14LFSPM)电机为原始结构,如图 2所示,主要参数见表 1。利用Ansoft有限元软件,采用较为通用的4种方法分步递进对12/14LFSPM电机推力脉动进行抑制和比较。
首先要改善12/14电机的端部效应。直线电机端部效应是由于动子(初级)电枢铁芯的两端断开,气隙磁场在电枢铁芯的端部发生畸变而产生的。端部效应会产生端部力。在直线电机中,齿槽力和端部力合称定位力(磁阻力),是直线电机推力脉动的主要成分[10]。直线电机端部效应还会引起三相空载磁链/反电势幅值不对称,这是因为直线电机端部磁路不对称,端部线圈的反电势幅值低于中间线圈的反电势幅值,使三相绕组空载反电势幅值不对称,从而降低推力平均值。
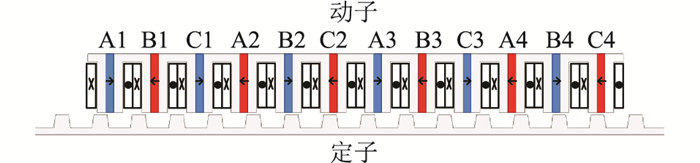
|
图 2 12/14LFSPM电机 Fig. 2 12/14LFSPM machine |
|
|
表 1 12/14LFSPM电机主要参数 Table 1 Main parameters of the 12/14LFSPM machine |
由于LFSPM电机的端部力仅与电机端部结构和端部磁场分布有关,目前抑制端部力的方法主要为削弱和抵消端部力。由于结构的限制,改变电机结构设计以减小端部力的选择较少,一般采用优化端部结构,如图 1所示。文献[19-20]研究的2种辅助齿结构可以减小端部力并平衡三相空载反电势幅值,且结构简单,所以文中比较了这2种结构,将其分别命名为辅助齿1和辅助齿2,如图 3(a)和图 3(b)所示,对应的电机命名为12/14LFSPM-E1和12/14LFSPM-E2。对这2台电机的辅助齿进行优化,端部尺寸标识如图 3(c)所示。其中,wt1为端部轭的宽度;wt2为端部齿的宽度;wpm为端部永磁体的宽度。
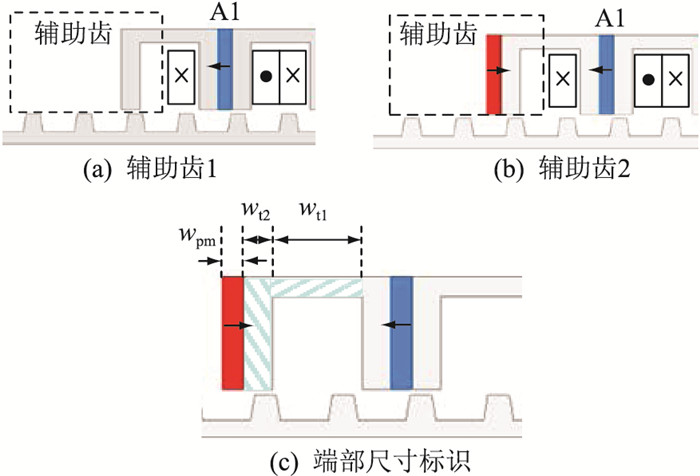
|
图 3 LFSPM电机辅助齿结构 Fig. 3 The assistant teeth structures of the LFSPM machine |
优化过程为:
(1) 先优化辅助齿1,设置2个比例参数,分别为r1和r2,其中,r1=wt1/τm,r2=wt2/τm,优化目标为使电机定位力最小,优化顺序为先r1后r2,r2的优化过程中采用优化好的r1。
(2) 然后在优化好的辅助齿1的基础上增加端部永磁体形成辅助齿2,优化辅助齿2中的永磁体宽度wpm,优化目标为使三相反电势幅值相等。
优化前后电机的定位力和空载反电势波形如图 4所示。由图 4(a)可知,辅助齿1和辅助齿2均可减小端部力,其中相对于原始结构12/14LFSPM,12/14LFSPM-E1和12/14LFSPM-E2的定位力峰峰值分别减小了约30%和21%。由图 4(b)—图 4(d)可以发现,辅助齿1和辅助齿2均可平衡三相空载反电势幅值,其中,12/14LFSPM、12/14LFSPM-E1和12/14LFSPM-E2的A相(端部相)反电势幅值与B相(中间相)反电势幅值比例分别约为94%,97%,100%。此外,由仿真可得12/14LFSPM、12/14LFSPM- E1和12/14LFSPM-E2的推力平均值分别为462 N,463 N,487 N,则3台电机定位力峰峰值占推力平均值比例为18%,13%,14%。
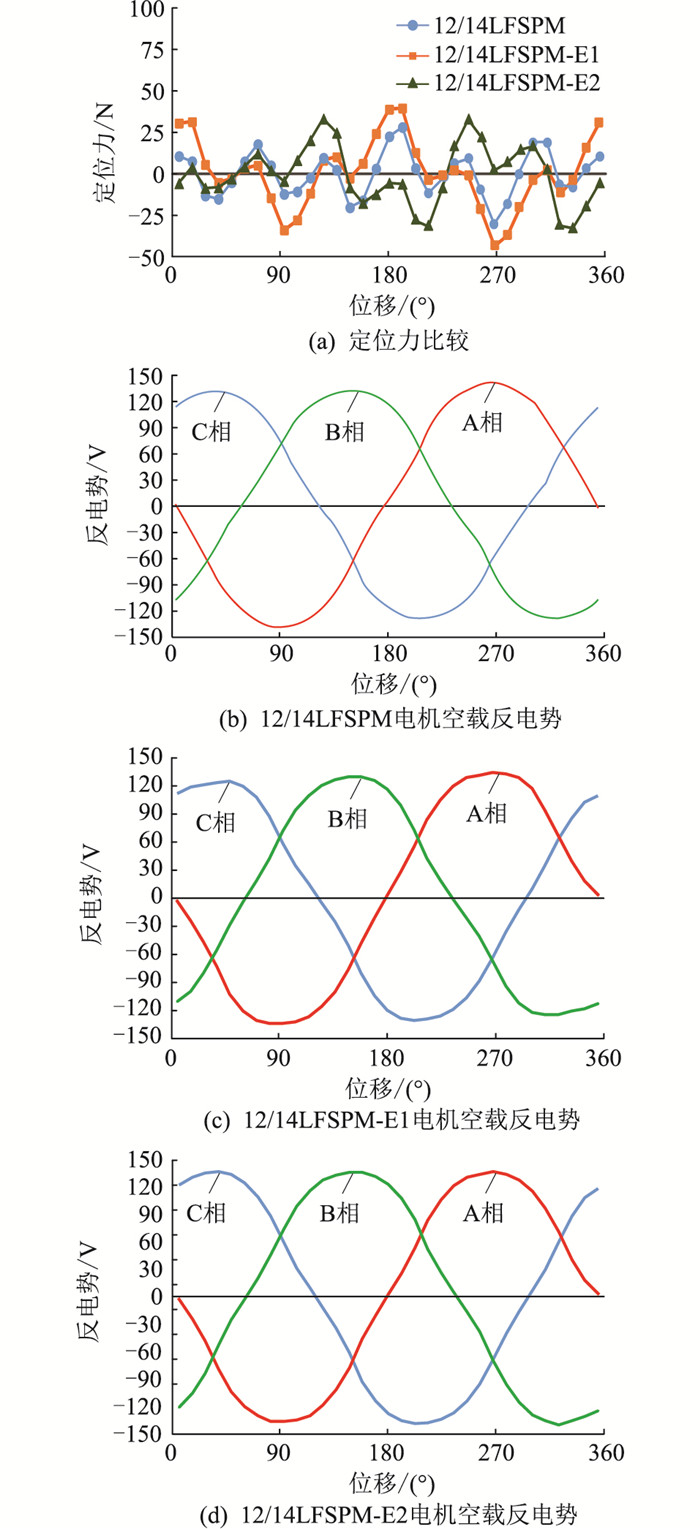
|
图 4 定位力与空载反电势 Fig. 4 Cogging force and no-load back-electromotive force (EMF) |
综上所述,2种辅助齿均可以有效地减小定位力中的端部力分量,同时平衡三相反电势幅值,提高输出推力平均值。
2 步进斜槽和分段错齿比较在抑制了12/14LFSPM电机的端部效应后,须对其进行进一步改进,来减小推力脉动。
直线电机的定位力由端部力和齿槽力组成,其中,齿槽力的成因与旋转电机的齿槽转矩(定位力矩)相同,是永磁体和电枢铁芯相互作用产生的,这与永磁同步电机类似。但LFSPM电机由于其双凸极结构,齿槽力比传统永磁同步电机要大。
文中将一种定子步进斜槽结构用于LFSPM电机来减小其定位力,尤其是其齿槽力分量。此外,综合考虑实现难度和抑制效果,定子步进斜槽采用三步斜槽结构(n=3)。同时,研究一种分段错齿结构,利用该结构分别对定子、动子进行改进,可有效减小LFSPM电机的定位力,尤其是齿槽力分量。因此,将辅助齿1和辅助齿2分别与定子三步斜槽和分段错齿结构组合起来,比较其组合后的效果。
为了方便分析,组合后的结构命名如下:(1) 12/14LFSPM-E1T,即辅助齿1与分段错齿结构组合;(2) 12/14LFSPM-E2T,即辅助齿2与分段错齿结构组合;(3) 12/14LFSPM-E1S,即辅助齿1与定子三步斜槽组合;(4) 12/14LFSPM-E2S,即辅助齿2与定子三步斜槽组合。
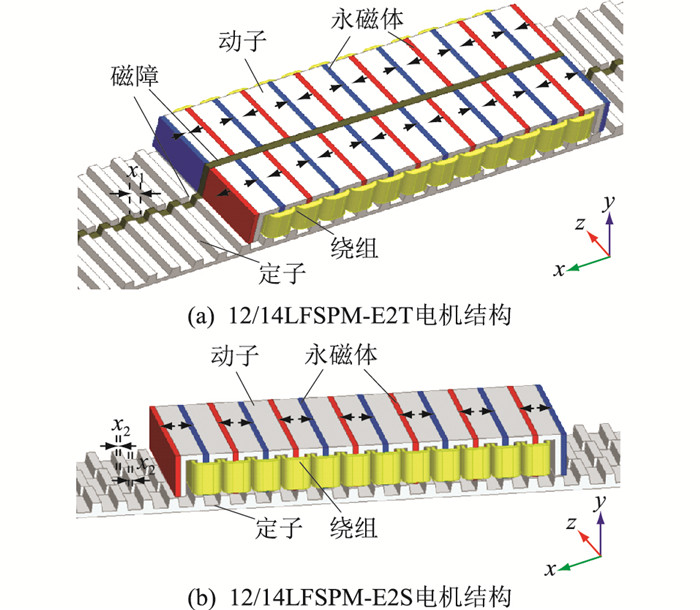
图 5以12/14LFSPM-E2T和12/14LFSPM-E2S为例,给出采用分段错齿和三步斜槽的电机结构,其中12/14LFSPM-E2T的2段定子错齿位移为x1,对应的电角度为θ1,12/14LFSPM-E2S定子斜槽的步进位移为x2,对应的电角度为θ2。
|
图 5 12/14LFSPM-E2T和12/14LFSPM-E2S电机结构 Fig. 5 Machine structures of 12/14LFSPM-E2T and 12/14LFSPM-E2S |
图 5(a)中,12/14LFSPM-E2T分段错齿结构的2段定子错开x1,2段动子相同位置永磁体充磁方向相反,前后2个动子极绕制1套线圈构成1个动子极,2段定动子分别由磁障来隔离(5 mm厚)。这种结构在2段定子错齿位移值为1/2极距(θ1=180°)或接近该值时可以抵消定位力,同时有效抑制反电势偶次谐波并保持基波幅值不变(θ1=180°时)或削弱很小。该电机1套线圈所匝链的永磁磁链表达式为(以只考虑二次谐波为例):
| $ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{\psi _{{\rm{A}}1}} = {\psi _{{\rm{A}}11}} + {\psi _{{\rm{A}}12}} = }\\ {\left( {{\psi _{\rm{m}}}\sin \left( {{\theta _{\rm{e}}} + {\varphi _1}} \right) + {\psi _{{\rm{m}}2}}\sin \left( {2{\theta _{\rm{e}}} + {\varphi _2}} \right)} \right) - }\\ {\left( {{\psi _{\rm{m}}}\sin \left( {{\theta _{\rm{e}}} + {\varphi _1} + {\theta _1}} \right) + {\psi _{{\rm{m}}2}}\sin \left( {2{\theta _{\rm{e}}} + {\varphi _2} + 2{\theta _1}} \right)} \right) = }\\ { - 2{\psi _{\rm{m}}}\sin \left( {{\theta _1}/2} \right)\cos \left( {{\theta _{\rm{e}}} + {\varphi _1} + {\theta _1}/2} \right) - } \end{array}}\\ {2{\psi _{{\rm{m}}2}}\sin \left( {{\theta _1}/2} \right)\cos \left( {2{\theta _{\rm{e}}} + {\varphi _2} + {\theta _1}} \right)} \end{array} $ | (1) |
式中:θe为定子位置对应的电角度;ψA11 ,ψA12分别为前、后2段动子极的永磁磁链;ψm,φ1分别为基波幅值和相位;ψm2,φ2分别为二次谐波幅值和相位。可以发现在理想情况下,当θ1=180°时,二次(偶次)谐波可以被消除,同时基波幅值不变。
由图 5(b)可知,12/14LFSPM-E2S的动子与12/14LFSPM-E2一样,而定子分为3段,每段之间错开x2,那么通过设置合适的x2,3段定子斜槽的定位力谐波分量就可以相互抵消,达到抑制定位力的目的。
下面通过仿真优化分别为分段错齿结构选择定子错齿位移x1以及为步进斜槽结构选择步进位移x2。在选择x1,x2时,除了要考虑定位力的减小程度,还要兼顾电机的输出推力平均值。为了方便分析,作如下定义。
(1) 定位力峰峰值比例:
| $ {\sigma _1} = \frac{{{F_{{\rm{cmax}}}} - {F_{{\rm{cmin}}}}}}{{{F_{{\rm{av}}}}}} \times 100\% $ | (2) |
(2) 推力平均值变化比例:
| $ {\sigma _2} = \frac{{{F_{{\rm{av}}1}} - {F_{{\rm{av}}2}}}}{{{F_{{\rm{av}}1}}}} \times 100\% $ | (3) |
(3) 推力脉动峰峰值比例:
| $ {\sigma _3} = \frac{{{F_{\max }} - {F_{\min }}}}{{{F_{{\rm{av}}}}}} \times 100\% $ | (4) |
式中:Fcmax,Fcmin,Fav分别为定位力正峰值、负峰值以及推力平均值;Fav1,Fav2分别为采用分段错齿结构或斜槽结构前、后的推力平均值;Fmax,Fmin分别为推力正峰值和负峰值。
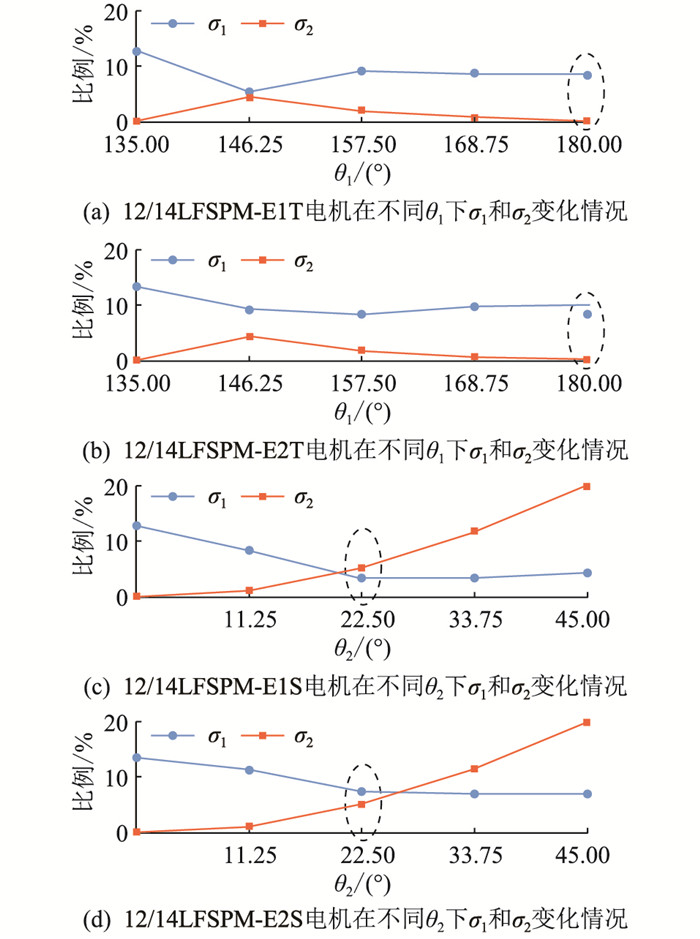
图 6给出了12/14LFSPM-E1T和12/14LFSPM-E2T在不同错齿位移对应的电角度θ1下以及12/14LFSPM-E1S和12/14LFSPM-E2S在不同步进位移对应的电角度θ2下,σ1和σ2的变化情况。算法采用Id=0矢量控制,假设注入的电枢电流为正弦波,θ1=0°和θ2=0°分别代表不采用分段错齿结构和斜槽结构时的电机。
|
图 6 不同θ1(θ2)下σ1和σ2变化情况 Fig. 6 The variation of σ1 and σ2 under different θ1(θ2) |
一般情况下,σ1和σ2越小越好,但往往不能兼得。这里以σ1与σ2之和最小作为选择依据,根据图 6,表 2给出4种电机选择结果。
|
|
表 2 θ1和θ2的选择结果 Table 2 Selection results of θ1 and θ2 |
根据表 2选择的结果,下面比较分析12/14LFSPM-E1T、12/14LFSPM-E2T、12/14LFSPM-E1S和12/14LFSPM-E2S与原始结构12/14LFSPM的定位力波形、推力波形、反电势谐波。
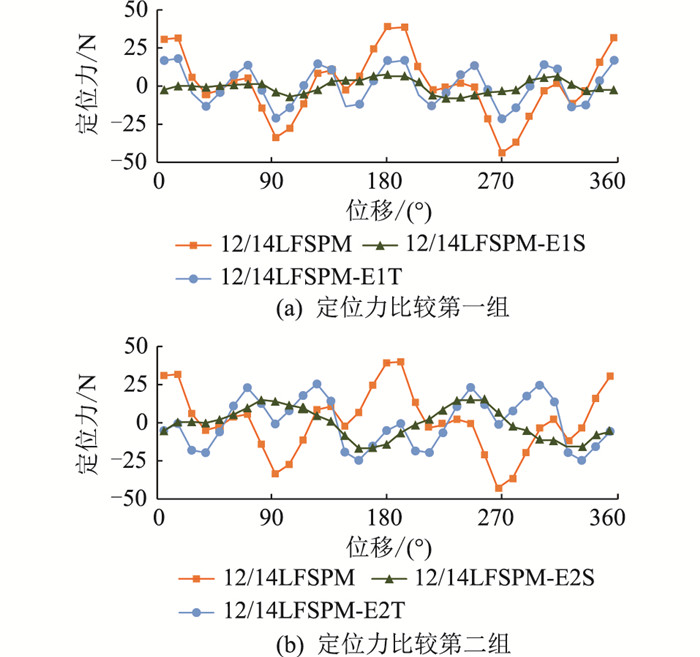
图 7给出了电机定位力的比较。可见,步进斜槽和分段错齿结构都可以进一步减小定位力,尤其是齿槽力分量,其中相对于原始结构12/14LFSPM,12/14LFSPM-E1T和12/14LFSPM-E1S的定位力峰峰值分别减小了约53%和82%,而12/14LFSPM-E2T和12/14LFSPM-E2S定位力峰峰值分别减小了约40%和60%。结合图 4(a)可以发现,采用分段错齿和三步斜槽结构后,定位力减小幅度更大。
|
图 7 定位力比较 Fig. 7 Comparison of cogging force |
图 8比较分析了A相空载反电势谐波。步进斜槽和分段错齿结构都可以抑制反电势谐波,其中,由于动子分段180°(电角度)的互补作用,12/14LFSPM-E1T和12/14LFSPM-E2T可以消除偶次谐波以及有效抑制部分奇次谐波,但是对于幅值最大的五次谐波没有抑制作用;而12/14LFSPM-E1S可以有效抑制奇次谐波,尤其是幅值最大的五次谐波;12/14LFSPM-E2S的偶次和部分奇次谐波都有很大程度减小,尤其是幅值最大的五次谐波。
|
图 8 A相反电势谐波分析比较 Fig. 8 Harmonic analysis of the A-phase back-EMF |
图 9比较了电机电磁推力。结合图 4、图 5和图 7可以发现,通过一系列的改进,相对于原始结构12/14LFSPM,12/14LFSPM-E1T、12/14LFSPM-E1S、12/14LFSPM-E2T和12/14LFSPM-E2S的推力脉动都得到有效减小。
|
图 9 电磁推力比较 Fig. 9 Comparison of the thrust force |
通过仿真计算和波形分析,表 3给出了12/14 LFSPM-E1T、12/14LFSPM-E2T、12/14LFSPM-E1S、12/14LFSPM-E2S和原始结构12/14LFSPM的比较结果。其中,ηTHD为A相空载反电势总的谐波畸变率;V为电机的有效体积;D为电机的推力密度。
|
|
表 3 12/14LFSPM电机各结构比较 Table 3 Structure comparison of the 12/14LFSPM machines |
根据前面的分析及表 3,得到如下结论:
(1) 通过改进结构,4台电机的推力脉动都显著减小,说明了改进结构的有效性,其中12/14LFSPM-E1T和12/14LFSPM-E1S电机的推力脉动比例最小,可以降低到7%。
(2) 分段错齿和斜槽结构在减小定位力的同时,对空载反电势谐波有一定的抑制效果,其中,12/14LFSPM-E2S反电势谐波可以抑制到1%左右。
(3) 定位力产生的推力脉动和反电势谐波产生的推力脉动存在互相抵消的情况,如12/14LFSPM-E1T和12/14LFSPM-E1S电机,其推力脉动峰峰值比例σ3小于定位力峰峰值比例σ1。
(4) 改进过程中,4台电机的体积都有不同程度的增大,其中12/14LFSPM-E2T由于改进时加了端部永磁体以及隔磁磁障,所以体积增加最大。由于体积的增加或者优化过程中推力平均值的削弱,4台电机的推力密度都减小了,其中12/14LFSPM-E1S的推力密度减小程度最大,减小了约12%。
改进过程中,电机结构的复杂程度都增加了,尤其是分段错齿结构,由于存在磁障,所以动子结构相对复杂。
4 结论对于LFSPM电机,研究其推力脉动的产生机理以及抑制方法是提升该电机应用潜力的重要手段。主要结论如下:
(1) 辅助齿结构和分段错齿结构或步进斜槽结构需要组合起来采用,才可以将LFSPM电机的推力脉动抑制到一个非常低的范围。
(2) 对于分段错齿结构和三步斜槽结构,将σ1与σ2之和的最小值作为错齿(斜槽)位移选择依据,得到的结构可以在抑制定位力的同时兼顾推力平均值的削弱程度。
(3) 分段错齿结构和三步斜槽结构在减小定位力的同时,也可以有效抑制空载反电势谐波,其中,分段错齿由于其动子结构互补,可以有效抑制或者消除偶次谐波,三步斜槽结构对奇次和偶次谐波都有抑制作用。
(4) 推力脉动抑制的代价就是会一定程度上减小推力密度,同时增加结构的复杂性。
分段错齿结构和斜槽结构具有通用性,可以根据不同的优化目标来选择错齿(斜槽)位移,适用于普通结构或者特殊结构,如C型铁芯、E型铁芯、模块化的LFSPM电机。
本文得到江苏省高校自然科学研究面上项目(19KJB470006),2019年江苏省高校“青蓝工程”项目资助,谨此致谢!
| [1] |
FAN H, CHAU K T, LIU C H, et al. Quantitative comparison of novel dual-PM linear motors for ropeless elevator system[J]. IEEE Transactions on Magnetics, 2018, 54(11): 1-6. (  0) 0) |
| [2] |
陈轶, 卢琴芬, 沈燚明. 双边水冷永磁直线电机的磁热耦合分析(英文)[J]. 中国电机工程学报, 2019, 39(7): 1852-1862. CHEN Yi, LU Qinfen, SHEN Yiming. Electromagnetic-thermalcoupled analysis of water-cooled double-sided permanent magnet linear synchronous machines[J]. Proceedings of the CSEE, 2019, 39(7): 1852-1862. (  0) 0) |
| [3] |
吕刚. 直线电机在轨道交通中的应用与关键技术综述[J]. 中国电机工程学报, 2020, 40(17): 5665-5675. LYU Gang. Review of the application and key technology in the linear motor for the rail transit[J]. Proceedings of the CSEE, 2020, 40(17): 5665-5675. (  0) 0) |
| [4] |
孙国斌. 日本直线电机制动技术的研究进展综述[J]. 铁道车辆, 2020, 58(1): 16-20, 4. SUN Guobin. Survey of research progress on linear motor braking technique in Japan[J]. Rolling Stock, 2020, 58(1): 16-20, 4. (  0) 0) |
| [5] |
姜岐广, 曲诗健, 姜涛, 等. 高速磁悬浮直线感应电机高精度推力控制[J]. 微电机, 2019, 52(10): 92-97. JIANG Qiguang, QU Shijian, JIANG Tao, et al. High-precision thrust control of high-speed maglev linear induction motor[J]. Micromotors, 2019, 52(10): 92-97. (  0) 0) |
| [6] |
许孝卓, 孙震, 汪旭东, 等. Halbach交替极永磁同步直线电机特性分析[J]. 电工技术学报, 2019, 34(9): 1825-1833. XU Xiaozhuo, SUN Zhen, WANG Xudong, et al. Characteristic of anovel permanent magnet linear synchronous motor with Halbach array consequent-pole[J]. Transactions of China Electrotechnical Society, 2019, 34(9): 1825-1833. (  0) 0) |
| [7] |
孙昌平, 谢贤飞, 于克训, 等. 脉冲发电机与直线感应电机直连供电系统建模与仿真[J]. 载人航天, 2020, 26(6): 696-701. SUN Changping, XIE Xianfei, YU Kexun, et al. Modeling and simulation of pulsed generator-linear induction motor directly connected power supply system[J]. Manned Spaceflight, 2020, 26(6): 696-701. DOI:10.3969/j.issn.1674-5825.2020.06.004 (  0) 0) |
| [8] |
潘剑飞, 邹宇, 曹广忠, 等. 一种直线开关磁阻电机发电研究[J]. 电机与控制学报, 2013, 17(2): 39-47. PAN Jianfei, ZOU Yu, CAO Guangzhong, et al. Study on the linear switched reluctance generator[J]. Electric Machines and Control, 2013, 17(2): 39-47. DOI:10.3969/j.issn.1007-449X.2013.02.007 (  0) 0) |
| [9] |
杜怿, 邹春花, 朱孝勇, 等. 初级永磁型游标直线电机绕组连接及其电磁特性比较[J]. 电工技术学报, 2017, 32(3): 130-138. DU Yi, ZOU Chunhua, ZHU Xiaoyong, et al. Comparison of winding arrangements and electromagnetic characteristics of a linear primary permanent magnet vernier machine[J]. Transactions of China Electrotechnical Society, 2017, 32(3): 130-138. (  0) 0) |
| [10] |
DU Y, YANG G, QUAN L, et al. Detent force reduction of a C-core linear flux-switching permanent magnet machine with multiple additional teeth[J]. Energies, 2017, 10(3): 318. DOI:10.3390/en10030318 (  0) 0) |
| [11] |
HAO W J, WANG Y. Analysis of double-sided sandwiched linear flux-switching permanent-magnet machines with staggered stator teeth for urban rail transit[J]. IET Electrical Systems in Transportation, 2018, 8(3): 175-181. DOI:10.1049/iet-est.2017.0062 (  0) 0) |
| [12] |
JIN M J, WANG C F, SHEN J X, et al. A modular permanent-magnet flux-switching linear machine with fault-tolerant capability[J]. IEEE Transactions on Magnetics, 2009, 45(8): 3179-3186. DOI:10.1109/TMAG.2009.2020090 (  0) 0) |
| [13] |
卢琴芬, 程传莹, 叶云岳, 等. 每极分数槽永磁直线电机的槽极数配合研究[J]. 中国电机工程学报, 2012, 32(36): 68-74, 12. LU Qinfen, CHENG Chuanying, YE Yunyue, et al. Slot/pole number combination research of PM linear motors with fractional slots per pole[J]. Proceedings of the CSEE, 2012, 32(36): 68-74, 12. (  0) 0) |
| [14] |
WANG C F, SHEN J X. A method to segregate detent force components in permanent-magnet flux-switching linear machines[J]. IEEE Transactions on Magnetics, 2012, 48(5): 1948-1955. DOI:10.1109/TMAG.2011.2177852 (  0) 0) |
| [15] |
HAO W J, WANG Y. Thrust force ripple reduction of two C-core linear flux-switching permanent magnet machines of high thrust force capability[J]. Energies, 2017, 10(10): 1608. DOI:10.3390/en10101608 (  0) 0) |
| [16] |
罗宏浩, 吴峻, 常文森. 动磁式永磁无刷直流直线电机的齿槽力最小化[J]. 中国电机工程学报, 2007, 27(6): 12-16. LUO Honghao, WU Jun, CHANG Wensen. Minimization of cogging force in moving magnet type PMBLDCLM[J]. Proceedings of the CSEE, 2007, 27(6): 12-16. DOI:10.3321/j.issn:0258-8013.2007.06.003 (  0) 0) |
| [17] |
REN N N, LI H S, XUE Z Q. Research of the cogging force in TPMLSM with unequal pole-pitch[C]//2016 IEEE Vehicle Power and Propulsion Conference. Hangzhou, China. IEEE, 2016: 1-5.
(  0) 0) |
| [18] |
CAO R W, CHENG M, MI C C, et al. Influence of leading design parameters on the force performance of a complementary and modular linear flux-switching permanent-magnet motor[J]. IEEE Transactions on Industrial Electronics, 2014, 61(5): 2165-2175. DOI:10.1109/TIE.2013.2271603 (  0) 0) |
| [19] |
MIN W, CHEN J T, ZHU Z Q, et al. Optimization and comparison of novel E-core and C-core linear switched flux PM machines[J]. IEEE Transactions on Magnetics, 2011, 47(8): 2134-2141. DOI:10.1109/TMAG.2011.2125977 (  0) 0) |
| [20] |
KROP D C J, ENCICA L, LOMONOVA E A. Analysis of a novel double sided flux switching linear motor topology[C]//The XIX International Conference on Electrical Machines-ICEM 2010. Rome, Italy. IEEE, 2010: 1-5.
(  0) 0) |
| [21] |
FEI W Z, LUK P C K, SHEN J X. Torque analysis of permanent-magnet flux switching machines with rotor step skewing[J]. IEEE Transactions on Magnetics, 2012, 48(10): 2664-2673. DOI:10.1109/TMAG.2012.2198223 (  0) 0) |
| [22] |
JIN M J, WANG Y, SHEN J X, et al. Cogging torque suppression in a permanent magnet flux-switching integrated-starter-generator[J]. IET Electric Power Applications, 2010, 4(8): 647-656. DOI:10.1049/iet-epa.2009.0176 (  0) 0) |
| [23] |
ISLAM M S, MIR S, SEBASTIAN T. Issues in reducing the cogging torque of mass-produced permanent-magnet brushless DC motor[J]. IEEE Transactions on Industry Applications, 2004, 40(3): 813-820. DOI:10.1109/TIA.2004.827469 (  0) 0) |
| [24] |
黄文美, 杨帅, 宋桂英. 永磁直线电动机削弱齿槽力的槽极数配合分析[J]. 微特电机, 2012, 40(4): 4-6. HUANG Wenmei, YANG Shuai, SONG Guiying. Analysis for reducing the cogging force using slot-poles number combination in permanent magnet linear motor[J]. Small & Special Electrical Machines, 2012, 40(4): 4-6. DOI:10.3969/j.issn.1004-7018.2012.04.002 (  0) 0) |
| [25] |
ZHOU S G, YU H T, HU M Q, et al. Reduction of cogging force in a linear flux-switching permanent-magnet brushless AC machine for direct-drive applications[J]. IEEE Transactions on Magnetics, 2011, 47(10): 3252-3255. DOI:10.1109/TMAG.2011.2151275 (  0) 0) |
2. College of Automation Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China
 2022, Vol. 41
2022, Vol. 41


 郝雯娟(1982),女,硕士,教授,研究方向为直线永磁磁通切换电机本体设计及控制算法(E-mail:
郝雯娟(1982),女,硕士,教授,研究方向为直线永磁磁通切换电机本体设计及控制算法(E-mail: