文章编号: 2096-3203(2022)02-0215-09 中图分类号: TM73
2. 西华大学电气与电子信息学院,四川 成都 610039
随着电力需求的增大,传统化石能源的大量使用造成严重的环境污染问题,基于智能电网和先进物联网技术的能源互联网能为解决能源危机提供有效手段[1-3],区域综合能源系统(regional integrated energy system,RIES)是能源互联网的一种重要实现形式[4-7]。目前针对RIES的运行、规划及优化配置等的研究成果充分说明了RIES建设的必要性和技术实现的可行性,但对其经济性评估的研究相对较少,而经济性对评判RIES的构架方案是否合理非常重要。当前,针对RIES效益评估的研究主要集中在评价指标搭建和权重求解方法两方面。
在评价指标体系搭建方面,文献[8-10]从不同维度构建了RIES的评估指标体系;文献[11]构建了拥有风光水储的微网经济运行评价指标体系;文献[12-13]面向多能互补,分别提出了不同能源形态的效率和可再生能源产能过剩率指标;文献[14]从投资者角度考虑银行贷款、内部收益率等经济参数,对微能源系统的投资效益进行分析。
在权重求解方法方面,RIES规划方案评估属于多属性群决策问题,其主要任务是确定相应的评价指标权重。主观权重赋权法反映决策专家的先验知识和自身经验,避免了指标主观权重和其实际重要程度相悖的现象,但评价结果具有较强的主观随意性,实际应用中有较大的局限性,具有代表性的方法有层次分析法[15]、最小平方和法[16]等。客观权重赋权法根据规划方案客观数据确定,但所得到的权重值可能违背决策者的主观意愿或无法真实准确反映规划的目的,具有代表性的方法有主成分分析法[17]、熵权法[18]等。为有效避免主、客观权重确定方法的缺点,需要将两者优点结合以构成综合赋权法来确定评估指标权重。
基于以上分析,文中从系统成本、系统收益及能源利用率3个维度建立RIES的经济效益评估指标体系,并搭建各指标模型。采用改进的最小叉熵法确定各指标的综合权重,实现主、客观权重之间内在联系的描述:一方面,该方法计及主观权重时,利用熵权法客观体现决策专家在各指标评价中的重要程度,避免了传统最小叉熵法中决策专家对评价结果影响度的模糊性;另一方面,在主、客观综合权重确定中,以指标的主、客观权重向量为基础构建二维平面坐标系确定每个指标的主、客观权重分配系数,降低了传统最小叉熵法中权重集成的主观性影响。最后结合优劣解距离法(technique for order preference by similarity to ideal solution, TOPSIS)和秩和比法(rank-sum ratio, RSR)建立RIES投资方案的决策评价模型,进行方案排序并选出最佳方案。
1 RIES的经济效益评估指标体系 1.1 RIES架构RIES的核心是集成物联网和能量管理技术,通过对某一指定区域内的化石能源、可再生能源等多类型能源进行充分调整和优化配置,实现多种能源的互补互济、交互响应、协调优化以及综合管理,在充分满足多层面、多元化用能的同时,可以有效提升综合能源利用率,缓解能源危机问题。RIES是典型的产供销一体化系统,计及的多种能源主要包括电能、热能、冷能和气能,电能生产设备主要包括风电和光伏机组,能源转换设备包括电转气(power to gas,P2G)装置、冷热电联产(combined cooling heating and power,CCHP)机组、电制冷/制热装置,电/燃气锅炉、热泵等,能源储存设备包括储热罐、储气罐和蓄电池等,各种能源形式的负荷中具有一定需求响应能力的负荷也可作为储能设备。
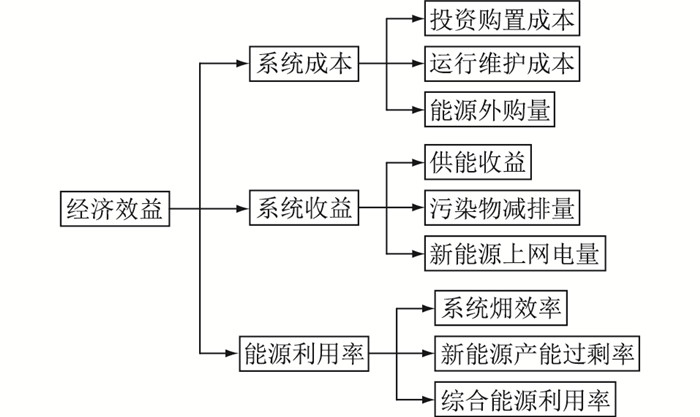
1.2 指标体系构建RIES的经济性评估指标体系可用于衡量评估区域系统内各种能源生产及相关转换设备的经济效益和利用率。文中根据RIES的系统架构,围绕投资运行的关注点,构建了两级评价指标体系,第一级指标分为系统成本、系统收益和能源利用率3个层面,在每一层面下分别建立了对应的3个二级指标,具体结构如图 1所示。
|
图 1 RIES评估指标体系 Fig. 1 The assessment index system for RIES |
设备的购买费用和安置费用包括风电机组、光伏机组、CCHP机组、储能装置、充电桩、加气站和P2G装置等设备分摊到生命周期年的购置费用,则投资购置费用C1为:
| $ \begin{aligned} C_{1}=Q_{\text {new }} & \sum\limits_{i=1}^{n_{1}}\left[\alpha_{i}\left(\beta_{i}+\gamma_{i}\right)\right]+\sum\limits_{j=1}^{n_{2}}\left(C_{\mathrm{CCHP}, j} \omega_{j} Q_{\mathrm{CCHP}, j}\right)+\\ & R_{\mathrm{P}} \sum\limits_{k=1}^{n_{3}}\left(\lambda_{k} \pi_{k}\right)+\sum\limits_{l=1}^{n_{4}}\left(Q_{\mathrm{G}, l} \varphi_{l}\right)+\\ & \sum\limits_{q=1}^{n_{5}}\left(Q_{\mathrm{C}, q} \delta_{q}\right)+\sum\limits_{y=1}^{n_{6}}\left(Q_{\mathrm{P} 2 \mathrm{G}, y} \sigma_{\mathrm{P} 2 \mathrm{G}, y}\right) \end{aligned} $ | (1) |
式中:Qnew为新能源机组容量;n1为新能源种类数;αi为第i种新能源装机比例;βi为第i种新能源发电机组单位容量成本系数;γi为第i种新能源机组安装成本系数;n2为CCHP中设备种类数;CCCHP, j为CCHP中第j种设备单位容量购置系数;ωj为CCHP中第j种设备附加设备成本系数;QCCHP, j为CCHP中第j种设备的容量;RP为储能系统总容量;n3为储能装置种类数;λk为第k种储能装置配比;πk为第k种储能装置单位容量购置价格;n4为加气站数;QG, l为第l个加气站容量;φl为第l个加气站设备单位容量购置系数;n5为系统内充电桩数量;QC, q为第q个充电桩安装容量;δq为第q个充电桩单位容量购置系数;n6为P2G设备数;QP2G, y为第y个P2G设备安装容量;σP2G, y为第y个P2G设备单位容量购置系数。RIES内组成部件的单位成本见表 1[10]。
|
|
表 1 RIES组件单位成本数据 Table 1 Unit cost data of RIES components |
RIES年运维费用可以分为不变费用和可变费用,不变费用是指人员工资和系统运行管理费,可变费用是指系统内设备的不定期检修维修等费用,则年运维费用C2为:
| $ \begin{gathered} C_{2}=Q_{\text {new }} \sum\limits_{i=1}^{n_{1}}\left[\alpha_{i}\left(C_{\mathrm{newc}, i}+T_{i} C_{\mathrm{newv}, i}\right)\right]+\sum\limits_{j=1}^{n_{2}}\left[Q_{\mathrm{CCHP}, j} \times\right. \\ \left.\left(C_{\mathrm{CCHPc}, j}+T_{j} C_{\mathrm{CCHPv}, j}\right)\right]+R_{\mathrm{P}} \sum\limits_{k=1}^{n_{3}}\left[\lambda _ { k } \left(C_{\mathrm{Pc}, k}+\right.\right. \\ \left.\left.T_{k} C_{\mathrm{Pv}, k}\right)\right]+\sum\limits_{l=1}^{n_{4}}\left[Q_{\mathrm{G}, l}\left(C_{\mathrm{Gc}, l}+T_{l} C_{\mathrm{Gv}, l}\right)\right]+\sum\limits_{q=1}^{n_{5}}\left[Q_{\mathrm{C}, q} \times\right. \\ \left.\left(C_{\mathrm{Cc}, q}+T_{q} C_{\mathrm{Cv}, q}\right)\right]+\sum\limits_{y=1}^{n_{6}}\left[Q_{\mathrm{P} 2 \mathrm{G}, y}\left(C_{\mathrm{P} 2 \mathrm{Gc}, y}+T_{y} C_{\mathrm{P} 2 \mathrm{Gv}, y}\right)\right] \end{gathered} $ | (2) |
式中:Cnewc, i,Cnewv, i分别为第i种可再生能源发电设备年单位容量不变成本和可变成本;CCCHPc, j,CCCHPv, j分别为CCHP中第j种能源转换设备年单位容量不变成本和可变成本;CPc, k,CPv, k分别为第k种储能设备年单位容量不变成本和可变成本;CGc, l,CGv, l分别为第l个加气站年单位容量不变成本和可变成本;CCc, q,CCv, q分别为第q个充电桩年单位容量不变成本和可变成本;CP2Gc, y,CP2Gv, y分别为第y个P2G设备单位容量不变成本和可变成本;T为各设备的平均年运行小时数。
1.3.3 能源外购量能源外购量主要包括CCHP机组的年耗气量,和新能源机组在供电不足情况下向大电网的购电量,没有考虑在实际运行情况下电制冷和电制热能效比不同对能源外购量的影响。能源外购量C3可描述为:
| $ \left\{\begin{array}{l} C_{3}=\left[(1-\upsilon-\theta) W_{\mathrm{E}}+\Delta W_{\mathrm{E}}\right]+(1-\tau) W_{\mathrm{G}} \frac{Q_{\mathrm{g}}}{Q_{\mathrm{e}}} \\ \Delta W_{\mathrm{E}}=\frac{\Delta W_{\mathrm{H}}}{\zeta_{\mathrm{H}}}+\frac{\Delta W_{\mathrm{C}}}{\zeta_{\mathrm{C}}} \end{array}\right. $ | (3) |
式中:υ为CCHP机组发电量占实际用电量比重;θ为新能源发电量占实际用电量比重;WE为年用电量,不包含因缺冷、缺热而由电制冷机、电制热机产生冷能、热能消耗的电能;ΔWE为CCHP机组在冷、热供应不足的情况下采用电制冷、电制热消耗的电能;τ为电转气量占实际用气负荷比重;WG为园区用气量;Qe为单位电量热值;Qg为单位立方的燃气热值;ΔWC,ΔWH分别为供应给用户的冷、热负荷不足量;ζH,ζC分别为电制热和电制冷的能效比。
1.3.4 供能收益供能收益是指RIES为终端用户提供电、气、冷、热等各种形式能源所获得的收益,其表示为:
| $ C_{4}=\sum\limits_{z=1}^{m}\left(W_{z} u_{z}\right) $ | (4) |
式中:m为供能种类;Wz为第z种能源形式用能量;uz为第z种能源单价。
1.3.5 污染气体减排量文中主要考虑将RIES区域内消纳风电、光伏电量按照热当量的方法折算成等值标准煤燃烧发电所产生的温室气体(CO2)和污染物气体(SO2,NOx)的排放量,并计及CCHP机组的CO2,SO2,NOx气体的排放量,则污染气体减排量C5为:
| $ \begin{aligned} C_{5}=\sum\limits_{p=1}^{n_{7}}&\left\{\left[\sum\limits_{i=1}^{n_{1}}\left(P_{i} T_{i}\right)+\sum\limits_{j=1}^{n_{2}}\left(P_{\mathrm{CCHP}, j} T_{j}\right)\right] m_{\mathrm{coal}, p}\right\}-\\ &\ \ \ \ \sum\limits_{p=1}^{n_{7}}\left[\sum\limits_{j=1}^{n_{2}}\left(P_{\mathrm{CCHP}, j} T_{j}\right)\right] m_{\mathrm{CCHP}, p} \end{aligned} $ | (5) |
式中:n7为污染物排放种类;Pi为第i种新能源年平均发电量;PCCHP, j为CCHP中第j种发电设备年平均发电量;mcoal, p为燃煤机组单位发电量对应的第p种排放污染物重量;mCCHP, p为CCHP单位发电量对应的第p种排放污染物重量。发电机组各污染排放系数见文献[19]。
1.3.6 新能源上网电量新能源上网电量是指在可再生能源产生的电量满足园区用电量且还有剩余情况下,并网后可卖给大电网的剩余电量,即:
| $ C_{6}=\sum\limits_{i=1}^{n_{1}} \Delta W_{\text {new }, i} $ | (6) |
式中:ΔWnew, i为第i种新能源剩余电量。
1.3.7 系统效率根据热力学第一定律,RIES的能量分析方法是借助能量转化之间的数学联系来评估能量利用热效率。对系统效率的分析是对能源的量和质的综合反映。系统效率C7为:
| $ \left\{\begin{array}{l} C_{7}=\frac{W_{\mathrm{E}} / 3\ 600+\varepsilon_{1} W_{\mathrm{H}}+\varepsilon_{2} W_{\mathrm{C}}}{W_{\mathrm{grid}} / 3\ 600+W_{\text {new }} / 3\ 600}+\frac{\varepsilon_{0} W_{\mathrm{G}}}{W_{\mathrm{gas}}} \\ \varepsilon_{1}=1-T_{\mathrm{0H}} / T_{\mathrm{H}} \\ \varepsilon_{2}=1-T_{0 \mathrm{C}} / T_{\mathrm{C}} \end{array}\right. $ | (7) |
式中:电能的能质系数为1,因此外购电量Wgrid、新能源发电量Wnew以及用电量WE的电量为其本身电量;WH为供热量;WC为供冷量;Wgas为总购气量;ε0,ε1,ε2分别为天然气能质系数、供热量能质系数、供冷量能质系数,且ε0=0.95;T0H,T0C分别为供热和供冷时的环境温度;TH,TC分别为供热、供冷温度。
1.3.8 新能源产能过剩率新能源产能过剩率可反映光伏、风电等可再生能源发电充裕情况,其值为正表明可再生能源发电量较为丰裕,可能有多余电量卖给大电网;其值为负代表可再生能源发电量匮乏,其计算为:
| $ C_{8}=\frac{W_{\text {new }}-\left(W_{\mathrm{E}}-W_{\mathrm{CCHP}}\right)}{W_{\mathrm{E}}} $ | (8) |
式中:WCCHP为CCHP机组发电量。
1.3.9 综合能源利用率RIES的能源利用率能够体现多能流在不同时间尺度上耦合互补、能量梯级应用的程度,根据文献[4]中提出的综合能源系统的总体能量效率指标,在考虑网损率影响的情况下,综合能源利用率C9为:
| $ C_{9}=\frac{W_{\mathrm{E}}+W_{\mathrm{H}}+W_{\mathrm{C}}}{W_{\mathrm{grid}} /\left(1-\eta^{\prime}\right)}+\frac{W_{\mathrm{G}}}{W_{\mathrm{gas}}} $ | (9) |
式中:η′为区域内的线损率。
2 RIES组成方案的评价指标权重确定RIES组成方案评估结果对权重确定方法和集成方法的依赖程度较高,采用主、客观权重综合赋权方法能有效兼顾主、客观信息,从而得到普遍认可。现有指标权重确定方法均添加了额外信息而导致最终决策结果不精确,采用具有信息熵原理的熵权法能够有效避免这一缺点,但信息熵因单纯依据距离来确定权重而存在一定的局限性,文中借助最小叉熵来寻求权重差异性最小的概率分布。
传统最小叉熵方法在确定评估指标的权重时存在2个明显的问题。一是在评估指标的主观权重确定过程中,通常会事先确定决策专家权重,无法体现其具体确定过程;二是在评估指标的综合权重确定过程中,主观权重分配系数是直接由专家的知识和经验来给定,无法体现指标主、客观权重的内在联系。针对以上2点不足,文中对最小叉熵法进行改进:在确定主、观权重时,利用熵权法体现专家评价的重要程度;在确定主、客观综合权重时,先构建主客观权重向量的二维平面,再计算主客观权重分配系数。
2.1 决策矩阵的标准化针对RIES方案决策问题,假设包含m个决策方案和n个评价指标(文中n=9),用A= {a1, a2, …, am} (m≥2)表示构成方案集,C= {c1, c2, …, cn }描述指标集,则形成原始数据矩阵X,其中xij为第i个方案中的第j个指标,X=(xij)(i=1, 2, …, m; j=1, 2, …, n)。
由于在实践工程中经济性指标通常会出现负值、零值或趋零值,因此线性比例变换法、偏差变换法、向量归一化法一般不适用,文中采用极差变换法,得到指标标准化后决策矩阵Z=(zij)。
其中,效益型指标为:
| $ z_{i j}=\frac{x_{i j}-\min \limits_{1 \leqslant i \leqslant m}\left(x_{i j}\right)}{\max \limits_{1 \leqslant i \leqslant m}\left(x_{i j}\right)-\min \limits_{1 \leqslant i \leqslant m}\left(x_{i j}\right)} $ | (10) |
成本型指标为:
| $ z_{i j}=\frac{\max \limits_{1 \leqslant i \leqslant m}\left(x_{i j}\right)-x_{i j}}{\max \limits_{1 \leqslant i \leqslant m}\left(x_{i j}\right)-\min \limits_{1 \leqslant i \leqslant m}\left(x_{i j}\right)} $ | (11) |
指标原始数据直接决定其客观权重的大小,因此根据标准化决策矩阵Z,用熵权法计算出客观权重向量ωo=(ωo, 1, ωo, 2, …, ωo, n),其中第j个指标的客观权重为:
| $ \omega_{0, j}=\frac{1+\frac{1}{\ln m} \sum\limits_{i=1}^{m}\left(s_{i j} \ln s_{i j}\right)}{\sum\limits_{j=1}^{n}\left[1+\frac{1}{\ln m} \sum\limits_{i=1}^{m}\left(s_{i j} \ln s_{i j}\right)\right]} $ | (12) |
其中:
| $ s_{i j}=z_{i j} / \sum\limits_{i=1}^{m} z_{i j} $ | (13) |
指标主观权重确定与决策者的主观认识和判断密切相关,对于不同的决策者,其认知程度不一样,判断结果也会有明显差异。文中采用相应的效用函数来描述不同决策者的判断。具体步骤为:
(1) 首先产生一个反映专家k对指标主观认识不同而产生差异的效用函数矩阵Uk,指标由标准化决策矩阵Z表示。假设效用函数大于等于0,且为简化采用了单变量形式,则对于第k个专家有Uk=(uk(zij))(k=1, 2, …, l),l为专家总人数。
(2) 根据效用函数矩阵Uk,利用熵权法得到不同专家对评估指标主观权重的判断矩阵β=(βkj)。其中:
| $ \beta_{k j}=\frac{1+\frac{1}{\ln m} \sum\limits_{i=1}^{m}\left(w_{k, i j} \ln w_{k, i j}\right)}{\sum\limits_{j=1}^{n}\left[1+\frac{1}{\ln m} \sum\limits_{i=1}^{m}\left(w_{k, i j} \ln w_{k, i j}\right)\right]} $ | (14) |
| $ w_{k, i j}=u_{k}\left(z_{i j}\right) / \sum\limits_{i=1}^{m} u_{k}\left(z_{i j}\right) $ | (15) |
(3) 最小叉熵法在确定指标主观权重的过程中,决策专家权重依据专家先验知识、工程经验,人为确定其重要程度,最终评价结果具有一定的模糊性且主观随意性较强。因此,在步骤(2)中求得的不同专家对评估指标主观权重判断矩阵β的基础上,运用熵权法确定决策专家权重向量α,以消除传统最小叉熵法中决策专家权重的模糊性对决策结果产生的不良影响。第k个决策专家的权重如式(16)所示。
| $ \alpha_{k}=\frac{1+\frac{1}{\ln n} \sum\limits_{j=1}^{n} g_{k j} \ln g_{k j}}{\sum\limits_{k=1}^{l}\left[1+\frac{1}{\ln n} \sum\limits_{j=1}^{n}\left(g_{k j} \ln g_{k j}\right)\right]} $ | (16) |
其中:
| $ g_{k j}=\beta_{k j} / \sum\limits_{k=1}^{l} \beta_{k j} $ | (17) |
(4) 构建以综合主观权重向量与每个专家的主观权重矩阵βk距离最小的最小叉熵模型,得到指标的综合主观权重向量βo=(βo, 1, βo, 2, …, βo, n)。目标函数为:
| $ \left\{\begin{array}{l} \min D=\sum\limits_{k=1}^{l}\left(\alpha_{k} D_{k}\left(\boldsymbol{\beta}_{\rm o}, \boldsymbol{\beta}_{k}\right)\right) \\ \text {s.t. } \sum\limits_{j=1}^{n} \beta_{{\rm o}, j}=1 \quad \beta_{{\rm o}, j} \geqslant 0 \end{array}\right. $ | (18) |
| $ D_{k}\left(\boldsymbol{\beta}_{\mathrm{o}}, \boldsymbol{\beta}_{k}\right)=\sum\limits_{j=1}^{n}\left(\beta_{{\mathrm{o}}, j} \ln \frac{\beta_{{\mathrm{o}}, j}}{\beta_{k j}}\right) $ | (19) |
计算得到第j个指标主观权重为:
| $ \beta_{\mathrm{o}, j}=\mathrm{e}^{\alpha_{k} \sum\limits_{k=1}^{l} \ln \beta_{k j}} / \sum\limits_{j=1}^{n} \mathrm{e}^{\sum\limits_{k=1}^{l} \alpha_{k} \ln \beta_{k j}} $ | (20) |
考虑到最小叉熵法的优势,文中仍然建立主客观权重差异最小的最小叉熵模型求得指标综合权重。而传统最小叉熵法在确定指标综合权重时,指标主、客观权重分配系数依据专家个人偏好给定,具有随意性,且不能反映主客观权重的内在联系。因此,以指标的主、客观权重向量为基础构建一个二维平面,并求取每个指标的主客观权重分配系数,以此降低传统最小叉熵法中指标综合权重集成的主观性影响。即:
| $ \left\{\begin{array}{l} \min \left[\boldsymbol{\gamma} D\left(\boldsymbol{\omega}, \boldsymbol{\beta}_{\mathrm{o}}\right)+(\bf{1}-\boldsymbol{\gamma}) D\left(\boldsymbol{\omega}, \boldsymbol{\omega}_{\mathrm{o}}\right)\right] \\ \text {s.t. } \sum\limits_{j=1}^{n} \omega_{j}=1 \quad \omega_{j} \geqslant 0 \end{array}\right. $ | (21) |
式中:ω=(ω1, ω2, …, ωn)为综合权重向量;γ=(γ1, γ2, …, γn)(0≤γj≤1),1 -γ分别为主观权重和客观权重分配系数向量;ωj为指标j的综合权重。
| $ \gamma_{j}=\frac{\beta_{\mathrm{o}, j}}{\beta_{\mathrm{o}, j}+\omega_{\mathrm{o}, j}} $ | (22) |
| $ 1-\gamma_{j}=\frac{\omega_{\mathrm{o}, j}}{\beta_{\mathrm{o}, j}+\omega_{\mathrm{o}, j}} $ | (23) |
| $ \begin{gathered} \omega_{j}=\mathrm{e}^{\gamma_{j} \ln \beta_{\mathrm{o}, j}+\left(1-\gamma_{j}\right) \ln \omega_{\mathrm{o}, j}} / \sum\limits_{j=1}^{n} \mathrm{e}^{\gamma_{j} \ln \beta_{\mathrm{o}, j}+\left(1-\gamma_{j}\right) \ln \omega_{\mathrm{o}, j}}= \\ \left(\beta_{\mathrm{o}, j}^{\gamma_{j}} \omega_{\mathrm{o}, j}^{1-\gamma_{j}}\right) / \sum\limits_{j=1}^{n}\left(\beta_{\mathrm{o}, j}^{\gamma_{j}} \omega_{\mathrm{o}, j}^{1-\gamma_{j}}\right) \end{gathered} $ | (24) |
TOPSIS[20-22]评估方法是常用的组内综合评价法,其优点是能充分利用原始数据,使得结果能精确反映评价对象之间的差距,但容易受指标异常值(零值或趋零值)影响。而RSR[23]是一种非参数统计评价方法,其特点是不受指标异常值影响,但计算值为秩次,不能对原始数据进行充分利用。因此,文中结合两者优点对决策方案进行综合评价。TOPSIS-RSR综合评价具体流程如下。
(1) 构建加权规范化矩阵。
| $ \boldsymbol{B}=\left[\begin{array}{cccc} b_{11} & b_{12} & \cdots & b_{1 n} \\ b_{21} & b_{22} & \cdots & b_{2 n} \\ \vdots & \vdots & & \vdots \\ b_{m 1} & b_{m 2} & \cdots & b_{m n} \end{array}\right] $ | (25) |
式中:bij=ωjzij; i=1, 2, …, m; j=1, 2, …, n。
(2) 确定正、负理想方案。
| $ \left\{\begin{array}{l} \boldsymbol{B}^{+}=\left(b_{1}^{+}, b_{2}^{+}, \cdots, b_{n}^{+}\right) \\ b_{j}^{+}=\max \limits_{1 \leqslant j \leqslant n}\left(b_{i j}\right) \end{array}\right. $ | (26) |
| $ \left\{\begin{array}{l} \boldsymbol{B}^{-}=\left(b_{1}^{-}, b_{2}^{-}, \cdots, b_{n}^{-}\right) \\ b_{j}^{-}=\min \limits_{1 \leqslant j \leqslant n}\left(b_{i j}\right) \end{array}\right. $ | (27) |
(3) 计算各评价方案与正负理想方案的贴近度,决策方案到正理想方案的距离为。
| $ D_{i}^{+}=\sqrt{\sum\limits_{j=1}^{n}\left(b_{j}^{+}-b_{i j}\right)^{2}} \quad i=1,2, \cdots, m $ | (28) |
决策方案到负理想方案的距离为:
| $ D_{i}^{-}=\sqrt{\sum\limits_{j=1}^{n}\left(b_{j}^{-}-b_{i j}\right)^{2}} \quad i=1,2, \cdots, m $ | (29) |
(4) 计算决策方案到负理想方案的相对贴近度。
| $ E_{i}=\frac{D_{i}^{-}}{D_{i}^{+}+D_{i}^{-}} \quad i=1,2, \cdots, m $ | (30) |
(5) 计算概率单位。将Ei的值替换成由RSR评价方法所得的各评价对象的加权秩和比WRSR, i;计算各评价对象出现的次数fi和累计次数∑fi,从而确定各评价对象RSR的秩次Ri及平均秩次Ri;计算各评价对象的累计频率Fi=Rim×100%,为保证WRSR, i的值小于1,最后一个对象的频率用1-1/(4m)计算;根据累计频率,查询百分率与概率单位对照表,得到对应的概率单位Pi。
(6) 将Pi作为自变量,Ei作为因变量,设置直线回归方程Ei=a+bPi,利用最小二乘法估计出a, b参数。
(7) 按照回归方程推算WRSR, i并排序,选择出最优方案T*。
| $ T^{*}=\max \limits_{1 \leqslant i \leqslant m}\left(W_{\mathrm{RSR}, i}\right) $ | (31) |
以某工业园区RIES为研究对象,该园区采光面积、光照辐射强度分别为20 000 m2和1 500 (kW ·h)/m2,平均风速约为5 m/s,系统的用电负荷为4.1 MW,冷热负荷分别为2.4 MW和3.1 MW,气负荷为4.2 MW,由光伏发电、风电、储能系统、CCHP机组以及天然气组成的RIES结构方案如表 2所示。其中,混合储能系统包括蓄电池、储热罐和储气罐。
|
|
表 2 RIES结构方案 Table 2 Structure plans of RIES |
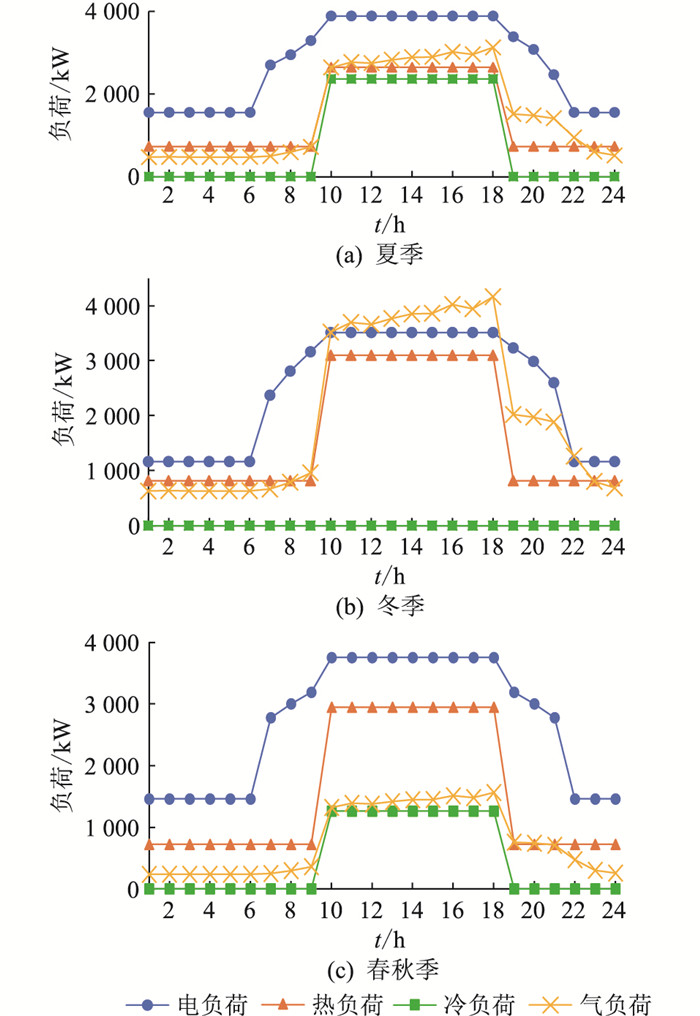
假设园区的气价为1.96元/m3,电网电价为0.64元/(kW ·h),网损率为5%,并且要求可再生能源供电自给率要达到40%及以上,外购电均来自燃煤火电厂,ξC和ξH均为3。参考文献[24]工业类负荷曲线,该工业园区夏季(6~8月)、冬季(12~1月)、春秋季(3~5月、9~11月)典型日负荷曲线如图 2所示。由式(1)—式(9)可计算出各能源系统组成方案的指标值如表 3所示。
|
图 2 某工业园区四季典型日负荷 Fig. 2 Typical daily load of an industrial park in four seasons |
|
|
表 3 不同RIES配置方案的指标值 Table 3 Indexes of the different RIES configuration plans |
假设分别取
|
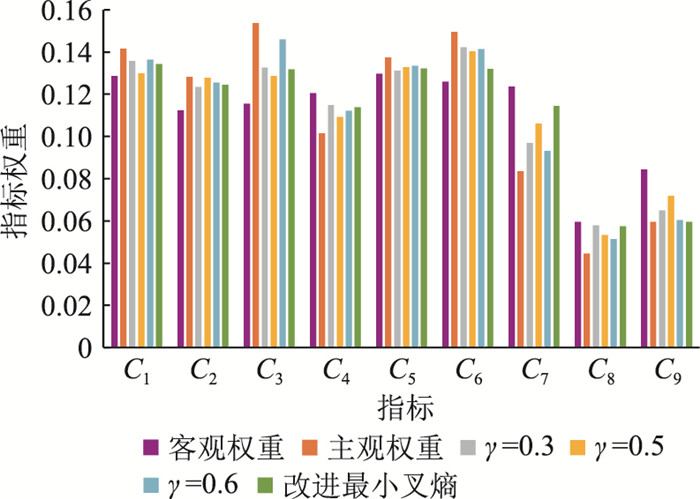
图 3 评估指标权重赋值比较 Fig. 3 Evaluation index weights comparison |
由图 3可知,最小叉熵法在确定指标综合权重的过程中因专家主观经验、先验知识影响,指标综合权重较为偏向指标主观权重或客观权重,影响了最终决策结果;而利用文中所提改进最小叉熵法得到的评价指标权重依则根据指标主、客观权重向量得出,不易受主观随意性影响,不刻意偏向主观或客观权重,得出的是一个较为折中的权重结果,且能够计及主观、客观权重之间蕴含的联系,保证了改进的合理性。
4.2 系统方案优选根据TOPSIS-RSR进行决策时,首先利用式(10)和式(11)计算标准化决策矩阵以求取变换的指标;然后通过所得指标权重和式(27)计算得到加权标准化评价矩阵B。利用式(28)和式(29),结合矩阵B中各评价指标的极大值、极小值,分别确定对应决策方案的正理想方案矩阵为B+=(0.039 8, 0.034 7, 0.043 6, 0.037 1, 0.035 9, 0.034 6, 0.035 6, 0.042 1, 0.032 9),负理想矩阵为B-=(0.014 7, 0.027 6, 0.025 8, 0.022 1, 0.027 0, 0.028 1)。借助B+和B-,根据式(30)—式(32)求取RIES组成方案与负理想方案的贴近度矩阵E=(0.204 9, 0.645 2, 0.673 1, 0.693 5, 0.792 9)。用Ei的值代替WRSR, i值后计算fi,∑fi,Ri,Ri,Fi,Pi及WRSR, i的结果如表 4所示。
|
|
表 4 各评价对象的计算变量值及结果 Table 4 Results and calculation values of all evaluation objects |
由表 4可知,各系统组成方案的综合评价结果为WRSR, i,则方案A5的值最大,因此RIES系统组成方案的优劣排序为A1 < A2 < A3 < A4 < A5,即A5为所有组成方案中的最优选择方案。
5 结论文中提出一种RIES组成方案经济性评价方法。建立适用于RIES组成方案经济性评价指标模型体系,利用基于改进最小叉熵法的TOPSIS-RSR方法对指标进行集成和方案评价。可以得出以下结论:
(1) 基于改进最小叉熵法可以量化多位专家的综合效用,客观、合理地进行不同系统组成方案的优劣排序,并确定最佳决策方案。
(2) 经济效益是综合能源网络投资运营主体的首要关注点,而综合的经济效益评估可以快速提供给投资商有价值的参考。
(3) 文中运用TOPSIS-RSR法进行综合评价,结合了TOPSIS、RSR两者的优点,评价结果既不受异常值影响,又能充分利用原始数据,对系统组成方案的综合评价更具有准确性、科学性。
本文得到国网甘肃省电力公司科技项目(52270819000A)资助,谨此致谢!
| [1] |
杨挺, 翟峰, 赵英杰, 等. 泛在电力物联网释义与研究展望[J]. 电力系统自动化, 2019, 43(13): 9-20, 53. YANG Ting, ZHAI Feng, ZHAO Yingjie, et al. Explanation and prospect of ubiquitous electric power Internet of Things[J]. Automation of Electric Power Systems, 2019, 43(13): 9-20, 53. DOI:10.7500/AEPS20190418015 (  0) 0) |
| [2] |
申洪, 周勤勇, 刘耀, 等. 碳中和背景下全球能源互联网构建的关键技术及展望[J]. 发电技术, 2021, 42(1): 8-19. SHEN Hong, ZHOU Qinyong, LIU Yao, et al. Key technologies and prospects for the construction of global energy internet under the background of carbon neutral[J]. Power Generation Technology, 2021, 42(1): 8-19. (  0) 0) |
| [3] |
张晶, 胡纯瑾, 于海玉, 等. 能源互联网重点领域标准国际化布局研究[J]. 供用电, 2021, 38(7): 3-8. ZHANG Jing, HU Chunjin, YU Haiyu, et al. Research on internationalization layout of energy internet technical standards in key areas[J]. Distribution & Utilization, 2021, 38(7): 3-8. (  0) 0) |
| [4] |
HUANG Z, FANG B L, DENG J. Multi-objective optimization strategy for distribution network considering V2G-enabled electric vehicles in building integrated energy system[J]. Protection and Control of Modern Power Systems, 2020, 5: 7. DOI:10.1186/s41601-020-0154-0 (  0) 0) |
| [5] |
陈云, 刘东, 高飞, 等. 考虑电转气环节氢能精细化利用的区域综合能源系统日前优化调度[J]. 供用电, 2021, 38(11): 59-67. CHEN Yun, LIU Dong, CHEN Fei, et al. Day-ahead optimal dispatching of regional integrated energy system considering refined utilization of hydrogen in power to gas process[J]. Distribution & Utilization, 2021, 38(11): 59-67. (  0) 0) |
| [6] |
卢炳文, 魏震波, 魏平桉, 等. 考虑消纳风电的区域综合能源系统电转气与储能设备优化配置[J]. 智慧电力, 2021, 49(5): 7-14. LU Bingwen, WEI Zhenbo, WEI Pingan, et al. Optimal configuration of PtG and energy storage equipment in regional integrated energy system considering wind power consumption[J]. Smart Power, 2021, 49(5): 7-14. DOI:10.3969/j.issn.1673-7598.2021.05.003 (  0) 0) |
| [7] |
帅轩越, 王秀丽, 黄晶. 多区域综合能源系统互联下的共享储能容量优化配置[J]. 全球能源互联网, 2021, 4(4): 382-392. SHUAI Xuanyue, WANG Xiuli, HUANG Jing. Optimal configuration of shared energy storage capacity under multiple regional integrated energy systems interconnection[J]. Journal of Global Energy Interconnection, 2021, 4(4): 382-392. (  0) 0) |
| [8] |
陈柏森, 廖清芬, 刘涤尘, 等. 区域综合能源系统的综合评估指标与方法[J]. 电力系统自动化, 2018, 42(4): 174-182. CHEN Baisen, LIAO Qingfen, LIU Dichen, et al. Comprehensive evaluation indices and methods for regional integrated energy system[J]. Automation of Electric Power Systems, 2018, 42(4): 174-182. (  0) 0) |
| [9] |
张玉莹, 李雷, 刘萧民. 计及不确定性的综合能源系统运行效益综合评估方法[J]. 可再生能源, 2019, 37(11): 1671-1678. ZHANG Yuying, LI Lei, LIU Xiaomin. Comprehensive evaluation method for integrated energy system operation benefits considering the impact of uncertainties[J]. Renewable Energy Resources, 2019, 37(11): 1671-1678. DOI:10.3969/j.issn.1671-5292.2019.11.015 (  0) 0) |
| [10] |
张世翔, 吕帅康. 面向园区微电网的综合能源系统评价方法[J]. 电网技术, 2018, 42(8): 2431-2439. ZHANG Shixiang, LYU Shuaikang. Evaluation method of park-level integrated energy system for microgrid[J]. Power System Technology, 2018, 42(8): 2431-2439. (  0) 0) |
| [11] |
夏永洪, 吴虹剑, 辛建波, 等. 考虑风/光/水/储多源互补特性的微网经济运行评价方法[J]. 电力自动化设备, 2017, 37(7): 63-69. XIA Yonghong, WU Hongjian, XIN Jianbo, et al. Evaluation of economic operation for microgrid with complementary DGs and energy storage[J]. Electric Power Automation Equipment, 2017, 37(7): 63-69. (  0) 0) |
| [12] |
郭艳飞, 吴强, 程林, 等. 基于效率的综合能源系统能效分析模型[J]. 可再生能源, 2017, 35(9): 1387-1394. GUO Yanfei, WU Qiang, CHENG Lin, et al. Efficiency analysis model of integrated energy system based on the exergy efficiency[J]. Renewable Energy Resources, 2017, 35(9): 1387-1394. (  0) 0) |
| [13] |
杜琳, 孙亮, 陈厚合. 计及电转气规划的综合能源系统运行多指标评价[J]. 电力自动化设备, 2017, 37(6): 110-116. DU Lin, SUN Liang, CHEN Houhe. Multi-index evaluation of integrated energy system with P2G planning[J]. Electric Power Automation Equipment, 2017, 37(6): 110-116. (  0) 0) |
| [14] |
李建林, 牛萌, 周喜超, 等. 能源互联网中微能源系统储能容量规划及投资效益分析[J]. 电工技术学报, 2020, 35(4): 874-884. LI Jianlin, NIU Meng, ZHOU Xichao, et al. Energy storage capacity planning and investment benefit analysis of micro-energy system in energy interconnection[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 874-884. (  0) 0) |
| [15] |
周剑, 罗添允, 李智勇, 等. 基于改进可拓层次分析的停电影响综合评估[J]. 电力系统保护与控制, 2019, 47(3): 31-38. ZHOU Jian, LUO Tianyun, LI Zhiyong, et al. Comprehensive evaluation of power failure based on improved extension analytic hierarchy process[J]. Power System Protection and Control, 2019, 47(3): 31-38. (  0) 0) |
| [16] |
周本金, 陶以政, 纪斌, 等. 最小化误差平方和k-means初始聚类中心优化方法[J]. 计算机工程与应用, 2018, 54(15): 48-52. ZHOU Benjin, TAO Yizheng, JI Bin, et al. Optimizing k-means initial clustering centers by minimizing sum of squared error[J]. Computer Engineering and Applications, 2018, 54(15): 48-52. DOI:10.3778/j.issn.1002-8331.1706-0223 (  0) 0) |
| [17] |
王维洲, 汤红卫, 刘福潮, 等. A+~E类区域配电网降损潜力评估模型研究[J]. 电力科学与技术学报, 2018, 33(2): 59-65. WANG Weizhou, TANG Hongwei, LIU Fuchao, et al. Study on the evaluation model of energy loss reduction potential for A+~E regional distribution network[J]. Journal of Electric Power Science and Technology, 2018, 33(2): 59-65. (  0) 0) |
| [18] |
南钰, 宋瑞卿, 陈鹏, 等. 基于改进熵权-灰色关联法的配电网可靠性影响因素分析[J]. 电力系统保护与控制, 2019, 47(24): 101-107. NAN Yu, SONG Ruiqing, CHEN Peng, et al. Study on the factors influencing the reliability analysis in distribution network based on improved entropy weight gray correlation analysis algorithm[J]. Power System Protection and Control, 2019, 47(24): 101-107. (  0) 0) |
| [19] |
吴耀文, 马溪原, 孙元章, 等. 微网高渗透率接入后的综合经济效益评估与分析[J]. 电力系统保护与控制, 2012, 40(13): 49-54. WU Yaowen, MA Xiyuan, SUN Yuanzhang, et al. Overall economic evaluation and analysis of accession of microgrids with high penetration[J]. Power System Protection and Control, 2012, 40(13): 49-54. (  0) 0) |
| [20] |
MIEJA M, GEIGER B C. Semi-supervised cross-entropy clustering with information bottleneck constraint[J]. Information Sciences, 2017, 421: 254-271. (  0) 0) |
| [21] |
MENG D, SHAO C, ZHU L. Ethylene cracking furnace TOPSIS energy efficiency evaluation method based on dynamic energy efficiency baselines[J]. Energy, 2018, 156: 620-634. (  0) 0) |
| [22] |
LI X Z, GAO Y L, ZHAO H L. Comparative research on the IOT industry competitiveness of eastern, central and western China: a comprehensive evaluation based on TOPSIS and GRA[C]//2015 IEEE International Conference on Grey Systems and Intelligent Services. Leicester, UK. IEEE, 2015: 187-193.
(  0) 0) |
| [23] |
周敏, 艾敬. 基于TOPSIS-RSR的中国省际能源生态效率评估[J]. 生态经济, 2019, 35(3): 45-50, 67. ZHOU Min, AI Jing. The provincial energy ecological efficiency evaluation in China based on TOPSIS-RSR method[J]. Ecological Economy, 2019, 35(3): 45-50, 67. (  0) 0) |
| [24] |
雷霞, 唐文左, 李逐云, 等. 考虑区域综合能源系统优化运行的配电网扩展规划[J]. 电网技术, 2018, 42(11): 3459-3470. LEI Xia, TANG Wenzuo, LI Zhuyun, et al. Distribution network expansion planning considering optimal operation of regional integrated energy system[J]. Power System Technology, 2018, 42(11): 3459-3470. (  0) 0) |
2. School of Electrical and Electronic Information, Xihua University, Chengdu 610039, China
 2022, Vol. 41
2022, Vol. 41


 赵尔敏(1974),男,学士,高级工程师,从事电网规划技术和管理相关工作(E-mail:
赵尔敏(1974),男,学士,高级工程师,从事电网规划技术和管理相关工作(E-mail: