文章编号: 2096-3203(2022)02-0037-08 中图分类号: TM732
2. 新疆大学电气工程学院,新疆维吾尔自治区 乌鲁木齐 830047
换相失败是依靠电网电压换相的高压直流输电技术中最为常见的故障类型之一[1-2]。随着我国特高压直流输电工程不断推进,换相失败引起的故障容量和发生频率有所增加,给混联系统的安全稳定带来极大的风险和挑战[3-6]。据国家电网公司统计,2004年至2018年,所投运的21个直流工程共发生1 353次换相失败,平均每个直流工程每年发生9.1次换相失败[7]。因此,开展换相失败的机理及抑制措施研究具有较高的理论、工程价值。
国内外学者针对直流电流的增加[8-9]、换相电压的降低[10]、换相电感的变化[11]、不对称故障下电压的偏移、谐波造成的电压畸变[12]以及故障合闸角[13]对换相过程的影响机理已进行了相关研究。现有文献针对电气量对换相过程的影响研究较为全面,针对控制量对换相失败的影响或锁相环误差、交流保护动作等间接影响因素仍缺乏相关定量计算方法。
目前换相失败抑制措施可分为2类:一类是通过增加设备或改变换流器的结构[14-15]等方法,增强系统的换相失败免疫能力,然而额外设备的加入会增加运行成本、损耗与新的运行风险;另一类是改进控制策略,这类换相失败抑制措施可以在稳态时维持一个较小的换相裕度,在故障暂态期间通过控制调节触发角、电流或电压的指令值,迅速增加换相裕度,抵御换相失败的发生,是一种灵活、经济的方式。
定关断角控制是逆变器的一种基本控制策略,可分为实测型和预测型2种[16]。文献[17]使用同步相量测量单元(phasor measurement unit,PMU)技术改进了实测型定关断角控制策略,但要事先获得系统的等值戴维南参数。相比实测型定关断角控制器,预测型定关断角控制器具有更好的速动性。文献[18-19]在预测型定关断角控制内部增加了直流电流预测模块,将实时计算控制转变为预测控制,实现首次换相失败的预测与抑制。文献[12]考虑了谐波,提出考虑直流电流变化和谐波影响的换相失败抑制策略。文献[20]利用关断角变化与电流偏差控制函数斜率关联关系,提出动态电流偏差控制方法,能够很好地抑制连续换相失败发生。
目前鲜有文献对预测型定关断角控制中电流偏差环节的暂态影响进行分析。文中分析了高压直流输电基本控制策略中预测型定关断角控制与电流偏差控制的关系,明确了电流偏差环节的功能。在此基础上,研究了故障暂态初期与恢复阶段,电流偏差环节中比例系数对换相失败抑制、系统恢复效果的影响,并提出一种自适应电流偏差环节,通过检测电气量判别系统状态并自适应输出比例系数,以兼顾换相失败的有效抑制与系统快速平稳恢复。最后,基于CIGRE标准测试系统的结构和基本参数,改变换流站控制策略,搭建了高压直流输电系统模型,验证了所提理论分析和自适应电流偏差控制的有效性。
1 HVDC系统换相失败及基本控制策略 1.1 HVDC系统换相失败高压直流输电系统中换流器的基本模块是Graetz桥,其包含6个晶闸管阀,连接于交流三相中某一相与直流正或负极间。通过调整晶闸管的触发角,可以实现功率在交、直流系统间的双向传导:当触发角α>90°时,换流器工作于逆变器状态,功率从直流流向交流;当α<90°时,换流器工作于整流器状态,功率从交流向直流系统传导。阀电流在共阴极组或共阳极组之间传导的过程被称为换相过程,由于线路、滤波器等的电感分量以及变压器存在的漏感,会使换相过程中存在等效换相电感,导致换相过程并不是瞬时完成的,这部分时间转化为电角度后被称为换相角μ。换相成功后,由于半控型元件的特性,换流阀需要承受一段时间的反向截止电压,使内部载流子复合以恢复其阻断能力,这部分时间转化为电角度后被称为关断角γ。
晶闸管元件中,载流子复合开关建立P-N结阻挡层以恢复正向阻断能力需要一定的时间,文中取400 μs,这部分时间对应的电角度被称为临界关断角γ0。当实际关断角小于γ0时,会出现下列2种情况:(1) 换相结束后,刚退出导通的阀在反向电压作用期间不能恢复阻断能力;(2) 2个桥臂的换相过程一直未能结束。这2种情况都会导致预期开通的阀未能开通,预期关断的阀未能关断,这种异常的工况被称为换相失败。
1.2 高压直流输电系统基本控制策略高压直流输电系统基本控制策略包含定电流、定电压和定关断角控制,均配备独立控制器并采用限幅相互嵌套的方式实现控制模式平滑切换,如图 1所示。
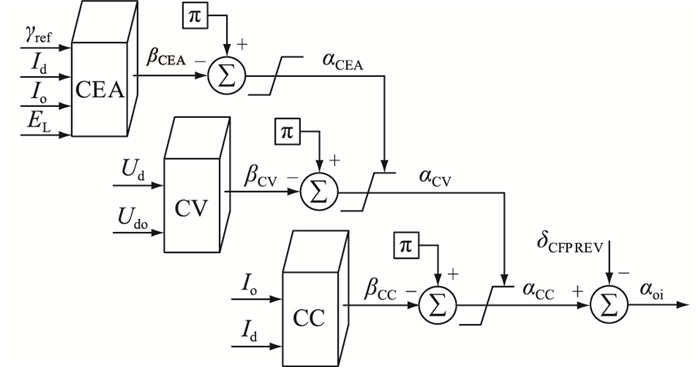
|
图 1 高压直流输电系统基本控制策略(逆变侧) Fig. 1 Basic control strategy of HVDC system (inverter side) |
图 1中,γref为预测型定关断角控制器中关断角整定值;Io,Id分别为低压限流控制(voltage dependent current order limiter, VDCOL)输出的逆变侧直流电流指令值与直流电流经一阶惯性环节后的实测值;EL为逆变侧交流系统线电压有效值;Udo,Ud分别为逆变侧直流电压指令值与经过一阶惯性环节后的逆变侧直流电压实测值;βCEA,αCEA,βCV,αCV,βCC,αCC分别为预测型定关断角、定电压、定电流控制器输出的超前触发角和触发角指令值,CEA,CV,CC分别为预测型定关断角、定电压、定电流控制器;δCFPREV为换相失败预测控制输出量;αoi为逆变器触发角指令值;此外还配备最小关断角(GAMMA0)控制功能,保证直流电压下降阶段逆变器触发角指令值由CEA提供,以改善交流电压稳定性[21]。
其中预测型定关断角控制可表示为:
| $ \beta {\rm{ = }}\arccos \left[ {\cos \;{\gamma _{{\rm{ref}}}} - 2{d_{\rm{x}}}\frac{{{I_{\rm{o}}}}}{{{I_{{\rm{dN}}}}}}\frac{{{U_{{\rm{di0N}}}}}}{{{U_{{\rm{di0}}}}}} - K\left( {{I_{\rm{o}}} - {I_{\rm{d}}}} \right)} \right] $ | (1) |
式中:dx为逆变侧等值换相电抗标幺值;Udi0N,Udi0分别为逆变侧理想空载直流电压的额定值、实际值;K为电流偏差比例系数;γref为关断角参考值;IdN为额定直流电流。
Udi0与EL关系为:
| $ {U_{{\rm{di0}}}} = \frac{{3\sqrt 2 N}}{{{\rm{ \mathsf{ π} }}T}}{E_{\rm{L}}} $ | (2) |
式中:N为串联六脉动桥的数量;T为换流变压器变比,阀侧电压/二次侧电压=1/T。dx计算方法为:
| $ {d_{\rm{x}}} = \frac{{3{X_{\rm{c}}}{I_{{\rm{dN}}}}}}{{{\rm{ \mathsf{ π} }}{U_{{\rm{di0N}}}}}} $ | (3) |
式中:Xc为换相电抗。将式(2)和式(3)代入式(1)可得:
| $ \beta {\rm{ = }}\arccos \left[ {\cos \;{\gamma _{{\rm{ref}}}} - \frac{{\sqrt 2 T{I_{\rm{o}}}{X_{\rm{c}}}}}{{N{E_{\rm{L}}}}} - K\left( {{I_{\rm{o}}} - {I_{\rm{d}}}} \right)} \right] $ | (4) |
忽略三相间的不平衡度及电压偏移角度,三相对称始终存在α+β=π,式(4)变为:
| $ \alpha {\rm{ = }}\arccos \left[ {\frac{{\sqrt 2 T{I_{\rm{o}}}{X_{\rm{c}}}}}{{N{E_{\rm{L}}}}} + K\left( {{I_{\rm{o}}} - {I_{\rm{d}}}} \right) - \cos \;{\gamma _{{\rm{ref}}}}} \right] $ | (5) |
根据式(5),预测型定关断角控制的原理仍然是经典关断角计算公式,通过获取直流电流、交流电压等信息,采用计算方式替代实时测量的方式,应用开环控制快速输出逆变器的触发角指令值。且在控制环节加入了电流偏差控制环节,并将电流偏差比例系数K设置为正,从而保证系统在暂态下具有一定的正斜率特征:当Io保持不变时,若系统实际电流受小干扰扰动而增大,根据式(5),控制器增大α,从而主动增大逆变侧直流电压,最终达到降低直流电流,将系统恢复至稳态工作点的作用。
采用式(5)表示的预测型定关断角控制,可以在小干扰下,通过主动控制直流电压的方式消除扰动的影响,但是在大暂态干扰下很难有效恢复至稳态工作点,极易引起换相失败,其主要是因为暂态期间系统选取了直流电流指令值。因此在文献[22]中,预测型关断角控制的表示为:
| $ \alpha {\rm{ = }}\arccos \left[ {\frac{{\sqrt 2 T{I_{\rm{d}}}{X_{\rm{c}}}}}{{N{E_{\rm{L}}}}} + K\left( {{I_{\rm{o}}} - {I_{\rm{d}}}} \right) - \cos \;{\gamma _{{\rm{ref}}}}} \right] $ | (6) |
无论是式(5)还是式(6),预测型定关断角控制内部嵌入了电流偏差控制环节,为了获得正斜率的特征,设置电流偏差系数为正常数,以保证小干扰下系统的稳定。但针对电流偏差环节引入的影响,目前鲜有文献给出具体分析并提出解决方案。
2 电流偏差环节的影响分析 2.1 电流偏差环节对换相失败抑制效果的影响当逆变侧交流系统发生故障并导致换流母线处电压跌落时,Id会迅速上升,而故障初期Io会保持不变或减小,因此电流偏差K(Io-Id)转变为负,引起触发角α不断增大,易导致换相失败。
式(6)对K求解偏导数有:
| $ \frac{{\partial \alpha }}{{\partial K}} = \frac{{{I_{\rm{d}}} - {I_{\rm{o}}}}}{{\sqrt {1 - {{\left[ {\frac{{\sqrt 2 T{I_{\rm{d}}}{X_{\rm{c}}}}}{{N{E_{\rm{L}}}}} + K\left( {{I_{\rm{o}}} - {I_{\rm{d}}}} \right) - \cos \;{\gamma _{{\rm{ref}}}}} \right]}^2}} }} $ | (7) |
故障初期Id增加,Io不变或降低,Id-Io为正,根据式(7)可知∂α/∂K为正,α与K呈现正相关函数关系,即α随着K增大而增大。因此,当K设置为正时,K越大,电流偏差环节在故障初期引起的触发角增量越大。为定量计算电流偏差环节的影响,可将式(6)转化为:
| $ \alpha {\rm{ = }}\arccos \left( {\frac{{\sqrt 2 T{I_{\rm{d}}}{X_{\rm{c}}}}}{{N{E_{\rm{L}}}}} - \cos \;{\gamma _{{\rm{target}}}}} \right) $ | (8) |
其中,关断角目标值γtarget计算公式为:
| $ {\gamma _{{\rm{target}}}}{\rm{ = }}\arccos \left[ {\cos \;{\gamma _{{\rm{ref}}}} + K\left( {{I_{\rm{d}}} - {I_{\rm{o}}}} \right)} \right] $ | (9) |
根据式(9),故障初期直流电流升高,电流偏差环节相当于主动将预测型定关断角控制的控制目标由γref调整为γtarget。由于K为正数,导致γtarge<γref,因此这种调整会增加系统换相失败的风险程度。由此可见,电流偏差环节的目标仅为使系统获得正斜率特征,以保证其在小干扰下可以回归至稳态状态。但在较大干扰的暂态过程中,若将比例系数设置为正数,该环节会导致换相失败的风险增加,且K越大,换相失败风险程度越高。
2.2 电流偏差环节对系统恢复过程的影响若系统经历换相失败,在恢复过程中,由预测型定关断角控制切换至定电流控制(情况一),定电流控制接管逆变器期间,逆变器控制目标变为使直流电流Id达到VDCOL输出的指令值Io,该阶段内Id在Io的带动下,按照设定的恢复速率进行恢复,Io大于Id。定电流控制期间,由于电流偏差环节嵌入于预测型定关断角控制中,预测型定关断角控制输出量为定电流控制输出的上限,并不会被选中,看似该阶段电流偏差控制并不会直接影响系统的恢复过程,但实际上电流偏差控制会通过改变预测型定关断角控制输出量间接影响预测型定关断角控制与定电流控制输出曲线交点,即定电流控制器起作用时刻。
当电流偏差系数K为正数时,根据式(7)可知,故障初期电流偏差环节将会导致触发角指令值增大,且K越大,该环节引起的触发角增量越大。因此,K为正时,K越大,预测型定关断角控制切换至定电流控制时刻越早。当K设置为正时,K越大对系统恢复过程越有利,但相应地系统后续换相失败的风险程度可能也会有所提高。
若系统未发生换相失败,系统恢复过程中逆变器始终为预测型定关断角控制(情况二),直流电流指令值Io不变或轻微减小,直流电流在故障初期后由最高值(大于1.0 p.u)开始降低,经过稳态值1.0 p.u后继续降低,并开始恢复。此过程中(Io-Id)由负转为正且始终增加,若K设置为正,根据式(9),γtarget会先大于γref,后小于γref,但一直在减小。
逆变器功率因数ϕ近似计算公式为[23]:
| $ \cos \;\phi \approx 0.5\left( {\cos \;{\gamma _{\rm{i}}} + \cos \left( {{\gamma _{\rm{i}}} + \mu } \right)} \right) $ | (10) |
式中:γi为逆变器关断角。根据式(10)可知,K设置为正数,恢复过程中定关断角控制器的控制目标γtarget始终保持减小的趋势,关断角的减小有助于增加逆变器功率因数,降低逆变器无功消耗,对恢复过程有利,但同时会增加后续换相失败风险。
3 自适应电流偏差环节电流偏差系数K设置为正,可令系统在小干扰下自动恢复稳定点,但若在大干扰情况下,会降低预测型定关断角控制对换相失败的抑制能力。在恢复过程中,虽然有助于系统恢复,但同时会增加后续换相失败的风险。因此在不同的阶段,识别系统状态,选取最为适合的电流偏差系数,可使电流偏差环节更具优势,起到兼顾换相失败抑制与系统快速恢复的效果。因此,改进后的电流偏差环节比例系数选取方法如图 2、图 3所示。其中,图 2为控制信号判别模块,其功能为判别系统当前状态;图 3为电流偏差比例系数输出模块,其功能为依据所判别状态,输出最为适合的比例系数。
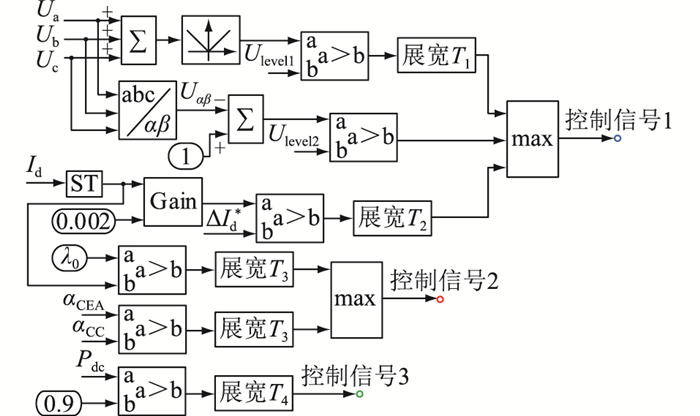
|
图 2 自适应电流偏差判断模块 Fig. 2 Judgment module in adaptive current error control |

|
图 3 自适应电流偏差输出模块 Fig. 3 Output module of adaptive current error control |
图 2中,Ua,Ub,Uc分别为逆变侧换流母线三相电压测量值;Ulevel1,Ulevel2分别为单相、三相故障下的启动阈值;abc/αβ为Clark变换模块;Uαβ为三相电压的αβ分量;ST为微分环节;Gain为增益;0.002 s为预测的换相时间(对应工频系统电角度为36°);λ0为电流微分门槛值;ΔId*为换相期间直流电流变化量启动阈值,计算方法可参考文献[18];Pdc为直流输送功率测量值,可选取上层定功率控制输入信号。图 3中,0.15为稳态时电流偏差环节比例系数;k1为故障初期电流偏差环节比例系数选取值;k2为恢复阶段电流偏差环节比例系数选取值。
自适应电流偏差判断模块中将故障暂态期间系统状态划分为三部分:第一部分为故障初期,通过检测三相电压的αβ分量与零序分量快速判别交流系统是否发生故障,通过预测直流电流初步判别该故障是否会引起换相失败;第二部分为故障恢复阶段,通过比较定电流控制与预测型定关断角控制输出判断定电流控制是否起作用,同时判别直流电流形态,在直流电流达到峰值后的下降阶段内同时发出启动信号,因此无论系统处于2.2节中2种情况中任何一种,均可有效识别;第三部分为故障恢复末期阶段,通过检测直流输送功率是否达到稳态值的90%[24]进行判别。
在检测系统处于故障初期阶段时,将电流偏差环节中比例系数调整为k1(k1可依据工程调试情况进行设定,可为负数);在检测系统处于恢复阶段时,将比例系数调整为k2,以改善系统恢复效果;当检测到系统处于恢复末期,将比例系数调整为稳态值,确保稳态下系统仍然具有预设的正斜率特征。其中k1,k2须设定单边界动态限幅klimit,其计算公式为:
| $ {k_{{\rm{limit}}}} = \frac{{\cos 7.2^\circ - \cos \;{\gamma _{{\rm{ref}}}}}}{{{I_{\rm{d}}} - {I_{\rm{o}}}}} $ | (11) |
为验证传统电流偏差环节的影响与所提出自适应电流偏差环节的有效性,在PSCAD/EMTDC中,基于CIGRE直流输电标准模型,通过修改整流、逆变站控制系统建立测试系统,其中模型参数依据文献[25],控制系统参数如表 1所示,仿真测试中晶闸管最小关断时间设置为400 μs。
|
|
表 1 整流侧和逆变侧控制参数 Table 1 Parameters of controllers on the rectifier side and inverter side |
为排除换相失败预测控制的干扰将其主动切除,为全面衡量换相失败可能性,在逆变侧换流母线处设置不同时刻(1.30~1.31 s)经过不同电感(1.2~1.5 H)接地的三相短路故障,故障持续时间为0.1 s,电流偏差环节中比例系统分别设置为0.15和-0.15,换相失败测试结果如图 4所示。在逆变侧换流母线处设置不同故障时刻(1.30~1.31 s)经过不同电感(0.6~0.9 H)单相(A相)接地故障,故障持续时间0.1 s,电流偏差环节比例系数分别设置为0.15和-0.15,换相失败情况如图 5所示。
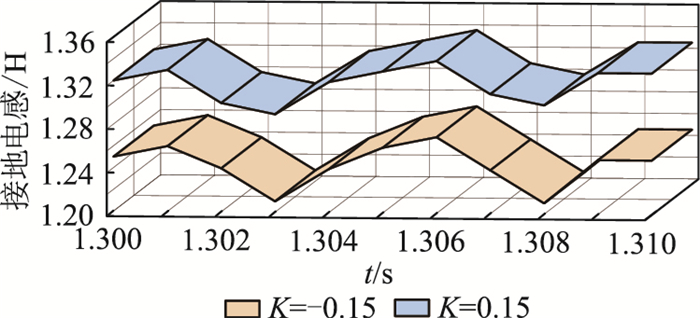
|
图 4 三相接地故障下不同比例系数的临界电感 Fig. 4 Critical inductance of commutation failure with different proportional coefficients under three-phase grounding fault |
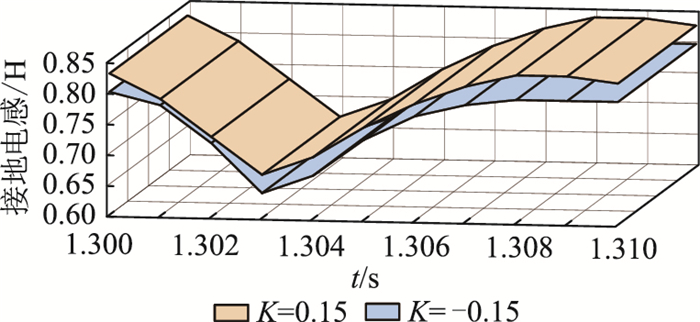
|
图 5 单相(A相)接地故障下不同比例系数的临界电感 Fig. 5 Critical inductance of commutation failure with different proportional coefficients under single phsae grounding fault (fault occurs in phase A) |
图 4、图 5中折面代表了临界换相电感,折面以上未发生换相失败,折面以下发生换相失败。测试结果表明,电流偏差环节比例系数会影响预测型定关断角控制器的换相失败抑制能力。三相故障下,当比例系数设置为0.15时,平均临界电压约为0.905 p.u.;当比例系数为-0.15时,平均临界电压变为0.897 p.u.。单相故障下,当比例系数为0.15时,平均临界电压约为0.938 p.u.;当比例系数为-0.15时,平均临界电压变为0.852 p.u.。可见,比例系数由0.15变为-0.15,系统的换相失败抵御能力明显提高。
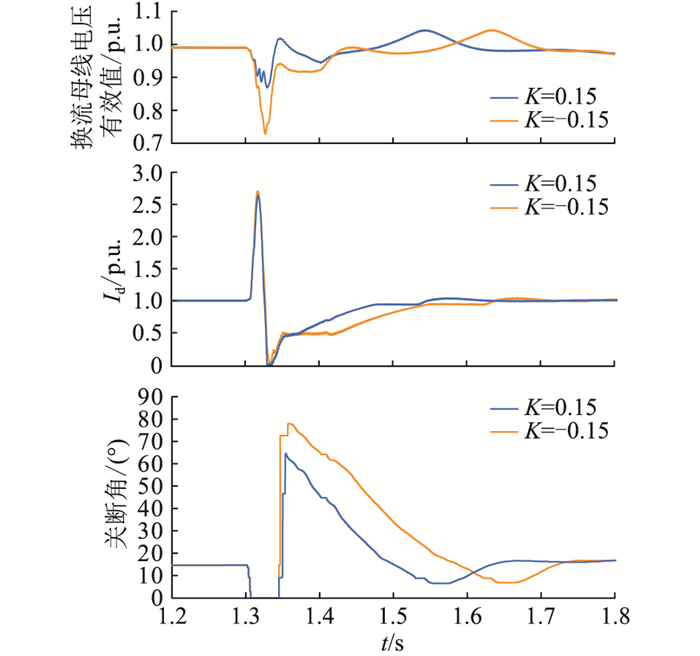
4.2.2 算例2:电流偏差环节对系统恢复影响(切换至定电流控制)设置逆变侧换流母线处1.3 s发生三相电感性接地故障,接地电感1.2 H,故障持续0.1 s。电流偏差环节比例系数分别设置为0.15和-0.15情况下,系统换流母线电压有效值、直流电流和逆变器关断角实测值如图 6所示。
|
图 6 三相故障下不同比例系数的系统恢复情况 Fig. 6 System recovery with different proportional coefficients under three-phase grounding fault |
根据图 6,在该故障下,无论比例系数为0.15或是-0.15,均发生了单次换相失败,在这种情况下,系统恢复过程中均由定关断角控制切换至定电流控制并在恢复末期切换至定电压控制,该测试情况对应了2.2节中的情况一。测试结果表明,比例系数由-0.15变为0.15,系统恢复阶段的交流电压水平、直流电流恢复速率、关断角超调量及其恢复速率有明显改善。
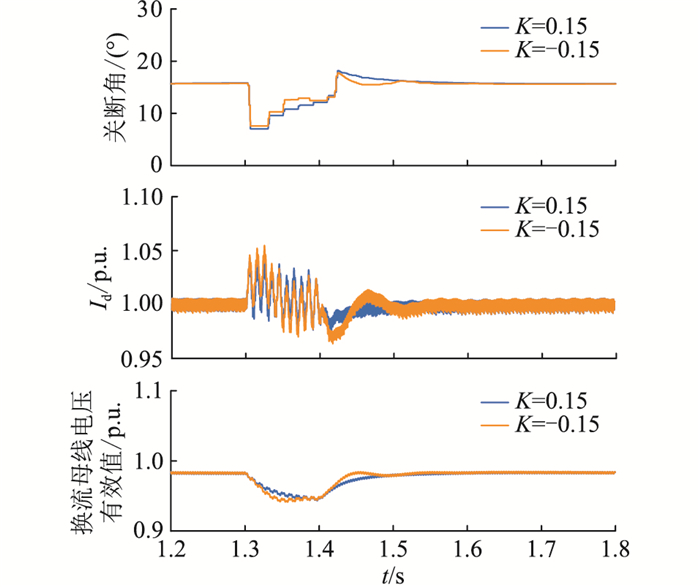
4.2.3 算例3:电流偏差环节对系统恢复影响(始终为预测型定关断角控制)设置逆变侧换流母线处1.3 s发生单相(A相)接地故障,接地电感0.9 H,故障持续0.1 s。电流偏差环节比例系数分别设置为0.15和-0.15情况下,逆变器关断角、直流电流和换流母线电压有效值如图 7所示。
|
图 7 单相故障下不同比例系数的系统恢复效果 Fig. 7 System recovery with different proportional coefficients under single phsae grounding fault |
根据图 7,该故障情况下,比例系数为0.15和-0.15均未发生换相失败,在这种情况下,系统恢复过程始终由定关断角控制器起作用,该测试算例对应2.2节中情况二。测试结果表明,相比-0.15,比例系数设置为0.15时,在恢复过程中关断角相对较低,导致了逆变器功率因数较大,消耗无功相对减小,因此换流母线处电压有效值更高,电流、电压的恢复效果更好。
4.3 自适应电流偏差控制效果验证自适应电流偏差控制中,k1设置为-0.15,k2设置为0.15,Ulevel1和Ulevel2分别设置为0.6和0.85,展宽统一选取20 ms。为全面衡量换相失败发生情况,故障发生时刻设置为(1.30~1.31 s),则传统电流偏差环节在比例系数分别为0.15,-0.15下和所提出的自适应电流偏差控制在三相、单相(A相)电感性接地故障下的临界故障电感如表 2所示。为了方便表示,表 2中传统电流偏差环节比例系数为0.15时的三相、单相电感性测试结果分别表示为A1,A2;传统比例系数为-0.15的三相、单相电感性测试结果分别表示为B1,B2;所提出电流偏差控制的三相电感性测试结果为C1,单相电感性测试结果为C2。
|
|
表 2 2种电流偏差控制下临界故障电感 Table 2 Critical fault inductance under two kinds of current error control strategies |
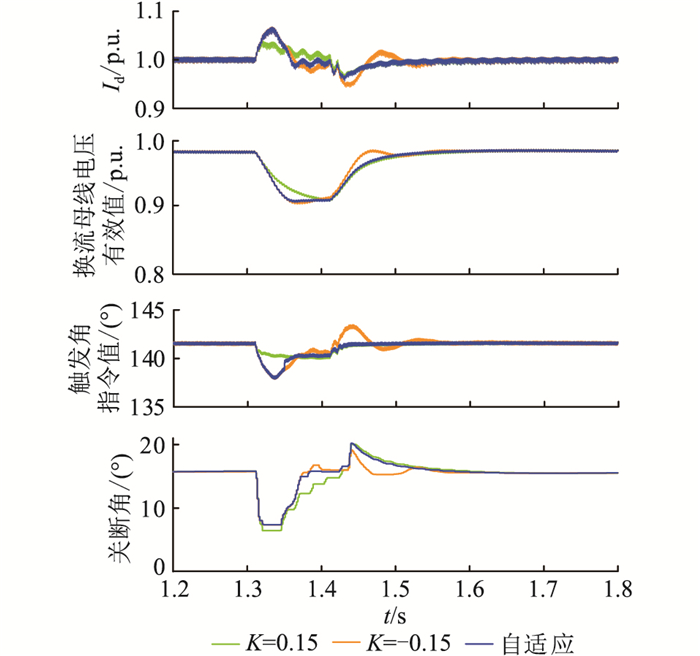
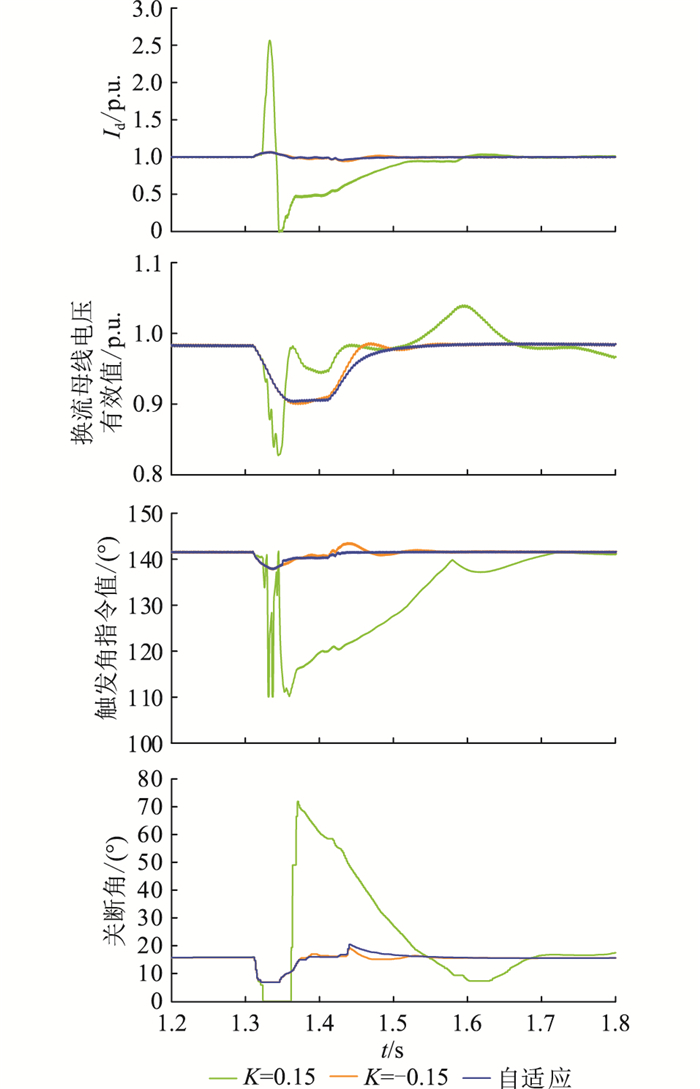
根据表 2可知,在三相、单相电感性故障下,所提出的自适应电流偏差控制的临界电感均不高于传统的电流偏差控制(K=0.15或-0.15),因此使用自适应电流偏差控制后,系统抵御换相失败的能力得到提升。为直观显示改进后电流偏差控制的系统响应,选取1.31 s换流母线处发生三相电感性接地故障,故障电感分别为1.35 H,1.3 H,持续0.1 s,传统电流偏差K设置为0.15,-0.15以及自适应电流偏差环节接入下,系统响应分别如图 8、图 9所示。
|
图 8 自适应电流偏差控制测试结果(故障电感为1.35 H) Fig. 8 Test results ofthe proposed adaptive current error control (fault inductance is 1.35 H) |
|
图 9 自适应电流偏差控制测试结果(故障电感为1.3 H) Fig. 9 Test results of the proposed adaptive current error control (fault inductance is 1.3 H) |
根据图 8可知,自适应电流偏差控制接入后,系统暂态期间直流电流、逆变侧换流母线电压及逆变器触发角指令值的波动相比传统电流偏差K设置为-0.15时小,且故障初期关断角实测值相比传统电流偏差K设置为0.15时更大。
根据图 9可知,自适应电流偏差控制接入后,系统暂态期间直流电流、逆变侧换流母线电压及逆变器触发角指令值的波动有所改善(相比K=-0.15),且在一定程度上可以增强系统换相失败的抵御能力。传统电流偏差K被设置为0.15时,系统发生首次换相失败,而使用所提出的自适应电流偏差控制的系统有效避免了换相失败的发生。
综上,所提出的自适应电流偏差控制兼顾了换相失败的抑制与系统的快速平稳恢复,可以在故障初期增强系统的换相失败抑制能力,在故障恢复阶段,抑制电流、电压波动,实现平稳恢复的目标。
5 结论针对预测型定关断角控制中电流偏差环节,分析了该环节中比例系数对故障初期换相失败抑制效果、系统恢复效果的影响,并提出了一种自适应电流偏差环节,得到如下结论:
(1) 电流偏差环节设定的目的为增强系统小干扰下稳定性,但在大的扰动下,正的比例系数会导致故障初期换相失败抑制效果变差,有利于系统的故障恢复,但须注意限制恢复速率防止后续换相失败的发生。
(2) 所提出的自适应电流偏差环节可以有效识别系统状态并输出合适的比例系数,起到兼顾换相失败抑制与系统快速稳定恢复的作用。
| [1] |
马星, 李凤婷, 尹纯亚, 等. 整流侧换流母线电压恢复导致逆变器换相失败的机理分析[J]. 电力工程技术, 2021, 40(4): 83-88. MA Xing, LI Fengting, YIN Chunya, et al. Mechanism analysis of inverter commutation failure caused by voltage recovery of commutation bus at rectifier side[J]. Electric Power Engineering Technology, 2021, 40(4): 83-88. (  0) 0) |
| [2] |
王勇, 尹纯亚, 石岩, 等. 抑制直流连续换相失败的直流电流指令值优化策略[J]. 电力工程技术, 2020, 39(3): 99-106. WANG Yong, YIN Chunya, SHI Yan, et al. Optimization strategy of DC current order value to restrain DC continuous commutation failure[J]. Electric Power Engineering Technology, 2020, 39(3): 99-106. (  0) 0) |
| [3] |
饶宇飞, 张鹏辉, 李程昊, 等. 励磁涌流对高压直流输电系统换相失败的影响机理及评估方法[J]. 电力系统保护与控制, 2019, 47(13): 54-61. RAO Yufei, ZHANG Penghui, LI Chenghao, et al. Mechanism and evaluating method for HVDC commutation failure caused by inrush current[J]. Power System Protection and Control, 2019, 47(13): 54-61. DOI:10.7667/PSPC20191308 (  0) 0) |
| [4] |
LIU L, LIN S, LIU J, et al. Analysis and prevention of subsequent commutation failures caused by improper inverter control interactions in HVDC systems[J]. IEEE Transactions on Power Delivery, 2020, 35(6): 2841-2852. (  0) 0) |
| [5] |
WANG J J, HUANG M H, FU C, et al. A new recovery strategy of HVDC system during AC faults[J]. IEEE Transactions on Power Delivery, 2019, 34(2): 486-495. DOI:10.1109/TPWRD.2019.2892410 (  0) 0) |
| [6] |
XIAO H Q, SUN K Q, PAN J P, et al. Review of hybrid HVDC systems combining line communicated converter and voltage source converter[J]. International Journal of Electrical Power & Energy Systems, 2021, 129: 106713. (  0) 0) |
| [7] |
阮思烨, 徐凯, 刘丹, 等. 直流输电系统换相失败统计分析及抵御措施建议[J]. 电力系统自动化, 2019, 43(18): 13-17, 34. RUAN Siye, XU Kai, LIU Dan, et al. Statistical analysis and suggestions on resistance measures for commutation failures of HVDC transmission system[J]. Automation of Electric Power Systems, 2019, 43(18): 13-17, 34. DOI:10.7500/AEPS20190130006 (  0) 0) |
| [8] |
THIO C V, DAVIES J B, KENT K L. Commutation failures in HVDC transmission systems[J]. IEEE Transactions on Power Delivery, 1996, 11(2): 946-957. DOI:10.1109/61.489356 (  0) 0) |
| [9] |
WEI Z N, YUAN Y, LEI X, et al. Direct-current predictive control strategy for inhibiting commutation failure in HVDC converter[J]. IEEE Transactions on Power Systems, 2014, 29(5): 2409-2417. DOI:10.1109/TPWRS.2014.2302010 (  0) 0) |
| [10] |
RAHIMI E, GOLE A M, DAVIES J B, et al. Commutation failure analysis in multi-infeed HVDC systems[J]. IEEE Transactions on Power Delivery, 2011, 26(1): 378-384. DOI:10.1109/TPWRD.2010.2081692 (  0) 0) |
| [11] |
MIRSAEIDI S, DONG X Z. An enhanced strategy to inhibit commutation failure in line-commutated converters[J]. IEEE Transactions on Industrial Electronics, 2020, 67(1): 340-349. DOI:10.1109/TIE.2019.2896328 (  0) 0) |
| [12] |
WANG Q, ZHANG C M, WU X Q, et al. Commutation failure prediction method considering commutation voltage distortion and DC current variation[J]. IEEE Access, 2019, 7: 96531-96539. DOI:10.1109/ACCESS.2019.2929301 (  0) 0) |
| [13] |
YAO W, LIU C, FANG J K, et al. Probabilistic analysis of commutation failure in LCC-HVDC system considering the CFPREV and the initial fault voltage angle[J]. IEEE Transactions on Power Delivery, 2020, 35(2): 715-724. DOI:10.1109/TPWRD.2019.2925399 (  0) 0) |
| [14] |
LEE H J, SON G T, YOO J I, et al. Effect of a SFCL on commutation failure in a HVDC system[J]. IEEE Transactions on Applied Superconductivity, 2013, 23(3): 5600104. DOI:10.1109/TASC.2012.2230291 (  0) 0) |
| [15] |
李春华, 孙宝奎, 赵成勇, 等. 半控型H桥子模块提高HVDC换相失败免疫力的机理[J]. 中国电机工程学报, 2016, 36(9): 2419-2427. LI Chunhua, SUN Baokui, ZHAO Chengyong, et al. Mechanism of semi-controlled H-bridge sub-module to improve commutation failure immunity of HVDC[J]. Proceedings of the CSEE, 2016, 36(9): 2419-2427. (  0) 0) |
| [16] |
JOVCIC D, AHMED K. High-voltage direct-current transmission[M]. Chichester, UK: John Wiley & Sons, Ltd, 2015.
(  0) 0) |
| [17] |
MIRSAEIDI S, DONG X Z, TZELEPIS D, et al. A predictive control strategy for mitigation of commutation failure in LCC-based HVDC systems[J]. IEEE Transactions on Power Electronics, 2019, 34(1): 160-172. DOI:10.1109/TPEL.2018.2820152 (  0) 0) |
| [18] |
周博昊, 李凤婷, 宋新甫, 等. 基于直流电流变化量的换相失败预测判别与控制系统优化[J]. 电网技术, 2019, 43(10): 3497-3504. ZHOU Bohao, LI Fengting, SONG Xinfu, et al. Commutationfailure prediction and control system optimization based on DC current variation[J]. Power System Technology, 2019, 43(10): 3497-3504. (  0) 0) |
| [19] |
周博昊, 李凤婷, 尹纯亚, 等. 基于直流电流有限时域预测算法的换相失败预防策略[J]. 电力系统自动化, 2020, 44(6): 178-185. ZHOU Bohao, LI Fengting, YIN Chunya, et al. Preventive strategy for mitigation of commutation failure based on finite time domain prediction algorithm of DC current[J]. Automation of Electric Power Systems, 2020, 44(6): 178-185. (  0) 0) |
| [20] |
戴志辉, 潘星宇, 王靖宇. 基于动态电流偏差控制的连续换相失败抑制方法[J]. 电力系统及其自动化学报, 2021, 33(3): 49-58. DAI Zhihui, PAN Xingyu, WANG Jingyu. Suppression method for continuous commutation failure based on dynamic current deviation control[J]. Proceedings of the CSU-EPSA, 2021, 33(3): 49-58. (  0) 0) |
| [21] |
王海军, 黄义隆, 周全. 高压直流输电换相失败响应策略与预测控制技术路线分析[J]. 电力系统保护与控制, 2014, 42(21): 124-131. WANG Haijun, HUANG Yilong, ZHOU Quan. Analysis of commutation failure response strategies and prediction control technology in HVDC[J]. Power System Protection and Control, 2014, 42(21): 124-131. DOI:10.7667/j.issn.1674-3415.2014.21.020 (  0) 0) |
| [22] |
汪娟娟, 王子民, 禤小聪, 等. 预测型定熄弧角控制及其改进策略[J]. 电网技术, 2018, 42(12): 3985-3991. WANG Juanjuan, WANG Zimin, XUAN Xiaocong, et al. Ex-tinction angle control based on predictive calculation and its improvement[J]. Power System Technology, 2018, 42(12): 3985-3991. (  0) 0) |
| [23] |
NIU C, WANG X, YANG M, et al. An improved start-up control method for hybrid cascaded multi-terminal HVDC transmission system[C]//The 16th IET International Conference on AC and DC Power Transmission (ACDC 2020). Online Conference, Institution of Engineering and Technology, 2021.
(  0) 0) |
| [24] |
张红丽, 刘福锁, 李威. 动态无功补偿装置提高多馈入直流恢复的布点方法[J]. 电力系统自动化, 2016, 40(5): 133-138. ZHANG Hongli, LIU Fusuo, LI Wei. Site selection for dynamic reactive power compensation and improvement of recovery from commutation failures in multi-infeed HVDC system[J]. Automation of Electric Power Systems, 2016, 40(5): 133-138. (  0) 0) |
| [25] |
SZECHTMAN M, WESS T, THIO C V. First benchmark model for HVDC control studied[J]. Electra, 1991, 135(4): 54-73. (  0) 0) |
2. School of Electrical Engineering, Xinjiang University, Urumqi 830047, China
 2022, Vol. 41
2022, Vol. 41


 宋新甫(1984),男,硕士,高级工程师,从事电力系统规划运行工作(E-mail:
宋新甫(1984),男,硕士,高级工程师,从事电力系统规划运行工作(E-mail: