文章编号: 2096-3203(2022)02-0060-07 中图分类号: TM721
基于电网换相换流器的高压直流(line commutated converter high voltage direct current, LCC-HVDC)输电系统已发展得较为成熟,被广泛应用于远距离大容量架空线输电场合,但其容易发生换相失败,影响系统的安全稳定运行[1-3]。近年来,基于模块化多电平换流器的高压直流(modular multilevel converter high voltage direct current, MMC-HVDC)输电发展迅速,不存在换相失败的风险,并且可以独立控制有功功率和无功功率。然而,MMC-HVDC存在建设成本较高、电压等级低和输送容量小等缺点[4-9]。因此,结合LCC-HVDC和MMC-HVDC的混合直流输电系统成为当前直流输电领域的研究热点[10-14]。
典型混合直流输电系统的送端为电网换相换流器(line commutated converter, LCC),受端为模块化多电平换流器(modular multilevel converter, MMC),可彻底避免换相失败,但其电压等级与输送功率均受限于MMC换流站[15-17]。为解决该问题并降低建设成本,近年来相关学者提出受端级联型混合直流输电技术,即送端为LCC,受端为LCC与MMC串联的混合拓扑结构,低端MMC扩展为多个MMC并联并落点于不同区域电网,在提高系统的电压等级和传输功率的同时,多落点结构也有利于工程的分期建设[18-23]。由于LCC的单相导电性,逆变侧直流故障回路中不存在故障电流,所以该系统
具有优良的直流故障穿越能力[24]。因此,受端级联型混合直流系统因其独特的优势被应用于高压大容量架空线路输电场合。
目前,针对受端级联型混合直流的相关研究较少。MMC的有功策略必须与送端LCC的有功指令相配合,否则将会出现各站功率协调不合理的现象。MMC可采用单点直流电压控制的主从控制,也可采用多点直流电压控制的下垂控制。文献[25-26]提出在主从控制下,定直流电压控制的MMC在发生故障时会出现功率反送现象,降低受端系统稳定性; 而在下垂控制方式下,MMC可以同时控制直流电压和直流功率,不存在上述问题。
文中明确了受端级联型混合直流系统的伏安特性,分析了系统的控制特性。基于特性分析发现,采用下垂控制的MMC无法实现直流电压的准确控制。因此,提出一种自适应下垂控制策略,可根据系统直流电流的变化实时自适应调节下垂特性,避免MMC的直流电压随直流电流变化而产生波动。最后,在PSCAD/EMTDC中对所提策略进行了算例分析和仿真验证。
1 受端级联混合直流输电系统的拓扑结构和控制方式 1.1 拓扑结构受端级联混合直流输电系统的拓扑结构如图 1所示。
|
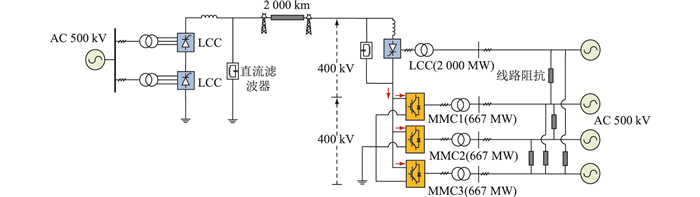
图 1 多落点受端级联混合直流系统拓扑结构 Fig. 1 The topology of hybrid HVDC with cascaded multi-infeed MMC inverters |
整流站由2组12脉动LCC串联构成,逆变站由1组12脉动LCC和MMC并联组串联构成,MMC并联组由3台半桥型MMC并联构成。混合直流系统的额定电压与有功功率分别为800 kV和4 000 MW,其中逆变侧高端LCC的额定电压与有功功率分别为400 kV与2 000 MW,低端3台MMC换流器的额定电压与有功功功率分别为400 kV与667 MW。另一方面,受端逆变站均馈入500 kV交流系统的不同地点。
1.2 控制方式 1.2.1 LCC控制方式LCC-HVDC的伏安特性如图 2所示[1],相关控制模式详见表 1。其中蓝色曲线代表整流侧的伏安特性,黄色曲线代表逆变侧的伏安特性,两曲线相交点为系统额定运行的工作点,对应的电压和电流分别为Udc_LCC和Id。

|
图 2 LCC的控制特性 Fig. 2 Control characteristic of LCC |
|
|
表 1 LCC控制模式 Table 1 The control modes of LCC |
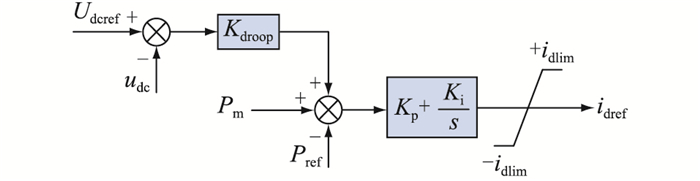
文中受端MMC采用下垂控制模式,其控制框图如图 3所示。其中,Udcref,udc分别为MMC的直流电压参考值和测量值; Pref,Pm分别为MMC输出的有功功率和测量值; Kdroop为下垂系数; Kp,Ki为外环控制的PI参数; idlim为有功电流限幅值; idref为输出的有功电流参考值。
|
图 3 下垂控制框图 Fig. 3 The droop control block diagram |
采用下垂控制MMC的有功功率和直流电压间的关系可表示为(MMC处于逆变状态,设置功率参考值为正值):
| $ P_{\mathrm{m}}-P_{\text {ref }}+K_{\text {droop }}\left(U_{\text {dcref }}-u_{\mathrm{dc}}\right)=0 $ | (1) |
设置受端各台MMC的参数都相同,则MMC均分输入的有功功率。下垂控制的控制特性如图 4所示,PMMC为输入MMC并联组的有功功率,Pm为MMC输出的有功功率。

|
图 4 MMC的下垂控制特性 Fig. 4 The control droop characteristics of MMC |
由于Pm=idc_MMCudc,式(1)可重新列写为:
| $ u_{\mathrm{dc}}=\frac{P_{\mathrm{ref}}-K_{\text {droop }} U_{\mathrm{dcref}}}{i_{\mathrm{dc} \text {_MMC }}-K_{\text {droop }}} $ | (2) |
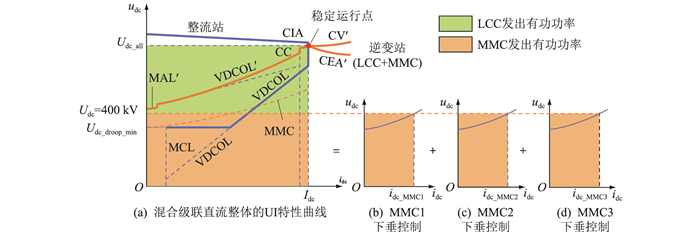
式中:idc_MMC为逆变侧MMC的直流电流。由式(2)可知,当MMC采用下垂控制时,其伏安特性曲线是一个双曲函数。因此,受端级联混合直流输电系统采用下垂控制方式的完整伏安特性曲线如图 5的左侧所示。在额定工作区间,MMC下垂控制的伏安特性曲线是一个曲线段,如图 5中左边黄色虚线所示。低端MMC的主从控制方式主要通过式(2)实现。对混合直流逆变侧伏安特性曲线的影响。图 5中,Udc_all为混合直流系统的额定直流电压; Idc为混合直流系统的额定直流电流; Udc_droop_min为MMC下垂控制允许的最低直流电压; Idc_MMC1,Idc_MMC2,Idc_MMC3分别为逆变侧MMC1、MMC2和MMC3的额定直流电流。
|
图 5 MMC采用下垂控制时混合直流系统的完整伏安特性 Fig. 5 Complete UI curves of hybrid HVDC when MMCs are in droop control |
高端LCC逆变站各段曲线的控制特性可由式(3)-式(6)描述。
| $ u_{\mathrm{dc}\_\mathrm{LCC}}=\frac{U_{\mathrm{d}\_\mathrm{rated}}}{2} $ | (3) |
| $ u_{\mathrm{dc}\_\mathrm{LCC}}=k_{\mathrm{CEA}}^{\prime} i_{\mathrm{dc}}+U_{\mathrm{dc}\_\mathrm{LCC}}^{\mathrm{CEA}} $ | (4) |
| $ u_{\mathrm{dc}\_\mathrm{LCC}}=k_{\mathrm{VDCOL}}^{\prime} i_{\mathrm{dc}}+U_{\mathrm{dc}\_\mathrm{LCC}}^{\mathrm{VDCOL}} $ | (5) |
| $ u_{\mathrm{dc}\_\mathrm{LCC}}=k_{\mathrm{MAL}}^{\prime} i_{\mathrm{dc}}+U_{\mathrm{dc}\_ \mathrm{LCC}}^{\mathrm{MAL}} $ | (6) |
式中:udc_LCC为逆变侧LCC的直流电压; idc为混合直流系统的测量直流电流; Ud_rated为混合直流系统额定直流电压; idc为混合直流系统的直流电流; k′CEA,k′VDCOL,k′MAL分别为逆变侧LCC的CEA控制段、VDCOL控制段和MAL控制段的斜率,上标“′”表示相关斜率是逆变侧LCC直流电压为400 kV的值,即相关斜率为800 kV额定电压值的一半; Udc_LCCCEA,Udc_LCCVDCOL,Udc_LCCMAL分别为各段控制曲线在udc轴的截距。
将式(2)与式(3)-式(6)依次相加,可得到下垂控制模式下的混合级联直流逆变侧直流电压表达式,如式(7)-式(10)所示。
| $ \begin{gathered} u_{\mathrm{dc\_a l l}}=u_{\mathrm{dc}\_\mathrm{LCC}}+u_{\mathrm{dc}}=\\ \frac{U_{\mathrm{d}\_\text {rated }}}{2}+\frac{P_{\text {ref }}-k_{\text {droop }} U_{\text {dcref }}}{i_{\text {dc_MMC }}-K_{\text {droop }}} \end{gathered} $ | (7) |
| $ \begin{gathered} u_{\mathrm{dc}\_\mathrm{all}}=u_{\mathrm{dc}\_\mathrm{LCC}}+u_{\mathrm{dc}}=\\ k_{\mathrm{CEA}}^{\prime} i_{\mathrm{dc}}+U_{\mathrm{dc}\_\mathrm{LCC}}^{\mathrm{CEA}}+\frac{P_{\text {ref }}-K_{\text {droop }} U_{\text {dcref }}}{i_{\mathrm{dc}_{-} \text {MMC }}-K_{\mathrm{droop}}} \end{gathered} $ | (8) |
| $ \begin{gathered} u_{\mathrm{dc} \text {_all }}=u_{\mathrm{dc}\_\mathrm{LCC}}+u_{\mathrm{dc}}=\\ k_{\mathrm{VDCOL}}^{\prime} \dot{l}_{\mathrm{dc}}+U_{\mathrm{dc}\_{\mathrm{LCC}}}^{\mathrm{VDCOL}}+\frac{P_{\text {ref }}-K_{\mathrm{droop}} U_{\mathrm{dcref}}}{i_{\mathrm{dc} \text {_MMC }}-K_{\mathrm{droop}}} \end{gathered} $ | (9) |
| $ \begin{gathered} u_{\mathrm{dc}\_\mathrm{all}}=u_{\mathrm{dc}\_\mathrm{LCC}}+u_{\mathrm{dc}}=\\ k_{\mathrm{MAL}}^{\prime} i_{\mathrm{dc}}+U_{\mathrm{dc}\_\mathrm{LCC}}^{\mathrm{MAL}}+\frac{P_{\text {ref }}-K_{\mathrm{droop}} U_{\mathrm{dcref}}}{i_{\mathrm{dc}_{-} \text {MMC }}-K_{\mathrm{droop}}} \end{gathered} $ | (10) |
式中:udc_all为混合直流系统的测量直流电压。因此式(7)-式(10)为混合直流逆变侧伏安特性曲线,如图 5(a)黄色实线所示。
在整流侧特性曲线影响方面,由于MMC主要通过式(2)影响混合直流电压特性,且半桥MMC没有低压限流等特性,因此整流侧特性曲线如图 5(a)蓝色实线所示。
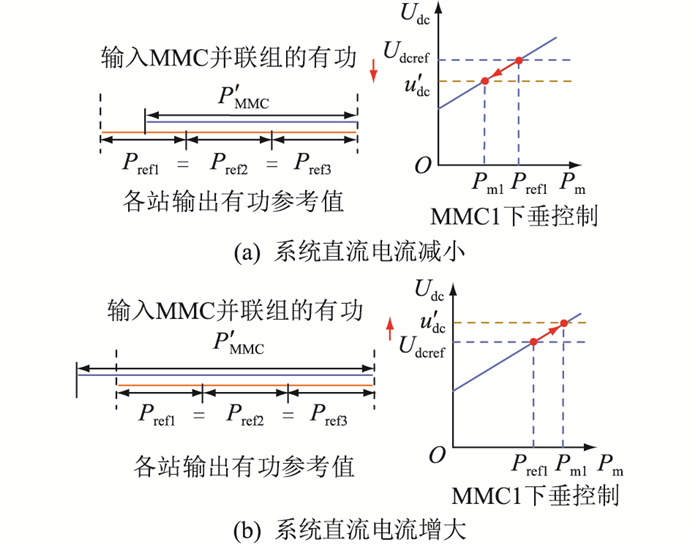
2 受端级联混合直流的下垂特性分析在受端MMC均采用下垂控制方式下,当系统直流电流发生变化时,输入MMC并联组的有功变化,会导致MMC直流电压的变化。由于各台MMC参数相同,其特性也相同,因此后续特性图仅给出一个MMC站进行说明。同时,特性图中虚线为MMC运行点对应的直流电压和输出有功功率。如图 6(a)所示,当系统直流电流减小时,输入MMC的有功功率减小为P'MMC,MMC的直流电压在下垂控制的作用下也相应减小为u'dc,无法控制直流电压保持为额定值。如图 6(b)所示,系统直流电流增大时,输入MMC的有功功率增大为P'MMC,MMC的直流电压在下垂控制的作用下也相应增大为u'dc。由上述分析可知,当系统直流电流波动时,会导致MMC直流电压产生波动,无法实现直流电压的精确控制。
|
图 6 直流电流变化时系统的下垂特性 Fig. 6 Characteristicof droop control when DC current changes |
为解决上述问题,提出自适应下垂控制策略以实现直流电压的精确控制,可根据系统的直流电流实时地上下平移下垂曲线。
由式(1)可知,若系统发生较大扰动,整个MMC并联组功率变化量可表示为:
| $ \begin{gathered} \Delta P_{\text {MMC }}=\sum\limits_{i=1}^{n} \Delta P_{i}=\Delta u_{\mathrm{dc}} \sum\limits_{i=1}^{n} K_{\text {droop_} i}=\\ \frac{\Delta P_{j}}{K_{\mathrm{droop}\_j}} \sum\limits_{i=1}^{n} K_{\mathrm{droop}\_i} \end{gathered} $ | (11) |
式中:n为MMC参与运行台数; Kdroop_j为第j台MMC的下垂系数; ΔPj为第j台MMC的不平衡功率。因此,换流站j承担的不平衡功率ΔPj为:
| $ \Delta P_{j}=P_{\mathrm{m} j}-P_{\mathrm{ref} j}=\frac{K_{\text {droop_}{j}} \Delta P_{\text {MMC }}}{\sum\limits_{i=1}^{n} K_{\text {droop_}{i}}} $ | (12) |
式中:Prefj为第j台MMC的有功功率参考值; Pmj为第j台MMC的有功功率测量值。为实现下垂特性的自动平移,对直流电压参考值进行补偿,mj为第j台MMC的电压补偿量,则下垂特性可改写为:
| $ u_{\mathrm{dc}}=\frac{P_{\mathrm{m} j}-P_{\mathrm{ref} j}}{K_{\mathrm{droop}\_j}}+U_{\mathrm{dcref}}+m_{j} $ | (13) |
为保持直流电压的稳定,移动后的下垂曲线应过点(Pmj,Udcref),同时将式(12)代入式(13)中,可得到补偿量m为:
| $ m_{j}=\frac{\left(I_{\mathrm{dcref}}-I_{\mathrm{dc}}\right) U_{\mathrm{dcref}}}{\sum\limits_{i=1}^{n} K_{\mathrm{droop}\_i}} $ | (14) |
式中:Idcref为系统直流电流额定参考值。由式(14)可知,所有MMC的补偿量m都相等。另一方面,对MMC的直流电压参考值进行补偿,本质上也相当于对有功功率参考值进行补偿。当Idc为额定值时,m=0,此时下垂特性不产生移动; 当Idc减小时,m>0,下垂特性曲线向上平移; 当Idc增大时,则m < 0,下垂特性曲线向下平移。
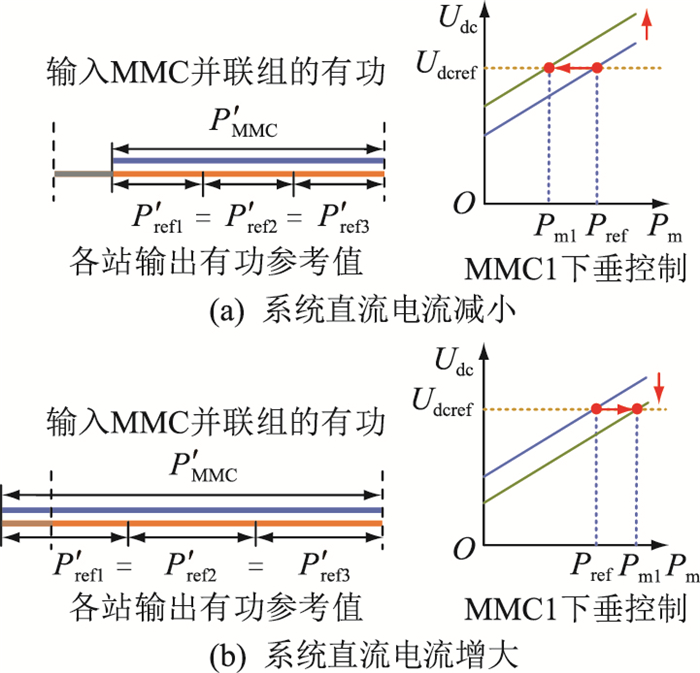
如图 7(a)所示,以n=3为例,当系统直流电流减小时,则m>0,此时下垂特性自动向上平移(本质上相当于减小了MMC的有功参考值),在保证直流电压仍然为参考电压Udcref的前提下,使得MMC输出的有功减小。同样地,如图 7(b)所示,当系统直流电流增大时,m < 0,此时下垂特性自动向下平移(本质上相当于增大了MMC的有功参考值),使得MMC增大有功输出,同时将直流电压保持为参考电压Udcref。
|
图 7 自适应下垂控制原理 Fig. 7 The principle of adaptive droop control |
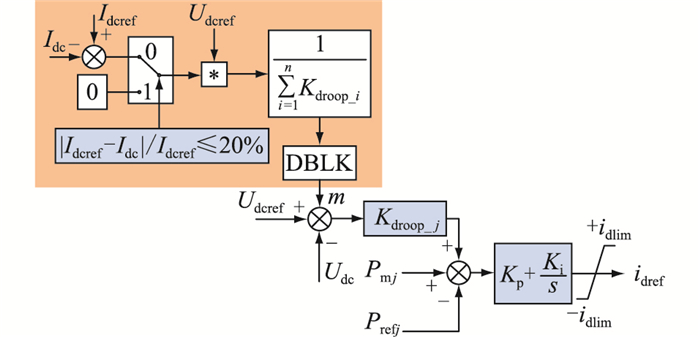
自适应下垂控制策略如图 8所示,通过在基本下垂控制上增加直流电压补偿量m,m根据系统直流电流Idc的变化进行调整,下垂特性可跟踪直流电流的值进行平移,实现自动调节。DBLK为控制解锁模块,当MMC解锁后再启动该控制。同时,为避免下垂特性的频繁移动,当|Idcref-Idc /Idcref≤2%时,闭锁该控制策略,使得m=0。
|
图 8 自适应下垂控制框图 Fig. 8 The adaptive droop control diagram |
为验证所提策略的有效性,在PSCAD/EMTDC软件平台搭建如图 1所示的多落点混合级联型直流输电模型进行仿真。设置受端3台MMC的参数都相同,下垂控制的直流电压参考值设置为400 kV,由于考虑到损耗,输出有功功率参考值均设置为650 MW。
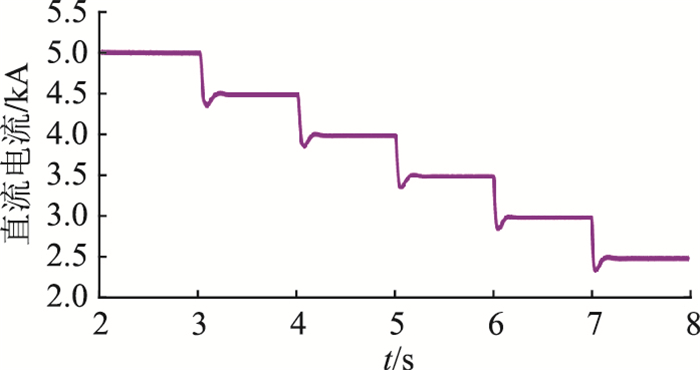
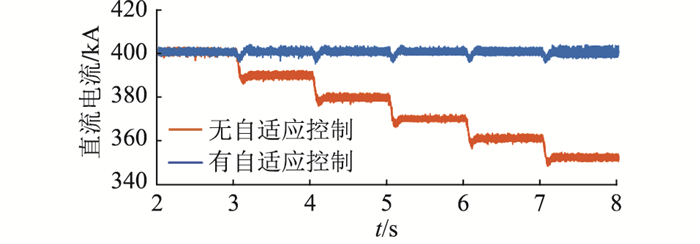
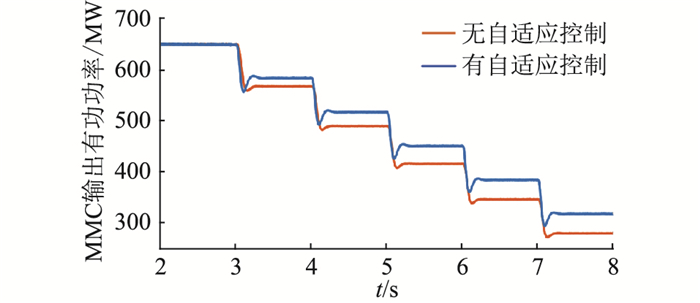
算例1:初始状态下,LCC电流指令值为1 p.u.,即5 kA。在3 s,4 s,5 s,6 s和7 s时依次改变LCC的直流电流指令值为0.9 p.u.,0.8 p.u.,0.7 p.u.,0.6 p.u.和0.5 p.u.,图 9为系统的直流电流。分别在无自适应下垂控制和采用自适应下垂控制的2种情况下进行仿真,仿真结果如图 9-图 11所示。无自适应下垂控制的情况下,MMC的直流电压随着系统直流电流的减小而降低,无法精确控制直流电压; 采取所提自适应下垂控制后,直流电压补偿量m根据系统直流电流Idc的变化进行实时调整,自动平移MMC的下垂特性,可控制直流电压保持为额定值。
|
图 9 混合直流系统直流电流(算例1) Fig. 9 DC current of the hybrid HVDC (case 1) |
|
图 10 MMC直流电压(算例1) Fig. 10 DC voltage of MMC (case 1) |
|
图 11 MMC输出有功功率(算例1) Fig. 11 Output active power of MMC (case 1) |
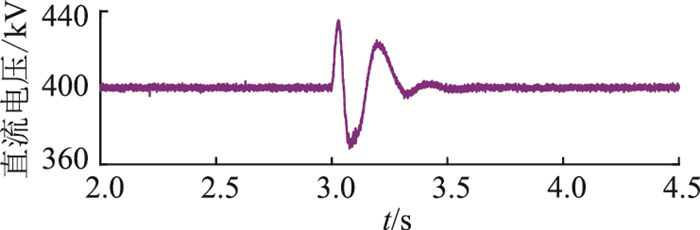
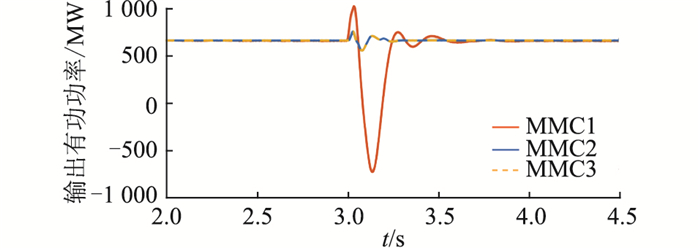
算例2:MMC采用主从控制方式下(MMC1定直流电压、MMC2和MMC3定有功功率),3 s时在LCC受端设置单相瞬时性接地故障,仿真结果如图 12和图 13所示。采用定直流电压控制方式的MMC1由于不具备控制直流功率的能力,其直流电流大小由系统总电流与定功率控制方式MMC2和MMC3的直流电流确定,因此在发生故障时MMC1会出现功率反送现象,由逆变切换至整流状态,不利于受端系统稳定。
|
图 12 MMC直流电压(算例2) Fig. 12 DC voltage of MMC (case 2) |
|
图 13 MMC输出有功功率(算例2) Fig. 13 Output active power of MMC (case 2) |
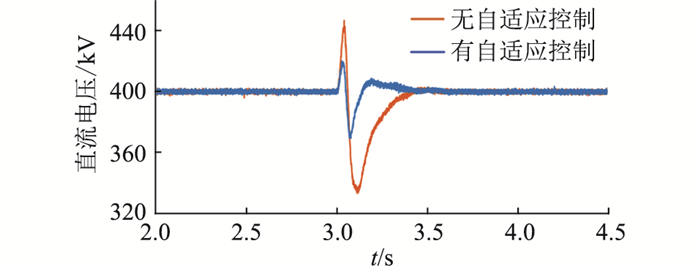
算例3:MMC采用下垂控制方式下,在3 s时设置同样的LCC受端单相瞬时性接地故障,分别在无自适应下垂控制和有自适应下垂控制进行仿真,仿真结果如图 14和图 15所示。
|
图 14 MMC直流电压(算例3) Fig. 14 DC voltage of MMC (case 3) |
|
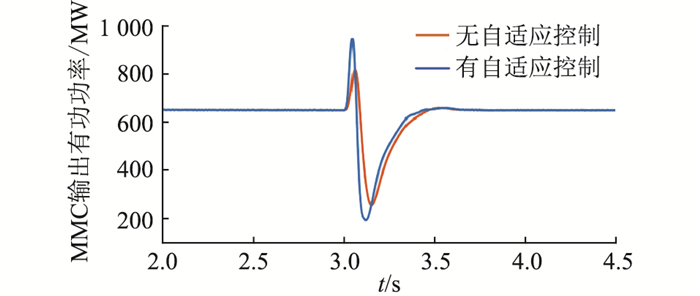
图 15 MMC输出有功功率(算例3) Fig. 15 Output active power of MMC (case 3) |
发生故障期间,采用下垂控制的MMC同时具有控制直流电压和直流功率的能力,不会出现功率反送的问题。由于LCC发生换相失败,系统直流电流会产生较大波动,在无控制策略下MMC直流电压的波动较大,而采取所提自适应下垂控制策略后,MMC直流电压的波动明显减小。
5 结语文中研究了受端级联型混合直流输电系统采用下垂控制的动态特性,提出了一种自适应下垂控制策略。通过算例分析与仿真验证可知,该策略可根据系统直流电流的变化实时自适应调节MMC的下垂特性,避免MMC的直流电压随直流电流的变化而产生波动,实现直流电压的准确控制。同时,在故障期间可有效减小MMC直流电压的波动,提高混合直流输电系统的稳定性,具有一定的工程应用价值。由于级联混合直流系统灵活性的增加带来了其控制方式和多换流器间协调控制策略的复杂性,因此,在未来的研究方向上还须深入研究该混合系统的控制方式,设计多换流器间的协调控制策略,以提高系统的稳定运行能力。
| [1] |
NI X J, GOLE A M, ZHAO C Y, et al. An improved measure of AC system strength for performance analysis of multi-infeed HVDC systems including VSC and LCC converters[J]. IEEE Transactions on Power Delivery, 2018, 33(1): 169-178. DOI:10.1109/TPWRD.2017.2711363 (  0) 0) |
| [2] |
LOU B L, ZHOU H, XU Z, et al. Fault response comparison of LCC-MMC hybrid topologies and conventional HVDC topology[J]. The Journal of Engineering, 2019(16): 2068-2073. (  0) 0) |
| [3] |
李猛, 夏成军, 杜兆斌. 混合直流双桥换相失败机理及抑制措施研究[J]. 电力工程技术, 2017, 36(1): 47-53. LI Meng, XIA Chengjun, DU Zhaobin. Research on the mechanism and suppression method of double bridge discontinuous commutation failure in hybrid HVDC[J]. Electric Power Engineering Technology, 2017, 36(1): 47-53. DOI:10.3969/j.issn.1009-0665.2017.01.011 (  0) 0) |
| [4] |
徐政, 屠卿瑞, 管敏渊. 柔性直流输电系统[M]. 北京: 机械工业出版社, 2013: 1-25. XU Zheng, TU Qingrui, GUAN Minyuan. Voltage source converter based HVDC power transmission systems[M]. Beijing: China Machine Press, 2013: 1-25. (  0) 0) |
| [5] |
王曦, 李兴源, 魏巍, 等. 柔性直流和常规直流互联输电系统协调控制策略[J]. 电力自动化设备, 2016, 36(12): 102-108. WANG Xi, LI Xingyuan, WEI Wei, et al. Coordinated control strategy for interconnected transmission system of VSC-HVDC and LCC-HVDC[J]. Electric Power Automation Equipment, 2016, 36(12): 102-108. (  0) 0) |
| [6] |
杨晓峰, 林智钦, 郑琼林, 等. 模块组合多电平变换器的研究综述[J]. 中国电机工程学报, 2013, 33(6): 1-15. YANG Xiaofeng, LIN Zhiqin, ZHENG Qionglin, et al. A review of modular multilevel converters[J]. Proceedings of the CSEE, 2013, 33(6): 1-15. (  0) 0) |
| [7] |
韦延方, 卫志农, 孙国强, 等. 一种新型的高压直流输电技术: MMC-HVDC[J]. 电力自动化设备, 2012, 32(7): 1-9. WEI Yanfang, WEI Zhinong, SUN Guoqiang, et al. New HVDC power transmission technology: MMC-HVDC[J]. Electric Power Automation Equipment, 2012, 32(7): 1-9. DOI:10.3969/j.issn.1006-6047.2012.07.001 (  0) 0) |
| [8] |
LI X Q, SONG Q, LIU W H, et al. Protection of nonpermanent faults on DC overhead lines in MMC-based HVDC systems[J]. IEEE Transactions on Power Delivery, 2013, 28(1): 483-490. DOI:10.1109/TPWRD.2012.2226249 (  0) 0) |
| [9] |
薛英林, 徐政. C-MMC直流故障穿越机理及改进拓扑方案[J]. 中国电机工程学报, 2013, 33(21): 63-70, 194. XUE Yinglin, XU Zheng. DC fault ride-through mechanism and improved topology scheme of C-MMC[J]. Proceedings of the CSEE, 2013, 33(21): 63-70, 194. (  0) 0) |
| [10] |
NGUYEN T H, LEE D C, KIM C K. A series-connected topology of a diode rectifier and a voltage-source converter for an HVDC transmission system[J]. IEEE Transactions on Power Electronics, 2014, 29(4): 1579-1584. DOI:10.1109/TPEL.2013.2283368 (  0) 0) |
| [11] |
XUE Y L, GE F L, ZHAO Z, et al. Control strategy for hybrid LCC-C-MMC HVDC system under AC fault at rectifier side[J]. The Journal of Engineering, 2019, 2019(16): 3259-3263. DOI:10.1049/joe.2018.8705 (  0) 0) |
| [12] |
陈睿, 孙仲卿, 杨银国, 等. 柔性直流与常规直流协调的紧急功率支援策略研究[J]. 电力工程技术, 2017, 36(6): 14-19, 26. CHEN Rui, SUN Zhongqing, YANG Yinguo, et al. Emergency power support control strategy of VSC-HVDC and LCC-HVDC coordination[J]. Electric Power Engineering Technology, 2017, 36(6): 14-19, 26. DOI:10.3969/j.issn.1009-0665.2017.06.003 (  0) 0) |
| [13] |
LIU Y, CHEN Z. A flexible power control method of VSC-HVDC link for the enhancement of effective short-circuit ratio in a hybrid multi-infeed HVDC system[J]. IEEE Transactions on Power Systems, 2013, 28(2): 1568-1581. DOI:10.1109/TPWRS.2012.2222057 (  0) 0) |
| [14] |
XIAO H, LI Y H, SHI D Y, et al. Evaluation of strength measure for static voltage stability analysis of hybrid multi-infeed DC systems[J]. IEEE Transactions on Power Delivery, 2019, 34(3): 879-890. DOI:10.1109/TPWRD.2019.2901831 (  0) 0) |
| [15] |
ZOU C Y, RAO H, XU S K, et al. Analysis of resonance between a VSC-HVDC converter and the AC grid[J]. IEEE Transactions on Power Electronics, 2018, 33(12): 10157-10168. DOI:10.1109/TPEL.2018.2809705 (  0) 0) |
| [16] |
RAO H, ZHOU Y B, XU S K, et al. Key technologies of ultra-high voltage hybrid LCC-VSC MTDC systems[J]. CSEE Journal of Power and Energy Systems, 2019, 5(3): 365-373. (  0) 0) |
| [17] |
LI B H, LIU T Q, ZHANG Y M. Unified adaptive droop control design based on dynamic reactive power limiter in VSC-MTDC[J]. Electric Power Systems Research, 2017, 148: 18-26. DOI:10.1016/j.epsr.2017.03.010 (  0) 0) |
| [18] |
YANG R Z, XIANG W, LIN W X, et al. Hybrid ultra-HVDC system with LCC and cascaded hybrid MMC[J]. The Journal of Engineering, 2019, 2019(16): 1112-1116. DOI:10.1049/joe.2018.8559 (  0) 0) |
| [19] |
GUO C Y, ZHANG Y, GOLE A M, et al. Analysis of dual-infeed HVDC with LCC-HVDC and VSC-HVDC[J]. IEEE Transactions on Power Delivery, 2012, 27(3): 1529-1537. DOI:10.1109/TPWRD.2012.2189139 (  0) 0) |
| [20] |
徐政, 王世佳, 李宁璨, 等. 适用于远距离大容量架空线路的LCC-MMC串联混合型直流输电系统[J]. 电网技术, 2016, 40(1): 55-63. XU Zheng, WANG Shijia, LI Ningcan, et al. A LCC and MMC series hybrid HVDC topology suitable for bulk power overhead line transmission[J]. Power System Technology, 2016, 40(1): 55-63. (  0) 0) |
| [21] |
郭贤珊, 刘路路, 周杨, 等. LCC-MMC混合级联系统MMC换流器过电压应力抑制策略[J]. 全球能源互联网, 2020, 3(4): 412-419. GUO Xianshan, LIU Lulu, ZHOU Yang, et al. Overvoltage mitigation control strategies of MMC converter in a hybrid LCC-MMC HVDC system[J]. Journal of Global Energy Interconnection, 2020, 3(4): 412-419. (  0) 0) |
| [22] |
徐政, 王世佳, 张哲任, 等. LCC-MMC混合级联型直流输电系统受端接线和控制方式[J]. 电力建设, 2018, 39(7): 115-122. XU Zheng, WANG Shijia, ZHANG Zheren, et al. Inverter station connection modes and control strategies of LCC-MMC hybrid HVDC systems[J]. Electric Power Construction, 2018, 39(7): 115-122. DOI:10.3969/j.issn.1000-7229.2018.07.014 (  0) 0) |
| [23] |
郭春义, 赵成勇, 彭茂兰, 等. 一种具有直流故障穿越能力的混合直流输电系统[J]. 中国电机工程学报, 2015, 35(17): 4345-4352. GUO Chunyi, ZHAO Chengyong, PENG Maolan, et al. A hybrid HVDC system with DC fault ride-through capability[J]. Proceedings of the CSEE, 2015, 35(17): 4345-4352. (  0) 0) |
| [24] |
刘杉, 余军, 贺之渊, 等. 基于VSC与LCC混合的多点传输直流输电系统拓扑结构研究与特性分析[J]. 中国电机工程学报, 2018, 38(10): 2980-2988, 3148. LIU Shan, YU Jun, HE Zhiyuan, et al. Research on the topology and characteristic of multi-terminal HVDC based on VSC and LCC[J]. Proceedings of the CSEE, 2018, 38(10): 2980-2988, 3148. (  0) 0) |
| [25] |
杨硕, 郑安然, 彭意, 等. 混合级联型直流输电系统直流故障特性及恢复控制策略[J]. 电力自动化设备, 2019, 39(9): 166-172, 179. YANG Shuo, ZHENG Anran, PENG Yi, et al. DC fault characteristic analysis and recovery control strategy for hybrid cascaded HVDC system[J]. Electric Power Automation Equipment, 2019, 39(9): 166-172, 179. (  0) 0) |
| [26] |
郭春义, 吴张曦, 赵成勇. 特高压混合级联直流输电系统中多MMC换流器间不平衡电流的均衡控制策略[J]. 中国电机工程学报, 2020, 40(20): 6653-6663. GUO Chunyi, WU Zhangxi, ZHAO Chengyong. Balancing control strategy for unbalanced current between multiple MMC converts in hybrid cascaded UHVDC system[J]. Proceedings of the CSEE, 2020, 40(20): 6653-6663. (  0) 0) |
| [27] |
姜田贵, 谢晔源, 姚宏洋, 等. 含直流断路器的双极接线柔性直流输电系统MMC交流侧单相接地故障研究[J]. 全球能源互联网, 2020, 3(2): 172-180. JIANG Tiangui, XIE Yeyuan, YAO Hongyang, et al. Single-phase-to-ground faults at AC side of MMC in bipolar HVDC system with DC circuit breakers[J]. Journal of Global Energy Interconnection, 2020, 3(2): 172-180. (  0) 0) |
 2022, Vol. 41
2022, Vol. 41


 曾蕊(1997),女,硕士在读,研究方向为混合直流输电(E-mail:
曾蕊(1997),女,硕士在读,研究方向为混合直流输电(E-mail: