文章编号: 2096-3203(2022)02-0075-08 中图分类号: TM73
2. 新疆大学电气工程学院,新疆维吾尔自治区 乌鲁木齐 830047;
3. 国网新疆电力有限公司奎屯供电公司,新疆维吾尔自治区 奎屯 831199
风电因其清洁、可再生等特性得到快速发展,对缓解能源短缺和减少环境污染有重要作用[1]。然而,风电出力固有的波动性和间歇性导致其可调度性差,弃风现象严重。因此,亟需考虑风电不确定性并制定鲁棒灵活的调度计划[2]。
传统的机组组合基于源荷预测信息,并配置一定容量的旋转备用以应对风电的不确定性[3],对风电不确定性考虑较为简单,难以应对大规模风电并网带来的挑战。有学者利用随机规划方法及机会约束规划来解决不确定优化调度问题,但风电概率信息难以准确获取、场景数量和求解精度存在矛盾等问题限制了这类方法的进一步应用[4]。近年来,鲁棒优化方法因其不依赖先验分布信息、易于实现等优点在优化调度问题中得到广泛应用[5-6]。文献[7]提出一种鲁棒风电调度模式,能够优化风电的允许出力区间,但采用固定的功率承担系数限制了运行灵活性。文献[8-9]建立了考虑仿射可调节策略的鲁棒调度模型。文献[10]构建了一种改进的两阶段鲁棒机组组合模型,能够保证解的可行性。但关于鲁棒优化调度的研究多关注火电机组与风电的协调优化,对其他源荷调节资源考虑较少。充分挖掘源荷双侧的调节潜力,实现良性互动,对提高电网运行经济性和鲁棒性具有重要作用[11]。抽水蓄能电站具有技术成熟、容量大、调节速度快等特点[12],应用前景广阔。文献[13-14]建立了考虑抽水蓄能机组的机组组合模型,能够提高系统运行经济性和清洁性。文献[15]提出了一种风电-抽水蓄能机组联合调度模式。需求响应能够挖掘负荷侧调节潜力,是重要的可灵活调节资源,分为价格型和激励型2种[16-19]。电价型需求响应基于用户自愿的原则开展,易受到各种随机因素影响,存在一定的响应不确定性[20-21]; 激励型需求响应可受电网直接控制,具有更大的调节潜力[22-24]。
为解决大规模风电接入电力系统带来的消纳问题,提出一种考虑需求响应及抽水蓄能的鲁棒机组组合优化方法。首先建立了考虑需求响应及抽水蓄能机组运行特性的数学模型,采用考虑不确定预算的风电功率不确定集合,基于仿射补偿策略,综合考虑预测场景约束和不确定场景的鲁棒可行性约束,构建鲁棒机组组合模型; 同时根据对偶原理将鲁棒优化模型转化为确定性数学规划问题; 在改进的IEEE 39节点系统中进行算例计算,对比分析不同场景下的经济性和鲁棒性,验证所提方法的正确性和有效性。
1 需求响应及抽水蓄能机组模型 1.1 需求响应运行特性及模型参与激励型需求响应(incentive-based demand response,IDR)的用户由代理商统一管理,与调度中心签订合同,明确通知时间、负荷调节量、补偿等信息。在满足自身约束的前提下,IDR用户能够响应系统的调度指令进行增/减电量,优化负荷曲线,缓解系统调峰压力,提高系统运行鲁棒性及风电消纳能力。基于提前通知时间的不同,将IDR分为日前IDR和日内IDR,日前IDR在日前调度中调整用电行为获得电量补偿,日内IDR在日前调度中提供一定的备用容量获得容量补偿。IDR的调度成本FIDR如式(1)所示。
| $ \begin{aligned} F_{\mathrm{IDR}} &=\sum\limits_{t=1}^{N_{\mathrm{T}}} \sum\limits_{k=1}^{N_{\mathrm{k}}} \sum\limits_{s=1}^{N_{\mathrm{s}}}\left(E_{k s}^{\mathrm{IDR},+} D_{k s, t}^{\mathrm{IDR},+}+E_{k s}^{\mathrm{IDR},-} D_{k s, t}^{\mathrm{IDR},-}\right)+\\ & \sum\limits_{t=1}^{N_{\mathrm{T}}} \sum\limits_{k=1}^{N_{\mathrm{k}}} \sum\limits_{s=1}^{N_{\mathrm{s}}}\left(C_{k s}^{\mathrm{IDR},+} d_{k s, t}^{\mathrm{IDR},+}+C_{k s}^{\mathrm{IDR},-} d_{k s, t}^{\mathrm{IDR},-}\right) \end{aligned} $ | (1) |
式中:NT为调度周期; Nk为参与IDR的代理商数目; Ns为IDR分段报价曲线的分段数; Dks, tIDR, +,EksIDR, +分别为t时段日前IDR的第k个代理商在报价曲线第s段的增加及其对应的电量补偿系数; Dks, tIDR, -,EksIDR, -分别为t时段日前IDR的第k个代理商在报价曲线第s段减少负荷量及其对应的电量补偿系数; dks, tIDR, -,CksIDR, -分别为t时段日内IDR的第k个代理商报价曲线第s段的向下备用容量及其对应的容量补偿系数; dks, tIDR, +,CksIDR, +分别为t时段日内IDR的第k个代理商报价曲线第s段的向上备用容量及其对应的容量补偿系数。
(1) 日前IDR调节功率约束。
| $ \left\{\begin{array}{l} 0 \leqslant \sum\limits_{s=1}^{N_{\mathrm{s}}} D_{k s, t}^{\mathrm{IDR},+} \leqslant D_{k, \max }^{\mathrm{IDR},+} \\ 0 \leqslant \sum\limits_{s=1}^{N_{\mathrm{s}}} D_{k s, t}^{\mathrm{IDR},-} \leqslant D_{k, \max }^{\mathrm{IDR},-} \end{array}\right. $ | (2) |
式中:Dk, maxIDR, +,Dk, maxIDR, -分别为日前IDR的第k个代理商增加、减小负荷的最大值。
(2) 日前IDR用电量约束。为不影响用户的正常用电需求,保证IDR需求响应前后的用电量不变,有:
| $ \sum\limits_{t=1}^{N_{\mathrm{T}}} \sum\limits_{s=1}^{N_{\mathrm{s}}}\left(D_{k s, t}^{\mathrm{IDR},+}-D_{k s, t}^{\mathrm{IDR},-}\right)=0 $ | (3) |
(3) 日内IDR备用容量约束。
| $ \begin{cases}{R}_{k, t}^{\mathrm{IDR,u}}=\sum\limits_{s=1}^{N_{\mathrm{s}}} d_{k s, t}^{\mathrm{IDR,+}} & 0 \leqslant R_{k, t}^{\mathrm{IDR,u}} \leqslant d_{k, \max }^{\mathrm{IDR},+} \\ {R}_{k, t}^{\mathrm{IDR,d}}=\sum\limits_{s=1}^{N_{\mathrm{s}}} d_{k s, t}^{\mathrm{IDR,-}} & 0 \leqslant R_{k, t}^{\mathrm{IDR, \textrm {d }}} \leqslant d_{k, \max }^{\mathrm{IDR},-}\end{cases} $ | (4) |
式中:Rk, tIDR, u,dk, maxIDR, +分别为t时段日内IDR的第k个代理商提供的向上备用容量及其对应的最大值; Rk, tIDR, d,dk, maxIDR, -分为t时段日内IDR的第k个代理商提供的向下备用容量及其对应的最大值。
1.2 抽水蓄能机组运行特性及模型抽水蓄能机组调节速度快,运行方式灵活,具备与电网双向互动的能力,可在负荷低谷存在弃风情况时抽水存储富余电量,在负荷高峰时发电以缓解系统调峰压力,并能为系统提供旋转备用,达到平抑风电出力波动、降低风电出力不确定性对电网运行的影响、提升风电消纳空间的目的。抽水蓄能机组的调度成本如式(5)所示。
| $ F_{\mathrm{g}-\mathrm{p}}=\sum\limits_{t=1}^{N_{\mathrm{T}}} \sum\limits_{m=1}^{N_{\mathrm{m}}}\left(C_{\mathrm{p}, m, t}+C_{\mathrm{g}, m, t}\right) $ | (5) |
式中:Fg-p为抽水蓄能机组的调度成本; Cp, m, t,Cg, m, t分别为抽水蓄能机组m抽水工况、发电工况的启动成本; Nm为抽水蓄能机组数量。
(1) 工作状态约束。
| $ u_{\mathrm{g}, m, t}+u_{\mathrm{p}, m, t} \leqslant 1 \quad u_{\mathrm{g}, m, t}, u_{\mathrm{p}, m, t} \in\{0,1\} $ | (6) |
式中:ug, m, t,up, m, t分别为抽水蓄能机组m的发电和抽水状态变量。抽水蓄能机组不能同时处于发电和抽水状态。当ug, m, t或up, m, t取值为1时,抽水蓄能机组m处于发电或抽水工况,否则抽水蓄能机组m处于停机状态。
(2) 抽水、发电功率约束。
| $ \left\{\begin{array}{l} P_{\mathrm{g}-\mathrm{p}, m, t}=P_{\mathrm{g}, m, t}-P_{\mathrm{p}, m, t} \\ u_{\mathrm{g}, m, t} P_{\mathrm{g}, m, \min } \leqslant P_{\mathrm{g}, m, t} \leqslant u_{\mathrm{g}, m, t} P_{\mathrm{g}, m, \max } \\ u_{\mathrm{p}, m, t} P_{\mathrm{p}, m, \min } \leqslant P_{\mathrm{p}, m, t} \leqslant u_{\mathrm{p}, m, t} P_{\mathrm{p}, m, \max } \end{array}\right. $ | (7) |
式中:Pg-p, m, t为抽水蓄能机组m的运行功率。Pg, m, t,Pp, m, t分别为抽水蓄能机组m的发电功率和抽水功率; Pg, m, max,Pg, m, min分别为抽水蓄能机组m的最大和最小发电功率; Pp, m, max,Pp, m, min分别为抽水蓄能机组m的最大和最小抽水功率。
(3) 抽水蓄能库容约束。
| $ \left\{\begin{array}{l} W_{m, t}=W_{m, t-1}+\eta_{\mathrm{p}, m} \Delta T P_{\mathrm{p}, m, t-1}-\eta_{\mathrm{g}, m} \Delta T P_{\mathrm{g}, m, t-1} \\ W_{m, \min } \leqslant W_{m, t} \leqslant W_{m, \max } \\ W_{m, 0}=W_{m, N_{\mathrm{T}}} \end{array}\right. $ | (8) |
式中:Wm, t为抽水蓄能机组m在t时段上水库蓄水池的库容; ηp, m, t,ηg, m, t分别为抽水蓄能机组m在抽水、发电状态的平均水量/电量转换系数; Wm, max,Wm, min,Wm, 0,Wm, NT分别为抽水蓄能机组m上水库蓄水池的最大库容、最小库容、初始库容和周期末库容; ΔT为调度时间间隔。
(4) 状态转换时间约束。抽水蓄能机组在抽水和发电工况下一般不进行连续启停转换,必须以停机状态作为中间状态才能进行转换。对于调度计划编制来说,需要至少一个时段的切换时间,选取一个时段为转换时间。
| $ \begin{cases}u_{\mathrm{p}, m, t}+u_{\mathrm{g}, m, t+1} \leqslant 1 & \forall t=1,2, \cdots, N_{\mathrm{T}}-1 \\ u_{\mathrm{p}, m, t+1}+u_{\mathrm{g}, m, t} \leqslant 1 & \forall t=1,2, \cdots, N_{\mathrm{T}}-1\end{cases} $ | (9) |
(5) 备用容量约束。抽水蓄能机组不仅能够对难以消纳的风电进行时空转移,提高风电可调度性,而且可为系统提供一定的备用容量,提高系统运行灵活性。
| $ \left\{\begin{aligned} R_{m, t}^{\mathrm{h}, \mathrm{u}} & \leqslant u_{\mathrm{g}, m, t}\left(P_{\mathrm{g}, m, \max }-P_{\mathrm{g}, m, t}\right)+\\ & u_{\mathrm{p}, m, t}\left(P_{\mathrm{p}, m, t}-P_{\mathrm{p}, m, \min }\right) \\ R_{m, t}^{\mathrm{h}, \mathrm{d}} & \leqslant u_{\mathrm{g}, m, t}\left(P_{\mathrm{g}, m, t}-P_{\mathrm{g}, m, \min }\right)+\\ & u_{\mathrm{p}, m, t}\left(P_{\mathrm{p}, m, \max }-P_{\mathrm{p}, m, t}\right) \end{aligned}\right. $ | (10) |
式中:Rm, th, u,Rm, th, d分别为抽水蓄能机组m预留的正、负备用容量。
2 鲁棒机组组合优化模型文中的鲁棒机组组合模型采用不确定集合刻画风电功率的随机波动,充分考虑需求响应和抽水蓄能机组的运行优势,满足系统功率平衡约束、火电机组运行约束、需求响应约束、抽水蓄能机组约束及鲁棒可行性约束等约束条件,制定机组组合及调度计划,在风电功率不确定集内任意可能风电场景都有再调度可行解,保证运行鲁棒性。
模型包括基于预测场景的机组组合及出力计划和日内再调度阶段的鲁棒可行性校验。由于考虑仿射策略的鲁棒优化模型具有简洁易处理、物理意义明确的特点,因此将再调度过程简化为仿射策略,并在风电功率不确定集合中计及不确定预算,灵活调节调度计划的保守性。
2.1 仿射调节策略将调度计划出力分解为预测场景下的预调度出力和误差场景的再调度调整出力。再调度调整出力与风电预测误差为仿射关系,即当风电出现误差波动时,源荷储按照一定比例承担系统失配量,保证系统的功率平衡。所提方法满足预测场景下的调度约束,可优化运行经济性并兼顾预测误差场景下的调度可行性,保证系统运行的鲁棒性。
再调度模型在决策阶段采用仿射调节策略,即t时段的再调度与t时段的不确定量为线性仿射关系,而与t时段后的不确定量无关,符合实际运行的时间因果性。火电机组、需求响应及抽水蓄能机组的再调度仿射策略如式(11)所示。
| $ \left\{\begin{array}{l} P_{i, t}^{\prime}=P_{0, i, t}-k_{i, t}^{\mathrm{g}} \sum\limits_{j=1}^{N_{\mathrm{w}}}\left(\tilde{P}_{j, t}^{\mathrm{w}}-\hat{P}_{j, t}^{\mathrm{w}}\right) \\ P_{\mathrm{g}-\mathrm{p}, m, t}^{\prime}=P_{\mathrm{g}-\mathrm{p}, 0, m, t}-k_{m, t}^{\mathrm{g}-\mathrm{p}} \sum\limits_{j=1}^{N_{\mathrm{w}}}\left(\tilde{P}_{j, t}^{\mathrm{w}}-\hat{P}_{j, t}^{\mathrm{w}}\right) \\ d_{k, t}^{\prime \mathrm{IDR}}=k_{k, t}^{\mathrm{IDR}} \sum\limits_{j=1}^{N_{\mathrm{w}}}\left(\tilde{P}_{j, t}^{\mathrm{w}}-\hat{P}_{j, t}^{\mathrm{w}}\right) \\ \sum\limits_{i=1}^{N_{\mathrm{g}}} k_{i, t}^{\mathrm{g}}+\sum\limits_{m=1}^{N_{\mathrm{m}}} k_{m, t}^{\mathrm{g}-\mathrm{p}}+\sum\limits_{k=1}^{N_{\mathrm{k}}} k_{k, t}^{\mathrm{IDR}}=1 \end{array}\right. $ | (11) |
式中:Nw为风电场数量; Ng为常规机组数量; P′ i, t, P′ g-p, m, t, d′k, tIDR分别为火电机组、抽水蓄能机组及日内IDR的再调度出力; P0, i, t, Pg-p, 0, m, t分别为火电机组和抽水蓄能机组在预测场景下的出力;
计及预测误差的风电出力约束构成盒式不确定集,如式(12)所示。
| $ P_{j, t}^{\mathrm{wl}} \leqslant \tilde{P}_{j, t}^{\mathrm{w}} \leqslant P_{j, t}^{\mathrm{wu}} $ | (12) |
式中:Pj, twu,Pj, twl分别为t时段风电出力区间上、下限。
考虑盒式不确定集合,鲁棒优化模型要保证最劣场景(即所有风电场出力均达到预测出力区间边界值)的系统运行可行性或经济最优。但由中心极限定理分析可知,实际运行中盒式不确定集合对应的最劣场景发生的概率几乎为零[25],基于盒式不确定集合的优化结果可能给调度带来严重的保守性。在风电功率不确定集合中引入不确定预算,实现对调度结果保守度的调节,风电功率不确定集合如式(13)所示。
| $ \varOmega=\left\{\begin{array}{c} \tilde{P}_{j, t}^{\mathrm{w}} \mid \tilde{P}_{j, t}^{\mathrm{w}} \geqslant \hat{P}_{j, t}^{\mathrm{w}}+\left(P_{j, t}^{\mathrm{wl}}-\hat{P}_{j, t}^{\mathrm{w}}\right) v_{j, t}^{\mathrm{w}} \\ \tilde{P}_{j, t}^{\mathrm{w}} \leqslant \hat{P}_{j, t}^{\mathrm{w}}+\left(P_{j, t}^{\mathrm{wu}}-\hat{P}_{j, t}^{\mathrm{w}}\right) v_{j, t}^{\mathrm{w}} \\ 0 \leqslant v_{j, t}^{\mathrm{w}} \leqslant 1 \\ \sum\limits_{j=1}^{N_{\mathrm{w}}} v_{j, t}^{\mathrm{w}} \leqslant \varGamma_{\mathrm{w}, \mathrm{s}} \end{array}\right\} $ | (13) |
式中:vj, tw为风电出力区间调节系数,用于调节风电出力边界值; Γw, s为对风电预测偏差的1-范数约束的参数,称为“不确定预算”,用以控制不确定集合所覆盖的场景空间,限制最劣场景下的风电功率偏差量,能够反映决策者对经济性和鲁棒性的偏好。当Γw, s=0时,不确定集合仅包含预测场景,在调度过程中不考虑风电功率不确定性,模型退化为传统的机组组合模型; 当Γw, s>0时,随着不确定预算增大,能够考虑更恶劣的运行场景,调度优化结果的鲁棒性增强,但同时保守度变大。
2.3 优化模型目标函数| $ F=\min \left(F_{\mathrm{g}}+F_{\mathrm{IDR}}+F_{\mathrm{g}-\mathrm{p}}\right) $ | (14) |
| $ \begin{gathered} F_{\mathrm{g}}=\sum\limits_{t=1}^{N_{\mathrm{T}}} \sum\limits_{i=1}^{N_{\mathrm{g}}}\left(a_{i} P_{0, i, t}^{2}+b_{i} P_{0, i, t}+c_{i} u_{i, t}^{\mathrm{g}}+\right. \\ \left.c_{\mathrm{u}, i} s_{\mathrm{u}, i, t}+c_{\mathrm{d}, i} s_{\mathrm{d}, i, t}+c_{i}^{\mathrm{ur}} R_{i, t}^{\mathrm{ur}}+c_{i}^{\mathrm{dr}} R_{i, t}^{\mathrm{dr}}\right) \end{gathered} $ | (15) |
式中:Fg为常规机组的发电成本; ai,bi,ci为机组i成本函数的系数; cu, i,cd, i分别为常规机组的开机成本和停机成本; su, i, t,sd, i, t分别为常规机组t时段的开机变量和停机变量; Ri, tur,Ri, tdr分别为火电机组i在t时段预留的正、负旋转备用容量,ciur,cidr分别为相应的备用成本系数; ui, tg为常规机组i在t时刻的运行状态,0表示机组停运,1表示机组运行。
2.4 优化模型约束条件 2.4.1 预测场景下的约束条件(1) 功率平衡约束。
| $ \sum\limits_{i=1}^{N_{\mathrm{g}}} P_{0, i, t}+\sum\limits_{j=1}^{N_{\mathrm{w}}} \hat{P}_{j, t}^{\mathrm{w}}+\sum\limits_{m}^{N_{\mathrm{m}}} P_{\mathrm{g}-\mathrm{p}, 0, m, t}=D_{t}-\sum\limits_{k=1}^{N_{\mathrm{k}}} D_{0, k, t}^{\mathrm{IDR}} $ | (16) |
式中:Dt为系统t时段初始负荷; D0, k, tIDR为日前IDR的响应负荷功率。
(2) 火电机组出力约束。
| $ P_{i, \min } \leqslant P_{0, i, t} \leqslant P_{i, \max } $ | (17) |
式中:Pi, max,Pi, min分别为机组i的出力上、下限。
(3) 火电机组爬坡约束。
| $ -\Delta T R_{\mathrm{D}, i} \leqslant P_{0, i, t}-P_{0, i, t-1} \leqslant \Delta T R_{\mathrm{U}, i} $ | (18) |
式中:RU, i,RD, i分别为机组i向上、向下爬坡速率限值。
(4) 火电机组备用约束。
| $ \left\{\begin{array}{l} R_{i, t}^{\mathrm{ur}} \leqslant \min \left(P_{i, \max }-P_{0, i, t}, \Delta T R_{\mathrm{U}, i}\right) \\ R_{i, t}^{\mathrm{dr}} \leqslant \min \left(P_{0, i, t}-P_{i, \min }, \Delta T R_{\mathrm{D}, i}\right) \end{array}\right. $ | (19) |
(5) 火电机组最小启停时间约束。
| $ \left\{\begin{array}{l} u_{i, t}^{\mathrm{g}}-u_{i,(t-1)}^{\mathrm{g}}=s_{\mathrm{u}, i, t}-s_{\mathrm{d}, i, t} \quad s_{\mathrm{u}, i, t}+s_{\mathrm{d}, i, t} \leqslant 1 \\ \sum\limits_{\tau=t-T_{\mathrm{U}}^{i}+1}^{t} s_{\mathrm{u}, i, \tau} \leqslant u_{i, t}^{\mathrm{g}} \quad \forall T_{\mathrm{U}}^{i}<t<N_{\mathrm{T}}, 1<i<N_{\mathrm{g}} \\ \sum\limits_{\tau=t-T_{\mathrm{D}}^{i}+1}^{t} s_{\mathrm{d}, i, \tau} \leqslant 1-u_{i, t}^{\mathrm{g}} \\ \ \ \ \ \ \ \ \ \ \ \forall T_{\mathrm{D}}^{i}<t<N_{\mathrm{T}}, 1<i<N_{\mathrm{g}} \end{array}\right. $ | (20) |
式中:TDi,TUi分别为常规机组i的最小停运时间和最小运行时间。
(6) 传输断面安全约束。
| $ \begin{aligned} &-F_{l, \max } \leqslant \sum\limits_{i=1}^{N_{\mathrm{g}}}\left(\lambda_{i, l} P_{0, i, t}\right)+\sum\limits_{j=1}^{N_{\mathrm{w}}}\left(\lambda_{j, l} \hat{P}_{j, t}^{\mathrm{w}}\right)+ \\ &\sum\limits_{m}^{N_{\mathrm{m}}}\left(\lambda_{m, l} P_{\mathrm{g}-\mathrm{p}, 0, m, t}\right)-\sum\limits_{d=1}^{N_{\mathrm{d}}}\left(\lambda_{d, l} D_{d, t}\right) \leqslant F_{l, \max } \end{aligned} $ | (21) |
式中:Nd为节点负荷数量; λi, l,λj, l,λm, l,λd, l分别为火电机组、风电场、抽水蓄能机组和节点负荷对线路l的功率转移分布因子; Fl, max为线路l的潮流上限; Dd, t为考虑日前IDR后t时段节点d的负荷值。
(7) 其他约束。抽水蓄能机组及IDR约束条件见1.1节和1.2节。
2.4.2 误差场景下的鲁棒可行性约束在满足中预测场景约束的基础上,增加鲁棒可行性约束,保证系统在任意不确定误差场景下均存在再调度解。
(1) 机组出力限制鲁棒约束。
| $ P_{i, \min } \leqslant P_{i, t}^{\prime} \leqslant P_{i, \max } \quad \forall \tilde{P}_{j, t}^{\mathrm{w}} \in \varOmega $ | (22) |
(2) 机组出力爬坡鲁棒约束。
| $ -\Delta T R_{\mathrm{D}, i} \leqslant P_{i, t}^{\prime}-P_{i, t-1}^{\prime} \leqslant \varDelta T R_{\mathrm{U}, i} \quad \forall \tilde{P}_{j, t}^{w} \in \varOmega $ | (23) |
(3) 备用容量鲁棒约束。
| $ \left\{\begin{array}{l} P_{i, t}^{\prime}-P_{0, i, t} \leqslant R_{i, t}^{\mathrm{ur}} \quad \forall \tilde{P}_{j, t}^{\mathrm{w}} \in \varOmega \\ -\left(P_{i, t}^{\prime}-P_{0, i, t}\right) \leqslant R_{i, t}^{\mathrm{dr}} \quad \forall \tilde{P}_{j, t}^{\mathrm{w}} \in \varOmega \\ P_{\mathrm{g}-\mathrm{p}, m, t}^{\prime}-P_{\mathrm{g}-\mathrm{p}, 0, m, t} \leqslant R_{m, t}^{\mathrm{h}, \mathrm{u}} \quad \forall \tilde{P}_{j, t}^{\mathrm{w}} \in \varOmega \\ -\left(P_{\mathrm{g}-\mathrm{p}, m, t}^{\prime}-P_{\mathrm{g}-\mathrm{p}, 0, m, t}\right) \leqslant R_{m, t}^{\mathrm{h}, \mathrm{d}} \quad \forall \tilde{P}_{j, t}^{\mathrm{w}} \in \varOmega \\ -R_{k, t}^{\mathrm{IDR, \textrm {d }}} \leqslant d_{k, t}^{\prime \mathrm{IDR}} \leqslant R_{k, t}^{\mathrm{IDR,u}} \quad \forall \tilde{P}_{j, t}^{\mathrm{w}} \in \varOmega \end{array}\right. $ | (24) |
(4) 传输断面安全鲁棒约束。
| $ \begin{gathered} -F_{l, \max } \leqslant \sum\limits_{i=1}^{N_{\mathrm{g}}}\left(\lambda_{i, l} P_{i, t}^{\prime}\right)+\sum\limits_{m=1}^{N_{\mathrm{w}}}\left(\lambda_{j, l} \tilde{P}_{j, t}^{\mathrm{w}}\right)+ \\ \sum\limits_{m}^{N_{\mathrm{m}}}\left(\lambda_{m, l} P_{\mathrm{g}-\mathrm{p}, m, t}^{\prime}\right)-\sum\limits_{d=1}^{N_{\mathrm{d}}}\left(\lambda_{d, l} D_{d, t}^{\prime}\right) \leqslant F_{l, \max } \\ \forall \tilde{P}_{j, t}^{\mathrm{w}} \in \varOmega \end{gathered} $ | (25) |
式中:D′ d, t为考虑日前IDR和日内IDR后t时段节点d的负荷值。
3 模型转换与求解应用对偶理论将含有不确定变量的鲁棒可行性约束式(22)-式(25)转化为确定性约束,以备用容量鲁棒约束(24)的第一个约束为例,其等价转化结果如式(26)所示。其他不确定约束等价转化方法相同,故不再赘述。
| $ \left\{\begin{array}{l} z^{\mathrm{w}} \varGamma_{\mathrm{w}, \mathrm{s}}+\sum\limits_{j=1}^{N_{\mathrm{w}}} p_{j}^{\mathrm{w}} \leqslant R_{i, t}^{\mathrm{ur}} \\ z^{\mathrm{w}}+p_{j}^{\mathrm{w}} \geqslant-\left(P_{j, t}^{\mathrm{wu}}-\hat{P}_{j, t}^{\mathrm{w}}\right) k_{i, t}^{\mathrm{g}} \\ z^{\mathrm{w}}+p_{j}^{\mathrm{w}} \geqslant\left(\hat{P}_{j, t}^{\mathrm{w}}-P_{j, t}^{\mathrm{wl}}\right) k_{i, t}^{{g}} \\ z^{\mathrm{w}} \geqslant 0, p_{j}^{\mathrm{w}} \geqslant 0 \end{array}\quad j=1, \cdots, N_{\mathrm{w}} \right. $ | (26) |
式中:zw,pwj为转化过程中引入的对偶变量。
经过约束条件的确定性等价转化,文中模型转换成等价的混合整数线性规划问题模型,使用成熟的求解器Cplex进行模型求解,优化火电机组的启停计划、出力计划、抽水蓄能出力计划及IDR调度计划等决策变量。
4 算例分析为了验证建立的鲁棒机组组合模型的可行性和有效性,在改进的IEEE 39节点系统中进行算例分析,每个时段15 min,共96个时段。仿真系统包含10台火电机组、4个风电场及1台抽水蓄能机组,其中火电机组采用文献[26]中的参数,抽水蓄能机组参数见表 1。算例中有2个日前IDR聚集商和1个日内IDR聚集商,其报价参数如表 2所示。风电场的装机容量分别为200 MW,200 MW,300 MW,200 MW,设置风电预测误差分布的95%置信区间作为风电功率不确定区间[27]。
|
|
表 1 抽水蓄能机组参数 Table 1 Parameters of pumped storage units |
|
|
表 2 IDR参数 Table 2 Parameters of IDR |
结合文中模型特点,针对以下4种运行场景进行仿真分析,不确定预算设置为4。场景1:仅含火电机组及风电场,不含抽水蓄能机组及IDR。场景2:在场景1的基础上加入IDR。场景3:在场景1的基础上加入抽水蓄能机组。场景4:在场景1的基础上同时考虑抽水蓄能机组、IDR。4种场景下的优化结果如表 3所示。
|
|
表 3 4种运行场景下的调度结果 Table 3 Scheduling results in four scenarios |
由表 3可知,场景1的总成本最高,这是因为仅有火电机组满足净负荷需求并提供备用容量,火电机组运行成本和备用成本远高于其他场景。场景2中引入IDR,通过优化日前IDR能够平抑负荷峰谷差,缓解了调峰压力,并且日内IDR提供了备用容量,增加了系统应对风电不确定性的能力,提高了系统运行经济性,总成本相比场景1降低了4.3%。场景3引入抽水蓄能机组,在负荷低谷时发电,在负荷高峰时抽水,实现对溢出风电的时空挪移,降低了负荷峰谷差,并提供了部分备用容量,缓解了火电机组的调节压力,总成本相比场景1降低了8.3%。场景4通过协调优化火电机组、抽蓄机组及IDR的出力计划,调节能力增强,系统总成本最小,相对场景1降低了10.9%,保证系统运行鲁棒性同时提高了经济性。
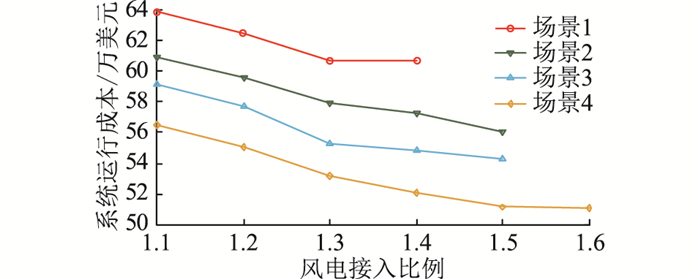
4.2 风电接入比例对调度结果影响分析随着风电接入比例的增加,对比分析不同场景下系统的风电消纳能力。风电装机容量在初始容量的1.1~1.6倍变化时,不同运行场景的运行成本及解的可行性如图 1所示。
|
图 1 不同风电接入比例下各场景调度结果 Fig. 1 Scheduling results of scenarios with different wind power access ratios |
由图 1可知,随着风电接入比例的增加,各场景的运行成本逐渐降低,其中场景4运行成本最低,场景2、3次之,场景1运行成本最高。当风电接入比达到1.4时,场景1单纯依靠火电机组的调节能力,无可行解,需要采取弃风或切负荷等调整措施保证调度计划可行性。而场景2和场景3在风电接入比增加至1.6时调节能力难以满足系统需求导致无可行解,只有场景4存在可行解,仍能够保证调度计划的可行性。因此相比于其他场景,考虑需求响应及抽水蓄能机组的场景4具有更充足的灵活调节能力,能够提升运行经济性和风电消纳能力。
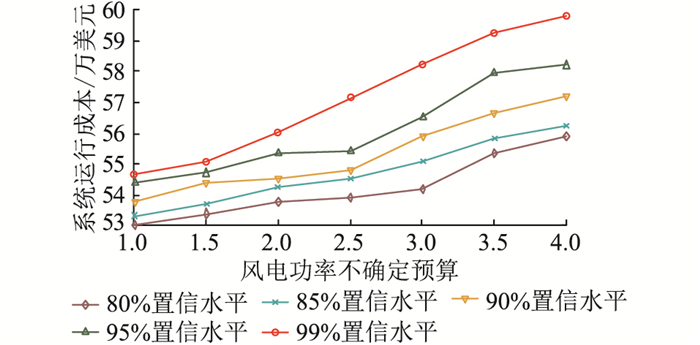
4.3 不确定性预算和置信区间影响分析基于场景分析风电功率不确定预算及风电出力置信区间对调度计划的影响,结果如图 2所示。由图 2可知,当风电出力置信区间相同时,随着不确定预算的增加,系统运行鲁棒性增强,同时总成本随之增加,系统运行经济性降低,调度计划趋于保守。而当不确定预算相同时,随着风电出力置信区间增加,系统能够应对更加极端的风电出力场景,运行的鲁棒性增强,但系统的运行成本增加,经济性变差。因此,在实际调度中可根据实际需求调节不确定预算和风电出力置信区间实现系统运行经济性和鲁棒性的调节折衷。
|
图 2 不确定预算及置信区间对调度结果的影响 Fig. 2 Impact of uncertainty budget and confidence interval on scheduling results |
采用新疆某区域电网进行仿真算例,进一步验证文中所提方法的有效性和可行性。该区域电网中含7 725 MW火电、2 663 MW风电,负荷和风电数据取自电网的实际运行数据,并增加1台200 MW的抽水蓄能机组、2个日前IDR聚集商和1个日内IDR聚集商。不同运行场景下,IEEE 39节点系统和实际电网的优化结果如表 4所示。
|
|
表 4 4种运行场景下不同系统的调度结果 Table 4 Different system scheduling results in four scenarios |
由表 4可知,对于IEEE 39节点系统而言,4种运行场景的平均计算时间为25.6 s,运行场景的计算时间最小为17.1 s,运行场景4的计算时间最大。这是由于考虑了抽水蓄能机组及需求响应后优化模型中的优化变量增多,计算量略有增加。实际电网优化模型的计算时间大于IEEE 39节点系统,最大计算时间和平均计算时间分别为73.7 s,64.2 s。可见,随着系统规模的增大,所建模型仍具有较好的计算效率,能够满足系统调度运行的时效性要求。
5 结语文中提出一种考虑需求响应及抽水蓄能的鲁棒机组组合优化方法。综合考虑需求响应及抽水蓄能机组的运行优势,采用考虑不确定预算的风电功率不确定集合,基于仿射补偿策略构建鲁棒机组组合模型,并转化为易于求解的形式。算例结果表明,需求响应及抽水蓄能机组能够优化负荷曲线,降低峰谷差,缓解火电机组调节压力,提高系统运行经济性、鲁棒性和风电消纳能力; 通过调节不确定预算和风电出力区间能够实现系统运行的经济性和鲁棒性的调节折衷。文中针对日前尺度调度阶段进行研究,后续将对需求响应及储能参与的多时间尺度鲁棒优化调度问题进行研究。
| [1] |
王耀华, 焦冰琦, 张富强, 等. 计及高比例可再生能源运行特性的中长期电力发展分析[J]. 电力系统自动化, 2017, 41(21): 9-16. WANG Yaohua, JIAO Bingqi, ZHANG Fuqiang, et al. Medium and long-term electric power development considering operating characteristics of high proportion of renewable energy[J]. Automation of Electric Power Systems, 2017, 41(21): 9-16. DOI:10.7500/AEPS20170612001 (  0) 0) |
| [2] |
林峰, 汪震, 王冠中, 等. 考虑风电降载的电力系统鲁棒备用调度模型[J]. 电力系统自动化, 2018, 42(19): 64-70, 154. LIN Feng, WANG Zhen, WANG Guanzhong, et al. Robust reserve scheduling model of electric power system considering WTG de-loading capability[J]. Automation of Electric Power Systems, 2018, 42(19): 64-70, 154. DOI:10.7500/AEPS20171011009 (  0) 0) |
| [3] |
朱光远, 林济铿, 罗治强, 等. 鲁棒优化在电力系统发电计划中的应用综述[J]. 中国电机工程学报, 2017, 37(20): 5881-5892. ZHU Guangyuan, LIN Jikeng, LUO Zhiqiang, et al. Review of robust optimization for generation scheduling in power systems[J]. Proceedings of the CSEE, 2017, 37(20): 5881-5892. (  0) 0) |
| [4] |
徐秋实, 邓长虹, 赵维兴, 等. 含风电电力系统的多场景鲁棒调度方法[J]. 电网技术, 2014, 38(3): 653-661. XU Qiushi, DENG Changhong, ZHAO Weixing, et al. A multi-scenario robust dispatch method for power grid integrated with wind farms[J]. Power System Technology, 2014, 38(3): 653-661. (  0) 0) |
| [5] |
仉梦林, 胡志坚, 李燕, 等. 基于可行性检测的考虑风电和需求响应的机组组合鲁棒优化方法[J]. 中国电机工程学报, 2018, 38(11): 3184-3194. ZHANG Menglin, HU Zhijian, LI Yan, et al. A robust optimization method for unit commitment considering wind power and demand response based on feasibility testing[J]. Proceedings of the CSEE, 2018, 38(11): 3184-3194. (  0) 0) |
| [6] |
黎静华, 文劲宇, 潘毅, 等. 面向新能源并网的电力系统鲁棒调度模式[J]. 电力系统保护与控制, 2015, 43(22): 47-54. LI Jinghua, WEN Jinyu, PAN Yi, et al. Robust dispatching mode of electrical power system to cope with renewable energy power[J]. Power System Protection and Control, 2015, 43(22): 47-54. DOI:10.7667/j.issn.1674-3415.2015.22.008 (  0) 0) |
| [7] |
李志刚, 吴文传, 张伯明. 消纳大规模风电的鲁棒区间经济调度(一)调度模式与数学模型[J]. 电力系统自动化, 2014, 38(20): 33-39. LI Zhigang, WU Wenchuan, ZHANG Boming. A robust interval economic dispatch method accommodating large-scale wind power generation part one dispatch scheme and mathematical model[J]. Automation of Electric Power Systems, 2014, 38(20): 33-39. DOI:10.7500/AEPS20131123001 (  0) 0) |
| [8] |
翟俊义, 周明, 李庚银, 等. 考虑可消纳风电区间的多区电力系统分散协调鲁棒调度方法[J]. 电网技术, 2018, 42(3): 747-755. ZHAI Junyi, ZHOU Ming, LI Gengyin, et al. A decentralized and robust dispatch approach for multi-area power system considering accommodated wind power interval[J]. Power System Technology, 2018, 42(3): 747-755. (  0) 0) |
| [9] |
吴巍, 汪可友, 李国杰, 等. 提升风电消纳区间的鲁棒机组组合[J]. 电工技术学报, 2018, 33(3): 523-532. WU Wei, WANG Keyou, LI Guojie, et al. Robust unit commitment to improve the admissible region of wind power[J]. Transactions of China Electrotechnical Society, 2018, 33(3): 523-532. (  0) 0) |
| [10] |
罗毅, 邵周策, 张磊, 等. 考虑风电不确定性和气网运行约束的鲁棒经济调度和备用配置[J]. 电工技术学报, 2018, 33(11): 2456-2467. LUO Yi, SHAO Zhouce, ZHANG Lei, et al. Robust economic dispatch and reserve configuration considering wind uncertainty and gas network constraints[J]. Transactions of China Electrotechnical Society, 2018, 33(11): 2456-2467. (  0) 0) |
| [11] |
ZHANG M L, FANG J K, AI X M, et al. Feasibility identification and computational efficiency improvement for two-stage RUC with multiple wind farms[J]. IEEE Transactions on Sustainable Energy, 2020, 11(3): 1669-1678. DOI:10.1109/TSTE.2019.2936581 (  0) 0) |
| [12] |
吕翔, 刘国静, 周莹. 含抽水蓄能的风水火联合机组组合研究[J]. 电力系统保护与控制, 2017, 45(12): 35-43. LYU Xiang, LIU Guojing, ZHOU Ying. Research on combined unit commitment of wind power-hydro power-thermal power for the power system with pumped hydro storage[J]. Power System Protection and Control, 2017, 45(12): 35-43. DOI:10.7667/PSPC160884 (  0) 0) |
| [13] |
JIANG R W, WANG J H, GUAN Y P. Robust unit commitment with wind power and pumped storage hydro[J]. IEEE Transactions on Power Systems, 2012, 27(2): 800-810. DOI:10.1109/TPWRS.2011.2169817 (  0) 0) |
| [14] |
HUANG H Y, ZHOU M, ZHANG L J, et al. Joint generation and reserve scheduling of wind-solar-pumped storage power systems under multiple uncertainties[J]. International Transactions on Electrical Energy Systems, 2019, 29(7): 1-21. (  0) 0) |
| [15] |
徐飞, 陈磊, 金和平, 等. 抽水蓄能电站与风电的联合优化运行建模及应用分析[J]. 电力系统自动化, 2013, 37(1): 149-154. XU Fei, CHEN Lei, JIN Heping, et al. Modeling and application analysis of optimal joint operation of pumped storage power station and wind power[J]. Automation of Electric Power Systems, 2013, 37(1): 149-154. (  0) 0) |
| [16] |
袁泉, 吴云亮, 李豹, 等. 计及源荷不确定性的多时间尺度滚动调度计划模型与方法[J]. 电力系统保护与控制, 2019, 47(16): 8-16. YUAN Quan, WU Yunliang, LI Bao, et al. Multi-timescale coordinated dispatch model and approach considering generation and load uncertainty[J]. Power System Protection and Control, 2019, 47(16): 8-16. (  0) 0) |
| [17] |
田壁源, 何峰, 常喜强, 等. 计及综合需求响应的电热气互联能源系统环保经济优化调度[J]. 电力需求侧管理, 2021, 23(1): 18-24. TIAN Biyuan, HE Feng, CHANG Xiqiang, et al. Environmental economic optimal dispatch of electricity-heat-gas integrated energy system considering integrated demand response[J]. Power Demand Side Management, 2021, 23(1): 18-24. (  0) 0) |
| [18] |
苏宜强, 刘盛松. 计及碳交易-绿证的"源-荷"互动优化调度策略[J]. 电力需求侧管理, 2021, 23(5): 35-39. SU Yiqiang, LIU Shengsong. Source-demand interactive optimal scheduling strategy considering carbon trading and green certificate[J]. Power Demand Side Management, 2021, 23(5): 35-39. (  0) 0) |
| [19] |
刘小聪, 王蓓蓓, 李扬, 等. 计及需求侧资源的大规模风电消纳随机机组组合模型[J]. 中国电机工程学报, 2015, 35(14): 3714-3723. LIU Xiaocong, WANG Beibei, LI Yang, et al. Stochastic unit commitment model for high wind power integration considering demand side resources[J]. Proceedings of the CSEE, 2015, 35(14): 3714-3723. (  0) 0) |
| [20] |
胡晶, 陈红坤, 陈磊, 等. 考虑多主体利益与需求响应的分布式电源优化配置[J]. 电力系统保护与控制, 2021, 49(15): 38-46. HU Jing, CHEN Hongkun, CHEN Lei, et al. Distributed generation planning in an active distribution network considering multi-agent interests and demand response[J]. Power System Protection and Control, 2021, 49(15): 38-46. (  0) 0) |
| [21] |
张涛, 郭玥彤, 李逸鸿, 等. 计及电气热综合需求响应的区域综合能源系统优化调度[J]. 电力系统保护与控制, 2021, 49(1): 52-61. ZHANG Tao, GUO Yuetong, LI Yihong, et al. Optimization scheduling of regional integrated energy systems based on electric-thermal-gas integrated demand response[J]. Power System Protection and Control, 2021, 49(1): 52-61. (  0) 0) |
| [22] |
曾博, 杨雍琦, 段金辉, 等. 新能源电力系统中需求侧响应关键问题及未来研究展望[J]. 电力系统自动化, 2015, 39(17): 10-18. ZENG Bo, YANG Yongqi, DUAN Jinhui, et al. Key issues and research prospects for demand-side response in alternate electrical power systems with renewable energy sources[J]. Automation of Electric Power Systems, 2015, 39(17): 10-18. (  0) 0) |
| [23] |
李政洁, 撖奥洋, 周生奇, 等. 计及综合需求响应的综合能源系统优化调度[J]. 电力系统保护与控制, 2021, 49(21): 36-43. LI Zhengjie, HAN Aoyang, ZHOU Shengqi, et al. Optimization of an integrated energy system considering integrated demand response[J]. Power System Protection and Control, 2021, 49(21): 36-43. (  0) 0) |
| [24] |
白浩, 袁智勇, 周长城, 等. 计及新能源波动与相关性的配电网最大供电能力调度方法[J]. 电力系统保护与控制, 2021, 49(8): 66-73. BAI Hao, YUAN Zhiyong, ZHOU Changcheng, et al. Dispatching method of maximum power supply capacity of a power distributed network considering fluctuation and correlation of renewable energy[J]. Power System Protection and Control, 2021, 49(8): 66-73. (  0) 0) |
| [25] |
魏韡, 刘锋, 梅生伟. 电力系统鲁棒经济调度(一)理论基础[J]. 电力系统自动化, 2013, 37(17): 37-43. WEI Wei, LIU Feng, MEI Shengwei. Robust and economical scheduling methodology for power systems part one theoretical foundations[J]. Automation of Electric Power Systems, 2013, 37(17): 37-43. (  0) 0) |
| [26] |
ONGSAKUL W, PETCHARAKS N. Unit commitment by enhanced adaptive Lagrangian relaxation[J]. IEEE Transactions on Power Systems, 2004, 19(1): 620-628. (  0) 0) |
| [27] |
WANG C, LIU F, WANG J H, et al. Robust risk-constrained unit commitment with large-scale wind generation: an adjustable uncertainty set approach[J]. IEEE Transactions on Power Systems, 2017, 32(1): 723-733. (  0) 0) |
2. School of Electrical Engineering, Xinjiang University, Urumqi 830047, China;
3. State Grid Kuitun Power Supply Company of Xinjiang Electric Power Co., Ltd., Kuitun 831199, China
 2022, Vol. 41
2022, Vol. 41


 陈伟伟(1989), 男, 硕士, 工程师, 从事电力系统优化与电网规划工作(E-mail:
陈伟伟(1989), 男, 硕士, 工程师, 从事电力系统优化与电网规划工作(E-mail: