0 引言

随着全球能源短缺和环境污染问题的日益突出，大力发展可再生能源发电技术已成为全世界的共识。然而，近年来风电并网引起电力系统事故时有发生^[1-2]，因此需要评估风电并网对电力系统的影响。双馈型风机具有成本低、控制灵活的特点^[3-4]，被广泛应用于风力发电系统中。然而，双馈型风机对电网电压变化敏感，在系统故障时会恶化系统的动态响应^[5-6]。因此，分析双馈型风机对电力系统的电压稳定性的影响具有重要意义^[7]。

目前，已有相关文献对双馈型风机并网的电力系统暂态稳定性分析和控制开展研究。文献[8]分析了风力发电系统接入对电力系统功角稳定性的影响。文献[9]提出一种基于修正暂态能量函数的量化暂态稳定性评估方法。文献[10]研究了双馈型风机接入系统比例的增加对电力系统暂态稳定性的影响。为了抑制双馈型风机自身不稳定运行带来的功率振荡，文献[11]提出一种改进的离散控制器。然而，以上文献并未涉及双馈型风机并网对电力系统电压动态的影响。文献[12]研究了风机非线性特性对系统电压的影响。文献[13]通过时域仿真研究了静止同步补偿器等无功补偿装置对系统电压的影响。文献[14]分析了无功补偿装置在增强电力系统短期电压稳定性方面的作用。文献[15]研究了双馈型风机造成系统电压振荡的机理。上述研究均使用时域仿真方法对系统电压动态进行分析，计算量大，难以实现对系统电压稳定性的在线判断，且无法获得系统稳定裕度的量化分析结果。Lyapunov理论是评估电力系统电压稳定性的另一种方法^[16]，通过计算初始状态到稳定域边界的距离可以得到量化的稳定性分析结果。然而，由于缺乏构造Lyapunov函数的系统算法，制约了该理论在实际系统中的应用。

输入-状态稳定(input-to-state stability, ISS)理论为研究非线性系统的稳定性问题提供了一种新的途径。该理论将状态空间稳定理论与输入-输出稳定理论相结合，通过将互联系统分解为若干子系统，利用子系统的ISS特性及其连接关系研究互联系统的稳定性^[17-18]。ISS理论可以研究非线性系统在外部扰动下的动态响应特性以及量化系统可承受的外部扰动的大小，因此，ISS理论适用于含双馈型风机的电力系统电压稳定性分析。

基于上述分析，文中提出一种双馈风力发电系统的电压稳定性量化分析方法。基于小增益定理，对双馈风力发电系统稳定特性进行量化分析，为其运行和控制提供指导。首先对ISS理论进行介绍; 其次以ISS理论为基础，提出了双馈风力发电系统的电压稳定性量化分析方法; 然后通过时域仿真验证了量化稳定性分析方法的有效性; 最后总结全文并指出未来的研究方向。

1 理论基础

文中给出局部输入-状态稳定(local input-to-state stability, LISS)和局部输入-输出稳定(local input-to-output stability, LIOS)的基本理论，并讨论与ISS等价的积分-积分估计，为子系统和互联系统的稳定性分析奠定基础。

考虑具有外部输入的非线性系统：

$ \left\{\begin{array}{l} \dot{\boldsymbol{x}}=f(\boldsymbol{x}, \boldsymbol{u}) \\ \boldsymbol{y}=h(\boldsymbol{x}, \boldsymbol{u}) \end{array}\right. $

(1)

式中：x∈Rⁿ; y∈R^p; u∈R^m; f: R^n×m→Rⁿ; h: R^n×m→R^p。f和h在x和u上连续且满足局部Lipschitz条件，且f(0, 0)=0, h(0, 0)=0。

定义1：取Ω_ISS为LISS初始状态域，U_ISS为LISS外部输入域，则对于任意x₀∈Ω_ISS∈Rⁿ, u∈U_ISS∈R^m，如果存在比较函数β_ISS∈K_L，γ_ISS∈K_∞，对于任意初始状态x₀和外部输入u，式(2)成立，则非线性系统(1)是LISS的。

$ \begin{gathered} \left|\boldsymbol{x}\left(t, \boldsymbol{x}_{0}, \boldsymbol{u}\right)\right| \leqslant \beta_{\mathrm{ISS}}\left(\left|\boldsymbol{x}_{0}\right|, t\right)+\gamma_{\mathrm{ISS}}\left(\|\boldsymbol{u}\|_{\infty}\right) \\ \forall t \geqslant 0 \end{gathered} $

(2)

式中：| · |为欧几里德范数; γ_ISS为输入到状态渐近增益; ‖u‖_∞为外部输入u的上确界。

定义2：取Ω_IOS为LIOS初始状态域，U_IOS为LOSS外部输入域，则对于任意x₀∈Ω_IOS∈Rⁿ, u∈U_IOS∈R^m，如果存在比较函数β_IOS∈K_L，γ_IOS∈K_∞，式(3)成立，则非线性系统(1)是LIOS的。

$ \begin{gathered} \left|\boldsymbol{y}\left(t, \boldsymbol{x}_{0}, \boldsymbol{u}\right)\right| \leqslant \beta_{\mathrm{IOS}}\left(\left|\boldsymbol{x}_{0}\right|, t\right)+\gamma_{\mathrm{IOS}}\left(\|\boldsymbol{u}\|_{\infty}\right) \\ \forall t \geqslant 0 \end{gathered} $

(3)

式中：γ_IOS为输入到输出渐近增益。

对于非线性系统的LISS/LIOS分析，估计初始状态的局部域和外部输入的局部域是至关重要的。在实际系统中，非线性系统的稳定域可以用Ω和U来表示，其中Ω=Ω_ISS∩Ω_IOS，U=U_ISS∩U_IOS。

渐近增益能反映外部输入对系统状态和输出的影响，并可量化系统对外部扰动的承受能力。由于定义1和2中外部输入由其上确界表示，因此仅能反映外部扰动的幅值信息，不能反映其随时间的波动信息。为解决该问题，文中采用与ISS等价的积分-积分估计^[19]。

定义3：对于任意x₀∈Ω_IOS∈Rⁿ, u∈U_IOS∈R^m，若式(4)成立，则称系统(1)满足局部状态积分-积分估计。

$ \begin{gathered} \int_{0}^{t} \alpha_{\mathrm{ISS}}|\boldsymbol{x}(s)| \mathrm{d} s \leqslant \\ \alpha_{\mathrm{ISS}}^{0}\left|\boldsymbol{x}_{0}\right|+\int_{0}^{t} \gamma_{\mathrm{ISS}}|\boldsymbol{u}(s)| \mathrm{d} s \end{gathered} $

(4)

式中：α_ISS，α_ISS⁰，γ_ISS∈K_∞。

定义4：对于任意x₀∈Ω_IOS∈Rⁿ, u∈U_IOS∈R^m，若式(5)成立，则称系统(1)满足局部输出积分-积分估计。

$ \begin{gathered} \int_{0}^{t} \alpha_{\operatorname{IOS}}|\boldsymbol{y}(s)| \mathrm{d} s \leqslant \\ \alpha_{\mathrm{IOS}}^{0}\left|\boldsymbol{x}_{0}\right|+\int_{0}^{t} \gamma_{\mathrm{IOS}}|\boldsymbol{u}(s)| \mathrm{d} s \end{gathered} $

(5)

式中：α_IOS，α_IOS⁰，γ_IOS∈K_∞。

由积分-积分估计的定义可见，系统状态、外部输入和系统输出均由积分表示，因此该分析方法能包含外部扰动的幅值信息以及在时间尺度上的波动信息。

文献[20]给出了子系统的量化LISS/LIOS评估的详细算法，基于此，提出互联系统的量化稳定性评估准则，量化评估双馈型风机接入对电网稳定性产生的影响。

2 双馈风力发电系统稳定性量化评估准则

考虑一个由n个子系统组成的互联系统，在双馈风力发电系统中，子系统可以选取双馈型风机、同步发电机、感应电动机等，其中第i个子系统数学模型表达式如下：

$ \left\{\begin{array}{l} \dot{\boldsymbol{x}}_{i}=f_{i}\left(\boldsymbol{x}_{i}, \boldsymbol{u}_{i}, \boldsymbol{\omega}_{i}\right) \\ \boldsymbol{y}_{i}=h_{i}\left(\boldsymbol{x}_{i}, \boldsymbol{u}_{i}, \boldsymbol{\omega}_{i}\right) \end{array}\right. $

(6)

式中：x_i∈R^N_i，u_i∈R^M_i为与其他子系统的状态和输出相关的内部输入; ω_i∈R^W_i为外部扰动; y_i∈R^P_i为各子系统的输出。研究双馈风力发电系统电压稳定性时，电源、负载子系统将选择电压、电流作为输入和输出，外部扰动对应双馈风力发电系统中受故障影响产生的电压波动。

由于最大输入与初始状态有关，因此用$\epsilon_{\tilde{\boldsymbol{x}}_{0}}$表示与|x₀|相关的最大输入，用$\boldsymbol{\mu}_{\tilde{\boldsymbol{x}}_{0}}$表示与|x₀|相关的最大输出。为满足LISS/LIOS的要求，子系统的输入需满足 $\int_{0}^{t}\left|\boldsymbol{u}_{i}(s)\right| \mathrm{d} s \leqslant \boldsymbol{\epsilon}_{\tilde{x}_{0}}$，对应的输出需满足$\int_{0}^{t}\left|\boldsymbol{y}_{i}(s)\right| \mathrm{d} s \leqslant \boldsymbol{\mu}_{\tilde{x}_{0}}$。

假设每个子系统都满足LISS/LIOS属性，并且子系统之间的连接关系可以表示为输入u_i和输出y_i的关系。通常，电力系统模型由微分代数方程组成，每个子系统的输入和输出满足一系列代数方程g(u, y)=0，子系统连接关系Z由系统的节点导纳矩阵消去运算获得^[21]。

文中给出基于积分-积分估计的互联系统量化稳定性评估准则如下。

如果由n个子系统组成的互联系统，满足下列2个准则，则该互联系统是LISS和LIOS的。

(1) 小增益条件成立，即：

$ G\left(\boldsymbol{v}^{*}\right)<\boldsymbol{v}^{*} $

(7)

$ G(\boldsymbol{p})<\boldsymbol{p} \quad \forall \boldsymbol{p} \in\left({\bf{0}}, \boldsymbol{v}^{*}\right] $

(8)

式中：G=Γ_IOS $ \circ $ Z, Γ_IOS为I/O增益矩阵; v^*为满足(7)的局部稳定域边界; p为(0, v^*]区域内一点。

(2) 系统稳定裕度M大于0，即：

$ \begin{gathered} M= \\ 1-\frac{\mu \circ\left(\alpha_{\mathrm{IOS}}^{0}\left|\boldsymbol{x}_{0}\right|+\vartheta_{\mathrm{IOS}} \circ \int_{0}^{t}|\boldsymbol{\omega}(s)| \mathrm{d} s\right)}{\min \left\{\boldsymbol{\mu}_{\tilde{\boldsymbol{x}}_{0}}, \gamma\right\}}>0 \end{gathered} $

(9)

式中：$\mu \in K_{\infty} ; \vartheta_{10 S} $为外部扰动的近似增益; γ为满足稳定性评估准则(1)的最大输出集合。

接下来证明量化稳定性评估准则。

第一步，证明当系统(6)即式(6)满足局部小增益定理，即稳定性评估准则(1)时，互联后子系统依然满足积分-积分估计。由文献[22]可知，当系统(6)满足量化稳定性评估准则(1)时，存在一个函数μ∈K_∞使得式(10)成立。

$ \begin{gathered} \int_{0}^{t}|\tilde{\boldsymbol{y}}(s)| \mathrm{d} s \leqslant \\ \mu \circ\left(\alpha_{\mathrm{IOS}}^{0}\left|\tilde{\boldsymbol{x}}_{0}\right|+\int_{0}^{t} \vartheta_{\mathrm{IOS}}|\tilde{\boldsymbol{\omega}}(s)| \mathrm{d} s\right) \end{gathered} $

(10)

令$ a=\left|\tilde{\boldsymbol{x}}_{0}\right|, b=\int_{0}^{t}|\tilde{\boldsymbol{\omega}}(s)| \mathrm{d} s$，则式(10)右侧表达式可转换为向量函数f(a, b)，即：

$ \mu \circ\left(\alpha_{\mathrm{IOS}}^{0}\left|\tilde{\boldsymbol{x}}_{0}\right|+\int_{0}^{t} \boldsymbol{\vartheta}_{\mathrm{IOS}}|\tilde{\boldsymbol{\omega}}(s)| \mathrm{d} s\right) \rightarrow f(a, b) $

(11)

考虑到$\mu, \boldsymbol{\vartheta}_{\mathrm{IOS}} $为K_∞函数，对于有界输入a≤A，b≤B，f(a, b)≤F，则f(a, b)单调有界，那么对于有界输入a≤A，b≤B，一定存在函数g(a, b)，满足g(a, b)≥f(a, b)。

令$ \alpha_{\mathrm{IOS}, s}^{0}\left|\tilde{\boldsymbol{x}}_{0}\right|+\int_{0}^{t} \vartheta_{\mathrm{IOS}, s}|\tilde{\boldsymbol{\omega}}(s)| \mathrm{d} s \rightarrow g(a, b)$，其中，$ \alpha_{\mathrm{IOS}, s}^{0}, \boldsymbol{\vartheta}_{\mathrm{IOS}, s} \in K_{\infty}$。考虑到g(a, b)≥f(a, b)，式(12)成立。

$ \begin{gathered} \int_{0}^{t}|\tilde{\boldsymbol{y}}(s)| \mathrm{d} s \leqslant \\ \alpha_{\mathrm{IOS}, s}^{0}\left|\tilde{\boldsymbol{x}}_{0}\right|+\int_{0}^{t} \boldsymbol{\vartheta}_{\mathrm{IOS}, s}|\tilde{\boldsymbol{\omega}}(s)| \mathrm{d} s \end{gathered} $

(12)

因此，互联系统(6)是LIOS的。接下来证明互联系统(6)是LISS的。

子系统满足式LISS属性，式(13)成立。

$ \begin{gathered} \int_{0}^{t}|\tilde{\boldsymbol{x}}(s)| \mathrm{d} s \leqslant \alpha_{\mathrm{ISS}}^{0}\left|\tilde{\boldsymbol{x}}_{0}\right|+ \\ \gamma_{\mathrm{ISS}} \circ \int_{0}^{t}|\tilde{\boldsymbol{u}}(s)| \mathrm{d} s+\int_{0}^{t} \vartheta_{\mathrm{ISS}}|\tilde{\boldsymbol{\omega}}(s)| \mathrm{d} s \end{gathered} $

(13)

将子系统连接关系Z代入式(12)，同时代入式(14)。

$ \begin{gathered} \gamma_{\mathrm{ISS}} \circ\left(\boldsymbol{Z} \int_{0}^{t}|\tilde{\boldsymbol{y}}(s)| \mathrm{d} s\right)=\lambda \circ \int_{0}^{t}|\tilde{\boldsymbol{y}}(s)| \mathrm{d} s \\ \lambda \in K_{\infty} \end{gathered} $

(14)

结合式(12)，可得：

$ \begin{gathered} \int_{0}^{t}|\tilde{\boldsymbol{x}}(s)| \mathrm{d} s \leqslant \alpha_{\mathrm{ISS}}^{0}\left|\tilde{\boldsymbol{x}}_{0}\right|+\int_{0}^{t} \vartheta_{\mathrm{ISS}}|\tilde{\boldsymbol{\omega}}(s)| \mathrm{d} s+ \\ \lambda \circ\left(\alpha_{\mathrm{IOS}, s}^{0}\left|\tilde{\boldsymbol{x}}_{0}\right|+\int_{0}^{t} \vartheta_{\mathrm{IOS}, s}|\tilde{\boldsymbol{\omega}}(s)| \mathrm{d} s\right) \end{gathered} $

(15)

令$ a=\left|\tilde{\boldsymbol{x}}_{0}\right|, b=\int_{0}^{t}|\tilde{\boldsymbol{\omega}}(s)| \mathrm{d} s$，则式(14)右侧表达式可转换为函数f(a, b)，即：

$ \begin{gathered} \alpha_{\mathrm{ISS}}^{0}\left|\tilde{\boldsymbol{x}}_{0}\right|+\int_{0}^{t} \vartheta_{\mathrm{ISS}}|\tilde{\boldsymbol{\omega}}(s)| \mathrm{d} s+ \\ \lambda \circ\left(\alpha_{\mathrm{IOS}, s}^{0}\left|\tilde{\boldsymbol{x}}_{0}\right|+\int_{0}^{t} \vartheta_{\mathrm{IOS}, s}|\tilde{\boldsymbol{\omega}}(s)| \mathrm{d} s\right) \rightarrow f(a, b) \end{gathered} $

(16)

考虑到$\lambda, \alpha_{\mathrm{ISS}}^{0}, \vartheta_{\mathrm{ISS}}, \alpha_{\mathrm{IOS}, s}^{0}, \vartheta_{\mathrm{IOS}, s} $为K_∞函数，对于有界输入a≤A，b≤B，f(a, b)≤F，f(a, b)单调有界，那么对于有界输入a≤A，b≤B，一定存在函数g(a, b)，满足g(a, b)≥f(a, b)。

令$\alpha_{\mathrm{ISS}, s}^{0}\left|\tilde{\boldsymbol{x}}_{0}\right|+\int_{0}^{t} \boldsymbol{\vartheta}_{\mathrm{ISS}, s}|\tilde{\boldsymbol{\omega}}(s)| \mathrm{d} s \rightarrow g(a, b) $，其中，$\boldsymbol{\alpha}_{\mathrm{ISS}, s}^{0}, \boldsymbol{\vartheta}_{\mathrm{ISS}, s} \in K_{\infty} $。考虑到g(a, b)≥f(a, b)，式(14)可以转换为：

$ \begin{gathered} \int_{0}^{t}|\tilde{\boldsymbol{x}}(s)| \mathrm{d} s \leqslant \\ \alpha_{\mathrm{ISS}, s}^{0}\left|\tilde{\boldsymbol{x}}_{0}\right|+\int_{0}^{t} \boldsymbol{\vartheta}_{\mathrm{ISS}, s}|\tilde{\boldsymbol{\omega}}(s)| \mathrm{d} s \end{gathered} $

(17)

因此，互联系统(6)是LISS的。

第二步，结合工程约束，考虑系统的最大干扰输出范围，证明互联系统(6)满足量化稳定性评估准则(2)时，系统满足工程约束。互联系统(6)满足量化稳定性评估准则(2)，则其输出范围为[0, v^*]，文中将该范围称为自然约束，该约束的集合记作Υ。区别地，文中将子系统的最大输入向量$ \epsilon_{\tilde{\boldsymbol{x}}_{0}}$和最大输出向量$\boldsymbol{\mu}_{\tilde{\boldsymbol{x}}_{0}}$ 称为工程约束。若稳定性评估准则(2)满足，即：

$ \begin{aligned} \mu \circ\left(\alpha_{\mathrm{IOS}}^{0}\left|\boldsymbol{x}_{0}\right|\right.&\left.+\boldsymbol{\vartheta}_{\mathrm{IOS}} \circ \int_{0}^{t}|\boldsymbol{\omega}(s)| \mathrm{d} s\right) \leqslant \\ & \min \left\{\boldsymbol{\mu}_{\tilde{\boldsymbol{x}}_{0}}, \varUpsilon\right\} \end{aligned} $

(18)

结合式(10)，可得：

$ \int_{0}^{t}|\tilde{\boldsymbol{y}}(s)| \mathrm{d} s \leqslant \min \left\{\boldsymbol{\mu}_{\tilde{\boldsymbol{x}}_{0}}, \varUpsilon\right\} $

(19)

式(18)表明输出既满足自然约束，也满足工程约束。

量化稳定性评估准则(2)可通过计算复合函数进行校验。因此，还需验证评估准则(1)中的局部小增益条件。

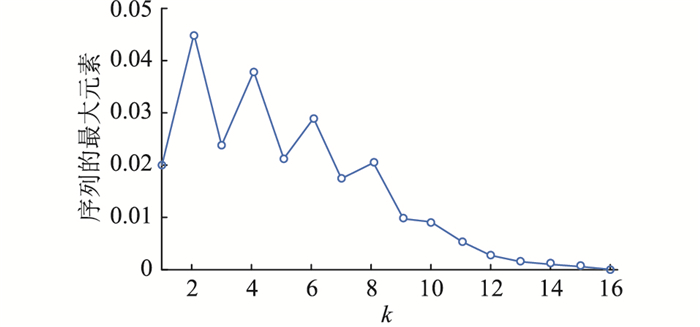
由文献[22]中的定理可知，小增益条件可以通过验证序列v(k) 的收敛性来判断。由于文中使用积分-积分估计，如果系统的状态和输出收敛到平衡点附近区域，则可认为该系统是稳定的。设系统存在保持稳定的最小输入能量v₀，则局部小增益的验证条件可以转换为当k→∞时，v(k)→v₀。

不动点v^*可由各子系统的输入向量表示。一般地，系统的安全运行约束范围总是小于系统的稳定范围，因此不动点v^*可以由系统的安全运行约束表示。在双馈风力发电系统中，设系统的电压、电流安全运行约束为U_lim和I_lim，则不动点v^*可表示为[I_lim, U_lim]^T。

综上所述，仅需验证序列{v(k)}的收敛性，其中v(k+1)=G(v(k))，v(0)=v^*。具体地，给定一个最大迭代次数k_max，校验序列{v(k)}是否能够在k_max次迭代内收敛至v₀的某一邻域内。若可以，则系统满足小增益条件; 反之，系统不稳定。

为验证小增益条件，增益函数应是平滑的。因此利用一个满足下列条件的光滑非线性增益函数来逼近分段线性渐近增益函数：

$ \gamma_{n, l}^{\operatorname{IOS}}(s) \leqslant \gamma_{p, l}^{\operatorname{IOS}}(s) $

(20)

式中：γ_{n, l}^IOS为光滑非线性增益函数; γ_{p, l}^IOS为分段线性渐近增益函数。

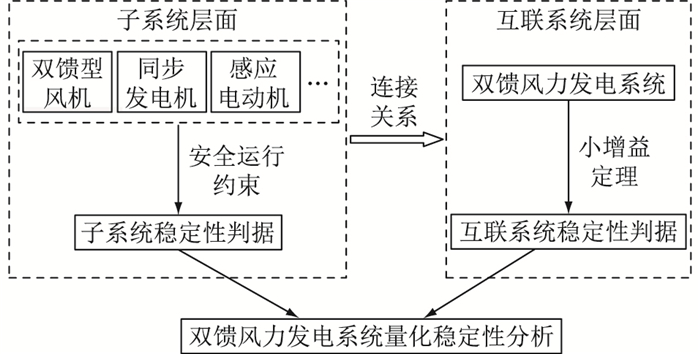
双馈风力发电系统可视作由双馈型风机、同步发电机、负载等子系统构成的互联系统，各子系统的LISS/LIOS属性均可通过估计得到，因此所提出的互联系统稳定性量化评估准则可应用于双馈风力发电系统的电压稳定性量化分析。具体地，对双馈风力发电系统的电压稳定性评估可从2个方面展开：(1) 在子系统层面，需研究各子系统在外部扰动下的稳定特性，根据式(4)、式(5)对其LISS/LIOS属性进行估计，结合运行约束得到各子系统的最大输入能量及输出能量; (2) 在互联系统层面，需充分考虑各子系统电压稳定特性及子系统间互联特征，根据式(8)、式(9)验证系统是否满足小增益定理以及对应的系统稳定裕度，进而得到互联系统电压稳定性判据，从而实现双馈风力发电系统电压稳定性的量化评估。双馈风力发电系统的电压稳定性量化分析研究框架如图 1所示。

3 双馈风力发电系统电压稳定性量化分析

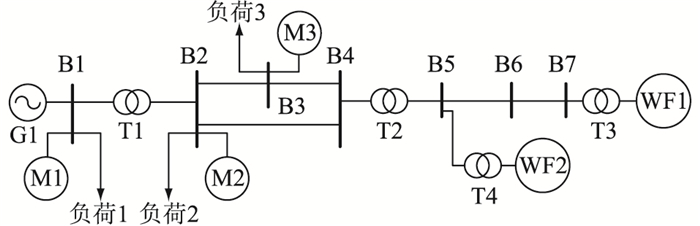
为验证所提出的互联系统稳定性量化评估准则的有效性，将在含双馈型风机的电力系统中进行测试及分析，测试系统的总体结构如图 2所示。

图 2所示电力系统的子系统包括双馈风机风场WF1、WF2，同步发电机G1，感应电动机M1、M2、M3和恒阻抗负载。为评估风电并网对电力系统电压稳定性的影响，须合理选择输入与输出，并且估计子系统外部输入和初始状态的局部域。其中，同步发电机的输入和输出分别选择为端电流和端电压，双馈型风机风场的输入和输出分别选择为端电压和定子电流，负载整体的输入和输出分别选择为端电压和端电流。设定电力系统的安全运行约束为：在故障清除后系统内各节点电压应不小于0.8 p.u.，双馈型风机的转子电流最大值为2.0 p.u.。

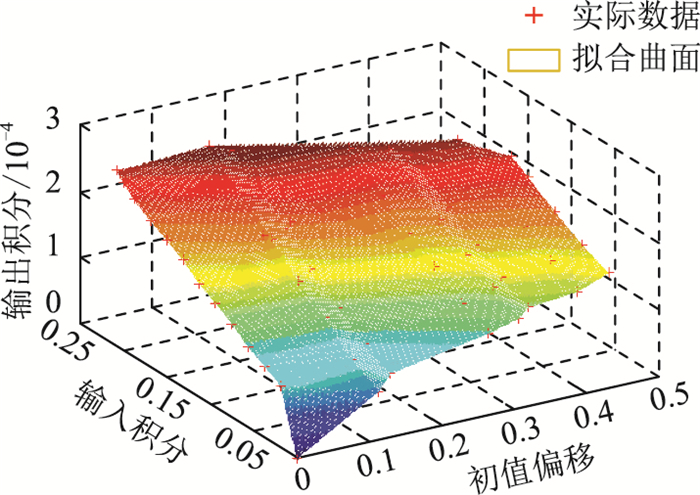
3.1 子系统的LISS/LIOS属性估计

文献[20]提出了不同控制策略的单台双馈型风机LIOS属性离线仿真估算方法，基于该方法对含有9台双馈型风机的风电场的LIOS属性进行估计，估计结果如图 3所示。其非线性渐近增益近似为γ_IOS(m₂): =l_Dm₂^0.5，其中l_D= 0.000 793，双馈型风机的其他LIOS特性通过求解分段线性渐近增益进行估计，其中α_IOS⁰(m₁): =k_Dm₁，优化结果为k_D= 0.000 86。图 4为当最大输出能量为σ_DFIG=0.002 5时初始状态、外部输入和系统输出之间的总体关系。

同步发电机的LIOS属性可以通过估计得到，其中，α_IOS⁰(m₁): =k_Gm₁，k_G>0，γ_IOS(m₂): =l_Gm₂。增益函数的估计结果为：k_G≈10^-6，l_G≈0.045 6，最大输入能量值φ_G=0.85，相应的最大输出能量δ_G=0.4。

将感应电动机和恒阻抗负载作为整体估计其LIOS属性，其中α_IOS⁰(m₁): =k_Lm₁，k_L>0，γ_IOS(m₂): = l_Lm₂。增益函数的估计结果：k_L≈ 0.000 43，l_L≈0.058 6。考虑到系统的安全运行约束，可得恒阻抗负载的最大的输入能量φ_L=0.43，相应的最大输出能量δ_L=0.182。

3.2 量化稳定性分析和仿真结果

算例研究故障清除后系统电压稳定性的量化结果。设定电力系统的安全运行约束为：在故障清除后系统内各节点电压应不小于0.8 p.u.，双馈型风机的转子电流最大值为2.0 p.u.。根据3.1节所得结果，得到最大输出能量为$\boldsymbol{\mu}_{\tilde{\boldsymbol{x}}_{0}}$ = [0.4, 0.002 5, 0.002 5, 0.182, 0.182, 0.182]。根据第2章所提方法，在给定的输入局部域内验证局部小增益条件。图 5描绘了双馈风力发电系统电压局部稳定域边界v(k)随迭代次数k的变化曲线，可以看出该结果满足小增益条件，并且$ \min \left\{\boldsymbol{\mu}_{\tilde{x}_{0}}, \gamma\right\}=\boldsymbol{\mu}_{\tilde{x}_{0}}$。因此，还需验证量化稳定性评估准则(2)，以保证系统输出在安全稳定约束内。

根据量化稳定性分析结果，定义：

$ \boldsymbol{\psi}=\mu \circ\left[\alpha_{\mathrm{IOS}}^{0}\left(\left|\boldsymbol{x}_{0}\right|\right)+\vartheta_{\mathrm{IOS}} \circ \int_{0}^{t}(|\boldsymbol{\omega}(s)|) \mathrm{d} s\right] $

(21)

研究初始状态对系统动态响应的影响。故障清除后双馈型风机的初始状态为$\left|\tilde{\boldsymbol{x}}_{02}\right| $ =0.23。由量化稳定性评估准则(2)可得：

$ \begin{gathered} \boldsymbol{\psi}= \\ {[0.000\ 3,0.002\ 47,0.002\ 41,0.003\ 9,0.003\ 8,0.004]<} \\ {[0.4,0.002\ 5,0.002\ 5,0.182,0.182,0.182]=} \\ \min \left\{\boldsymbol{\mu}_{\tilde{\boldsymbol{x}}_{0}}, \gamma\right\} \end{gathered} $

(22)

系统状态将保持在安全约束内，但是ψ第2个元素接近安全约束边界。增大外部扰动，寻找临界稳定点。当$ \left|\tilde{\boldsymbol{x}}_{02}\right|$=0.24时，上述条件计算为：

$ \begin{gathered} \boldsymbol{\psi}= \\ {[0.000\ 3,0.002\ 58,0.002\ 51,0.003\ 9,0.003\ 8,0.004] \leqslant} \\ \min \left\{\boldsymbol{\mu}_{\tilde{\boldsymbol{x}}_{0}, \gamma}\right\} \end{gathered} $

(23)

不满足量化稳定性评估准则(2)。

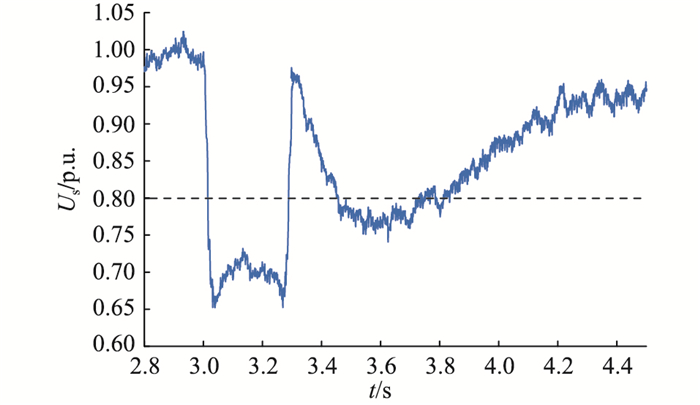
时域仿真验证上述理论分析结果，首先设置风电场均含9台双馈型风机，在t=3 s时，B4发生三相接地短路故障，短路故障持续时间为0.27 s，风电场端电压的动态响应如图 6所示。由图 6可知，在故障清除后，端电压降到0.8 p.u.以下，电压越过安全稳定约束，与理论分析结果一致。

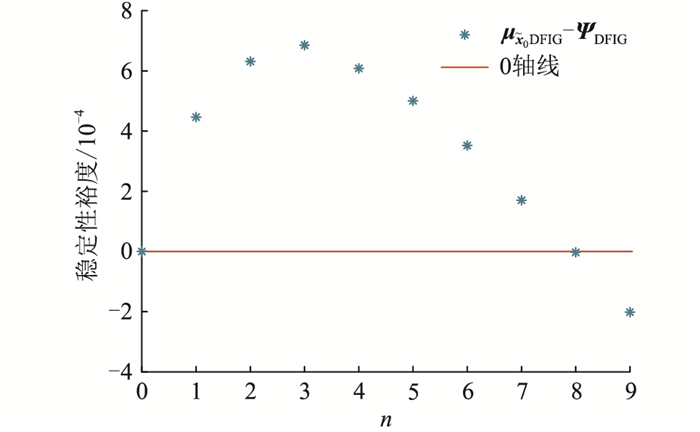
为了进一步验证所提量化稳定性分析方法的有效性，固定风电场2中双馈型风机数量，分析风电场1中风机数量对系统电压稳定性的影响。在上述分析中，ψ中第2个元素超出了限值，而其他元素则在给定的范围内。令ψ和$\boldsymbol{\mu}_{\tilde{\boldsymbol{x}}_{0}} $中的第2个元素分别为ψ_DFIG和$\boldsymbol{\mu}_{\tilde{\boldsymbol{x}}_{0} \mathrm{DFIG}} $，图 7描述了$\boldsymbol{\mu}_{\tilde{\boldsymbol{x}}_{0} \mathrm{DFIG}} $-ψ_DFIG的值随双馈型风机数量n的变化曲线，其中，$\boldsymbol{\mu}_{\tilde{\boldsymbol{x}}_{0} \mathrm{DFIG}} $-ψ_DFIG>0，说明系统是满足安全稳定约束的，并且该值越大，裕度越大。

由图 7可得，n=8是双馈型风机临界数量，适当减少双馈型风机的个数，可以提高系统故障清除后的动态响应性能。假设初始状态$ \left|\tilde{\boldsymbol{x}}_{02}\right|$ =0.238，将风电场1中风机数目降至到n=7，计算结果为：

$ \begin{gathered} \boldsymbol{\psi}= \\ {[0.000\ 28,0.002\ 26,0.002\ 38,0.002\ 9,0.002\ 8,0.003\ 1]<} \\ \min \left\{\boldsymbol{\mu}_{\tilde{\boldsymbol{x}}_{0}}, \gamma\right\} \end{gathered} $

(24)

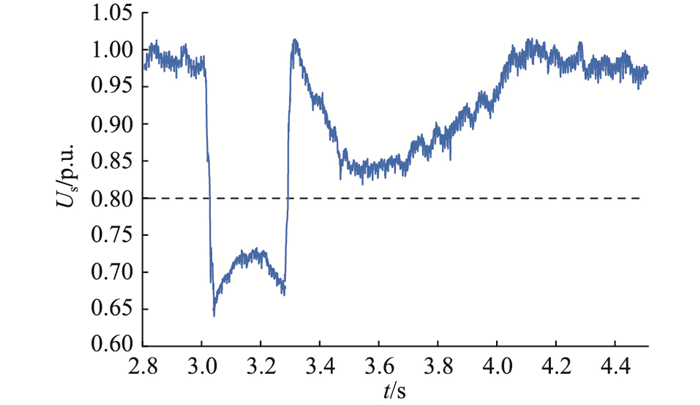
分析结果表明，当n=7时，系统在故障清除后将满足安全稳定约束。仿真设置相同的故障条件，风场的端电压仿真结果如图 8所示。由图 8可知，将风电场1中双馈型风机的数量减少到7台时，风场的端电压保持在安全稳定约束内，仿真结果验证了理论分析的正确性。

由算例结果可知，文中所提互联系统稳定性量化分析方法可在互联系统层面对双馈风力发电系统的电压稳定性进行定量评估，揭示了系统的动态响应与外部扰动之间的关系，同时量化系统能够承受的最大扰动，从而能够有效促进双馈型风机在电力系统中的应用。此外，由于子系统的稳定性特征可通过离线仿真获得，降低了互联系统稳定性分析的计算量，从而使系统电压稳定性的在线判断成为可能。

4 结语

文中提出了含双馈型风机的电力系统电压稳定性量化评估方法，该方法的主要优点是能从子系统层面和互联系统层面2个角度对系统的稳定性进行量化评估, 并用渐近增益量化外部扰动对系统电压稳定性的影响，用外部输入和初始状态的局部域量化系统的稳定域。时域仿真验证了该方法的有效性。

降低这种方法的保守性是值得进一步研究的工作。同时，如果系统的维数较高，则式(9)中μ函数的计算会比较复杂。因此，未来还需要研究μ函数估计的一般算法。

本文得到国网陕西省电力公司科技项目(B626KY190005)资助，谨此致谢！