文章编号: 2096-3203(2022)01-0002-09 中图分类号: TM73
“双碳”战略目标下,构建新能源为主体的新型电力系统成为未来趋势。大规模消纳新能源的需求与传统电厂占比下降的行业前景对电网调控提出了更高的要求。协同电力系统中大量的可调负荷资源主动参与调控是提高电网调节能力、减少弃风弃光的一种有效手段。然而用户侧资源存在单个资源功率较小、难以被直接调控、负荷具有随机性等特点,因此,将大量用户侧资源整合为可调节容量较大、功率较为稳定、控制成本较低的聚合体是实现需求响应的必要技术。负荷聚合商(load aggre ̄gator,LA)基于价格信号自主申报参与电能量市场的负荷削减投标(load curtailment bidding,LCB)是一类有效的需求响应[1]。一方面,LA通过代理电力用户在电力批发市场中统一购电并从中收取服务费进行盈利;另一方面,电力零售市场存在竞争,因此LA常与用户签订中长期负荷响应合同以降低代理成本。
当前已经有许多学者围绕用户侧资源聚合参与需求响应展开研究。文献[2]提出实时价格信号是激励需求响应的有效措施;文献[3]提出将具体的实际负荷按可控特性进行聚合以简化建模;文献[4]提出将电力市场中的需求响应总体分为能量市场需求响应与辅助服务市场需求响应2种;文献[5]对负荷资源聚合的分类、控制方式、建模与应用场景等方面的研究成果进行了综述;文献[6]针对LA的策略用电行为,电价差与理论负荷转移率如何影响实际负荷转移率的问题进行了研究;文献[7]考虑综合能源系统,将需求响应分为价格型和其他能源替代型。
LA向电网提供调节服务时,通常需要面对市场价格与负荷功率的不确定问题。当前研究者已从不同的角度对这些不确定性进行建模。文献[8-10]基于模糊机会约束规划,用模糊变量描述聚合体响应行为的不确定。文献[11]在考虑了现货市场价格波动风险的情况下对微电网参与日前、实时电能量市场进行了优化调度。文献[12]讨论了光伏发电功率不确定性带来的履约能力不足问题,基于鲁棒优化提出了一种电力市场投标策略。文献[13]则利用了鲁棒优化来处理调节服务价格的不确定性,并结合博弈论获得最优竞价策略。文献[14]考虑了实时现货市场的价格波动性,认为负荷在市场中的利润最大化行为可通过求解马尔科夫决策过程得到。文献[15-19]以随机分布描述电动汽车的充电行为。文献[15]以弹性矩阵来近似可调电力负荷的需求响应行为,文献[19]则结合了基于蒙特卡洛的多场景法与二阶段随机线性规划。
上述研究多仅考虑确定的电能量价格或跟踪调度需求,与成熟电力市场中用户可进行LCB等操作的实际情况有所差异。部分研究虽然涉及申报行为,但只单一地考虑价格或负荷波动[12-14]。此外,电力用户通常同时拥有可调负荷与不可调负荷且不能够被分别代理,因此有必要针对二者并存的聚合体进行研究。
文中针对LA参与电能量市场LCB时面临双重不确定性的问题,考虑负荷波动带来的不确定性建立双层规划;提出了基于神经网络的场景缩减方法以处理电力市场价格的不确定性,最终构建了混合整数线性规划模型。通过求解模型,LA可得出代理成本与风险损失更低的LCB申报方案。
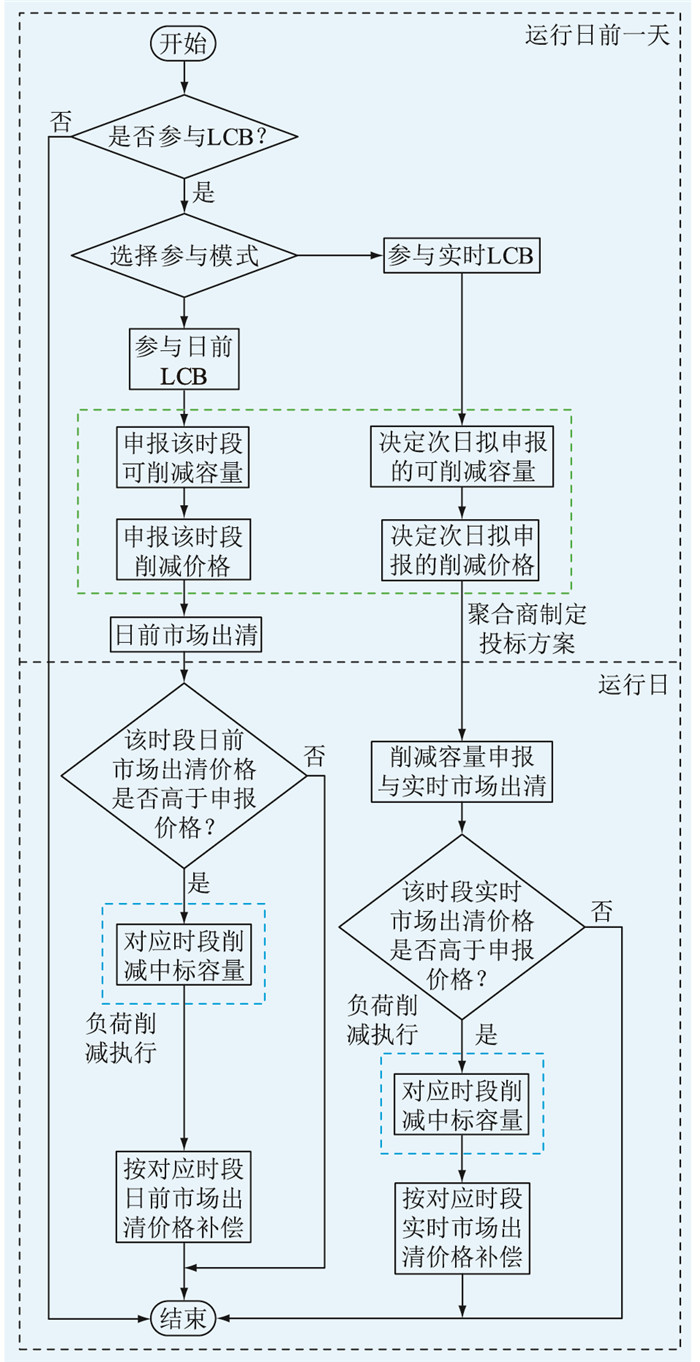
1 LA参与LCB 1.1 LA参与LCB流程LA参与LCB流程见图 1。LA在运行日前一天须根据所签订的响应合同、调节成本与预计收入决定次日的负荷曲线调整方案并通知用户,同时在市场上进行投标。当参与日前LCB时,LA在当天的日前市场出清后即获得中标信息。参与实时LCB时,LA在运行日当天对应时段的实时市场出清后才能获得中标信息。市场通常不允许用户同时参与同一时段的日前与实时LCB。运行日当天,若LA的实际负荷削减容量未达到中标容量的一定比例,则不能获得削减收入且需要为差额支付罚金。
|
图 1 LA参与LCB流程 Fig. 1 Process of LA participating in LCB |
当不考虑不确定因素时,LA计及LCB的代理成本计算方式如式(1)—式(4)所示。
| $ f=\sum\limits_{t \in T}\left(\gamma_{t}-\mu_{t}+\delta_{t}\right) $ | (1) |
| $ \gamma_{t}=\left(\pi_{t}^{\mathrm{da}}-\pi_{t}^{\mathrm{rt}}\right) P_{t}^{\mathrm{da}}+\pi_{t}^{\mathrm{rt}} L_{t} $ | (2) |
| $ \mu_{t}= \begin{cases}\pi_{t}^{\mathrm{da}} \min \left\{\bar{L}_{t}-L_{t}, P_{t}^{\mathrm{da}, \mathrm{cur}}\right\} \ \ \ \ P_{t}^{\mathrm{da}, \mathrm{cur}}>0 \\ \pi_{t}^{\mathrm{rt}} \min \left\{\bar{L}_{t}-L_{t}, P_{t}^{\mathrm{rt}, \mathrm{cur}}\right\} \ \ \ \ P_{t}^{\mathrm{rt}, \mathrm{cur}}>0 \\ 0 \ \ \ \ \text { 其他 } \end{cases} $ | (3) |
| $ \begin{gathered} \delta_{t}= \\ \begin{cases}\xi_{2} \pi_{t}^{\mathrm{da}} \max \left\{\xi_{1} P_{t}^{\mathrm{da}, \mathrm{cur}}-\left(\bar{L}_{t}-L_{t}\right), 0\right\} & P_{t}^{\mathrm{da}, \mathrm{cur}}>0 \\ \xi_{2} \pi_{t}^{\mathrm{rt}} \max \left\{\xi_{1} P_{t}^{\mathrm{rt}, \mathrm{cur}}-\left(\bar{L}_{t}-L_{t}\right), 0\right\} & P_{t}^{\mathrm{rt}, \mathrm{cur}}>0 \\ 0 \quad \text { 其他 } & \end{cases} \end{gathered} $ | (4) |
式中:f为代理成本;T为总时段数;γt为t时段的电能量市场支出;μt为LCB收入;δt为t时段的LCB罚金;πtda,πtrt分别为日前市场与实时市场的电能量价格;Ptda为t时段的日前市场申报购电量,出于风险管控需要,市场常对主体的购售电行为进行限制,如果算例中无特别说明则每个时段的申报购电量不超过基线负荷功率的1.5倍;Lt为用户聚合体t时段的实际负荷功率曲线;Lt为t时段的基线负荷功率曲线,文中以负荷期望值作为基线负荷;Ptda, cur,Ptrt, cur分别为t时段的日前市场与实时市场中的LCB中标容量,且有Ptda, curPtrt, cur=0;ξ1,ξ2分别为削减考核系数与惩罚价格系数,如果算例中无特别说明则分别取0.9与1。
2 电能量市场下LA参与LCB 2.1 目标函数LA的代理成本F由每个场景下的现货电能量市场购电支出、改变负荷用电模式带来的支出及参与LCB带来的收入组成,其数学表达式见式(5)。
| $ \begin{gathered} F\left(x, y_{s}, L_{s, t}^{\mathrm{u}} ; \pi_{s, t}^{\mathrm{da}}, \pi_{s, t}^{\mathrm{rt}}\right)= \\ \min \limits_{x, y_{s}} \max \limits_{L_{s, t}^{\mathrm{u}}} \sum\limits_{s \in S}\left[w_{s}\left(C_{s}-B_{s}^{\mathrm{rt}}-B_{s}^{\mathrm{da}}\right)\right] \end{gathered} $ | (5) |
| $ x=\left\{I_{t}^{\mathrm{DA}, \mathrm{par}}, I_{t}^{\mathrm{RT}, \mathrm{par}}, P_{t}^{\mathrm{da}, \text { sub }}, P_{t}^{\mathrm{rt}, \text { sub }}, \pi_{t}^{\mathrm{da}, \text { curt }}, \pi_{t}^{\mathrm{rt}, \text { curt }}, P_{t}^{\mathrm{da}}\right\} $ | (6) |
| $ y_{s}=\left\{P_{s, t}^{\mathrm{ESS}}, P_{s, t}^{\mathrm{IL}}, P_{s, t}^{\mathrm{TL}}\right\} $ | (7) |
式中:πs, tda,πs, trt分别为场景s中t时段的日前市场与实时市场价格;S为缩减后的场景集;Bsrt,Bsda分别为场景s中的实时与日前市场中的LCB收入;Cs为场景s中的购电商支出;ws为场景s的权重,且有
聚合商在场景s中的支出Cs的数学表达式如式(8)所示。
| $ C_{s}=\sum\limits_{t=1}^{T}\left[\pi_{s, t}^{\mathrm{da}} P_{t}^{\mathrm{da}}+\pi_{s, t}^{\mathrm{rt}}\left(L_{s, t}-P_{t}^{\mathrm{da}}\right)\right]+C_{s}^{\mathrm{IL}}+C_{s}^{\mathrm{TL}} $ | (8) |
| $ L_{s, t} \geqslant L_{s, t}^{\mathrm{u}}+P_{s, t}^{\mathrm{ESS}}+P_{s, t}^{\mathrm{IL}}+P_{s, t}^{\mathrm{TL}} $ | (9) |
式中:Ls, t为场景s中t时段的实时负荷功率;CsIL为可中断负荷的调节成本;CsTL为可转移负荷的调节成本。
2.2.2 可调负荷运行约束(1) 储能设备运行约束。
| $ \left\{\begin{array}{l} P_{s, t}^{\mathrm{ESS}}=P_{s, t}^{\mathrm{cha}}-P_{s, t}^{\mathrm{dis}} \\ P_{\mathrm{cha}, \min } I_{s, t}^{\mathrm{cha}} \leqslant P_{s, t}^{\mathrm{cha}} \leqslant P_{\mathrm{cha}, \max } I_{s, t}^{\mathrm{cha}} \\ P_{\mathrm{dis}, \min } \mathrm{I}_{s, t}^{\mathrm{ds}} \leqslant P_{s, t}^{\mathrm{dis}} \leqslant P_{\mathrm{dis}, \max } I_{s, t}^{\mathrm{dis}} \\ I_{s, t}^{\mathrm{cha}}+I_{s, t}^{\mathrm{dis}} \leqslant 1 \end{array}\right. $ | (10) |
式中:Ps, tcha为储能充电功率;Ps, tdis为场景s中t时段的储能放电功率;Is, tcha,Is, tdis为场景s中t时段的储能充放电状态的0-1变量;Pcha, min,Pcha, max分别为充电功率的最小值与最大值;Pdis, min,Pdis, max分别为储能放电功率的最小值与最大值。
| $ \left\{\begin{array}{l} S_{s, t+1}^{\mathrm{SOC}}=S_{s, t}^{\mathrm{SOC}}(1-\sigma)-\frac{1}{C_{\mathrm{ap}}}\left(\frac{1}{\eta_{\mathrm{d}}} P_{s, t}^{\mathrm{dis}}-\eta_{\mathrm{c}} P_{s, t}^{\mathrm{cha}}\right) \Delta t \\ S_{\mathrm{SOC}, \min } \leqslant S_{s, t}^{\mathrm{SOC}} \leqslant S_{\mathrm{SOC}, \max } \end{array}\right. $ | (11) |
式中:Δt为时间段长度;Ss, tSOC为储能在场景s中t时段的荷电状态(state of charge,SOC);σ为储能设备Δt内的自放电率;Cap为储能设备的额定能量;ηd,ηc分别为放电效率与充电效率;SSOC, min,SSOC, max分别为控制过程中荷电状态需要满足的最小值与最大值。
(2) 可中断负荷运行约束。可中断负荷功率与成本约束如式(12)所示。
| $ \left\{\begin{array}{l} P_{s, t}^{\mathrm{IL}}=I_{s, t}^{\mathrm{IL}} P_{t}^{\mathrm{IL}, \mathrm{ORI}} \\ C_{s}^{\mathrm{IL}} \geqslant \sum\limits_{t=1}^{T} C_{s, t}^{\mathrm{IL}} \\ C_{s, t}^{\mathrm{IL}} \geqslant\left(I_{s, t-1}^{\mathrm{IL}}-I_{s, t}^{\mathrm{IL}}\right) \pi_{\mathrm{IL}} \\ C_{s, t}^{\mathrm{IL}} \geqslant 0 \end{array}\right. $ | (12) |
式中:PtIL, ORI为可中断负荷在t时段的的额定负荷功率;Cs, tIL为可中断负荷在场景s中t时段的调节成本;Is, tIL为0-1变量,取1时代表可中断负荷在场景s中t时段没有中断,取0时代表中断;πIL为可中断负荷单次中断成本。
可中断负荷的最小连续关停时间与最小累计运行时间约束如式(13)所示。
| $ \left\{\begin{array}{l} T_{s, t}^{\mathrm{L}}-\left(I_{s, t}^{\mathrm{IL}}-I_{s, t-1}^{\mathrm{IL}}\right) T_{\mathrm{IL}, \mathrm{D}} \geqslant 0 \\ T_{s, t}^{\mathrm{IL}}=\sum\limits_{k=t-T_{\mathrm{IL}, \mathrm{D}}}^{t-1}\left(1-I_{s, k}^{\mathrm{IL}}\right) \\ \sum\limits_{t=1}^{T} I_{s, t}^{\mathrm{IL}} \geqslant T_{\mathrm{IL}, \min } \end{array}\right. $ | (13) |
式中:TIL, D为可中断负荷的最小连续关停时间;TIL, min为可中断负荷的最小累计运行时间;Ts, tIL为辅助变量。
(3) 可转移负荷运行约束。
| $ \left\{\begin{array}{l} P_{\mathrm{TL}, \min } \leqslant P_{s, t}^{\mathrm{TL}} \leqslant P_{\mathrm{TL}, \max } \\ \sum\limits_{t=1}^{T} P_{s, t}^{\mathrm{TL}}=W_{\mathrm{TL}} \\ C_{s}^{\mathrm{TL}} \geqslant \sum\limits_{t=1}^{T} C_{s, t}^{\mathrm{TL}} \\ C_{s, t}^{\mathrm{TL}} \geqslant\left(P_{t}^{\mathrm{TL}, \mathrm{ORI}}-P_{s, t}^{\mathrm{TL}}\right) \pi_{\mathrm{TL}} \Delta t \\ C_{s, t}^{\mathrm{TL}} \geqslant 0 \end{array}\right. $ | (14) |
式中:PTL, max,PTL, min分别为可转移负荷功率的调节上限与下限;WTL为可转移负荷需要保证的总耗能;πTL为可转移负荷下调单位负荷功率对应的调节成本;Cs, tTL为可转移负荷在场景s中t时段的调节成本。
2.2.3 LCB约束(1) LCB实际执行量约束。
| $ \left\{\begin{array}{l} D_{s, t}^{\mathrm{rt}}+D_{s, t}^{\mathrm{da}} \leqslant \bar{L}_{t}-L_{s, t}+\left(1-I_{t}^{\mathrm{RT}, \mathrm{par}}-I_{t}^{\mathrm{DA}, \mathrm{par}}\right) M \\ I_{t}^{\mathrm{RT}, \mathrm{par}}+I_{t}^{\mathrm{DA}, \mathrm{par}} \leqslant 1 \\ -I_{t}^{\mathrm{DA}, \mathrm{par}} M \leqslant D_{s, t}^{\mathrm{da}} \leqslant I_{t}^{\mathrm{DA}, \mathrm{par}} M \\ -I_{t}^{\mathrm{RT}, \mathrm{par}} M \leqslant D_{s, t}^{\mathrm{rt}} \leqslant I_{t}^{\mathrm{RT}, \mathrm{par}} M \\ \bar{L}_{t}=\bar{L}{}_{t}^{\mathrm{u}}+P_{t}^{\mathrm{IL}, \mathrm{ORI}}+P_{t}^{\mathrm{TL}, \mathrm{ORI}} \end{array}\right. $ | (15) |
式中:M为足够大的正整数,文中所有M取105;Ds, tda为场景s中t时段的日前LCB实际执行量;Ds, trt为场景s中t时段的实时LCB实际执行量;Lt为t时段的聚合商代理的所有用户侧资源的总体基线负荷;Ltu为t时段的不可调负荷的期望功率。
(2) LCB中标约束。因实时与日前类似,仅对日前LCB中标约束进行说明。
| $ \left\{\begin{array}{l} -M I_{s, t}^{\mathrm{da}, \mathrm{cur}} \leqslant \pi_{t}^{\mathrm{da}, \mathrm{curt}}-\pi_{s, t}^{\mathrm{da}} \leqslant M\left(1-I_{s, t}^{\mathrm{da}, \mathrm{cur}}\right) \\ 0 \leqslant P_{t}^{\mathrm{da}, \mathrm{cur}} \leqslant I_{t}^{\mathrm{DA}, \mathrm{par}} P_{\mathrm{cur}} \\ P_{t}^{\mathrm{da}, \mathrm{cur}}-M\left(1-I_{s, t}^{\mathrm{da}, \mathrm{cur}}\right) \leqslant P_{s, t}^{\mathrm{da}, \mathrm{cur}} \leqslant \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ P_{t}^{\mathrm{da}, \mathrm{cur}}+M\left(1-I_{s, t}^{\mathrm{da}, \mathrm{cur}}\right) \\ 0 \leqslant P_{s, t}^{\mathrm{da}, \mathrm{cur}} \leqslant I_{s, t}^{\mathrm{da}, \mathrm{cur}} M \end{array}\right. $ | (16) |
式中:Is, tda, cur为0-1变量,取1表示场景s中t时段的日前LCB中标,取0表示未中标;Pcur为申报削减容量的上限;Ps, tda, cur为场景s中t时段的日前中标容量;πtda, curt为申报的日前削减价格。
(3) LCB免除考核约束。
| $ \left\{\begin{array}{l} M\left(I_{s, t}^{\mathrm{da}, \mathrm{sat}}-1\right) \leqslant D_{s, t}^{\mathrm{da}}-\xi_{1} P_{s, t}^{\mathrm{da}, \mathrm{cur}} \leqslant M I_{s, t}^{\mathrm{da}, \mathrm{sat}} \\ M\left(I_{s, t}^{\mathrm{t}, \mathrm{sat}}-1\right) \leqslant D_{s, t}^{\mathrm{rt}}-\xi_{1} P_{s, t}^{\mathrm{rt}, \mathrm{cur}} \leqslant M I_{s, t}^{\mathrm{t}, \mathrm{sat}} \end{array}\right. $ | (17) |
式中:Is, tda, sat,Is, trt, sat为0-1变量,取1分别表示场景s中t时段的日前LCB与实时LBC符合补偿标准,取0表示不符合补偿标准;Ps, tda, cur,Ps, trt, cur分别为场景s中t时段的日前与实时LCB中标容量。
(4) LCB收入约束。聚合商在场景s中的日前LCB收入Bsda的数学表达式如式(18)所示,实时LCB收入Bsrt与日前类似。
| $ B_{s}^{\mathrm{da}}=\sum\limits_{t=1}^{T}\left(B_{s, t}^{\mathrm{da}}-\delta_{s, t}^{\mathrm{da}}\right) $ | (18) |
| $ \left\{\begin{array}{l} B_{s, t}^{\mathrm{da}} \leqslant \pi_{s, t}^{\mathrm{da}} P_{s, t}^{\mathrm{da}, \mathrm{cur}} \\ B_{s, t}^{\mathrm{da}} \leqslant M I_{s, t}^{\mathrm{da}, \mathrm{sat}} \\ B_{s, t}^{\mathrm{da}} \leqslant \pi_{s, t}^{\mathrm{da}} D_{s, t}^{\mathrm{da}}+M\left(1-I_{s, t}^{\mathrm{da}, \mathrm{sat}}\right) \\ \delta_{s, t}^{\mathrm{da}} \geqslant \xi_{2} \pi_{s, t}^{\mathrm{da}}\left(\xi_{1} P_{s, t}^{\mathrm{da}, \mathrm{cur}}-D_{s, t}^{\mathrm{da}}\right) \\ \delta_{s, t}^{\mathrm{da}} \geqslant 0 \end{array}\right. $ | (19) |
式中:Bs, tda为场景s中t时段的日前LCB收入;δs, tda为场景s中t时段的日前LCB违约罚金。
2.3 优化问题求解由式(5)—式(19)所描述的优化问题不仅需要合理的场景数据,且属于min-max型双层规划问题,不能直接求解。对文中采用的场景缩减方案与双层规划转化方法进行说明。
2.3.1 基于深度神经网络的场景缩减方法文中利用深度神经网络(deep neural networks,DNN)进行场景缩减。神经网络输出见式(20)。
| $ \begin{gathered} u_{n, k}\left(s_{n}\right)=\mathrm{e}^{h_{k}\left(s_{n}\right)} / \sum\limits_{j=1}^{K} \mathrm{e}^{h_{j}\left(s_{n}\right)} \\ n=1,2, \cdots, N ; k=1,2, \cdots, K \end{gathered} $ | (20) |
式中:R为实数集;R2T为长度为2T的实数质量空间;sn∈R2T,为原场景集中的第n个场景,在文中代表一天内的日前价格与实时价格序列;T为总时段数;un, k∈ R,为输出层Softmax激活函数针对输入sn的第k个输出,代表输入场景sn关于第k个聚类中心的隶属度;hk(sn)为输出层第k个神经元针对输入sn的输出;K为缩减后的场景个数;N为原场景集中的场景个数。
聚类中心ck∈R2T,为缩减后的场景,其计算方式及对应的场景权重wk分别如式(21)和式(22)所示。
| $ c_{k}=\sum\limits_{n=1}^{N}\left(u_{n, k} s_{n}\right) / \sum\limits_{n=1}^{N} u_{n, k} $ | (21) |
| $ w_{k}=\sum\limits_{n=1}^{N} u_{n, k} / \sum\limits_{j=1}^{K} \sum\limits_{n=1}^{N} u_{n, j} $ | (22) |
隶属于某一类的场景应该尽可能接近聚类中心,因此将式(23)所示损失加入损失函数。
| $ L_{\mathrm{e}}=\frac{1}{N} \sum\limits_{k=1}^{K} w_{k} \sum\limits_{n=1}^{N}\left\|s_{n}-c_{k}\right\|_{2} $ | (23) |
考虑缩减后的场景集须保持原场景集的差异性,因此文中构造如式(24)所示的聚类中心分离度损失函数。
| $ L_{\mathrm{s}}=\frac{1}{2} \sum\limits_{j=1}^{K} \sum\limits_{k=1}^{K} \frac{c_{k} c_{j}}{\left\|c_{k}\right\|_{2}\left\|c_{j}\right\|_{2}} $ | (24) |
有时神经网络不会对部分场景明确地划分隶属,因为上述损失函数对模糊隶属关系不敏感。故构造如式(25)所示的模糊隶属关系损失函数。
| $ L_{\mathrm{p}}=-\sum\limits_{n=1}^{N} \ln \left(\min \left(\max \limits_{1 \leqslant k \leqslant K}\left(2 u_{n, k}\right), 1\right)\right) $ | (25) |
综上,文中所提出的DNN采用的损失函数LDNN如式(26)所示。
| $ L_{\mathrm{DNN}}=L_{\mathrm{e}}+L_{\mathrm{s}}+L_{\mathrm{p}} $ | (26) |
DNN拓扑如表 1所示。迭代次数α为400次,采用全批次训练,优化器选用Adam[20],学习率为4×10-3-2×10-6α。
|
|
表 1 DNN拓扑 Table 1 Topology of DNN |
文中采用Bertsimas与Sim提出的方法对原问题进行转化[21]。内层变量Ls, tu反映了不可调负荷的不确定性,若假设其期望值为Ls, tu,取值范围为[Ltu-ΔLs, tu, Ltu+ΔLs, tu],则可用式(27)替换式(9)。替换后的模型中不再存在变量Ls, tu,双层规划转化为单层规划,且能直接用Cplex进行求解。
| $ \left\{\begin{array}{l} -L_{s, t}+P_{s, t}^{\mathrm{ESS}}+P_{s, t}^{\mathrm{IL}}+P_{s, t}^{\mathrm{TL}}+z_{s, t} \varGamma+q_{s, t} \leqslant-\bar{L}{}_{s, t}^{\mathrm{u}} \\ z_{s, t}+q_{s, t} \geqslant \Delta \bar{L}{}_{s, t}^{\mathrm{u}} g_{s, t} \\ g_{s, t} \geqslant 1, z_{s, t} \geqslant 0, q_{s, t} \geqslant 0 \end{array}\right. $ | (27) |
式中:Γ为调节变量Ls, tu不确定程度的系数,在文中的取值范围为Γ Γ=0.1k, k∈[0, 10]∩Z;zs, t,qs, t,gs, t为辅助变量。
3 算例分析 3.1 算例设置 3.1.1 聚合商可调资源设置选取具有储能资源、可中断负荷资源、可转移负荷资源与不可调负荷资源的电力LA作为研究对象。其中,不可控负荷在每个时段的负荷功率期望值为40 MW,每个时段的负荷功率服从均匀分布U(30, 50)。参照文献[22]对可调电力资源的参数进行配置,其中储能设备额定能量为60 MW ·h,储能最大充放电功率为10 MW,充电效率与放电效率为95%,起始SOC为0.7,SOC允许范围为[0.2, 0.9],其他资源的参数如表 2、表 3所示。
|
|
表 2 可中断负荷参数 Table 2 Interruptible load parameters |
|
|
表 3 可转移负荷参数 Table 3 Transferable load parameters |
测试场景可用于评测求解形成的LCB申报方案在不同价格场景与负荷场景下对LA代理成本的影响。测试场景集由原市场价格场景与负荷偏差场景的组合生成。文中随机生成1 000个负荷场景,分别结合1月份与8月份的原市场价格场景组合生成2组各含31 000个测试场景的测试场景集。
在测试时,首先基于缩减后的价格场景集与不确定系数Γ求解LA的LCB方案,其次计算LA在测试场景中执行LCB方案后的实际代理成本,最终计算平均代理成本。其数学表达式如式(28)所示。
| $ \left\{\begin{array}{l} \beta\left(\varGamma, S_{m}, \hat{S}\right)=\frac{1}{\hat{N}} \sum\limits_{s \in \hat{S}} f\left(x^{*}, y_{s}^{*} ; L_{s, t}^{\mathrm{u}}, \pi_{s, t}^{\mathrm{da}}, \pi_{s, t}^{\mathrm{rt}}\right) \\ x^{*}=\arg \min \limits_{x} F\left(x, y_{s} ; \varGamma, \pi_{s, t}^{\mathrm{da}}, \pi_{s, t}^{\mathrm{rt}}\right) \quad s \in S_{m} \\ y_{s}^{*}=\arg \min \limits_{y_{s}} f\left(x^{*}, y_{s} ; \bar{L}{}_{t}^{\mathrm{u}}, \pi_{s, t}^{\mathrm{da}}, \pi_{s, t}^{\mathrm{rt}}\right) \quad s \in \hat{S} \end{array}\right. $ | (28) |
式中:β为测试场景集
电力市场价格的历史场景集分别选择美国宾夕法尼亚州-新泽西州-马里兰州(Pennsylvania-New Jersey-Maryland,PJM)电力市场2018年1月份与8月份的逐时价格数据。采用2.3.1节所述场景缩减模型分别将所选取的历史场景集缩减成2组各含3个场景的缩减场景集。
为了说明文中所采用的场景缩减方法的有效性,选取5种场景缩减方法进行相同的缩减,所选取方法包括基于动态时间规整(dynamic time warping,DTW)、主成分分析(principal component analysis,PCA)以及l2范数的3种K-means方法、同步向后缩减法[23](simultaneous backward reduction,SBR)与一种考虑相关性损失的综合场景缩减方法[24](comprehensive optimal scenario reduction,COSR)。评价指标的计算如式(29)所示[25]。
| $ e_{m}(\hat{S})=\left(\frac{\min \limits_{\varGamma} \beta\left(\varGamma, S_{m}, \hat{S}\right)}{\min \limits_{\varGamma, m} \beta\left(\varGamma, S_{m}, \hat{S}\right)}-1\right) \times 100 \% $ | (29) |
式中:
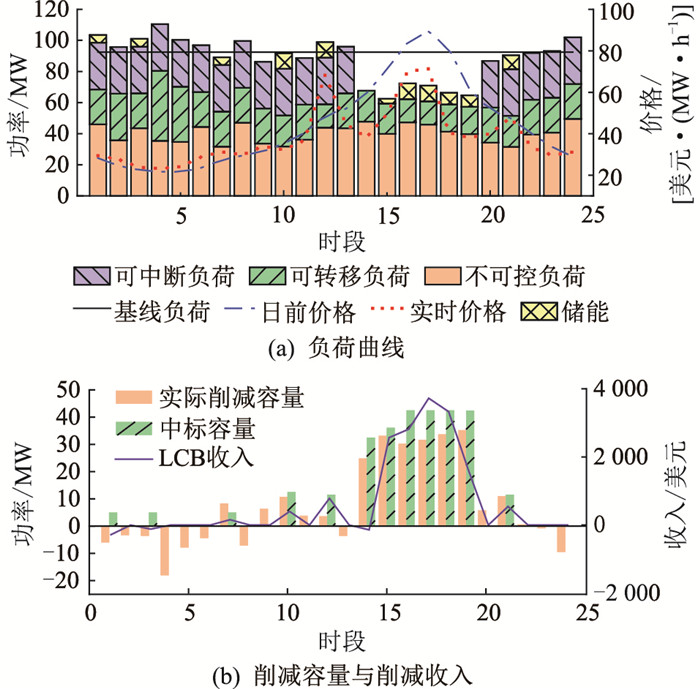
LA在8月份的某具体测试场景中的用电行为如图 2(a)所示,LA根据对价格的预测,在市场价格较高的14—20时段削减了用电。LA参与LCB的情况如图 2(b)所示,LA主要在市场价格较高的时段进行投标,并在中标时段削减可调负荷以获得削减补偿。由于不可调负荷的预测偏差,LA可能无法执行削减承诺,因此对应时段的LCB收入为负,如第1、3和14时段。
|
图 2 LA在测试场景中的行为 Fig. 2 Behavior of LA in test scenarios |
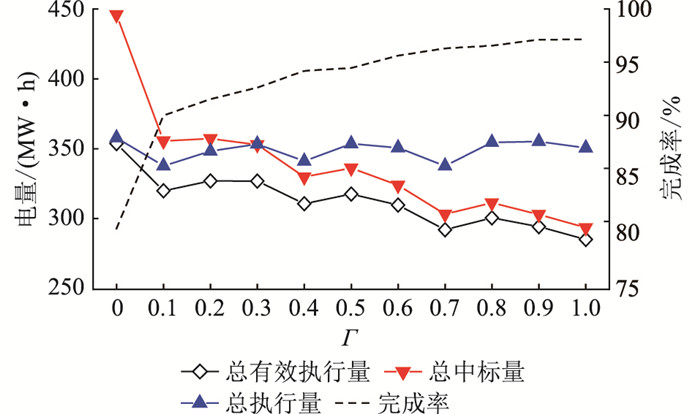
以1月份为例,对每个时段的LCB申报量、各个测试场景下的中标量与执行量进行加权求和,结果如图 3所示。计算结果表明,随着Γ的增大,LA参与LCB的总中标量与有效执行量总体都呈现下降趋势,这说明计及负荷不确定性使LA降低预期负荷削减能力并减少了投标。这一行为提高了最多17.8%的完成率。
|
图 3 测试场景集(1月份)中LA参与LCB情况 Fig. 3 LCB participation of LA in test scenario set (January) |
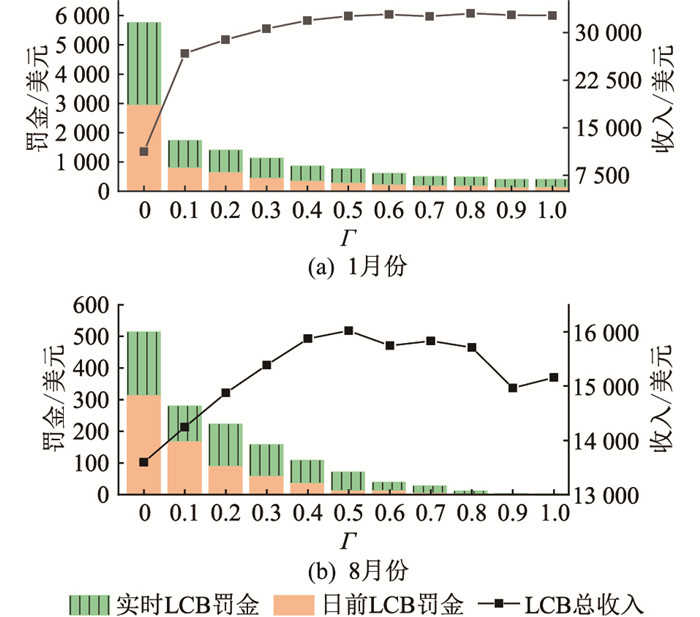
图 4(a)与图 4(b)分别为1月份与8月份测试场景集下LA因未完成削减承诺平均需缴纳的LCB罚金。结果表明考虑负荷的不确定性后需缴纳的违约罚金大幅度减少,Γ为1时可减少99%以上的违约罚金,但过于保守的LCB策略可能会影响总收入。
|
图 4 测试场景集中的平均LCB违约罚金 Fig. 4 Average LCB penalty in test scenario set |
基于式(29)对文中所采用的场景缩减方法、3.1.2节提及的5种方法及仅针对期望场景进行优化的投标策略进行评价,其评价结果如表 4所示。在2个测试场景集中,基于文中所采用的场景缩减方法DNN的投标策略均优于所选对照方法。计算结果还表明不适合的场景缩减方法会对策略造成负面影响。
|
|
表 4 场景缩减方法评价结果 Table 4 Evaluation results of scene reduction methods |
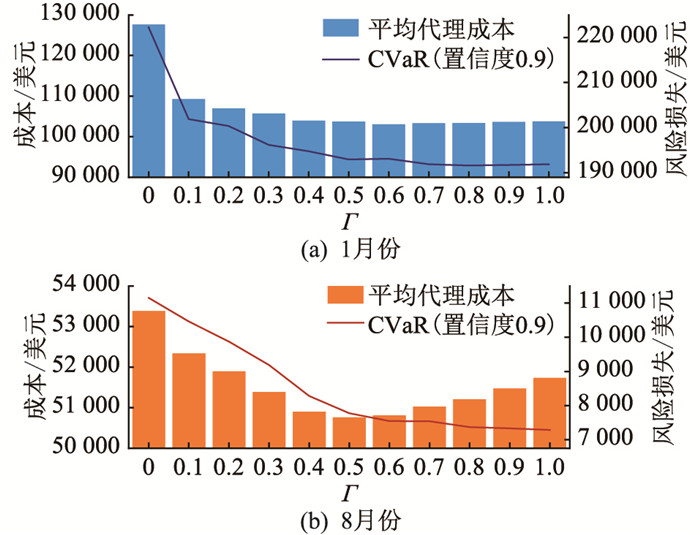
根据式(28)计算不同Γ下的平均代理成本,结果如图 5所示。由图 5可知,加权总代理成本随着Γ增大总体呈现先减再增的趋势,最高能减少19.25%(1月份)和4.91%(8月份),且考虑负荷波动时的平均成本都低于完全不考虑负荷波动时的结果。利用条件风险价值(conditional value at risk,CVaR)计量LA的代理成本超出期望值的风险,结果表明,考虑负荷波动更有利于控制风险,在测试场景集中最高可降低13.80%(1月份)和34.69%(8月份)的风险损失。
|
图 5 测试场景集中的平均代理成本与CVaR Fig. 5 Average agency cost and CVaR in test scenario set |
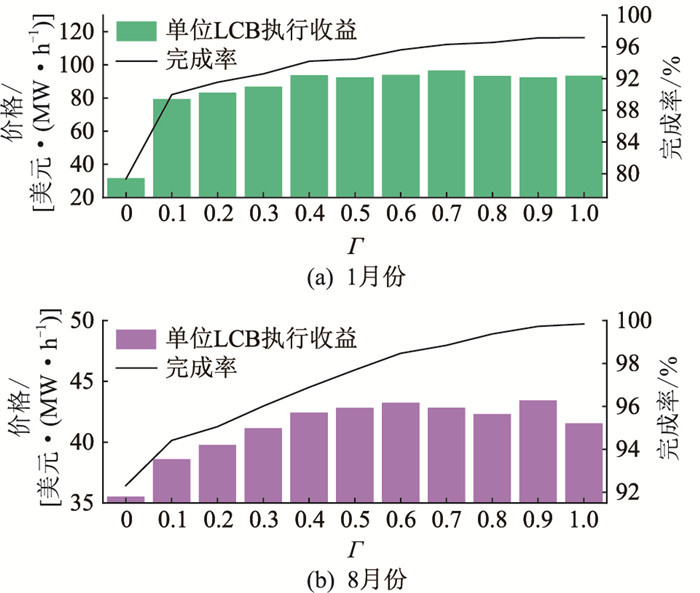
LA在测试场景集下的LCB完成率与单位执行收益如图 6所示。完成率随着Γ的增大逐渐趋向于1。单位LCB收入呈现先增再减的趋势,先增大是由于考虑负荷的不确定性使得聚合商缴纳的罚金减少;后减少是由于过于保守的投标策略使得LA中标容量偏低,部分实际削减容量没有被认定为LCB下的负荷削减容量从而减少了获利。
|
图 6 测试场景集中的单位负荷削减收入与完成率 Fig. 6 Unit load curtailment revenue and completion ratein test scenario set |
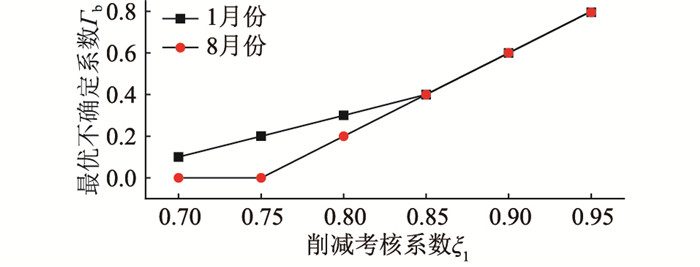
最优不确定系数Γb与考核削减系数ξ1的关系如图 7所示,所提策略在测试场景集中的最优不确定系数Γb随着考核削减系数ξ1增大呈现单调非递减趋势。因为ξ1的大小反映了市场对LCB考核的严格程度,更严格的考核下LA会更充分地考虑负荷的不确定性以减免罚金。
|
图 7 最优不确定系数Γb与考核削减系数ξ1的关系 Fig. 7 Relationship between optimal uncertainty coefficient Γb and assessment reduction coefficient ξ1 |
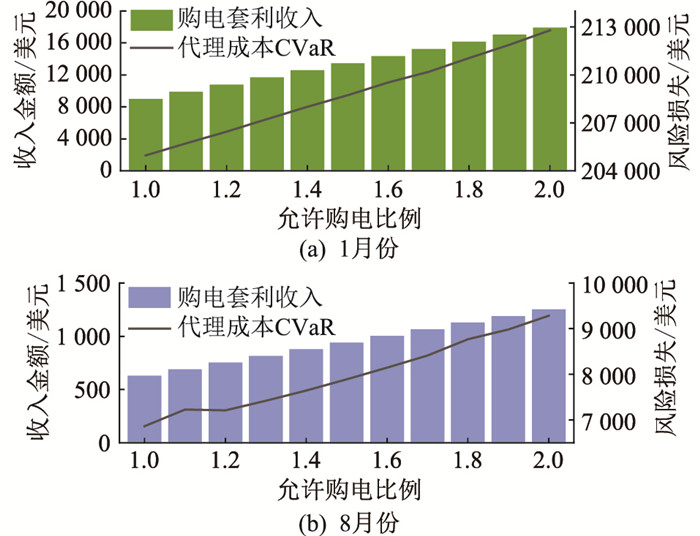
当缩减场景集能反应测试场景集的价格特征时,LA的购电方案能在测试场景集中进行套利。如图 8所示,允许购电比例从1倍提高至2倍时,LA策略购电行为带来的收入也提高了100%,这使得平均代理成本分别降低了7.52%(1月份)与1.13%(8月份),但其CVaR分别提高了3.82%(1月份)与35.24%(8月份)。
|
图 8 允许购电比例对聚合商的影响 Fig. 8 Impact of allowable power purchase ratio on LA |
文中研究了LA参与电能量市场面临双重不确定性的问题,且考虑了LA同时参与日前与实时LCB的情况,构建了混合整数线性规划模型。首先提出用双层规划与多场景法来解决价格与负荷的双重不确定性;其次提出一种基于神经网络的场景缩减方法;最后采用PJM市场数据围绕所提策略模型及场景缩减方法进行算例分析,并得出以下结论:
(1) 不同的场景缩减方法会影响求解出的LCB策略在测试场景集中的表现优劣。文中所用场景集中,基于DNN的缩减方法的投标策略相较于对比方法可减少0.02%至12.28%不等的代理成本。
(2) 对负荷波动的考虑程度会影响聚合商的LCB行为,随着前者的增大,聚合商在制订策略时倾向于减少承诺的削减容量以保证LCB的完成率,同时提高了最多196.49%的单位LCB执行收益。
(3) 相对于完全不考虑负荷波动风险,通过选取合适的考量负荷不确定性的系数求解出的LCB策略最多可让聚合商减少19.25%的代理成本,同时也可降低风险损失。
| [1] |
王健, 梁华彬, 杜兆斌. 考虑CBL误差不确定性的PJM电力市场经济需求响应模型研究[J]. 电力建设, 2016, 37(10): 137-143. WANG Jian, LIANG Huabin, DU Zhaobin. Economic demand response modeling in PJM electric market considering CBL error uncertainty[J]. Electric Power Construction, 2016, 37(10): 137-143. DOI:10.3969/j.issn.1000-7229.2016.10.019 (  0) 0) |
| [2] |
AGHAEI J, ALIZADEH M I. Demand response in smart electricity grids equipped with renewable energy sources: a review[J]. Renewable and Sustainable Energy Reviews, 2013, 18: 64-72. DOI:10.1016/j.rser.2012.09.019 (  0) 0) |
| [3] |
袁晓冬, 费骏韬, 胡波, 等. 资源聚合商模式下的分布式电源、储能与柔性负荷联合调度模型[J]. 电力系统保护与控制, 2019, 47(22): 17-26. YUAN Xiaodong, FEI Juntao, HU Bo, et al. Joint scheduling model of distributed generation, energy storage and flexible load under resource aggregator mode[J]. Power System Protection and Control, 2019, 47(22): 17-26. (  0) 0) |
| [4] |
徐小涵. 需求响应集成服务商参与电力市场的运行机制研究[D]. 南京: 东南大学, 2018. XU Xiaohan. Research on operation mode and decision-making strategy for demand response aggregator in power market[D]. Nanjing: Southeast University, 2018. (  0) 0) |
| [5] |
孙玲玲, 高赐威, 谈健, 等. 负荷聚合技术及其应用[J]. 电力系统自动化, 2017, 41(6): 159-167. SUN Lingling, GAO Ciwei, TAN Jian, et al. Load aggregation technology and its applications[J]. Automation of Electric Power Systems, 2017, 41(6): 159-167. (  0) 0) |
| [6] |
赵冬梅, 宋原, 王云龙, 等. 考虑柔性负荷响应不确定性的多时间尺度协调调度模型[J]. 电力系统自动化, 2019, 43(22): 21-30. ZHAO Dongmei, SONG Yuan, WANG Yunlong, et al. Coordinated scheduling model with multiple time scales considering response uncertainty of flexible load[J]. Automation of Electric Power Systems, 2019, 43(22): 21-30. DOI:10.7500/AEPS20190428008 (  0) 0) |
| [7] |
尹硕, 张鹏, 杨萌, 等. 计及需求侧响应的综合能源系统多时间尺度优化调度[J]. 电力系统及其自动化学报, 2020, 32(11): 35-42. YIN Shuo, ZHANG Peng, YANG Meng, et al. Multi-time scale optimal scheduling of integrated energy system considering demand-side response[J]. Proceedings of the CSU-EPSA, 2020, 32(11): 35-42. (  0) 0) |
| [8] |
张晶晶, 张鹏, 吴红斌, 等. 负荷聚合商参与需求响应的可靠性及风险分析[J]. 太阳能学报, 2019, 40(12): 3526-3533. ZHANG Jingjing, ZHANG Peng, WU Hongbin, et al. Reliability and risk analysis of load aggregators in demand response[J]. Acta Energiae Solaris Sinica, 2019, 40(12): 3526-3533. (  0) 0) |
| [9] |
曹彬, 吕干云, 王楠, 等. 综合能源系统优化调度下的需求响应研究与应用[J]. 电力需求侧管理, 2021, 23(4): 45-50. CAO Bin, LYU Ganyun, WANG Nan, et al. Research and application of demand response based on optimal scheduling of integrated energy system[J]. Power Demand Side Management, 2021, 23(4): 45-50. DOI:10.3969/j.issn.1009-1831.2021.04.009 (  0) 0) |
| [10] |
ZENG B, WEI X, ZHAO D B, et al. Hybrid probabilistic-possibilistic approach for capacity credit evaluation of demand response considering both exogenous and endogenous uncertainties[J]. Applied Energy, 2018, 229: 186-200. DOI:10.1016/j.apenergy.2018.07.111 (  0) 0) |
| [11] |
郭红霞, 高瑞, 杨苹. 基于条件风险价值的微电网现货市场两阶段调度[J]. 电网技术, 2019, 43(8): 2665-2674. GUO Hongxia, GAO Rui, YANG Ping. Two-stage dispatch of microgrid based on CVaR theory under electricity spot market[J]. Power System Technology, 2019, 43(8): 2665-2674. (  0) 0) |
| [12] |
HE G N, CHEN Q X, KANG C Q, et al. Optimal offering strategy for concentrating solar power plants in joint energy, reserve and regulation markets[J]. IEEE Transactions on Sustainable Energy, 2016, 7(3): 1245-1254. DOI:10.1109/TSTE.2016.2533637 (  0) 0) |
| [13] |
ABAPOUR S, MOHAMMADI-IVATLOO B, TARAFDAR HAGH M. Robust bidding strategy for demand response aggregators in electricity market based on game theory[J]. Journal of Cleaner Production, 2020, 243: 118393. DOI:10.1016/j.jclepro.2019.118393 (  0) 0) |
| [14] |
WANG S Y, BI S Z, ZHANG Y J A. Demand response management for profit maximizing energy loads in real-time electricity market[J]. IEEE Transactions on Power Systems, 2018, 33(6): 6387-6396. DOI:10.1109/TPWRS.2018.2827401 (  0) 0) |
| [15] |
阎怀东, 马汝祥, 柳志航, 等. 计及需求响应的电动汽车充电站多时间尺度随机优化调度[J]. 电力系统保护与控制, 2020, 48(10): 71-80. YAN Huaidong, MA Ruxiang, LIU Zhihang, et al. Multi-time scale stochastic optimal dispatch of electric vehicle charging station considering demand response[J]. Power System Protection and Control, 2020, 48(10): 71-80. (  0) 0) |
| [16] |
王妍, 吴传申, 高山. 基于电动汽车行驶数据快速聚类的充电站选址优化[J]. 电力需求侧管理, 2021, 23(3): 8-12. WANG Yan, WU Chuanshen, GAO Shan. Site selection optimization of charging station based onrapid clustering of electric vehicle driving data[J]. Power Demand Side Management, 2021, 23(3): 8-12. DOI:10.3969/j.issn.1009-1831.2021.03.003 (  0) 0) |
| [17] |
刘坚, 熊英, 金亨美, 等. 电动汽车参与电力需求响应的成本效益分析——以上海市为例[J]. 全球能源互联网, 2021, 4(1): 86-94. LIU Jian, XIONG Ying, KIM H M, et al. Economic assessment of demand response delivered by electric vehicles in Shanghai[J]. Journal of Global Energy Interconnection, 2021, 4(1): 86-94. (  0) 0) |
| [18] |
高红, 廖斌, 屈东明. 基于电动汽车云平台的大数据存储与管理[J]. 电力信息与通信技术, 2018, 16(4): 45-49. GAO Hong, LIAO Bin, QU Dongming. The big data storage and management based on the electric vehicles cloud platform[J]. Electric Power Information and Communication Technology, 2018, 16(4): 45-49. (  0) 0) |
| [19] |
WANG Z F, JOCHEM P, FICHTNER W. A scenario-based stochastic optimization model for charging scheduling of electric vehicles under uncertainties of vehicle availability and charging demand[J]. Journal of Cleaner Production, 2020, 254: 119886. DOI:10.1016/j.jclepro.2019.119886 (  0) 0) |
| [20] |
KINGMA D, BA J. Adam: a method for stochastic optimization[C]//2015 International Conference on Learning Representations(ICLR). San Diego, CA, USA: 2015: 1-15.
(  0) 0) |
| [21] |
BERTSIMAS D, SIM M. Robust discrete optimization and network flows[J]. Mathematical Programming, 2003, 98(1/2/3): 49-71. (  0) 0) |
| [22] |
PARVANIA M, FOTUHI-FIRUZABAD M, SHAHIDEHPOUR M. Optimal demand response aggregation in wholesale electricity markets[J]. IEEE Transactions on Smart Grid, 2013, 4(4): 1957-1965. (  0) 0) |
| [23] |
HEITSCH H, RÖMISCH W. Scenario reduction algorithms in stochastic programming[J]. Computational Optimization and Applications, 2003, 24(2/3): 187-206. (  0) 0) |
| [24] |
HU J X, LI H R. A new clustering approach for scenario reduction in multi-stochastic variable programming[J]. IEEE Transactions on Power Systems, 2019, 34(5): 3813-3825. (  0) 0) |
| [25] |
LIANG J K, TANG W Y. Scenario reduction for stochastic day-ahead scheduling: a mixed autoencoder based time-series clustering approach[J]. IEEE Transactions on Smart Grid, 2021, 12(3): 2652-2662. (  0) 0) |
 2022, Vol. 41
2022, Vol. 41


 杨苹(1967),女,博士,教授,研究方向为可再生能源并网和微电网技术;
杨苹(1967),女,博士,教授,研究方向为可再生能源并网和微电网技术;