文章编号: 2096-3203(2022)01-0026-08 中图分类号: TM732
2. 北京清能互联科技有限公司, 北京 100084
新型电力系统核心特征在于新能源占据主导地位,高比例新能源的大规模并网将进一步加剧新能源的消纳压力[1-3]。在“碳达峰、碳中和”目标下,我国新能源装机容量和占比都将快速增长,2030年风电和太阳能发电总装机容量预计将超过12亿kW[4]。为满足高比例新能源的并网消纳需求、最大程度降低弃风弃光率,迫切需要充分挖掘系统中的灵活性调节资源。发电侧由于受到机组出力限制以及机组自身性能的影响,可提供的调峰资源有限,难以为新型电力系统下的新能源消纳提供足够的空间[5]。为此,应积极挖掘电力用户的调峰潜力[6-7],建立需求响应市场化交易机制[8],用市场化手段调动用户侧参与调峰辅助服务的积极性,从而引导用户侧资源公平、有序参与电网灵活互动。目前,相关学者对用户侧参与调峰的优化调度策略[9-11]和发用两侧参与调峰的模式[12-17]进行了研究。
调峰辅助服务市场是在我国尚未建设现货市场时提出的,本质仍是电能量市场。国外成熟电力市场并没有调峰这一辅助服务品种,系统调峰问题主要通过现货市场解决[18]。但是,我国火电机组中可作为灵活调节资源的燃气机组占比较少,不能频繁启停的燃煤机组占比较高,仅通过现货市场无法解决调峰问题,仍需研究调峰辅助服务市场。如果现货市场和调峰辅助服务市场先后独立出清,调峰
市场需以现货市场出清结果为基础。在调峰市场中,假如机组在某一时段本可调减出力进行调峰,但由于受机组爬坡约束限制,调减出力之后的下一时段可能无法达到现货出清的设定出力,从而失去该时段的调峰能力。调峰市场和现货电能量市场联合优化,统一优化目标和约束条件可获得更好的优化结果,同时保证出清结果的可行性。
目前,相关学者对调峰市场和现货市场联合优化的市场模式进行了相关研究,包括考虑用户侧参与调峰的现货市场模式[19-20]和考虑发电侧参与调峰的现货市场模式[21]。文献[19]针对三北地区风电消纳问题,在电力用户与发电企业直接交易的基础上,设计了电力用户参与风电消纳的日前市场模式,深入挖掘用户侧的调峰潜力,并设计了调峰成本在市场主体间的分摊机制。文献[20]在安全约束机组组合(security constrained unit commitment,SCUC)模型的基础上加入了用户侧互动负荷,形成发用电一体化调度计划模型。文献[21]设计了考虑火电机组深度调峰和可再生能源避免削减降价的日前市场机制,将可再生能源出让的发电上网红利补偿给深度调峰的火电机组。
现有研究中,缺乏考虑发电侧和用户侧共同参与的调峰市场与现货市场联合出清模式。同时在用户侧参与调峰市场的相关研究中,没有考虑储能的参与,且对调节不同用户侧调峰资源的能力差异考虑不充分,未能精细且合理地挖掘用户侧调峰潜力。
为此,文中针对新能源大规模并网条件下电网调峰能力不足的问题,根据用户是否具有跟踪实时调度指令的能力,将用户侧调峰资源分为灵活调节用户和非灵活调节用户,在此基础上设计了一种发用两侧参与调峰的现货市场模式,将调峰辅助服务市场、新能源消纳与现货市场相结合,充分发挥常规机组和柔性负荷的调峰能力,提升新能源消纳水平。
1 发用两侧参与调峰的现货市场联合出清模式设计 1.1 基本原则发用两侧参与调峰的现货市场联合出清模式将现货市场和调峰辅助服务市场进行联合出清,并在优化时考虑新能源消纳。火电机组、独立储能和用户作为调峰辅助服务提供者,在调峰辅助服务市场中同台竞价。其中,用户根据其是否具有跟踪实时调度指令的能力,分为灵活调节用户和非灵活调节用户。火电机组、独立储能和灵活调节用户按照实时市场出清结果执行;非灵活调节用户不参与实时市场,按照日前市场出清结果执行,其日前市场出清结果作为实时市场的边界条件。
1.2 交易申报 1.2.1 能量申报火电机组在日前申报“电能量-价格”曲线时,最多可申报n段,每段需申报出力区间起点、出力区间终点以及该区间报价。每段报价均不可超过申报价格的上、下限。最小技术出力不为零的发电机组,第一段出力区间起点为机组的最小技术出力,最后一段出力区间终点为机组的最大技术出力。随着出力增加,报价曲线必须单调非递减。每段报价段的长度不能低于[(机组最大技术出力-机组最小技术出力)/n]%,这是为了防止机组进行高价试探,对可申报高价的报价段区间终点和区间起点间的长度设置过长,抬高市场出清价格。
为了促进新能源消纳,在文中所设计的现货市场模式下,风电、光伏采用报量不报价的方式参与市场,按零价在现货市场中优先出清。
1.2.2 调峰申报发电侧主体和用户侧主体调峰均采用“阶梯式”分档报价,以“调峰贡献-价格”曲线形式和报量报价方式来参与市场。
火电机组的调峰贡献是最小技术出力以下的发电电力,日前在最小技术出力的基础上,采用下调容量比率的形式报价,以k%额定容量作为一个报价区间,直至最小深调出力为止。用户的调峰贡献是负荷基准以上的用电负荷,日前在负荷基准的基础上,采用上调用电负荷的形式报价,由用户自行确定报价区间分段。独立储能采用充电负荷的方式进行调峰贡献,报价区间分段由独立储能自行确定。“调峰贡献-价格”曲线为单调连续非递减曲线,最多可分为m段,每段曲线包含调峰贡献起点、终点以及该区间的报价。为了保障市场的稳定运行以及考虑到调峰的经济性,需对每段报价设置上、下限。
负荷基准是用户在正常无约束条件下负荷变动习惯的量化数据,是用于衡量用户参与电力市场程度的基准。为保证用户侧响应的有效性,调度机构应在调峰辅助服务市场开展前对用户侧进行负荷基准测试,以验证其具有相对稳定的用电规律,并要求用户侧依照测试负荷基准进行市场申报。
1.3 交易组织 1.3.1 日前市场交易组织(1) 信息发布。日前市场开市前,市场运营机构发布交易的边界条件、电网调峰需求等信息。
(2) 交易申报。火电机组进行日前现货市场申报;风电、光伏申报出力预测曲线;有意参与深度调峰的火电机组、独立储能和用户依据自身能力,进行深度调峰交易申报。
(3) 日前市场出清。市场运营机构执行日前市场交易出清,生成交易出清结果,包括次日火电机组出力计划及出清价格、深度调峰火电机组中标调峰电量、独立储能中标调峰电量、灵活调节用户中标调峰电量、非灵活调节用户中标调峰电量、深度调峰市场出清价格。
1.3.2 实时市场交易组织(1) 交易申报。实时市场采用日前市场封存的报价信息进行出清;风电、光伏申报超短期出力预测曲线;非灵活调节用户不参与实时市场,在日前市场的出清结果作为实时市场的边界条件。
(2) 实时市场出清。市场运营机构执行实时市场交易出清,生成交易出清结果,包括未来2 h的火电机组出力计划和出清价格、深度调峰火电机组中标调峰电量、独立储能中标调峰电量、灵活调节用户中标调峰电量、深度调峰市场出清价格。
2 发用两侧参与调峰的现货市场联合出清模型 2.1 日前市场出清模型 2.1.1 目标函数目前市场出清模型的目标函数如式(1)所示。
| $ \begin{gathered} \min \sum\limits_{t=1}^{T}\left[\sum\limits_{i=1}^{I} \sum\limits_{n=1}^{N}\left(p_{i, n}^{\mathrm{G}} P_{i, t, n}^{\mathrm{G}, \mathrm{a}}\right)+\sum\limits_{i=1}^{I}\left(\alpha_{i, t} U_{i}^{\mathrm{G}, \mathrm{start}}+\right.\right. \\ \left.\beta_{i, t} U_{i}^{\mathrm{G}, \mathrm{finish}}\right)+\sum\limits_{j=1}^{J} \sum\limits_{h=1}^{H}\left(p_{j, t, h}^{\mathrm{U}_{1}} P_{j, t, h}^{\mathrm{U}_{1}, \mathrm{a}}\right)+ \\ \sum\limits_{f=1}^{F} \sum\limits_{r=1}^{R}\left(p_{f, t, r}^{\mathrm{U}_{2}} P_{f, t, r}^{\mathrm{U}_{2}, \mathrm{a}}\right)+\sum\limits_{q=1}^{Q} \sum\limits_{e=1}^{E}\left(p_{q, t, e}^{\mathrm{Z}} P_{q, t, e}^{\mathrm{Z}, \mathrm{a}}\right)+ \\ \left.\sum\limits_{i=1}^{I} \sum\limits_{m=1}^{M}\left(r_{i, t, m}^{\mathrm{G}} R_{i, t, m}^{\mathrm{G}, \mathrm{a}}\right)+\lambda\left(\sum\limits_{k=1}^{K} P_{k, t}^{\mathrm{W}, \mathrm{a}}+\sum\limits_{v=1}^{V} P_{v, t}^{\mathrm{S}, \mathrm{a}}\right)\right] \end{gathered} $ | (1) |
式中:T为总时段数;I为火电机组台数;N为火电机组能量报价的总段数;pi, nG,Pi, t, nG, a分别为火电机组i的第n段能量报价和在t时段的日前市场中标出力;αi, t,βi, t分别为火电机组i在t时段的启、停状态变量,为0-1变量;UiG, start,UiG, finish分别为火电机组i的启、停成本;J为灵活调节用户总数;H为灵活调节用户的报价总段数;pj, t, hU1,Pj, t, hU1, a分别为灵活调节用户j在t时段的第h段调峰报价和日前市场中标调峰电力;F为非灵活调节用户总数;R为非灵活调节用户的报价总段数;pf, t, rU2,Pf, t, rU2, a分别为非灵活调节用户f在t时段的第r段调峰报价和日前中标调峰电力;Q为独立储能总数;E为独立储能的报价总段数;pq, t, eZ,Pq, t, eZ, a分别为独立储能q在t时段的第e段调峰报价和日前中标调峰电力;M为火电机组参与深度调峰的报价的总段数;ri, t, mG,Ri, t, mG, a分别为火电机组i在t时段的第m段深度调峰报价和日前中标调峰电力;K,V分别为风电和光伏的数量;λ为弃风弃光惩罚因子;Pk, tW, a为日前风机k在t时段的弃风电力;Pv, tS, a为日前光伏v在t时段的弃光电力。
上述目标函数有2层,火电机组的发电成本、启停成本以及灵活调节用户、非灵活调节用户、独立储能、火电机组的调峰成本为第1层,弃风、弃光惩罚为第2层,第2层的优先级高于第1层的优先级。设置弃风弃光惩罚因子λ,使得优先调用各种资源进行调峰,最大化消纳新能源,保障系统弃风弃光电量最小。
2.1.2 约束条件(1) 系统负荷平衡约束。
| $ \begin{array}{c} \sum\limits_{i=1}^{I} \sum\limits_{n=1}^{N} P_{i, t, n}^{\mathrm{G}, \mathrm{a}}+\sum\limits_{k=1}^{K}\left(P_{k, t}^{\mathrm{W}, \mathrm{F}, \mathrm{a}}-P_{k, t}^{\mathrm{W}, \mathrm{a}}\right)+\sum\limits_{v=1}^{V}\left(P_{v, t}^{\mathrm{S}, \mathrm{F}, \mathrm{a}}-\right. \\ \left.P_{v, t}^{\mathrm{S}, \mathrm{a}}\right)+\sum\limits_{q=1}^{Q} P_{q, t}^{\mathrm{Z}, \mathrm{Y}, \mathrm{a}}=D_{t}^{\mathrm{a}}+\sum\limits_{j=1}^{J} \sum\limits_{h=1}^{H} P_{j, t, h}^{\mathrm{U}_{1}, \mathrm{a}}+ \\ \sum\limits_{f=1}^{F} \sum\limits_{r=1}^{R} P_{f, t, r}^{\mathrm{U}_2, \mathrm{a}}+\sum\limits_{q=1}^{Q} \sum\limits_{e=1}^{E} P_{q, t, e}^{\mathrm{Z}, \mathrm{a}} \quad \forall t \end{array} $ | (2) |
式中:Pk, tW, F, a,Pv, tW, F, a分别为风电k和光伏v在t时段的日前预测出力;Pq, tZ, Y, a为独立储能q在t时段的日前放电负荷;Dta为t时段的系统总负荷日前预测值。式(2)左边为考虑弃风弃光的火电、风电、光伏以及储能放电的总出力,式(2)右边为考虑用户侧参与调峰的系统总负荷。
(2) 线路有功潮流约束。
| $ \begin{gathered} f_{l}^{\mathrm{min}} \leqslant \sum\limits_{i=1}^{I} \sum\limits_{n=1}^{N}\left(G_{i, l}^{\mathrm{G}} P_{i, t, n}^{\mathrm{G}, \mathrm{a}}\right)+\sum\limits_{k=1}^{K}\left[G_{k, l}^{\mathrm{W}}\left(P_{k, t}^{\mathrm{W}, \mathrm{F}, \mathrm{a}}-P_{k, t}^{\mathrm{W}, \mathrm{a}}\right)\right]+ \\ \sum\limits_{v=1}^{V}\left[G_{v, l}^{\mathrm{S}}\left(P_{v, t}^{\mathrm{S}, \mathrm{F}, \mathrm{a}}-P_{v, t}^{\mathrm{S}, \mathrm{a}}\right)\right]+\sum\limits_{q=1}^{Q}\left(G_{q, l}^{\mathrm{Z}} P_{q, t}^{\mathrm{Z}, \mathrm{Y}, \mathrm{a}}\right)- \\ \sum\limits_{b=1}^{B}\left(G_{b, l}^{\mathrm{D}} D_{b, t}^{\mathrm{a}}\right)-\sum\limits_{j=1}^{J} \sum\limits_{h=1}^{H}\left(G_{j, l}^{\mathrm{U}_{1}} P_{j, t, h}^{\mathrm{U}_{1}, \mathrm{a}}\right)- \\ \sum\limits_{f=1}^{F} \sum\limits_{r=1}^{R}\left(G_{f, l}^{\mathrm{U}_{2}} P_{f, t, r}^{\mathrm{U}_{2}, \mathrm{a}}\right)-\sum\limits_{q=1}^{Q} \sum\limits_{e=1}^{E}\left(G_{q, l}^{\mathrm{Z}} P_{q, t, e}^{\mathrm{Z}, \mathrm{a}}\right) \leqslant f_{l}^{\max } \\ \forall l, \forall t \end{gathered} $ | (3) |
式中:Gi, lG,Gk, lW,Gv, lS,Gb, lD,Gj, lU1,Gf, lU2,Gq, lZ分别为火电机组i、风电k、光伏v、负荷节点b、灵活调节用户j、非灵活调节用户f、独立储能q所在节点对线路l的发电转移分布因子;Db, ta为t时段节点b的日前预测负荷;B为负荷节点总数;f lmin,f lmax分别为线路l的最小、最大传输功率。
(3) 火电机组约束。
| $ \left\{\begin{array}{l} P_{i}^{\min } \tau_{i, t} \leqslant \sum\limits_{n=1}^{N} P_{i, t, n}^{G, \mathrm{a}} \leqslant P_{i}^{\max } \tau_{i, t} \\ \sum\limits_{m=1}^{M} R_{i, t, m}^{\mathrm{G}, \mathrm{a}}=0 \\ \sum\limits_{n=1}^{N} P_{i, t, n}^{\mathrm{G}, \mathrm{a}}+\sum\limits_{m=1}^{M} R_{i, t, m}^{\mathrm{G}, \mathrm{a}}=P_{i}^{\min } \tau_{i, t} \quad \forall t \\ \sum\limits_{n=1}^{N} P_{i, t, n}^{\mathrm{G}, \mathrm{a}} \geqslant R_{i}^{\min } \tau_{i, t} \\ \sum\limits_{m=1}^{M} R_{i, t, m}^{\mathrm{G}, \mathrm{a}}>0 \end{array}\right. $ | (4) |
式中:Pimax,Pimin,Rimin分别为火电机组i的最大技术出力、最小技术出力和最小深调出力;τi, t为火电机组i在时段t的开停机状态。
式(4)为火电机组约束,当火电机组未参与调峰,则只需满足最大、最小技术出力约束;当火电机组参与调峰,则要求火电机组的出力中标量和调峰中标量相加要等于机组的最小技术出力,且出力中标量要大于最小深调出力。
(4) 其他约束条件。系统正备用容量约束、系统负备用容量约束、机组爬坡约束等约束条件与常规SCUC模型一致[22],文中不再赘述。
2.2 实时市场出清模型 2.2.1 目标函数实时市场出清模型的目标函数如式(5)所示。
| $ \begin{array}{c} \min \sum\limits_{t=1}^{T}\left[\sum\limits_{i=1}^{I} \sum\limits_{n=1}^{N}\left(p_{i, n}^{\mathrm{G}} P_{i, t, n}^{\mathrm{G}, \mathrm{o}}\right)+\sum\limits_{j=1}^{J} \sum\limits_{h=1}^{H}\left(p_{j, t, h}^{\mathrm{U}_{1}} P_{j, t, h}^{\mathrm{U}_{1}, \mathrm{o}}\right)+\right. \\ \sum\limits_{q=1}^{Q} \sum\limits_{e=1}^{E}\left(p_{q, t, e}^{\mathrm{Z}} P_{q, t, e}^{\mathrm{Z}, \mathrm{o}}\right)+\sum\limits_{i=1}^{I} \sum\limits_{m=1}^{M}\left(r_{i, t, m}^{\mathrm{G}} R_{i, t, m}^{\mathrm{G}, \mathrm{o}}\right)+ \\ \left.\lambda\left(\sum\limits_{k=1}^{K} P_{k, t}^{\mathrm{W}, \mathrm{o}}+\sum\limits_{v=1}^{V} P_{v, t}^{\mathrm{S}, \mathrm{o}}\right)\right] \end{array} $ | (5) |
式中:Pi, t, nG, o为火电机组i在t时段的第n段能量报价的实时市场中标出力;Pj, t, hU1, o为灵活调节用户j在t时段的第h段调峰报价区间的实时中标调峰电力;Pq, t, eZ, o为独立储能q在t时段的第e段调峰报价区间的实时中标调峰电力;Ri, t, mG, o为火电机组i在t时段的第m段深度调峰报价区间的实时中标调峰电力;Pk, tW, o为风机k在t时段的实时弃风电力;Pv, tS, o为光伏v在t时段的实时弃光电力。
非灵活调节用户不参加实时市场,实时市场出清模型的目标函数包括火电机组发电成本、灵活调节用户调峰成本、独立储能调峰成本、火电机组深度调峰成本、弃风、弃光惩罚。
2.2.2 约束条件(1) 系统负荷平衡约束。
| $ \begin{array}{c} \sum\limits_{i=1}^{I} \sum\limits_{n=1}^{N} P_{i, t, n}^{\mathrm{G}, \mathrm{o}}+\sum\limits_{k=1}^{K}\left(P_{k, t}^{\mathrm{W}, \mathrm{F}, \mathrm{o}}-P_{k, t}^{\mathrm{W}, \mathrm{o}}\right)+\sum\limits_{v=1}^{V}\left(P_{v, t}^{\mathrm{S}, \mathrm{F}, \mathrm{o}}-\right. \\ \left.P_{v, t}^{\mathrm{S}, \mathrm{o}}\right)+\sum\limits_{q=1}^{Q} P_{q, t}^{\mathrm{Z}, \mathrm{Y}, \mathrm{o}}=D_{t}^{\mathrm{o}}+\sum\limits_{j=1}^{J} \sum\limits_{h=1}^{H} P_{j, t, h}^{\mathrm{U}_{1}, \mathrm{o}}+ \\ \sum\limits_{f=1}^{F} \sum\limits_{r=1}^{R} P_{f, t, r}^{\mathrm{U}_{2}, \mathrm{a}'}+\sum\limits_{q=1}^{Q} \sum\limits_{e=1}^{E} P_{q, t, e}^{\mathrm{Z}, \mathrm{o}} \quad \forall t \end{array} $ | (6) |
式中:Pk, tW, F, o,Pv, tS, F, o分别为风电k和光伏v在t时段的实时预测出力;Pq, tZ, Y, o为独立储能q在t时段的实时放电负荷;Dto为t时段的系统总负荷实时预测值;Pf, t, rU2, a′为日前市场中非灵活调节用户f在t时段第r段调峰报价的中标电力。
实时市场的系统负荷平衡约束与日前市场的区别在于非灵活调节用户只参与日前市场,因此实时市场中非灵活调节用户的中标调峰电力Pf, t, rU2, a不再是决策变量,而是直接将日前市场优化结果代入。
(2) 线路有功潮流约束。
| $ \begin{gathered} f_{l}^{\min } \leqslant \sum\limits_{i=1}^{I} \sum\limits_{n=1}^{N}\left(G_{i, l}^{\mathrm{G}} P_{i, t, n}^{\mathrm{G}, \mathrm{o}}\right)+\sum\limits_{k=1}^{K}\left[G_{k, l}^{\mathrm{W}}\left(P_{k, t}^{\mathrm{W}, \mathrm{F}, \mathrm{o}}-P_{k, t}^{\mathrm{W}, \mathrm{o}}\right)\right]+ \\ \sum\limits_{v=1}^{V}\left[G_{v, l}^{\mathrm{S}}\left(P_{v, t}^{\mathrm{S}, \mathrm{F}, \mathrm{o}}-P_{v, t}^{\mathrm{S}, \mathrm{o}}\right)\right]+\sum\limits_{q=1}^{Q}\left(G_{q, l}^{\mathrm{Z}} P_{q, t}^{\mathrm{Z}, \mathrm{Y}, \mathrm{o}}\right)- \\ \sum\limits_{b=1}^{B}\left(G_{b, l}^{\mathrm{D}} D_{b, t}^{\mathrm{o}}\right)-\sum\limits_{j=1}^{J} \sum\limits_{h=1}^{H}\left(G_{j, l}^{\mathrm{U}_{1}} P_{j, t, h}^{\mathrm{U}_{1}, \mathrm{o}}\right)- \\ \sum\limits_{f=1}^{F} \sum\limits_{r=1}^{R}\left(G_{f, l}^{\mathrm{U}_{2}} P_{f, t, r}^{\mathrm{U}_{2}, \mathrm{a}'}\right)-\sum\limits_{q=1}^{Q} \sum\limits_{e=1}^{E}\left(G_{q, l}^{\mathrm{Z}} P_{q, t, e}^{\mathrm{Z}, \mathrm{o}}\right) \leqslant f_{l}^{\max } \\ \forall l, \forall t \end{gathered} $ | (7) |
式中:Db, to为t时段节点b的实时预测负荷。
与系统负荷平衡约束的区别类似,实时市场的线路有功潮流约束与日前市场的区别在于非灵活调节用户的中标调峰电力不再是决策变量。
(3) 火电机组约束。实时市场中,火电机组的出力上、下限约束条件与日前市场相同。
(4) 其他约束条件。机组爬坡约束等约束条件与常规安全约束经济调度模型一致[22],文中不再赘述。
3 发用两侧参与调峰的现货市场交易结算 3.1 现货市场结算火电机组在日前市场的出清电量按照日前市场的出清价格结算,实际执行电量与日前市场出清电量的偏差部分按照实时市场出清价格结算。
| $ F_{i}^{\mathrm{G}}=\sum\limits_{t=1}^{T}\left[Q_{t, i}^{\mathrm{E}, \mathrm{a}} p_{t}^{\mathrm{E}, \mathrm{a}}+\left(Q_{t, i}^{\mathrm{E}, \mathrm{o}}-Q_{t, i}^{\mathrm{E}, \mathrm{a}}\right) p_{t}^{\mathrm{E}, \mathrm{o}}\right] $ | (8) |
式中:FiG为火电机组i在现货市场的收益;Qt, iE, a为火电机组i在日前市场t时段的中标电量;Qt, iE, o为火电机组i在t时段的实际执行电量;ptE, a,ptE, o分别为日前市场和实时市场出清的t时段的电能量价格。
3.2 调峰辅助服务市场结算 3.2.1 调峰辅助服务费用结算深度调峰采用边际价格进行结算,计算深度调峰市场每档中最后一台中标火电机组/独立储能/用户的报价,得到该档的市场出清价。深度调峰火电机组和灵活调节用户按照实时市场出清的中标调峰电量和出清价格进行结算;非灵活调节用户按照日前市场出清的中标调峰电量和出清价格进行结算,并乘以比例系数φ。
| $ F_{i}^{\mathrm{D}, \mathrm{G}} =\sum\limits_{t=1}^{T}\left(Q_{t, i}^{\mathrm{D}, \mathrm{G}, \mathrm{o}} p_{t, m, i}^{\mathrm{D}, \mathrm{o}}\right) $ | (9) |
| $ F_{q}^{\mathrm{D}, \mathrm{Z}} =\sum\limits_{t=1}^{T}\left(Q_{t, q}^{\mathrm{D}, \mathrm{Z}, \mathrm{o}} p_{t, m, q}^{\mathrm{D}, \mathrm{o}}\right) $ | (10) |
| $ F_{j}^{\mathrm{D}, \mathrm{U}_{1}} =\sum\limits_{t=1}^{T}\left(Q_{t, j}^{\mathrm{D}, \mathrm{U}_{1}, \mathrm{o}} p_{t, m, j}^{\mathrm{D}, \mathrm{o}}\right) $ | (11) |
| $ F_{f}^{\mathrm{D}, \mathrm{U}_{2}} =\sum\limits_{t=1}^{T}\left(\varphi Q_{t, f}^{\mathrm{D}, \mathrm{U}_{2}, \mathrm{a}} p_{t, m, f}^{\mathrm{D}, \mathrm{a}}\right) $ | (12) |
式中: FiD, G, FqD, Z, FjD, U2, FfD, U2分别为火电机组、独立储能、灵活调节用户和非灵活调节用户的调峰收益;Qt, iD, G, o, Qt, qD, Z, o, Qt, jD, U1, o, Qt, fD, U2, a分别为火电机组i、独立储能q、灵活调节用户j、非灵活调节用户f在t时段的调峰贡献电量;pt, m, iD, o, pt, m, qD, o, pt, m, jD, o分别为火电机组、独立储能、灵活调节用户在t时段的实时市场最高调峰出清价格;pt, m, fD, a为非灵活调节用户f在t时段的日前市场最高调峰出清价格,其中标的最高档为m;φ为比例系数,0 < φ < 1,用于在结算中体现调峰资源调节性能的差异性,调节性能好的资源可以获得更多的调峰补偿。
3.2.2 调峰辅助服务费用分摊在市场深度调峰服务交易时段内的网内非调峰机组分摊调峰辅助服务费用。
(1) 火电机组。火电机组按照高于最小技术出力的上网电量部分参与分摊。
| $ C_{i}^{\mathrm{G}}=\sum\limits_{t=1}^{T} \frac{Q_{i, t}^{\mathrm{G}} F_{t}}{\sum\limits_{i=1}^{N_{t}^{\mathrm{G}}} Q_{i, t}^{\mathrm{G}}+\sum\limits_{j=1}^{N_{t}^{\mathrm{C}}} Q_{j, t}^{\mathrm{C}}+\sum\limits_{k=1}^{N_{t}^{\mathrm{O}}} Q_{k, t}^{\mathrm{O}}} $ | (13) |
式中:CiG为火电机组i的分摊金额;Qi, tG为火电机组在t时段的高于最小技术出力的上网电量;Qj, tC为风电/光伏机组在t时段的上网电量;Qk, tO为其他类型机组在t时段的修正后的上网电量;NtG,NtC,NtO分别为t时段的在运火电机组数量、风电/光伏机组数量、其他类型机组数量;Ft为t时段的调峰服务总费用。
(2) 风电、光伏机组。风电、光伏机组按照实际上网电量进行分摊。
| $ C_{j}^{\mathrm{C}}=\sum\limits_{t=1}^{T} \frac{Q_{j, t}^{\mathrm{C}} F_{t}}{\sum\limits_{i=1}^{N_{t}^{\mathrm{G}}} Q_{i, t}^{\mathrm{G}}+\sum\limits_{j=1}^{N_{t}^{\mathrm{C}}} Q_{j, t}^{\mathrm{C}}+\sum\limits_{k=1}^{N_{i}^{\mathrm{O}}} Q_{k, t}^{\mathrm{O}}} $ | (14) |
式中:CjC为风电/光伏机组的分摊金额。
(3) 其他机组。水电等其他类型机组按照修正后的上网电量进行分摊。修正后的上网电量等于实际上网电量乘以修正系数。
| $ C_{k}^{\mathrm{O}}=\sum\limits_{t=1}^{T} \frac{Q_{k, t}^{\mathrm{O}} F_{t}}{\sum\limits_{i=1}^{N_{t}^{\mathrm{G}}} Q_{i, t}^{\mathrm{G}}+\sum\limits_{j=1}^{N_{t}^{\mathrm{C}}} Q_{j, t}^{\mathrm{C}}+\sum\limits_{k=1}^{N_{t}^{\mathrm{O}}} Q_{k, t}^{\mathrm{O}}} $ | (15) |
| $ Q_{k, t}^{\mathrm{O}}=\alpha Q_{k, t}^{\mathrm{O}^{\prime}} $ | (16) |
式中:CkO为水电等其他类型机组的分摊金额;Qk, tO′为其他类型机组在t时段的上网电量;α为修正系数,0 < α < 1。
3.2.3 调峰辅助服务偏差考核如果火电机组、独立储能、用户的实际调峰贡献量小于市场出清的中标调峰电量,且电量偏差率大于一定值时,需要对偏差部分进行考核。
| $ \eta_{i, t}=\frac{Q_{i, t}^{\mathrm{w}}-Q_{i, t}^{\mathrm{r}}}{Q_{i, t}^{\mathrm{w}}} $ | (17) |
式中:ηi, t为火电机组/独立储能/用户在t时段的调峰贡献量偏差率;Qi, tw为火电机组/独立储能/用户在t时段的中标调峰电量,其中,火电机组、独立储能和灵活调节用户按照实时市场中标调峰电量进行计算,非灵活调节用户按照日前市场中标调峰电量进行计算;Qi, tr为火电机组/独立储能/用户在t时段的实际调峰贡献量。
偏差考核罚金按照火电机组/独立储能/用户的调峰偏差电量收取。
| $ E_{i, t}=\tau Q_{i, t} p_{t}^{\mathrm{D}} $ | (18) |
式中:Ei, t为火电机组/独立储能/用户在t时段的调峰偏差考核罚金;τ为惩罚系数,τ>1;Qi, t为火电机组/独立储能/用户在t时段的调峰偏差电量;ptD为t时段的调峰市场最高档出清价格,其中,火电机组、独立储能和灵活调节用户按照实时市场出清价格进行计算,非灵活调节用户按照日前市场出清价格进行计算。
4 算例分析算例分析采用IEEE 39节点模型构建一个处于供热期的电力系统,设置机组1、8、9为非供热火电机组,机组7为光伏机组,机组10为风电机组,其余为供热火电机组。系统数据、机组参数等参考文献[19]。交易申报数据参考某地区调峰辅助服务市场和现货市场的历史报价数据,能量报价可最多申报10段,调峰报价可最多申报5段。调峰报价区间划分及报价范围见表 1,P为火电机组额定容量。值得注意的是,交易申报数据只是为了对所提市场模式进行验证,取值合理即可。目标函数中的λ取105,非灵活调节用户结算时的φ取0.8,水电等其他类型机组调峰费用的α取0.3,调峰辅助服务的τ取2。混合整数规划模型采用Cplex求解器进行求解。
|
|
表 1 调峰报价区间划分及报价范围 Table 1 Peak regulation quotation interval and scope |
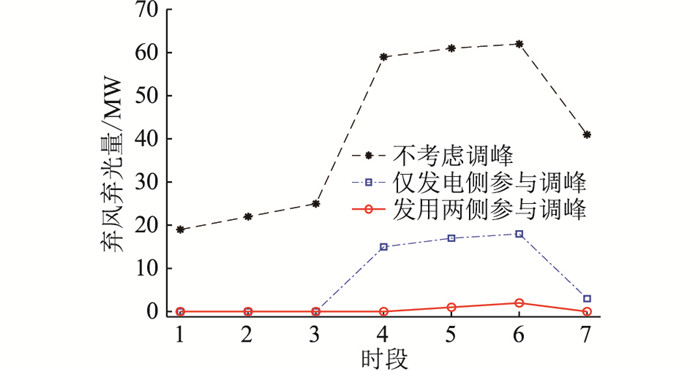
图 1对比了在典型弃风弃光时段不考虑调峰、仅发电侧参与调峰、发用两侧参与调峰3种现货市场模式下系统的弃风弃光情况。从图中可知,仅发电侧参与调峰和发用两侧参与调峰的现货市场模式下,系统的弃风弃光量均有所降低。发用两侧参与调峰的模式相比于仅发电侧参与调峰的模式可以降低17.3%的弃风弃光量。这是由于发电侧调峰资源不足,发用两侧参与调峰之后,增加了系统调峰资源,进一步提升了新能源消纳量。
|
图 1 系统弃风弃光情况 Fig. 1 Wind and light abandonment of the system |
在图 1中的时段4时,调峰市场的报价情况如表 2所示,在该时段,仅发电侧参与调峰和发用两侧参与调峰的现货市场模式下,调峰市场5段分段报价区间的出清价格如表 3所示。
|
|
表 2 时段4时调峰市场报价情况 Table 2 Quotation of peak regulation market in the fourth period |
|
|
表 3 调峰市场出清价格 Table 3 Peak market clearing price |
由表 3可知,发用两侧参与调峰的模式较仅发电侧参与调峰的模式,第一段和第三段的出清价格有所升高,这是由于柔性负荷参与调峰竞价之后,2段中报价高于火电机组的独立储能/用户在调峰市场中被调用,从而提高了出清的边际价格;第二段和第四段的出清价格一致,这是由于这2段中参与调峰的独立储能和用户报价均不高于火电机组的报价;第五段的出清价格有所降低,这是由于报价较低的独立储能和用户替代了原来报价较高的火电机组提供调峰辅助服务,从而降低了调峰市场出清的边际价格。
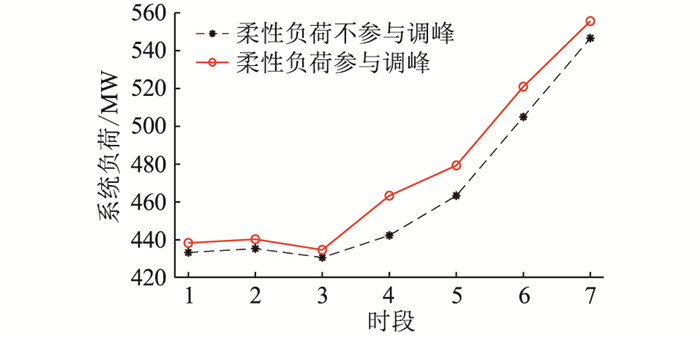
发用两侧参与调峰辅助服务前后的负荷曲线如图 2所示,从图中可知,柔性负荷参与调峰之后,系统负荷有所增加。
|
图 2 柔性负荷参与调峰辅助服务前后的负荷曲线 Fig. 2 Load curves before and after the flexible load participating in peak regulation anxiliary service |
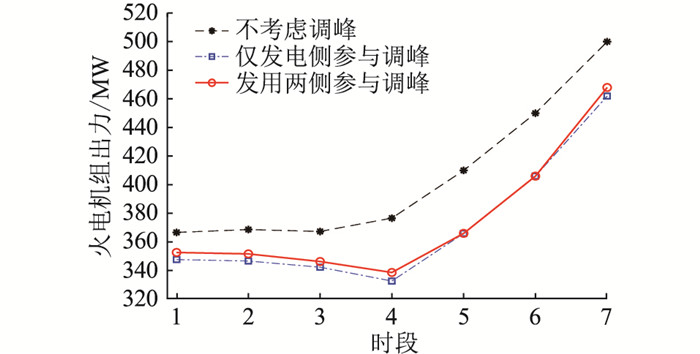
火电机组参与调峰辅助服务前后的出力曲线如图 3所示,从图中可知,火电机组参与深度调峰之后,整体出力有所降低。发用两侧参与调峰的模式较仅发电侧参与调峰的模式,在除时段5和时段6之外,火电机组压减出力较少,这是由于柔性负荷参与调峰之后,替代了部分火电机组的调峰贡献量。在时段5和时段6中,2种模式的火电机组出力相同,这是由于调峰资源不足,所有火电机组申报的调峰贡献量均被调用。
|
图 3 火电机组参与调峰辅助服务前后的出力曲线 Fig. 3 Power curves before and after thermal power units participating in peak regulation anxiliary service |
发用两侧参与调峰的现货市场模式下,系统新能源消纳量增加286 MW ·h,调峰总成本为12.76万元。调峰总成本在非调峰机组中的分摊结果见表 4。
|
|
表 4 调峰成本分摊结果 Table 4 Peak regulation cost allocation |
文中根据用户侧调峰资源调节能力的差异性对用户侧资源进行分类,并设计了针对性的市场参与机制,以便精细化地挖掘用户侧调峰潜力。在此基础上设计了一种发用两侧参与调峰的现货市场模式,将发电侧和用户侧的调峰资源纳入市场机制竞价,实现调峰辅助服务市场与现货市场联合出清。仿真结果表明,文中所提市场模式可充分挖掘用户侧调峰能力,有效降低弃风弃光量,提升新能源消纳水平,可为新能源高占比地区的电力市场设计提供有益借鉴。
需要说明的是,文中引入柔性负荷与发电侧共同参与调峰的模式不一定可以降低系统的调峰成本。为保障市场稳定运行,市场运营机构应根据市场的模拟运行情况对调峰申报价格进行调整。
本文得到国家电网有限公司西北分部科技项目(52250119000J)资助,谨此致谢!
| [1] |
舒印彪, 张智刚, 郭剑波, 等. 新能源消纳关键因素分析及解决措施研究[J]. 中国电机工程学报, 2017, 37(1): 1-9. SHU Yinbiao, ZHANG Zhigang, GUO Jianbo, et al. Study on key factors and solution of renewable energy accommodation[J]. Proceedings of the CSEE, 2017, 37(1): 1-9. (  0) 0) |
| [2] |
李国栋, 李庚银, 周明, 等. 国外促进新能源消纳的典型市场机制分析[J]. 中国电力, 2019, 52(2): 46-52, 60. LI Guodong, LI Gengyin, ZHOU Ming, et al. Analysis on foreign typical market mechanisms for promoting new energy consumptive[J]. Electric Power, 2019, 52(2): 46-52, 60. DOI:10.3969/j.issn.1007-3361.2019.02.019 (  0) 0) |
| [3] |
李国栋, 李庚银, 严宇, 等. 新能源跨省区消纳交易方式研究与应用分析[J]. 中国电力, 2017, 50(4): 39-44. LI Guodong, LI Gengyin, YAN Yu, et al. Research and application of trans-province trading modes of renewable energy[J]. Electric Power, 2017, 50(4): 39-44. (  0) 0) |
| [4] |
胡鞍钢. 中国实现2030年前碳达峰目标及主要途径[J]. 北京工业大学学报(社会科学版), 2021, 21(3): 1-15. HU Angang. China's goal of achieving carbon peak by 2030 and its main approaches[J]. Journal of Beijing University of Technology (Social Sciences Edition), 2021, 21(3): 1-15. (  0) 0) |
| [5] |
范高锋, 张楠, 梁志锋, 等. 我国"三北"地区弃风弃光原因分析[J]. 华北电力技术, 2016(12): 55-59. FAN Gaofeng, ZHANG Nan, LIANG Zhifeng, et al. Analysis on the 'three norths' region wind and PV power limitation[J]. North China Electric Power, 2016(12): 55-59. (  0) 0) |
| [6] |
党东升, 韩松, 周珏, 等. 需求响应参与系统调峰研究综述[J]. 电力需求侧管理, 2017, 19(5): 13-17. DANG Dongsheng, HAN Song, ZHOU Jue, et al. Review of demand response participating in power system peak shifting[J]. Power Demand Side Management, 2017, 19(5): 13-17. (  0) 0) |
| [7] |
潘尔生, 王新雷, 徐彤, 等. 促进可再生能源电力接纳的技术与实践[J]. 电力建设, 2017, 38(2): 1-11. PAN Ersheng, WANG Xinlei, XU Tong, et al. Technology and practice of promoting renewable energy power accommodation[J]. Electric Power Construction, 2017, 38(2): 1-11. (  0) 0) |
| [8] |
张高, 薛松, 范孟华, 等. 面向我国电力市场的需求响应市场化交易机制设计[J]. 电力建设, 2021, 42(4): 132-140. ZHANG Gao, XUE Song, FAN Menghua, et al. Design of demand-response market mechanism in accordance with China power market[J]. Electric Power Construction, 2021, 42(4): 132-140. (  0) 0) |
| [9] |
曹年林. 与大规模新能源发电相适应的用户侧联合调峰技术研究[D]. 北京: 北京交通大学, 2015. CAO Nianlin. Research on customer side participating in peak-load regulating under conditions of large-scale renewable energy integration[D]. Beijing: Beijing Jiaotong University, 2015. (  0) 0) |
| [10] |
刘小聪. 基于需求响应的大规模风电消纳调度策略研究[D]. 南京: 东南大学, 2015. LIU Xiaocong. Scheduling strategy based on demand response for high wind power integration[D]. Nanjing: Southeast University, 2015. (  0) 0) |
| [11] |
张强, 代建. 基于WSR的用户参与新能源发电并网调峰系统研究[J]. 智慧电力, 2018, 46(6): 27-33. ZHANG Qiang, DAI Jian. Study on end-user's participation in new energy power generation and network peaking based on WSR methodology[J]. Smart Power, 2018, 46(6): 27-33. (  0) 0) |
| [12] |
封圆. 广域源荷互动调峰模式研究[D]. 北京: 华北电力大学, 2013. FENG Yuan. Theoretical study on wide area source and load interactive scheduling mode[D]. Beijing: North China Electric Power University, 2013. (  0) 0) |
| [13] |
薛晨, 任景, 张小东, 等. 含虚拟储能的新能源高渗透电网深度调峰备用决策模型[J]. 中国电力, 2019, 52(11): 35-43. XUE Chen, REN Jing, ZHANG Xiaodong, et al. A reserve decision model for high-proportional renew energy integrated power grid based on deep peak-shaving and virtual storage[J]. Electric Power, 2019, 52(11): 35-43. (  0) 0) |
| [14] |
欧阳婷. 考虑需求响应资源的电网调峰模型与方法研究[D]. 北京: 华北电力大学, 2017. OUYANG Ting. Research on model and method of power peak regulation considering demand response resource[D]. Beijing: North China Electric Power University, 2017. (  0) 0) |
| [15] |
任大鹏. 源荷协调的调峰模式研究[D]. 北京: 华北电力大学, 2014. REN Dapeng. Study on the peak load regulation modes considering coordination between load and distributed generation[D]. Beijing: North China Electric Power University, 2014. (  0) 0) |
| [16] |
邓婷婷, 娄素华, 田旭, 等. 计及需求响应与火电深度调峰的含风电系统优化调度[J]. 电力系统自动化, 2019, 43(15): 34-41. DENG Tingting, LOU Suhua, TIAN Xu, et al. Optimal dispatch of power system integrated with wind power considering demand response and deep peak regulation of thermal power units[J]. Automation of Electric Power Systems, 2019, 43(15): 34-41. (  0) 0) |
| [17] |
张志, 邵尹池, 伦涛, 等. 电化学储能系统参与调峰调频政策综述与补偿机制探究[J]. 电力工程技术, 2020, 39(5): 71-77, 84. ZHANG Zhi, SHAO Yinchi, LUN Tao, et al. Review on the policies and compensation mechanism of BESS participation in the auxiliary service of frequency and peak modulation[J]. Electric Power Engineering Technology, 2020, 39(5): 71-77, 84. (  0) 0) |
| [18] |
杨超, 孙谊媊, 王勇, 等. 国外典型调频辅助服务市场综述与启示[J]. 电力需求侧管理, 2021, 23(5): 96-100. YANG Chao, SUN Yiqian, WANG Yong, et al. Review and enlightenment of foreign typical frequency regulation auxiliary service market[J]. Power Demand Side Management, 2021, 23(5): 96-100. (  0) 0) |
| [19] |
夏叶, 康重庆, 陈天恩, 等. 电力用户参与风电消纳的日前市场模式[J]. 电力系统自动化, 2015, 39(17): 120-126. XIA Ye, KANG Chongqing, CHEN Tian'en, et al. Day-ahead market mode with power consumers participation in wind power accommodation[J]. Automation of Electric Power Systems, 2015, 39(17): 120-126. (  0) 0) |
| [20] |
夏叶, 康重庆, 宁波, 等. 用户侧互动模式下发用电一体化调度计划[J]. 电力系统自动化, 2012, 36(1): 17-23. XIA Ye, KANG Chongqing, NING Bo, et al. A generation and load integrated scheduling on interaction mode on customer side[J]. Automation of Electric Power Systems, 2012, 36(1): 17-23. (  0) 0) |
| [21] |
李嘉龙, 陈雨果, 刘思捷, 等. 考虑深度调峰的电力日前市场机制设计[J]. 电力系统自动化, 2019, 43(4): 9-15, 78. LI Jialong, CHEN Yuguo, LIU Sijie, et al. Mechanism design of day-ahead market considering deep peak regulation[J]. Automation of Electric Power Systems, 2019, 43(4): 9-15, 78. (  0) 0) |
| [22] |
彭超逸, 顾慧杰, 朱文, 等. 交直流混联区域电网现货市场出清模型研究[J]. 电网技术, 2020, 44(1): 323-331. PENG Chaoyi, GU Huijie, ZHU Wen, et al. Study on spot market clearing model of regional power grid considering AC/DC hybrid connection[J]. Power System Technology, 2020, 44(1): 323-331. (  0) 0) |
2. Beijing TsIntergy Technology Co., Ltd., Beijing 100084, China
 2022, Vol. 41
2022, Vol. 41


 任景(1982), 女, 硕士, 高级工程师, 从事调度计划和新能源消纳管理工作(E-mail:
任景(1982), 女, 硕士, 高级工程师, 从事调度计划和新能源消纳管理工作(E-mail: