文章编号: 2096-3203(2022)01-0019-07 中图分类号: TM715;F426
2. 南京工程学院电力工程学院, 江苏 南京 211167
2015年,国务院出台《关于进一步深化电力体制改革的若干意见》(中发〔2015〕9号文),这标志着我国新一轮电改正式拉开帷幕。随着改革的深化,售电商必须全面了解用户需求,以用户为出发点,通过分时电价和激励引导用户积极参与用户响应,主动避峰用电,降低售电商的购电成本和风险,实现售电商与用户的双赢[1-4]。
近年来,售电套餐的优化设计是售电服务的研究重点。文献[5-6]以固定电价套餐为基础,优化设计了分时电价套餐、季节电价套餐等多种套餐。文献[7]建立以售电商利润最大化和工业用户成本最小化为目标的双层优化模型,通过算例仿真验证了该套餐有利于买卖双方的利益并起到削峰填谷的作用。文献[8]通过用户效用最大化模型和售电商利润最大化模型优化电力用户的用电量和售电商的购电决策,根据提出的用户贡献度指标,设计个性化的零售电价套餐。
需求侧响应分为价格型响应和激励型响应,可以提高电网经济运行效率[9]。文献[10-11]基于需求侧响应模型优化综合发电资源的调度。文献[12]基于需求侧响应提出了储能容量的识别方法。文献[13-15]基于需求侧响应减少电力用户的峰谷差,降低售电商参与中长期市场的购电成本,以此来优化设计售电套餐。
以上研究均未考虑需求侧响应对现货市场交易的影响,缺乏售电商参与现货市场交易的方法指导,因此文中设计基于售电商参与现货市场的售电套餐。首先,基于售电套餐激励计算电力用户的响应情况;然后,依据用户的需求响应情况建立电力用户套餐决策模型,并以套餐激励和用户避峰响应系数为决策变量、以售电商利益驱动量最大化为目标建立售电套餐的优化模型;最后,通过寻优算法求解目标优化函数。算例结果证明了套餐优化的可行性以及合理性。
1 需求侧响应以及套餐决策模型 1.1 假定条件(1) 电力负荷与现货市场的电价存在强耦合关系,即现货市场电价在用电负荷大的时段偏高。
(2) 不考虑谷时段用电量的加权系数时,电力用户会均匀转移负荷。
(3) 售电商通过中长期合约购买其所代理的电力用户的负荷,通过现货市场交易电力用户所转移的用电负荷。
(4) 电费占生产成本比例越大的电力用户越注重电费节省满意度,即电费占生产成本比例越大,电力用户对电费节省满意度赋予的权重越大。
1.2 用户避峰响应系数以及售电套餐激励分时电价是我国电价的一种重要形式,电力用户一般会按照峰谷平3个时段合理安排自己的生产。然而电力用户的负荷曲线仍然存在较大的峰谷差,须采取进一步的激励措施,提高用户转移负荷的积极性,以避峰用电。为了衡量用户的避峰用电行为,文中引入用户避峰响应系数,根据不同范围的避峰响应系数,售电商制定多种售电套餐激励,通过给予电力用户套餐自主选择权来吸引用户转移负荷。
| $ \mu_{i}^{\prime}=\frac{a q_{i, \mathrm{~g}}^{\prime}+(1-a) q_{i, \mathrm{p}}^{\prime}}{q_{i, \mathrm{f}}^{\prime}+q_{i, \mathrm{p}}^{\prime}+q_{i, \mathrm{~g}}^{\prime}} $ | (1) |
式中:μ′ i为套餐优化前用户i的避峰响应系数;a为谷时段用电量的加权系数;q′ i, f,q′ i, p,q′ i, g分别为套餐优化前用户i在峰时段、平时段、谷时段的用电量。
根据用户每日的避峰响应系数,售电商给予用户相应的电费激励。则用户每日的电费为:
| $ p_{i j}=\left(p_{\mathrm{f}} q_{i j, \mathrm{f}}+p_{\mathrm{p}} q_{i j, \mathrm{p}}+p_{\mathrm{g}} q_{i j, \mathrm{~g}}\right) x_{i j} $ | (2) |
式中:pij为用户i选择套餐j后的电费;pf,pp,pg分别为峰时段、平时段、谷时段电价;qij, f,qij, p,qij, g分别为用户i选择套餐j后在峰时段、平时段、谷时段的用电量;xij为电力用户i选择套餐j对应的激励系数。
1.3 基于售电套餐激励的需求侧响应为了满足售电套餐的要求,用户将部分峰时段用电量转移至平时段和谷时段。同时,负荷转移前后的总电量保持不变,则电力用户的峰、平、谷用电量为:
| $ \left\{\begin{array}{l} q_{i j, \mathrm{f}}=q_{i, \mathrm{f}}^{\prime}-\Delta q_{i j, \mathrm{fp}}-\Delta q_{i j, \mathrm{fg}} \\ q_{i j, \mathrm{p}}=q_{i, \mathrm{p}}^{\prime}+\Delta q_{i j, \mathrm{fp}} \\ q_{i j, \mathrm{g}}=q_{i, \mathrm{~g}}^{\prime}+\Delta q_{i j, \mathrm{fg}} \\ q_{i j, \mathrm{f}}+q_{i j, \mathrm{p}}+q_{i j, \mathrm{~g}}=q_{i, \mathrm{f}}^{\prime}+q_{i, \mathrm{p}}^{\prime}+q_{i, \mathrm{~g}}^{\prime} \end{array}\right. $ | (3) |
式中:Δqij, fp为峰平时段的负荷转移量;Δqij, fg为峰谷时段的负荷转移量。
为了引导电力用户积极转移负荷,售电商需要将电力用户的避峰响应系数分为数个范围来设计套餐,每一个套餐对应一个套餐激励。当电力用户将自身的避峰响应系数提高到售电商设定的避峰响应系数范围的最小值时,就可以获得套餐激励。如果电力用户在该避峰响应系数范围内继续提高自身的避峰响应系数,不仅无法获得额外的套餐激励,还会导致用电方式满意度下降。文中定义售电商设定的套餐的避峰响应系数范围的最小值为该套餐的避峰响应系数的标准值。套餐的避峰响应系数的标准值作为分段点,可以将电力用户的避峰响应系数划分为数个范围。
为了获得套餐激励,电力用户需要调整自身的用电量情况。随着电力用户平时段和谷时段用电量占比的增大,该用户的避峰响应系数也相应增大。因此,在初始用电负荷的基础上,电力用户将峰时段的用电量向平时段和谷时段转移,使负荷转移后的电力用户i的避峰响应系数等于其所选套餐的避峰响应系数的标准值,则:
| $ \frac{a\left(q_{i, \mathrm{~g}}^{\prime}+\Delta q_{i j, \mathrm{fg}}\right)+(1-a)\left(q_{i, \mathrm{p}}^{\prime}+\Delta q_{i j, \mathrm{fp}}\right)}{q_{i, \mathrm{f}}^{\prime}+q_{i, \mathrm{p}}^{\prime}+q_{i, \mathrm{~g}}^{\prime}}=\mu_{i j} $ | (4) |
式中:μij为用户i选择套餐j的避峰响应系数的标准值。
文中引入电力用户在不考虑谷时段用电量的加权系数时的转移负荷分配系数b。当0 < b < 0.5时,表示电力用户偏向于将负荷向平时段转移。当0.5 < b < 1时,表示电力用户偏向于将负荷向谷时段转移。则峰谷时段和峰平时段用电量转移为:
| $ \left\{\begin{array}{l} \Delta q_{i j, \mathrm{fg}}=\frac{b\left(\mu_{i j}-\mu_{i}^{\prime}\right)\left(q_{i, \mathrm{f}}^{\prime}+q_{i, \mathrm{p}}^{\prime}+q_{i, \mathrm{~g}}^{\prime}\right)}{a} \\ \Delta q_{i j, \mathrm{fp}}=\frac{(1-b)\left(\mu_{i j}-\mu_{i}^{\prime}\right)\left(q_{i, \mathrm{f}}^{\prime}+q_{i, \mathrm{p}}^{\prime}+q_{i, \mathrm{~g}}^{\prime}\right)}{1-a} \end{array}\right. $ | (5) |
通常,用效用函数来衡量用户对某一商品或服务的偏好,可以表示电力用户选择某一售电套餐后的满意度。根据电力用户对每种套餐的满意度,建立电力用户对售电套餐的决策模型。
效用函数包括电费节省满意度和用电方式改变满意度。电费节省满意度取决于初始电费和选择套餐后电费支出的差值,设定初始电费的电费满意度为1,电力用户转移负荷后,可获得套餐激励以及峰时段负荷转移节省的电费。电力用户负荷转移后电费与初始电费的差值越大,用户越倾向选择这个套餐。则电费节省满意度表示为[16]:
| $ B_{i j}=1+\delta \frac{p_{i}^{\prime}-p_{i j}}{p_{i}^{\prime}} $ | (6) |
式中:Bij为用户i选择套餐j的电费节省满意度;δ为节省的电费与用户满意度之间的比例系数;p′ i为用户i每日初始电费;pij为用户i选择套餐j后的电费。
以初始用电方式的满意度为标准值,设定为1。当电力用户为了获得需求侧响应激励而进行负荷转移时,与初始负荷曲线相比,新的负荷曲线产生部分偏移,造成满意度下降。因此,用该偏移量衡量用户用电方式改变满意度,其表达式如下[17]:
| $ \begin{gathered} C_{i j}=1-\varepsilon_{i}\left(\left|q_{i j, \mathrm{f}}-q_{i, \mathrm{f}}^{\prime}\right|+\right. \\ \left.\left|q_{i j, \mathrm{p}}-q_{i, \mathrm{p}}^{\prime}\right|+\left|q_{i j, \mathrm{~g}}-q_{i, \mathrm{~g}}^{\prime}\right|\right)^{\theta_{i}} \end{gathered} $ | (7) |
式中:Cij为用户i选择套餐j的用电方式改变满意度;εi为用电方式偏移量与用户满意度之间的比例系数;θi为用电方式偏移量与用户满意度之间的指数系数。
综上可知,效用的表达式如下:
| $ U_{i j}=\gamma_{i} B_{i j}+\left(1-\gamma_{i}\right) C_{i j} $ | (8) |
式中:Uij为用户i选择套餐j的效用;γi为用户i对电费支出满意度赋予的权重,反映不同类型的用户对电费支出和用电方式改变的重视程度不同。
根据电力用户选择各个售电套餐所带来的效用,售电商可以选择初始售电套餐,也可以选择优化后的各种售电套餐。而初始售电套餐的用户效用为1,用户效用越大,用户选择的概率就越大。则用户对售电套餐的决策模型如下[18]:
| $ d_{i j}=\mathrm{e}^{\beta U_{i j}} /\left(\mathrm{e}^{\beta}+\sum\limits_{j=1}^{K} \mathrm{e}^{\beta U_{i j}}\right) $ | (9) |
式中:dij为用户i选择套餐j的概率;β为用户效用与套餐决策概率之间的比例系数;K为优化后的售电套餐数。
2 现货市场交易下售电套餐优化模型与发电商不同,售电商参与电力现货市场,既可以卖电,也可以买电。售电商通过套餐激励引导电力用户将峰时段负荷往平时段和谷时段转移,通过现货市场卖出峰时段负荷转移量并购买谷时段负荷转移量,以此来提高售电商利益。文中以用户避峰响应系数标准值和套餐激励系数为决策变量,以售电商利益驱动量最大化为目标函数,建立基于售电商参与现货市场的售电套餐优化模型,即:
| $ \begin{gathered} \max E=\sum\limits_{i=1}^{L} \sum\limits_{j=1}^{K}\left\{\left[\left(\Delta q_{i j, \mathrm{fp}} \Delta p_{\mathrm{fp}}+\Delta q_{i j, \mathrm{fg}} \Delta p_{\mathrm{fg}}\right)-\right.\right. \\ \left.\left.\left(p_{i}^{\prime}-p_{i j}\right)\right] d_{i j}\right\} \end{gathered} $ | (10) |
式中:E为售电商套餐优化的利益驱动量;L为电力用户数;Δpfp为现货市场峰时段和平时段的平均电价差;Δpfg为现货市场峰时段和谷时段的平均电价差。
约束条件如下:(1) 用户避峰响应系数约束。用户会根据自身用电习惯选择适合自己的售电套餐并转移负荷。因此套餐优化后的用户避峰响应系数标准值不小于套餐优化前的用户避峰系数,即:
| $ \mu_{j} \geqslant \mu_{i}^{\prime} $ | (11) |
式中:μj为套餐j的用户避峰响应系数标准值。
考虑到极端的情况,当电力用户将所有用电负荷转移到谷时段时,该用户避峰响应系数最大,即:
| $ \mu_{j}^{\prime}=\frac{a q_{i, \mathrm{~g}}+(1-a) q_{i, \mathrm{p}}}{q_{i, \mathrm{f}}+q_{i, \mathrm{p}}+q_{i, \mathrm{~g}}}=a $ | (12) |
式中:μ′ j为极端情况下的避峰响应系数标准值。
售电商设计的套餐的用户避峰响应系数标准值需要小于极端情况下的用户避峰系数,即:
| $ \mu_{j}<a $ | (13) |
(2) 用户响应激励系数约束。用户避峰响应系数越大,售电商给予的用户响应激励系数越小,为此设定第j+1个售电套餐的避峰响应系数大于第j个售电套餐的避峰响应系数,第j+1个售电套餐的激励系数小于第j个售电套餐的激励系数,则应当满足以下约束:
| $ \mu_{j+1}>\mu_{j} $ | (14) |
| $ x_{j+1}<x_{j} $ | (15) |
| $ 0<x_{j}<1 $ | (16) |
式中:xj为第j个售电套餐的套餐激励;μj+1,xj+1分别为第j+1个售电套餐的避峰响应系数标准值和套餐激励。
3 模型求解为验证套餐优化模型的可行性,文中采用混沌粒子群优化(chaos particle swarm optimization,CPSO)算法对目标优化函数进行寻优。CPSO算法在粒子群的每次迭代中都对每个粒子进行混沌映射,避免粒子群迭代时陷入局部,与传统的遗传算法(genetic algorithm,GA)和粒子群优化(particle swarm optimization,PSO)算法相比,CPSO算法提高了算法的搜索速度和精度[19-22]。CPSO算法采用一维混沌Logistic映射,如式(17)所示。
| $ y_{t+1}=\nu y_{t}\left(1-y_{t}\right) $ | (17) |
式中:yt, yt+1分别为第t次,第t+1次迭代的混沌Logistic映射值;ν为控制系数。
通过混沌序列对粒子的位置和算法的惯性因子进行混沌映射,如式(18)、式(19)所示。
| $ z_{t}=y_{t}\left(z_{\max }-z_{\min }\right)+z_{\min } $ | (18) |
| $ \omega= \begin{cases}\omega_{\min }+\frac{\left(\omega_{\max }-\omega_{\min }\right)\left(\lambda_{k}-\lambda_{\min }\right)}{\lambda_{\mathrm{av}}-\lambda_{\min }} & \lambda_{k} \leqslant \lambda_{\mathrm{av}} \\ \omega_{\min } \lambda_{k}>\lambda_{\mathrm{av}} & \end{cases} $ | (19) |
式中:zt为第t次迭代时粒子的位置;zmax,zmin分别为初始化设置的粒子位置极大值和极小值;ω为算法的惯性权重;ωmax,ωmin分别为初始化设置的惯性权重极大值和极小值;λk为粒子k的适应度;λav为粒子群适应度的平均值;λmin为粒子群适应度的最小值。
算法主要流程如下。
步骤1:用户数据初始化,算法参数初始化。
步骤2:进入迭代循环。
步骤3:根据式(17)—式(19)混沌初始化粒子群的位置和惯性权重。
步骤4:根据式(3)—式(5)计算用户的需求侧响应。
步骤5:根据式(6)—式(9)计算用户的售电套餐决策模型。
步骤6:根据式(10)计算目标函数值,确定个体最优位置和全局最优位置。
步骤7:判断是否达到最大迭代次数,若是,则结束迭代,否则根据算法规则,更新粒子位置和速度,返回步骤2重新计算。
4 套餐优化模型下的算例分析 4.1 参数设定文中选取某地区电力用户的典型日负荷曲线作为用户负荷的初始数据,通过K-means聚类法可将用户分为3类典型日负荷曲线。第1类用户为早高峰型,第2类用户为晚高峰型,第3类用户为双峰型,如图 1所示。
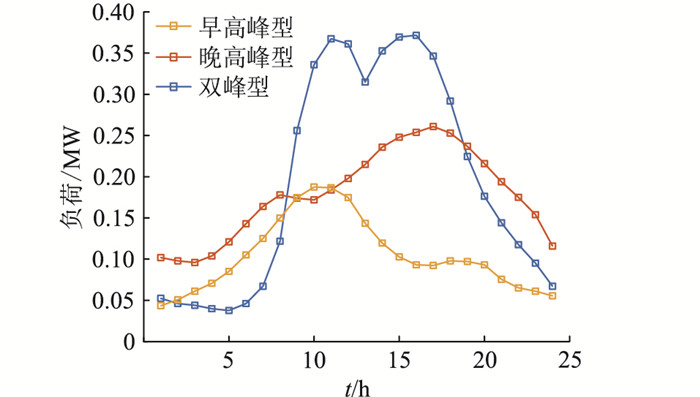
|
图 1 不同类型的用户负荷 Fig. 1 Different types of user load |
电力现货市场以日为市场交易周期,采用集中出清的交易形式,产生面向次日各个时段的分时电价。2019年,中国在广东等8个试点地区的电力现货市场基本建成,目前均已完成了电力现货市场交易机制的构建并实现了月度以上的试运营阶段[23]。图 2为广东电力现货市场某一周的实时电价曲线,由图 2可知,现货市场的实时价格在一天中波动剧烈,并且峰值通常出现在白天用电高峰期,谷值出现在晚上用电低谷期,峰谷差明显。
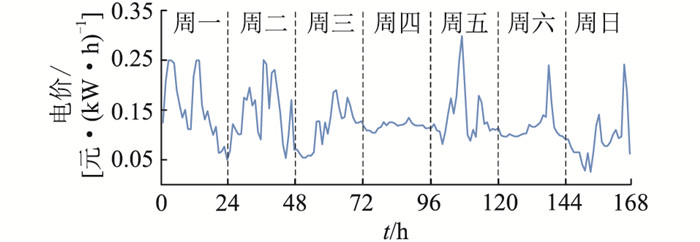
|
图 2 广东现货市场实时电价 Fig. 2 Real-time electricity price in Guangdong spot market |
随着电力现货市场的成熟,参与市场交易的主体增加,现货市场竞争愈发激烈,峰谷电价差进一步增加。综合考虑,文中设定现货市场峰平电价差为0.5元/(kW ·h)、峰谷电价差为1.0元/(kW ·h)。
由于现货市场的市场价格与电力用户的用电负荷存在强耦合关系,根据某地区的电力现货市场的市场价格和电力用户的用电负荷情况划分峰、平、谷时段,如表 1所示。
|
|
表 1 分时电价的时段划分与价格 Table 1 Time division and price of time-of-use electricity price |
分别使用CPSO算法、PSO算法、GA求解目标函数,其迭代过程如图 3所示。由图可知,CPSO算法的收敛速度和精度明显优于PSO算法和GA。
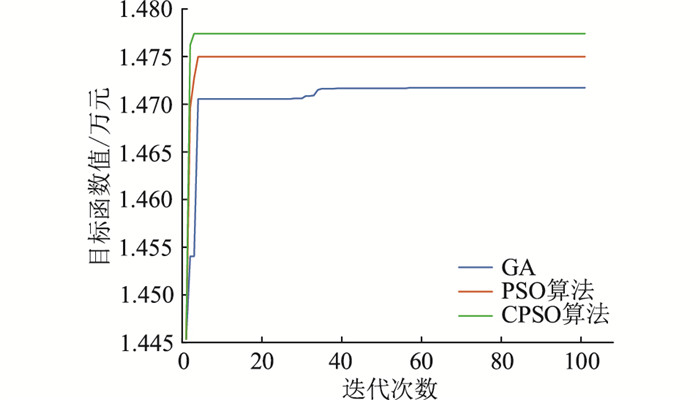
|
图 3 不同算法迭代过程对比 Fig. 3 Comparison of iterative process based on different algorithms |
通过CPSO算法求解用户避峰响应系数标准值和套餐激励系数,得到最优售电套餐,如表 2所示。
|
|
表 2 售电套餐优化设计 Table 2 Optimized design of electricity sales package |
根据优化设计的售电套餐的避峰响应系数标准值,如果电力用户选择相应的套餐,需要转移负荷以满足套餐的要求,3类电力用户分别选择4种售电套餐所需的负荷转移量构成12种情景,如图 4所示。由图 4可知,电力用户希望获得的套餐激励越多,其转移负荷就越大。同时,电力用户偏向于将电力负荷从峰时段往与之相邻的平时段转移,平时段的用电增量要高于谷时段的用电增量。
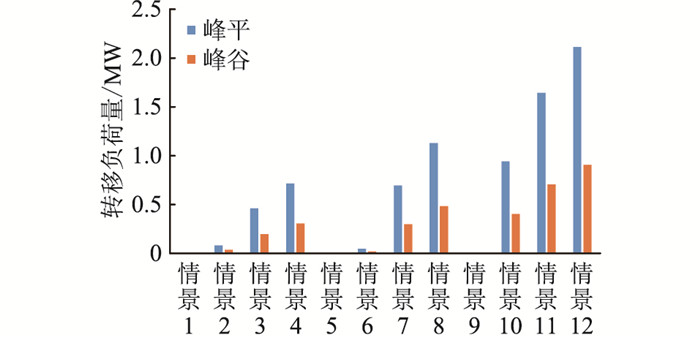
|
图 4 用户负荷转移量 Fig. 4 Transfer volume of user load |
根据电力用户选择售电套餐的负荷转移情况,计算出3类电力用户选择4种售电套餐的电费节省满意度和用电方式满意度,如表 3和表 4所示。由表 3和表 4可知,电力用户选择套餐4的电费节省满意度最高,选择套餐1的电费节省满意度最低。而选择套餐4的用电方式满意度最低,选择套餐1的用电方式满意度最高。
|
|
表 3 电力用户电费节省满意度 Table 3 Satisfaction of power users with electricity charges |
|
|
表 4 电力用户用电方式满意度 Table 4 Satisfaction situation of power users |
根据每一类用户转移负荷导致的电费节省满意度的提高和用电方式满意度的下降,计算每一类用户的效用,并得到3类用户的套餐决策情况,如表 5所示。
|
|
表 5 电力用户的套餐决策 Table 5 Package decision of power users |
由表 5可知,第1类电力用户作为早高峰型用户,其用户效用更注重用电方式满意度,选择套餐2的概率最大。第2类电力用户作为晚高峰型用户,其用户效用均衡考虑用电方式满意度和电费节省满意度,选择套餐3的概率最大。第3类电力用户作为双峰型用户,其用户效用注重电费节省满意度,选择套餐4的概率最大。4.4售电商的套餐优化的利益驱动分析
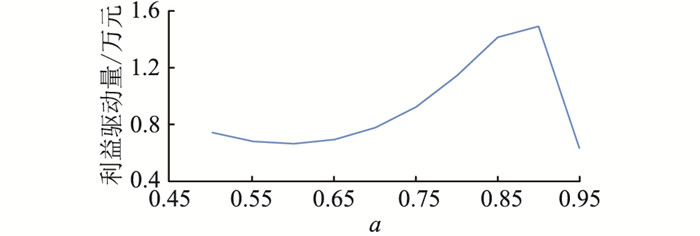
谷时段加权系数a影响着用户的负荷转移情况,a越大,电力用户的峰谷负荷转移量越大。通过改变系数a的取值,计算售电商的利益驱动量,得到利益驱动量随系数a的变化情况如图 5所示。由图 5可知,当系数a增长时,电力用户偏向于将负荷往谷时段转移,这样不但能节省更多的电费,还可以最低限度地改变用电方式。但是当a>0.9时,电力用户想要获得套餐激励需要向谷时段大量转移用电负荷,导致用电方式满意度过低而使用户的负荷转移积极性下降,用户将更愿意选择原套餐,售电商的利益驱动量快速下降。售电商设计售电套餐时需要注意指标的制定,避免损害售电商和电力用户的利益。
|
图 5 售电商利益驱动量 Fig. 5 Profit-driven volume of sellers |
文中从售电商参与现货市场交易的角度提出一种提高售电商利益的方法。首先,从用户侧出发,分析了电费支出和用电方式对用户效用的影响,并以此建立用户的售电套餐决策模型。然后,分析售电商优化套餐的利益驱动,以此为目标函数优化设计多种售电套餐,促使电力用户积极转移负荷,提高售电商的利益,并减小用户负荷曲线的峰谷差,实现削峰填谷。这为售电服务的发展提供可靠的依据和实际参考,为售电商开展业务提供新的思路。同时,文中在分析现货市场价格的实时电价情况时存在一定的局限性,忽略了现货市场价格的波动对售电套餐优化的影响。未来可以利用大数据对现货市场的实时电价进行预测,建立实时电价的动态指标,通过预测的实时电价优化设计售电套餐。
本文得到江苏省高校哲学社会科学研究重点项目(2018SJZDI097),江苏省高校哲学社会科学优秀创新团队建设项目(2017ZSTD025)资助,谨此致谢!
| [1] |
林卫斌, 李妙华, 陈昌明. 新一轮电力体制改革的逻辑与进展[J]. 价格理论与实践, 2016(9): 8-13. LIN Weibin, LI Miaohua, CHEN Changming. The logic and progress of the new round of power system reform[J]. Price: Theory & Practice, 2016(9): 8-13. (  0) 0) |
| [2] |
丁一, 惠红勋, 林振智, 等. 面向电力需求侧主动响应的商业模式及市场框架设计[J]. 电力系统自动化, 2017, 41(14): 2-9, 189. DING Yi, HUI Hongxun, LIN Zhenzhi, et al. Design of business model and market framework oriented to active demand response of power demand side[J]. Automation of Electric Power Systems, 2017, 41(14): 2-9, 189. DOI:10.7500/AEPS20170218001 (  0) 0) |
| [3] |
王宝, 叶斌, 朱刘柱, 等. 市场环境下我国电力需求响应实践与探索[J]. 电力需求侧管理, 2021, 23(5): 91-95. WANG Bao, YE Bin, ZHU Liuzhu, et al. Practice and exploration of China's power demand response in electricity market[J]. Power Demand Side Management, 2021, 23(5): 91-95. DOI:10.3969/j.issn.1009-1831.2021.05.018 (  0) 0) |
| [4] |
高政南, 周飞航, 葛根塔娜, 等. 多维电力市场风险综合评价研究[J]. 电力需求侧管理, 2021, 23(6): 26-30. GAO Zhengnan, ZHOU Feihang, GE Gentana, et al. Research on comprehensive evaluation of multi dimensional power market's risks[J]. Power Demand Side Management, 2021, 23(6): 26-30. DOI:10.3969/j.issn.1009-1831.2021.06.006 (  0) 0) |
| [5] |
焦哲. 新电改条件下负荷特性及零售电价套餐设计分析[D]. 北京: 华北电力大学, 2019. JIAO Zhe. Load characteristic and retail price package design and analysis under the new electricity reform conditions[D]. Beijing: North China Electric Power University, 2019. (  0) 0) |
| [6] |
初保驹, 朱少林. 新电改背景下阶梯分时电价模型优化研究[J]. 价格理论与实践, 2020(2): 43-46, 174. CHU Baoju, ZHU Shaolin. Research on optimization of stepped time-of-use electricity price model under the background of new electricity reform[J]. Price: Theory & Practice, 2020(2): 43-46, 174. (  0) 0) |
| [7] |
曹敏, 段艳娜, 贾天圣, 等. 工业园区配售电公司分时电价双层优化模型[J]. 数学的实践与认识, 2019, 49(17): 132-143. CAO Min, DUAN Yanna, JIA Tiansheng, et al. Bi-level programming model of time-of-use power price for distribution companies in industrial estate[J]. Mathematics in Practice and Theory, 2019, 49(17): 132-143. (  0) 0) |
| [8] |
窦迅, 王俊, 邵平, 等. 考虑用户贡献度的售电商购售电策略[J]. 电网技术, 2019, 43(8): 2752-2760. DOU Xun, WANG Jun, SHAO Ping, et al. Purchase-sale strategy of power retailers considering user contribution degree[J]. Power System Technology, 2019, 43(8): 2752-2760. (  0) 0) |
| [9] |
曾博, 杨雍琦, 段金辉, 等. 新能源电力系统中需求侧响应关键问题及未来研究展望[J]. 电力系统自动化, 2015, 39(17): 10-18. ZENG Bo, YANG Yongqi, DUAN Jinhui, et al. Key issues and research prospects for demand-side response in alternate electrical power systems with renewable energy sources[J]. Automation of Electric Power Systems, 2015, 39(17): 10-18. (  0) 0) |
| [10] |
刘旭, 杨德友, 刘铖, 等. 考虑用户满意度的含风电场多目标环境经济调度[J]. 现代电力, 2017, 34(3): 44-51. LIU Xu, YANG Deyou, LIU Cheng, et al. Multi-objective economic emission dispatching for power grid integrated with wind farms by considering customers' satisfaction[J]. Modern Electric Power, 2017, 34(3): 44-51. (  0) 0) |
| [11] |
朱伟业, 罗毅, 胡博, 等. 热负荷弹性与分时电价需求侧响应协同促进碳减排的电热优化调度[J]. 电网技术, 2021, 45(10): 3803-3813. ZHU Weiye, LUO Yi, HU Bo, et al. Thermal load elasticity and time-of-use electricity price demand-side response synergistically promote optimal electric and thermal dispatch for carbon emission reduction[J]. Power System Technology, 2021, 45(10): 3803-3813. (  0) 0) |
| [12] |
方逸波, 袁晓冬, 费骏韬, 等. 基于需求侧响应的配电网储能容量识别[J]. 电力工程技术, 2019, 38(6): 61-68. FANG Yibo, YUAN Xiaodong, FEI Juntao, et al. Capacity identification of energy storage in distribution grids based on demand response[J]. Electric Power Engineering Technology, 2019, 38(6): 61-68. (  0) 0) |
| [13] |
肖白, 崔涵淇, 姜卓, 等. 基于有限理性用户选择行为的定制化电价套餐设计[J]. 电网技术, 2021, 45(3): 1050-1058. XIAO Bai, CUI Hanqi, JIANG Zhuo, et al. Customized electricity price package design based on limited rational user selection behavior[J]. Power System Technology, 2021, 45(3): 1050-1058. (  0) 0) |
| [14] |
张智, 卢峰, 林振智, 等. 考虑用户有限理性的售电公司峰谷组合电力套餐设计[J]. 电力系统自动化, 2021, 45(16): 114-123. ZHANG Zhi, LU Feng, LIN Zhenzhi, et al. Design of peak-valley combined power package of electricity sales company considering user's bounded rationality[J]. Automation of Electric Power System, 2021, 45(16): 114-123. (  0) 0) |
| [15] |
侯佳萱, 林振智, 杨莉, 等. 面向需求侧主动响应的工商业用户电力套餐优化设计[J]. 电力系统自动化, 2018, 42(24): 11-19. HOU Jiaxuan, LIN Zhenzhi, YANG Li, et al. Design of electricity plans for industrial and commercial customers oriented to active demand response on power demand side[J]. Automation of Electric Power Systems, 2018, 42(24): 11-19. (  0) 0) |
| [16] |
丁伟, 袁家海, 胡兆光. 基于用户价格响应和满意度的峰谷分时电价决策模型[J]. 电力系统自动化, 2005, 29(20): 14-18. DING Wei, YUAN Jiahai, HU Zhaoguang. Time-of-use price decision model considering users reaction and satisfaction index[J]. Automation of Electric Power Systems, 2005, 29(20): 14-18. (  0) 0) |
| [17] |
王刚, 董亦华, 王珂, 等. 计及网络约束的发用电一体化综合优化调度模型[J]. 电力系统自动化, 2017, 41(14): 105-111. WANG Gang, DONG Yihua, WANG Ke, et al. Comprehensive optimal scheduling model for integration of power generation and consumption considering network constraints[J]. Automation of Electric Power Systems, 2017, 41(14): 105-111. (  0) 0) |
| [18] |
聂冲, 贾生华. 离散选择模型的基本原理及其发展演进评介[J]. 数量经济技术经济研究, 2005, 22(11): 151-159. NIE Chong, JIA Shenghua. Research on the theoretical basis and evolution of discrete choice models[J]. Quantitative & Technica Economics, 2005, 22(11): 151-159. (  0) 0) |
| [19] |
周立栋. 基于改进混沌粒子群算法的多源微网优化运行模型[D]. 北京: 华北电力大学, 2018. ZHOU Lidong. The optimized operation model of multi-sources micro-grid based on modified chaos particle swarm optimization algorithm[D]. Beijing: North China Electric Power University, 2018. (  0) 0) |
| [20] |
余明明. 基于混沌粒子群算法的大型水电站自动电压控制优化研究[D]. 武汉: 华中科技大学, 2013. YU Mingming. The study of automatic voltage control in large-scale hydro power station based on chaos particle swarm optimization[D]. Wuhan: Huazhong University of Science and Technology, 2013. (  0) 0) |
| [21] |
司风琪, 顾慧, 叶亚兰, 等. 基于混沌粒子群算法的火电厂厂级负荷在线优化分配[J]. 中国电机工程学报, 2011, 31(26): 103-109. SI Fengqi, GU Hui, YE Yalan, et al. Online unit load economic dispatch based on chaotic-particle swarm optimization algorithm[J]. Proceedings of the CSEE, 2011, 31(26): 103-109. (  0) 0) |
| [22] |
贠保记, 白森珂, 张国. 基于混沌自适应粒子群算法的冷热电联供系统优化[J]. 电力系统保护与控制, 2020, 48(10): 123-130. YUN Baoji, BAI Senke, ZHANG Guo. Optimization of CCHP system based on a chaos adaptive particle swarm optimization algorithm[J]. Power System Protection and Control, 2020, 48(10): 123-130. (  0) 0) |
| [23] |
关玉衡, 何宇俊, 肖云鹏, 等. 广东电力现货市场环境下的需求响应交易机制设计[J]. 电力需求侧管理, 2021, 23(6): 15-20. GUAN Yuheng, HE Yujun, XIAO Yunpeng, et al. Design of demand response trading mechanism under Guangdong spot energy market environment[J]. Power Demand Side Management, 2021, 23(6): 15-20. (  0) 0) |
2. School of Electrical Engineering, Nanjing Institute of Technology, Nanjing 211167, China
 2022, Vol. 41
2022, Vol. 41


 刘秋华(1963), 女, 博士, 教授, 研究方向为电力市场需求侧分析(E-mail:
刘秋华(1963), 女, 博士, 教授, 研究方向为电力市场需求侧分析(E-mail: