文章编号: 2096-3203(2022)01-0108-09 中图分类号: TM61
极地地区蕴含丰富的自然资源,具有较强的科考价值,许多国家在极地设立科考站进行科学考察。极地环境气象十分复杂,常年低温且伴有极夜现象,因此大多数科考站依旧依靠柴油发电机进行供电,对极地环境造成严重污染。此外,在极地的极端低温环境下,柴油发电机效率较低,燃料流动性差,清理工作极其困难,使用寿命受到很大影响。根据极地特殊的地理位置和气象环境,利用可再生能源代替传统柴油发电机进行供电迫在眉睫[1-4]。极地一整年中有一半时间处于极夜,光照资源不足,且环境气温较低,因此无法在极地利用光伏系统供电。但极地地理位置独特,风资源十分丰富,因此采用风力发电作为主要电源是解决极地环境供电的有效方式[5]。
独立微电网系统中常以蓄电池作为储能装置,极地低温环境下,若采用大量的蓄电池作为储能装置将会降低供电系统的经济性[6-8],且蓄电池存在自放电问题,不能长期储存电能。氢气作为清洁能源,可直接通过电解水获得,易于储存,且其作为燃料发电只产生电能和水。文献[9]提出风氢系统,将风机产生的多余电能通过电解槽电解水制氢储存,然后以氢气作为燃料,利用燃料电池对微网系统进行供电。文献[10]提出将氢作为储能介质,利用燃氢燃气轮机弥补风电不足,以安装成本最低、负载缺电率(loss of load probability,LPSP)与风氢互补系统输出功率波动率最小为目标对供电系统容量进行优化配置。
在诸多微电网规划设计中,为了简化模型而忽略了相关环境条件对微电网系统的影响。文中考虑低温环境对风机输出功率、蓄电池容量以及用电负荷的影响,提出利用富余风电制氢,并配置蓄电池储能装置的风氢储微电网容量优化模型;研究了含风机、蓄电池储能、燃料电池、电解槽、储氢罐的极地低温环境下独立微电网供电系统容量优化配置方法;以年度平均成本最小为目标,全年LPSP为约束,对极地环境下风氢储微电网系统进行容量优化配置。
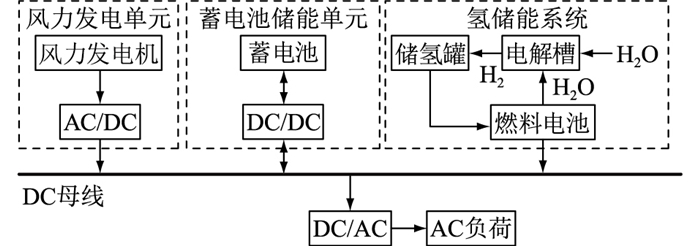
1 极地环境风氢储微电网电源模型 1.1 微电网系统结构微电网系统主要由风机、蓄电池储能装置、燃料电池、电解槽、储氢罐、逆变器及本地负荷组成[11-13],其系统结构如图 1所示。氢储能系统的充电优先级高于蓄电池储能系统,当风机出力大于负荷时,利用富余风电制氢储存后对蓄电池储能装置进行充电。在负荷高峰期,利用蓄电池及燃料电池对系统进行供电,燃料电池的供电优先级大于蓄电池。即当风机出力小于负荷,且储氢罐储氢量大于其下限时,优先启用燃料电池供电,启用燃料电池后,缺额功率由蓄电池提供。当储氢量低于允许下限时,停用燃料电池发电,缺额功率由蓄电池补偿。
|
图 1 风氢储微电网系统结构 Fig. 1 Structure of wind-hydrogen-storage microgrid system |
随着高度的不断变化,风速也会相应地发生改变,因此须对所测量的风速数据进行修正[14]。风速随高度的变化可以用对数定律进行修正,假定风速与地面以上高度的对数成正比,则风力发电机轮毂高度处的风速与测量风速之比为:
| $ \frac{v}{v_{1}}=\frac{\ln \left(z / z_{0}\right)}{\ln \left(z_{1} / z_{0}\right)} $ | (1) |
式中:v为风机轮毂所在高度处的实际风速;v1为所测量的实际风速;z1为风力计所在高度;z为风机实际安装高度;z0为地面粗糙度,由于极地地区地势平坦,故文中取0.003。
1.2.2 极地低温环境下风机输出功率修正由于低温环境会对风机实际出力产生一定影响,因此须对风机的输出功率进行修正。对于一台特定的风力发电机,其输出功率为:
| $ P_{\mathrm{WT}}=\frac{1}{8} \rho D^{2} v^{3} C_{\mathrm{p}} \eta_{\mathrm{WT}} $ | (2) |
式中:PWT为风机输出功率;ρ为空气密度;D为风轮直径;CP为风能利用系数;ηWT为风机效率。
风速一定时,修正后风机输出功率与标准状况下输出功率之比为:
| $ \frac{P_{\mathrm{WT}}}{P_{\mathrm{WT} 0}}=\frac{\frac{1}{8} \rho D^{2} v^{3} C_{\mathrm{p}} \eta_{\mathrm{WT}}}{\frac{1}{8} \rho_{0} D^{2} v^{3} C_{\mathrm{p}} \eta_{\mathrm{WT}}}=\frac{\rho}{\rho_{0}} $ | (3) |
其中:
| $ \rho=\frac{p}{R T} $ | (4) |
式中:PWT0为标准状况下风机输出功率;ρ0为标准状况下空气密度,取1.255 kg/m3;p为大气压,通过查询计算得中山站年平均气压为981.64 hPa;T为温度;R为普适气体常数。
标准气温、气压下一般典型风机的输出功率与风速之间关系可以表示如下[15-17]:
| $ P_{\mathrm{WT} 0}=\left\{\begin{array}{l} a P_{\mathrm{r}} \quad v_{\mathrm{ci}} \leqslant v \leqslant v_{\mathrm{r}} \\ P_{\mathrm{r}} \quad v_{\mathrm{r}}<v \leqslant v_{\mathrm{co}} \\ 0 \quad v<v_{\mathrm{ci}} \text { 或 } v>v_{\mathrm{co}} \end{array}\right. $ | (5) |
| $ a=\frac{v^{3}-v_{\mathrm{ci}}^{3}}{v_{\mathrm{r}}^{3}-v_{\mathrm{ci}}^{3}} $ | (6) |
式中:Pr为风机额定功率;vci为切入风速;vco为切出风速;vr为额定风速。
一般低温型风机运行温度为-30~40 ℃,故将正常运行最低温度设置为-30 ℃。结合式(3),修正后的风机输出功率为:
| $ P_{\mathrm{WT}}=\left\{\begin{array}{l} \frac{\rho}{\rho_{0}} P_{\mathrm{WT0}} \quad T(t) \geqslant-30℃ \\ 0 \quad T(t)<-30℃ \end{array}\right. $ | (7) |
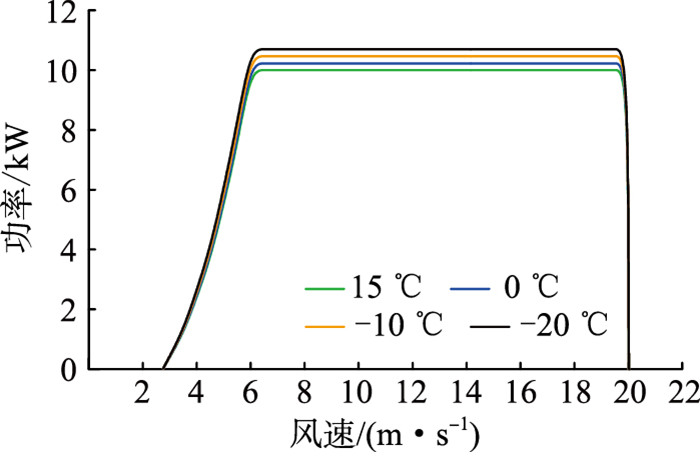
由于极地环境复杂且运输不便,为方便运输安装及维护,文中选用小型风机,额定功率10 kW,轮毂高度16 m,切入风速2.75 m/s,额定风速6 m/s,切出风速20 m/s。图 2为不同低温环境下风机功率特性曲线。
|
图 2 不同温度下风机功率特性 Fig. 2 Power characteristics of wind turbines at different temperatures |
氢储系统包含电解槽、储氢罐以及燃料电池三部分。文中利用风机产生的富余电量,采用碱式电解槽电解水制氢,以压缩气态方式储氢。当风机出力不足时,利用燃氢燃料电池对微网系统进行供电。
燃料电池输出功率PFC为:
| $ P_{\mathrm{FC}}=\eta_{\mathrm{FC}} Q_{\mathrm{H}} / \mu $ | (8) |
式中:ηFC为燃料电池效率;QH为氢气进气量;μ为燃料电池生产1 kW·h电能所需氢气量。
电解槽电解水制氢模型可表示为:
| $ Q_{\mathrm{E}}=\eta_{\mathrm{E}} P_{\mathrm{E}} \xi $ | (9) |
式中:QE为制氢量;ηE为电解槽效率;PE为电解槽输入功率;ξ为1 kW·h电能制氢量。
储氢罐t时刻的容量大小QTank(t)为:
| $ Q_{\mathrm{Tank}}(t)=Q_{\mathrm{Tank}}(t-\Delta t)+Q_{\mathrm{E}}(t) \Delta t-\frac{P_{\mathrm{FC}}(t) \mu \Delta t}{\eta_{\mathrm{FC}} \eta_{\mathrm{Tank}}} $ | (10) |
式中:ηTank为储氢罐效率。文中燃料电池的额定功率为100 kW, 寿命为20 a。单个电解槽最大输入功率PE, max=50 kW, ηE=70%, ξ=0.127 Nm3/(kW·h)。单个储氢罐体积5 m3, 最大储氢量为500 Nm3,储氢罐初始容量为0。
1.4 蓄电池储能模型采用蓄电池作为储能元件,蓄电池容量对温度极其敏感,由于极地环境气温极低,故在规划建设中须考虑极地气温环境对蓄电池储能装置的影响。蓄电池实际容量与温度的关系如下[18]:
| $ C_{\mathrm{bat}}(T)=C_{\mathrm{STC}}\left[1+k\left(T-T_{\mathrm{STC}}\right)\right] $ | (11) |
式中:Cbat(T)为蓄电池在环境温度为T时的实际容量;CSTC为标准状况下蓄电池额定容量;k为温度系数,取值约为0.005~0.008 ℃-1;TSTC为标准状况下温度,取25 ℃。
蓄电池充电条件及充电状态模型为:
| $ \left\{\begin{array}{l} P_{\mathrm{WT}}(t) \eta_{\mathrm{inv}}-P_{\mathrm{load}}(t)>0 \\ C_{\mathrm{bat}}(t-1)<C_{\mathrm{bat}, \mathrm{max}} \end{array}\right. $ | (12) |
| $ \begin{aligned} &C_{\mathrm{bat}}(t)=(1-\delta) C_{\mathrm{bat}}(t-1)+ \\ &\quad\left(P_{\mathrm{WT}}(t) \eta_{\mathrm{inv}}-P_{\mathrm{load}}(t)\right) \eta_{\mathrm{c}} \end{aligned} $ | (13) |
蓄电池放电条件及放电状态模型为:
| $ \left\{\begin{array}{l} \left(P_{\mathrm{WT}}(t)+P_{\mathrm{FC}}(t)\right) \eta_{\mathrm{inv}}-P_{\mathrm{load}}(t)<0 \\ C_{\mathrm{bat}}(t-1)>C_{\mathrm{bat}, \min } \end{array}\right. $ | (14) |
| $ \begin{gathered} C_{\mathrm{bat}}(t)=(1-\delta) C_{\mathrm{bat}}(t-1)+ \\ {\left[\left(P_{\mathrm{WT}}(t)+P_{\mathrm{FC}}(t)\right) \eta_{\mathrm{inv}}-P_{\mathrm{load}}(t)\right] / \eta_{\mathrm{d}}} \end{gathered} $ | (15) |
式中:Cbat(t),Cbat(t-1)分别为t时刻,t-1时刻蓄电池储能大小;Cbat,max,Cbat,min分别为蓄电池的最大、最小容量;Pload(t)为t时刻的负载功率;δ为蓄电池自放电率;ηc,ηd分别为蓄电池的充、放电效率;ηinv为变换器效率,文中为98%;PWT(t)为t时刻风机输出功率。
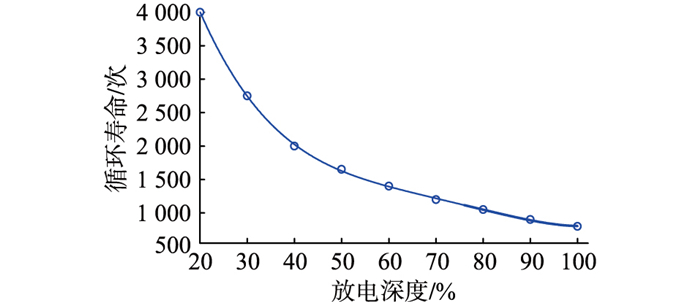
选用蓄电池类型为铅酸蓄电池,其额定容量为5 kW·h,最大放电功率为5 kW,充放电效率为97%,自放电率为0.01%, 蓄电池使用寿命根据等效循环次数进行计算,计算过程参考文献[19],蓄电池放电深度与循环寿命关系如图 3所示。
|
图 3 放电深度与循环寿命对应关系 Fig. 3 Correspondence between depth of discharge and cycle life |
微电网容量优化配置的目的是使微电网系统成本和可靠性指标达到一个最佳平衡点。采用年度平均成本Cacs作为微电网系统的经济性评价指标[20],其表示如下:
| $ C_{\mathrm{acs}}=\min \left(C_{\mathrm{ic}}+C_{\mathrm{rc}}+C_{\mathrm{mc}}\right) $ | (16) |
式中:Cic,Crc,Cmc分别为微网系统的年度初始投资成本、年度置换成本和年度运维成本。
2.1.1 年度初始投资成本极地环境温度低,对蓄电池容量及其充、放电效率有较大影响,因此需要对蓄电池储能装置采取保温措施。初始投资成本除考虑微网系统内风机、电解槽、储氢罐、燃料电池、蓄电池的购置成本外,还须考虑蓄电池保温成本,其计算如下:
| $ C_{\mathrm{ic}}=\left(\sum\limits_{k=1}^{5} C_{k, \mathrm{ic}}+N_{\mathrm{bat}} C_{\mathrm{T}}\right) f_{\mathrm{CRF}} $ | (17) |
| $ \left\{\begin{array}{l} f_{\mathrm{CRF}}=i(1+i)^{y} /\left[(1+i)^{y}-1\right] \\ i=\left(i^{\prime}-f\right) /(1+f) \end{array}\right. $ | (18) |
式中:Ck, ic分别为风机、电解槽、储氢罐、燃料电池、蓄电池的初始投资成本;Nbat,CT分别为蓄电池数量和蓄电池单块保温成本,CT=500元/块;fCRF为资金回收系数;i为年实际利率;y为部件使用寿命;i′为名义利率;f为通货膨胀率。
2.1.2 年度置换成本微网系统的年度置换成本定义为项目全寿命周期内各部件更换所产生的年度平均成本。文中项目周期为20 a,除蓄电池外,其余部件寿命周期均为20 a,故年度置换成本仅须考虑蓄电池更换所产生的成本费用,计算如下:
| $ C_{\mathrm{rc}}=n C_{\mathrm{BAT}} \frac{i}{(1+i)^{y}-1} $ | (19) |
式中:n为需更换的蓄电池个数;CBAT为单块蓄电池成本。
2.1.3 年度运维成本年度运维成本定义为微网系统各部件1 a运行维护成本总和。由于风机暴露于低温自然环境中,在计算风机运维成本时,除考虑常规运维成本外,还需考虑低温环境对风机的不利影响所带来的维修成本,文中只考虑风机在0 ℃以下运行的维修成本,其计算如下:
| $ C_{\mathrm{mc}}=\sum\limits_{k=1}^{5}\left(N_{k} C_{k}\right)+\int_{0}^{8\ 760} \varPhi P_{\mathrm{WT}}(t) \frac{T(t)}{T_{\mathrm{set}}} \mathrm{d} t $ | (20) |
式中:Nk为第k种设备数目;Ck为第k种设备的单个年运维成本;Φ为低温运行所需维护成本系数,取0.1;T(t)为t时刻对应环境温度;Tset为允许运行最低温度。
微电网系统各相关设备成本数据如表 1所示。
|
|
表 1 微网系统相关设备成本数据 Table 1 Cost data of equipments in microgrid system |
进行微电网设计时,系统的供电可靠性是一个很重要的指标,采用全年LPSP为微电网供电可靠性目标函数[21],用符号δLPSP表示。其定义为1 a(8 760 h)内负载缺电量与1 a内负载正常运行所需电量之比,δLPSP越小,系统供电可靠性越高。
| $ \delta_{\mathrm{LPSP}}=\frac{\sum\limits_{i=1}^{8\ 760}\left(P_{\mathrm{load}}(t)-\sum P_{s}(t)\right)}{\sum\limits_{t=1}^{8\ 760} P_{\mathrm{load}}(t)} \times 100 \% $ | (21) |
式中:Ps(t)为第s种电源在t时刻的输出功率。
2.2.2 能源浪费率能源浪费率指微电网系统内浪费电能与可再生能源发电总量之比。在Δt时间内系统能量浪费率计算如下:
| $ \delta_{\mathrm{Excess}}=\left[\sum\limits_{t=t_{0}}^{t_{0}+\Delta t} Q_{\mathrm{Excess}}(t) / \sum\limits_{t=t_{0}}^{t_{0}+\Delta t}\left(P_{\mathrm{WT}}(t) \Delta t\right)\right] \times 100 \% $ | (22) |
| $ Q_{\mathrm{Excess}}(t)=\left(P_{\mathrm{WT}}(t)-P_{\mathrm{load}}(t)-P_{\mathrm{E}}(t)-P_{\mathrm{c}}(t)\right) \Delta t $ | (23) |
式中:Pc(t)为t时刻蓄电池的充电功率。QExcess(t)为正数,当QExcess(t)<0时,令QExcess(t)=0。
2.3 约束条件 2.3.1 功率平衡约束为满足独立微电网系统发电单元出力平衡负荷需求,保证系统稳定运行,允许系统切负荷和弃风,约束表示为:
| $ \begin{gathered} P_{\mathrm{WT}}(t)+P_{\mathrm{FC}}(t)+P_{\mathrm{d}}(t)+P_{\text {loss }}(t)= \\ P_{\text {load }}(t)+P_{\mathrm{c}}(t)+P_{\text {dump }}(t) \end{gathered} $ | (24) |
式中:Pd(t)为t时刻蓄电池的放电功率;Ploss(t)为t时刻切负荷大小;Pdump(t)为t时刻微网系统丢弃的风机出力。
2.3.2 分布式电源安装数量及输出功率约束| $ 0 \leqslant N_{s} \leqslant N_{s, \max } $ | (25) |
| $ 0 \leqslant P_{\mathrm{WT}} \leqslant \lambda P_{\mathrm{WT}, \max } $ | (26) |
| $ 0 \leqslant P_{\mathrm{FC}} \leqslant P_{\mathrm{FC}, \max } $ | (27) |
式中:Ns为第s种电源设备的安装数量;Ns, max为第s种电源的最大安装数量;λ为风机功率最大修正系数,其表示环境温度-20 ℃时,空气密度的相对变化值;PWT, max为标准状况下风机最大输出功率;PFC, max为燃料电池最大输出功率。
2.3.3 蓄电池约束从蓄电池使用寿命及运行安全角度考虑,蓄电池储能装置在运行时需满足以下约束条件。
(1) 储能装置充放电深度约束。
| $ S_{\mathrm{soc}, \min } \leqslant S_{\mathrm{soc}}(t) \leqslant S_{\mathrm{soc}, \max } $ | (28) |
式中:Ssoc(t)为蓄电池荷电状态大小,表示蓄电池当前储能大小所占总容量比例;Ssoc, min,Ssoc, max分别为荷电状态下限、上限,文中上限为1,下限为0.3。
(2) 蓄电池储能装置充、放电功率约束。
| $ \left|P_{\mathrm{bat}}(t)\right| \leqslant\left|P_{\mathrm{bat}, \mathrm{lim}}(t)\right| $ | (29) |
充电过程:
| $ \begin{gathered} \left|P_{\mathrm{bat}, \mathrm{lim}}(t)\right|= \\ \min \left\{P_{\max , \mathrm{c}}, \frac{C_{\mathrm{bat}}\left[S_{\mathrm{soc}, \max }-(1-\delta) S_{\mathrm{soc}}(t-\Delta t)\right]}{\Delta t \eta_{\mathrm{c}}}\right\} \end{gathered} $ | (30) |
放电过程:
| $ \begin{gathered} \left|P_{\mathrm{bat}, \mathrm{lim}}(t)\right|= \\ \min \left\{P_{\max , \mathrm{d}}, \frac{\eta_{\mathrm{d}} C_{\mathrm{bat}}\left[(1-\delta) S_{\mathrm{soc}}(t-\Delta t)-S_{\mathrm{soc}, \min }\right]}{\Delta t}\right\} \end{gathered} $ | (31) |
式中:|Pbat, lim(t)|为蓄电池所允许的最大充放电功率;Pmax, c,Pmax, d分别为蓄电池储能装置的最大充电、放电功率。
2.3.4 氢储系统容量约束| $ Q_{\mathrm{Tank}, \min } \leqslant Q_{\mathrm{Tank}}(t) \leqslant Q_{\mathrm{Tank}, \max } $ | (32) |
式中:QTank, max,QTank, min分别为储氢罐容量上限和下限,上限等于额定容量,下限为额定容量的20%。
2.3.5 供电可靠性约束| $ \delta_{\mathrm{LPSP}} \leqslant \delta_{\mathrm{LPSP}, \mathrm{set}} $ | (33) |
式中:δLPSP, set为所设置的最大全年LPSP。
3 求解流程采用遗传算法对文中所建模型进行求解,遗传算法作为一种常见的群优化算法,能较好地求解微电网容量优化配置问题[22-23]。决策变量为风机、蓄电池、电解槽、储氢罐、燃料电池数量;目标函数作为适应度函数,在约束条件下求解出最佳配置组合,使得目标函数最小。
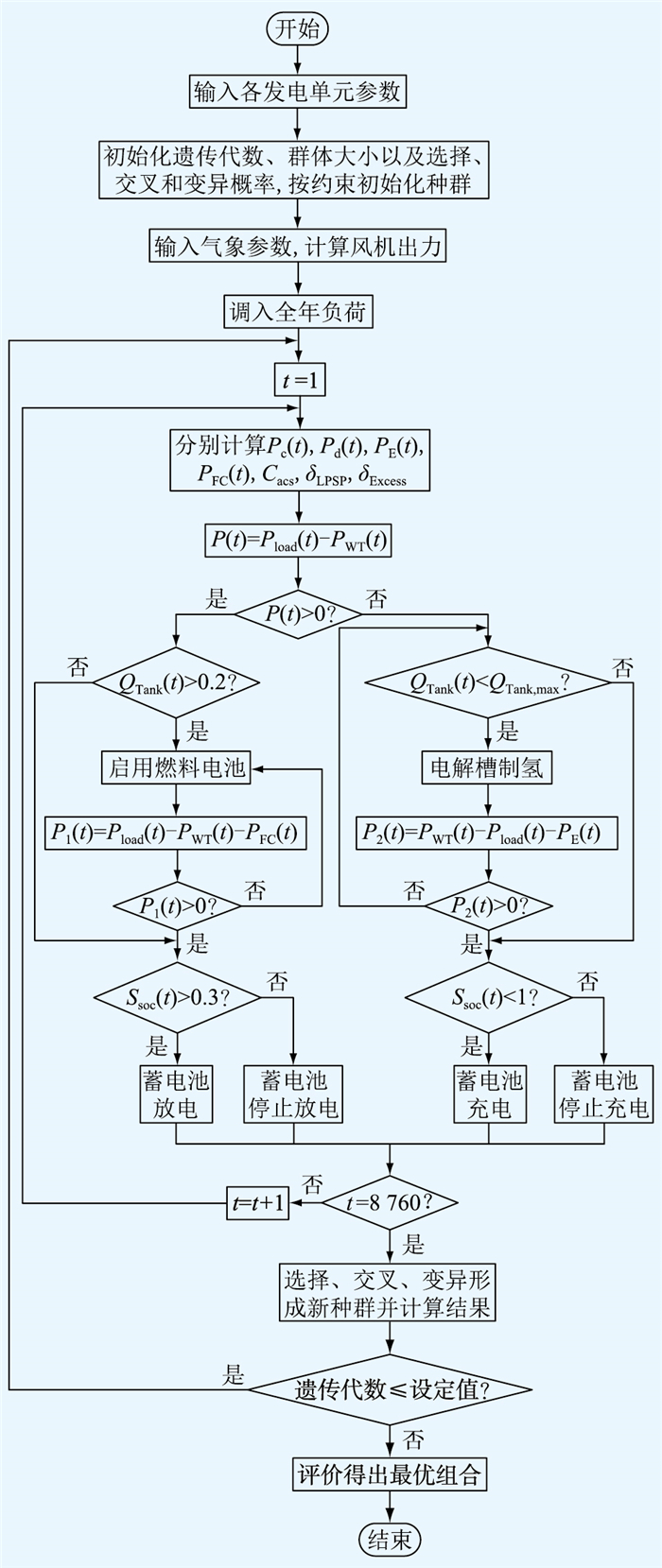
遗传算法种群大小设置为100,遗传代数为200,交叉概率为0.8,变异概率为0.1,优化配置流程如图 4所示。
|
图 4 容量优化配置流程 Fig. 4 Flow chart of capacity optimization configuration |
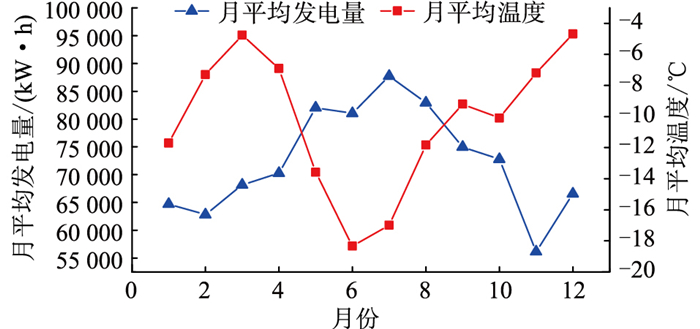
利用皮尔逊相关系数法对中山站负荷与其环境温度之间的关系进行分析。综合文献[24]得到中山站月平均气温和柴油发电机月平均发电量数据,如图 5所示。
|
图 5 中山站月发电量及月平均温度曲线 Fig. 5 Monthly power generation and temperature curves of Zhongshan station |
以月平均温度X和月平均发电量Y为变量,X与Y之间的皮尔逊相关系数ρX, Y可以表示为:
| $ \rho_{X, Y}=\frac{\operatorname{cov}(X, Y)}{\sigma_{X} \sigma_{Y}}=\frac{\sum\limits_{j=1}^{n}\left(X_{j}-\bar{X}\right)\left(Y_{j}-\bar{Y}\right)}{\sqrt{\sum\limits_{j=1}^{n}\left(X_{j}-\bar{X}\right)^{2}} \sqrt{\sum\limits_{j=1}^{n}\left(Y_{j}-\bar{Y}\right)^{2}}} $ | (34) |
式中:cov(X, Y)为协方差;σX, σY分别为X,Y的标准差;Xj,Yj分别为第j个月的平均温度和平均发电量;n为月数。ρX, Y∈[-1, 1],为正表示正相关,为负表示负相关,其绝对值位于0.8~1表示极强相关;0.6~0.8表示强相关;0.4~0.6表示中等程度相关;0.2~0.4表示弱相关;0.0~0.2表示两者之间极弱相关或不相关。
根据式(34)以及中山站月平均温度和月平均发电量数据,计算得ρX, Y=-0.68,可知中山站温度与负荷之间相关性为强相关,温度越低,发电量越大,故判断中山站极低气温将导致负荷增加。据此文中考虑的负荷数学模型如下:
| $ P_{\text {load }}(t)=P_{0}(t)(1+\varphi)+a\left|\rho_{X, Y}\right||X| $ | (35) |
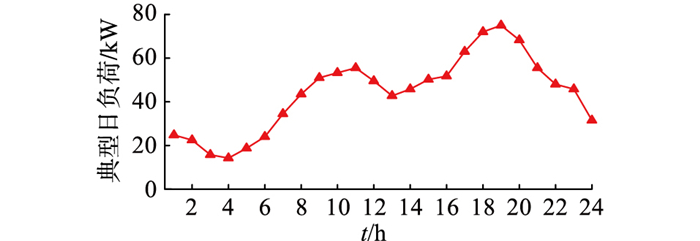
式中:P0(t)为不考虑温度影响的典型日负荷,如图 6所示;φ为负荷变化量,φ∈[-0.1, 0.1];a为常数,取值为4。
|
图 6 典型日负荷曲线 Fig. 6 Typical daily load curve |
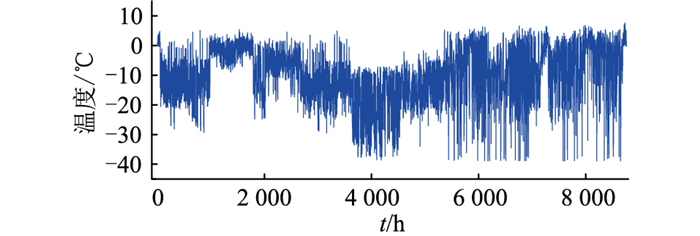
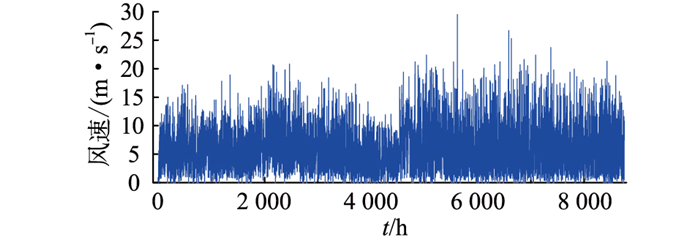
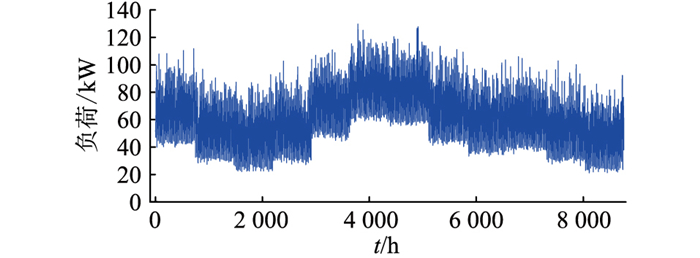
中山站位于东南极大陆伊丽莎白公主地拉斯曼丘陵的维斯托登半岛上,水资源丰富,其地理坐标为南纬69°22′24.76″, 东经76°22′14.28″。通过我国极地实时气象系统查询到2016年内中山站所在位置全年温度、风速数据如图 7、图 8所示。根据式(35),模拟计算得到中山站全年负荷数据曲线,如图 9所示。由图 7可知,6月中山站平均气温达全年最低,导致用电负荷全年最大。同时,6月中山站风速相比其他月份较小。
|
图 7 中山站全年温度曲线 Fig. 7 The annual temperature curve of Zhongshan station |
|
图 8 中山站全年风速曲线 Fig. 8 The annual wind speed curve of Zhongshan station |
|
图 9 中山站全年负荷曲线 Fig. 9 The annual load curve of Zhongshan station |
运用文中方法对极地环境微电网电源容量进行优化配置,仿真时间为1 a,采样时间间隔为1 h, Ssoc(0)=0.85。根据文中建立的发电单元数学模型,以气象数据和相关成本作为输入,计算出微电网发电单元出力,并计算微电网系统δLPSP, 将其作为约束条件。用表 1给出的各设备相关成本数据计算微电网的年度平均成本, 并将其作为目标函数,利用遗传算法求解多元非线性整数规划问题。
为分析温度对风机及蓄电容量影响,更好地选择适用于极地环境的微电网电源供电系统,分别计算以下4种不同配置方案的优化结果。
(1) 方案1:不考虑低温对风机出力及蓄电池容量影响的风氢储微电网电源容量优化配置。
(2) 方案2:只考虑低温对风机出力影响的风氢储微电网电源容量优化配置。
(3) 方案3:考虑低温对风机出力及蓄电池容量影响的风氢储微电网电源容量优化配置。
(4) 方案4:考虑低温对风机出力及蓄电池容量影响的风储微电网电源容量优化配置。
4种配置方案均要求系统供电可靠性为99%,即微电网δLPSP, set=1%。不同方案的容量优化配置结果及成本见表 2。
|
|
表 2 微电网容量优化配置结果 Table 2 Capacity optimization results of microgrid |
由表 2可知,方案1、方案2及方案3中除蓄电池配置数量不同,其他配置均相同。与方案1相比,方案2考虑低温对风机的出力影响,低温下风机出力有所增加,故所需蓄电池容量小于方案1,导致方案2年度平均成本低于方案1。方案3在方案2的基础上增加低温环境对蓄电池容量的影响,在低温环境下蓄电池容量减小,所需蓄电池数量较多,需要投入较大的投资成本以及运行维护成本,年度平均成本高于方案2。
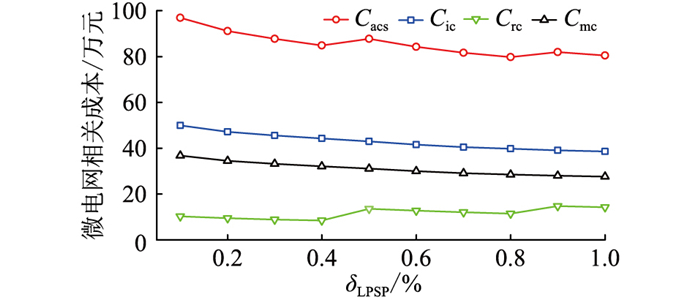
方案3与方案4在同等环境条件下,针对不同供电系统进行优化对比。由表 2可知,方案4(风储系统)中风机及蓄电池配置数量均高于方案3(风氢储系统),年度平均成本为85.763万元,比方案3高出5.246万元,说明利用富余风电制氢可以提高微网系统的经济性。此外,风氢储系统的供电可靠性略高于风储供电系统。在风氢储系统中,用电负荷主要由风电机组满足,风电富余时,先利用电解槽进行制氢储存,然后对蓄电池进行充电;风电不足时,由燃料电池和蓄电池进行供电,氢储系统与风电实现有效互补,提高了微电网系统的供电可靠性。且合理配置一定容量的氢储装置,还能减少系统的电能浪费。在风氢储系统中,配置的蓄电池容量和氢储容量越高,供电可靠性越高,能量浪费率越低。以极地低温环境下的风氢储系统为例,计算δLPSP与微电网相关成本关系,结果如图 10所示。可以看出微电网系统的年度初始投资成本以及年度运维成本随着δLPSP的增加平稳降低,而系统年度置换成本的变换呈现出阶段性,在一定范围内随着δLPSP的增加平稳降低,在大的趋势上则表现为置换成本随δLPSP增加而增加,原因在于δLPSP增加导致蓄电池配置容量减少,相同负荷下蓄电池放电深度越大,蓄电池使用寿命减小,在项目周期内需要多次更换,产生大额的置换成本。微电网系统年度平均成本随δLPSP增加总体呈减少趋势,当δLPSP为0.8%和1%时,系统年度平均成本差异不大,故取在δLPSP为0.8%时的容量配置为微电网的最佳配置,即:风机20台,蓄电池266个,燃料电池1台,电解槽3台,储氢罐1个,Cacs为79.820万元。
|
图 10 δLPSP与微电网相关成本关系 Fig. 10 Relationship between δLPSP and microgrid-related costs |
由于极地地区常年低温,需要保证不间断供电,满足科考人员取暖及科考设备用电需求,因此微电网系统供电可靠性至关重要。为研究系统的真实工作状态,选取文中最佳配置方案对风机、蓄电池以及储氢系统的工作状态进行进一步分析。
微电网某日仿真结果如图 11所示,当风机实际发电量大于负荷需求时,蓄电池会对多余电量进行储存,同时富余电能将输入电解槽电解水制氢。当风机出力低于微电网负荷时,系统启用蓄电池和燃料电池进行不间断供电。

|
图 11 某日仿真结果 Fig. 11 Simulation results on a certain day |
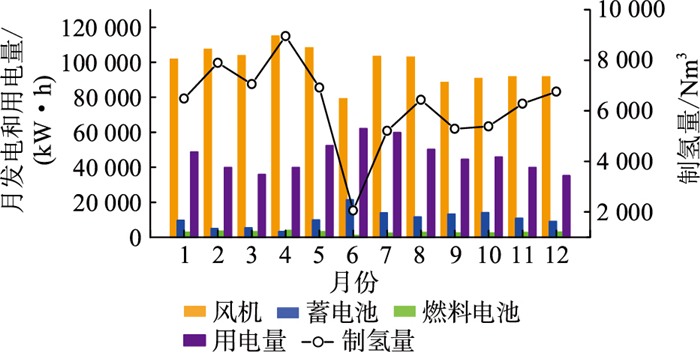
图 12为发电单元逐月能量输出及负荷需求,6月中山站进入寒冬,月平均气温为-18.34 ℃,为全年最低月平均气温,导致用电负荷全年最大。同时,月平均风速仅为4.5 m/s,风机出力较低,制氢量大幅减少,不得不长时间启用蓄电池储能装置对负载进行供电。在文中最佳方案配置下,系统缺电时间集中于6月,其他时间完全可以保证不间断供电,系统供电可靠性得到充分保障。
|
图 12 各发电单元能量输出及负荷需求 Fig. 12 Power output and load demand of each power generation unit |
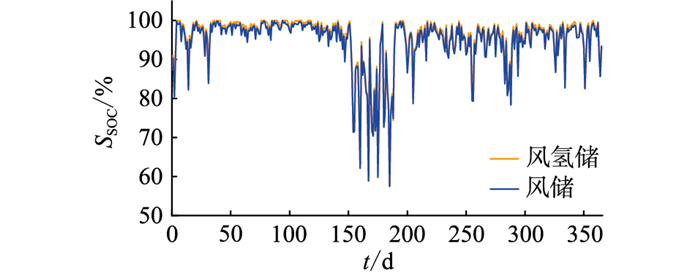
为比较风储和风氢储2种配置方案对蓄电池使用寿命的影响,在考虑温度影响,δLPSP为0.8%时求解风储系统容量配置,与文中最佳配置进行比较。图 13为2种配置方案下蓄电池日平均荷电状态,由图可知单一风储系统由于缺少燃料电池供电,风机出力不足时蓄电池需长时间放电,导致蓄电池荷电状态略低于风氢储系统。因此,在实际运用中,采用风氢储配置方案可以提高蓄电池的使用寿命,进而可以降低系统费用。
|
图 13 蓄电池日平均荷电状态 Fig. 13 Daily average state of charge of storage battery |
文中针对极地低温环境,考虑低温对风机出力、蓄电池实际容量和微电网负荷的影响,对极地低温环境下独立微电网电源优化配置问题进行求解。对比不同方案下的优化配置结果,得出以下结论:
(1) 极地低温环境对风机尤其是蓄电池有一定影响,低温下蓄电池配置数量远大于标准状况下配置数量。在微电网实际规划过程中,必须将温度影响因素考虑在内,才能更合理地对低温环境下的微电网供电系统容量进行配置。
(2) 风氢储系统更适用于极地环境,不仅能有效减少能源浪费,提高系统经济性,还能提高微电网系统供电可靠性。
(3) 风氢储供电系统可以减小蓄电池放电深度,延长蓄电池使用寿命。
| [1] |
郑凌蔚, 刘士荣, 周文君, 等. 并网型可再生能源发电系统容量配置与优化[J]. 电力系统保护与控制, 2014, 42(17): 31-37. ZHENG Lingwei, LIU Shirong, ZHOU Wenjun, et al. Capacity configuration and optimization of grid-connected renewable energy power generation system[J]. Power System Protection and Control, 2014, 42(17): 31-37. DOI:10.7667/j.issn.1674-3415.2014.17.005 (  0) 0) |
| [2] |
卞艺衡, 别朝红, 黄格超, 等. 弹性配电网分布式可再生能源电源最优配置模型[J]. 全球能源互联网, 2020, 3(3): 213-221. BIAN Yiheng, BIE Zhaohong, HUANG Gechao, et al. Optimal renewable energy distributed generators placement for resilient distribution system[J]. Journal of Global Energy Interconnection, 2020, 3(3): 213-221. (  0) 0) |
| [3] |
鲁宗相, 李昊, 乔颖. 从灵活性平衡视角的高比例可再生能源电力系统形态演化分析[J]. 全球能源互联网, 2021, 4(1): 12-18. LU Zongxiang, LI Hao, QIAO Ying. Morphological evolution of power systems with high share of renewable energy generations from the perspective of flexibility balance[J]. Journal of Global Energy Interconnection, 2021, 4(1): 12-18. (  0) 0) |
| [4] |
马锐, 李相俊, 李文启, 等. 可再生能源供电区域电网中储能系统协同调度策略[J]. 发电技术, 2021, 42(1): 31-39. MA Rui, LI Xiangjun, LI Wenqi, et al. Cooperative scheduling strategy of energy storage systems for regional grid supplied by renewable energy[J]. Power Generation Technology, 2021, 42(1): 31-39. (  0) 0) |
| [5] |
刘艳平, 贾春娟. 基于遗传算法的独立型风光互补发电容量优化[J]. 电力系统及其自动化学报, 2015, 27(10): 69-74. LIU Yanping, JIA Chunjuan. Capacity optimization of independent wind/PV hybrid power generation system based on GA[J]. Proceedings of the CSU-EPSA, 2015, 27(10): 69-74. DOI:10.3969/j.issn.1003-8930.2015.10.11 (  0) 0) |
| [6] |
周志超, 郭力, 王成山, 等. 风柴储生物质独立微电网系统的优化规划设计[J]. 电力系统自动化, 2014, 38(7): 16-22. ZHOU Zhichao, GUO Li, WANG Chengshan, et al. Optimal planning and design of a wind/biomass/diesel/battery stand-alone microgrid[J]. Automation of Electric Power Systems, 2014, 38(7): 16-22. (  0) 0) |
| [7] |
汤翔鹰, 胡炎, 郑棣, 等. 考虑电网灵活性的微电网储能优化配置方法[J]. 供用电, 2020, 37(12): 54-60. TANG Xiangying, HU Yan, ZHENG Di, et al. Research on optimal configuration of energy storage in microgrid considering grid flexibility[J]. Distribution&Utilization, 2020, 37(12): 54-60. (  0) 0) |
| [8] |
王晨, 李海军, 徐光福, 等. 含多元储能交直流混合微电网系统控制策略研究[J]. 供用电, 2020, 37(6): 74-81. WANG Chen, LI Haijun, XU Guangfu, et al. Research on control strategy of AC/DC hybrid microgrid system with multi-type energy storage[J]. Distribution&Utilization, 2020, 37(6): 74-81. (  0) 0) |
| [9] |
GUTIERREZ-MARTIN F, CONFENTE D, GUERRA I. Management of variable electricity loads in wind-hydrogen systems: the case of a Spanish wind farm[J]. International Journal of Hydrogen Energy, 2010, 35(14): 7329-7336. DOI:10.1016/j.ijhydene.2010.04.181 (  0) 0) |
| [10] |
马榕谷, 陈洁, 赵军超, 等. 非并网风氢互补系统的容量多目标优化[J]. 太阳能学报, 2019, 40(2): 422-429. MA Ronggu, CHEN Jie, ZHAO Junchao, et al. Multi-objective optimization for capacity of non-grid-connected wind/hydrogen hybrid power system[J]. Acta Energiae Solaris Sinica, 2019, 40(2): 422-429. (  0) 0) |
| [11] |
马溪原, 吴耀文, 方华亮, 等. 采用改进细菌觅食算法的风/光/储混合微电网电源优化配置[J]. 中国电机工程学报, 2011, 31(25): 17-25. MA Xiyuan, WU Yaowen, FANG Hualiang, et al. Optimal sizing of hybrid solar-wind distributed generation in an islanded microgrid using improved bacterial foraging algorithm[J]. Proceedings of the CSEE, 2011, 31(25): 17-25. (  0) 0) |
| [12] |
于东霞, 张建华, 王晓燕, 等. 并网型风光储互补发电系统容量优化配置[J]. 电力系统及其自动化学报, 2019, 31(10): 59-65. YU Dongxia, ZHANG Jianhua, WANG Xiaoyan, et al. Optimal capacity configuration of grid-connected wind-PV-storage hybrid power generation system[J]. Proceedings of the CSU-EPSA, 2019, 31(10): 59-65. (  0) 0) |
| [13] |
李奇, 赵淑丹, 蒲雨辰, 等. 考虑电氢耦合的混合储能微电网容量配置优化[J]. 电工技术学报, 2021, 36(3): 486-495. LI Qi, ZHAO Shudan, PU Yuchen, et al. Capacity optimization of hybrid energy storage microgrid considering electricity-hydrogen coupling[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 486-495. (  0) 0) |
| [14] |
李益民, 王关平, 马建立, 等. 基于天牛须搜索遗传算法的风光柴储互补发电系统容量优化配置研究[J]. 储能科学与技术, 2020, 9(3): 918-926. LI Yimin, WANG Guanping, MA Jianli, et al. Study on optimal capacity in the construction of wind-solar-diesel battery hybrid power system based on bettle antennae search algorithm improved genetic algorithm[J]. Energy Storage Science and Technology, 2020, 9(3): 918-926. (  0) 0) |
| [15] |
李彦哲, 郭小嘉, 董海鹰, 等. 风/光/储微电网混合储能系统容量优化配置[J]. 电力系统及其自动化学报, 2020, 32(6): 123-128. LI Yanzhe, GUO Xiaojia, DONG Haiying, et al. Optimal capacity configuration of wind/PV/storage hybrid energy storage system in microgrid[J]. Proceedings of the CSU-EPSA, 2020, 32(6): 123-128. (  0) 0) |
| [16] |
AMROLLAHI M H, BATHAEE S M T. Techno-economic optimization of hybrid photovoltaic/wind generation together with energy storage system in a stand-alone micro-grid subjected to demand response[J]. Applied energy, 2017, 202: 66-77. DOI:10.1016/j.apenergy.2017.05.116 (  0) 0) |
| [17] |
张文杰, 吴杰康, 赵俊浩, 等. 考虑源-荷不确定性的水风柴微电网优化配置[J]. 电力工程技术, 2020, 39(2): 117-126. ZHANG Wenjie, WU Jiekang, ZHAO Junhao, et al. Optimal capacity configuration of hydro-wind-diesel microgrid considering uncertainty of renewable energy and load[J]. Electric Power Engineering Technology, 2020, 39(2): 117-126. (  0) 0) |
| [18] |
王斯成, 陈子平, 杨军, 等. 蓄电池剩余容量(SOC)数学模型探讨和在线测试仪的开发[J]. 太阳能学报, 2005, 26(1): 6-13. WANG Sicheng, CHEN Ziping, YANG Jun, et al. SOC modeling for lead-acid battery and developments of SOC on-line tester[J]. Acta Energiae Solaris Sinica, 2005, 26(1): 6-13. DOI:10.3321/j.issn:0254-0096.2005.01.002 (  0) 0) |
| [19] |
韩晓娟, 程成, 籍天明, 等. 计及电池使用寿命的混合储能系统容量优化模型[J]. 中国电机工程学报, 2013, 33(34): 91-97, 16. HAN Xiaojuan, CHENG Cheng, JI Tianming, et al. Capacity optimal modeling of hybrid energy storage systems considering battery life[J]. Proceedings of the CSEE, 2013, 33(34): 91-97, 16. (  0) 0) |
| [20] |
刘峪涵, 汪沨, 谭阳红. 并网型微电网多目标容量优化配置及减排效益分析[J]. 电力系统及其自动化学报, 2017, 29(9): 70-75. LIU Yuhan, WANG Feng, TAN Yanghong. Multi-objective optimal capacity configuration and emission reduction benefit analysis of grid-connected microgrid[J]. Proceedings of the CSU-EPSA, 2017, 29(9): 70-75. DOI:10.3969/j.issn.1003-8930.2017.09.012 (  0) 0) |
| [21] |
吴小刚, 刘宗歧, 田立亭, 等. 独立光伏系统光储容量优化配置方法[J]. 电网技术, 2014, 38(5): 1271-1276. WU Xiaogang, LIU Zongqi, TIAN Liting, et al. Optimized capacity configuration of photovoltaic generation and energy storage device for stand-alone photovoltaic generation system[J]. Power System Technology, 2014, 38(5): 1271-1276. (  0) 0) |
| [22] |
YANG H X, ZHOU W, LU L, et al. Optimal sizing method for stand-alone hybrid solar-wind system with LPSP technology by using genetic algorithm[J]. Solar Energy, 2008, 82(4): 354-367. DOI:10.1016/j.solener.2007.08.005 (  0) 0) |
| [23] |
AL-SHAMMA'A A A, ADDOWEESH K E. Techno-economic optimization of hybrid power system using genetic algorithm[J]. International Journal of Energy Research, 2014, 38(12): 1608-1623. DOI:10.1002/er.3191 (  0) 0) |
| [24] |
席晓琴. 南极中山站风光互补供电系统设计[D]. 太原: 太原理工大学, 2018. XI Xiaoqin. Design of wind and solar complementary power supply system in Antarctica Zhongshan station[D]. Taiyuan: Taiyuan University of Technology, 2018. (  0) 0) |
 2022, Vol. 41
2022, Vol. 41


 张长云(1996), 男, 硕士在读, 研究方向为新能源发电技术、微电网优化运行(E-mail:
张长云(1996), 男, 硕士在读, 研究方向为新能源发电技术、微电网优化运行(E-mail: