文章编号: 2096-3203(2022)01-0180-05 中图分类号: TM743
2. 国网山西省电力公司, 山西 太原 030021;
3. 河海大学能源与电气学院, 江苏 南京 211100
随着分布式发电的技术进步和成本降低,分布式电源(distributed generation,DG)在配电网中的安装比例逐年增加[1-4]。DG的大量接入使配电系统从无源网络转变为有源网络,配电网的无功优化问题也变得更加复杂[5-9],配电网网损分摊的公平性问题日益突出。将含DG的配电网网损进行合理分摊,有利于负荷和DG对网损的责任划定[10-11],以及终端用能价格和结算机制的合理制定[12]。
针对含DG的配电网网损分摊,文献[13]提出一种改进平均网损法,解决了原始平均网损法中没有考虑的双向潮流问题,但功率相同而位置不同的参与者会分摊到相同的损耗,分摊的公平性无法保证。文献[14]提出一种含DG的辐射型配电网网损分摊新方法,其优点是不考虑任何额外假设和近似来分配损失,但未考虑无功传输对网损的影响。文献[15]提出利用Shapley值和电路定律进行网损分摊,将支路电流分解为每个参与者的电流再进行网损分摊,但负荷和DG较多时,工作量较大,计算负担大。文献[16]考虑到配电网的谐波,将损耗分为基波损耗和谐波损耗进行分摊,但未考虑DG接入有利于网损减小,须对DG进行奖励的情况。
边际损耗系数(marginal loss coefficients, MLC)法是一种对各节点上负荷或发电机进行网损分摊的灵敏度方法,广泛应用于国际电力市场[17]。文献[18]指出,MLC法不能保证所计算出的总网损与系统实际总网损一致。因此,用比例系数来调整网损分摊量,可避免网损的过度回收,但将该方法应用于含DG的配电网网损分摊时,会出现成员间的分摊差距过大的情况,有失分摊的公平性。
针对以上问题,以基于比例系数的MLC法为基础,进一步引入奖惩系数。既保留了避免网损过度回收的优势,又能解决正、负分摊量相互抵消而导致成员间分摊差距过大的问题,旨在寻求更合理的含DG配电网损耗分摊方法。
1 基于比例系数的MLC法 1.1 原理分析MLC法考虑节点有功功率和无功功率与网络总有功功率损耗之间的非线性函数关系,根据系统中节点功率与总有功功率损耗的变化关系分摊损耗。
配电网总有功功率损耗可记为L(Pi, Qi),可通过定义MLC,计算出由网络中节点i的有功功率Pi和无功功率Qi的边际变化所引起的总有功功率损耗L的变化量。定义MLC为:
| $ \left\{\begin{array}{l} \lambda_{p_{i}}=\frac{\partial L}{\partial P_{i}} \quad i=1,2, \cdots, N \\ \lambda_{q_{i}}=\frac{\partial L}{\partial Q_{i}} \quad i=1,2, \cdots, N \end{array}\right. $ | (1) |
式中:λpi,λqi分别为节点i有功功率、无功功率的MLC值;N为节点个数。
基于极坐标的总有功功率损耗计算公式[18],应用标准链式规则,可建立以下线性方程组计算MLC值:
| $ \frac{\partial L}{\partial V_{i}}=\sum\limits_{j=1}^{N}\left(\frac{\partial L}{\partial P_{j}} \frac{\partial P_{j}}{\partial V_{i}}+\frac{\partial L}{\partial Q_{j}} \frac{\partial Q_{j}}{\partial V_{i}}\right) $ | (2) |
| $ \frac{\partial L}{\partial \theta_{i}}=\sum\limits_{j=1}^{N}\left(\frac{\partial L}{\partial P_{j}} \frac{\partial P_{j}}{\partial \theta_{i}}+\frac{\partial L}{\partial Q_{j}} \frac{\partial Q_{j}}{\partial \theta_{i}}\right) $ | (3) |
式中:Vi为节点i的电压幅值;θi为节点i的相角。
将式(2)和式(3)写成矩阵形式为:
| $ \left[\begin{array}{cccccccc} \frac{\partial P_{1}}{\partial V_{1}} & \frac{\partial P_{2}}{\partial V_{1}} & \cdots & \frac{\partial P_{N}}{\partial V_{1}} & \frac{\partial Q_{1}}{\partial V_{1}} & \frac{\partial Q_{2}}{\partial V_{1}} & \cdots & \frac{\partial Q_{N}}{\partial V_{1}} \\ \vdots & \vdots & & \vdots & \vdots & \vdots & & \vdots \\ \frac{\partial P_{1}}{\partial V_{N}} & \frac{\partial P_{2}}{\partial V_{N}} & \cdots & \frac{\partial P_{N}}{\partial V_{N}} & \frac{\partial Q_{1}}{\partial V_{N}} & \frac{\partial Q_{2}}{\partial V_{N}} & \cdots & \frac{\partial Q_{N}}{\partial V_{N}} \\ \frac{\partial P_{1}}{\partial \theta_{1}} & \frac{\partial P_{2}}{\partial \theta_{1}} & \cdots & \frac{\partial P_{N}}{\partial \theta_{1}} & \frac{\partial Q_{1}}{\partial \theta_{1}} & \frac{\partial Q_{2}}{\partial \theta_{1}} & \cdots & \frac{\partial Q_{N}}{\partial \theta_{1}} \\ \vdots & \vdots & & \vdots & \vdots & \vdots & & \vdots \\ \frac{\partial P_{1}}{\partial \theta_{N}} & \frac{\partial P_{2}}{\partial \theta_{N}} & \cdots & \frac{\partial P_{N}}{\partial \theta_{N}} & \frac{\partial Q_{1}}{\partial \theta_{N}} & \frac{\partial Q_{2}}{\partial \theta_{N}} & \cdots & \frac{\partial Q_{N}}{\partial \theta_{N}} \end{array}\right]\left[\begin{array}{c} \frac{\partial L}{\partial P_{1}} \\ \vdots \\ \frac{\partial L}{\partial P_{N}} \\ \frac{\partial L}{\partial Q_{1}} \\ \vdots \\ \frac{\partial L}{\partial Q_{N}} \end{array}\right]=\left[\begin{array}{c} \frac{\partial L}{\partial V_{1}} \\ \vdots \\ \frac{\partial L}{\partial V_{N}} \\ \frac{\partial L}{\partial \theta_{1}} \\ \vdots \\ \frac{\partial L}{\partial \theta_{N}} \end{array}\right] $ | (4) |
用J表示式(4)中的系数矩阵,则MLC值的计算如下:
| $ \left[\begin{array}{c} \lambda_{p_{i}} \\ \lambda_{q_{i}} \end{array}\right]=\left[\begin{array}{c} \frac{\partial L}{\partial P_{i}} \\ \frac{\partial L}{\partial Q_{i}} \end{array}\right]=\boldsymbol{J}^{-1}\left[\begin{array}{c} \frac{\partial L}{\partial V_{i}} \\ \frac{\partial L}{\partial \theta_{i}} \end{array}\right] $ | (5) |
根据实际运行数据经验可知,MLC法计算得到的总损耗大于实际总损耗,即:
| $ \sum\limits_{i=1}^{N-1}\left[\frac{\partial L}{\partial P_{i}} P_{i}+\frac{\partial L}{\partial Q_{i}} Q_{i}\right]>L $ | (6) |
为了使采用MLC法计算出的各节点分摊损耗之和等于系统实际总损耗,采用比例系数对边际分摊量进行相应调整,得到基于比例系数的MLC法。比例系数定义为实际总损耗与MLC分摊量总和之比,其计算如下[18]:
| $ k=\frac{L}{\sum\limits_{i=1}^{N-1}\left(\frac{\partial L}{\partial P_{i}} P_{i}+\frac{\partial L}{\partial Q_{i}} Q_{i}\right)} $ | (7) |
则节点i注入有功、无功功率的MLC值为:
| $ \left\{\begin{array}{l} \lambda_{p i}^{\prime}=k \lambda_{p i} \\ \lambda_{q i}^{\prime}=k \lambda_{q i} \end{array}\right. $ | (8) |
对调整后各节点的分摊损耗量进行求和,计算得到的总损耗与系统实际总损耗相等。
1.2 存在问题在进行损耗分摊时,对功率增大使总损耗增加的节点进行正分摊,对功率减小使总损耗减少的节点进行负分摊。在含DG的配电网络中,运用MLC法进行损耗分摊时,用户的分摊量可能会出现负值。主要原因为:
(1) 为了奖励DG而出现负分摊。在DG接入的容量较小时,DG离负荷较近,输送同样大小的功率比平衡节点引起的损耗小,此时DG容量的增加会减少配电网损耗。
(2) 为了奖励负荷而出现负分摊。DG接入的容量较大时存在一个使网损最小的容量,超过该容量后,若DG容量继续增大,配电网的损耗将增大。此时负荷如果增加,可进一步减少DG剩余功率,从而减少线路上流动功率,减少网络损耗,负荷的损耗分摊量会减少。
在配电网中引入DG后存在某些节点分摊量为负值的情况,仍用比例系数k进行放缩存在正、负分摊量抵消的问题。即MLC法不区分分摊量正、负直接进行放缩处理,会造成某一用户分摊量过大,成员之间的分摊差距过大。
例如一个包含负荷节点和DG节点的网络,设网络实际损耗为100 kW,通过MLC法计算得到负荷节点分摊量为180 kW,DG节点分摊量为-50 kW,此时存在过度回收问题。采用比例系数进行修正时,由式(7)计算比例系数,正分摊180 kW和负分摊-50 kW相加会有一部分抵消,使得比例系数k较大,虽然能保证分摊量总和等于实际损耗,但也会使各用户正分摊量和负分摊量较大,分摊差距过大。
2 改进MLC法为了使各用户分摊比例在可接受的范围内,同时不改变对用户的奖惩属性,对基于比例系数的MLC法进行改进。首先通过基于比例系数的MLC法计算出各节点的有功、无功MLC值,即λ′ pi和λ′ qi,则各节点的有功、无功功率传输边际系数分摊量为:
| $ L_{p i}^{\prime}=\lambda_{p i}^{\prime} P_{i} $ | (9) |
| $ L_{q i}^{\prime}=\lambda_{q i}^{\prime} Q_{i} $ | (10) |
将节点有功传输分摊量和无功传输分摊量以正和非正划分为2个子集,即LA和LB,假设LA中有m个元素,LB中有n个元素,其关系满足m+n=2(N-1),即把正分摊量放入LA,非正分摊量放入LB。由于将每个节点的有功功率和无功功率分开考虑,且平衡节点不参与分摊,故共有2(N-1)个分摊量。
为便于表示,记|Lsum|为所有分摊量的绝对值之和,|LAS|(|LAS|>0)为集合LA中所有值之和,|LBS|(|LBS|≥0)为集合LB中所有值之和。
分2步计算每个用户的分配系数。首先,根据边际法分摊量的绝对值大小,得到初始分配系数。如果初始分配系数下损耗不能完全分摊,则引入奖惩系数,让正分摊量除以奖惩系数,负分摊量乘以奖惩系数,以此使回收的损耗等于实际损耗,具体步骤如下。
(1) 计算初始分配系数。
| $ \left\{\begin{array}{l} k_{p i}=\frac{L_{p i}^{\prime}}{\sum\limits_{i=1}^{N-1}\left(\left|L_{p i}^{\prime}\right|+\left|L_{q i}^{\prime}\right|\right)}=\frac{L_{p i}^{\prime}}{\left|L_{\mathrm{sum}}\right|} \\ k_{q i}=\frac{L_{q i}^{\prime}}{\sum\limits_{i=1}^{N-1}\left(\left|L_{p i}^{\prime}\right|+\left|L_{q i}^{\prime}\right|\right)}=\frac{L_{q i}^{\prime}}{\left|L_{\mathrm{sum}}\right|} \end{array}\right. $ | (11) |
式中:kpi为初始有功功率分配系数;kqi为初始无功功率分配系数。
各节点有功传输、无功传输初始损耗分摊量计算如下:
| $ L_{p i}=k_{p i} L=\frac{L_{p i}^{\prime}}{\left|L_{\text {sum }}\right|} L $ | (12) |
| $ L_{q i}=k_{q i} L=\frac{L_{q i}^{\prime}}{\left|L_{\text {sum }}\right|} L $ | (13) |
若Lpi,Lqi全部大于零,即网络中没有负分摊,则完成了分摊。若Lpi,Lqi中存在负值,即网络中有用户负分摊,此时各节点初始分摊量相加小于实际总损耗,为了完全回收损耗成本,还要进行第二步。
(2) 计算各节点最终分摊量。以初始分摊量为基础,引入奖惩系数β(0 < β≤1),通过奖惩系数来增加正分摊量,减小负分摊量,具体如下:
| $ L_{p i}^{\prime \prime}=\left\{\begin{array}{l} L_{p i} \beta \quad L_{p i} \leqslant 0 \\ \frac{L_{p i}}{\beta} \quad L_{p i}>0 \end{array}\right. $ | (14) |
| $ L_{q i}^{\prime \prime}=\left\{\begin{array}{l} L_{q i} \beta \quad L_{q i} \leqslant 0 \\ \frac{L_{q i}}{\beta} \quad L_{q i}>0 \end{array}\right. $ | (15) |
按照式(14)和式(15)计算各节点有功传输、无功传输最终的损耗分摊量,相加等于网络实际损耗,即满足:
| $ \sum\limits_{i=1}^{N-1}\left(L_{p i}^{\prime \prime}+L_{q i}^{\prime \prime}\right)=L $ | (16) |
将式(16)代入式(14)和(15),对此一元二次方程进行求解,可以计算出奖惩系数β:
| $ \left|L_{\mathrm{BS}}\right| \beta^{2}+\left|L_{\text {sum }}\right| \beta-\left|L_{\mathrm{AS}}\right|=0 $ | (17) |
解得:
| $ \beta=\frac{-\left|L_{\text {sum }}\right|+\sqrt{\left|L_{\text {sum }}\right|^{2}+4\left|L_{\mathrm{BS}}\right|\left|L_{\mathrm{AS}}\right|}}{2\left|L_{\mathrm{BS}}\right|} $ | (18) |
显然β>0,由|Lsum|,|LAS|,|LBS|的定义可得:
| $ \begin{gathered} \beta= \\ \frac{\sqrt{\left(\left|L_{\mathrm{AS}}\right|+\left|L_{\mathrm{BS}}\right|\right)^{2}+4\left|L_{\mathrm{BS}}\right|\left|L_{\mathrm{AS}}\right|}-\left(\left|L_{\mathrm{AS}}\right|+\left|L_{\mathrm{BS}}\right|\right)}{2\left|L_{\mathrm{BS}}\right|} \end{gathered} $ | (19) |
令
| $ \beta=\frac{2}{\sqrt{t^{2}+6 t+1}+t+1} $ | (20) |
而t≥0,因此β≤1。通过式(18)和式(19)可以证明0 < β≤1,且β=1时|LBS|=0,即网络中没有进行奖励的用户。
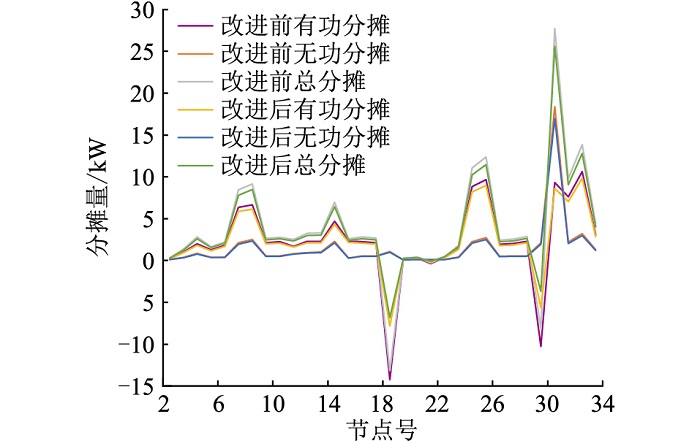
3 IEEE 33节点算例及分析以IEEE 33节点标准算例系统为例进行损耗分摊计算[19]。该配电网电压等级为10 kV,共有33个节点,32条支路。在原系统上接入3个DG,其中节点18接入容量为480 kW的光伏电源,节点21接入容量为200 kW的光伏电源,节点29接入容量为360 kW的光伏电源。分布式光伏电源在各节点消纳后剩余量(功率基值为100 kV ·A)为:节点18注入功率为-0.39+j0.04 MV ·A,节点21注入功率为-0.11+j0.04 MV ·A,节点29注入功率为-0.24+j0.07 MV ·A。用改进后的MLC法对该算例进行损耗分摊,与比例法计算结果对比如图 1所示。
|
图 1 2种分摊方法节点分摊量对比 Fig. 1 Node allocation amount comparison of two allocation methods |
由图 1可知,改进后的MLC法相较于基于比例系数的MLC法,各成员分摊量之间的差距减小。改进前分摊结果中,通过式(7)计算出节点30的MLC值为0.048 3,进而得到节点30分摊功率为27.705 kW,节点18计算出的MLC值为0.036 6,对节点18奖励-13.168 kW,成员分摊差距最大可达40.873 kW,各节点在计算MLC值时,由于节点18、节点21和节点29注入有功为负,所以在计算总损耗时存在正负量抵消的情况,导致计算出的MLC值偏大。改进后的MLC法计算得节点30的MLC值为0.045 1,节点30分摊量为25.619 kW,节点18的MLC为0.021,对节点18进行奖励-6.843 kW,成员间分摊差距最大为32.462 kW。通过改进MLC法,能够解决正负量抵消导致的MLC值偏大的问题,并且能够保证分摊量总和与实际损耗相等。
比较分摊结果可得,改进后的MLC法能修正基于比例系数的MLC法中用户损耗分摊量或奖励过多的情况。改进后的MLC法不仅能真实反映各成员对网络损耗的贡献,保证市场成员内部公平性,还能使市场整体分摊差距减小,保证市场成员外部合理性。
4 结语针对含DG配电网损耗分摊时存在的正、负分摊量抵消的情况,在基于比例系数的MLC法的基础上,按分摊量绝对值大小分摊网络损耗,引入奖惩系数,通过减小奖励,增加惩罚,使得回收损耗等于网络实际损耗,建立适用于含DG配电网损耗分摊计算的模型。
分析IEEE 33节点网络算例的计算结果,可知改进的分摊方法既体现了MLC法能够提供明显经济信号的优点,又保留了基于比例系数的MLC法能避免过度回收的优势,还能减小成员之间的分摊差距,将系统中的损耗按实际贡献合理地分摊(或奖励)给各节点成员,对含DG配电网的网络损耗分配的公平合理性具有重要意义。
| [1] |
杨振铨, 项基, 李艳君. 配合主网调度的配电网分布式电源主动控制策略[J]. 中国电机工程学报, 2019, 39(11): 3176-3186. YANG Zhenquan, XIANG Ji, LI Yanjun. Active control strategy of distributed generations for utility grid cooperation in distribution network[J]. Proceedings of the CSEE, 2019, 39(11): 3176-3186. (  0) 0) |
| [2] |
WANG Z J, MADAWALA U K. Modelling and analysis of grid integrated TSCAOI generators for renewable distributed generation systems[J]. CPSS Transactions on Power Electronics and Applications, 2020, 5(4): 372-387. DOI:10.24295/CPSSTPEA.2020.00031 (  0) 0) |
| [3] |
朱星旭, 韩学山, 杨明, 等. 含分布式光伏与储能配电网时变最优潮流追踪的分布式算法[J]. 中国电机工程学报, 2019, 39(9): 2644-2658. ZHU Xingxu, HAN Xueshan, YANG Ming, et al. A distributed algorithm for time-varying optimal power flow tracking in distribution networks with photovoltaics and energy storage[J]. Proceedings of the CSEE, 2019, 39(9): 2644-2658. (  0) 0) |
| [4] |
陆永耕, 李建刚, 黄禹铭, 等. 高渗透率分布式电源控制方法[J]. 发电技术, 2021, 42(1): 103-114. LU Yonggeng, LI Jiangang, HUANG Yuming, et al. High-permeability distributed power control method[J]. Power Generation Technology, 2021, 42(1): 103-114. (  0) 0) |
| [5] |
寇凌峰, 吴鸣, 李洋, 等. 主动配电网分布式有功无功优化调控方法[J]. 中国电机工程学报, 2020, 40(6): 1856-1865. KOU Lingfeng, WU Ming, LI Yang, et al. Optimization and control method of distributed active and reactive power in active distribution network[J]. Proceedings of the CSEE, 2020, 40(6): 1856-1865. (  0) 0) |
| [6] |
GANGULY S, SAMAJPATI D. Distributed generation allocation on radial distribution networks under uncertainties of load and generation using genetic algorithm[J]. IEEE Transactions on Sustainable Energy, 2015, 6(3): 688-697. DOI:10.1109/TSTE.2015.2406915 (  0) 0) |
| [7] |
范明天, 张祖平, 苏傲雪, 等. 主动配电系统可行技术的研究[J]. 中国电机工程学报, 2013, 33(22): 12-18, 5. FAN Mingtian, ZHANG Zuping, SU Aoxue, et al. Enabling technologies for active distribution systems[J]. Proceedings of the CSEE, 2013, 33(22): 12-18, 5. (  0) 0) |
| [8] |
裴哲义, 丁杰, 李晨, 等. 分布式光伏并网问题分析与建议[J]. 中国电力, 2018, 51(10): 80-87. PEI Zheyi, DING Jie, LI Chen, et al. Analysis and suggestions for distributed photovoltaic generation[J]. Electric Power, 2018, 51(10): 80-87. DOI:10.3969/j.issn.1007-3361.2018.10.023 (  0) 0) |
| [9] |
郭清元, 莫超, 吴杰康, 等. 分布式电源接入的配电系统多类型无功源出力优化方法[J]. 电力工程技术, 2020, 39(5): 211-219. GUO Qingyuan, MO Chao, WU Jiekang, et al. Multi-type reactive power output optimization method of distribution system with distributed generations[J]. Electric Power Engineering Technology, 2020, 39(5): 211-219. (  0) 0) |
| [10] |
DASHTAKI A K, HAGHIFAM M R. A new loss estimation method in limited data electric distribution networks[J]. IEEE Transactions on Power Delivery, 2013, 28(4): 2194-2200. DOI:10.1109/TPWRD.2013.2273103 (  0) 0) |
| [11] |
张琦, 陈谦, 周聪, 等. 基于机会约束的含分布式电源配电网网损优化[J]. 供用电, 2020, 37(12): 8-15, 30. ZHANG Qi, CHEN Qian, ZHOU Cong, et al. Loss optimization of distribution network with distributed power source based on chance constraint[J]. Distribution & Utilization, 2020, 37(12): 8-15, 30. (  0) 0) |
| [12] |
陈星莺, 郁清云, 谢俊, 等. 基于利用Aumann-Shapley值分摊网损和排放减少量的DLMP计算研究[J]. 电力自动化设备, 2019, 39(4): 17-23. CHEN Xingying, YU Qingyun, XIE Jun, et al. DLMP calculation based on power loss and emission reduction allocation using Aumann-Shapley method[J]. Electric Power Automation Equipment, 2019, 39(4): 17-23. (  0) 0) |
| [13] |
何引生, 张越. 一种基于改进平均网损的含源配电网网损分摊方法[C]//用电与能效专题讲座暨智能用电及能效管理技术研讨会论文集. 南京, 2019: 269-273, 296. HE Yinsheng, ZHANG Yue. A method for loss allocation of sourced distribution network based on improved average power loss[C]//Special Lectures on Power Consumption and Energy Efficiency and Proceedings of Seminar on Smart Power Consumption and Energy Efficiency Management Technology. Nanjing, 2019: 269-273, 296. (  0) 0) |
| [14] |
JAGTAP K M, KHATOD D K. Current summation based approach for loss allocation with distributed generation[C]//2018 International Conference on Power, Instrumentation, Control and Computing (PICC). Thrissur, India. IEEE, 2018: 1-5.
(  0) 0) |
| [15] |
SHARMA S, ABHYANKAR A R. Loss allocation for weakly meshed distribution system using analytical formulation of shapley value[J]. IEEE Transactions on Power Systems, 2017, 32(2): 1369-1377. (  0) 0) |
| [16] |
ZHANG S, CHEN F, WANG X Z, et al. Study on loss allocation method of distribution network with considering of distributed generation[C]//2020 IEEE/IAS Industrial and Commercial Power System Asia (I & CPS Asia). Weihai, China. IEEE, 2020: 508-512.
(  0) 0) |
| [17] |
YANG T S, GUO Y, DENG L R, et al. A distribution system loss allocation approach based on a modified DistFlow model[C]//2020 IEEE Power & Energy Society General Meeting (PESGM). Montreal, QC, Canada. IEEE, 2020: 1-5.
(  0) 0) |
| [18] |
吴泽穹, 滕欢, 李基康, 等. 配电网节点边际容量成本研究[J]. 科学技术与工程, 2017, 17(8): 176-181. WU Zeqiong, TENG Huan, LI Jikang, et al. Research on locational marginal capacity cost of distribution network[J]. Science Technology and Engineering, 2017, 17(8): 176-181. DOI:10.3969/j.issn.1671-1815.2017.08.029 (  0) 0) |
| [19] |
向明旭, 杨知方, 余娟, 等. 配电网线性潮流模型通式及误差分析[J]. 中国电机工程学报, 2021, 41(6): 2053-2064. XIANG Mingxu, YANG Zhifang, YU Juan, et al. Linear power flow model in distribution network: unified expression and error analysis[J]. Proceedings of the CSEE, 2021, 41(6): 2053-2064. (  0) 0) |
2. State Grid Shanxi Electric Power Company, Taiyuan 030021, China;
3. College of Energy and Electrical Engineering, Hohai University, Nanjing 211100, China
 2022, Vol. 41
2022, Vol. 41


 李蒙赞(1975), 女, 学士, 高级工程师, 从事电力系统分析相关工作(E-mail:
李蒙赞(1975), 女, 学士, 高级工程师, 从事电力系统分析相关工作(E-mail: