文章编号: 2096-3203(2022)01-0084-09 中图分类号: TM711
2. 广东省新能源 电力系统智能运行与控制企业重点实验室, 广东 广州 510663
近年来,国内外发生了多起由连锁故障引发的大停电事故[1-3],造成了巨大的经济损失与恶劣的社会影响。研究表明,在连锁故障的发展过程中极少数线路有至关重要的作用[4],高效且准确地识别出这些关键线路,对于揭示电网薄弱环节、提高电力系统可靠性具有重要的意义。
基于复杂网络理论的关键线路辨识算法首先将电力系统简化为抽象模型,再依据节点介数[5]、线路效能权值[6]、潮流熵[7]等拓扑特征对线路进行重要性排序。此外,亦有学者建立了如ORNL-PSERC-Alaska(OPA)模型[8]、Manchester模型[9]、基于直流潮流法的电力系统解列模拟器(direct current power flow simulator of power system separation,DCSS)模型[10]等连锁故障仿真模型,试图刻画电力系统连锁故障的演化过程,并从中找出对故障发展具有推波助澜作用的关键线路。
上述仿真模型或电力系统实际运行所产生的故障链数据蕴含了丰富的连锁故障信息,通过分析不同故障链间的共同特征及发展规律,同样能实现关键线路的辨识。文献[11]利用Apriori算法对交直流连锁故障链进行频繁项挖掘,有效地识别出危及系统安全的强关联规则;文献[12]通过FP-growth算法对故障链集合进行数据挖掘,辨识出了不同故障发展过程中的危险线路;文献[13]根据故障链集合构建了连锁故障时空图,并从触发与扩大连锁故障2个角度出发,分类辨识出了系统中的脆弱线路。然而,故障链集合中的数据可能由不同的连锁故障演化模式产生,各模式下起主导作用的关键线路亦不尽相同[13]。若在进行关键线路辨识前,预先对故障链序列的相似性进行度量,根据序列间相似的演化规律或关联特征进行聚类,并对相似度较高的故障链集合进行分类评估,可进一步提高关键线路辨识精度与效率[14]。
文中首先根据热量累积效应构建了改进DCSS连锁故障仿真模型,并与随机化学(random chemistry,RC)法相互配合,高效生成了含丰富时序信息的故障链集合。在此基础上,文中引入编辑距离(edit distance, ED)衡量故障链间的相似程度,并通过凝聚式层次聚类算法实现了故障链集合聚类。将完成聚类后的故障链集合分别进行线路风险重要度排序,名次靠前的线路即为相应连锁故障演化模式中起主导作用的关键线路。以Matpower 2 383节点系统为例,对不同算法所辨识的关键线路进行容量扩建,并根据扩容后系统连锁故障风险水平的下降量化比较了所辨识线路的重要程度,对比结果进一步证明了文中所提模型及算法的有效性。
1 连锁故障仿真模型 1.1 故障链集合生成DCSS[10]是一种基于直流潮流法建立的连锁故障仿真模型,主要面向过载主导型连锁故障,考虑在无功较为充足的纯交流系统中因线路过载而发生相继失效的连锁故障过程,其仿真速度快且没有收敛性问题。DCSS模型通过对线路过载功率进行时间积分,模拟反时限保护机制,但当重载线路处于临界状态时,累计积分值可能被多次清零,所求线路跳闸的用时变长,使得模型所描述的故障时序特性可能与实际情况存在较大出入。因此,文中根据热量累积效应[15]建立更合理的改进DCSS连锁故障仿真模型。
首先,假设线路L的潮流PL超过限值Pmax, L,根据线路流过潮流对导线的热效应,可近似计算出线路L在t时刻的瞬时温度TL(t)。
| $ \left\{ \begin{array}{l} {T_L}\left( t \right) = {{\rm{e}}^{ - \nu t}}\left( {{T_L}\left( 0 \right) - {T_{\rm{e}}}\left( {{P_L}} \right)} \right) + {T_{\rm{e}}}\left( {{P_L}} \right)\\ {T_{\rm{e}}}\left( {{P_L}} \right) = \frac{\alpha }{\nu }{\rm{ }}P_L^2 + {T_{{\rm{env}}}} \end{array} \right. $ | (1) |
式中:TL(t)为线路的瞬时温度;PL为线路L流过的功率;Te(PL)为线路流过该功率时的平衡温度;ν,α为线路热效应的相关参数,皆取决于线路本身;Tenv为环境温度;TL(0)为初始温度。
将线路过热保护的温度触发阈值Tmax, L代入式(1),可算得线路L的过热保护动作时间Δttrip, L。
| $ \Delta {t_{{\rm{trip}}, L}} = - {\rm{ }}\frac{1}{\nu }{\rm{ln}}\left( {\frac{{{T_{{\rm{max}}, L}} - {T_{\rm{e}}}\left( {{P_L}} \right)}}{{{T_L}\left( 0 \right) - {T_{\rm{e}}}\left( {{P_L}} \right)}}} \right) $ | (2) |
在给定电网参数的前提下,通过式(2)可快速计算出下一次故障跳闸线路及相应动作时刻。
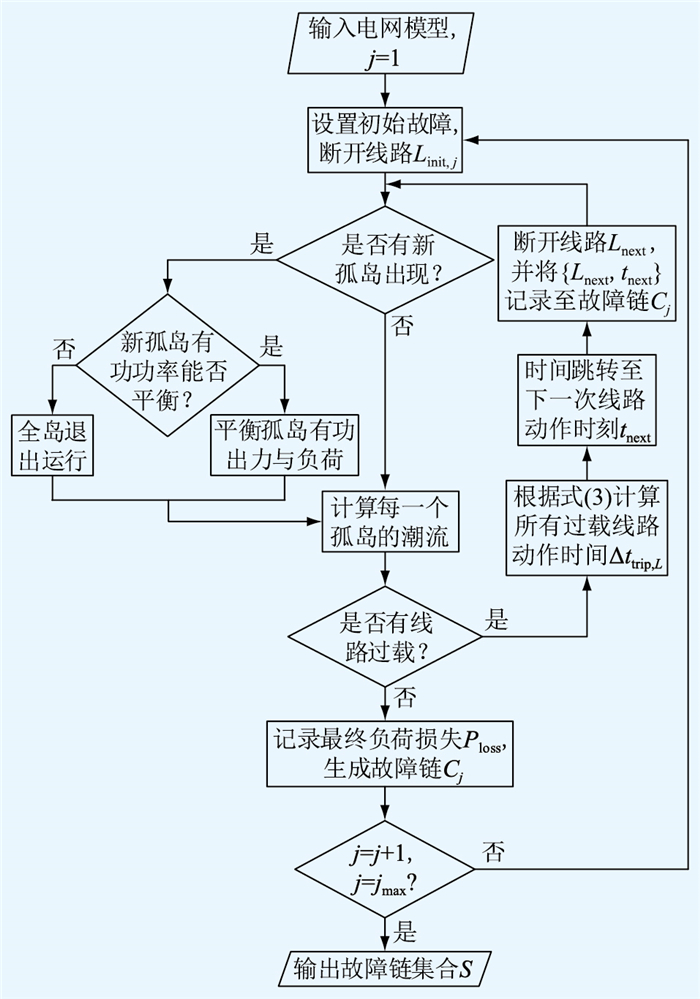
上述所建立的改进DCSS模型能高效且准确地生成故障链集合,具体流程见图 1,具体步骤为:
|
图 1 故障链集合生成流程 Fig. 1 Flow chart of fault chain set generation |
(1) 载入电网模型,初始化电网的运行状态。
(2) 设置初始故障,将相应故障线路作为初始扰动进行开断,第j条故障链Cj的初始故障线路集合为Linit, j。
(3) 通过孤岛判定程序对线路开断后的电网进行孤岛判定。假如有新的孤岛生成则进行发电机有功出力调整,如不能在规定时间内实现负荷与出力之间的平衡,则进行切机切负荷操作;假如没有新的孤岛出现,则直接转至步骤(4)。
(4) 对每一个仍处于运行状态的孤岛执行直流潮流运算。
(5) 依据步骤(4)所算得的潮流结果判断是否有线路过载,如果仍有过载线路,则转至步骤(6),否则转至步骤(7)。
(6) 将过载线路的潮流PL代入式(2),计算下一次线路动作时间Δttrip, L,相应开断线路记为Lnext,总仿真时间跳转至tnext。记录跳闸线路与相应的动作时刻{Lnext, tnext}后跳转至步骤(3)。
(7) 连锁故障仿真过程结束,根据步骤(6)所记录的所有线路开断信息{Lnext, tnext}及最终负荷损失Ploss生成故障链Cj。
(8) 重新选取初始故障线路形成初始故障集Linit, j,并重复步骤(2)~(7)生成故障链Cj,直至故障链样本足够多或满足仿真退出条件。
对于较小的系统,或对计算速度无较高要求的搜索过程,初始故障集Linit, j可设定为系统中所有线路组合,通过遍历法来进行连锁故障分析,但当电网规模较大时,组合规模及计算量急剧增加,将面临“维数灾”的挑战。为兼顾搜索时间与搜索精度,文中采用效率较高的RC法[16]来提高故障链的生成效率。RC法属于无偏抽样,即所得的初始故障集不依赖于任何先验的概率或者指标,生成的故障链集合样本较为全面地涵盖了多种故障演化路径,为后续的聚类分析及数据挖掘提供了更加丰富的数据样本。
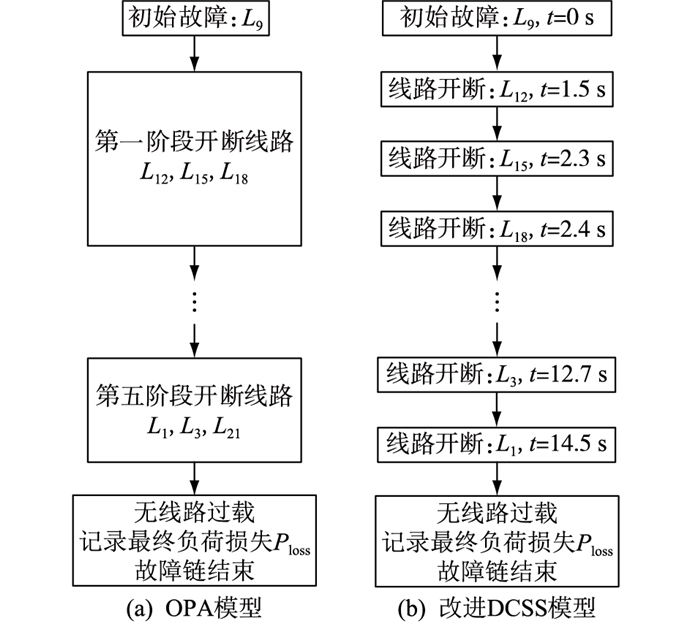
如图 2所示,某些连锁故障仿真模型按故障演化阶段进行线路开断。以OPA快动态过程模型[8]生成的故障链如图 2(a)所示,其同一阶段中多条线路开断,不区分先后顺序,此类故障链易造成无效规则的误筛,增大后续数据挖掘难度。相比之下,如图 2(b)所示的通过改进DCSS模型仿真生成的故障链物理含义明确,包含更丰富的时序信息,既有线路开断的先后顺序,又记录了相应的开断时刻,能较真实地刻画连锁故障的演化过程,为后续分析提供更合理的样本依据。
|
图 2 2类连锁故障仿真模型所生成故障链的对比 Fig. 2 Comparison of fault chains generated by two kinds of cascading failure models |
文中采用文献[17]中的概率风险法进行故障链的风险评估,定义故障链Cj造成的后果与发生概率分别为E(Cj),p(Cj)。
1.2.1 连锁故障后果连锁故障后果通常以系统负荷总损失、电网解列程度、故障链长度(停电线路数)等指标来衡量。负荷损失是连锁故障在电力系统中造成的最直接后果,因此文中采用系统负荷总损失来衡量连锁故障的后果。
| $ E\left( {{C_j}} \right) = {P_{{\rm{loss}}, j}} $ | (3) |
式中:Ploss, j为第j条故障链Cj最终所造成的系统负荷总损失。
1.2.2 连锁故障概率根据1.1节中的定义可知,改进DCSS模型对于任意给定的N-k初始故障能且仅能生成唯一的故障链Cj及相应的负荷损失Ploss, j,即连锁故障的发生概率由N-k初始故障所决定,文中定义故障链概率p(Cj)为:
| $ p\left( {{C_j}} \right) = \prod\limits_{i = 1}^k {} U({L_{{\rm{init}}, i}}) $ | (4) |
式中:k为初始故障元件数;Linit, i为初始故障集Linit, j中的第i线路;U(Linit, i)为线路Linit, i的不可用率,可通过式(5)求得。
| $ U\left( {{L_{{\rm{init}}, i}}} \right) = \lambda {t_{{\rm{Dur}}}}/8\;760 $ | (5) |
式中:λ为线路的平均失效频率;tDur为平均修复时间。独立事件的不可用率乘积表示多条线路同时失效的概率,即为以N-k故障为初始故障的连锁故障发生概率。
将上述的故障链后果和故障链概率相乘,则可计算出事故链的负荷损失期望值R(Cj),用于表征事故链的风险。
| $ R\left( {{C_j}} \right) = E\left( {{C_j}} \right)p({C_j}) $ | (6) |
故障链集合S的连锁故障风险等于所含全部故障链的风险之和。
| $ R\left( S \right) = \sum\limits_{{C_j} \in S}^{} {} R({C_j}) $ | (7) |
在时间序列数据挖掘的诸多任务和问题中,序列相似性度量是最基础的问题。以动态时间归整(dynamic time warping,DTW)算法为代表的时间序列度量方法已广泛应用在电力系统中,其通过对电流、电压等时间序列的波形轮廓进行匹配,完成故障源辨识[18]、扰动分类[19]等任务。而改进DCSS模型所生成的故障链本质是事件序列,如图 2(b)所示,此类序列具有不等长、离散性等特点,因此文中引入更直观的ED算法,计算故障链事件序列间的相似程度,为后续的分类过程提供聚类依据。
ED[20]是指将某一序列Cx通过插入、删除与替换3种编辑操作转换至另一序列Cy所需要的最小操作步数。假设存在2条由改进DCSS模型生成的故障链Cx,Cy,按线路先后开断的次序可表示为:
| $ \left\{ \begin{array}{l} {C_x} = {\rm{ }}\left\{ {{L_{x, 1}}, {L_{x, 2}}, \cdots , {L_{x, m}}} \right\}\\ {C_y} = {\rm{ }}\left\{ {{L_{y, 1}}, {L_{y, 2}}, \cdots , {L_{y, n}}} \right\} \end{array} \right. $ | (8) |
式中:Lx, 1为故障链序列Cx中第1条开断的线路;m为Cx中开断线路的总数(Cy同理)。Cx与Cy之间的ED可通过构造一个(m+1)×(n+1)维矩阵D递归求取,矩阵元素di, j的计算公式为:
| $ \begin{array}{l} {d_{i, j}} = {\rm{min}}({d_{i - 1, j}} + 1, {d_{i, j - 1}} + 1, \\ \;\;\;\;\;\;\;\;\;{d_{i - 1, j - 1}} + {L_{x, i}} \oplus {L_{y, j}}) \end{array} $ | (9) |
特别地,当i=0或j=0时,di, j= max(i, j)。其中,
当故障链序列长度不一致的时候,长序列之间的ED将远大于短序列之间的ED,因此需要对ED进行归一化处理:
| $ d'{_{m, n}} = \frac{{{d_{m, n}}}}{{{\rm{min}}(m, n)}} $ | (10) |
归一化后的ED能较为准确地度量具有不等长、离散性等特点的故障链相似性,提高后续聚类分析的准确性与数据挖掘的效率。
2.2 基于AGNES算法的故障链聚类文中采用凝聚式层次聚类(AGglomerative NESting, AGNES)算法[21],根据2.1节所得的故障链间的ED,完成对故障链集合的聚类分析。
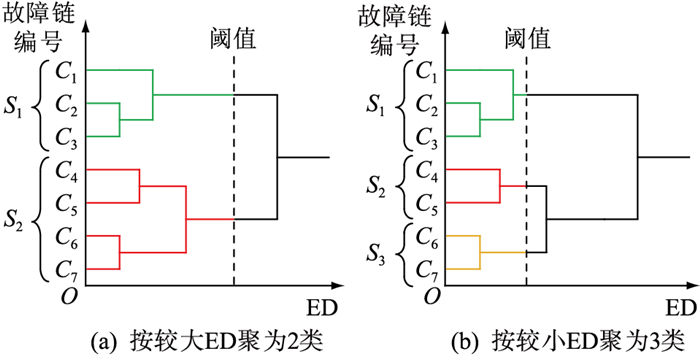
AGNES算法“自底而上”的聚类过程如图 3所示。随着ED的增加,故障链序列逐渐合并,直至最后聚至同一类中。聚类簇数可通过改变截取阈值来灵活调整,而最优聚类簇数可通过Calinski-Harabaz(CH)指标[22]进行评估求取。其中,S为由故障链Cj组成的故障链集合。
|
图 3 层次聚类 Fig. 3 Tree diagram of hierarchical clustering |
以CH指标较高的簇数对故障链集合进行划分后,同集合内故障链相似度较高,即线路开断的先后次序相近,则可近似认为此类故障链在同一连锁故障演化模式下产生。对各类故障链集合分别进行关键线路辨识,找出各连锁故障演化模式下具有推波助澜作用的薄弱环节,能有效提高辨识精度。
3 连锁故障关键线路辨识 3.1 线路风险重要度假设故障链集合S共有m条故障链,其中有h(h≤m)条故障链包含线路Li,即满足:
| $ {L_i} \in {C_j}\;\;\;j = 1, 2, \cdots , h $ | (11) |
则线路Li的风险重要度的计算公式为:
| $ I\left( {{L_i}} \right) = \sum\limits_{j = 1}^h {} {\rm{ }}(\omega \left( {{L_i}, {C_j}} \right)E({C_j})) $ | (12) |
式中:ω(Li, Cj)为线路Li在故障链Cj中的重要度权重。考虑到最终负荷损失是由故障链中所有线路开断造成的,且连锁故障演变过程存在级联性,因此认为先开断线路对负荷损失的影响高于后开断线路,相应权重也更高。文中假设重要度权重随开断顺序按指数分布递减,则计算公式为:
| $ \omega \left( {{L_i}, {C_j}} \right) = {{\rm{e}}^{ - \mu (X({L_i}, {C_j}) - 1)}} $ | (13) |
式中:X(Li, Cj)为线路Li在故障链Cj中的顺序;μ为调节系数,用于调整重要度权重递减的速度,μ越小,故障链中的线路权重分布就越均衡。当μ=0.1时,按开断顺序算得的权重依次为1.000,0.915,0.819,0.741,0.670等。
综合来看,线路所涉及的连锁故障越多、引起的故障越严重、开断顺序越靠前,则对应的线路风险重要度也会更高。按I(Li)对所有线路进行排序,排名靠前的线路即为连锁故障演化过程中的关键线路。
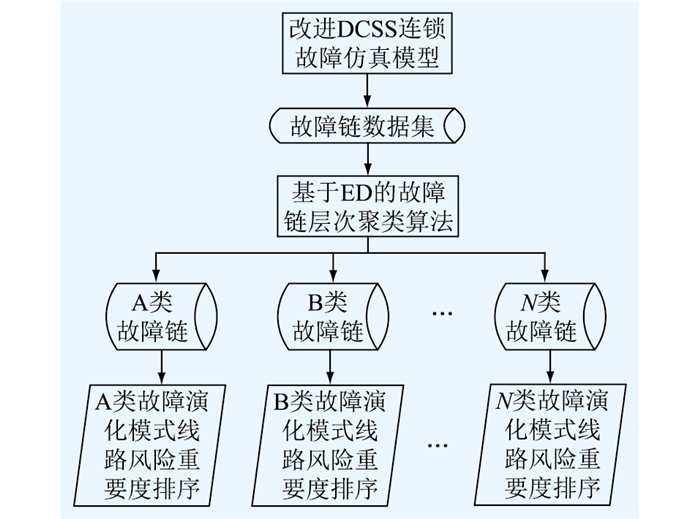
3.2 关键线路辨识流程关键线路辨识流程如图 4所示。首先通过改进DCSS模型生成故障链集合,然后计算故障链之间的ED,并通过选取合适的ED阈值,应用AGNES算法完成对故障链的聚类,分别计算出同类故障链集合中各线路的风险重要度,识别出各类故障演化模式下的关键线路。
|
图 4 关键线路辨识流程 Fig. 4 Flow chart of critical line identification |
为了进一步证明文中算法在大电网中的有效性,文中采用Matpower软件包中的算例case2383wp进行仿真研究,该算例的详细数据参见文献[23]。
4.1 故障链集合生成文中采用抽样效率较高的RC法,通过调用改进DCSS连锁故障仿真程序对Matpower软件包中的2 383节点模型(满足“N-1”准则)进行模拟。
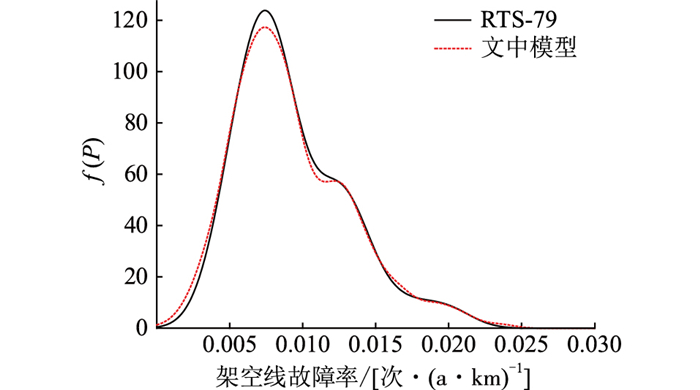
2 383节点模型数据不包含线路平均故障频率等参数,因此文中将IEEE RTS-79可靠性标准测试模型的架空线故障率随机映射至文中模型的2 896条线路上,使得2个模型的线路故障率概率密度分布函数f(P)相近,如图 5所示。
|
图 5 RTS-79与文中模型的线路故障率概率密度曲线对比 Fig. 5 Comparison of line failure rate probability density function of RTS-79 and the model in this paper |
将映射所得的故障率与实际线路长度相乘得到平均失效频率λ之后,根据式(5)可算得相应线路的不可用率U(Linit, i),其中线路平均修复时间tDur取IEEE RTS-79标准数据的中位值10 h。
为平衡故障链搜索时间与搜索广度,文中以负荷损失超过2 701 MW(占总负荷的10%)为筛选阈值,经过10万次RC法循环仿真,共生成424条由不同N-2初始故障引发的故障链。对所生成的故障链进行线路频次统计,统计情况如表 1所示。
|
|
表 1 故障链集合中线路出现频次统计 Table 1 Frequency statistics of occurrence of lines in fault chain set |
由表 1可知,仅有极少数线路在故障链集合中出现超过300次,而同时有多达397条线路出现小于27次。线路的频次分布具有明显的“长尾效应”,即故障链集合中很少一部分线路的出现次数远高于其他线路,表明这些线路与严重连锁故障的触发与演化存在密切关系。
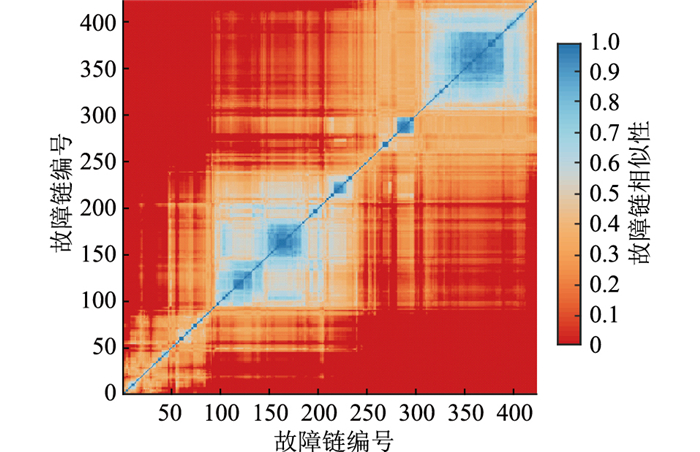
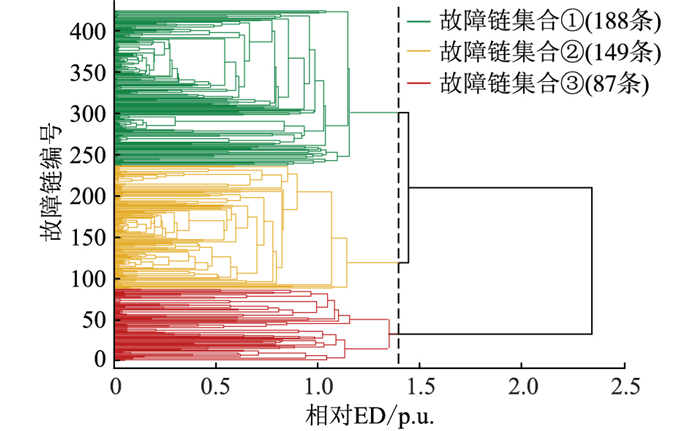
4.2 故障链聚类结果对4.1节所得的故障链集合采用ED算法,根据424条故障链之间的相似性可绘制出如图 6所示的热力图。以故障链间的ED为依据进行层次聚类,可得如图 7所示的聚类过程树状图。
|
图 6 故障链相似性热力图 Fig. 6 Fault chain similarity heat map |
|
图 7 故障链集合层次聚类 Fig. 7 Hierarchical clustering of fault chain set |
不同簇数的聚类方案所得的CH评估指标如图 8所示,由图 8可知,当簇数为3时,CH指标最高,表明相应的聚类方案最优。3类故障链已在图 7中以不同颜色标注,分别记为故障链集合①~③,同类集合中的故障链相似性较高,表明所涉及的连锁故障演化路径重合度较高。

|
图 8 不同聚类簇数对应的CH指标 Fig. 8 CH index corresponding to different cluster numbers |
对故障链集合①~③分别进行信息统计,所得结果如表 2所示,其中平均故障链长度是指集合内每条故障链所开断线路条数的平均值。
|
|
表 2 不同故障链集合的基本信息统计 Table 2 Basic information statistics of different fault chain sets |
根据式(12)-式(13)分别计算各故障链集合中的线路风险重要度I(Li),调节系数μ取0.1。将所有线路按I(Li)进行降序排列,排名靠前的线路即为相应故障链集合中的关键线路。表 3中分别列出了聚类前后各类故障链集合中线路风险重要度排名前5的关键线路,括号内的数字表示对应线路在未聚类时故障链总集合中的重要度排名。
|
|
表 3 不同故障链集合中的关键线路排序 Table 3 Critical lines rank in different fault chain sets |
结合表 2、表 3可知,由于故障链集合①中的故障链占比较大(44.3%),若直接对未聚类的故障链总集合进行关键线路辨识,前5名分别为{L15, L96, L680, L113, L8},此结果与故障集合①中的关键线路前5名{L15, L96, L113, L24, L680}高度重合,但故障链集合②与③中的关键线路在未聚类故障链总集合中的排名普遍较低,意味着若不进行聚类极有可能造成故障链集合②与③中关键线路的漏选。
4.4 辨识结果有效性验证文中参考文献[24],对算法所辨识的关键线路进行容量扩建,并基于相同的初始故障集重新进行连锁故障仿真,扩容后故障链集合的连锁故障风险R(S)下降得越多,证明相应算法所辨识的线路在故障链集合中的重要性越高。
线路容量的调整在实际系统中可通过更换线路、增加并行线路等措施实现[25]。在文中的算例中,线路扩建容量设定为额定容量的2倍,根据4.3节的关键线路辨识结果分别设置以下2组扩容方案。
(1) 扩容方案一。按未聚类时的辨识结果取线路风险重要度排序的前3名,具体扩容线路为{L15, L96, L680}。
(2) 扩容方案二。按聚类后的辨识结果分别取各故障链集合中的线路风险重要度排序第1名,具体扩容线路为{L15, L250, L169}。
另设置随机扩容方案,即随机选取3条故障链集合中所涉及的线路进行扩容。
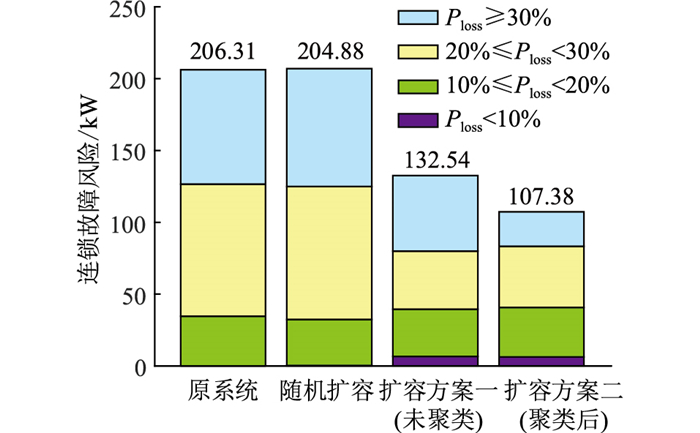
对上述3种方案扩容后的2 383节点系统重新进行424组连锁故障仿真并进行风险评估,其中随机扩容的连锁故障风险由20次仿真后取平均值所得,原系统及3类方案下的风险如图 9所示。
|
图 9 不同扩容方案下系统连锁故障风险比较 Fig. 9 Comparison of system cascading failure risks under different expansion plans |
由图 9可知,上述的3种扩容方案将连锁故障整体风险由206.31 kW分别降至204.88 kW,132.54 kW,107.38 kW。随机扩容方案下,整体风险平均仅降低了1.43 kW,证明随机选取的线路重要性较低。这是因为线路的重要性分布与4.1节所述的频次分布类似,皆具有“长尾效应”,随机选取线路大概率为重要性不高的非关键线路。而在基于线路风险重要度排序的2种扩容方案中,方案二能最大程度地降低连锁故障风险,其中Ploss≥30%的大规模连锁故障风险由79.8 kW减少至24.1 kW,明显低于方案一的52.6 kW,证明分类辨识所得关键线路的重要性更高。
为进一步探究辨识结果对连锁故障风险的影响,按故障链集合①~③对原系统及扩容方案一、二下的连锁故障风险进行分类统计,对比结果如表 4所示,其中,括号内表示相较于原系统连锁故障风险下降的百分比。
|
|
表 4 不同扩容方案对特定故障链集合风险的影响 Table 4 The impact of different expansion schemes on the specific failure chain set risk |
由表 4可知,在未聚类时,方案一使得故障链集合①中的连锁故障风险下降了50.7%,但同时仅让故障链集合③的连锁故障风险降低了0.36%。因此未聚类时所辨识的线路对大规模故障链集合而言重要性较高,对其他规模较小故障链集合的影响力则相对有限。相比之下,方案二下的整体风险下降了48.0%,故障链集合①~③的风险分别下降了58.6%,74.4%,11.0%,皆优于方案一,证明分类辨识的线路集合{L15, L250, L169}在各类集合中的重要程度皆高于未聚类前的辨识结果。
上述结果说明,若直接对未聚类的424条故障链进行关键线路辨识,辨识结果将倾向于占比较大的故障链集合,难以全面顾及各类连锁故障演化模式,所辨识的线路在规模较小集合中的重要性也相对较低。相比之下,基于故障链聚类算法的分类辨识结果使得各类连锁故障风险的下降程度更高,进一步证明了故障链聚类算法对于提高关键线路辨识效果的有效性。
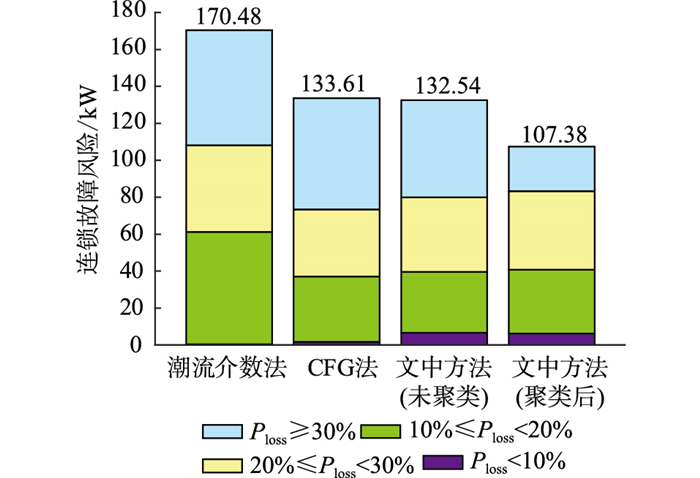
4.5 与其他关键线路辨识算法的比较为进一步验证文中所提关键线路分类辨识算法的有效性,文中针对2 383节点模型采用潮流介数法[26-27]与连锁故障关系图(cascading failure graph,CFG)法[25],分别得到线路重要性排序,根据排序结果前3名分别设置相应的线路扩容方案。其中潮流介数法具体扩容线路为{L169, L52, L23},CFG法具体扩容线路为{L8, L38, L90}。对扩容后的系统重新进行仿真与连锁故障风险评估,所得结果与4.4节的扩容方案一、二比较,对比结果如图 10所示。
|
图 10 不同算法所辨识线路扩容后的连锁故障风险比较 Fig. 10 Comparison of cascading failure risks of lines identified by different algorithms after capacity expansion s |
由图 10可知,由于潮流介数法未考虑连锁故障的演化过程,因此辨识结果对降低系统连锁故障风险的作用较小;CFG法与文中所提方法(未聚类)虽能一定程度降低系统连锁故障风险,但缺乏对各类连锁故障演化模式的综合考虑,作用依然有限;相比之下,基于故障链聚类的关键线路扩容方案能够最大程度地降低系统的连锁故障风险,证明文中方法(聚类后)所辨识线路的重要程度更高。
5 结语文中首先建立了改进DCSS仿真模型,并对过载主导型连锁故障进行仿真,生成含丰富时序信息的故障链集合。针对现有关键线路辨识算法未能对各类故障演化模式予以全面考虑的不足,文中提出了基于ED的故障链聚类算法,对相似度较高的故障链集合进行分类评估,能够更加精确地揭露特定演化路径下的薄弱环节,可进一步提高关键线路的辨识精度与效率。以Matpower 2 383节点系统为例,通过对关键线路进行扩建,以扩容前后的连锁故障风险水平为依据,量化比较了各类算法所辨识线路的重要性,进一步证明了所提模型及算法的有效性。文中的研究工作还可从以下方面进一步完善和深入:
(1) 随着高压直流的投运及大量电力电子器件在电力系统中应用,连锁故障过程中的无功问题、交直流耦合问题日益突出,基于更复杂模型及其故障链数据集的关键线路辨识将是后续研究的要点。
(2) 文中从故障演化路径相似性的角度进行聚类,后续可进一步考虑如失负荷量、系统解列程度等其他变量作为聚类依据。
| [1] |
李保杰, 李进波, 李洪杰, 等. 土耳其"3.31"大停电事故的分析及对我国电网安全运行的启示[J]. 中国电机工程学报, 2016, 36(21): 5788-5795, 6021. LI Baojie, LI Jinbo, LI Hongjie, et al. Analysis of Turkish blackout on March 31, 2015 and lessons on China power grid[J]. Proceedings of the CSEE, 2016, 36(21): 5788-5795, 6021. (  0) 0) |
| [2] |
汤涌, 卜广全, 易俊. 印度"7.30"、"7.31"大停电事故分析及启示[J]. 中国电机工程学报, 2012, 32(25): 167-174, 23. TANG Yong, BU Guangquan, YI Jun. Analysis and lessons of the blackout in Indian power grid on July 30 and 31, 2012[J]. Proceedings of the Chinese Society for Electrical Engineering, 2012, 32(25): 167-174, 23. (  0) 0) |
| [3] |
严道波, 文劲宇, 杜治, 等. 2021年得州大停电事故分析及其对电网规划管理的启示[J]. 电力系统保护与控制, 2021, 49(9): 121-128. YAN Daobo, WEN Jinyu, DU Zhi, et al. Analysis of Texas blackout in 2021 and its enlightenment to power system planning management[J]. Power System Protection and Control, 2021, 49(9): 121-128. (  0) 0) |
| [4] |
YANGY F, GUAN X H, ZHAI Q Z. Fast grid security assessment with N-K contingencies[J]. 2017 IEEE Power & Energy Society General Meeting, 2017, 1. (  0) 0) |
| [5] |
梁颖, 方瑞明, 卢小芬, 等. 基于复杂网络理论的电力系统脆弱线路辨识研究现状[J]. 电力系统保护与控制, 2012, 40(20): 151-155. LIANG Ying, FANG Ruiming, LU Xiaofen, et al. Research status of power system vulnerable line identification based on complex-network theory[J]. Power System Protection and Control, 2012, 40(20): 151-155. DOI:10.7667/j.issn.1674-3415.2012.20.027 (  0) 0) |
| [6] |
吴晨, 韩海腾, 祁万春, 等. 基于改进线路效能的电网脆弱性辨识方法研究[J]. 电力工程技术, 2018, 37(5): 64-68. WU Chen, HAN Haiteng, QI Wanchun, et al. Vulnerability identification in power systems based on an improved line-efficiency evaluation approach[J]. Electric Power Engineering Technology, 2018, 37(5): 64-68. DOI:10.3969/j.issn.1009-0665.2018.05.013 (  0) 0) |
| [7] |
李勇, 刘俊勇, 刘晓宇, 等. 基于潮流熵的电网连锁故障传播元件的脆弱性评估[J]. 电力系统自动化, 2012, 36(19): 11-16. LI Yong, LIU Junyong, LIU Xiaoyu, et al. Vulnerability assessment in power grid cascading failures based on entropy of power flow[J]. Automation of Electric Power Systems, 2012, 36(19): 11-16. (  0) 0) |
| [8] |
张振安, 郭金鹏, 张雪敏, 等. 考虑频率稳定的大停电事故模型及应用[J]. 电力系统及其自动化学报, 2015, 27(4): 26-32. ZHANG Zhen'an, GUO Jinpeng, ZHANG Xuemin, et al. Blackout model and its application considering frequency stability[J]. Proceedings of the CSU-EPSA, 2015, 27(4): 26-32. DOI:10.3969/j.issn.1003-8930.2015.04.005 (  0) 0) |
| [9] |
ALIZADEH MOUSAVI O, CHERKAOUI R, BOZORG M. Blackouts risk evaluation by Monte Carlo simulation regarding cascading outages and system frequency deviation[J]. Electric Power Systems Research, 2012, 89: 157-164. DOI:10.1016/j.epsr.2012.03.004 (  0) 0) |
| [10] |
EPPSTEIN M, HINES P. A ″random chemistry″ algorithm for identifying collections of multiple contingencies that initiate cascading failure[J]. 2013 IEEE Power & Energy Society General Meeting, 2013, 1. (  0) 0) |
| [11] |
肖遥, 过羿, 谢佳, 等. 基于Apriori算法的连锁故障机理研究[J]. 电力学报, 2017, 32(1): 22-27, 69. XIAO Yao, GUO Yi, XIE Jia, et al. Esearch on the mechanism of cascading failure based on Apriori algorithm[J]. Journal of Electric Power, 2017, 32(1): 22-27, 69. (  0) 0) |
| [12] |
周强明, 姜盛波, 鲁鸿毅, 等. 基于FP-growth算法的大电网关键线路辨识方法[J]. 电力自动化设备, 2018, 38(4): 89-95. ZHOU Qiangming, JIANG Shengbo, LU Hongyi, et al. Critical line identification method based on FP-growth algorithm for large power grid[J]. Electric Power Automation Equipment, 2018, 38(4): 89-95. (  0) 0) |
| [13] |
刘豫航, 黄少伟, 梅生伟, 等. 基于序列模式挖掘的电力系统连锁故障模式分析方法[J]. 电力系统自动化, 2019, 43(6): 34-40. LIU Yuhang, HUANG Shaowei, MEI Shengwei, et al. Analysis on pattern of power system cascading failure based on sequential pattern mining[J]. Automation of Electric Power Systems, 2019, 43(6): 34-40. (  0) 0) |
| [14] |
陈海燕, 刘晨晖, 孙博. 时间序列数据挖掘的相似性度量综述[J]. 控制与决策, 2017, 32(1): 1-11. CHEN Haiyan, LIU Chenhui, SUN Bo. Survey on similarity measurement of time series data mining[J]. Control and Decision, 2017, 32(1): 1-11. (  0) 0) |
| [15] |
ANGHEL M, WERLEY K A, MOTTER A E. Stochastic model for power grid dynamics[C]//2007 40th Annual Hawaii International Conference on System Sciences (HICSS'07). Waikoloa, HI, USA. IEEE, 2007: 113.
(  0) 0) |
| [16] |
REZAEI P, HINES P D H, EPPSTEIN M J. Estimating cascading failure risk with random chemistry[J]. IEEE Transactions on Power Systems, 2015, 30(5): 2726-2735. DOI:10.1109/TPWRS.2014.2361735 (  0) 0) |
| [17] |
李文沅. 电力系统风险评估: 模型方法和应用[M]. 北京: 科学出版社, 2006. LI Wenxuan. Power system risk assessment: model method and application[M]. Beijing: Science Press, 2006. (  0) 0) |
| [18] |
邱海峰, 陈兵, 袁晓冬, 等. 基于动态时间弯曲距离的电压暂降源辨识方法[J]. 电力系统保护与控制, 2017, 45(13): 7-13. QIU Haifeng, CHEN Bing, YUAN Xiaodong, et al. Identification of voltage sag sources based on DTW[J]. Power System Protection and Control, 2017, 45(13): 7-13. DOI:10.7667/PSPC161018 (  0) 0) |
| [19] |
吴杰, 吕春媚, 崔彪. 基于小波轮廓描述符和动态时间扭曲的电压扰动分类[J]. 电工电能新技术, 2015, 34(4): 62-67, 80. WU Jie, LYU Chunmei, CUI Biao. Identification of disturbance signals based on wavelet boundary descriptors and dynamic time warping[J]. Advanced Technology of Electrical Engineering and Energy, 2015, 34(4): 62-67, 80. DOI:10.3969/j.issn.1003-3076.2015.04.011 (  0) 0) |
| [20] |
RISTAD E S, YIANILOS P N. Learning string-edit distance[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1998, 20(5): 522-532. DOI:10.1109/34.682181 (  0) 0) |
| [21] |
孙即祥. 现代模式识别[M]. 2版. 北京: 高等教育出版社, 2008. SUN Jixiang. Modern pattern recognition[M]. 2nd ed. Beijing: Higher Education Press, 2008. (  0) 0) |
| [22] |
CALINSKI T, HARABASZ J. A dendrite method for cluster analysis[J]. Communications in Statistics-Simulation and Computation, 1974, 3(1): 1-27. DOI:10.1080/03610917408548446 (  0) 0) |
| [23] |
RAY Z. CASE2383WP power flow data for polish system-winter 1999-2000 peak[EB/OL]. (2018-10-09)[2021-04-10]. https://github.com/MATPOWER/matpower/blob/master/data/case2383wp.m.
(  0) 0) |
| [24] |
LI L Z, WU H, SONG Y H, et al. A state-failure-network method to identify critical components in power systems[J]. Electric Power Systems Research, 2020, 181: 106192. DOI:10.1016/j.epsr.2019.106192 (  0) 0) |
| [25] |
HINES P D H, DOBSON I, REZAEI P. Cascading power outages propagate locally in an influence graph that is not the actual grid topology[J]. IEEE Transactions on Power Systems, 2017, 32(2): 958-967. (  0) 0) |
| [26] |
刘文颖, 梁才, 徐鹏, 等. 基于潮流介数的电力系统关键线路辨识[J]. 中国电机工程学报, 2013, 33(31): 90-98, 11. LIU Wenying, LIANG Cai, XU Peng, et al. Identification of critical line in power systems based on flow betweenness[J]. Proceedings of the CSEE, 2013, 33(31): 90-98, 11. (  0) 0) |
| [27] |
陶鸿飞, 谢栋, 赵福林, 等. 含大规模风电并网电力系统的关键线路综合辨识[J]. 电力系统保护与控制, 2020, 48(6): 115-123. TAO Hongfei, XIE Dong, ZHAO Fulin, et al. Comprehensive identification of critical line in power systems with large-scale wind power integration[J]. Power System Protection and Control, 2020, 48(6): 115-123. (  0) 0) |
2. Guangdong Province Key Laboratory of Intelligent Operation and Control for New Energy Power System, Guangzhou 510663, China
 2022, Vol. 41
2022, Vol. 41


 黎寿涛(1996), 男, 硕士在读, 研究方向为连锁故障仿真及风险评估(E-mail:
黎寿涛(1996), 男, 硕士在读, 研究方向为连锁故障仿真及风险评估(E-mail: