文章编号: 2096-3203(2022)01-0093-08 中图分类号: TM732
2. 国网山西省电力公司朔州供电公司, 山西 朔州 036004
近年来,风电入网规模日益增大,为应对风电大规模并网带来的问题,配置储能系统成为减少弃风和增强系统安全可靠性的一项重要措施。储能系统具有时空转移特性,不仅能减少弃风,还能利用峰谷电价提高电网经济性[1]。抽水蓄能电站具有启停迅速、灵活可靠、绿色环保的特点,可以作为风电并网的储能系统。
目前,国内外对风电并网和风蓄联合运行进行了大量研究。文献[2]针对风电并网制定负荷需求对峰谷时段的电价响应策略,降低风电机组的运行成本。文献[3-4]指出,在风电场中加入抽水蓄能系统,配置不同抽水和发电容量可以不同程度地增加系统综合效益,并确定了风电场中最优的抽水蓄能容量。文献[5]建立风-光-水-气-火-储联合优化调度模型,能提高可再生能源的消纳能力,降低系统运行成本。文献[6-7]建立含抽水蓄能机组的安全约束机组组合模型,充分发挥抽水蓄能机组的削峰填谷能力以应对风电的不确定性所带来的问题。文献[8]利用多种能源的时空互补特性来充分消纳新能源,减少弃风量,提高系统运行效益。上述研究均从风电消纳最多和抽水蓄能的容量配置最优进行分析,并未考虑在风蓄火联合运行情况下,运用抽水蓄能机组的储能作用减少弃风,提高系统经济效益,增加旋转备用容量,减少火电机组出力波动,增加系统安全可靠性。
文中综合考虑风蓄火联合优化运行的风电消纳、机组组合和系统旋转备用容量问题,将风蓄作为整体,风蓄火联合出力,增加了火电机组出力的平稳性,可为系统提供充足的旋转备用容量,提高系统的安全性和可靠性。采用内外两层模型嵌套求解思想使基于风电不确定性的风蓄火联合优化调度收益最大化。内层以风蓄联合机组收益最大和风电并网出力波动最小为目标确定调度周期内抽水蓄能机组的抽水功率和发电功率;外层在此基础上计及不同置信水平下的风电预测误差,建立包含系统旋转备用成本的以风蓄火联合收益最大为目标的模型。模型中的风蓄火机组分别接在IEEE 30节点系统相对应的节点上,运用粒子群优化-遗传算法(particle swarm optimization and genetic algorithm,PSO-GA)混合优化算法求解该模型,分析有无抽水蓄能机组在不同置信水平下对系统风电消纳和经济收益的影响。
1 风电出力概率分布特性风电出力的不确定性对电网调度的影响日益加剧,降低出力不确定性引起的电网调度运行风险已经迫在眉睫。风电出力预测主要有点预测[9]、区间预测[10]和概率预测[11],这些预测方法都不能忽略预测误差。正态分布拟合常用于研究风电功率预测误差和负荷预测误差[12-13],但有别于风电出力区间的实际情况。文献[14]采用Beta概率密度函数拟合风电出力,优点为:(1) 服从Beta分布对象的自变量的取值范围是[0, 1],与风电出力标幺值区间一致;(2) Beta分布的2个形状参数不同,可描述不同情况下的风电出力曲线。
综上所述,文中选择Beta概率密度函数拟合风电出力。风电出力具有较大的随机性和波动性,可选择将风电出力预测分为多个预测区间,不同区间分别进行Beta拟合,得到不同的拟合参数,从而减小风电拟合误差。根据文献[15]假设一个预测区间段的风电预测值相同,即等于该区间范围内的预测平均值。服从Beta分布的风电出力的概率密度函数如式(1)所示。
| $ F(p)=\frac{p^{\alpha-1}(1-p)^{\beta-1}}{B(\alpha, \beta)} $ | (1) |
其中:
| $ B(\alpha, \beta)=\int_{0}^{1} p^{\alpha-1}(1-p)^{\beta-1} \mathrm{~d} p $ | (2) |
式中:p为风电实际出力标幺值,是一个服从Beta分布的随机变量;B(α, β)为Beta函数,α,β为参数。α,β和风电预测出力的方差σ2、均值μ有关,如式(3)和式(4)所示。
| $ \alpha=\frac{(1-\mu) \mu^{2}}{\sigma^{2}}-\mu $ | (3) |
| $ \beta=\frac{1-\mu}{\mu} \alpha $ | (4) |
系统中若仅考虑风电机组和火电机组,则风电场的随机性和波动性以及风电并网给系统带来的反调峰特性,会造成一系列不良影响。如使火电机组频繁启停,降低火电机组使用年限,还可能会由于风电机组在短时间内出力波动巨大,导致火电机组备用不足,产生大量弃风,降低联合运行的经济效益,使利用新能源降低环境污染达不到预期效果。因此,考虑加入较大规模的储能系统,用于系统调峰及为系统提供备用容量。抽水蓄能机组启停迅速,具有分钟级别的响应能力,故选择抽水蓄能作为文中储能系统。电网负荷处于低谷时段时,抽水蓄能机组处于抽水状态,用水泵将下游的水抽到上水库中,将多余的电能转化为具有势能的水能存储起来;电网负荷处于高峰时段时,抽水蓄能机组处于发电状态,将存储在上水库中的水能转化为电能。
2.1 模型搭建采用内外两层嵌套模型,内层模型优化结果作为已知值代入外层模型,外层模型优化结果反馈在内层模型中,进行迭代寻优。反复迭代直到达到结束条件,结束寻优,获得目标所求最优值。内外两层嵌套模型的求解流程如图 1所示。
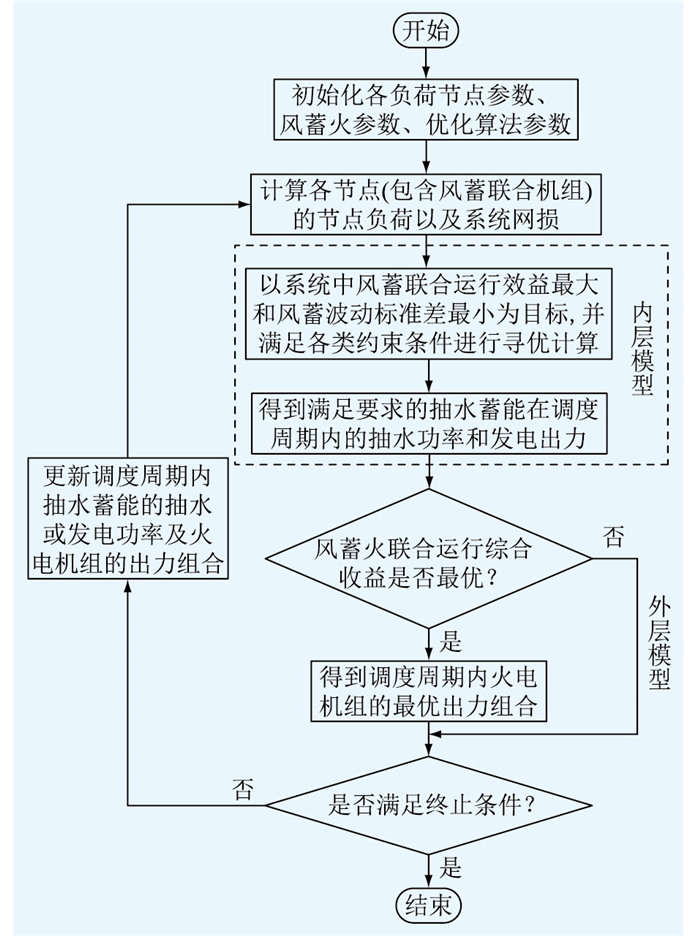
|
图 1 内外两层嵌套模型求解流程 Fig. 1 Flow chart for solving the internal and external nested model |
(1) 风蓄联合运行效益最大。为了减少风电的波动性和随机性给系统带来的不确定性,文中将抽水蓄能机组和风电机组当成一个整体,利用风电出力补偿抽水蓄能机组抽水的储能。
| $ \max F_{\text {whep }}=\sum\limits_{t=1}^{T}\left(P_{\mathrm{wh}, t} C_{\mathrm{f}, t}\right)-\sum\limits_{t=1}^{T}\left(P_{\mathrm{p}, t} C_{\mathrm{p}, t}\right) $ | (5) |
| $ P_{\mathrm{wh}, t}= \begin{cases}P_{\mathrm{w}, t}-P_{\mathrm{p}, t} u_{\mathrm{p}, t} & P_{\mathrm{w}, t} \geqslant \bar{P}_{\mathrm{w}} \\ P_{\mathrm{w}, t}+P_{\mathrm{g}, t} u_{\mathrm{g}, t} & P_{\mathrm{w}, t}<\bar{P}_{\mathrm{w}}\end{cases} $ | (6) |
| $ u_{\mathrm{g}, t}+u_{\mathrm{p}, t} \leqslant 1 $ | (7) |
| $ \bar{P}_{\mathrm{w}}=\sum\limits_{t=1}^{T} P_{\mathrm{w}, t} / T $ | (8) |
| $ P_{\mathrm{dl}, t}=P_{\mathrm{w}, t}-P_{\mathrm{p}, t}-P_{\mathrm{wc}, t} $ | (9) |
式中:Fwhep为风蓄联合运行收益;Pwh, t为t时段风蓄联合机组的并网出力;Cf, t,Cp, t分别为t时段的上网电价和抽水蓄能机组的抽水电价;Pp, t,Pg, t分别为t时段抽蓄机组的抽水功率和发电功率;Pw, t,Pw分别为t时段风电机组的预测功率和风电机组在调度周期内的平均预测功率;up, t,ug, t为0-1变量,分别表示抽水蓄能机组是否处于抽水状态和发电状态,为1表示处于该状态,为0表示不处于该状态;T=24,为1个调度周期(即24 h的总时段数);Pdl, t为t时段风电弃风功率;Pwc, t为风电并网出力,系统中含有抽水蓄能机组时,表示t时段的风蓄联合出力,即Pwh, t,不含抽水蓄能机组时,表示风电的并网出力,即Pw, t。
(2) 风蓄联合运行波动标准差最小。风蓄联合运行波动标准差越小,风蓄联合并网功率越平滑。
| $ \min F_{\mathrm{whvv}}=\sqrt{\frac{1}{T} \sum\limits_{t=1}^{T}\left(P_{\mathrm{wh}, t}-\bar{P}_{\mathrm{wh}}\right)^{2}} $ | (10) |
| $ \bar{P}_{\mathrm{wh}}=\sum\limits_{t=1}^{T} P_{\mathrm{wh}, t} / T $ | (11) |
式中:Fwhvv为风蓄联合运行的波动标准差;Pwh为风蓄联合机组的平均并网出力。
2.2.2 约束条件(1) 风蓄联合运行并网出力在抽水蓄能机组抽水状态和发电状态下的约束。
| $ u_{\mathrm{g}, t} P_{\mathrm{w}, t} \leqslant P_{\mathrm{wh}, t}^{\mathrm{g}} \leqslant P_{\mathrm{wh}, \max } $ | (12) |
| $ P_{\mathrm{wh}, \min } \leqslant P_{\mathrm{wh}, t}^{\mathrm{p}} \leqslant u_{\mathrm{p}, t} P_{\mathrm{w}, t} $ | (13) |
式中:Pwh, min,Pwh, max分别为风蓄机组联合运行并网出力的最小值和最大值;Pwh, tg,Pwh, tp分别为t时段抽水蓄能机组处于发电状态和抽水状态下的风蓄联合运行并网出力。
(2) 上水库储能约束。
| $ E_{\min } \leqslant E_{t} \leqslant E_{\max } $ | (14) |
| $ E_{t+1}=E_{t}+\Delta t\left(P_{\mathrm{p}, t} \eta_{\mathrm{p}} u_{\mathrm{p}, t}-\frac{P_{\mathrm{g}, t}}{\eta_{\mathrm{g}}} u_{\mathrm{g}, t}\right) $ | (15) |
式中:Emax,Emin分别为上水库最大储能和最小储能;Et为t时段上水库储能;Δt为1个调度时段长度,即1 h;ηg,ηp分别为抽水蓄能机组的发电效率和抽水效率。
(3) 抽水蓄能机组在抽水状态和发电状态下的功率约束。
| $ P_{\mathrm{g}, \min } \leqslant P_{\mathrm{g}, t} \leqslant \min \left(P_{\mathrm{g}, \max }, \frac{E_{t}}{\Delta t} \eta_{\mathrm{g}}\right) $ | (16) |
| $ P_{\mathrm{p}, \min } \leqslant P_{\mathrm{p}, t} \leqslant \min \left(P_{\mathrm{p}, \max }, \frac{E_{\max }-E_{t-1}}{\Delta t \eta_{\mathrm{p}}}\right) $ | (17) |
式中:Pg, max,Pp, max分别为抽蓄机组发电功率最大值和抽水功率最大值;Pg, min,Pp, min分别为抽蓄机组发电功率最小值和抽水功率最小值。
(4) 风电机组预测功率约束。
| $ 0 \leqslant P_{\mathrm{w}, t} \leqslant P_{\mathrm{we}} $ | (18) |
式中:Pwe为风电机组额定出力。
2.3 外层模型 2.3.1 目标函数外层模型的目标是系统的风蓄火综合运行收益最大,即:
| $ \max F_{\text {whef }}=C_{\text {whf }}-C_{\text {fuel }}-C_{\text {envir }}-C_{\mathrm{r}}-C_{\mathrm{Aw}} $ | (19) |
式中:Fwhfef为风蓄火综合运行收益;Cwhf为风蓄火联合运行并网收益;Cfuel为火电机组的燃料成本;Cenvir为火电机组的环境成本;Cr为旋转备用成本;CAw为弃风成本。
风蓄火联合运行并网的收益为:
| $ C_{\mathrm{whf}}=\sum\limits_{t=1}^{T}\left(P_{\mathrm{wh}, t} \lambda_{\mathrm{wh}}+\sum\limits_{i=1}^{N} P_{i, t} \lambda_{\mathrm{G}}\right) $ | (20) |
式中:λwh,λG分别为风蓄联合运行电价和火电上网电价;N为火电机组的机组数;Pi, t为火电机组i在t时段的出力。
火电机组的燃料成本为:
| $ C_{\text {fuel }}=\sum\limits_{t=1}^{T} \sum\limits_{i=1}^{N}\left(a_{i} u_{i, t}+b_{i} P_{i, t}+c_{i} P_{i, t}^{2}\right) $ | (21) |
式中:ai,bi,ci为火电机组i的燃料成本系数;ui, t为0-1变量,表示火电机组i在t时段的开停机状态,为1表示处于运行状态,为0表示处于停机状态。
火电机组的环境成本为:
| $ \begin{aligned} C_{\text {envir }}=& \sum\limits_{i=1}^{N} \sum\limits_{t=1}^{T}\left[\lambda_{\text {envir }, \mathrm{c}}\left(\alpha_{\mathrm{c}, i} u_{i, t}+\beta_{\mathrm{c}, i} P_{i, t}+\gamma_{\mathrm{c}, i} P_{i, t}^{2}\right)+\right.\\ &\left.\lambda_{\text {envir}, \mathrm{s}}\left(\alpha_{\mathrm{s}, i} u_{i, t}+\beta_{\mathrm{s}, i} P_{i, t}+\gamma_{\mathrm{s}, i} P_{i, t}^{2}\right)\right] \end{aligned} $ | (22) |
式中:λenvir, c,λenvir, s分别为火电发电产生CO2和SO2的环境成本系数;αc, i,βc, i,γc, i为火电机组i的CO2排放系数;αs, i,βs, i,γs, i为火电机组i的SO2排放系数。
旋转备用成本为:
| $ C_{\mathrm{r}}=\sum\limits_{t=1}^{T}\left(R_{\mathrm{u}, t} \lambda_{\mathrm{u}}+R_{\mathrm{d}, t} \lambda_{\mathrm{d}}\right) $ | (23) |
式中:Ru,t,Rd,t分别为t时段系统的上、下旋转备用需求;λu,λd分别为上、下旋转备用需求成本系数。
弃风成本为:
| $ C_{\mathrm{Aw}}=k_{\mathrm{w}} \sum\limits_{t=1}^{T}\left(P_{\mathrm{w}, t}-P_{\mathrm{wcr}, t}\right) $ | (24) |
式中:kw为弃风惩罚成本系数;Pwcr, t为t时段风电并网限制出力。
2.3.2 约束条件(1) 系统功率平衡约束。
| $ \sum\limits_{t=1}^{T}\left(P_{\mathrm{wh}, t}+\sum\limits_{i=1}^{N} P_{i, t}\right)=\sum\limits_{t=1}^{T} P_{\mathrm{load}, t} $ | (25) |
式中:Pload, t为t时段系统负荷功率。
(2) 火电机组的出力约束。
| $ u_{i, t} P_{i, \min } \leqslant P_{i, t} \leqslant u_{i, t} P_{i, \max } $ | (26) |
式中:Pi, max,Pi, min分别为火电机组i的出力最大值和最小值。
(3) 火电机组爬坡约束[16]。
| $ \left\{\begin{array}{l} P_{i, t+1}-P_{i, t} \leqslant r_{\text {up }, i} \Delta t u_{i, t}+P_{i, \max }\left(1-u_{i, t}\right) \\ P_{i, t}-P_{i, t+1} \leqslant r_{\mathrm{dn}, i} \Delta t u_{i, t+1}+P_{i, \max }\left(1-u_{i, t+1}\right) \end{array}\right. $ | (27) |
式中:rup, i,rdn, i分别为火电机组i的向上、向下爬坡速率。
(4) 旋转备用约束。上旋转备用约束:
| $ \begin{gathered} P\left\{\sum\limits_{i=1}^{N} S_{\mathrm{up}, i, t}+R_{\mathrm{up}, \mathrm{wh}, t} \geqslant R_{\mathrm{up}, \mathrm{load}, t}+\right. \\ \left.\max \left(P_{\mathrm{w}, t}-p^{\prime}, 0\right)\right\} \geqslant \alpha \end{gathered} $ | (28) |
| $ S_{\text {up }, i, t}=\min \left(P_{i, \max }-P_{i, t}, r_{\text {up }, i} T_{10}\right) $ | (29) |
| $ R_{\text {up }, \text { wh }, t}=\min \left(P_{\mathrm{g}, \max }-P_{\mathrm{g}, t}, E_{t} \eta_{\mathrm{g}}\right) $ | (30) |
下旋转备用约束:
| $ \begin{gathered} P\left\{\sum\limits_{i=1}^{N} S_{\mathrm{dn}, i, t}+R_{\mathrm{dn}, \mathrm{wh}, t} \geqslant R_{\mathrm{dn}, \mathrm{load}, t}+\right. \\ \left.\max \left(p^{\prime}-P_{\mathrm{w}, t}, 0\right)\right\} \geqslant \alpha \end{gathered} $ | (31) |
| $ S_{\mathrm{dn}, i, t}=\min \left(P_{i, t}-P_{i, \min }, r_{\mathrm{dn}, i} T_{10}\right) $ | (32) |
| $ R_{\mathrm{dn}, \mathrm{wh}, t}=\min \left(P_{\mathrm{p}, \max }-P_{\mathrm{p}, t}, \frac{E_{\max }-E_{t}}{\eta_{\mathrm{p}}}\right) $ | (33) |
式中:Sup, i, t,Sdn, i, t分别为火电机组i在t时段能够提供的上、下旋转备用容量;Rup, load, t,Rdn, load, t为t时段系统负荷的备用需求容量,一般取该时段系统总负荷的5%;Rup, wh, t,Rdn, wh, t分别为t时段抽水蓄能机组提供的上、下旋转备用容量;P{·}为事件的可信性;p′为风电实际出力;α为上、下旋转备用约束置信水平;T10为系统旋转备用响应时间,文中取10 min。
2.4 随机变量的处理采用机会约束规划处理随机变量,机会约束规划是随机规划的一个分支,主要用来解决含有随机变量且不利情况下可能不满足约束条件的模型,要求约束条件成立的概率不小于一定的置信水平[17-19]。机会约束规划求解含有随机变量的模型如式(34)所示。
| $ \begin{cases}\max \bar{f} \\ {\rm{s.t.}}\ \ \ \ P\{f(\boldsymbol{x}, \boldsymbol{\xi}) \geqslant \bar{f}\} \geqslant \alpha \\ \ \ \ \ \ \ \ \ \ \ P\left\{g_{j}(\boldsymbol{x}, \boldsymbol{\xi}) \leqslant 0\right\} \geqslant \beta \quad j=1,2, \cdots, m\end{cases} $ | (34) |
式中:f(x, ξ)为目标函数;f为目标函数的置信水平不低于α时所取的最大值;gj(x, ξ)为约束函数;x为决策向量;ξ为随机参数向量;α,β为决策者事先给定的置信水平。
文中模型的随机变量为风电实际出力标幺值p,风电出力是满足Beta分布的概率密度函数。因此,在给定置信水平α时,可通过机会约束规划,将上、下旋转备用约束转换为确定性约束。将式(29)、式(32)转换为式(36)、式(37)。
| $ \begin{aligned} &P\left\{\sum\limits_{i=1}^{N} S_{\mathrm{up}, i, t}+R_{\mathrm{up}, \mathrm{wh}, t} \geqslant R_{\mathrm{up}, \mathrm{load}, t}+\right. \\ &\left.P_{\mathrm{we}} \int_{a}^{P_{\mathrm{wn}, t}}\left(P_{\mathrm{wn}, t}-p\right) F(p) \mathrm{d} p\right\} \geqslant \alpha \end{aligned} $ | (35) |
| $ \begin{aligned} &P\left\{\sum\limits_{i=1}^{N} S_{\mathrm{dn}, i, t}+R_{\mathrm{dn}, \mathrm{wh}, t} \geqslant R_{\mathrm{dn}, \mathrm{load}, t}+\right. \\ &\left.P_{\mathrm{we}} \int_{P_{\mathrm{wn}, t}}^{b}\left(p-P_{\mathrm{wn}, t}\right) F(p) \mathrm{d} p\right\} \geqslant \alpha \end{aligned} $ | (36) |
| $ P_{\mathrm{wn}, t}=P_{\mathrm{w}, t} / P_{\mathrm{we}} $ | (37) |
式中:Pwn, t为风电预测出力标幺值;a,b分别为风电出力满足置信水平α时对应区间的下限和上限。a,b与置信水平α有如下关系:
| $ \int_{0}^{a} f(p) \mathrm{d} p=(1-\alpha) \int_{0}^{P_{\mathrm{wn}, t}} f(p) \mathrm{d} p $ | (38) |
| $ \int_{0}^{b} f(p) \mathrm{d} p=\alpha+(1-\alpha) \int_{0}^{P_{\mathrm{wn}, t}} f(p) \mathrm{d} p $ | (39) |
内外两层模型的目标都是求最优值,可采用PSO-GA混合优化算法[20]对其进行求解。GA具有较优的全局搜索能力,不易陷入局部最优,但计算时间较长,求解效率低。PSO算法具有快速寻优能力,但优化模式单一,易陷入局部最优解。因此可将2种算法相结合,则该混合算法既有快速寻优能力,又有全局搜索能力,弥补了单一算法的不足。
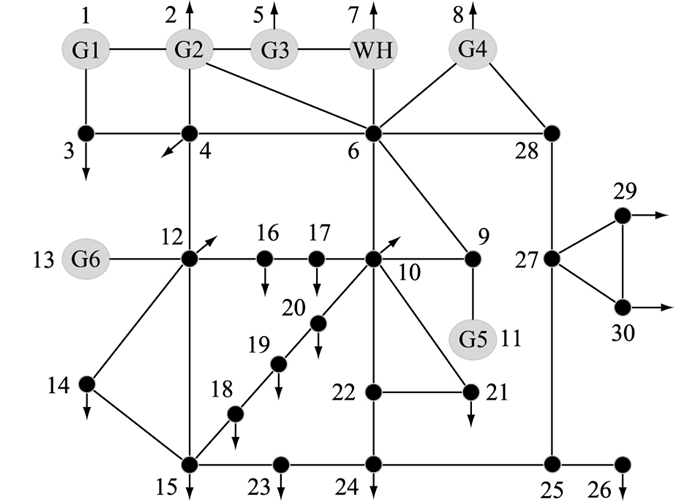
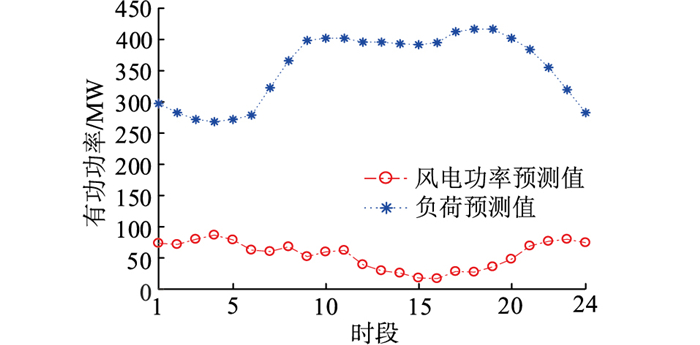
3 算例分析 3.1 参数设定为验证文中内外两层模型的有效性,采用IEEE 30节点6机系统进行仿真检验运算。火电机组参数见表 1。节点7接入风蓄联合运行机组,修改后的IEEE 30节点系统示意见图 2。风电场的额定容量为100 MW,抽水蓄能的最大发电功率为40 MW,最大抽水功率为60 MW,可逆式水轮机的发电效率为0.8,抽水效率为0.85,上游水库的初始储能为50 MW·h。为简化模型,风电24个时段的发电功率均满足参数α=2.767,β=2.517的Beta概率密度函数。24 h风电功率预测与负荷预测见图 3。采用CO2和SO2的环境成本来量化火电机组对环境的影响,环境成本系数均为3.5元/kg,上、下旋转备用成本系数分别取140元/(MW·h)和80元/(MW·h),弃风惩罚成本系数取210元/(MW·h)。
|
|
表 1 火电机组参数 Table 1 Thermal unit parameters |
|
图 2 修改后的IEEE 30节点示意 Fig. 2 Schematic diagram of modified IEEE 30-bus distribution system |
|
图 3 风电功率预测与负荷预测 Fig. 3 Wind power prediction and load prediction |
选用PSO-GA混合优化算法,PSO初始规模取100个,PSO迭代次数取20次。依照目标要求选取M个最优粒子作为遗传操作的初始值,M取40,然后再经过遗传操作生成L个粒子,L取60。重新生成100个粒子作为下一次迭代时粒子群算法更新的粒子速度和位置的初始值,依次继续优化,直到满足优化算法停止条件。学习因子c1,c2均取2,惯性权重最大值wmax和最小值wmin分别取0.9和0.3,速度最大、最小更新值vmax和vmin分别取10和-10, GA的交叉概率pc和变异概率pm分别取0.7和0.3[16]。
风蓄火的峰、谷上网电价Ct,以及抽水蓄能机组的抽水电价Cp, t参考国外的风电价格体系,具体如下:
| $ \left\{\begin{array}{l} C_{t}=540 \text { 元 } /(\mathrm{MW} \cdot \mathrm{h}) \quad 0 \leqslant t<8 \\ C_{t}=1038.4 \text { 元 } /(\mathrm{MW} \cdot \mathrm{h}) \quad 8 \leqslant t<22 \\ C_{t}=540 \text { 元 } /(\mathrm{MW} \cdot \mathrm{h}) \quad 22 \leqslant t<24 \\ C_{\mathrm{p}, t}=0.25 C_{t} \end{array}\right. $ | (41) |
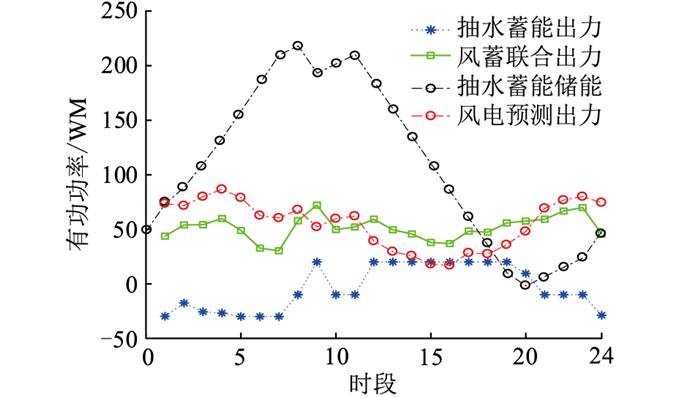
文中通过内层所建模型,采用PSO-GA混合优化算法求得风蓄并网情况下,抽水蓄能在整个调度周期(24 h)的抽水功率、发电功率、风蓄联合出力以及抽水蓄能的储能,具体如图 4所示。
|
图 4 风蓄联合运行时各有功功率曲线 Fig. 4 Active power curves during wind-storage combined operation |
图 4中,抽水蓄能出力为正表示抽水蓄能机组处于发电状态,为负表示抽水蓄能机组处于抽水状态。在日前风电预测功率中,时段1-8中风电预测功率大于风电平均预测功率,此时抽水蓄能机组处于抽水状态;时段9中风电预测功率小于风电平均预测功率,此时抽水蓄能机组处于发电状态;时段12-20中风力发电较少,低于平均预测功率,且负荷处于较高的状态,此时抽水蓄能机组以较高的发电功率运行。由于受到上水库储能约束的影响,时段20的抽水蓄能发电功率降低。为了比较加入抽水蓄能前后,不是多余的水能发电替代风电和火电机组出力,要求调度周期末的上水库储能不低于调度周期前上水库的初始储能。从图 4中可以看出,抽水蓄能储能在调度周期始末时刻都是50 MW,整个风蓄联合运行过程,体现了抽水蓄能的时空转移特性,把多余的风电转换为水能储存在上水库中用于补充风电出力不足的时段。风蓄合作调度过程中,在满足模型约束条件下,总弃风量为0 MW·h,风电的并网出力标准差为14 MW。而无抽水蓄能的风电并网中,总弃风量为47 MW·h,风电的并网出力标准差为19.7 MW。
综上可知,在风电并网中加入抽水蓄能作为储能不但可以改善风电的反调峰特性,减小风电并网的标准差和常规机组的出力波动,还可以减少弃风量,增加发电企业的经济收益,同时减少环境污染,实现从传统能源向清洁能源改革的环境效益。
在外层模型中,求得整个调度周期中不同置信水平下风蓄火联合运行的经济收益和上、下旋转备用需求容量,如表 2所示。
|
|
表 2 不同置信水平下风蓄火联合运行的优化结果 Table 2 Optimization results of combined operation of wind, storage and fire under different confidence levels |
可知,随着置信水平的降低,上、下旋转备用需求容量也在降低,发电企业的收益增加。置信水平的高低反映系统可靠性的高低,置信水平越高,系统可靠性越高。由表 2可知,系统可靠性的高低与收益成反比,发电企业在尽力获得最大经济收益的同时须考虑系统的可靠性高低。在整个调度周期中,火电机组和抽水蓄能可以提供较大的下旋转备用容量,用来满足负荷和风电不确定性带来的下旋转备用需求容量。调度周期内,不同置信水平下系统上旋转备用需求容量和风蓄火运行提供的上旋备用容量对比如图 5所示。
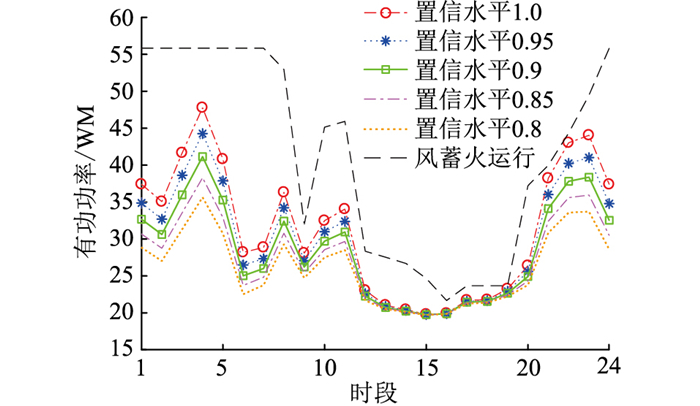
|
图 5 上旋转备用和需求容量对比 Fig. 5 Comparison of upper rotary reserve and required capacity |
图 5中,风蓄火联合运行提供的上旋转备用满足所有置信水平下的系统上旋转备用需求容量。系统中含抽水蓄能机组时,系统的可靠性高。此时发电企业在寻求更大收益的同时也可以在满足较高的置信水平下安排机组出力,使发电策略处于较高的可靠性。文中发电企业可选择在置信水平处于0.9时安排机组出力,此时发电收益较大,且备用需求也满足整个调度周期时段要求。置信水平为0.9时火电机组的出力策略如图 6所示。结果显示,在调度周期的时段1-7和时段21-24,负荷处于较低状态,机组4处于下边界状态,没有选择停机,原因是此时系统收益较大且系统需要火电机组为系统提供上旋转备用,提高系统的可靠性。时段9-20中,由于系统负荷较大,机组G5和G6基本都处于完全出力状态。
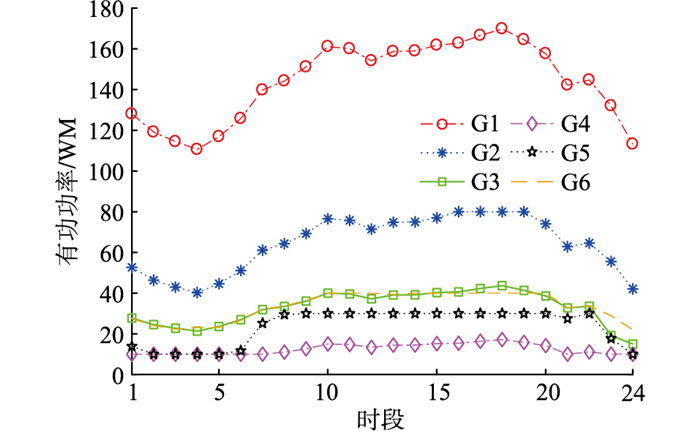
|
图 6 置信水平为0.9时各时段的机组出力计划 Fig. 6 Unit output plan for 24 hours under 0.9 confidence level |
当发电系统中不考虑抽水蓄能机组,只有风电和火电机组出力时,风电的波动性较大,为了满足系统可靠性,必须满足该时间段风电和负荷的备用需求容量,此时会有弃风现象,并且目标中考虑了弃风惩罚,所以在相应置信水平下对比可知,含有抽水蓄能的系统收益高于仅含风火系统的收益。各个置信水平下,不含抽水蓄能机组的系统收益和含有抽水蓄能机组的经济收益如表 3所示。
|
|
表 3 不同置信水平下有无抽蓄机组的系统收益对比 Table 3 Comparison of system revenue with and without pumping unit under different confidence level |
随着置信水平的降低, 系统的经济收益增加。在最终作决策时要在两者之间进行权衡,满足可靠性的同时又要使经济性达到较高的要求,实现发电企业和用户的利益最大化。
4 结论文中提出了考虑风电不确定性的风蓄火联合调度优化模型,通过建立内外双层嵌套求解模型研究系统中有无抽水蓄能机组在不同置信水平下的发电企业经济收益。采用Beta概率密度函数拟合不同时期的风电出力,将抽水蓄能机组和风电打捆处理,利用机会约束规划处理风电的不确定性,分析求解随机变量处于不同置信水平、系统中有无抽水蓄能机组对系统旋转备用、风电消纳以及经济调度的影响,并采用PSO-GA混合优化算法在IEEE 30节点系统上求解。通过以上仿真分析,得出如下结论:(1) 通过对比一般风电系统的调度,系统中加入抽水蓄能机组,利用储能系统的时空转移特性,减少了风电的弃风量和传统机组的燃煤量,保护环境的同时增加了发电企业的经济收益。(2) 采用风蓄联合运行,可降低风电并网的波动性,提高整个系统的机组运行平稳性。
| [1] |
佟晶晶, 温俊强, 王丹, 等. 基于分时电价的电动汽车多目标优化充电策略[J]. 电力系统保护与控制, 2016, 44(1): 17-23. TONG Jingjing, WEN Junqiang, WANG Dan, et al. Multi-objective optimization charging strategy for plug-in electric vehicles based on time-of-use price[J]. Power System Protection and Control, 2016, 44(1): 17-23. (  0) 0) |
| [2] |
刘军, 宋词, 程军照, 等. 考虑风电及分时电价的机组组合问题研究[J]. 智慧电力, 2020, 48(5): 14-20, 33. LIU Jun, SONG Ci, CHENG Junzhao, et al. Unit combination considering wind power and time-sharing electricity price[J]. Smart Power, 2020, 48(5): 14-20, 33. DOI:10.3969/j.issn.1673-7598.2020.05.003 (  0) 0) |
| [3] |
易琛, 任建文, 于佳. 风蓄联合系统的抽水蓄能容量优化[J]. 中国电力, 2018, 51(2): 99-104, 124. YI Chen, REN Jianwen, YU Jia. Research on capacity optimization of pumped-storage power station with wind farm[J]. Electric Power, 2018, 51(2): 99-104, 124. (  0) 0) |
| [4] |
盛四清, 孙晓霞. 利用风蓄联合削峰的电力系统经济调度[J]. 电网技术, 2014, 38(9): 2484-2489. SHENG Siqing, SUN Xiaoxia. An economic dispatching strategy of peak load shifting by wind farm and pumped storage plant[J]. Power System Technology, 2014, 38(9): 2484-2489. (  0) 0) |
| [5] |
李志伟, 赵书强, 刘金山. 基于机会约束目标规划的风-光-水-气-火-储联合优化调度[J]. 电力自动化设备, 2019, 39(8): 214-223. LI Zhiwei, ZHAO Shuqiang, LIU Jinshan. Coordinated optimal dispatch of wind-photovoltaic-hydro-gas-thermal-storage system based on chance-constrained goal programming[J]. Electric Power Automation Equipment, 2019, 39(8): 214-223. (  0) 0) |
| [6] |
卢艺, 卢苑, 梁俊文, 等. 含抽水蓄能电网安全约束机组组合问题的混合整数线性规划算法[J]. 电力系统保护与控制, 2019, 47(3): 39-47. LU Yi, LU Yuan, LIANG Junwen, et al. Mixed integer linear programming algorithm for solving security constrained unit commitment problem of power grid with pumped storage hydro[J]. Power System Protection and Control, 2019, 47(3): 39-47. (  0) 0) |
| [7] |
夏沛, 邓长虹, 龙志君, 等. 含抽水蓄能机组的风电消纳鲁棒机组组合[J]. 电力系统自动化, 2018, 42(19): 41-49. XIA Pei, DENG Changhong, LONG Zhijun, et al. Robust unit commitment with pumped storage units for wind power accommodation[J]. Automation of Electric Power Systems, 2018, 42(19): 41-49. DOI:10.7500/AEPS20171217002 (  0) 0) |
| [8] |
夏新华, 高宗和, 李恒强, 等. 考虑时空互补特性的风光水火多能源基地联合优化调度[J]. 电力工程技术, 2017, 36(5): 59-65. XIA Xinhua, GAO Zonghe, LI Hengqiang, et al. Combined optimization dispatching of multi-source hybrid power bases considering the time-space complementary characteristics[J]. Electric Power Engineering Technology, 2017, 36(5): 59-65. DOI:10.3969/j.issn.1009-0665.2017.05.010 (  0) 0) |
| [9] |
王松峰, 蔺红. 考虑气象相似日GA-BP预测风电短期出力[J]. 水力发电, 2019, 45(7): 120-124. WANG Songfeng, LIN Hong. GA-BP prediction on short-term output of wind power considering the weather similarity day[J]. Water Power, 2019, 45(7): 120-124. DOI:10.3969/j.issn.0559-9342.2019.07.026 (  0) 0) |
| [10] |
陈好杰, 程浩忠, 徐国栋, 等. 基于云理论的风电场群长期出力区间预测[J]. 电力系统保护与控制, 2019, 47(3): 110-117. CHEN Haojie, CHENG Haozhong, XU Guodong, et al. Interval prediction for long-term wind power of wind farm clusters based on cloud theory[J]. Power System Protection and Control, 2019, 47(3): 110-117. (  0) 0) |
| [11] |
叶一达, 魏林君, 乔颖, 等. 非参数条件概率预测提高风电消纳的优化方法[J]. 电网技术, 2017, 41(5): 1443-1450. YE Yida, WEI Linjun, QIAO Ying, et al. Optimal method of improving wind power accommodation by nonparametric conditional probabilistic forecasting[J]. Power System Technology, 2017, 41(5): 1443-1450. (  0) 0) |
| [12] |
刘燕华, 李伟花, 刘冲, 等. 短期风电功率预测误差的混合偏态分布模型[J]. 中国电机工程学报, 2015, 35(10): 2375-2382. LIU Yanhua, LI Weihua, LIU Chong, et al. Mixed skew distribution model of short-term wind power prediction error[J]. Proceedings of the CSEE, 2015, 35(10): 2375-2382. (  0) 0) |
| [13] |
张刘冬, 殷明慧, 宋坤隆, 等. 基于净负荷分步建模的旋转备用优化确定风险分析方法[J]. 电力系统自动化, 2015, 39(24): 16-22. ZHANG Liudong, YIN Minghui, SONG Kunlong, et al. Risk analysing method of optimizing spinning reserve requirements based on multi-step modeling of net demand[J]. Automation of Electric Power Systems, 2015, 39(24): 16-22. DOI:10.7500/AEPS20150307005 (  0) 0) |
| [14] |
DOQUET M. Use of a stochastic process to sample wind power curves in planning studies[C]//2007 IEEE Lausanne Power Tech. Lausanne, Switzerland. IEEE, 2007: 663-670.
(  0) 0) |
| [15] |
BLUDSZUWEIT H, DOMINGUEZ-NAVARRO J A, LLOMBART A. Statistical analysis of wind power forecast error[J]. IEEE Transactions on Power Systems, 2008, 23(3): 983-991. DOI:10.1109/TPWRS.2008.922526 (  0) 0) |
| [16] |
雷宇, 杨明, 韩学山. 基于场景分析的含风电系统机组组合的两阶段随机优化[J]. 电力系统保护与控制, 2012, 40(23): 58-67. LEI Yu, YANG Ming, HAN Xueshan. A two-stage stochastic optimization of unit commitment considering wind power based on scenario analysis[J]. Power System Protection and Control, 2012, 40(23): 58-67. DOI:10.7667/j.issn.1674-3415.2012.23.011 (  0) 0) |
| [17] |
赵冬梅, 殷加玞. 考虑源荷双侧不确定性的模糊随机机会约束优先目标规划调度模型[J]. 电工技术学报, 2018, 33(5): 1076-1085. ZHAO Dongmei, YIN Jiafu. Fuzzy random chance constrained preemptive goal programming scheduling model considering source-side and load-side uncertainty[J]. Transactions of China Electrotechnical Society, 2018, 33(5): 1076-1085. (  0) 0) |
| [18] |
李捷, 杨霖. 基于小波变换与机会约束规划的风电储能容量配置[J]. 电力需求侧管理, 2021, 23(2): 37-42. LI Jie, YANG Lin. Wind power storage capacity configuration based on wavelet transform and chance constrained programming[J]. Power Demand Side Management, 2021, 23(2): 37-42. DOI:10.3969/j.issn.1009-1831.2021.02.007 (  0) 0) |
| [19] |
张琦, 陈谦, 周聪, 等. 基于机会约束的含分布式电源配电网网损优化[J]. 供用电, 2020, 37(12): 8-15, 30. ZHANG Qi, CHEN Qian, ZHOU Cong, et al. Loss optimization of distribution network with distributed power source based on chance constraint[J]. Distribution & Utilization, 2020, 37(12): 8-15, 30. (  0) 0) |
| [20] |
於世为, 魏一鸣, 诸克军. 基于粒子群-遗传的混合优化算法[J]. 系统工程与电子技术, 2011, 33(7): 1647-1652. YU Shiwei, WEI Yiming, ZHU Kejun. Hybrid optimization algorithms based on particle swarm optimization and genetic algorithm[J]. Systems Engineering and Electronics, 2011, 33(7): 1647-1652. DOI:10.3969/j.issn.1001-506X.2011.07.41 (  0) 0) |
2. State Grid Shuozhou Power Supply Company of Shanxi Electric Power Company, Shuozhou 036004, China
 2022, Vol. 41
2022, Vol. 41


 王博(1996), 男, 硕士, 研究方向为新能源接入下的运行与控制(E-mail:
王博(1996), 男, 硕士, 研究方向为新能源接入下的运行与控制(E-mail: