文章编号: 2096-3203(2022)01-0207-06 中图分类号: TM744
2. 广东电网有限责任公司广州供电局, 广东 广州 510620;
3. 福州大学电气工程与自动化学院, 福建 福州 350116
若电力系统稳定性受到破坏,不仅会给人民生活带来不便,而且会造成巨大的经济损失,因此有必要进一步加强电力系统监控[1-3]。目前,传统的暂态稳定性评估方法主要有时域仿真法[4]和直接法[5]。随着大规模电网复杂性的增加,这些传统方法的耗时逐步增加,难以满足在线评估应用的要求。
随着电网同步相量测量装置(phasor measurement unit, PMU)的逐步安装以及通信技术的快速发展,控制中心已经能够实时获取系统各个动态过程的响应信息,这为电力系统的在线监测与分析奠定了基础[6-7]。机器学习算法凭借其计算速度快、准确性高等优点,被广泛应用于电力系统暂态稳定的在线评估。浅层学习算法在暂态稳定评估应用方面已经有了大量研究[8-13]。浅层学习算法需要先进行特征量的提取,特征量提取的合理性影响着判别结果的准确性。而深度学习模型具有多隐藏层的网络结构,将高维度的原始特征量输入到模型中,深度学习算法便能够实现相关特征量的快速分离和提取[14]。常用的深度学习模型有深度置信网络[15-16]、卷积神经网络[17-19]和堆叠自动编码器[20-21]等。
已有的研究成果在无噪声的情况下,均有着不错的表现,但若要将机器学习算法应用到在线监测上,采样或传输过程中产生的噪声就不能被忽略[22-23]。同时,训练模型无法涵盖系统所有的突发状况,在应用过程中,遇到新的工况或故障时,其准确性不能太低,因此模型的泛化能力也很重要。
文中提出了一种基于堆叠稀疏降噪自编码器(stacked sparse denoising auto-encoder, SSDAE)的暂态稳定评估模型。首先对SSDAE评估模型的算法和原理进行了介绍,通过改进自编码器,减少了输入数据中的噪声对特征提取的干扰,增强模型的鲁棒性。同时,SSDAE对原始数据进行了稀疏表达,有利于模型在训练过程中抓住主导特征,从而提高模型的泛化能力。然后介绍了基于SSDAE的评估模型的具体实现过程,包括离线训练和在线应用,并给出评估训练结果的指标。最后通过仿真验证了文中方法的有效性。
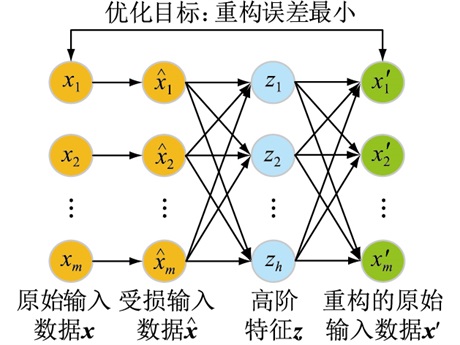
1 基于SSDAE的模型原理 1.1 稀疏降噪自编码器模型稀疏降噪自编码器(sparse denoising auto-encoder,SDAE)由编码器和解码器两部分构成。SDAE首先将噪声加入原始输入数据得到受损数据样本,编码器对受损数据样本进行特征提取,解码器将提取的高阶特征重构成未受损的数据,这一训练过程大大提高了模型的抗噪能力。SDAE提取的高阶特征具有极强的鲁棒性,能够对高维原始特征进行抽象表达而不受噪声的干扰,因此SDAE模型具有很好的抗噪能力。SDAE结构如图 1所示。
|
图 1 SDAE结构 Fig. 1 Structure of SDAE |
SDAE首先对原始输入数据样本x ∈ Rm进行“破坏和污染”得到受损数据样本
| $ \mathit{\boldsymbol{z}} = {f_\varphi }\left( {\mathit{\boldsymbol{\hat x}}} \right) = \frac{1}{{1 + {{\rm{e}}^{ - \mathit{\boldsymbol{W\hat x}} + \mathit{\boldsymbol{B}}}}}} $ | (1) |
式中:W ∈ R h×m为连接输入层和隐藏层的权重矩阵;B ∈ Rh×1为连接输入层和隐藏层的偏置向量矩阵。
解码器通过式(2)将隐藏层向量z映射到一个与输入层相同维度的输出层,得到重构的原始输入特征x ′。
| $ \mathit{\boldsymbol{x'}} = {q_\alpha }\left( \mathit{\boldsymbol{z}} \right) = \frac{1}{{1 + {{\rm{e}}^{ - \mathit{\boldsymbol{W'z}} + \mathit{\boldsymbol{B'}}}}}} $ | (2) |
式中:W ′∈ Rm×h为连接隐藏层和输出层的权重矩阵;B ′∈ R m×1为连接隐藏层和输出层的偏置向量矩阵。
SDAE训练的目标是将受损样本
| $ {L_{{\rm{re}}{\mathop{\rm construction}\nolimits} }} = \frac{1}{m}\sum\limits_{i = 1}^m {{{\left( {{{x'}_i} - {x_i}} \right)}^2}} $ | (3) |
式中:x′ i为重构的输入特征的第i维特征量;xi为未受损原始输入特征的第i维特征量。
电力系统运行时的电压、电流和不平衡功率等信息之间具有相关性,导致高维原始输入信息中包含了大量的冗余特征。对SDAE模型加入稀疏化限制,能迫使SDAE模型在训练的过程中自动去除冗余特征,提取出对暂态稳定性评估具有高区分度的特征,从而提高暂态稳定评估的性能。同时,稀疏化使得网络的部分参数为0,提高了使用反向传播(back propagation, BP)算法对网络进行训练的速度。
1.2 SSDAE分类模型SSDAE是由多个SDAE的编码器有机组合,并在最后加入一层Logistic分类器组成的深度神经网络。通过这样的堆叠结构,充分发挥了SDAE的特征提取能力,使得SSDAE具有很强的拟合高维非线性函数的能力。
为了对SSDAE进行有效训练,首先,将多个SDAE串联起来,前一级SDAE编码器的输出特征作为下一级SDAE的输入特征,逐个对SDAE进行无监督的预训练。经过无监督预训练的SDAE能够将受损数据恢复成原始数据。此时,SDAE的编码器部分便能够从受损的数据中提取出能反映未受损数据信息的高阶特征。将每个经过预训练的SDAE的编码器串联起来,并在最后加入一层Logistic分类器,使用BP算法,对SSDAE分类模型进行有监督的训练。模型的最优参数θ*可通过式(4)得到。
| $ {\theta ^*} = \arg \mathop {\min }\limits_\theta \left( { - y\ln y' - \left( {1 - y} \right)\ln \left( {1 - y'} \right)} \right) $ | (4) |
式中:y为训练样本的真实标签值;y′为预测标签值;θ为SSDAE分类模型的网络参数。
逐层贪婪无监督预训练与有监督微调的训练相结合,能对SSDAE模型进行有效训练,充分发挥深度神经网络对于高维非线性函数强大的拟合能力[24]。由于SDAE提取的特征具有强鲁棒性,以及SDAE激活程度的稀疏化限制,使得SSDAE分类模型具有较强的抗噪声能力和泛化能力,且训练样本不容易过拟合。
2 基于SSDAE的暂态稳定性评估 2.1 离线训练通过仿真数据和历史运行数据构建训练样本集。提取故障发生前时刻、故障发生时刻、故障清除时刻、故障清除后0.1 s这4个时刻所有发电机的功角、角速度、机械功率、电磁功率,作为评估模型的输入特征,并对所有特征进行归一化预处理。
根据式(5)判断每一例样本为稳定样本或不稳定样本。若φ≥0,则为稳定样本,标签为1;否则为不稳定样本,标签为0。
| $ \varphi = 360^\circ - \left| {\Delta {\delta _{\max }}} \right| $ | (5) |
式中:Δδmax为任意时刻所有发电机间的最大功角差值。
文中使用BPA仿真软件在IEEE 39节点系统和华东某省电网上进行仿真。在IEEE 39节点系统中,故障情况为永久性三相短路故障,系统负荷水平分别为90%,100%,110%,故障位置分别位于线路10%,30%,50%,70%,90%处,故障持续时间为100~300 ms。通过仿真共生成样本4 950个,其中稳定样本2 933个,不稳定样本2 017个。将所有样本按照4 ∶1的比例分成训练集和测试集,训练集用于离线训练,测试集用于评价模型的性能。在华东某省电网中,只考虑了系统100%的负载水平。故障设置为220 kV及以上的输电线路的10%,50%,90%处发生永久性三相短路故障。故障持续时间为8个周波。随机模拟了18 204种故障情况。将所有样本分为训练集和测试集。其中训练集中有6 000个样本,测试集中有12 204个样本。
使用训练集样本对SSDAE评估模型进行训练,网络的超参数由5折交叉验证结合随机搜索确定。最终确定SSDAE的隐藏层神经元个数依次为500,500,250,50,25;批样本大小为128;使用Adam方法进行网络优化,学习率为0.001;无监督预训练次数为200;有监督训练次数为300。
2.2 在线应用借助电网中广泛分布的电力系统同步PMU,可以实时收集发电机和母线的动态信息。然后,实时监测数据可以通过高速通信网络发送到控制中心。在控制中心,当故障被清除5周波后,从接收动态信息中提取出评估模型的输入特征,并进行预处理。将预处理后的特征量输入离线训练好的基于SSDAE的暂态稳定评估模型中。SSDAE评估模型本质上是输入特征与输出结果之间的高维非线性映射。当这种映射关系被确定后,只需要将当前的特征量输入SSDAE评估模型,就能够快速完成电力系统暂态稳定性的预测。
当电力系统发生新的故障情况时,评估当前的基于SSDAE的暂态稳定评估模型对新故障的评估效果。若当前评估模型对新故障的评估正确率能够满足要求,则不更新当前评估模型。否则,将基于这批新的故障,仿真生成相近或相同运行情况的故障样本,并标记稳定情况,构建成补充训练样本集。利用补充训练样本集对当前暂态稳定评估模型进行微调,得到更新后的暂态稳定评估模型,并用于在线评估。
2.3 模型性能评价指标对于暂态稳定评估模型,文中使用以下指标对模型性能进行评估。
(1) 全局正确率ηAC。
| $ {\eta _{{\rm{AC}}}} = \frac{{{N_R}}}{{{N_{{\rm{all}}}}}} $ | (6) |
式中:NR为预测正确的样本数量;Nall为样本总数。
| $ {\eta _{{\rm{FD}}}} = \frac{{{N_{{\rm{UF}}}}}}{{{N_{\rm{U}}}}} $ | (7) |
式中:NUF为预测错误的不稳定样本数量;NU为不稳定样本总数。
(3) 误警率ηFA。
| $ {\eta _{{\rm{FA}}}} = \frac{{{N_{{\rm{SF}}}}}}{{{N_{\rm{S}}}}} $ | (8) |
式中:NSF为预测错误的稳定样本数量;NS为稳定样本总数。
全局正确率ηAC体现了模型的综合性能,漏警率ηFD体现了模型对于不稳定样本的评估性能,误警率ηFA体现了模型对于稳定样本的评估性能,综合考察这3个指标能够全面评价模型性能。
3 仿真算例 3.1 无噪声数据实验结果 3.1.1 IEEE 39节点系统将SSDAE与堆叠稀疏自编码器(stacked sparse auto-encoder, SSAE)[17]、支持向量机(support vector machine, SVM)、决策树算法(decision tree, DT)、人工神经网络(artificial neural network, ANN)、朴素贝叶斯(naive bayes, NB)的实验结果作比较。其中,DT使用分类回归树算法;SVM使用径向基核函数,通过5折交叉验证和网格搜索法确定参数C为500,γ为0.1;ANN为单隐藏层结构,训练次数为300,批样本大小为128,通过5折交叉验证和网格搜索法确定学习率为0.5,隐藏层神经元个数为200;SSAE使用和SSDAE相同的超参数。
由于抽样具有随机性,为了更加可靠地评估模型性能,所有算法均进行5次随机抽样,以5次测试集评估结果的平均值作为最终评估结果。评估结果如表 1所示。
|
|
表 1 不同分类模型在无噪声情况下的评估结果 Table 1 Evaluation results of different models without noise |
可以看出,SSDAE和SSAE的评估性能明显高于其他浅层学习算法。而SSDAE和SSAE采用相同的结构和参数,在无噪声情况下,两者的性能指标基本相同。
模型计算时间如表 2所示,SSDAE模型训练500次的时间为147.65 s,其在应用过程中每个测试样本的计算速度非常快,仅为2.99 ms,可以满足在线计算的需求。
|
|
表 2 不同模型的训练和测试时间 Table 2 Training and testing time of different models |
在华东某省电网中,将SSDAE,SSAE,ANN的实验结果相比较。进行5次随机抽样,以5次测试集评估结果的平均值作为最终评估结果,结果如表 3所示。
|
|
表 3 实际电网仿真结果 Table 3 Simulation results of different models in actual grid |
在华东某省电网中,输入特征量仍然为各发电机组的功角、角速度、机械功率、电磁功率,但该电网系统包含183台发电机组,因此输入特征量维数变大,各样本平均测试时间多了0.99 ms,但总体来说,SSDAE的计算速度仍满足在线计算的需求。
3.2 噪声干扰对评估模型的影响由于在实际应用中,数据的采集、传输等过程均有可能受到不同程度的干扰[19],因此需要检验评估模型对含噪声数据评估的准确性。在训练评估模型时,训练集的数据采用无噪声的实验数据,而在测试过程中,对IEEE 39节点系统测试样本分别加入信噪比为20 dB,15 dB,10 dB,8 dB的高斯白噪声,来模拟数据在实际应用时伴随的噪声干扰。不同分类模型对含噪声数据的评估结果见表 4。
|
|
表 4 不同分类模型在有噪声情况下的评估结果 Table 4 Evaluation results of different models with noise |
可以看出,当信噪比为20 dB时,DT,NB这2种模型的评估性能受影响很大,准确率下降很多。而SSDAE,SSAE,SVM,ANN这4种模型受影响并不大,说明这4种模型均有一定的抗噪能力。当信噪比为10 dB时,SVM和ANN的评估结果受到了较大影响。而SSDAE和SSAE的评估准确性仍然很高,SSAE的准确性在96.5%以上,SSDAE的准确性保持在97%以上。当信噪比为8 dB时,SSDAE的评估准确性仍然可以达到96.38%,而SSAE的准确性为95.77%。由此可见,SSDAE在训练时对数据加入噪声重构成无噪声数据的过程大大提高了模型的抗噪能力。
3.3 SSDAE评估模型的泛化能力在IEEE 39节点系统中,随机抽取200~1 200个样本作为训练集;在剩余的样本集中,抽取800个样本作为测试集,测试样本不被训练。以未训练测试样本的准确性评估SSDAE模型的泛化能力。不同数量的训练样本,其对未知样本的评估准确性如表 5所示。
|
|
表 5 不同数量训练样本的评估结果 Table 5 Evaluation results of different training samples |
样本数量对于模型的训练具有重要影响,当样本数量较小时,使用高维输入特征对模型进行训练容易导致模型过拟合,从而影响评估模型的泛化性能。当训练样本数量仅为200个时,SSDAE模型准确率超过92%,相较于SVM和DT拥有明显的优势;而SVM由于过拟合最为严重,泛化能力最差,相较于使用400个训练样本时,其测试集准确率低了8.57%。随着训练样本数量的增加,3种模型在测试集上的评估准确率也逐渐上升,其中,SSDAE一直拥有最高的准确率。当训练集样本数量达到1 200个时,SSDAE的评估准确率超过97%。这是由于大量的训练样本可以更加有效地训练评估模型,使评估模型泛化能力越来越强,模型对系统暂态稳定性的评估性能越来越好。
4 结语在实际应用过程中,不仅仅要考虑机器学习算法在无噪声情况下的准确率,同时也要考虑噪声干扰的影响,以及算法的泛化能力。文中基于SSDAE分类模型,提出一种具有较好抗噪性能和泛化能力的暂态稳定性评估模型。在无噪声的情况下,该模型的准确率略高于其他机器学习算法;含噪声干扰时,其准确率要大大高于其他机器学习算法。仿真结果表明,SSDAE分类模型在有噪声和无噪声的情况下,均有着较高的准确率。不同训练样本数量的评估结果验证了SSDAE分类模型具有很好的泛化能力。
文中利用SSDAE算法独特的训练方式降低了数据噪声对结果的影响,未来可以考虑通过机器学习算法对噪声数据进行去噪处理,进一步提高机器学习模型在应用过程中的实用能力。
本文得到福建省中青年教师教育科研项目(JT180018)资助,谨此致谢!
| [1] |
CARRERAS B A, NEWMAN D E, DOBSON I. North American blackout time series statistics and implications for blackout risk[J]. IEEE Transactions on Power Systems, 2016, 31(6): 4406-4414. DOI:10.1109/TPWRS.2015.2510627 (  0) 0) |
| [2] |
王怀远, 张保会, 杨松浩, 等. 电力系统暂态稳定切机控制策略表的快速整定方法[J]. 电力系统自动化, 2016, 40(11): 68-72, 79. WANG Huaiyuan, ZHANG Baohui, YANG Songhao, et al. Fast setting method of generator tripping strategy tables in transient stability control of power systems[J]. Automation of Electric Power Systems, 2016, 40(11): 68-72, 79. DOI:10.7500/AEPS20150921009 (  0) 0) |
| [3] |
王怀远, 张保会, 杨松浩, 等. 基于相平面特性的切机切负荷紧急控制方法[J]. 中国电机工程学报, 2016, 36(15): 4144-4152. WANG Huaiyuan, ZHANG Baohui, YANG Songhao, et al. Combined emergency control strategy of generator tripping and loadshedding based on the characteristics of state plane[J]. Proceedings of the CSEE, 2016, 36(15): 4144-4152. (  0) 0) |
| [4] |
黄天罡, 薛禹胜, 林振智, 等. 动态EEAC的自适应分段映射[J]. 电力系统自动化, 2018, 42(21): 21-27. HUANG Tiangang, XUE Yusheng, LIN Zhenzhi, et al. Dynamic EEAC with adaptive subsection mapping[J]. Automation of Electric Power Systems, 2018, 42(21): 21-27. DOI:10.7500/AEPS20180903005 (  0) 0) |
| [5] |
夏小琴, 徐伟. 考虑调整变化量和变步长的暂态稳定约束最优潮流模型[J]. 电力工程技术, 2018, 37(6): 115-119. XIA Xiaoqin, XU Wei. Transient stability constrained optimal power flow model considering power adjustments and variable step size[J]. Electric Power Engineering Technology, 2018, 37(6): 115-119. DOI:10.3969/j.issn.1009-0665.2018.06.019 (  0) 0) |
| [6] |
AGHAMOHAMMADI M R, ABEDI M. DT based intelligent predictor for out of step condition of generator by using PMU data[J]. International Journal of Electrical Power & Energy Systems, 2018, 99: 95-106. (  0) 0) |
| [7] |
PAL A, SANCHEZ-AYALA G A, CENTENO V A, et al. A PMU placement scheme ensuring real-time monitoring of critical buses of the network[J]. IEEE Transactions on Power Delivery, 2014, 29(2): 510-517. DOI:10.1109/TPWRD.2013.2279172 (  0) 0) |
| [8] |
HASHIESH F, MOSTAFA H E, KHATIB A R, et al. An intelligent wide area synchrophasor based system for predicting and mitigating transient instabilities[J]. IEEE Transactions on Smart Grid, 2012, 3(2): 645-652. DOI:10.1109/TSG.2012.2187220 (  0) 0) |
| [9] |
SIDDIQUI S A, VERMA K, NIAZI K R, et al. Real-time monitoring of post-fault scenario for determining generator coherency and transient stability through ANN[J]. IEEE Transactions on Industry Applications, 2018, 54(1): 685-692. DOI:10.1109/TIA.2017.2753176 (  0) 0) |
| [10] |
朱利鹏, 陆超, 黄河, 等. 基于广域时序数据挖掘策略的暂态电压稳定评估[J]. 电网技术, 2016, 40(1): 180-185. ZHU Lipeng, LU Chao, HUANG He, et al. Wide-area time series data mining based transient voltage stability assessment[J]. Power System Technology, 2016, 40(1): 180-185. (  0) 0) |
| [11] |
LI Y, YANG Z. Application of EOS-ELM with binary jaya-based feature selection to real-time transient stability assessment using PMU data[J]. IEEE Access, 2017, 5: 23092-23101. DOI:10.1109/ACCESS.2017.2765626 (  0) 0) |
| [12] |
ZHOU Y Z, WU J Y, JI L Y, et al. Transient stability preventive control of power systems using chaotic particle swarm optimization combined with two-stage support vector machine[J]. Electric Power Systems Research, 2018, 155: 111-120. DOI:10.1016/j.epsr.2017.10.007 (  0) 0) |
| [13] |
陈厚合, 王长江, 姜涛, 等. 基于投影能量函数和Pin-SVM的电力系统暂态稳定评估[J]. 电工技术学报, 2017, 32(11): 67-76. CHEN Houhe, WANG Changjiang, JIANG Tao, et al. Transient stability assessment in bulk power grid using projection energy function and support vector machine with pinball loss[J]. Transactions of China Electrotechnical Society, 2017, 32(11): 67-76. (  0) 0) |
| [14] |
赵晶晶, 贾然, 陈凌汉, 等. 基于深度学习和改进K-means聚类算法的电网无功电压快速分区研究[J]. 电力系统保护与控制, 2021, 49(14): 89-95. ZHAO Jingjing, JIA Ran, CHEN Linghan, et al. Research on fast partition of reactive power and voltage based on deep learning and an improved K-means clustering algorithm[J]. Power System Protection and Control, 2021, 49(14): 89-95. (  0) 0) |
| [15] |
朱乔木, 党杰, 陈金富, 等. 基于深度置信网络的电力系统暂态稳定评估方法[J]. 中国电机工程学报, 2018, 38(3): 735-743. ZHU Qiaomu, DANG Jie, CHEN Jinfu, et al. A method for power system transient stability assessment based on deep belief networks[J]. Proceedings of the CSEE, 2018, 38(3): 735-743. (  0) 0) |
| [16] |
胡婧, 周洋, 何志强, 等. 基于深度置信网络和随机森林的电力扰动检测方法[J]. 供用电, 2020, 37(9): 17-22, 28. HU Jing, ZHOU Yang, HE Zhiqiang, et al. Power quality disturbance detection method using deep belief network[J]. Distribution & Utilization, 2020, 37(9): 17-22, 28. (  0) 0) |
| [17] |
周悦, 谭本东, 李淼, 等. 基于深度学习的电力系统暂态稳定评估方法[J]. 电力建设, 2018, 39(2): 103-108. ZHOU Yue, TAN Bendong, LI Miao, et al. Transient stability assessment of power system based on deep learning technology[J]. Electric Power Construction, 2018, 39(2): 103-108. DOI:10.3969/j.issn.1000-7229.2018.02.013 (  0) 0) |
| [18] |
许若冰, 王璇, 赵倩宇, 等. 基于卷积神经网络和深度置信网络的多类型能源需求预测方法[J]. 供用电, 2020, 37(10): 65-70. XU Ruobing, WANG Xuan, ZHAO Qianyu, et al. A multi-energy demand prediction method based on convolutional neural network and deep belief network[J]. Distribution & Utilization, 2020, 37(10): 65-70. (  0) 0) |
| [19] |
田芳, 周孝信, 史东宇, 等. 基于卷积神经网络的电力系统暂态稳定预防控制方法[J]. 电力系统保护与控制, 2020, 48(18): 1-8. TIAN Fang, ZHOU Xiaoxin, SHI Dongyu, et al. A preventive control method of power system transient stability based on a convolutional neural network[J]. Power System Protection and Control, 2020, 48(18): 1-8. (  0) 0) |
| [20] |
朱乔木, 陈金富, 李弘毅, 等. 基于堆叠自动编码器的电力系统暂态稳定评估[J]. 中国电机工程学报, 2018, 38(10): 2937-2946, 3144. ZHU Qiaomu, CHEN Jinfu, LI Hongyi, et al. Transient stability assessment based on stacked autoencoder[J]. Proceedings of the CSEE, 2018, 38(10): 2937-2946, 3144. (  0) 0) |
| [21] |
MAHDI M, GENC V M I. Post-fault prediction of transient instabilities using stacked sparse autoencoder[J]. Electric Power Systems Research, 2018, 164: 243-252. DOI:10.1016/j.epsr.2018.08.009 (  0) 0) |
| [22] |
张俊峰, 杨婷, 陈珉, 等. 基于Prony滑动平均窗算法的电力系统低频振荡特征分析[J]. 电力自动化设备, 2018, 38(10): 178-183. ZHANG Junfeng, YANG Ting, CHEN Min, et al. Power system low-frequency oscillation characteristic analysis based on Prony moving average window algorithm[J]. Electric Power Automation Equipment, 2018, 38(10): 178-183. (  0) 0) |
| [23] |
熊思宇, 符玲, 张佳怡, 等. 基于测量值波动特性的PMU测量性能在线评价方法[J]. 电网技术, 2017, 41(7): 2332-2339. XIONG Siyu, FU Ling, ZHANG Jiayi, et al. Online assessment for PMU measurement performance based on phasor measurement volatility characteristics[J]. Power System Technology, 2017, 41(7): 2332-2339. (  0) 0) |
| [24] |
HINTON G E, SALAKHUTDINOV R R. Reducing the dimensionality of data with neural networks[J]. Science, 2006, 313(5786): 504-507. DOI:10.1126/science.1127647 (  0) 0) |
2. Guangdong Power Grid Co., Ltd. Guangzhou Power Supply Bureau, Guangzhou 510620, China;
3. College of Electrical Engineering and Automation, Fuzhou University, Fuzhou 350116, China
 2022, Vol. 41
2022, Vol. 41


 温涛(1988), 男, 硕士, 工程师, 从事电力系统运行与控制、继电保护相关工作(E-mail:
温涛(1988), 男, 硕士, 工程师, 从事电力系统运行与控制、继电保护相关工作(E-mail: