文章编号: 2096-3203(2022)01-0165-08 中图分类号: TM74
2. 中铁上海设计院集团有限公司, 上海 200070;
3. 东方电气中央研究院, 四川 成都 611731
随着信息通信技术的发展,现代电力系统成为信息物理融合系统。但由于信息通信系统存在漏洞不可避免,电力系统遭受信息攻击的可能性不断增加[1-3]。恶意的信息攻击对电力系统的安全稳定运行危害极大,严重时可能导致重大事故,如2015年的乌克兰大停电事故[4]。其中,虚假数据注入攻击是一种较为常见的网络攻击,攻击者利用电力系统状态估计的检测漏洞,恶意篡改测量数据。电力系统的许多应用,如经济调度、应急分析等都依赖于状态估计的结果,而错误的状态估计结果会影响控制中心的操作和控制功能[5-9]。
为构建一次成功的虚假数据注入攻击,攻击者需要篡改一个子集的测量数据,并绕过基于残差的不良数据检测算法[10-12]。为简化问题,研究大多采用基于直流潮流的线性状态估计模型[13]。文献[14]指出,攻击者若能完全掌握系统的网络拓扑和支路参数,就可利用精心设计的数据来篡改仪表的量测值并且不被检测到[15]。但在实际情况中,攻击者还受到许多其他限制。文献[16]指出,当攻击者获取的数据有所缺失时,攻击向量可能被轻易检测出来。当一些仪表进行了加密设置,攻击者无法访问时,则需要篡改更多其他仪表的数据来达到相同目的[17-18]。
现有研究中攻击者使用较多的是针对线性状态估计的虚假数据注入攻击,若实际的状态估计是非线性状态估计,则攻击很容易被检测到[6],因此许多学者专门设计了针对非线性状态估计的攻击策略。文献[19]提出了一种基于图论的算法,得到攻击所需篡改的测量数据子集;文献[20]指出,攻击者需要了解部分节点的电压幅值和相角,以便确定攻击向量;文献[7]指出虚假数据注入攻击在攻击前后,不良数据检测算法的结果会有较小偏差。以上关于虚假数据注入攻击的构建方法均针对交流系统,目前尚无以交直流混联系统为研究场景的攻击方法。然而,已有的攻击方法并不完全适用于交直流混联系统。一方面,交直流混联系统交流部分的状态估计模型基于非线性的交流潮流,因此攻击方法并不适用于线性状态估计;另一方面,当攻击涉及到换流母线节点的量测量和状态变量时,既要考虑直流部分的有功、无功功率变化对交流部分的影响,又要考虑交流部分的电压幅值变化对直流部分的影响。
高压直流输电在全国联网和西电东送工程中广泛应用[21-22],近年来,我国已陆续建成酒泉-湖南直流、山西-江苏直流等输电工程[23]。随着高压直流输电在电力系统中的占比越来越大,目前的电力系统已成为交直流混联系统。研究以交直流混联系统为场景的虚假数据注入攻击方法,有利于制定相应的检测和防御方法,提高系统的安全性。
基于此,文中在现有交流系统攻击模型的基础上,提出了面向交直流混联系统的虚假数据注入攻击方法。首先,基于交替迭代算法的交直流混联状态估计,分析在换流母线附近进行攻击的策略;然后,构建针对交直流混联系统的虚假数据注入攻击模型,计算实现攻击所要篡改的测量数据大小;最后,利用Matlab仿真软件,通过改进的IEEE 30节点系统对文中方法的有效性进行验证。
1 交直流混联系统量测方程状态估计的基本原理是根据收集到的测量数据来推断电力系统的运行状态。量测量和状态变量之间的关系可用量测方程来描述。文中将交直流混联系统量测方程分为交流部分、直流部分、交直流耦合部分介绍。
1.1 交流部分在交直流混联系统中,交流部分状态估计采用交流潮流模型,因此测量数据包括节点有功、无功注入功率,节点电压幅值,支路有功、无功潮流;状态变量为各个节点的电压幅值和相角[24]。
对于节点i与节点j之间线路的潮流,量测方程可由式(1)-式(2)确定。
| $ P_{i, j}=V_{i}^{2} g_{i, j}-V_{i} V_{j}\left(g_{i, j} \cos \theta_{i, j}+b_{i, j} \sin \theta_{i, j}\right) $ | (1) |
| $ \begin{gathered} Q_{i, j}=-V_{i}^{2}\left(b_{i, j}+b_{i, j}^{\mathrm{sh}}\right)-V_{i} V_{j} \times \\ \left(g_{i, j} \sin \theta_{i, j}-b_{i, j} \cos \theta_{i, j}\right) \end{gathered} $ | (2) |
对于节点i的有功、无功注入功率,量测方程可由式(3)-式(4)确定。
| $ P_{i}=\sum\limits_{j \in S_{i}} P_{i, j} $ | (3) |
| $ Q_{i}=\sum\limits_{j \in S_{i}} Q_{i, j} $ | (4) |
式中:Pi, j,Qi, j分别为节点i与节点j之间线路的有功、无功功率潮流;Pi,Qi分别为节点i的有功、无功注入功率;gi, j,bi, j分别为节点i与节点j之间线路的电导和电纳;bi, jsh为对地电纳;θi, j为节点i与节点j电压相角的差值,即θi, j=θi-θj;Vi,Vj分别为节点i与节点j的电压幅值;Si为所有与节点i直接相连的节点集合。由于在形成节点导纳矩阵时已考虑变压器的电抗以及变比,因此式(1)-式(4)同样适用于变压器支路。
1.2 直流部分直流部分的量测方程较为复杂。对于双端直流输电系统,量测量包括:直流侧有功功率Pdc_recm,Pdc_invm;交流侧有功功率Pac_recm,Pac_invm;交流侧无功功率Qac_recm,Qac_invm;直流电压Vrecm,Vinvm;直流电流Idm。状态变量包括:直流电压Vrec,Vinv;直流电流Id;交流侧电流Iac_rec,Iac_inv;整流侧触发延迟角α;逆变侧熄弧角γ;功率因数角Φrec,Φinv。其中,上标m表示量测量,下标rec表示整流侧变量,下标inv表示逆变侧变量。则量测方程可表示为:
| $ V_{\text {rec }}=k_{1} B_{\text {rec }} T_{\text {rec }} E_{\text {ac_rec }} \cos \alpha-k_{2} B_{\text {rec }} X_{\text {c_rec }} I_{\mathrm{d}}+\eta_{1} $ | (5) |
| $ V_{\text {inv }}=k_{1} B_{\text {inv }} T_{\text {inv }} E_{\text {ac_inv }} \cos \gamma+k_{2} B_{\text {inv }} X_{\text {c_inv }} I_{\mathrm{d}}+\eta_{2} $ | (6) |
| $ V_{\text {rec }}=V_{\text {inv }}+R I_{\mathrm{d}}+\eta_{3} $ | (7) |
| $ V_{\text {rec }}=k_{1} B_{\text {rec }} T_{\text {rec }} E_{\text {ac_rec }} \cos \varPhi_{\text {rec }}+\eta_{4} $ | (8) |
| $ V_{\text {inv }}=k_{1} B_{\text {inv }} T_{\text {inv }} E_{\text {ac_inv }} \cos \varPhi_{\text {inv }}+\eta_{5} $ | (9) |
| $ I_{\text {ac_rec }}=k_{3} B_{\text {rec }} T_{\text {rec }} I_{\mathrm{d}}+\eta_{6} $ | (10) |
| $ I_{\text {ac_inv }}=k_{3} B_{\text {inv }} T_{\text {inv }} I_{\mathrm{d}}+\eta_{7} $ | (11) |
| $ P_{\text {de_rec }}^{\mathrm{m}}=V_{\text {rec }} I_{\mathrm{d}}+\eta_{8} $ | (12) |
| $ P_{\text {dc_inv }}^{\mathrm{m}}=V_{\text {inv }} I_{\mathrm{d}}+\eta_{9} $ | (13) |
| $ P_{\text {ac_rec }}^{\mathrm{m}}=\sqrt{3} E_{\text {ac_rec }} I_{\text {ac_rec }} \cos \varPhi_{\text {rec }}+\eta_{10} $ | (14) |
| $ P_{\text {ac_inv }}^{\mathrm{m}}=\sqrt{3} E_{\text {ac_inv }} I_{\text {ac_inv }} \cos \varPhi_{\text {inv }}+\eta_{11} $ | (15) |
| $ Q_{\text {ac_rec }}^{\mathrm{m}}=\sqrt{3} E_{\text {ac_rec }} I_{\text {ac_rec }} \sin \varPhi_{\text {rec }}+\eta_{12} $ | (16) |
| $ Q_{\text {ac_inv }}^{\mathrm{m}}=\sqrt{3} E_{\text {ac_inv }} I_{\text {ac_inv }} \sin \varPhi_{\text {inv }}+\eta_{13} $ | (17) |
式中:
另外,为了使该模型更加贴近实际,需要考虑直流换流站的运行方式。例如,当换流站整流侧定电流运行,逆变侧定熄弧角运行时,有:
| $ I_{\mathrm{d}}=I_{\text {ord }}+\eta_{14} $ | (18) |
| $ \gamma=\gamma_{\text {ord }}+\eta_{15} $ | (19) |
式中:Iord为人为设定的直流电流;γord为人为设定的逆变侧熄弧角;η14,η15为量测误差。
1.3 交直流耦合部分对于交直流耦合部分,需充分考虑直流部分有功、无功功率的影响。量测方程可表示为:
| $ P_{i} \pm P_{\mathrm{dc}}=\sum\limits_{j \in S_{i}} P_{i, j} $ | (20) |
| $ Q_{i}-Q_{\mathrm{dc}}=\sum\limits_{j \in S_{i}} Q_{i, j} $ | (21) |
式中:Pdc,Qdc分别为直流有功、无功功率。式(20)在整流侧时取-,在逆变侧时取+;由于直流部分无论在整流侧还是逆变侧,都吸收无功功率,因此式(21)始终取-。
由上述量测方程可知,在进行状态估计时,交流部分的估计结果(换流母线节点电压幅值)将影响直流部分的状态估计,而直流部分的估计结果(直流有功、无功功率)将影响交流部分的状态估计。这是基于交流系统的虚假数据注入攻击不能完全适用于交直流混联系统的原因,也是文中主要解决的问题。
2 交直流混联系统攻击原理交直流混联状态估计模型可简单表示为:
| $ \boldsymbol{z}=h(\boldsymbol{x})+\boldsymbol{\eta} $ | (22) |
为方便说明,将量测量分为交流部分有功、无功量测量和直流部分量测量;将状态变量分为交流部分电压幅值、相角以及直流部分状态变量,如式(23)所示。
| $ \boldsymbol{z}=\left[\begin{array}{l} \boldsymbol{z}_{\mathrm{p}} \\ \boldsymbol{z}_{\mathrm{q}} \\ \boldsymbol{z}_{\mathrm{d}} \end{array}\right]=\left[\begin{array}{l} h_{\mathrm{p}}\left(\boldsymbol{\theta}, \boldsymbol{v}, \boldsymbol{x}_{\mathrm{dc}}\right) \\ h_{\mathrm{q}}\left(\boldsymbol{\theta}, \boldsymbol{v}, \boldsymbol{x}_{\mathrm{dc}}\right) \\ h_{\mathrm{d}}\left(\boldsymbol{\theta}, \boldsymbol{v}, \boldsymbol{x}_{\mathrm{dc}}\right) \end{array}\right]+\left[\begin{array}{l} \boldsymbol{\eta}_{\mathrm{p}} \\ \boldsymbol{\eta}_{\mathrm{q}} \\ \boldsymbol{\eta}_{\mathrm{d}} \end{array}\right] $ | (23) |
式中:zp,zq分别为交流部分有功、无功量测量;z d为直流部分量测量;hp,hq,hd分别为状态变量和量测量关系的函数,hd的元素可由直流部分的量测方程确定;θ为电压相角;v为电压幅值;xdc为直流部分状态变量;ηp,ηq,ηd为量测误差。
常见的交直流混联系统状态估计算法有统一求解法、交替迭代法等[25]。交替迭代法将直流部分和交流部分解耦开来,分别求解,能减小状态估计维数,并能充分利用现有状态估计程序,因此文中选用这种方法作为交直流混联系统状态估计算法。篇幅所限,在此不作详细介绍。
由于设备故障、通信干扰等因素可能会产生不良数据,因此在状态估计时需进行不良数据检测。在电力系统中,常用残差的2-范数来进行不良数据检测,可表示为:
| $ L_{\mathrm{NR}}=\|\boldsymbol{z}-h(\hat{\boldsymbol{x}})\|_{2}<\tau $ | (24) |
式中:LNR为残差的2-范数;τ为人为设置的不良数据检测门槛值。由于
将状态估计所得状态变量代入式(1)-式(21)的量测方程中,可得到量测量的估计值。将估计值与实际量测量进行比较,利用2-范数得到的结果来判断是否存在不良数据。若检测结果满足式(24),则说明状态估计的结果是可靠的;若检测结果大于τ,则说明状态估计过程中包含错误的测量数据,估计结果是不可靠的。
若攻击者想要进行一次成功的虚假数据注入攻击,就必须使攻击绕过不良数据检测机制。文中假设攻击者掌握系统的拓扑和参数,也了解状态估计与不良数据检测机制。当系统受到虚假数据注入攻击时,攻击向量为a。此时,系统的量测量由z变为zT,其中zT= z + a;状态变量由
| $ \begin{gathered} L_{\mathrm{NRbad}}=\left\|\boldsymbol{z}^{\mathrm{T}}-h\left(\hat{\boldsymbol{x}}^{\mathrm{T}}\right)\right\|= \\ \left\|\boldsymbol{z}^{\mathrm{T}}-h\left(\hat{\boldsymbol{x}}^{\mathrm{T}}\right)+h(\hat{\boldsymbol{x}})-h(\hat{\boldsymbol{x}})\right\|= \\ \left\|\boldsymbol{z}+\boldsymbol{a}-h\left(\hat{\boldsymbol{x}}^{\mathrm{T}}\right)+h(\hat{\boldsymbol{x}})-h(\hat{\boldsymbol{x}})\right\|= \\ \left\|\boldsymbol{z}-h(\hat{\boldsymbol{x}})+\boldsymbol{a}-h\left(\hat{\boldsymbol{x}}^{\mathrm{T}}\right)+h(\hat{\boldsymbol{x}})\right\| \end{gathered} $ | (25) |
当满足
| $ \boldsymbol{a}=\left[\begin{array}{c} \boldsymbol{z}_{\mathrm{p}}^{\mathrm{T}} \\ \boldsymbol{z}_{\mathrm{q}}^{\mathrm{T}} \\ \boldsymbol{z}_{\mathrm{d}}^{\mathrm{T}} \end{array}\right]-\left[\begin{array}{l} \boldsymbol{z}_{\mathrm{p}} \\ \boldsymbol{z}_{\mathrm{q}} \\ \boldsymbol{z}_{\mathrm{d}} \end{array}\right]=\left[\begin{array}{l} h_{\mathrm{p}}\left(\boldsymbol{\theta}^{\mathrm{T}}, \boldsymbol{v}^{\mathrm{T}}, \boldsymbol{x}_{\mathrm{dc}}^{\mathrm{T}}\right)-h_{\mathrm{p}}\left(\boldsymbol{\theta}, \boldsymbol{v}, \boldsymbol{x}_{\mathrm{dc}}\right) \\ h_{\mathrm{q}}\left(\boldsymbol{\theta}^{\mathrm{T}}, \boldsymbol{v}^{\mathrm{T}}, \boldsymbol{x}_{\mathrm{dc}}^{\mathrm{T}}\right)-h_{\mathrm{q}}\left(\boldsymbol{\theta}, \boldsymbol{v}, \boldsymbol{x}_{\mathrm{dc}}\right) \\ h_{\mathrm{d}}\left(\boldsymbol{\theta}^{\mathrm{T}}, \boldsymbol{v}^{\mathrm{T}}, \boldsymbol{x}_{\mathrm{dc}}^{\mathrm{T}}\right)-h_{\mathrm{d}}\left(\boldsymbol{\theta}, \boldsymbol{v}, \boldsymbol{x}_{\mathrm{dc}}\right) \end{array}\right] $ | (26) |
其中,上标T表示攻击后的量测量和状态变量。
式(26)表明,攻击者在进行一次虚假数据注入攻击时,若能篡改交流部分和直流部分的测量数据使之满足一定条件,就能发动隐蔽的攻击,在不良数据检测结果保持不变的情况下使状态估计输出攻击者想要的结果。
3 交直流混联系统攻击模型第三章介绍式(26)在不同攻击场景下的具体模型。通过推导状态变量和量测量的关系得到精心构建的攻击向量,使之满足式(26)的等式关系,以绕过不良数据检测机制。当虚假数据注入攻击远离直流输电线路时,攻击的构建方法与普通的交流系统攻击方法类似,因此文中侧重于介绍发生在直流输电线路附近的攻击。
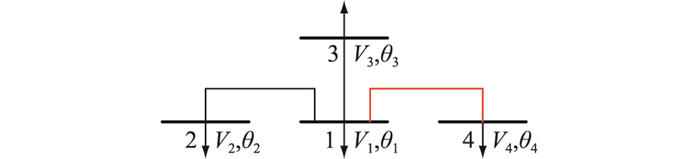
由于估计的量测值是通过状态变量计算得到的,文中仅介绍以改变状态变量为目的的攻击方法,以改变量测值为目的的攻击方法同理可得。假设攻击者不仅要在状态估计中注入错误的量测量,还要使某些状态变量达到预期的偏差,在文中,这些状态变量指的是换流母线节点的电压幅值和相角。通过篡改这些状态变量的估计值,攻击者可达到破坏电网稳定、经济运行或是自身获取利益的目的。以图 1为例,进一步说明式(26)攻击原理。
|
图 1 发生在换流母线的攻击说明 Fig. 1 Illustration of an attack on a converter bus |
图 1中,V,θ分别为节点的电压幅值和相角;红线表示直流线路,其中节点1为整流侧,节点4为逆变侧;黑色箭头表示节点负荷。假设攻击发生在整流侧换流母线节点1处,攻击者想要通过篡改节点1附近量测量的方式来改变状态估计的结果。为方便说明,假设仅有节点1的电压幅值或相角的估计值发生了改变,而其他状态变量在攻击前后保持不变。
3.1 改变电压幅值的攻击攻击者的目的是改变节点1的电压幅值估计值,改变的幅度为V1T。为了使攻击不被检测到,攻击的具体方法如下。
3.1.1 确定电压幅值攻击篡改的量测量对于交流部分,由式(1)-式(4)可知,节点1电压幅值的改变会影响与该节点直接相连节点的有功、无功注入功率,即P1,Q1,P2,Q2,P3,Q3;以及与节点1直接相连支路的有功、无功功率潮流,即P1, 2,Q1, 2,P1, 3,Q1, 3,因此需要篡改这些量测量以实现攻击。
对于直流部分,由1.2节的量测方程可知,直流部分量测量受换流母线节点电压幅值的影响。当攻击发生在整流侧换流母线节点1处时,由于逆变侧换流母线节点电压V4保持不变,且换流站为整流侧定电流运行,逆变侧定熄弧角运行,由式(6)可知,逆变侧电压Vinv保持不变;此时由式(7)可知,整流侧电压Vrec保持不变。
当Vrec保持不变时,由式(5)可知在攻击前后需要满足:
| $ E_{\text {ac_rec }}^{\mathrm{T}} \cos \alpha^{\mathrm{T}}=E_{\text {ac_rec }} \cos \alpha $ | (27) |
当Vinv,Vrec保持不变时,由式(8)、式(9)可知Φinv保持不变,Φrec需要满足:
| $ E_{\text {ac_rec }}^{\mathrm{T}} \cos \varPhi_{\text {rec }}^{\mathrm{T}}=E_{\text {ac_rec }} \cos \varPhi_{\text {rec }} $ | (28) |
式中:Eac_recT为攻击后整流侧换流母线电压;αT为攻击后整流侧触发延迟角;ΦrecT为攻击后整流侧功率因数角。
由式(10)-式(13)可知,状态变量Iac_rec,Iac_inv以及量测量Pdc_recm,Pdc_invm在攻击前后保持不变。由式(14)、式(15)以及式(28)可知,量测量Pac_recm,Pac_invm在攻击前后保持不变。根据式(16)可知,量测量Qac_recm在攻击时需要篡改,以满足式(31)的条件。由式(17)可知,量测量Qac_invm在攻击前后保持不变。
根据上述推导可知,当攻击发生在节点1处时,直流部分需要篡改量测量Qac_recm,并且α,Φrec在状态估计时会发生相应改变。
3.1.2 确定电压幅值攻击向量对于交流部分,以节点1与节点2之间的有功、无功功率潮流P1, 2与Q1, 2为例,假设P1, 2与Q1, 2需要篡改的大小分别为ΔP1, 2T,ΔQ1, 2T,由式(29)-式(30)确定。
| $ \begin{aligned} \Delta P_{1,2}^{\mathrm{T}}=&\left(V_{1}+V_{1}^{\mathrm{T}}\right)^{2} g_{1,2}-\left(V_{1}+V_{1}^{\mathrm{T}}\right) V_{2} g_{1,2} \cos \theta_{1,2}-\\ &\left(V_{1}+V_{1}^{\mathrm{T}}\right) V_{2} b_{1,2} \sin \theta_{1,2}-V_{1}^{2} g_{1,2}+\\ & V_{1} V_{2} g_{1,2} \cos \theta_{1,2}+V_{1} V_{2} b_{1,2} \sin \theta_{1,2} \end{aligned} $ | (29) |
| $ \begin{gathered} \Delta Q_{1,2}^{\mathrm{T}}=-\left(V_{1}+V_{1}^{\mathrm{T}}\right)^{2}\left(b_{1,2}+b_{1,2}^{\mathrm{sh}}\right)- \\ \left(V_{1}+V_{1}^{\mathrm{T}}\right) V_{2} g_{1,2} \sin \theta_{1,2}+ \\ \left(V_{1}+V_{1}^{\mathrm{T}}\right) V_{2} b_{1,2} \cos \theta_{1,2}+V_{1}^{2}\left(b_{1,2}+b_{1,2}^{\mathrm{sh}}\right)+ \\ V_{1} V_{2} g_{1,2} \sin \theta_{1,2}-V_{1} V_{2} b_{1,2} \cos \theta_{1,2} \end{gathered} $ | (30) |
节点1与节点3之间需要篡改的有功、无功功率潮流ΔP1, 3T与ΔQ1, 3T同理可得。
由于节点有功、无功注入功率的大小分别为各支路有功、无功功率的总和,且换流母线节点还需考虑直流功率的影响,因此节点1需要篡改的有功、无功注入功率ΔP1T与ΔQ1T可由式(31)和式(32)确定。
| $ \Delta P_{1}^{\mathrm{T}}=\Delta P_{1,2}^{\mathrm{T}}+\Delta P_{1,3}^{\mathrm{T}} $ | (31) |
| $ \Delta Q_{1}^{\mathrm{T}}=\Delta Q_{1,2}^{\mathrm{T}}+\Delta Q_{1,3}^{\mathrm{T}}+\Delta Q_{\text {ac_rec }}^{\mathrm{T}} $ | (32) |
式中:ΔQac_recT为需要篡改的整流侧无功功率。节点2与节点3需要篡改的有功、无功注入功率同理可得。
对于直流部分,需要篡改的整流侧无功功率ΔQac_recT为:
| $ \begin{gathered} \Delta Q_{\mathrm{ac}_{-} \mathrm{rec}}^{\mathrm{T}}=\sqrt{3}\left(V_{\mathrm{inv}}+V_{\mathrm{inv}}^{\mathrm{T}}\right) I_{\mathrm{ac}_{-} \mathrm{rec}} \sin \left(\varPhi_{\mathrm{rec}}+\varPhi_{\mathrm{rec}}^{\mathrm{T}}\right)- \\ \sqrt{3} V_{\mathrm{inv}} I_{\mathrm{ac}\_{\mathrm{rec}}} \sin \varPhi_{\mathrm{rec}} \end{gathered} $ | (33) |
其中,ΦrecT的大小可根据式(28)得到。
当攻击者用上述方法确定攻击向量时,能达到使节点1电压相角的估计值改变V1T的目的,并能绕过不良数据检测。同时,攻击者在进行攻击时需要了解节点1,2,3的电压相角与幅值,否则无法精确计算出所要篡改的具体数值。
3.2 改变电压相角的攻击攻击者的目的是改变节点1的电压相角估计值,改变的幅度为θ1T。同样,为了使攻击不被检测到,攻击的具体方法如下。
3.2.1 确定电压相角攻击篡改的量测量对于交流部分,同理,需要篡改的量测量为相关节点注入功率P1,Q1,P2,Q2,P3,Q3,以及与节点1直接相连支路的有功、无功功率潮流P1, 2,Q1, 2,P1, 3,Q1, 3。
对于直流部分,由直流量测方程可知,换流母线电压相角的改变不影响直流部分的量测量,因此攻击者无需篡改直流部分的量测量。
3.2.2 确定电压相角攻击向量对于交流部分,仍以节点1与节点2之间的有功、无功功率潮流P1, 2与Q1, 2为例,ΔP1, 2T,ΔQ1, 2T的大小可由式(34)和式(35)确定。
| $ \begin{gathered} \Delta P_{1,2}^{\mathrm{T}}=V_{1}^{2} g_{1,2}-V_{1} V_{2} g_{1,2} \cos \left(\theta_{1,2}+\theta_{1}^{\mathrm{T}}\right)- \\ V_{1} V_{2} b_{1,2} \sin \left(\theta_{1,2}+\theta_{1}^{\mathrm{T}}\right)-V_{1}^{2} g_{1,2}+ \\ V_{1} V_{2} g_{1,2} \cos \theta_{1,2}+V_{1} V_{2} b_{1,2} \sin \theta_{1,2} \end{gathered} $ | (34) |
| $ \begin{gathered} \Delta Q_{1,2}^{\mathrm{T}}=-V_{1}^{2}\left(b_{1,2}+b_{1,2}^{\mathrm{sh}}\right)-V_{1} V_{2} g_{1,2} \sin \left(\theta_{1,2}+\theta_{1}^{\mathrm{T}}\right)+ \\ V_{1} V_{2} b_{1,2} \cos \left(\theta_{1,2}+\theta_{1}^{\mathrm{T}}\right)+V_{1}^{2}\left(b_{1,2}+b_{1,2}^{\mathrm{sh}}\right)+ \\ V_{1} V_{2} g_{1,2} \sin \theta_{1,2}-V_{1} V_{2} b_{1,2} \cos \theta_{1,2} \end{gathered} $ | (35) |
节点1与节点3之间需要篡改的有功、无功功率潮流ΔP1, 3T与ΔQ1, 3T同理可得。
节点1需要篡改的有功、无功注入功率ΔP1T与ΔQ1T可由式(36)和式(37)确定。
| $ \Delta P_{1}^{\mathrm{T}}=\Delta P_{1,2}^{\mathrm{T}}+\Delta P_{1,3}^{\mathrm{T}} $ | (36) |
| $ \Delta Q_{1}^{\mathrm{T}}=\Delta Q_{1,2}^{\mathrm{T}}+\Delta Q_{1,3}^{\mathrm{T}} $ | (37) |
同理可得节点2与节点3需要篡改的有功、无功注入功率。
由此确定了攻击向量a。当攻击者使用该方法确定攻击向量时,能达到使节点1的电压相角估计值改变θ1T的目的,并能绕过不良数据检测。这同样要求攻击者在进行攻击时事先了解相关节点的电压相角与幅值。
上述虚假数据注入攻击的构建也可延伸至改变多个节点的状态变量,并且电压幅值和电压相角可同时改变,这要求攻击者要获知更多节点的状态变量估计值,以及篡改更多量测值才能够实现。
4 仿真算例文中采用改进IEEE 30节点系统,分别以改变电压相角与幅值为攻击目的,通过分析攻击状态估计结果与迭代过程中的残差2-范数结果对文中所提攻击策略进行验证。对比每次迭代过程中攻击前后残差2-范数,能体现出攻击策略的有效性。
4.1 仿真系统介绍文中将IEEE 30节点系统节点2与节点6之间的交流线路替换为双端直流输电线路,并保证构造的系统与原来的交流系统具有相同的潮流状况,以此作为交直流混联系统,如图 2所示。其中,与节点2相连的换流站为整流侧,与节点6相连的换流站为逆变侧。双端直流输电系统参数如下:换流变压器变比为525 kV/209 kV,电抗为200 Ω;换流器直流电压额定值为500 kV,直流电压最大值为525 kV;整流器超前触发角α范围为5°~57.1°;额定触发角为15°;逆变侧熄弧角γ限值为15°;额定熄弧角为18°;直流线路电阻为100 Ω;直流输送容量为30 000 MW。

|
图 2 改进的IEEE 30节点系统 Fig. 2 Improved IEEE 30-bus system |
假设攻击者的目的是改变节点2的电压幅值,改变的大小为0.03。其中节点1~8和节点28的电压等级为500 kV,其余节点电压等级为220 kV。攻击者需要篡改的量测值如表 1所示。
|
|
表 1 进行电压幅值攻击时需要篡改的量测量 Table 1 The measurement volume that needs to be tampered when conducting voltage amplitude attacks |
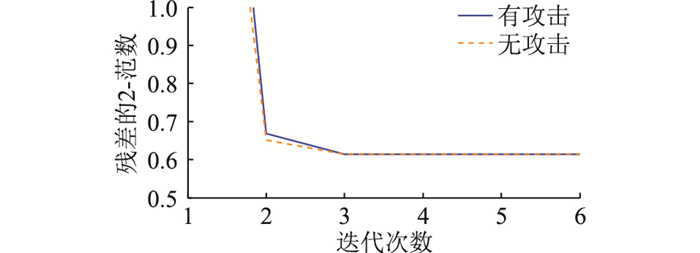
表 1为攻击需要篡改的量测量以及篡改的大小,其他量测量保持不变。篡改后的量测量与其他量测量形成攻击向量。分别用篡改前后的量测值进行状态估计,并进行对比,所得结果如图 3、表 2、表 3所示,其中表 2仅列出与节点2关联的几个节点状态变量。表 3中的状态变量直流电流在电压幅值攻击前后均为60 A。
|
图 3 电压幅值攻击下不良数据检测结果 Fig. 3 Results of bad data detection under voltage amplitude attack |
|
|
表 2 电压幅值攻击下交流部分状态估计结果 Table 2 State estimation results of AC part under voltage amplitude attack |
|
|
表 3 电压幅值攻击下直流部分状态估计结果 Table 3 State estimation results of DC part under voltage amplitude attack |
由图 3可知,利用攻击后的量测量进行状态估计时,前2次迭代的不良数据检测结果与攻击前相比有较小偏差,但在第3次迭代后结果保持一致,并且很快收敛,说明攻击能绕过不良数据检测机制。由表 2、表 3可知,在状态估计后节点2的电压幅值变为1.059 3。自动调压装置根据状态估计结果降低节点2的电压,导致这一节点甚至周围节点的实际电压低于安全电压下限。另外,由于节点2的有功功率注入量测大幅增加,这将误导调度中心调整机组出力。以上均说明该攻击策略能影响电力系统运行的安全性与经济性。
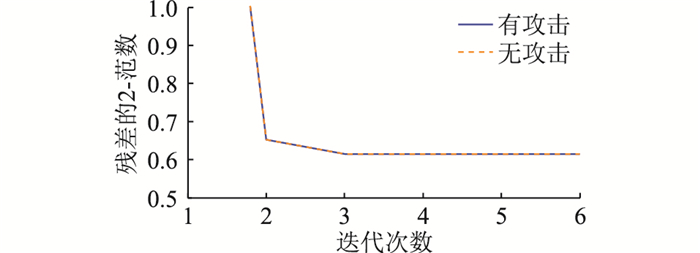
4.3 改变电压相角攻击仿真分析假设攻击者的目的是改变节点2的电压相角,改变的大小为0.5°。为达到攻击目的,攻击者需要篡改的量测量如表 4所示。分别将篡改前后的量测值进行状态估计,并进行对比,所得结果如图 4、表 5、表 6所示。表 6中状态变量直流电流在电压相角攻击前后均为60 A。
|
|
表 4 进行电压相角攻击时需要篡改的量测量 Table 4 The measurement volume that needs to be tampered when conducting voltage phase angle attacks |
|
图 4 电压相角攻击下不良数据检测结果 Fig. 4 Results of bad data detection under voltage phase angle attack |
|
|
表 5 电压相角攻击下交流部分状态估计结果 Table 5 State estimation results of AC part under voltage phase angle attack |
|
|
表 6 电压相角攻击下直流部分状态估计结果 Table 6 State estimation results of DC part under voltage phase angle attack |
由图 3可知,利用攻击后的量测量进行状态估计时,迭代过程中不良数据检测结果与攻击前几乎保持一致,并且很快收敛,说明攻击能绕过不良数据检测机制。由表 5、表 6可知,攻击能使节点2的电压相角变化量达到预期的结果,同时其他状态变量在攻击前后基本保持不变。
5 结语电力系统状态估计容易受到虚假数据注入攻击,输出错误的系统运行状态。文中提出了在交直流混联系统中构建虚假数据注入攻击的策略。利用文中所提攻击策略,可计算出当改变状态估计结果并不被检测到时,攻击者所需要篡改的量测值。以改进的IEEE 30节点系统为场景进行的仿真结果表明,这一攻击策略可以成功绕过不良数据检测机制,达到攻击者的目的。
文中研究以攻击者完全掌握交直流混联系统的运行信息为前提,后续研究将会考虑攻击者在信息不完全的情况下构建虚假数据注入攻击,使得攻击策略更加贴近实际。同时,考虑状态估计采用如抗差方法时如何构建攻击。针对该攻击策略的防御方法也将进一步研究。
| [1] |
WANG W Y, LU Z. Cyber security in the smart grid: survey and challenges[J]. Computer Networks, 2013, 57(5): 1344-1371. DOI:10.1016/j.comnet.2012.12.017 (  0) 0) |
| [2] |
ALGULIYEV R, IMAMVERDIYEV Y, SUKHOSTAT L. Cyber-physical systems and their security issues[J]. Computers in Industry, 2018, 100: 212-223. DOI:10.1016/j.compind.2018.04.017 (  0) 0) |
| [3] |
ABUSORRAH A, ALABDULWAHAB A, LI Z Y, et al. Minimax-regret robust defensive strategy against false data injection attacks[J]. IEEE Transactions on Smart Grid, 2019, 10(2): 2068-2079. DOI:10.1109/TSG.2017.2788040 (  0) 0) |
| [4] |
郭庆来, 辛蜀骏, 王剑辉, 等. 由乌克兰停电事件看信息能源系统综合安全评估[J]. 电力系统自动化, 2016, 40(5): 145-147. GUO Qinglai, XIN Shujun, WANG Jianhui, et al. Comprehensive security assessment for a cyber physical energy system: a lesson from Ukraine's blackout[J]. Automation of Electric Power Systems, 2016, 40(5): 145-147. (  0) 0) |
| [5] |
XIE L, MO Y L, SINOPOLI B. False data injection attacks in electricity markets[C]//2010 First IEEE International Conference on Smart Grid Communications. Gaithersburg, MD, USA. IEEE, 2010: 226-231.
(  0) 0) |
| [6] |
陆东生, 马龙鹏. 基于增广状态估计的混合不良数据诊断与参数辨识[J]. 电力工程技术, 2019, 38(2): 99-104. LU Dongsheng, MA Longpeng. Hybrid bad-data detection and parameter identification based on augmented state estimation[J]. Electric Power Engineering Technology, 2019, 38(2): 99-104. (  0) 0) |
| [7] |
LIANG G Q, ZHAO J H, LUO F J, et al. A review of false data injection attacks against modern power systems[J]. IEEE Transactions on Smart Grid, 2017, 8(4): 1630-1638. DOI:10.1109/TSG.2015.2495133 (  0) 0) |
| [8] |
CHE L, LIU X, LI Z Y, et al. False data injection attacks induced sequential outages in power systems[J]. IEEE Transactions on Power Systems, 2019, 34(2): 1513-1523. DOI:10.1109/TPWRS.2018.2871345 (  0) 0) |
| [9] |
肖飞, 叶康, 邓祥力, 等. 基于最优编码集及智能状态估计的电网故障诊断方法[J]. 电力系统保护与控制, 2021, 49(2): 89-97. XIAO Fei, YE Kang, DENG Xiangli, et al. A fault diagnosis method of a power grid based on an optimal coding set and intelligent state estimation[J]. Power System Protection and Control, 2021, 49(2): 89-97. (  0) 0) |
| [10] |
朱杰, 张葛祥, 王涛, 等. 电力系统状态估计欺诈性数据攻击及防御综述[J]. 电网技术, 2016, 40(8): 2406-2415. ZHU Jie, ZHANG Gexiang, WANG Tao, et al. Overview of fraudulent data attack on power system state estimation and defense mechanism[J]. Power System Technology, 2016, 40(8): 2406-2415. (  0) 0) |
| [11] |
WANG H Z, RUAN J Q, WANG G B, et al. Deep learning-based interval state estimation of AC smart grids against sparse cyber attacks[J]. IEEE Transactions on Industrial Informatics, 2018, 14(11): 4766-4778. DOI:10.1109/TII.2018.2804669 (  0) 0) |
| [12] |
黄冬梅, 何立昂, 孙锦中, 等. 基于边缘计算的电网假数据攻击分布式检测方法[J]. 电力系统保护与控制, 2021, 49(13): 1-9. HUANG Dongmei, HE Li'ang, SUN Jinzhong, et al. Distributed detection method for a false data attack in a power grid based on edge computing[J]. Power System Protection and Control, 2021, 49(13): 1-9. (  0) 0) |
| [13] |
代明明. 电力系统局部区域假数据注入攻击研究[D]. 成都: 西南交通大学, 2016. DAI Mingming. Research on fake data injection attack in local area of power system[D]. Chengdu: Southwest Jiaotong University, 2016. (  0) 0) |
| [14] |
LIU Y, NING P, REITER M K. False data injection attacks against state estimation in electric power grids[J]. ACM Transactions on Information and System Security, 2011, 14(1): 1-33. (  0) 0) |
| [15] |
SANDBERG H, TEIXEIRA A, JOHANSSON K H. On security indices for state estimators in power networks[C]//Preprints of the First Workshop on Secure Control Systems, CPSWEEK 2010, Stockholm, Sweden. 2011.
(  0) 0) |
| [16] |
RAHMAN M A, MOHSENIAN-RAD H. False data injection attacks with incomplete information against smart power grids[C]//2012 IEEE Global Communications Conference (GLOBECOM). Anaheim, CA, USA. IEEE, 2012: 3153-3158.
(  0) 0) |
| [17] |
BI S Z, ZHANG Y J. Graphical methods for defense against false-data injection attacks on power system state estimation[J]. IEEE Transactions on Smart Grid, 2014, 5(3): 1216-1227. DOI:10.1109/TSG.2013.2294966 (  0) 0) |
| [18] |
ANWAR A, MAHMOOD A N, TARI Z. Identification of vulnerable node clusters against false data injection attack in an AMI based smart grid[J]. Information Systems, 2015, 53: 201-212. (  0) 0) |
| [19] |
HUG G, GIAMPAPA J A. Vulnerability assessment of AC state estimation with respect to false data injection cyber-attacks[J]. IEEE Transactions on Smart Grid, 2012, 3(3): 1362-1370. (  0) 0) |
| [20] |
RAHMAN M A, MOHSENIAN-RAD H. False data injection attacks against nonlinear state estimation in smart power grids[C]//2013 IEEE Power & Energy Society General Meeting. Vancouver, BC, Canada. IEEE, 2013: 1-5.
(  0) 0) |
| [21] |
申志鹏, 熊会, 朱介北, 等. 影响特高压直流输电工程安全高效运行评估因素集的建模与分析[J]. 发电技术, 2021, 42(1): 48-59. SHEN Zhipeng, XIONG Hui, ZHU Jiebei, et al. Modelling and analysis on evaluation factor sets affecting the safe and high-efficiency operation of UHVDC transmission project[J]. Power Generation Technology, 2021, 42(1): 48-59. (  0) 0) |
| [22] |
孙广, 王阳, 薛枫, 等. 特高压直流输电线路改进双端行波故障定位方法研究[J]. 电力系统保护与控制, 2020, 48(14): 113-120. SUN Guang, WANG Yang, XUE Feng, et al. Research on an improved double-terminal traveling wave fault location method for UHVDC project[J]. Power System Protection and Control, 2020, 48(14): 113-120. (  0) 0) |
| [23] |
艾红杰, 黄金海, 吴金波, 等. 陕北—武汉特高压直流输电工程无功控制策略研究[J]. 电力系统保护与控制, 2021, 49(14): 149-156. AI Hongjie, HUANG Jinhai, WU Jinbo, et al. Reactive power control strategy for the Shanbei-Wuhan UHVDC transmission project[J]. Power System Protection and Control, 2021, 49(14): 149-156. (  0) 0) |
| [24] |
杨波. 电力系统状态估计不同类型量测权重研究[D]. 大连: 大连海事大学, 2013. YANG Bo. Research of different measurement weights in power system state estimation[D]. Dalian: Dalian Maritime University, 2013. (  0) 0) |
| [25] |
王磊. 交直流混合系统状态估计研究[D]. 北京: 中国电力科学研究院, 2005. WANG Lei. Research on state estimation of AC/DC hybrid system[D]. Beijing: China Electric Power Research Institute, 2005. (  0) 0) |
2. China Railway Shanghai Design Institute Group Co., Ltd., Shanghai 200070, China;
3. Central Research Academy of DEC, Chengdu 611731, China
 2022, Vol. 41
2022, Vol. 41


 谢云云(1985), 男, 博士, 副教授, 研究方向为电力系统停电恢复控制(E-mail:
谢云云(1985), 男, 博士, 副教授, 研究方向为电力系统停电恢复控制(E-mail: