文章编号: 2096-3203(2022)01-0070-07 中图分类号: TM131.1
如今数据中心作为一种经济基础设施,其快速发展给社会的生产和生活都带来了极大的便利。随着计算设备的更新换代以及高密度计算设备的广泛应用,数据中心所需的能量不断增加。据估计,到2025年,数据中心的能量消耗将达到世界电能总量的20%。目前,数据中心能耗增长带来的成本问题已成为各行业关注的焦点,因此企业在能耗和散热等能源管理方面提出了新的要求,迫使数据中心必须立即对能耗管理作出战略性变革。AC/DC开关变换器作为现代电源被广泛应用于数据中心应用及数据通信设备等领域,在电网和用电设备之间担任至关重要的过渡角色。电源的好坏不仅直接决定用电设备能否正常工作,甚至会威胁电网的稳定运行。随着技术要求的不断提高,高效率和高功率密度已成为驱使技术创新革命的重要因素[1-5]。为了保证电源符合电磁兼容规范和绿色能源要求,抑制谐波污染成为AC/DC开关变换器不可或缺的环节[6-9]。功率因数校正(power factor correction, PFC)电路具有抑制甚至消除谐波对电网污染的作用。
PFC可分为无源PFC和有源PFC。由于无源PFC的输出纹波大、电流畸变校正及功率因数补偿的能力差,有源PFC被广泛应用于AC/DC变换器中。传统的有源PFC电路由不控整流桥和Boost升压电路组成,但随着功率等级的提高,整流桥的损耗在很大程度上阻碍了系统效率和功率等级的提升。与传统的Boost型PFC电路相比,采用氮化镓器件的图腾柱式无桥Boost PFC拓扑具有元器件数量少、器件利用率高及电磁干扰(electromagnetic interference, EMI)噪声低等优点。为打破开关损耗对高频化、高功率密度化的限制,利用谐振原理的软开关技术[10-16]已广泛应用于开关器件设计中。通过在开关过程前后加入谐振环节,使开关管实现零电压条件下的开通或零电流条件下的关断,进而有效降低开关损耗。
文中采用图腾柱无桥PFC拓扑实现高效高功率密度的要求,通过全数字控制满足电路在具备PFC功能的同时实现开关管零电压开关(zero voltage switch, ZVS)。首先介绍了图腾柱无桥PFC电路拓扑,分析了电路暂态情况下零电压条件;其次介绍了系统参数优化设计以及双闭环控制原理;然后通过仿真软件对系统在不同情况下进行数学仿真,从理论上证明系统运行的可行性;最后通过搭建样机,在实际应用中验证系统的可行性。
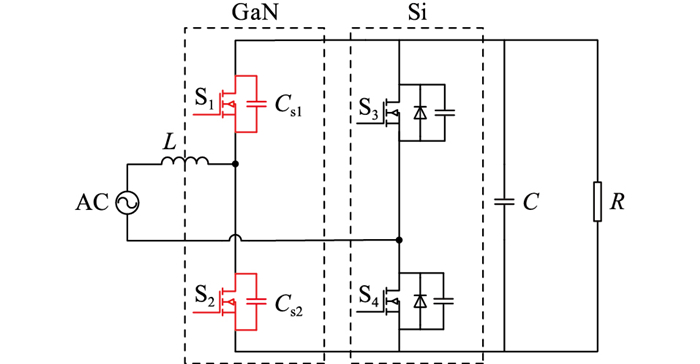
1 拓扑结构及电路暂态分析 1.1 拓扑结构结合应用新型开关器件氮化镓的图腾柱无桥PFC电路不存在反向恢复问题,可以适用于更广泛的场合。图腾柱无桥PFC电路结构如图 1所示,S1,S2为工作在高频状态的氮化镓主开关管;S3,S4为工作在工频状态的开关管;Cs1,Cs2分别为开关管S1和S2的寄生电容;L为输入滤波电感;C为输出低频滤波电容;R为等效负载。
|
图 1 图腾柱软开关无桥PFC电路 Fig. 1 Totem pole soft switch of bridgless PFC circuit |
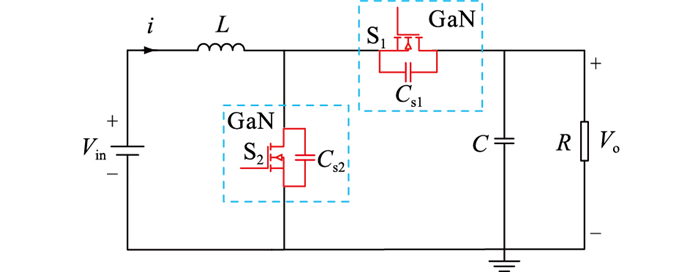
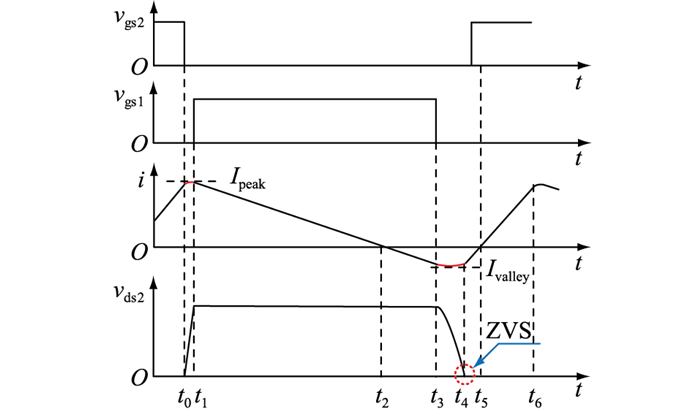
以正半周期为例对一个高频周期内电路中各器件工作模式进行具体分析,此阶段S4保持导通,S3关断,开关管S2为主功率开关管,S1为辅助续流开关管。图 2为正半周期等效电路,图 3为一个高频周期中电感电流波形及开关管栅源极和漏源极电压波形。其中,Vin为输入电压;Vo为输出电压;Ipeak为峰值电流;Ivalley为谷底电流;Vgs2为开关管S2的驱动电压;Vgs1为开关管S1的驱动电压;Vds2为开关管S2的漏源电压。
|
图 2 GaN图腾柱PFC等效电路(正半周) Fig. 2 PFC equivalent circuit of GaN totem pole (positive half cycle) |
|
图 3 主要电压及电流波形 Fig. 3 Waveforms of main voltage and current |
(1) t0~t1时段:S2关断,L与Cs1,Cs2发生谐振。在t=t0时刻前,开关管S2栅源极间存在正向电压,开关管处于导通状态,电感电流i线性增加。在t=t0时刻,开关管S2驱动电压消失,S2截止,同时i的上升过程停止。此时Cs1,Cs2与L发生谐振,S1漏源极端电压下降到零,S2漏源极端电压上升至Vo。
(2) t1~t2时段:辅助管S1反向导通,电感电流i线性减小。当t=t1时,S2漏源极两端的电压值达到母线电压。此时S1两端电压为零,S1等效体二极管导通,电感经S1续流,i开始线性减小。t=t2时刻,电感电流i减小至零。
(3) t2~t3时段:S1持续导通,电感电流i反向。辅助续流管S1受栅源极电压控制正向导通,电感电流i继续减小,此时i反向。
(4) t3~t4时段:S1驱动信号消失,S1关断,L与Cs1,Cs2发生谐振。t3时刻,L与Cs1,Cs2进入谐振状态,主功率管S2的漏源极电压开始降低,辅助管S1的漏源极电压开始升高。在t=t4时刻,S2漏极间电压减小至零,此工作阶段结束
(5) t4~t5时段:S2反向导通,电感L经S2续流。当t=t4时,主功率开关管S2两端电压已经谐振至零,此时电感电流仍为负,S2等效体二极管导通,须在电感电流上升至零之前在开关管两端加上驱动信号。此阶段S2漏源极电压一直为零,电感经S2续流。
(6) t5~t6时段:S2实现ZVS,电感电流流经S2线性增加。当开关管受栅极驱动信号控制开通时,S2两端电压为零,实现ZVS,i继续保持线性上升。当电路达到t6时,驱动信号消失,S2关断,电感电流i上升到最大值,完成一个高频周期的工作过程。
2 系统参数优化设计及双闭环控制 2.1 系统参数优化设计在基于氮化镓器件的图腾柱软开关PFC电路中,电感L作为正负半周Boost电路的限流电感,决定电路的工作频率范围。过大的电感会限制变换器功率密度的提升,而当电感值偏小时,过高的工作频率会增加电路采样和控制的难度。因此,L的感值设计十分重要。同样,以电路工作在正半周期为例,可以得到:
| $ I_{\text {peak }}=I_{\text {valley }}+\frac{V_{\text {in }}}{L} t_{\text {on }} $ | (1) |
| $ I_{\text {valley }}=I_{\text {peak }}-\frac{V_{\mathrm{o}}-V_{\text {in }}}{L} t_{\text {off }} $ | (2) |
| $ T \approx t_{\text {on }}+t_{\text {off }} $ | (3) |
式中:ton为开关管导通时间;toff为开关管关断时间;T为开关管工作周期。
由电感伏秒平衡原理可得:
| $ V_{\text {in }} t_{\text {on }}+\left(V_{\text {in }}-V_{\mathrm{o}}\right) t_{\text {off }}=0 $ | (4) |
由式(3)和式(4)可得开关管工作频率fs为:
| $ f_{\mathrm{s}}=\frac{1}{T}=\frac{1}{t_{\mathrm{on}}}\left(1-\frac{\sqrt{2} V_{\mathrm{rms}} \sin \left(\omega_{\mathrm{L}} t\right)}{V_{\mathrm{o}}}\right) $ | (5) |
式中:ωL为工频角频率;Vrms为输入交流电压有效值。
当Vin<0.5Vo时,有:
| $ t_{\mathrm{on}}=t_{\mathrm{on}_{-} \mathrm{ac}}=\frac{2 P_{\mathrm{o}} L}{\eta V_{\mathrm{rms}}^{2}} $ | (6) |
式中:ton_ac为高频周期的导通时间。
文中设定电路稳定工作时的输入电压有效值为220 V,输出电压为400 V,因此可得到此阶段开关管工作频率范围为:
| $ \frac{\eta V_{\mathrm{rms}}^{2}}{4 P_{\mathrm{o}} L}<f_{\mathrm{s}}<\frac{\eta V_{\mathrm{rms}}^{2}}{2 P_{\mathrm{o}} L} $ | (7) |
式中:Po为系统输出功率;η为系统效率。
当Vin>0.5Vo时,有:
| $ t_{\mathrm{on}}=t_{\mathrm{on\_ac}}+t_{\mathrm{ZVS}}=\frac{2 P_{\mathrm{o}} L}{\eta V_{\mathrm{rms}}^{2}}+\left(\sqrt{k^{2}-1}+k\right) \sqrt{2 L C_{\mathrm{s}}} $ | (8) |
式中:tZVS为系统实现ZVS时间。
此阶段开关管工作频率范围为:
| $ \begin{gathered} \frac{89}{\frac{800 P_{\mathrm{o}} L}{\eta V_{\mathrm{rms}}^{2}}+400\left(\sqrt{k^{2}-1}+k\right) \sqrt{2 L C_{\mathrm{s}}}}<f_{\mathrm{s}}<\\ \frac{1}{\frac{4 P_{\mathrm{o}} L}{\eta V_{\mathrm{rms}}^{2}}+\left(\sqrt{k^{2}-1}+k\right) \sqrt{8 L C_{\mathrm{s}}}} \end{gathered} $ | (9) |
式中:Cs为谐振电容,取150 pF;k为软开关实现条件,应满足k>1,过大的k值会造成反向电流过大、电流纹波大,因此k取1.1。
综合式(7)和式(9),考虑到开关频率对系统功率密度及控制难度的影响,文中最终选取电感L=135 μH,此时开关频率范围为98~450 kHz。
对于PFC变换器的输出电容,设计时一般需要考虑2个条件:输出电压的纹波大小Vripple和掉电保持时间thold。
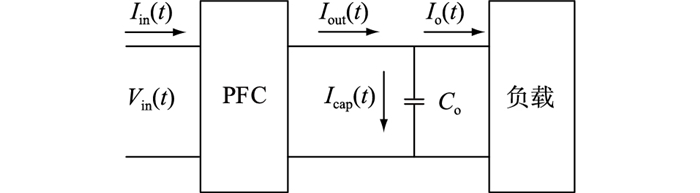
纹波方面,PFC作为前级电路,其输出纹波大小对于后级DC-DC电路的设计十分重要,较大的纹波会导致后级电路输入电压范围变宽,难以优化设计。相比于典型开关电源变换器,PFC变换器的输出纹波包含2种:第一种为高频的开关纹波,其幅值较小,可通过在输出端加很小的电容滤除;第二种是由输入造成的频率为输入电压频率2倍的低频纹波,此类纹波频率低,幅值较大,如图 4所示。
|
图 4 PFC电路纹波分析框图 Fig. 4 Block diagram of ripple analysis of PFC circuit |
为具备PFC功能,可认为变换器的输入电流与电压同相位,此时输入电流可表示为:
| $ I_{\mathrm{in}}(t)=\sqrt{2} I_{\mathrm{rms}} \sin \left(\omega_{\mathrm{L}} t\right) $ | (10) |
式中:Irms为输入交流电流有效值。
由能量守恒定律可得:
| $ P_{\text {in }} \eta=P_{\mathrm{o}} $ | (11) |
即:
| $ V_{\mathrm{rms}} I_{\mathrm{rms}} \eta=V_{\mathrm{o}} I_{\mathrm{o}} $ | (12) |
由图 4可得流经滤波电容Co前电流及电压满足:
| $ V_{\text {in }}(t) I_{\text {in }}(t)=V_{\text {rms }} I_{\text {rms }}\left(1-\cos \left(2 \omega_{\mathrm{L}} t\right)\right)=V_{\mathrm{o}}(t) I_{\text {out }}(t) $ | (13) |
式中:Iout(t)为输出电流值。
由式(12)及式(13)可得:
| $ I_{\text {out }}(t)=\frac{V_{\text {rms }} I_{\text {rms }} \eta}{V_{\mathrm{o}}}\left(1-\cos \left(2 \omega_{\mathrm{L}} t\right)\right) $ | (14) |
由此得到流过输出电容的纹波电流Icap为:
| $ \begin{gathered} I_{\text {cap }}(t)=I_{\text {out }}(t)-I_{\mathrm{o}}= \\ \frac{V_{\text {rms }} I_{\text {rms }} \eta}{V_{\mathrm{o}}} \cos \left(2 \omega_{\mathrm{L}} t\right)=I_{\mathrm{o}} \cos \left(2 \omega_{\mathrm{L}} t\right) \end{gathered} $ | (15) |
因此输出电压纹波Vripple为:
| $ V_{\text {ripple }}=2 \frac{\Delta Q}{C_{\mathrm{o}}}=2 \frac{\int_{0}^{\frac{{\rm{ \mathsf{ π} }}}{\omega_{\mathrm{L}}}} I_{\mathrm{o}} \cos \left(2 \omega_{\mathrm{L}} t\right) \mathrm{d} t}{C_{\mathrm{o}}}=\frac{V_{\mathrm{rms}} I_{\mathrm{rms}} \eta}{V_{\mathrm{o}} \omega_{\mathrm{L}} C_{\mathrm{o}}} $ | (16) |
式中:ΔQ为电容电荷变化量;Co为输出电容值。
由式(15)可以看出,当输入功率因数为1时,在变换器输出端必会引入2倍于输入电压频率的电压纹波,且其振幅与输出电流大小成正比,与输出滤波电容值大小成反比。一般根据4%的纹波指标计算电容值,由此可以计算输出电容取值范围如下:
| $ C_{\mathrm{o}} \geqslant \frac{P_{\mathrm{o}}}{2 {\rm{ \mathsf{ π} }} f_{\mathrm{L}} V_{\mathrm{o}} V_{\text {ripple }} / 2}=100 $ | (17) |
掉电保持时间thold是指当变换器的输入电源突然切断后,输出电压可以稳定在调整范围内的时间。thold的取值范围通常要求在15~50 ms,大多数商用电源的掉电保持时间指标是输入电压的一个周期,即20 ms。
对于有一个固定容值的电容,充满电时所包含的能量大小为:
| $ E=\frac{1}{2} C U^{2} $ | (18) |
式中:E为电容能量;C为电容数值;U为电容电压。
则电容值可以计算为:
| $ C_{\mathrm{o}} \geqslant \frac{2 P_{\mathrm{o}} t_{\text {hold }}}{V_{\mathrm{o}}^{2}-V_{\mathrm{o}\_\min }^{2}}=228 $ | (19) |
式中:Vo_min为保持时间内的系统允许的最低输出电压,文中设定为300 V。
要求稳态情况下PFC变换器的输出电压稳定在400 V,考虑到输出滤波电容的耐压值需要在此基础上留取一定的裕量,同时参考电解电容的规格等级,实际选取规格为450 V/300 μF的电解电容作为PFC变换器的输出滤波电容。
2.2 双闭环系统的控制传统的控制方法[17-20]通过使电路在电流临界模式下工作以实现主开关管ZVS,但其只适用于部分输入电压(Vin≤0.5Vo)范围内[21-24]。为保证在全输入电压范围内实现ZVS,系统在电流过零检测的基础上实现数字化双闭环控制。
控制系统外环为电压环,通过将电压环给定值与母线电压采样值作差,得到误差信号作为电压环比例积分(proportional integral, PI)调节器的输入,调节器的输出决定每一高频周期的导通时间ton_ac。系统通过计算电流内环采样得到的输入电压值、母线电压值及电压环输出值,从而得到主功率管和整流管的开通关断时刻信号。以电流过零信号(zero crossing detect, ZCD)作为每个开关周期的时间基准,控制高频开关管和整流管的工作时间。
3 系统仿真分析通过数学分析分别对图腾柱软开关无桥Boost PFC电路在开环和闭环条件下输入电流、输出功率及输出电压进行模拟。图 5与图 6分别为氮化镓型图腾柱软开关无桥Boost PFC电路输入电压与输入电流及母线电压与输出功率的仿真波形,iL为电感电流。
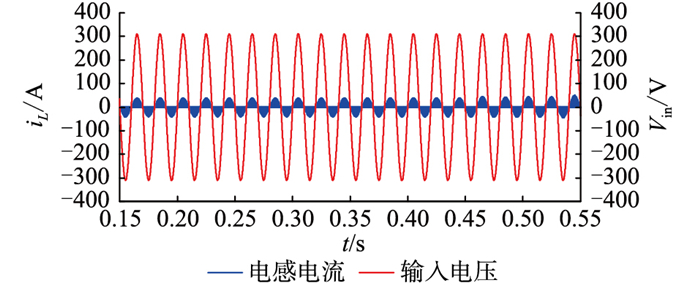
|
图 5 图腾柱软开关无桥Boost PFC电路输入电压和电感电流仿真波形 Fig. 5 Input voltage inductor current simulation waveforms of totem pole soft switch without bridge Boost PFC circuit |
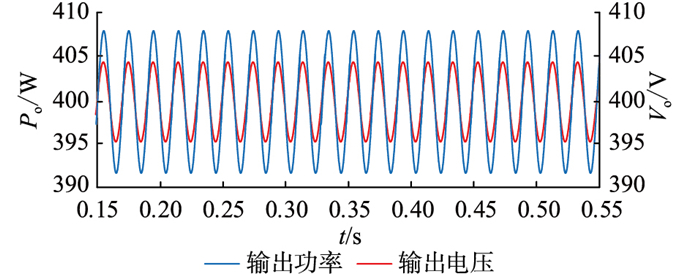
|
图 6 图腾柱软开关无桥Boost PFC电路输出功率和输出电压仿真波形 Fig. 6 Output power and output voltage simulation waveforms of totem pole soft switch bridged Boost PFC circuit |
从图中可以直观看出,电感电流能够保持与输入电压相位相同,且具有较高的正弦度。并且在额定功率400 W下,输出电压可稳定在400 V,电压纹波较小,达到了较好的电压和电流双闭环控制效果。
由于在实际应用中电网电压存在实时波动,当电网交流电压出现波动时,变换器仍须保持稳定的输出。图 7、图 8为模拟电网电压波动时的仿真波形,在t=0.3 s时刻,电网电压有效值由220 V突变至180 V。
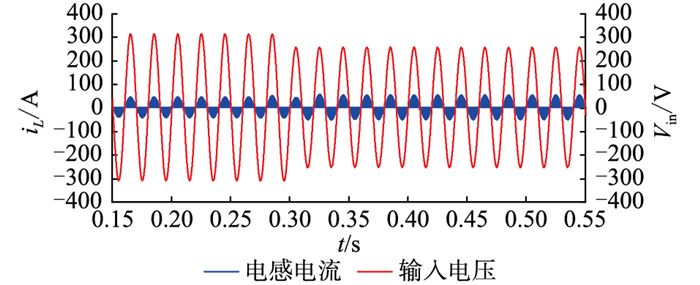
|
图 7 电网电压波动时输入电压和电感电流仿真波形 Fig. 7 Simulation waveforms of input voltage and inductor current when the grid voltage fluctuates |
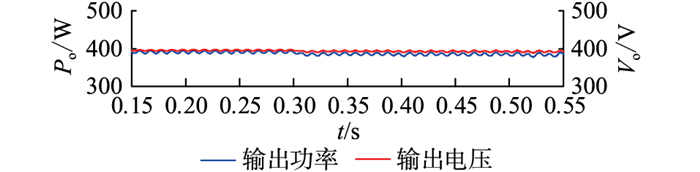
|
图 8 电网电压波动时输出功率及输出电压仿真波形 Fig. 8 Simulation waveforms of output power and output voltage when the grid voltage fluctuates |
由图 7、图 8中的波形可得,输入电压发生波动后,电感电流波形无过冲现象,能始终以正弦型跟随输入电压变化。变换器输出功率及输出电压在波动出现后能够迅速调节,最终恢复并保持在波动前的值。
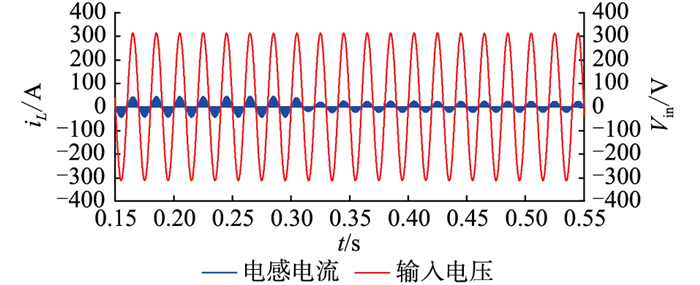
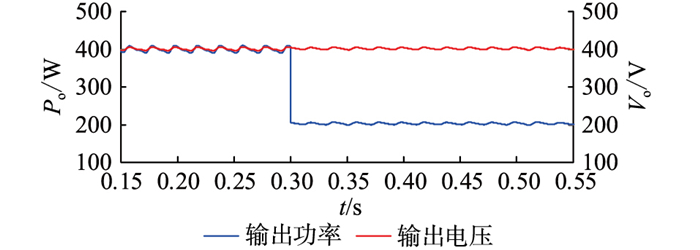
此外,为了满足负载不同功率等级要求,需要保证当系统负载发生波动时,变换器仍能保证正常稳定工作。图 9、图 10分别为负载波动时变换器输入电压电流及输出功率和电压的仿真波形。考虑在t=0.3 s时刻,变换器负载功率由满载400 W波动至半载状态。
|
图 9 负载波动时输入电压及输入电流仿真波形 Fig. 9 Simulation waveforms of input voltage and current when load fluctuates |
|
图 10 负载波动时输出功率及输出电压仿真波形 Fig. 10 Simulation waveforms of output power and output voltage with load fluctuation |
由图 9、图 10中的波形可以得知,在系统负载突变至半载后,输出功率突变至原来的一半,但母线电压仍保持在400 V,同时输入电流波形无出现明显过冲现象,能够始终跟随输入电压并以正弦波形变化。
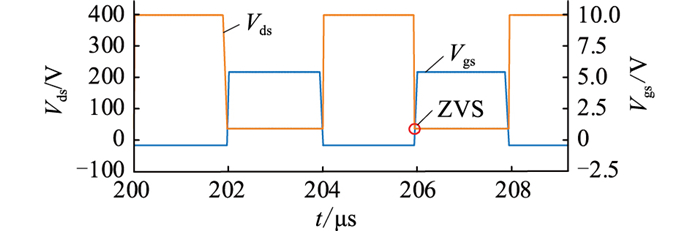
结合PSIM电路仿真软件,在输入电压大于输出电压的一半的情况下针对主开关管进行电路仿真,如图 11所示。辅助开关管通过延长导通时间以获得更多反向电流从而保证主开关两端电容能谐振到零实现ZVS。
|
图 11 输入电压为280V时ZVS的仿真波形图 Fig. 11 Simulation waveforms of ZVS when input voltage is 280V |
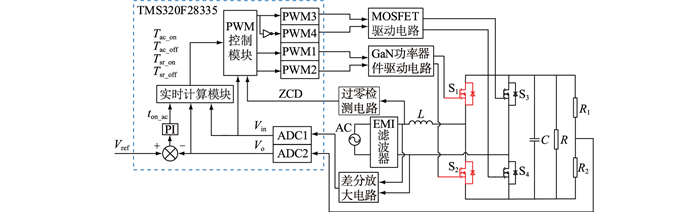
为验证所选择拓扑、参数设计的可行性,搭建输入电压有效值220 V,额定功率400 W的实验样机。图 12为样机原理图,在图腾柱式PFC电路中,由于正负周期内主开关管交替工作同时开关频率较高且变换范围较大,为准确获得ZCD,系统以交流电感侧作为采样点进行采样电阻Rsen采样,与在直流续流回路侧采样电流相比,交流侧采样具有采样电流连续、无明显振荡且电流检测无延时等优点。由运算放大器、比较器及数字隔离器三部分组成电流过零检测电路,其中运算放大器采用AD8061,比较器采用TLV3501。样机选用的芯片型号及参数如表 1所示。
|
图 12 图腾柱软开关PFC电路原理 Fig. 12 Schematic diagram of totem pole soft switch PFC circuit |
|
|
表 1 样机选用的芯片型号及无源器件参数 Table 1 Chip models and passive device parameters selected by the prototype |
图 13为图腾柱型无桥PFC电路主功率回路波形。图 13(a)为电感电流波形,可以看出,此模式下电感电流包络呈正弦型,且与输入电压同相位,功率校正效果较好。同时,在过电流抑制策略的控制下,输入电压过零处电流冲击得到了抑制,电路可以正常稳定工作。图 13(b)为额定工作条件下的输入电压及输出电压波形,此时输入为有效值220 V的单相正弦交流电,输出电压可以稳定在400 V左右,纹波较低可忽略不计。
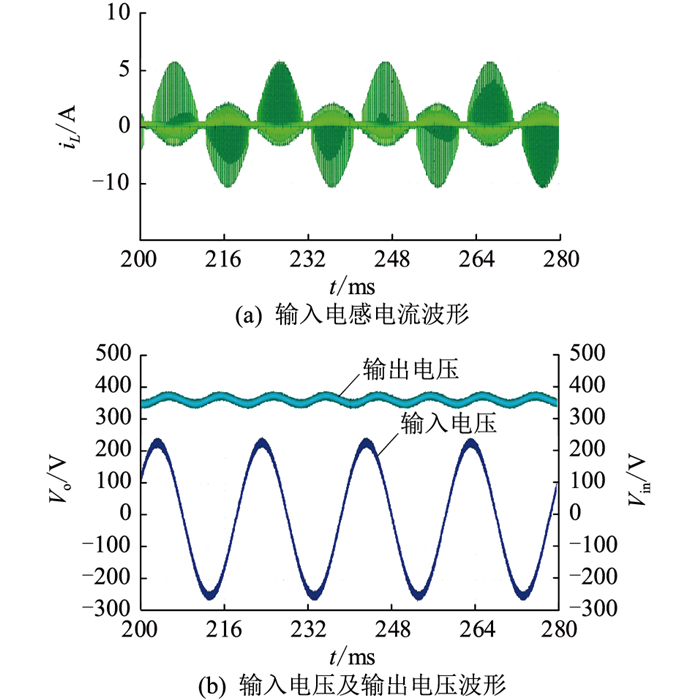
|
图 13 满载情况下PFC电路主要电压及电流波形 Fig. 13 Main voltage and current waveforms of PFC circuit under full load |
文中设计了1台400 W基于图腾柱结构实现高效高功率密度的软开关PFC电路,输入电压220 V,输出电压400 V。该电路采用无桥PFC拓扑结合第三代宽禁带氮化镓器件,通过全数字双闭环控制方法实现电路在电流临界和准方波2种状态下切换工作,保证变换器在具备PFC功能的同时实现开关管ZVS。该电路的数学仿真模型从理论上证明了其设计的可行性。后续进一步针对大功率情况下图腾柱软开关电路进行理论分析及实验验证。
| [1] |
FU M F, FEI C, YANG Y C, et al. Optimal design of planar magnetic components for a two-stage GaN-based DC-DC converter[J]. IEEE Transactions on Power Electronics, 2019, 34(4): 3329-3338. DOI:10.1109/TPEL.2018.2849741 (  0) 0) |
| [2] |
PARK C W, HAN S K. Design of an integrated magnetics structure for LLC resonant converter[C]//IECON 2017-43rd Annual Conference of the IEEE Industrial Electronics Society. Beijing, China. IEEE, 2017: 1888-1893.
(  0) 0) |
| [3] |
YANG B, CHEN R G, LEE F C. Integrated magnetic for LLC resonant converter[C]//APEC. Seventeenth Annual IEEE Applied Power Electronics Conference and Exposition (Cat. No. 02CH37335). Dallas, TX, USA. IEEE, 2002: 346-351.
(  0) 0) |
| [4] |
HUANG D C, JI S, LEE F C. LLC resonant converter with matrix transformer[J]. IEEE Transactions on Power Electronics, 2014, 29(8): 4339-4347. DOI:10.1109/TPEL.2013.2292676 (  0) 0) |
| [5] |
PARK H P, CHOI H J, JUNG J H. Design and implementation of highswitching frequency LLC resonant converter for high power density[C]//2015 9th International Conference on Power Electronics and ECCE Asia (ICPE-ECCE Asia). Seoul, Korea (South). IEEE, 2015: 502-507.
(  0) 0) |
| [6] |
AHMED M H, FEI C, LEE F C, et al. 48 V voltage regulator module with PCB winding matrix transformer for future data centers[J]. IEEE Transactions on Industrial Electronics, 2017, 64(12): 9302-9310. DOI:10.1109/TIE.2017.2711519 (  0) 0) |
| [7] |
SHAHABI A, LEMMON A, GRAVES R, et al. A SiC-based isolated DC/DC converter for high density data center applications[C]//2018 IEEE Applied Power Electronics Conference and Exposition. San Antonio, TX, USA. IEEE, 2018: 2294-2301.
(  0) 0) |
| [8] |
LIY C, LYU X F, CAO D, et al. A high efficiency resonant switched-capacitor converter for data center[C]//2017 IEEE Energy Conversion Congress and Exposition. Cincinnati, OH, USA. IEEE, 2017: 4460-4466.
(  0) 0) |
| [9] |
WARREN J R, ROSOWSKI K A, PERREAULT D J. Transistor selection and design of a VHF DC-DC power converter[J]. IEEE Transactions on Power Electronics, 2008, 23(1): 27-37. DOI:10.1109/TPEL.2007.911773 (  0) 0) |
| [10] |
OUYANG Z W, THOMSEN O C, ANDERSEN M A E. Optimal design and tradeoff analysis of planar transformer in high-power DC-DC converters[C]//IEEE Transactions on Industrial Electronics. IEEE, 2012: 2800-2810.
(  0) 0) |
| [11] |
WANG Y J, GUAN Y S, REN K L, et al. A single-stage LED driver based on BCM boost circuit and LLC converter for street lighting system[J]. IEEE Transactions on Industrial Electronics, 2015, 62(9): 5446-5457. DOI:10.1109/TIE.2015.2416341 (  0) 0) |
| [12] |
WANG Y J, GUAN Y S, HUANG J P, et al. A single-stage LED driver based on interleaved buck-boost circuit and LLC resonant converter[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2015, 3(3): 732-741. DOI:10.1109/JESTPE.2015.2421342 (  0) 0) |
| [13] |
LI Y C, CHEN C L. A novel primary-side regulation scheme for single-stage high-power-factor AC-DC LED driving circuit[J]. IEEE Transactions on Industrial Electronics, 2013, 60(11): 4978-4986. DOI:10.1109/TIE.2012.2224080 (  0) 0) |
| [14] |
陈子健. 高效率软开关图腾柱PFC交错并联控制策略分析及优化[D]. 杭州: 浙江大学, 2021. CHEN Zijian. Analysis and optimization of high efficiency ZVS totem-pole PFC interleaving control[D]. Hangzhou: Zhejiang Universitu, 2021. (  0) 0) |
| [15] |
李力超, 何维, 吴新科. 基于软开关图腾柱拓扑的AC/DC电源[J]. 电力电子技术, 2021, 55(2): 77-79. LI Lichao, HE Wei, WU Xinke. AC/DC power supply based on soft switching totem-pole topology[J]. Power Electronics, 2021, 55(2): 77-79. DOI:10.3969/j.issn.1000-100X.2021.02.020 (  0) 0) |
| [16] |
赵臣凯. 临界导通图腾柱Boost功率因数校正器研究[D]. 杭州: 浙江大学, 2018. ZHAO Chenkai. Research on boundary conduction mode totem-pole boost power factor correction rectifier[D]. Hangzhou: Zhejiang University, 2018. (  0) 0) |
| [17] |
王寅浩. 一种新型软开关无桥Dual-Boost PFC变换器研究[D]. 成都: 西南交通大学, 2012. WANG Yinhao. Research of a novel soft-switching bridgeless Dual-Boost PFC converter technology[D]. Chengdu: Southwest Jiaotong University, 2012. (  0) 0) |
| [18] |
MUSAVI F, EDINGTON M, EBERLE W, et al. Evaluation and efficiency comparison of front end AC-DC plug-in hybrid charger topologies[J]. IEEE Transactions on Smart Grid, 2012, 3(1): 413-421. DOI:10.1109/TSG.2011.2166413 (  0) 0) |
| [19] |
SU B, LU Z Y. An interleaved totem-pole boost bridgeless rectifier with reduced reverse-recovery problems for power factor correction[J]. IEEE Transactions on Power Electronics, 2010, 25(6): 1406-1415. DOI:10.1109/TPEL.2010.2040633 (  0) 0) |
| [20] |
HUANG L, YAO W X, LU Z Y. Interleaved totem-pole bridgeless PFC rectifier with ZVS and low input current ripple[C]//2015 IEEE Energy Conversion Congress and Exposition. Mon-treal, QC, Canada. IEEE, 2015: 166-171.
(  0) 0) |
| [21] |
ZHOU L, WU Y F, HONEA J, et al. High-efficiency true bridgeless totem pole PFC based on GaN HEMT: design challenges and cost-effective solution[C]//Proceedings of PCIM Europe 2015;International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management. Nuremberg, Germany. VDE, 2015: 1-8.
(  0) 0) |
| [22] |
ZHU K, O'GRADY M, DODGE J, et al. 1.5 kW single phase CCM totem-pole PFC using 650 V SiC cascodes[C]//2016 IEEE 4th Workshop on Wide Bandgap Power Devices and Applications (WiPDA). Fayetteville, AR, USA. IEEE, 2016: 90-94.
(  0) 0) |
| [23] |
WU W. 1.5 kW digital totem pole PFC design for air-conditioner and perforance comparison using IGBT, SiC and GaN[C]//PCIM Europe 2017;International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management. Nuremberg, Germany. VDE, 2017: 1-5.
(  0) 0) |
| [24] |
TSAI H Y, HSIA T H, CHEN D. A family of zero-voltage-transition bridgeless power-factor-correction circuits with a zero-current-switching auxiliary switch[J]. IEEE Transactions on Industrial Electronics, 2011, 58(5): 1848-1855. DOI:10.1109/TIE.2010.2053335 (  0) 0) |
 2022, Vol. 41
2022, Vol. 41


 孙战(1997), 男, 硕士在读, 研究方向为高频开关电源(E-mail:
孙战(1997), 男, 硕士在读, 研究方向为高频开关电源(E-mail: