文章编号: 2096-3203(2022)01-0156-09 中图分类号: TM844
2. 国网安徽省电力有限公司合肥供电公司, 安徽 合肥 230061;
3. 国网安徽省电力有限公司, 安徽 合肥 230022
由于交联聚乙烯电缆具有占地面积小、运行可靠性高等优点,其在城市输配电系统中得到了广泛应用[1-2]。但是受施工工艺和运行环境等因素的影响,交联聚乙烯电缆的绝缘性能会降低,最终出现短路故障[3]。因此,为了确保电缆的稳定运行,需要定期对电缆进行绝缘检测,而通过检测工频电压下的电缆局部放电可以判断其绝缘性能。目前,该方法被广泛研究和使用[4-6]。近年来,振荡波电压法在电缆局部放电检测中开始广泛应用,通过产生阻尼振荡电压对电缆进行加压试验。与传统工频电源相比,其工频等效性好,对电缆绝缘损伤小,试验时间短且操作方便[7-10]。
在采用振荡波电压法检测电缆局部放电时,可以通过局部放电脉冲信号在时域上的反射时间差进行绝缘缺陷定位[11-13]。采用该方法进行局部放电定位的关键在于正确匹配放电脉冲的入射波和反射波,从而计算得出准确的时间差。文献[14]利用脉冲信号的幅值突变特点及传播特性进行脉冲匹配,并通过聚类方法修正定位结果。文献[15]采用连续小波变换的方法提取脉冲信号的高频分量,并通过能量峰值特征进行脉冲匹配,在短距离电缆局部放电中有较好的定位精度。文献[16]通过提取单个局部放电脉冲信号的特征进行匹配,可以实现局部放电的自动定位。文献[17]采用经验模态分解(empirical mode decomposition,EMD)对局部放电信号进行去噪预处理,再利用Teager能量算子和动态时间规整法进行脉冲匹配,可以有效实现局部放电的定位。但是上述信号匹配和定位方法均需要先对信号进行去噪处理,在去噪过程中会造成脉冲信号畸变,增加定位计算时间的同时也会降低定位精度[18-19]。
文中提出一种基于集合经验模态分解(ensemble empirical mode decomposition,EEMD)算法与Hilbert边际谱能量的局部放电入射脉冲和反射脉冲匹配方法,可以在振荡波电压下准确进行电缆局部放电定位。首先,基于提出的移动窗口阈值(move window threshold,MWT)法提取出局部放电脉冲;其次,采用EEMD算法对局部放电脉冲信号进行分解,得到若干本征模态函数(instrinsic mode function,IMF)分量;然后,对各IMF分量进行Hilbert变换获得其边际谱并计算出对应分量的边际谱能量值。选择不同IMF分量在原始信号边际谱能量值的占比作为特征量,进行入射脉冲信号和反射脉冲信号匹配,最终采用时域反射法进行定位。试验结果表明,所提方法可以在高斯白噪声较强的情况下实现电缆绝缘缺陷定位。
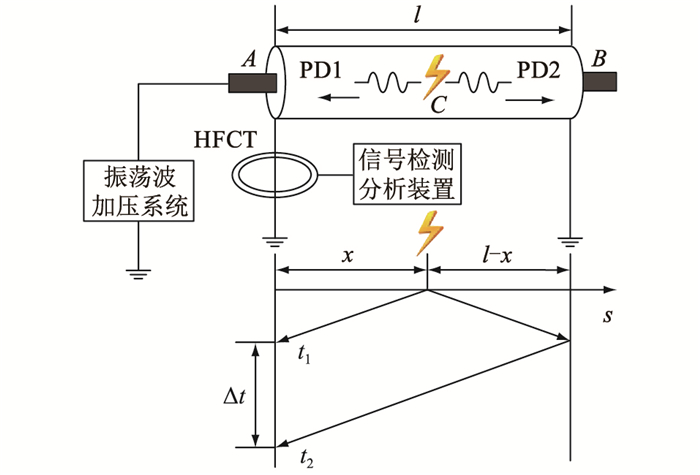
1 定位原理由于振荡波电压下电缆的局部放电检测属于离线测试,因此局部放电脉冲信号会在电缆中发生反射,如图 1所示。电缆A点与振荡波产生装置连接,电缆B点开路,C点处存在绝缘缺陷,检测系统传感器为电缆两端接头地线上安装的高频电流互感器(high frequency current transformer,HFCT)。电缆在振荡波电压下,C点处产生局部放电高频脉冲信号,并分别向电缆两端传输,其中向B点传输的高频脉冲信号PD2会发生反射并最终到达A点。因此,在A点利用HFCT即可分别检测到局部放电高频脉冲信号PD1和PD2。
|
图 1 时域反射局部放电定位方法 Fig. 1 Partial discharge localization method based on time domain reflection |
通过分析局部放电高频脉冲信号的波形参数,结合设备台账中电缆的长度,即可利用时域反射法对局部放电点进行定位。图 1中,l为电缆长度;t1,t2分别为脉冲信号PD1和PD2到达A点检测装置的时间;Δt为局部放电脉冲信号入射波和反射波的时间差。则局部放电点x的位置可以通过求解式(1)得出。
| $ x=l-c \Delta t / 2 $ | (1) |
式中:c为电脉冲在电缆中的传播速度。采用时域反射法进行电缆局部放电定位计算简单且定位精度高,但是在实际检测和定位计算中,一组振荡波电压下产生的局部放电信号由多个高频脉冲组成。局部放电脉冲信号受到背景噪声的影响以及反射传输过程中出现的信号畸变影响,给在脉冲信号中匹配入射脉冲信号和反射脉冲带来困难。
在局部放电脉冲信号传播过程中,信号高频分量衰减较快,低频分量衰减较慢。基于此原理,不同信号的高频分量占比不同,且在相同的传输过程中,反射波的高频分量占比与入射波接近[20-21]。因此,文中提出一种基于IMF分量在原始信号边际谱能量值的占比的入射脉冲信号和反射脉冲信号匹配方法,可以实现电缆中局部放电点的准确定位。
2 局部放电脉冲匹配 2.1 方法总述文中提出局部放电脉冲匹配和定位的具体计算流程,如图 2所示。首先采用MWT算法提取出局部放电脉冲,其次采用EEMD算法对各脉冲信号进行分解,然后基于IMF分量在原始信号边际谱能量值的占比完成入射和反射脉冲信号的匹配,最后采用时域反射法进行定位。

|
图 2 局部放电定位算法流程 Fig. 2 The flow chat of partial discharge location algorithm |
在采用振荡波电压法检测电缆局部放电时,一般会在一个振荡周期内获得一组局部放电高频电流信号。但是在定位计算中,需要提取出单个局部放电信号脉冲,并获得该信号准确的产生时间。因此,文中基于高斯白噪声信号与局部放电信号的典型特征,提出一种基于MWT算法的局部放电高频脉冲信号提取方法。该方法通过在时间坐标上建立移动窗口,计算幅值的方差和平均值,判定脉冲信号起始和截止时间,完成脉冲信号提取,具体计算步骤如下。
步骤一:建立移动窗口,窗口长度与该组局部放电信号最大幅值相同,窗口宽度与信号50个采样点对应的时间长度相同。其中,窗口长度和窗口宽度分别指移动窗口在纵坐标(幅值坐标)上和横坐标(时间坐标)上的最大尺寸。
步骤二:选取该组局部放电信号中的一段高斯白噪声信号,信号长度为50个采样点,计算窗口中信号幅值方差Ex和平均值Av。
步骤三:从0时刻开始移动窗口,并计算每个移动窗口的方差和平均值。当方差和平均值均大于ny倍的Ex和Av时,将第一个采样点记录为需要提取脉冲信号的起始时刻;当方差和平均值均小于ny倍的Ex和Av时,将最后一个采样点记录为需要提取脉冲信号的截止时刻。移动窗口时间间隔为1/2个窗口宽度。
步骤四:根据脉冲信号的起始截止时刻,完成信号提取。
由于高斯白噪声与局部放电信号的特征有明显区别,当移动窗口移动到局部放电信号对应的采样点时,窗口信号的方差和平均值会明显增大,因此,文中提出的MWT法可以有效提取出局部放电脉冲。其中,ny为阈值,可以根据所提取信号的放电量进行设置。
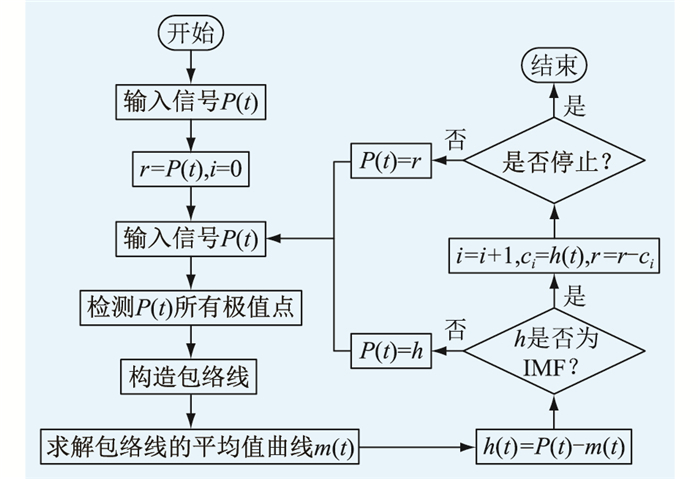
2.3 信号分解EMD算法是EEMD算法的基础,常用于局部放电信号分解计算[22]。EMD算法的计算流程如图 3所示。
|
图 3 EMD算法流程 Fig. 3 The flow chart of EMD algorithm |
但是,EMD算法在处理包含高斯白噪声的局部放电高频脉冲信号时,分解结果会出现模态混叠(mode mixing,MM),这会导致单个IMF分量中存在多种频率分量,或者相近频率分量分布在不同的IMF分量中,不利于后续局部放电的进一步分析,会导致信号定位和识别的误差增大[23-24]。因此,文中选择EEMD算法对局部放电高频脉冲信号进行分解。EEMD算法基于噪声辅助分析,可以有效降低高斯白噪声对EMD算法的干扰,避免出现MM现象。EEMD算法向原始局部放电高频脉冲信号中增加了辅助白噪声,从而改变了原信号中的极值点分布,使不同尺度的信号成分被分配到对应的尺度空间中,解决了MM问题。同时,EEMD算法基于高斯白噪声零均值的统计特性,对染噪局部放电信号分解得到的多组IMF求平均值,可以抑制高斯白噪声对IMF分解结果的不利影响[25]。EEMD算法的具体步骤如下。
步骤一:算法中输入电缆局部放电脉冲信号P(t),添加白噪声的次数N和所接白噪声的幅值系数E。
步骤二:按照式(2)对原始局部放电信号P(t)添加白噪声。
| $ P_{j}(t)=P(t)+g_{j}(t) E $ | (2) |
式中:gj(t)为第j次添加的白噪声信号;Pj(t)为染噪信号。
步骤三:采用EMD算法对染噪信号Pj(t)进行分解,得到一组i阶IMF分量ci, j(t)。
步骤四:重复步骤二和步骤三N次,且每次添加不同的高斯白噪声序列gj(t)。
步骤五:按照式(3)对所有IMF分量按阶求平均值。
| $ a_{i}(t)=\frac{1}{N} \sum\limits_{j=1}^{N} c_{i, j}(t) $ | (3) |
式中:ci, j(t)为第j次得到的第i阶IMF分量。
步骤六:按照式(4)得到P(t)的分解结果。
| $ P(t)=\sum\limits_{i=1}^{N} a_{i}(t)+r(t) $ | (4) |
式中:r(t)为除IMF分量ai(t)外的剩余分量。
在EEMD算法中添加高斯白噪声的次数N越大,采用平均计算得到IMF分量白噪声均值越接近0。
2.4 边际谱能量值为了获得各IMF分量的特征,需要求解其边际谱能量值。对各IMF分量ai(t)进行Hilbert变换,计算过程参见文献[22]。基于式(9)中瞬时频率ωi(t)的求解结果,局部放电高频脉冲信号可以表示为:
| $ \omega_{i}(t)=\mathrm{d} \theta_{i}(t) / \mathrm{d} t $ | (9) |
| $ P(t)=\operatorname{Re} \sum\limits_{i=1}^{n}\left(A_{i}(t) \mathrm{e}^{k \theta_{i}(t)}\right) $ | (10) |
其中,Re为对其取实部计算,因此Hilbert谱为:
| $ H(\omega, t)=\operatorname{Re} \sum\limits_{i=1}^{n}\left(A_{i}(t) \mathrm{e}^{k\int\omega_{i}(t) \mathrm{d} t}\right) $ | (11) |
则Hilbert边际谱h(ω)和边际谱能量E(ω)分别为:
| $ h(\omega)=\int_{0}^{t} H(\omega, t) \mathrm{d} t $ | (12) |
| $ E(\omega)=\int_{\omega_{1}}^{\omega_{2}} h^{2}(\omega) \mathrm{d} \omega $ | (13) |
式中:ω1,ω2分别为边际谱h(ω)的起始和截止频率。
根据式(12)和式(13)可以得出,边际谱能量E(ω)对边际谱h(ω)进行了平方计算。由于边际谱h(ω)可以反映出局部放电高频脉冲信号中的频率成分,文中通过Hilbert边际谱能量将实际频率成分再次放大,可以降低高斯白噪声干扰对信号处理的影响。
2.5 信号匹配文中对局部放电高频脉冲信号进行EEMD分解,可以得到除余量r(t)外的n个IMF分量,求解各IMF分量的边际谱能量Ei(ω),i=1, …, n。选择该IMF分量在原始信号边际谱能量值的占比作为特征,如式(14)所示。
| $ f_{i}=E_{i}(\omega) / \sum\limits_{i=1}^{n} E_{i}(\omega) $ | (14) |
可以得到入射局部放电脉冲信号的特征向量F =(f1, f2, …, fn)和后一个局部放电脉冲信号的特征向量F ′=(f′ 1, f′ 2, …, f′ n)。计算F与F ′之间的脉冲相似度,如式(15)所示。
| $ S=\sum\limits_{i=1}^{n} \frac{f_{i}}{\left|f_{i}-f_{i}^{\prime}\right|} $ | (15) |
在局部放电脉冲信号传播过程中,信号高频分量衰减较快,低频分量衰减较慢,且不同局部放电信号源的高频分量占比不同,在相同的传输过程中,反射波的高频分量占比与入射波最为接近[20]。对后续所有局部放电脉冲按照上述方法依次进行相似度计算和比对,最大S值对应的脉冲信号为该入射脉冲的反射脉冲信号,完成信号匹配计算。通过求解入射和反射脉冲信号的时间差以及式(1),可以实现电缆绝缘缺陷位置定位。
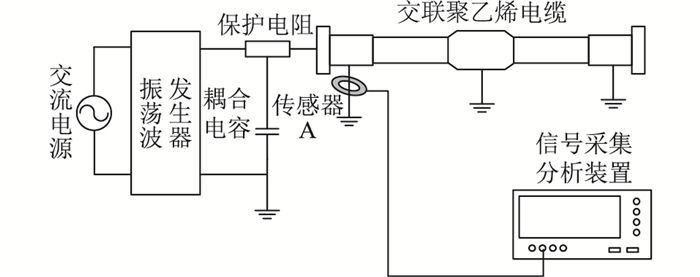
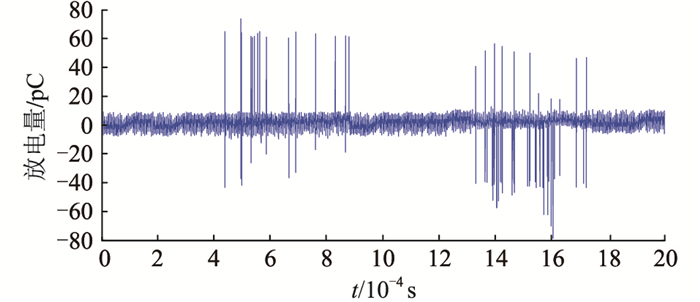
3 试验及分析 3.1 试验设备及解析利用实际中的35 kV单芯电缆进行振荡波耐压试验,电缆中间存在一处人工预制绝缘缺陷,缺陷类型为绝缘介质间包裹金属微粒。通过检测局部放电信号进行分析,对提出的定位算法进行验证。电缆型号为YJLV22-35 kV,长度为502.4 m,预制绝缘缺陷位置为376.1 m,试验电压为1.5U0,U0为电缆缆芯导体与金属护层间的设计额定电压。利用HFCT在电缆接地线上检测局部放电高频脉冲信号。试验接线见图 4。经过校准试验获得电缆的衰减系数为2×104 s-1,放电脉冲在电缆中的传播速度为180 m/μs。传感器检测到局部放电信号见图 5,为一个振荡波周期下产生的多组局部放电脉冲。
|
图 4 试验接线 Fig. 4 Test wiring |
|
图 5 振荡波电压下局部放电信号 Fig. 5 Partial discharge signals under oscillating wave voltage |
由于阈值ny会对定位精度造成影响,文中分别在不同阈值的情况下对所有定位结果的平均误差wav进行了定位计算,结果如表 1所示。定位误差w和平均误差wav的计算公式分别为:
| $ w=\frac{\left|x_{\mathrm{r}}-x_{\mathrm{c}}\right|}{x_{\mathrm{r}}} \times 100 \% $ | (16) |
| $ w_{\mathrm{av}}=\left(\sum\limits_{i=1}^{n_{\mathrm{p}}} w_{i}\right) / n_{\mathrm{p}} $ | (17) |
式中:xr,xc分别为绝缘缺陷实际位置和缺陷定位位置;np为进行定位计算脉冲的数量;wi为第i个脉冲定位计算误差结果。
|
|
表 1 阈值ny对定位精度的影响 Table 1 Influence of threshold ny on localization accuracy |
考虑到单一变量便于分析,表 1中的wav在np=10的情况下计算[26]。由于ny为局部放电信号与白噪声脉冲幅值方差Ex和平均值Av的倍数,所以ny大于1。而当ny大于一定值时,会导致提取信号幅值较低部分波形不完整,甚至部分波形无法提取,因此文中对ny取值从1.2~4.6(间隔0.2)的定位误差进行了计算。结果表明,当ny为2.0~2.4时定位结果较为准确。这是由于ny较小时,无法有效分辨白噪声和局部放电脉冲波型,导致提取出的局部放电信号起始时间错误;ny较高时,无法有效提取出全部局部放电脉冲信号,导致匹配结果出现错误,从而出现较大的定位误差。
确定阈值ny设为2后,采用文中方法对该信号进行脉冲提取,所提取出的前2个局部放电脉冲信号如图 6所示。结果表明,采用MWT法提取脉冲信号波形完整,波形起始时间、结束时间、最高幅值等关键参数均可得出,可以进行后续信号处理分析。
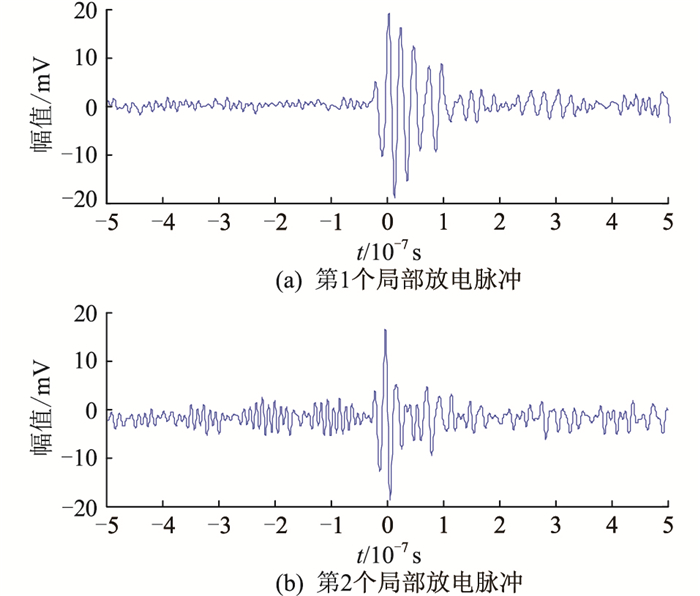
|
图 6 提取出的局部放电脉冲 Fig. 6 Extracted partial discharge pulses |
根据文献[26-27]中的结论,选择振荡波电压下EEMD分解层数为10可以有效提取出局部放电信号特征量。因此,采用EEMD算法对提取出的第1个局部放电脉冲信号进行分解,分解层数设为10,可以得到10个IMF分量和1个残余项(residual term,RES)。信号构造包络线如图 7所示,最终分解结果如图 8所示。
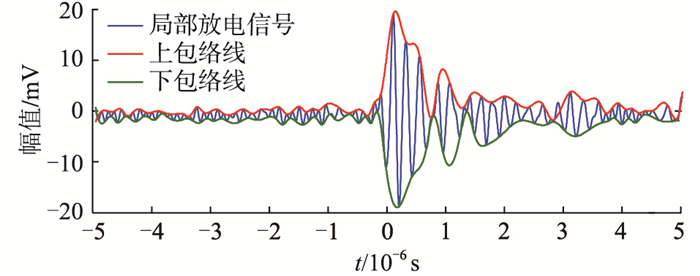
|
图 7 信号构造包络线 Fig. 7 Envelope of the signal construction |
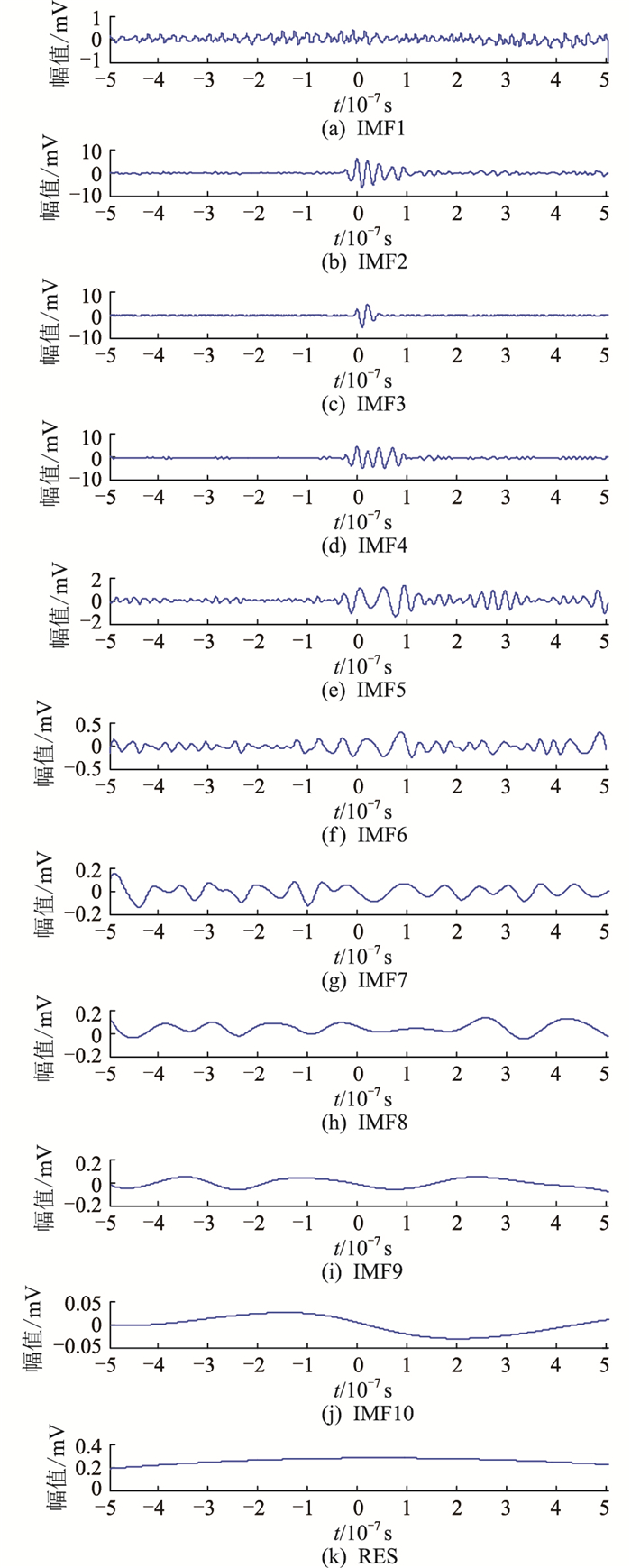
|
图 8 EEMD算法分解结果 Fig. 8 EEMD algorithm decomposition results |
图 8中,IMF1和IMF2为高斯白噪声信号,虽然与局部放电脉冲信号相关度较低,但是凭借其幅值变化范围小、频率覆盖范围广的特性,可以作为IMF分量边际谱能量占比计算,且各脉冲的IMF分量占比值相同[28-29]。
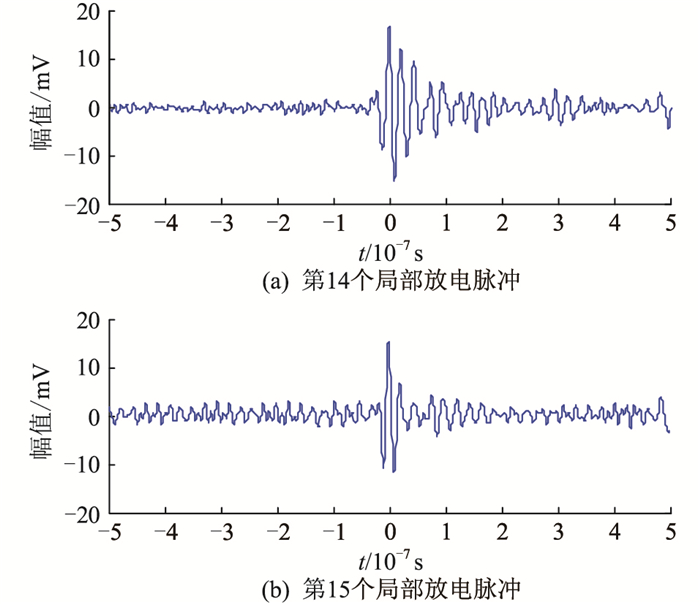
采用文中算法进行脉冲匹配计算和定位计算。图 6中提取出的2个局部放电脉冲信号与后续放电脉冲的相似度S计算结果如图 9所示,选择最大S值对应的脉冲信号为入射脉冲的反射脉冲信号,分别为第14和15个局部放电信号脉冲,其波形见图 10。其中第1个局部放电脉冲与其匹配的反射脉冲时间差为2.062 μs,第2个局部放电脉冲与其匹配的反射脉冲时间差为2.060 μs。根据图 1中的时间到达差法和式(1),最终计算得到的定位位置分别为371.2 m和370.8 m,误差分别为1.3%和1.4%。
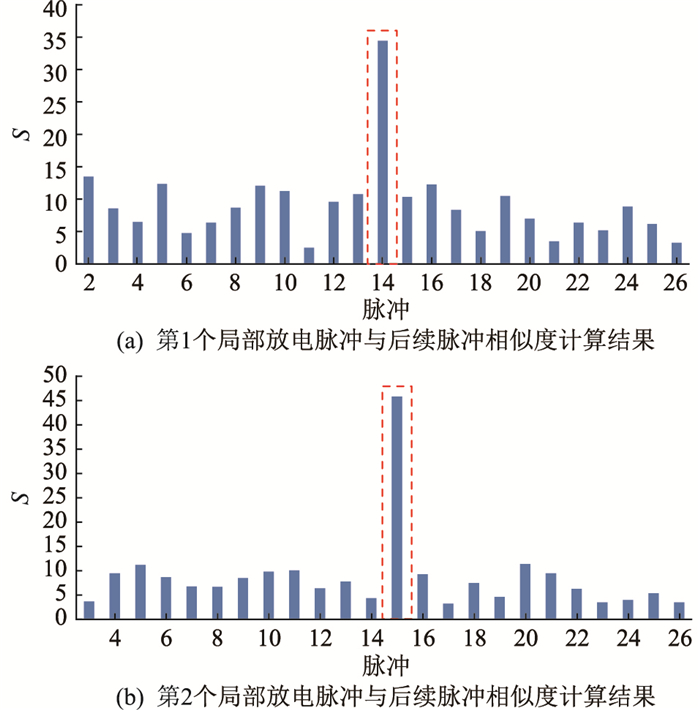
|
图 9 相似度S计算结果 Fig. 9 The similarity S calculation results |
|
图 10 匹配所得反射脉冲 Fig. 10 The matched reflected pulses |
文中所提算法无需对高斯白噪声进行抑制或消除等预处理,这是由于高斯脉冲信号频率范围广、幅值低且稳定,各脉冲信号分解出的高斯白噪声IMF分量边际谱能量占比也基本相同,进行相似度计算时可以忽略其干扰。对提取出的信号人工加入不同幅值的高斯白噪声干扰信号,分析文中方法抗干扰能力,结果见表 2。可以看出,与传统方法相比,文中所提定位算法具有较好的抗白噪声干扰能力。此外,对于其他类型的干扰,如果是脉冲噪声干扰,在后续计算中是无法匹配到反射波形的,因此不会对定位结果造成影响;如果是周期性窄带干扰,采用EEMD计算时会和高斯白噪声干扰一样被分解处理,不影响脉冲信号相似度计算[30-32]。
|
|
表 2 不同幅值白噪声信号干扰下定位误差 Table 2 The localization error under the white noise signal interference of different amplitudes |
按照文中算法依次对入射脉冲信号进行提取,并进行反射脉冲信号进行匹配计算,得到定位结果如表 3所示。从定位结果可以看出,局部放电主要集中在电缆370~381 m的范围内,定位误差范围为0.82%~1.54%,平均误差wav为1.15%。这表明文中提出的振荡波电压下电缆绝缘缺陷定位方法准确度较高,适用于现场绝缘缺陷查找。此外,由于只有局部放电信号波形提取完整,且入射和反射局部放电脉冲匹配正确,使用时间到达差法定位才会进行准确定位,因此试验结果也说明文中所提信号脉冲提取方法及射脉冲匹配方法是准确且有效的。
|
|
表 3 定位结果 Table 3 Localization results |
文中提出了一种基于EEMD与Hilbert边际谱能量的电缆振荡波局部放电定位方法,可以准确匹配局部放电入射和反射脉冲,通过计算到达时间差实现局部放电定位。在实验室内对预制绝缘缺陷35 kV电缆进行振荡波耐压试验,验证了提出方法的准确性,并得到以下结论:
(1) MWT法可以有效提取局部放电脉冲信号,并确保脉冲信号波形完整;基于边际谱能量值占比的脉冲信号匹配方法,可以准确匹配对应的入射和反射脉冲信号,为后续定位计算奠定基础。
(2) 提出的振荡波电压下电缆局部放电定位方法,可以在高斯白噪声干扰下对电缆绝缘缺陷进行有效定位,平均定位误差可达到1.15%。
文中提出的定位算法具有较高的准确性与参考性,在振荡波电缆局部放电定位测试中可降低人工和时间成本,具有较好的应用前景。后续将从加快计算速度和降低现场复杂干扰对定位结果的影响2个方面开展研究。
本文得到国网安徽省电力有限公司科技项目(52120517000F)资助,谨此致谢!
| [1] |
马星河, 朱昊哲, 刘志怀, 等. 基于VMD的电力电缆局部放电信号自适应阈值降噪方法[J]. 电力系统保护与控制, 2019, 47(23): 145-151. MA Xinghe, ZHU Haozhe, LIU Zhihuai, et al. An adaptive threshold value noise suppression method for detecting partial discharge of power cables based on variational mode decomposition[J]. Power System Protection and Control, 2019, 47(23): 145-151. (  0) 0) |
| [2] |
马星河, 张登奎, 朱昊哲, 等. 基于EWT的高压电缆局部放电信号降噪研究[J]. 电力系统保护与控制, 2020, 48(23): 108-114. MA Xinghe, ZHANG Dengkui, ZHU Haozhe, et al. Research on noise reduction of a partial discharge signal of a high voltage cable based on EWT[J]. Power System Protection and Control, 2020, 48(23): 108-114. (  0) 0) |
| [3] |
汪颖, 孙建风, 肖先勇, 等. 基于优化卷积神经网络的电缆早期故障分类识别[J]. 电力系统保护与控制, 2020, 48(7): 10-18. WANG Ying, SUN Jianfeng, XIAO Xianyong, et al. Cable incipient fault classification and identification based on optimized convolution neural network[J]. Power System Protection and Control, 2020, 48(7): 10-18. (  0) 0) |
| [4] |
吴童, 孙抗, 师文文. 基于AVMD-自适应小波包法的电缆局部放电去噪研究[J]. 电力系统保护与控制, 2020, 48(14): 95-103. WU Tong, SUN Kang, SHI Wenwen. Research on cable partial discharge denoising based on an AVMD-adaptive wavelet packet method[J]. Power System Protection and Control, 2020, 48(14): 95-103. (  0) 0) |
| [5] |
GULSKI E, WESTER F J, SMIT J J, et al. Advanced partial discharge diagnostic of MV power cable system using oscillating wave test system[J]. IEEE Electrical Insulation Magazine, 2000, 16(2): 17-25. DOI:10.1109/57.833657 (  0) 0) |
| [6] |
张若兵, 陈子豪, 杜钢. 适用于振荡波电缆局放测试的π型检测阻抗设计[J]. 高电压技术, 2019, 45(5): 1503-1509. ZHANG Ruobing, CHEN Zihao, DU Gang. Design of π-type detection impedance for oscillatory wave cable partial discharge test[J]. High Voltage Engineering, 2019, 45(5): 1503-1509. (  0) 0) |
| [7] |
薛荣, 张龙, 黄志伟, 等. 阻尼振荡波电压和工频电压下XLPE电缆局部放电特性的对比研究[J]. 绝缘材料, 2015, 48(1): 43-48. XUE Rong, ZHANG Long, HUANG Zhiwei, et al. Comparative study on partial discharge characteristics of XLPE cable under damped oscillating wave voltage and AC voltage[J]. Insulating Materials, 2015, 48(1): 43-48. DOI:10.3969/j.issn.1009-9239.2015.01.011 (  0) 0) |
| [8] |
赵铁军, 王秀斌, 虞跃. 基于金属护层模型参数辨识的电缆单相故障单端测距方法[J]. 电力系统保护与控制, 2019, 47(21): 83-91. ZHAO Tiejun, WANG Xiubin, YU Yue. A single terminal fault location method for single phase fault of cable based on parameter identification of metal sheath model[J]. Power System Protection and Control, 2019, 47(21): 83-91. (  0) 0) |
| [9] |
李旭, 郗晓光, 朱明正, 等. 两起不同工艺35 kV电缆中间接头振荡波局部放电缺陷对比分析[J]. 高压电器, 2018, 54(11): 260-264, 272. LI Xu, XI Xiaoguang, ZHU Mingzheng, et al. Comparative analysis of oscillating wave induced partial discharge defects in two 35 kV cable joints with different processes[J]. High Voltage Apparatus, 2018, 54(11): 260-264, 272. (  0) 0) |
| [10] |
陆国俊, 熊俊, 李光茂, 等. 振荡波电压下XLPE电缆局部放电模式识别研究[J]. 高压电器, 2017, 53(2): 95-100, 107. LU Guojun, XIONG Jun, LI Guangmao, et al. Pattern recognition of XLPE cable partial discharge under oscillating voltage[J]. High Voltage Apparatus, 2017, 53(2): 95-100, 107. (  0) 0) |
| [11] |
GHASSEMI F, DENNIS S, AINSLEY A, et al. 275 kV cable discharge field measurement and analysis of SVLs chain failure using ATP[J]. Electric Power Systems Research, 2018, 161: 95-102. DOI:10.1016/j.epsr.2018.04.009 (  0) 0) |
| [12] |
林桂辉, 朱鹏宇, 王灿, 等. 基于Carson理论和EMTP的220 kV多回电缆线路电气参数及不平衡度分析[J]. 电力系统保护与控制, 2019, 47(20): 142-148. LIN Guihui, ZHU Pengyu, WANG Can, et al. Analysis of electrical parameters and unbalance factors of 220 kV multi-circuit transmission cable based on Carson theory and EMTP simulation[J]. Power System Protection and Control, 2019, 47(20): 142-148. (  0) 0) |
| [13] |
KIM Y H, YOUN Y W, YI S H, et al. High-resolution partial discharge location estimation in power cables[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2014, 21(2): 758-765. DOI:10.1109/TDEI.2013.004176 (  0) 0) |
| [14] |
刘鸿. 基于振荡波的电缆多源局放检测及定位方法[D]. 成都: 西南交通大学, 2017. LIU Hong. Cable multi-source PD detection and location based on oscillating wave[D]. Chengdu: Southwest Jiaotong University, 2017. (  0) 0) |
| [15] |
周凯, 赵世林, 何珉, 等. 考虑短距离电缆中行波特性的振荡波局部放电定位方法[J]. 电网技术, 2017, 41(6): 2047-2054. ZHOU Kai, ZHAO Shilin, HE Min, et al. An oscillating wave test method based on traveling wave characteristics of partial discharges for defect location in short cables[J]. Power System Technology, 2017, 41(6): 2047-2054. (  0) 0) |
| [16] |
张若兵, 陈子豪, 杜钢. 基于行波法的振荡波电压下电缆局部放电自动定位算法[J]. 高电压技术, 2019, 45(4): 1289-1296. ZHANG Ruobing, CHEN Zihao, DU Gang. Partial discharge automatic locating algorithm for cable under oscillatory wave voltage conditions based on traveling wave method[J]. High Voltage Engineering, 2019, 45(4): 1289-1296. (  0) 0) |
| [17] |
张若兵, 金森, 杜钢. 基于EMD与DTW算法的振荡波下电缆局部放电定位方法[J]. 高电压技术, 2020, 46(1): 273-281. ZHANG Ruobing, JIN Sen, DU Gang. Method ofpartial discharge localization for cable under oscillatory wave voltage conditions based on EMD and DTW algorithm[J]. High Voltage Engineering, 2020, 46(1): 273-281. (  0) 0) |
| [18] |
刘宇舜, 程登峰, 夏令志, 等. 基于单通道盲源分离算法的局部放电特高频信号去噪方法[J]. 电工技术学报, 2018, 33(23): 5625-5636. LIU Yushun, CHENG Dengfeng, XIA Lingzhi, et al. Partial discharge ultra-high frequency signal de-noising method based on single-channel blind source separation algorithm[J]. Transactions of China Electrotechnical Society, 2018, 33(23): 5625-5636. (  0) 0) |
| [19] |
GHORAT M, GHAREHPETIAN G B, LATIFI H, et al. A new partial discharge signal denoising algorithm based on adaptive dual-tree complex wavelet transform[J]. IEEE Transactions on Instrumentation and Measurement, 2018, 67(10): 2262-2272. DOI:10.1109/TIM.2018.2816438 (  0) 0) |
| [20] |
彭超, 雷清泉. 局部放电超高频信号时频特性与传播距离的关系[J]. 高电压技术, 2013, 39(2): 348-353. PENG Chao, LEI Qingquan. Relationship between characteristic in time and frequency domain of partial discharge ultra-high frequency signals and the radiation distance[J]. High Voltage Engineering, 2013, 39(2): 348-353. DOI:10.3969/j.issn.1003-6520.2013.02.014 (  0) 0) |
| [21] |
杜浩, 关弘路, 玉林威, 等. 直流电压下10 kV交联聚乙烯电缆气隙缺陷局部放电特性研究[J]. 浙江电力, 2019, 38(9): 74-80. DU Hao, GUAN Honglu, YU Linwei, et al. Investigation of partial discharge characteristics of void defects in 10 kV XLPE cable under DC voltage[J]. Zhejiang Electric Power, 2019, 38(9): 74-80. (  0) 0) |
| [22] |
王永强, 李长元, 胡芳芳, 等. 基于改进EMD的GIS局部放电特高频信号降噪方法研究[J]. 电测与仪表, 2017, 54(9): 1-5, 29. WANG Yongqiang, LI Changyuan, HU Fangfang, et al. Study on noise reduction method for PD ultra-high frequency signal based on the improved EMD[J]. Electrical Measurement & Instrumentation, 2017, 54(9): 1-5, 29. DOI:10.3969/j.issn.1001-1390.2017.09.001 (  0) 0) |
| [23] |
杨秋玉, 阮江军, 黄道春, 等. 基于改进Hilbert-Huang变换和支持向量机的高压断路器触头超程状态识别[J]. 电力自动化设备, 2019, 39(1): 198-204. YANG Qiuyu, RUAN Jiangjun, HUANG Daochun, et al. Over-travel detection of electrical contact for high-voltage circuit breaker based on improved HHT and SVM[J]. Electric Power Automation Equipment, 2019, 39(1): 198-204. (  0) 0) |
| [24] |
MOTIN M A, KARMAKAR C K, PALANISWAMI M. Ensemble empirical mode decomposition with principal component analysis: a novel approach for extracting respiratory rate and heart rate from photoplethysmographic signal[J]. IEEE Journal of Biomedical and Health Informatics, 2018, 22(3): 766-774. DOI:10.1109/JBHI.2017.2679108 (  0) 0) |
| [25] |
朱永利, 王刘旺. 并行EEMD算法及其在局部放电信号特征提取中的应用[J]. 电工技术学报, 2018, 33(11): 2508-2519. ZHU Yongli, WANG Liuwang. Parallel ensemble empirical mode decomposition and its application in feature extraction of partial discharge signals[J]. Transactions of China Electrotechnical Society, 2018, 33(11): 2508-2519. (  0) 0) |
| [26] |
王泽雄, 张冠一, 黄晟, 等. 基于改进EEMD的电缆振荡波局放信号特征提取方法[C]//2017智能电网信息化建设研讨会论文集. 北京, 2017: 101-104, 108. WANG Zexiong, ZHANG Guanyi, HUANG Sheng, et al. Feature extraction method of cable oscillating wave local discharge signal based on improved EEMD[C]//2017 Proceedings of the Symposium on Smart Grid Informatization Construction. Beijing, 2017: 101-104, 108. (  0) 0) |
| [27] |
张讥培. 电缆局部放电高频信号的提取及处理技术研究[D]. 成都: 西南交通大学, 2018: 32-41. ZHANG Jipei. The study on extraction and processing technology of high frequency signal of partial discharge in cable[D]. Chengdu: Southwest Jiaotong University, 2018: 32-41. (  0) 0) |
| [28] |
王恩俊, 张建文, 马晓伟, 等. 基于CEEMD-EEMD的局部放电阈值去噪新方法[J]. 电力系统保护与控制, 2016, 44(15): 93-98. WANG Enjun, ZHANG Jianwen, MA Xiaowei, et al. A new threshold denoising algorithm for partial discharge based on CEEMD-EEMD[J]. Power System Protection and Control, 2016, 44(15): 93-98. DOI:10.7667/PSPC151487 (  0) 0) |
| [29] |
韩宏志, 唐振浩. 基于CEEMDAN与回声状态网络的风速预测方法[J]. 电力系统保护与控制, 2020, 48(12): 90-96. HAN Hongzhi, TANG Zhenhao. Wind speed prediction method based on CEEMDAN and echo state network[J]. Power System Protection and Control, 2020, 48(12): 90-96. (  0) 0) |
| [30] |
姚林朋, 郑文栋, 钱勇, 等. 基于集合经验模态分解的局部放电信号的窄带干扰抑制[J]. 电力系统保护与控制, 2011, 39(22): 133-139. YAO Linpeng, ZHENG Wendong, QIAN Yong, et al. A narrow-band interference suppression method based on EEMD for partial discharge[J]. Power System Protection and Control, 2011, 39(22): 133-139. (  0) 0) |
| [31] |
韩宝国, 马驰, 李静鹏, 等. 基于DTCWT与LLE算法的变压器局部放电特高频信号特征参数提取方法[J]. 电力系统保护与控制, 2019, 47(20): 65-72. HAN Baoguo, MA Chi, LI Jingpeng, et al. A feature parameters extraction method of PD UHF signal based on DTCWT and LLE algorithm[J]. Power System Protection and Control, 2019, 47(20): 65-72. (  0) 0) |
| [32] |
刘宝升, 王涤, 马爱军, 等. 封闭环境空气局部放电组分研究[J]. 电力系统保护与控制, 2021, 49(9): 21-28. LIU Baosheng, WANG Di, MA Aijun, et al. Study on the components of air under partial discharge condition in closed space[J]. Power System Protection and Control, 2021, 49(9): 21-28. (  0) 0) |
2. State Grid Hefei Power Supply Company of Anhui Electric Power Co., Ltd., Hefei 230061, China;
3. State Grid Anhui Electric Power Co., Ltd., Hefei 230022, China
 2022, Vol. 41
2022, Vol. 41


 刘宇舜(1990), 男, 博士, 工程师, 从事电力设备状态评价和故障诊断工作(E-mail:
刘宇舜(1990), 男, 博士, 工程师, 从事电力设备状态评价和故障诊断工作(E-mail: