文章编号: 2096-3203(2022)01-0134-07 中图分类号: TM247
复合绝缘子广泛应用于高压输电线的绝缘部分,其良好的疏水性能保证其在污秽条件下保持较好的绝缘性能。然而在严重污秽条件下,绝缘子表面会形成一层潮湿污层,增加表面泄漏电流。电流的热效应使绝缘子表面形成干区,最终引发电弧。局部电弧逐渐发展连接两端电极形成闪络。
国内外有较多研究关注干区形成及其影响。污秽会影响干区的形成[1]。文献[2]从温度分布和泄漏电流角度,细致地分析了干区的形成过程;文献[3]表明了容易产生干区的条件;文献[4-5]利用ANSYS分析了存在干区时绝缘子的温度分布。
与此同时,较多学者分析了电弧的发展机理,通过建立污秽绝缘子仿真模型,分析不同天气条件、不同干区数量及位置下污秽绝缘子的电场分布[6-9]。文献[10-11]研究了绝缘子界面出现气隙、水汽等缺陷以及绝缘子表面存在水珠凝结时的电场分布特性;文献[12]通过人工污秽试验记录了局部电弧形成、短接伞裙、发展为沿面闪络的过程;文献[13]提出了饱和湿度条件下局部电弧会影响绝缘子表面电导率;文献[14]提出了局部电弧的弧根前端可能发生电击穿;文献[15]研究了污层宽度与附着金属相对尺寸造成放电现象差异的原因。
上述研究对干区形成和放电现象有较为深入的分析,但针对干区形成和电弧发展2个随机过程的统计性综合研究并不多。因此,文中采用电热耦合方法,对积污条件下复合绝缘子干区形成和电弧发展的机理进行理论分析和仿真建模,并开展实验对仿真模型进行验证。
1 复合绝缘子电热耦合模型与仿真 1.1 绝缘子模型文中110 kV输电线路复合绝缘子模型根据IEC 60815标准选择尺寸和几何形状。该绝缘子有15个大伞裙和14个小伞裙。由于复合绝缘子的轴对称几何形状,文中使用二维模型来模拟干区形成和电弧发展过程,既满足了计算精度又降低计算复杂度。
环境温度和气压分别为293 K和101.325 kPa。在环境温度和空气湿度的影响下,文中用等值盐密(equivalent salt deposit density, ESDD)评估绝缘子表面的污秽程度。由于污秽层在绝缘子表面上并非均匀分布,绝缘子伞裙上表面和下表面等值盐密比值为KESDD,文献[16]表明当该比值接近1时,闪络击穿发生概率最高。因此文中选取等值盐密为0.1 mg/cm2且KESDD=1用于模拟较为严重的积污情况,模型中未考虑空气中的水颗粒。绝缘子模型如图 1所示。其中,θ为伞裙倾斜角;d为绝缘子伞裙间的干弧距离;r1,r2分别为大伞裙和小伞裙的半径。

|
图 1 复合绝缘子模型示意 Fig. 1 Schematic diagram of composite insulator model |
爬电系数KCF定义为绝缘子爬电距离与干弧距离之比:
| $ K_{\mathrm{CF}}=\left(l_{1}+l_{2}\right) / d $ | (1) |
式中:l1+l2为绝缘子相邻2个大伞裙之间的总爬电距离。
伞裙比KS为r2与r1之比:
| $ K_{\mathrm{S}}=r_{2} / r_{1} $ | (2) |
为了降低干区电弧和电弧传播的可能性,在保持爬电距离不变的前提下优化绝缘子的几何结构。绝缘子几何形状的优化变量分别为KCF,KS和θ。
1.2 场域计算方法文中电场与热场的数值计算方法均采用广义时域有限差分法,此方法是一种无网格的差分方法。相较于传统的有限差分法,广义有限差分法离散计算点的布置不受网格剖分制约,可以根据计算区域内的物体形状,灵活选取离散点的布置位置以及疏密程度。因此,广义有限差分法适用于复杂边界形状的场域计算问题,同时减少计算量。
1.2.1 电场计算模型绝缘子附近的电场计算式如下:
| $ \left\{\begin{array}{l} \nabla^{2} \varphi=\frac{\partial^{2} \varphi}{\partial x^{2}}+\frac{\partial^{2} \varphi}{\partial y^{2}}=-\frac{\rho_{\mathrm{c}}}{\varepsilon} \\ \left.\varphi(x, y)\right|_{\varGamma}=f_{1}(\varGamma) \\ \left.\frac{\partial \varphi}{\partial n}\right|_{\varGamma}=f_{2}(\varGamma) \end{array}\right. $ | (3) |
式中:φ为电势;ρc为体电荷密度;ε为介电常数;Γ为场域边界几何形状。场域中第一类边界条件包括电势已知的电极,以及电势为0的场域边界;第二类边界条件为绝缘子与空气交界面电场法向分量连续。
为了确定干区形成和电弧过程中绝缘子表面的电弧传播方向和泄漏电流密度,文中采用广义时域有限差分方法计算复合绝缘子附近的瞬时电场。广义时域有限差分的优点是,根据精度要求和边界条件,在场域中离散计算点分布的疏密程度可以不同。由于需要着重计算靠近电弧的电场,且要降低其他区域中的计算复杂度,所以靠近电弧的点的分布应比场域其他区域的点更加密集。
电弧附近通过广义时域有限差分方法计算场域的离散点分布,如图 2所示。

|
图 2 电场计算中的广义时域有限差分 Fig. 2 Generalized finite different-time domain method in electric field calculation |
其中,Pi是P1~Pn之间的点;Pi和P1~Pn的每个点的函数值为ui和u1~un;P1~Pn到Pi的距离为r1~rn,最远的距离为rmax。
根据泰勒级数展开式,Pi附近的点Pj处的函数值uj表示如下:
| $ \begin{gathered} u_{j}=u_{i}+h_{i j} \frac{\partial u_{i}}{\partial x}+k_{i j} \frac{\partial u_{i}}{\partial y}+\frac{1}{2}\left(h_{i j}^{2} \frac{\partial^{2} u_{i}}{\partial x^{2}}+k_{i j}^{2} \frac{\partial^{2} u_{i}}{\partial y^{2}}\right)+ \\ h_{i j} k_{i j} \frac{\partial^{2} u_{i}}{\partial x \partial y} \quad i=1,2, \cdots, m \end{gathered} $ | (4) |
其中,hij, kij分别为x和y坐标差的绝对值,如式(5)所示。
| $ \left\{\begin{array}{l} h_{i j}=\left|x_{j}-x_{i}\right| \\ k_{i j}=\left|y_{j}-y_{i}\right| \end{array}\right. $ | (5) |
两点的残差函数B(u)[17]如式(6)所示。
| $ \begin{gathered} B(u)=\sum\limits_{j=1}^{n}\left[\left(u_{i}-u_{j}+h_{i j} \frac{\partial u_{j}}{\partial x}+\right.\right. \\ \left.\left.k_{i j} \frac{\partial u_{j}}{\partial y}+\frac{h_{i j}^{2}}{2} \frac{\partial^{2} u_{j}}{\partial x^{2}}+\frac{k_{i j}^{2}}{2} \frac{\partial^{2} u_{j}}{\partial y^{2}}\right) w_{j}\right]^{2} \end{gathered} $ | (6) |
第j个点的权重函数wj计算如下:
| $ w_{j}=1-6\left(\frac{r_{j}}{r_{\max }}\right)^{2}+8\left(\frac{r_{j}}{r_{\max }}\right)^{3}-3\left(\frac{r_{j}}{r_{\max }}\right)^{4} $ | (7) |
将B(u) 中的∂2u/∂x2,∂2u/∂y2,∂u/∂2和∂u/∂y分离出来,然后得到ADu = b,其中矩阵A,Du和b如式(8)-式(10)所示。
| $ \begin{array}{c} \boldsymbol{A}=\\ \left[\begin{array}{cccc} \sum\limits_{j=1}^{n} \frac{h_{i j}^{4} w_{j}^{2}}{4} & \sum\limits_{j=1}^{n} \frac{h_{i j}^{2} k_{i j}^{2} w_{j}^{2}}{4} & 0 & 0 \\ \sum\limits_{j=1}^{n} \frac{h_{i j}^{2} k_{i j}^{2} w_{j}^{2}}{4} & \sum\limits_{j=1}^{n} \frac{k_{i j}^{4} w_{j}^{2}}{4} & 0 & 0 \\ 0 & 0 & \sum\limits_{j=1}^{n}\left(h_{i j}^{2} w_{j}^{2}\right) & \sum\limits_{j=1}^{n}\left(h_{i j} k_{i j} w_{j}^{2}\right) \\ 0 & 0 & \sum\limits_{j=1}^{n}\left(h_{i j} k_{i j} w_{j}^{2}\right) & \sum\limits_{j=1}^{n}\left(k_{i j}^{2} w_{j}^{2}\right) \end{array}\right] \end{array} $ | (8) |
| $ \boldsymbol{D}_{u}=\left[\begin{array}{llll} \frac{\partial^{2} u}{\partial x^{2}} & \frac{\partial^{2} u}{\partial y^{2}} & \frac{\partial u}{\partial x} & \frac{\partial u}{\partial y} \end{array}\right]^{\mathrm{T}} $ | (9) |
| $ \boldsymbol{b}=\left[\begin{array}{c} \sum\limits_{j=1}^{n}\left(\left(u_{j}-u_{i}\right) \frac{h_{i j}^{2} w_{j}^{2}}{2}\right) \\ \sum\limits_{j=1}^{n}\left(\left(u_{j}-u_{i}\right) \frac{k_{i j}^{2} w_{j}^{2}}{2}\right) \\ \sum\limits_{j=1}^{n}\left(\left(u_{j}-u_{i}\right) h_{i j} w_{j}^{2}\right) \\ \sum\limits_{j=1}^{n}\left(\left(u_{j}-u_{i}\right) k_{i j} w_{j}^{2}\right) \end{array}\right] $ | (10) |
将矩阵b分解为b = Bu,其中:
| $ \begin{array}{c} \boldsymbol{B}=\\ \left[\begin{array}{ccccccc} \sum\limits_{j=1}^{n} \frac{-h_{i j}^{2} w_{j}^{2}}{2} & \frac{h_{i 1}^{2} w_{1}^{2}}{2} & \frac{h_{i 2}^{2} w_{2}^{2}}{2} & \cdots & \frac{h_{i j}^{2} w_{j}^{2}}{2} & \cdots & \frac{h_{i n}^{2} w_{n}^{2}}{2} \\ \sum\limits_{j=1}^{n} \frac{-k_{i j}^{2} w_{j}^{2}}{2} & \frac{k_{i 1}^{2} w_{1}^{2}}{2} & \frac{k_{i 2}^{2} w_{2}^{2}}{2} & \cdots & \frac{k_{i j}^{2} w_{j}^{2}}{2} & \cdots & \frac{k_{i n}^{2} w_{n}^{2}}{2} \\ \sum\limits_{j=1}^{n}\left(-h_{i j} w_{j}^{2}\right) & h_{i 1} w_{1}^{2} & h_{i 2} w_{2}^{2} & \cdots & h_{i j} w_{j}^{2} & \cdots & h_{i n} w_{n}^{2} \\ \sum\limits_{j=1}^{n}\left(-k_{i j} w_{j}^{2}\right) & k_{i 1} w_{1}^{2} & k_{i 2} w_{2}^{2} & \cdots & k_{i j} w_{j}^{2} & \cdots & k_{i n} w_{n}^{2} \end{array}\right] \end{array} $ | (11) |
| $ \boldsymbol{u}=\left[\begin{array}{lllllll} u_{i} & u_{1} & u_{2} & \cdots & u_{j} & \cdots & u_{n} \end{array}\right]^{\mathrm{T}} $ | (12) |
矩阵Du也可表达为Du= A-1b = A-1Bu = Du,其中:
| $ \begin{gathered} \boldsymbol{D}=\boldsymbol{A}^{-1} \boldsymbol{B}= \\ {\left[\begin{array}{cccc} \sum\limits_{i=1}^{4}\left(a_{1, i} b_{i, 1}\right) & \sum\limits_{i=1}^{4}\left(a_{1, i} b_{i, 2}\right) & \cdots & \sum\limits_{i=1}^{4}\left(a_{1, i} b_{i, n+1}\right) \\ \sum\limits_{i=1}^{4}\left(a_{2, i} b_{i, 1}\right) & \sum\limits_{i=1}^{4}\left(a_{2, i} b_{i, 2}\right) & \cdots & \sum\limits_{i=1}^{4}\left(a_{2, i} b_{i, n+1}\right) \\ \sum\limits_{i=1}^{4}\left(a_{3, i} b_{i, 1}\right) & \sum\limits_{i=1}^{4}\left(a_{3, i} b_{i, 2}\right) & \cdots & \sum\limits_{i=1}^{4}\left(a_{3, i} b_{i, n+1}\right) \\ \sum\limits_{i=1}^{4}\left(a_{4, i} b_{i, 1}\right) & \sum\limits_{i=1}^{4}\left(a_{4, i} b_{i, 2}\right) & \cdots & \sum\limits_{i=1}^{4}\left(a_{4, i} b_{i, n+1}\right) \end{array}\right]} \end{gathered} $ | (13) |
其中,ar, c和br, c分别为矩阵A-1和B中的第r行和第c列的元素。
∂2u/∂x2,∂2u/∂y2,∂u/∂x和∂u/∂y分别可写为:
| $ \left\{\begin{array}{l} \frac{\partial^{2} u}{\partial x^{2}}=d_{1,1} u_{i}+\sum\limits_{j=1}^{n}\left(d_{1, j+1} u_{j}\right) \\ \frac{\partial^{2} u}{\partial y^{2}}=d_{2,1} u_{i}+\sum\limits_{j=1}^{n}\left(d_{2, j+1} u_{j}\right) \\ \frac{\partial u}{\partial x}=d_{3,1} u_{i}+\sum\limits_{j=1}^{n}\left(d_{3, j+1} u_{j}\right) \\ \frac{\partial u}{\partial y}=d_{4,1} u_{i}+\sum\limits_{j=1}^{n}\left(d_{4, j+1} u_{j}\right) \end{array}\right. $ | (14) |
式中:dr, c为矩阵D第r行和第c列的元素。
将式(14)代入式(3),泊松方程可写为:
| $ \begin{gathered} d_{1,1} \varphi_{i, t_{n}}+\sum\limits_{j=1}^{n}\left(d_{1, j+1} \varphi_{j, t_{n}}\right)+d_{2,1} \varphi_{i, t_{n}}+ \\ \sum\limits_{j=1}^{n}\left(d_{2, j+1} \varphi_{j, t_{n}}\right)=-\frac{\rho_{i, t_{n}}}{\varepsilon_{i}} \end{gathered} $ | (15) |
式中:ρi, tn为第i个离散点在tn阶段的电荷密度;tn为当前阶段。
随机漫步理论用于计算所有方向的电弧传播概率。在电弧传播的每个步骤都生成随机数,以确定下一步的确切方向。因此,即使电场分布保持不变,电弧的发展方向也可能不同,这体现了电弧传播的随机性[18-19]。
| $ P=\frac{E^{2}}{\sum E^{2}} a\left(E-E_{\mathrm{c}}\right) $ | (16) |
式中:P为电弧传播过程中向各个方向发展的概率;E为E>Ec时所有可能方向的电场强度总和;Ec(2.1 kV/mm)为空气电绝缘强度的均方根值;a为阶跃函数。
1.2.2 热传递模型受污染绝缘子表面的传热过程包括泄漏电流注入过程、热传导和对流过程、电弧辐射过程以及水蒸发过程。
在电弧产生之前,热传导和热对流是复合绝缘子表面热传递的主要形式。热传导和热对流偏微分方程以及边界条件如式(17)所示。
| $ \left\{\begin{array}{l} \rho c\left(\frac{\partial T}{\partial t}+v_{x} \frac{\partial T}{\partial x}+v_{y} \frac{\partial T}{\partial y}\right)=\lambda\left(\frac{\partial^{2} T}{\partial x^{2}}+\frac{\partial^{2} T}{\partial y^{2}}\right)+\varPhi \\ \left.T(x, y)\right|_{\varGamma}=f_{1}(\varGamma) \\ \left.\frac{\partial T}{\partial n}\right|_{\varGamma}=f_{2}(\varGamma) \end{array}\right. $ | (17) |
式中:T为热温度;t为时间;ρ,c,λ分别为不同绝缘材料的密度、比热容和热导率;vx,vy分别为流体速度在x轴和y轴上的分量;Φ为由干区电弧和绝缘子表面的漏电流密度引起的内部热源。场域中第一类边界条件包括温度为室温的场域边界,以及初始时刻场域内的温度分布;第二类边界条件为绝缘子与空气交界面热流密度连续。
导热计算中的广义时域有限差分方法类似于电场计算。离散形式的热传导偏微分方程如下:
| $ \begin{gathered} \rho_{i} c_{i}\left[\frac{T_{i, t_{n+1}}-T_{i, t_{n}}}{\Delta t}+d_{3,1} T_{i, t_{n+1}}+\sum\limits_{j=1}^{n}\left(d_{3, j+1} T_{j, t_{n+1}}\right)+\right. \\ \left.d_{4,1} T_{i, t_{n+1}}+\sum\limits_{j=1}^{n}\left(d_{4, j+1} T_{j, t_{n+1}}\right)\right]= \\ \lambda_{i} d_{1,1} T_{i, t_{n+1}}+\sum\limits_{j=1}^{n}\left(\lambda_{j} d_{1, j+1} T_{j, t_{n+1}}\right)+ \\ \lambda_{i} d_{2,1} T_{i, t_{n+1}}+\sum\limits_{j=1}^{n}\left(\lambda_{j} d_{2, j+1} T_{j, t_{n+1}}\right) \end{gathered} $ | (18) |
式中:tn+1为离散时域中的下一个阶段。
离散形式的Φ计算如下:
| $ \varPhi_{i}=E_{i, t_{n}} J_{i, t_{n}}=E_{i, t_{n}}^{2} / \rho_{r} $ | (19) |
式中:Ei, tn为第i个离散点在tn阶段的电场强度;Ji, tn为第i个离散点在tn阶段的漏电流密度;ρr为绝缘子表面的电阻率。
泄漏电流注入能量的计算如下:
| $ W_{\text {leakage }}=\sum\limits_{t=0}^{t_{0}} \sum\limits_{i=1}^{l} \frac{E_{i, t_{n}}^{2}}{\rho_{r}} $ | (20) |
绝缘子表面的热传导和对流能量计算如下:
| $ W_{\text {conduction }}=\sum\limits_{t=0}^{t_{0}} \sum\limits_{i=0}^{l} \lambda \Delta T_{i, t_{n}} $ | (21) |
| $ W_{\text {convention }}=\sum\limits_{t=0}^{t_{0}} \sum\limits_{i=0}^{l} h\left(T_{i, t_{n}}-T_{0}\right) $ | (22) |
式中:l为绝缘子爬电距离的长度;t0为持续时间;Ti, tn为绝缘子表面第i个离散点在tn阶段的热温度;ΔT为随距离和时间变化的温度差;T0为环境温度,取273 K;h为对流的传热系数。
电弧产生后,热辐射成为导致绝缘子表面传热的主要因素。热辐射是电弧产生辐射能的过程。电弧辐射能量Warc的计算如下:
| $ W_{\mathrm{arc}}=\sum\limits_{t=0}^{t_{0}} \sum\limits_{i=0}^{l} \varepsilon_{\mathrm{emit}} \sigma T_{i, t_{n}}^{4} $ | (23) |
式中:εemit为实际物体的发射率;σ为斯特番-波尔茨曼常数,σ= 5.67×10-8 W ·m-2 ·K-4。
污层中的水在传热过程中蒸发。克劳修斯-克拉伯龙方程描述了基于气压和热温度的焓变:
| $ \ln \frac{P_{2}}{P_{1}}=\frac{\Delta H_{\text {water }}^{\text {steam }}}{R}\left(\frac{1}{T_{1}}-\frac{1}{T_{2}}\right) $ | (24) |
| $ \Delta H_{\text {water }}^{\text {steam }}=R T_{1} / T_{2} $ | (25) |
式中:ΔHwatersteam为水的相变焓;R为通用气体常数,R= 8.314;P1,P2保持与标准大气压(101.325 kPa)相同;T1,T2分别为电弧产生前后的热温度。因此,ΔH是干区形成和电弧传播过程中热温度的函数。Vwater为蒸发水物质的量,蒸发能量为:
| $ W_{\text {water }}^{\text {steam }}=\Delta H_{\text {water }}^{\text {steam }} V_{\text {water }} $ | (26) |
绝缘子表面干区形成的热平衡方程为:
| $ W_{\text {water }}^{\text {steam }}+W_{\text {conduction }}+W_{\text {convection }}=W_{\text {arc }}+W_{\text {leakage }} $ | (27) |
首先,模拟了污层从初始时刻(t=0 s)到电弧产生时刻的干区形成过程,以分析泄漏电流密度对干区形成的影响。然后,在电弧产生之后模拟电弧传播过程,以研究电弧能量耗散对干区进一步形成和闪络的影响。
当t=0 s和t=2.4 s时,在电弧产生之前形成干区的2个阶段如图 3所示。

|
图 3 绝缘子表面干区形成过程 Fig. 3 Dry band formation process on the insulator surface |
在形成干区前t=0 s时的电场和热场分布如图 4所示。由图 3(b)和图 4(b)可知,干区最先在最大热场的位置出现。

|
图 4 污层产生之前的电场和热场分布 Fig. 4 Electric and thermal field distributions before the pollutant layer generation |
当污染物层中的水继续蒸发时,干区面积继续扩大。比较干区形成的3个不同时刻靠近高压电极的绝缘子表面上的电场分布,如图 5所示,存在干区时的最大电场高于没有干区时的最大电场,当干区扩大时,最大电场减小。

|
图 5 不同干区长度的电场比较 Fig. 5 Electric field comparison with different lengths of the dry band |
当最大电场超过空气的电绝缘强度(t=4.28 s)时,电弧产生。最初的电弧产生和热场分布见图 6。

|
图 6 高电压电极附近的电弧轨迹和热场分布 Fig. 6 Arc trajectory and thermal field distributions close to the HV electrode |
电弧产生在绝缘子表面上最大电场的位置。可以看出,当电弧产生时,热温度显著升高,电弧热辐射将能量从电弧耗散到空气和绝缘体表面。在传播过程中电弧能量辐射成为干区形成的主要因素。然而,当干区的长度和数量增加时,电弧会熄灭,因为干区的表面电阻率显著高于污染物层的电阻率,从而泄漏电流减小。
如图 7(a)所示,当t等于7.69 s时,在产生多个干区后,电弧在绝缘子表面的不同位置出现。电弧的出现伴随着干区的扩张,靠近干区的位置出现电场畸变,从而引发新的电弧。经过6次迭代,得到的结果是,每次迭代后电弧的数量均显著增加。如图 7(b)所示,当t等于17.23 s时,彼此分离的电弧最终会连在一起,形成从复合绝缘子的高压电极到接地电极的导电路径,并引起闪络。

|
图 7 高电压电极附近的电弧轨迹 Fig. 7 Arc trajectory close to the HV electrode |
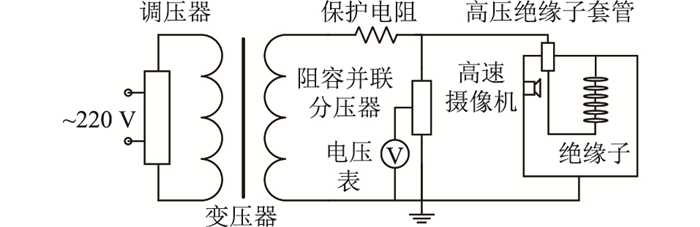
实验系统的原理如图 8所示。高速摄像机用于捕获电弧的传播过程。
|
图 8 实验系统 Fig. 8 Experiment system |
干区形成和电弧传播过程的实验结果见图 9。比较了不同时间范围的电弧传播,以分析干区位置和电弧现象。图 9(a)显示了由于靠近高电压电极的干区而引发的第一个电弧,图 9(b)显示了由于绝缘子表面上存在多个干区,电弧在不同位置重新出现,图 9(c)显示了分离的电弧连接并导致闪络。各个现象出现的时刻与模型中的仿真结果一致。

|
图 9 干区形成和电弧发展过程的实验结果 Fig. 9 Experiment results of dry band formation and arc propagation process |
该模型可较为准确地模拟复合绝缘子污闪过程,通过改变绝缘子结构并多次重复电弧发展过程可计算得到击穿概率,从而优化爬电系数KCF,伞裙比KS和伞裙倾角θ。在爬电距离不变的情况下,优化后的爬电系数KCF=2.89,伞裙倾角θ=12.3°,伞裙比KS在0.7~0.9范围内变化时对闪络概率影响较小。
4 结论文中对污秽复合绝缘子的干区形成和电弧过程进行了建模。通过广义时域有限差分方法计算了瞬时电场和热场,以研究干区电弧和闪络的机理。通过实验验证了理论结果。最终得出结论:
(1) 广义时域有限差分方法适用于绝缘子几何结构的电场和热场的计算。该方法可提高关键区域的计算精度,并降低非关键区域的计算复杂度。
(2) 仿真和实验结果均表明,与绝缘子爬电距离上其他位置相比,2个电极周围的电场和泄漏电流密度更高,因此2个电极附近有较大概率形成干区。
(3) 最大电场值随着干区的扩大而减小,同时最大热场值随着绝缘体表面上干区的扩大而连续增大。
(4) 通过干区形成与电弧发展模型优化绝缘子爬电系数、伞裙倾角和伞裙比,能够在不增加绝缘子爬电距离的条件下有效降低闪络击穿的概率。此外,对于具有新的几何形状和结构设计的绝缘子,研究干区形成机理,有助于预测其干区和电弧形成的特征,评估其绝缘性能。
| [1] |
梁飞, MacAlpine Mark, 关志成, 等. 污秽绝缘子表面干区形成的影响因素[J]. 高电压技术, 2012, 38(10): 2604-2610. LIANG Fei, MARK M, GUAN Zhicheng, et al. Factors affecting dry-band formation on the surface of polluted insulator[J]. High Voltage Engineering, 2012, 38(10): 2604-2610. (  0) 0) |
| [2] |
梁飞, MacAlpine Mark, 关志成, 等. 基于红外热像分析的绝缘子污闪过程中干区形成过程分析[J]. 高电压技术, 2014, 40(1): 138-146. LIANG Fei, MARK M, GUAN Zhicheng, et al. Formation of dry-band in the process of pollution flashover based on infrared thermal image analysis[J]. High Voltage Engineering, 2014, 40(1): 138-146. (  0) 0) |
| [3] |
张达. 湿污绝缘子发热及污秽放电机理[J]. 高电压技术, 2018, 44(3): 787-795. ZHANG Da. Heating and discharge mechanism of wet contaminated insulators[J]. High Voltage Engineering, 2018, 44(3): 787-795. (  0) 0) |
| [4] |
孟繁萃, 张达, 赵洪博, 等. 干燥带对绝缘子温度场影响的研究[J]. 机械与电子, 2018, 36(7): 22-27. MENG Fancui, ZHANG Da, ZHAO Hongbo, et al. Research on influence of drying zone on insulator temperature field[J]. Machinery & Electronics, 2018, 36(7): 22-27. DOI:10.3969/j.issn.1001-2257.2018.07.006 (  0) 0) |
| [5] |
张明, 祝新飞, 张达. 湿污绝缘子的温度场研究[J]. 绝缘材料, 2017, 50(10): 37-42, 47. ZHANG Ming, ZHU Xinfei, ZHANG Da. Research on temperature field of polluted and wetted insulators[J]. Insulating Materials, 2017, 50(10): 37-42, 47. (  0) 0) |
| [6] |
李静, 许鹏娟, 杨光, 等. 盐密对污秽复合绝缘子电场与温度场的影响研究[J]. 电气工程学报, 2018, 13(7): 23-30. LI Jing, XU Pengjuan, YANG Guang, et al. Study on the effect of salt density on electric and temperature field of contaminated composite insulator[J]. Journal of Electrical Engineering, 2018, 13(7): 23-30. (  0) 0) |
| [7] |
刘向实. 污秽条件下复合绝缘子电场仿真研究[J]. 电瓷避雷器, 2014(5): 31-36. LIU Xiangshi. Study on electric field distribution of composite insulator under pollution conditions[J]. Insulators and Surge Arresters, 2014(5): 31-36. (  0) 0) |
| [8] |
DHAHBI-MEGRICHE N, SLAMA M E A, BEROUAL A. Influence of dry bands on polluted insulator performance[C]//2017 International Conference on Engineering & MIS (ICEMIS). Monastir, Tunisia. IEEE, 2017: 1-4.
(  0) 0) |
| [9] |
ARSHAD, NEKAHI A, MCMEEKIN S G, et al. Effect of dry band location on electric field distribution along a polymeric insulator under contaminated conditions[C]//2015 50th International Universities Power Engineering Conference (UPEC). Stoke on Trent, UK. IEEE, 2015: 1-4.
(  0) 0) |
| [10] |
江渺, 李黎, 华奎, 等. 复合绝缘子界面缺陷对电场分布特性影响的仿真研究[J]. 电力工程技术, 2019, 38(4): 138-144. JIANG Miao, LI Li, HUA Kui, et al. Influence of interface defect on the electric field distribution of composite insulator[J]. Electric Power Engineering Technology, 2019, 38(4): 138-144. (  0) 0) |
| [11] |
吕玉坤, 王佳文, 宋庆壮, 等. 水珠对复合绝缘子表面电场畸变特性的影响[J]. 电网技术, 2021, 45(3): 1201-1207. LYU Yukun, WANG Jiawen, SONG Qingzhuang, et al. Effect of water drop on electric field distortion of composite insulator[J]. Power System Technology, 2021, 45(3): 1201-1207. (  0) 0) |
| [12] |
李静, 许鹏娟, 刘树鑫, 等. 复合绝缘子污闪动态发展过程与影响因素[J]. 沈阳工业大学学报, 2019, 41(5): 481-488. LI Jing, XU Pengjuan, LIU Shuxin, et al. Dynamic development process and influencing factors of pollution flashover for composite insulators[J]. Journal of Shenyang University of Technology, 2019, 41(5): 481-488. (  0) 0) |
| [13] |
王黎明, 李旭, 曹彬, 等. 局部电弧对绝缘子泄漏电流和表面电导率关系的影响[J]. 高电压技术, 2019, 45(5): 1624-1629. WANG Liming, LI Xu, CAO Bin, et al. Influence of partial arc on leakage current and surface conductivity of insulators[J]. High VoltageEngineering, 2019, 45(5): 1624-1629. (  0) 0) |
| [14] |
李健, 周军, 黄瑞平, 等. 沿绝缘表面空气间隙击穿特性的试验研究[J]. 高压电器, 2017, 53(5): 1-6. LI Jian, ZHOU Jun, HUANG Ruiping, et al. Experimental study of the breakdown characteristic of the air gap along dielectric surface[J]. High Voltage Apparatus, 2017, 53(5): 1-6. (  0) 0) |
| [15] |
王羽, 牟霖, 王万昆, 等. 附着金属体染污绝缘表面局部电弧特性研究[J]. 中国电机工程学报, 2019, 39(11): 3253-3262. WANG Yu, MU Lin, WANG Wankun, et al. Research on cha-racteristics of partial electric arc on contaminated insulating surface attached with floating potential metal[J]. Proceedings of the CSEE, 2019, 39(11): 3253-3262. (  0) 0) |
| [16] |
JIANG X L, ZHANG Z J, HU J L. Investigation on flashover voltage and non-uniform pollution correction coefficient of DC composite insulator[C]//2008 International Conference on High Voltage Engineering and Application. Chongqing, China. IEEE, 2008: 104-108.
(  0) 0) |
| [17] |
CHAN H F, FAN C M, KUO C W. Generalized finite difference method for solving two-dimensional non-linear obstacle problems[J]. Engineering Analysis With Boundary Elements, 2013, 37(9): 1189-1196. DOI:10.1016/j.enganabound.2013.05.004 (  0) 0) |
| [18] |
NOSKOV M D, MALINOVSKI A S, SACK M, et al. Self-consistent modeling of electrical tree propagation and PD activity[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2000, 7(6): 725-733. DOI:10.1109/94.891982 (  0) 0) |
| [19] |
NOSKOV M D, MALINOVSKI A S, SACK M, et al. Modelling of partial discharge development in electrical tree channels[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2003, 10(3): 425-434. DOI:10.1109/TDEI.2003.1207468 (  0) 0) |
 2022, Vol. 41
2022, Vol. 41


 何嘉弘(1988), 男, 博士, 副教授, 研究方向为高电压与绝缘技术(E-mail:
何嘉弘(1988), 男, 博士, 副教授, 研究方向为高电压与绝缘技术(E-mail: