文章编号: 2096-3203(2022)01-0185-07 中图分类号: TM342
近些年,由于国内西电东送的实施,特高压直流输电工程正大规模地建设,其直流端的无功调节需求越来越大[1-3]。同步调相机相较于其他无功补偿方式具有更大的容量,尤其可以解决特高压变电站直流端换相失败的问题,因而在电网中的应用逐步扩大。但调相机长时间运行后,极易出现轴承座振动超标的情况,导致系统轴系支撑磨损,甚至轴承故障,而载荷分配不均便是常见的引发轴承座振动超标的原因之一[4-5]。因此,研究一种针对同步调相机载荷分配的故障诊断方法,对提高调相机机组的安全性十分重要。
对调相机等旋转设备而言,振动法是一种非常有效的在线监测手段。目前已有大量学者在各类旋转机械设备及其轴承的故障诊断中应用振动信号分析法,如经验模态分解(empirical mode decomposition, EMD)、快速傅里叶变换(fast fourier transform, FFT)、小波分解等。相对于其他信号处理方法,EMD在振动信号的处理中有较好的效果,但易出现模态混淆且耗时过长;而变分模态分解(variational mode decomposition,VMD)具有更好的信号处理能力,可以避免模态混叠,拥有较强的鲁棒性。文献[6]通过对风力数据分别进行VMD和EMD分析,说明了VMD在预测诊断中有更好的效果。VMD在分解过程中,将固有模态分量(intrinsic mode function, IMF)分解的同时,还提取了中心频率,可将信号中各个IMF隔开,避免端点效应和频率混叠等EMD中常见问题,因此文中采用VMD对采集到的轴承座振动信号进行特征提取。
在机器学习中,随着训练数据的规模逐渐扩大,单一核函数的支持向量机(support vector ma ̄chine, SVM)已不再适用于很多复杂的数据集,因此可将现有的核函数进行组合,运用不同的核函数处理不同特征的数据样本,构建多核支持向量机(multiple-kernel support vector machine,MSVM)。文献[7]通过相空间重构和最小二乘支持向量机(least squares support vector machine,LS-SVM)对网络控制系统的时延进行预测分析,仿真验证了该方法具有更高的精度和更低的误差;文献[8]通过粒子群优化LS-SVM参数,建立模型识别刀具磨损状态,实验结果证明该方法具有更高的识别率。MSVM是在SVM的基础上组合多种核函数进行学习,可以克服SVM在对异构性复杂数据进行分析时的不足,同时由于核函数的使用决策不同,多核学习在分类识别中有更高的正确率。
综上所述,文中提出了一种基于VMD-MSVM的同步调相机载荷分配故障诊断方法,对调相机载荷分配故障进行诊断识别。实验分析结果表明,所提方法能够准确有效地对载荷分配不均的故障进行诊断识别。
1 调相机轴承振动分析在调相机内部,轴承是转子转动的关键部件,一旦出现诸如轴瓦磨损、温度过高、甚至碎裂等问题,都会引发振动超标,并对机组的运行产生不确定性,因此其稳定运行对机组整体的安全具有重要作用。在调相机运行中,其轴承振动超标的原因有以下方面:
(1) 调相机转子内部冷却系统故障,导致其铁芯过热,从而出现形变,引发轴承振动超标。
(2) 调相机内部气隙偏心,转子不平衡,导致转子本身出现机械振动,引发轴承振动超标。
(3) 调相机载荷分配不平衡导致定子底座刚性连接不足,引发轴承振动超标。
在实际运行中,载荷对轴承的运行状况会有很大影响,文中实验针对调相机载荷分配故障进行,因此主要分析载荷对轴承振动超标的影响。
轴承座的底部支撑一般由基础面、垫铁、台板和灌浆浇筑构成。基础面和台板中间由垫铁进行支撑调整,垫铁需要和台板平整紧固接触,受力均匀。轴承座和台板则通过刚性连接,并有垫片置于其中,但垫片仅用来弥补接触面的不规则性,过多过少或形变都会对整体载荷产生影响,一旦载荷分配不均,就会直接作用在轴承上引发振动问题。
2 基于能量熵的VMD特征提取 2.1 VMD算法VMD于2014年被Konstantin Dragomiretskiy等人提出,是一种非递归、具有自适应性的信号分解方法[9-13]。在其应用过程中,首先将序列信号分解为k个IMF, 再计算出每个模态分量的中心频率,将各个IMF分离,然后根据频域提取信号中的有效特征,获取最优解。
VMD得到的IMF可表示为:
| $ u_{k}=B_{k}(t) \sin \varphi_{k}(t) $ | (1) |
式中:uk为分解出的第k个离散信号;Bk(t)为该离散信号的幅值;φk(t)为角度函数。
每一个IMF都聚集在中心频率处,且其带宽均不一样,可通过平滑偏移信号来进行计算。由于得到的各个IMF有不同的稀疏性,因而在进行VMD的k层分解的过程中,使用的约束变分模型为:
| $ \left\{\begin{array}{l} \min \limits_{\left\{u_{k}\right\},\left\{\omega_{k}\right\}} \sum\limits_{k}\left\|\partial_{t}\left[\left(\sigma(t)+\frac{\mathrm{j}}{{\rm{ \mathsf{ π} }} t}\right) u_{k}\right] \mathrm{e}^{k-\mathrm{j} \omega_{k}}\right\|^{2} \\ \sum\limits_{k} u_{k}=f \end{array}\right. $ | (2) |
式中:
引入如式(3)所示的拉格朗日增广函数求取上述模型的最优解。
| $ \begin{gathered} L\left(\left\{u_{k}\right\},\left\{\omega_{k}\right\}, \lambda\right)= \\ \alpha \sum\limits_{k}\left\|\partial_{t}\left[\left(\sigma(t)+\frac{\mathrm{j}}{{\rm{ \mathsf{ π} }} t}\right) u_{k}\right] \mathrm{e}^{k-\mathrm{j} \omega_{k}}\right\|^{2}+ \\ \left\|f-\sum\limits_{k} u_{k}\right\|^{2}+\lambda f-\sum\limits_{k} u_{k} \end{gathered} $ | (3) |
式中:λ为拉格朗日算子;α为二次惩罚因子。
通过交替方向的乘子算法对式(3)的鞍点进行求解,交替计算uk, n+1,ωk, n+1,λn+1:
| $ \left\{\begin{array}{l} u_{k, n+1}=\frac{f(\omega)-\sum\limits_{i \neq k} u_{i}(\omega)+\lambda(\omega) / 2}{1+2 \alpha\left(\omega-\omega_{k}\right)^{2}} \\ \omega_{k, n+1}=\int_{0}^{\infty} \omega\left|u_{k}(\omega)\right|^{2} \mathrm{~d} \omega / \int_{0}^{\infty}\left|u_{k}(\omega)\right|^{2} \mathrm{~d} \omega \\ \lambda_{n+1}=\lambda_{n}(\omega)+\tau\left(f(\omega)-\sum\limits_{k} u_{k, n+1}(\omega)\right) \end{array}\right. $ | (4) |
式中:ui为Wiener滤波;n为迭代次数;τ为噪声容限。
具体的求解过程为:(1) 初始化uk, 1,ωk, 1,λ1;(2) 令n=n+1,k=k+1,并根据式(4)进行迭代;(3) 给定一个趋近于零的值ε>0,若满足如式(5)所示的条件,则完成迭代过程。
| $ \frac{\sum\limits_{k}\left\|u_{k, n+1}-u_{k, n}\right\|^{2}}{\left\|u_{k, n}\right\|}<\varepsilon $ | (5) |
对于不同故障,分解调相机轴承振动信号得到的各层IMF所蕴含的能量熵[14-16]也有所不同,但对于相同故障,各层IMF所蕴含的能量熵具有一定关联,故可将能量熵作为调相机载荷分配故障诊断中的特征量。
对调相机轴承振动信号进行VMD,计算各IMF的能量。
| $ E_{m}=\sqrt{\sum\limits_{i=1}^{h} x^{2}(i) / h} $ | (6) |
式中:Em为分解后第m层IMF的能量值;x(i)为离散振动信号样本;h为x(i)中的离散点数。
可将所得各层IMF的能量值构成特征向量E =[E1 E2 … Em],并将经VMD后振动信号的能量熵定义为:
| $ \left\{\begin{array}{l} H_{E}=-\sum\limits_{i=1}^{m}\left(p_{i} \lg p_{i}\right) \\ p_{i}=E_{i} / \sum\limits_{i=1}^{m} E_{i} \end{array}\right. $ | (7) |
式中:pi为第i层IMF的能量占整个特征样本总体能量的比值。
根据时频可将各层IMF分为K个部分,每部分的能量为Ek,则某一层IMF的总体能量是
| $ H_{\mathrm{IMF}}=-\sum\limits_{k=1}^{K}\left(P_{k} \lg P_{k}\right) $ | (8) |
振动信号经过VMD后得到了各层IMF,因而各层IMF能量熵的总和与振动信号整体的能量熵是等价的。若某层IMF能量熵贡献较大,则其频率簇的一致性较大,该层IMF更能反映实际的故障特征。
3 多核组合SVM由于仅有单一的核函数,传统的SVM[17]在处理较为复杂且非线性程度高的数据时效果不理想,尤其是当样本分布较为不均时,最终的分类正确率会大幅度下降。针对上述问题,有众多学者提出了MSVM[18-20],相较于SVM具有更高的灵活性,可以根据需求选择不同的核函数进行组合学习。
传统SVM中常用的单核函数为:
| $ \left\{\begin{array}{l} K_{\mathrm{g}}(\boldsymbol{x}, \boldsymbol{y})=\mathrm{e}^{-\|\boldsymbol{x}-\boldsymbol{y}\|^{2 /\left(2 \sigma^{2}\right)}} \\ K_{\mathrm{p}}(\boldsymbol{x}, \boldsymbol{y})=\left[\lambda\left(\boldsymbol{x}^{\mathrm{T}} \boldsymbol{y}\right)+c\right]^{d} \\ K_{\mathrm{s}}(\boldsymbol{x}, \boldsymbol{y})=\tanh \left[a\left(\boldsymbol{x}^{\mathrm{T}} \boldsymbol{y}\right)+b\right] \end{array}\right. $ | (9) |
式中:Kg为高斯函数;Kp为多项式函数;Ks为双曲正切函数(即Sigmoid函数);x, y为核函数的输入向量;σ, λ, a, b, c, d为各个核函数参数。
可将单一核函数进行线性组合来构建多核函数,表达式如下:
| $ K(\boldsymbol{x}, \boldsymbol{y})=\sum\limits_{i=1}^{k}\left(w_{i} K_{i}(\boldsymbol{x}, \boldsymbol{y})\right) $ | (10) |
式中:Ki(x, y)为不同的核函数;wi为核函数相对应的权值。
在选取核函数时,可根据样本数据的类型来选择适合的核函数。根据风险最小化原则和优化方法,可将MSVM的模型构造为:
| $ \left\{\begin{array}{l} \min \limits_{f_{l}, b, \xi_{i}, w_{i}} J(w)=\frac{1}{2} \sum\limits_{i=1}^{k} \frac{1}{w_{i}}\left\|f_{l}\right\|^{2}+C \sum\limits_{i=1}^{I} \xi_{i} \\ \text { s.t. } y_{i} \sum\limits_{i=1}^{n}\left(f_{l}+y_{i} b\right) \geqslant 1-\xi_{i} \quad \xi_{i} \geqslant 0 \\ \ \ \ \ \ \ \sum\limits_{i=1}^{k} w_{i}=1 \quad w_{i} \geqslant 0 \end{array}\right. $ | (11) |
式中:J(w)为模型的最优解;C为惩罚系数;ξi为松弛量;fl为跟核函数Ki相应的特征空间。
通过Karush Kuhn Tucker条件和拉格朗日乘数法推导出对偶问题为:
| $ \begin{array}{c} W(w)=\\ \left\{\begin{array}{l} \max \limits_{\alpha}\left[\sum\limits_{i=1}^{p} \alpha_{i}-\frac{1}{2} \sum\limits_{j=1}^{n} \sum\limits_{i=1}^{n}\left(\alpha_{i} \alpha_{j} y_{i} y_{j}\right) \sum\limits_{i=1}^{k}\left(w_{i} K_{i}\left(y_{i}, y_{j}\right)\right)\right] \\ \text { s.t. } y_{i} \sum\limits_{i=1}^{n}\left(\alpha_{i} y_{i}\right)=0 \quad 0 \leqslant \alpha_{i} \leqslant C \\ \ \ \ \ \ \ \sum\limits_{i=1}^{k} w_{i}=1 \quad w_{i} \geqslant 0 \end{array}\right. \end{array} $ | (12) |
最终求取式(12)和权值w的最优解,得到MSVM的分类结果:
| $ f(x)=\sum\limits_{i=1}^{n}\left(\alpha_{i}^{\prime} y_{i}\right) \sum\limits_{i=1}^{k}\left(w_{i}^{\prime} K_{i}\left(y_{i}, y_{j}\right)\right)+b $ | (13) |
式中:w′ i为w的最优解;α′ i为式(13)的最优解。
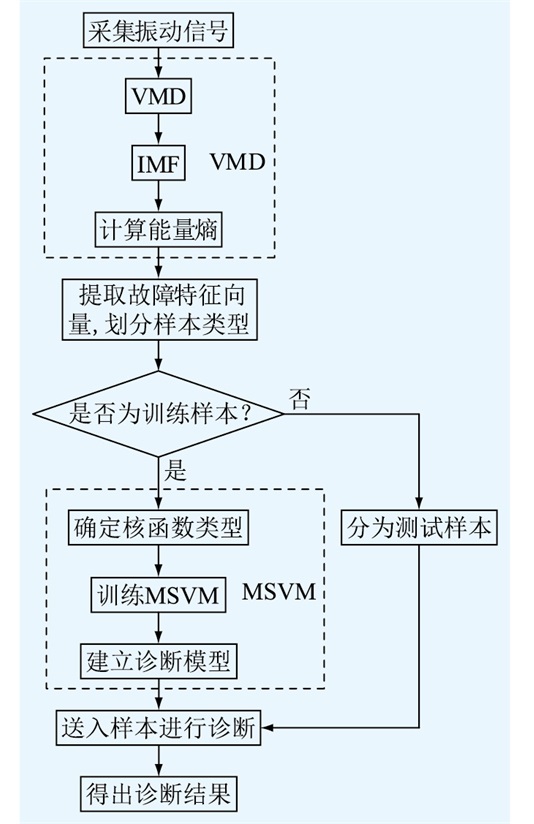
4 基于VMD-MSVM的故障诊断模型文中提出一种基于VMD-MSVM的调相机载荷分配故障诊断方法,整体的故障诊断流程见图 1。
|
图 1 基于VMD-MSVM的调相机载荷分配故障诊断流程 Fig. 1 Flow chart of load distribution fault diagnosis for synchronous condenser based on VMD-MSVM |
具体的诊断过程为:
(1) 在调相机轴承座表面布置多个测点,并利用振动传感器采集所需的振动信号。
(2) 对振动信号进行VMD,根据频域提取有效特征,计算分解得到各层IMF的能量熵,提取故障特征向量,并将完成处理的数据分为训练样本和测试样本。
(3) 确定核函数类型,并通过训练样本对MSVM进行训练,建立诊断模型。
(4) 向完成训练的模型送入测试样本进行诊断,根据诊断的结果可以判断出调相机载荷分配是否出现故障。
5 实验分析与结果为检验基于VMD-MSVM的同步调相机载荷分配故障诊断方法的有效性,在泰州特高压变电站例行检修期间对一号调相机进行载荷分配实验,并在轴承座外部布置多个测点用以采集振动信号。
在各个测点安装磁吸式加速度传感器,并通过东华DH5922采集仪采集振动信号,设置采样频率为10 kHz,现场采集过程如图 2所示,振动传感器分布位置如图 3所示。

|
图 2 现场采集过程 Fig. 2 The process of field acquisition |
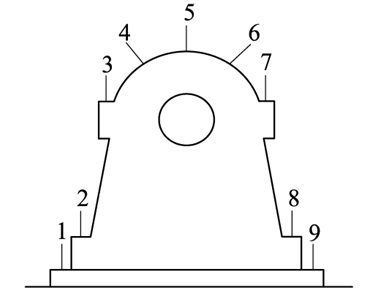
|
图 3 轴承座表面测点位置分布 Fig. 3 Location distribution of measuring points on bearing housing surface |
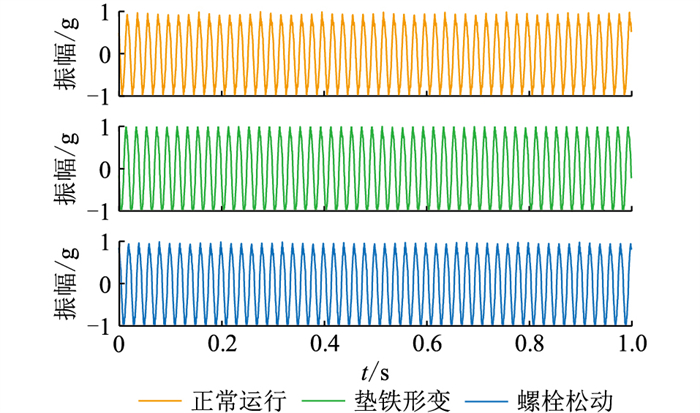
实验为模拟调相机载荷分配故障,设置了2种方案:一是调整垫铁,使垫铁受力不均匀,结合面出现空隙;二是松动螺栓,使台板与轴承座之间连接松动。实验设置时调整的垫铁和螺栓均靠右侧边缘位置,因此选取8号测点采集数据,分别采集垫铁形变和松动半圈螺栓情况下的振动信号进行分析。图 4为调相机在正常运行、垫铁形变、螺栓松动3种情况下的振动信号波形,发现在轻微的载荷分配不平衡故障下,仅通过振动波形无法识别各个故障。
|
图 4 调相机在3种情况下的部分振动信号 Fig. 4 Partial vibration signals of synchronous condenser bearing in three cases |
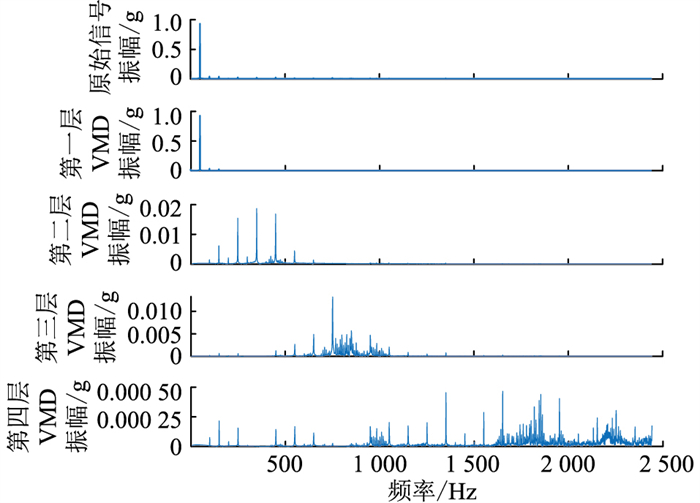
为验证所提方法的有效性,以垫铁形变时的振动信号为例进行特征提取,同时为便于FFT,选取8 192个点为一组样本。图 5为原始信号及其4层VMD的时域图,图 6为VMD对应的频谱图。

|
图 5 垫铁形变情况下振动信号的VMD Fig. 5 VMD diagram of vibration signal under deformation of cushion iron |
|
图 6 VMD各模态对应的频谱图 Fig. 6 The corresponding spectrum diagram of each mode obtained by VMD |
根据图 5、图 6,相较于EMD,VMD得到的模态数量较少,没有模态混叠现象,且在高频频率附近可以有效分别。
VMD得到4层模态,以上述垫铁形变时的样本为例计算各个模态的能量值和能量熵,结果见表 1。
|
|
表 1 样本各层模态参数 Table 1 Modal parameters of each layer of the sample |
从表 1可以看出,第4层模态的能量熵较低,且其能量值比其余3层模态小了2个数量级,再结合图 6可知,第4层模态信号中包含了大量的高频成分,说明其中含有大量噪声信号,需将其去除。将余下3层模态的能量熵构成特征向量,输入MSVM进行故障诊断。
实验过程中,为方便计算,选取8 192个振动信号的数据点作为一组样本。分别取调相机处于正常运行、垫铁形变、螺栓松动3种运行状况下各180组有标签的样本数据对VMD-MSVM模型进行训练,并额外提取每种工况各60组数据,共计180组数据作为测试样本,以检验模型的精度。最终诊断结果如表 2所示,其中,正确样本的统计值为总计,正确率的统计值为平均值。
|
|
表 2 基于VMD-MSVM模型的诊断结果 Table 2 Diagnosis results based on VMD-MSVM model |
为了进一步验证基于VMD-MSVM的调相机载荷分配故障诊断方法的有效性以及优越性,同时采用EMD-MSVM、EMD-SVM和小波分解-MSVM进行对比分析。将相同的训练样本和测试样本输入上述3种模型进行训练诊断,得到的结果见表 3。
|
|
表 3 3种对比模型的故障诊断结果 Table 3 Fault diagnosis results of three comparative models |
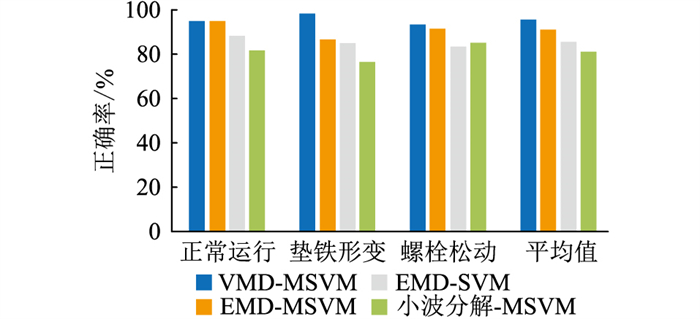
图 7展示了基于VMD-MSVM的调相机载荷分配故障诊断方法与其他3种模型的结果对比。
|
图 7 4种诊断模型的结果对比 Fig. 7 Comparison of the results of four diagnostic models |
根据图 7,文中所提基于VMD-MSVM的调相机载荷分配故障诊断方法对各类故障均有较高的识别率,尤其对垫铁形变产生的载荷分配故障。从整体上来看,基于VMD-MSVM模型的诊断正确率高于95%,而其他3种模型的诊断正确率均低于92%。在EMD过程中,其每层模态都有部分重叠,小波分解也在高频段时区分度较差,故在特征提取的过程中对于某种故障会出现混淆的情况。对比图 7中EMD-SVM和EMD-MSVM模型发现,MSVM因具有多种核函数,在数据具体处理过程中拥有不同的分辨能力,所以最终的分类性能更好,优于单核的标准SVM。
综上所述,基于VMD-MSVM的模型对调相机载荷分配故障具有更好的识别能力,充分说明了该方法优于传统的诊断方法,且更适用于载荷分配故障的诊断。
6 结语文中结合VMD和SVM 2种算法的优势,提出了一种基于VMD-MSVM的同步调相机载荷分配故障诊断方法。通过VMD实验中采集到的振动信号,计算能量熵并构建特征向量,再利用MSVM对故障进行分类诊断。实验将文中所提方法与EMD-MSVM,EMD-SVM和小波分解-MSVM 3种模型作对比分析,结果表明,基于VMD-MSVM的调相机载荷分配故障诊断方法诊断正确率较高,高于另外3种模型的诊断正确率,且对于轻微载荷分配故障具有较好的识别效果。
本文得到国网江苏省电力有限公司科技项目(J2019114)资助,谨此致谢!
| [1] |
张开宇, 崔勇, 庄侃沁, 等. 加装同步调相机对多直流馈入受端电网的影响分析[J]. 电力系统保护与控制, 2017, 45(22): 139-143. ZHANG Kaiyu, CUI Yong, ZHUANG Kanqin, et al. Analysis of the influence of synchronous condensers on receiving-end grid with multi-infeed HVDC[J]. Power System Protection and Control, 2017, 45(22): 139-143. DOI:10.7667/PSPC160632 (  0) 0) |
| [2] |
王少雄, 潘学萍, 颜君凯, 等. 大容量调相机参与下特高压交直流电力系统稳态电压协同控制[J]. 电力系统保护与控制, 2020, 48(24): 120-127. WANG Shaoxiong, PAN Xueping, YAN Junkai, et al. Coordinated control of steady-state voltage for UHVDC/AC power systems with large-scale synchronous condenser integration[J]. Power System Protection and Control, 2020, 48(24): 120-127. (  0) 0) |
| [3] |
邹欣, 蒋维勇, 李亚男. ±800 kV酒泉-湖南特高压直流工程无功补偿优化配置方案[J]. 电力建设, 2015, 36(9): 43-49. ZOU Xin, JIANG Weiyong, LI Ya'nan. Reactive power configuration scheme of ±800 kV Jiuquan-Hunan UHVDC project[J]. Electric Power Construction, 2015, 36(9): 43-49. DOI:10.3969/j.issn.1000-7229.2015.09.007 (  0) 0) |
| [4] |
柴岩, 钟良, 杨建刚. 汽轮机低压缸轴承座振动分析和动平衡试验研究[J]. 汽轮机技术, 2017, 59(1): 50-52. CHAI Yan, ZHONG Liang, YANG Jiangang. Bearing pedestal vibration analysis and balance test of a turbine low pressure rotor with bearing located on the exhaust cylinder[J]. Turbine Technology, 2017, 59(1): 50-52. DOI:10.3969/j.issn.1001-5884.2017.01.013 (  0) 0) |
| [5] |
俎海东, 朱生华, 李晓波, 等. 汽轮发电机组轴系支撑系统连接刚度不足引起的轴承座振动分析[J]. 内蒙古电力技术, 2018, 36(5): 23-26. ZU Haidong, ZHU Shenghua, LI Xiaobo, et al. Analysis of vibration problems caused by insufficient joint stiffness of bearing block of steam turbine generator set[J]. Inner Mongolia Electric Power, 2018, 36(5): 23-26. (  0) 0) |
| [6] |
ZHANG G, LIU H C, ZHANG J B, et al. Wind power prediction based on variational mode decomposition multi-frequency combinations[J]. Journal of Modern Power Systems and Clean Energy, 2019, 7(2): 281-288. DOI:10.1007/s40565-018-0471-8 (  0) 0) |
| [7] |
田中大, 张超, 李树江, 等. 基于相空间重构与最小二乘支持向量机的时延预测[J]. 电子学报, 2017, 45(5): 1044-1051. TIAN Zhongda, ZHANG Chao, LI Shujiang, et al. Time-delay prediction based on phase space reconstruction and least squares support vector machine[J]. Acta Electronica Sinica, 2017, 45(5): 1044-1051. DOI:10.3969/j.issn.0372-2112.2017.05.003 (  0) 0) |
| [8] |
刘成颖, 吴昊, 王立平, 等. 基于PSO优化LS-SVM的刀具磨损状态识别[J]. 清华大学学报(自然科学版), 2017, 57(9): 975-979. LIU Chengying, WU Hao, WANG Liping, et al. Tool wear state recognition based on LS-SVM with the PSO algorithm[J]. Journal of Tsinghua University (Science and Technology), 2017, 57(9): 975-979. (  0) 0) |
| [9] |
刘建华. 相空间重构和SVR联合优化的短时交通流预测[J]. 计算机工程与应用, 2014, 50(3): 13-17. LIU Jianhua. Short-term traffic flow prediction model of phase space reconstruction and support vector regression with combination optimization[J]. Computer Engineering and Applications, 2014, 50(3): 13-17. DOI:10.3778/j.issn.1002-8331.1306-0339 (  0) 0) |
| [10] |
姜佳辉, 包永强, 邵琪. 基于VMD-FHT的风机齿轮箱故障特征提取方法[J]. 机床与液压, 2020, 48(23): 202-207. JIANG Jiahui, BAO Yongqiang, SHAO Qi. Fault feature extraction method for wind turbine gearbox based on VMD-FHT[J]. Machine Tool & Hydraulics, 2020, 48(23): 202-207. DOI:10.3969/j.issn.1001-3881.2020.23.038 (  0) 0) |
| [11] |
何刘, 林建辉, 丁建明, 等. 调幅-调频信号的经验模态分解包络技术和模态混叠[J]. 机械工程学报, 2017, 53(2): 1-10. HE Liu, LIN Jianhui, DING Jianming, et al. Empirical mode decomposition envelope technique and mode mixing problem in amplitude modulation-frequency modulation signals[J]. Journal of Mechanical Engineering, 2017, 53(2): 1-10. (  0) 0) |
| [12] |
TSENG C C, LEE S L. Fractional Hilbert transform sampling method and its filter bank reconstruction[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2017, 64(5): 1214-1224. DOI:10.1109/TCSI.2016.2629086 (  0) 0) |
| [13] |
谷紫文, 李鹏, 郎恂, 等. 基于变分模态分解和密度峰值快速搜索的电力负荷曲线可控聚类模型[J]. 电力系统保护与控制, 2021, 49(8): 118-127. GU Ziwen, LI Peng, LANG Xun, et al. A controllable clustering model of the electrical load curve based on variational mode decomposition and fast search of the density peak[J]. Power System Protection and Control, 2021, 49(8): 118-127. (  0) 0) |
| [14] |
齐咏生, 白宇, 高胜利, 等. 基于VMD与熵价值的风电机组轴承故障诊断[J]. 控制工程, 2020, 27(12): 2055-2062. QI Yongsheng, BAI Yu, GAO Shengli, et al. Fault diagnosis of wind turbine bearing based on VMD and entropy value[J]. Control Engineering of China, 2020, 27(12): 2055-2062. (  0) 0) |
| [15] |
王恒迪, 邓四二, 杨建玺, 等. 基于参数优化变分模态分解的滚动轴承早期故障诊断[J]. 振动与冲击, 2020, 39(23): 38-46. WANG Hengdi, DENG Sier, YANG Jianxi, et al. Incipient fault diagnosis of rolling bearing based on VMD with parameters optimized[J]. Journal of Vibration and Shock, 2020, 39(23): 38-46. (  0) 0) |
| [16] |
ZHANG X, MIAO Q, ZHANG H, et al. A parameter-adaptive VMD method based on grasshopper optimization algorithm to analyze vibration signals from rotating machinery[J]. Mechanical Systems and Signal Processing, 2018, 108: 58-72. DOI:10.1016/j.ymssp.2017.11.029 (  0) 0) |
| [17] |
方涛, 钱晔, 郭灿杰, 等. 基于天牛须搜索优化支持向量机的变压器故障诊断研究[J]. 电力系统保护与控制, 2020, 48(20): 90-96. FANG Tao, QIAN Ye, GUO Canjie, et al. Research on transformer fault diagnosis based on a beetle antennae search optimized support vector machine[J]. Power System Protection and Control, 2020, 48(20): 90-96. (  0) 0) |
| [18] |
徐蕙, 陈平, 李海涛, 等. MPSR-MKSVM电力负荷预测综合优化策略[J]. 电测与仪表, 2022, 59(1): 77-83. XU Hui, CHEN Ping, LI Haitao, et al. Comprehensive optimization strategy of power load forecasting based on MPSR-MKSVM[J]. Electrical Measurement & Instrumentation, 2022, 59(1): 77-83. (  0) 0) |
| [19] |
朱晓玲, 李琨, 张长胜, 等. 基于Gabor小波变换和多核支持向量机的电梯导靴故障诊断方法[J]. 计算机科学, 2020, 47(12): 258-261. ZHU Xiaoling, LI Kun, ZHANG Changsheng, et al. Elevator boot fault diagnosis method based on Gabor wavelet transform and multi-core support vector machine[J]. Computer Science, 2020, 47(12): 258-261. DOI:10.11896/jsjkx.200700039 (  0) 0) |
| [20] |
臧博研. 多核支持向量机关键技术研究[D]. 西安: 西安邮电大学, 2019. ZANG Boyan. Research on multi kernel support vector mach-ine[D]. Xi'an: Xi'an University of Posts and Telecommunications, 2019. (  0) 0) |
 2022, Vol. 41
2022, Vol. 41


 张玉良(1997), 男, 硕士在读, 研究方向为大型电力设备故障诊断(E-mail:
张玉良(1997), 男, 硕士在读, 研究方向为大型电力设备故障诊断(E-mail: