文章编号: 2096-3203(2022)01-0077-07 中图分类号: TM714
2. 江苏省配电网智能技术与装备协同创新中心, 江苏 南京 211167
IEEE将电压暂降定义为在系统频率时供电电压有效值瞬时减小到额定值的10%~90%,其持续时间一般为0.5~30个工频周波[1]。电力系统中数字化的新型负荷比起传统用电负荷,对电压暂降更加敏感[2]。据统计,每年因发生电压暂降而造成的经济损失巨大。因此,电压暂降是最严重的电能质量问题之一,对不同电压暂降源进行准确分类识别具有重大意义,是抑制和缓解电压暂降的前提[3]。
目前常用方法是先运用希尔伯特黄变换、小波变换、S变换及改进S变换等时频分析方法提取电压暂降信号曲线的相关特征值,再通过支持向量机、神经网络、模糊综合评价、深度学习模型等学习算法完成对电压暂降源的识别[4-11]。文献[12-14]分别通过标准S变换和小波变换提取不同类型电压暂降信号的相关特征指标,利用灰狼优化算法和支持向量机构建分类器和自组织竞争性神经网络以及概率神经网络,实现电压暂降扰动源的识别。
文献[15]用深度置信网络替换深度学习算法中的卷积神经网络,提高了最终分类识别能力;文献[16]通过综合指标的隶属度判定暂降源类型;文献[17]应用随机森林模型完成对电压暂降的分类;文献[18]通过瞬时对称分量法检测发生不同扰动时正序电流的幅值以及相位,从而建立对应的识别模式;文献[19]通过改进S变换提取能量熵等特征指标,利用支持向量机实现扰动源的识别工作。
反向传播(back propagation,BP)神经网络可以有效识别不同类型的电压暂降源,但其初始阈值和权值对分类效果有较大的影响。天牛须搜索(beetle antennae search,BAS)算法是一种模拟天牛觅食过程的智能算法,可有效解决多目标参数的寻优问题。
为进一步提高电压暂降源的精确识别率,文中基于BAS算法对BP神经网络的初始权值和阈值进行寻优,构建BAS-BP分类器模型,仿真结果表明,与已有的神经网络分类器模型相比,该新型分类器具有更高的分类识别正确度。
1 特征指标提取及筛选 1.1 指标提取标准S变换存在对暂降误判、对噪声敏感等缺点,而改进S变换通过调节高斯窗函数,可以有效克服标准S变换的缺点,具有良好的时频分析能力,可以提取任意频率分量特征,更加精确地提取电压暂降信号的特征指标。
因此文中采用改进S变换提取电压暂降特征指标数据。在标准S变换高斯窗函数的基础上,引入调节因子a和b,得到改进S变换表达式如下[20]:
| $ S(t, f)=\int_{-\infty}^{+\infty} h(\tau) \frac{a|f|^{b}}{\sqrt{2 {\rm{ \mathsf{ π} }}}} \mathrm{e}^{-\frac{a^{2}(t-\tau)^{2} f^{2 b}}{2}} \mathrm{e}^{-\mathrm{j}(2 {\rm{ \mathsf{ π} }} f \tau)} \mathrm{d} \tau $ | (1) |
式中:h(τ)为信号表达式;t为时间;f为频率;τ为高斯窗函数的中心位置;a为高斯窗幅度调节系数;b为高斯窗指数调节系数。不同的a,b对应不同的时频分辨率[21]。
在大量实验和仿真的基础上,对由短路故障和感应电动机启动引起的电压暂降波形进行特征提取时取a=5,b=0.87;对变压器投运引起的电压暂降波形进行特征提取时取a=1,b=0.87。
图 1和图 2分别为短路故障、感应电动机启动和变压器投运时改进S变换所提取到的基频幅值曲线和频率幅值包络线。
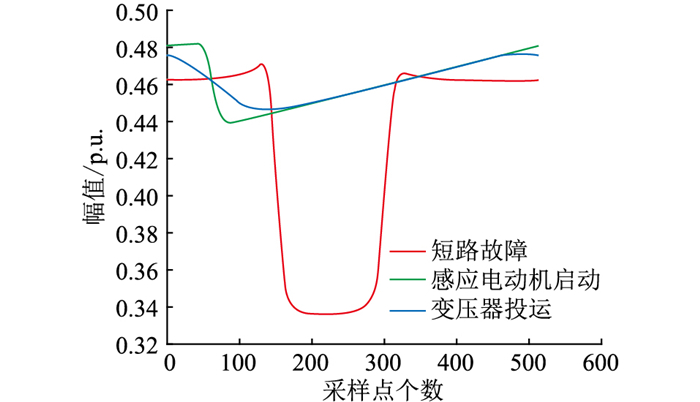
|
图 1 基频幅值曲线 Fig. 1 The curves of fundamental-frequency amplitude |
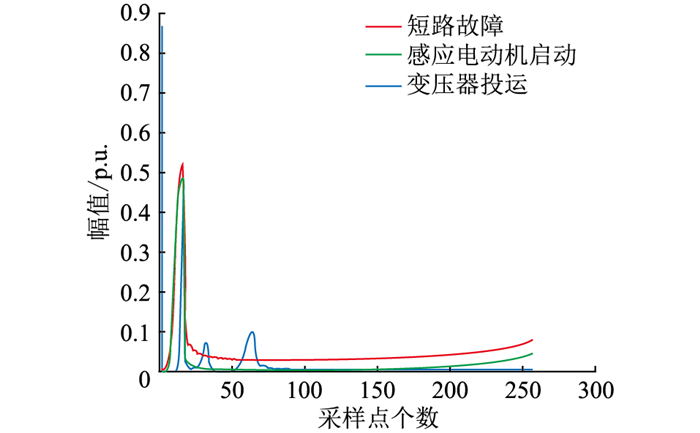
|
图 2 频率幅值包络线 Fig. 2 Frequency amplitude envelope |
基于配电网发生单相短路故障、两相短路故障、三相短路故障、感应电动机启动以及变压器投运5种类型引起的电压暂降幅值、波形、相位跳变和所含谐波分量的不同,选取均值F1,标准差F2,均方根值F3,暂降深度F4,能量F5,峰度F6,突变点个数F7,香农熵F8,对数能量熵F9,基频幅值上升和下降斜率F10,F11,二次谐波含有率F12,偏度F13,波形系数F14,波峰系数F15和暂降时间比F16这16个指标构建电压暂降源识别特征指标体系。
1.2 指标筛选由于特征指标数目较多,为防止各电压暂降源识别特征指标之间信息重叠、特征指标的数据提取速度过慢而造成的分类识别正确率降低问题,文中采用相应的赋权法对16个特征指标进行降维处理。为克服主客观赋权法各自的缺点,采用结合层次分析法与熵值法的组合赋权方法,其步骤如下。
(1) 数据标准化。由于各特征指标具有不同的性质和量纲,其数据大小相差较大,因此需要对原始指标数据进行标准化处理,以保证结果的可靠性。
| $ A_{i j}^{*}=\frac{A_{i j}-\bar{A}_{j}}{f_{\text {std }}\left(A_{j}\right)} \quad i=1,2, \cdots, m ; j=1,2, \cdots, n $ | (2) |
式中:Aij*为第j个样本的第i个特征指标原始数据;Aij为第j个样本第i个特征指标值;Aj为第j个样本的均值;fstd(·)为标准差函数。
(2) 采用层析分析法确定各特征指标的主观权重。根据标度表对各特征指标进行两两比较,得到判断矩阵A=(aij)n×n。其中,aij为与指标j相比,指标i的重要程度,aii为1,aij>0且满足aij×aji=1。一致性检验为:
| $ C_{1}=\left(\lambda_{\max }-n\right) /(n-1) $ | (3) |
| $ C_{2}=C_{1} / R $ | (4) |
式中:C1为一致性指标;λmax为判断矩阵A的最大特征值;C2为一致性比例;R为平均随机一致性指标,可通过查表得到。
若C2<0.1,则可认为所求权重有意义;否则需要对判断矩阵A=(aij)n×n进行调整。
利用算数平均法求权重值:
| $ \omega_{1 i}=\frac{1}{n} \sum\limits_{j=1}^{n}\left(a_{i j} / \sum\limits_{k=1}^{n} a_{k j}\right) $ | (5) |
(3) 采用熵值法确定各特征指标的客观权重。
计算第i个特征指标的熵值:
| $ H_{i}=-k \sum\limits_{j=1}^{n}\left(F_{i j} \ln F_{i j}\right) $ | (6) |
其中:
| $ F_{i j}=A_{i j} / \sum\limits_{j=1}^{n} A_{i j} $ | (7) |
| $ k=\frac{1}{\ln n} $ | (8) |
式中:Fij为第i项指标下第j个样本的比重;n为特征指标矩阵A的行数,即样本数。
熵值法权重为:
| $ \omega_{2 i}=\left(1-H_{i}\right) / \sum\limits_{i=1}^{m}\left(1-H_{i}\right) $ | (9) |
式中:m为特征指标个数。
(4) 最后得到组合赋权权重为:
| $ \omega_{i}=\omega_{1 i} \omega_{2 i} / \sum\limits_{i=1}^{m}\left(\omega_{1 i} \omega_{2 i}\right) $ | (10) |
由此可计算得到各个特征指标的组合权重,具体如表 1所示。
|
|
表 1 各特征指标权重值 Table 1 Weight values of each characteristic index |
根据各特征指标权重可知,为了避免重复信息对分类结果的干扰,选取标准差、峰度、基频幅值上升和下降斜率、偏度、暂降深度、暂降时间比、突变点个数和二次谐波含有率共9个特征指标作为分类器的输入量。
2 建立BAS-BP分类器模型 2.1 BP神经网络分类模型BP神经网络是一种多层的,不断向前反馈的神经网络[22],且当下每一层神经元的状态只影响下一层的神经元状态。该网络的显著特点是输入信号从输入层向前传递,经过隐含层,最终到达输出层。当输出层的值与设定值或预期值不符时,则开始传播误差,而误差的传播方向与信号的传播方向相反,从输出层经隐含层最终传播到输入层。BP神经网络的权值和阈值大小根据反馈的误差不断调整,最终使其输出值与期望值的差逐渐减小。
采用BP神经网络进行分类可分为三部分,即BP神经网络的构建、训练和分类,如图 3所示。
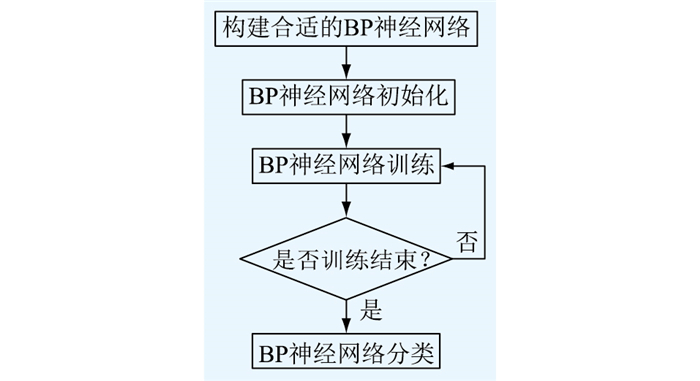
|
图 3 BP神经网络分类流程 Fig. 3 Classification process of BP neural network |
BAS算法[23-24]起源于天牛的觅食过程: 天牛在觅食过程中,起初并不能确定食物的方位,而天牛的2只长触角可以嗅到食物的气味,当右边的长触角接收到比左边更强的食物气味时,那么天牛就会向右边飞,反之则向左边向飞。天牛依据这一原理便可以找到食物。BAS算法模型如下。
(1) 将天牛须的朝向定义为一个经归一化处理得到的随机向量,如式(11)所示。
| $ \boldsymbol{b}=\frac{f_{\text {rands }}(k, 1)}{\left\|f_{\text {rands }}(k, 1)\right\|} $ | (11) |
式中:frands(·)为随机函数;k为空间维度。
(2) 天牛左右2只长触角的空间坐标见式(12)。
| $ \left\{\begin{array}{l} \boldsymbol{x}_{\mathrm{r} t}=\boldsymbol{x}_{t}+d_{0} \boldsymbol{b} / 2 \\ \boldsymbol{x}_{\mathrm{l} t}=\boldsymbol{x}_{t}-d_{0} \boldsymbol{b} / 2 \end{array} \quad t=0,1,2, \cdots, n\right. $ | (12) |
式中:t为迭代次数;xrt为在第t次迭代时天牛右长触角的空间坐标;xlt为在第t次迭代时天牛左长触角的空间坐标;d0为天牛左右2只长触角之间的距离;xt为在第t次迭代时天牛的质心坐标。
(3) 求解适应度函数值。
| $ \left\{\begin{array}{l} f_{\text {right }}=f\left(x_{\mathrm{r}}\right) \\ f_{\text {left }}=f\left(x_{\mathrm{l}}\right) \end{array}\right. $ | (13) |
式中:fright为当前空间坐标下天牛右长触角的适应度函数值;fleft为当前空间坐标下天牛左长触角的适应度函数值;f(·)为适应度函数;xl,xr分别为左、右触角位置。
(4) 更新天牛的空间位置。
| $ \boldsymbol{x}_{t}=\boldsymbol{x}_{t-1}-\delta_{t} \boldsymbol{b} f_{\text {sign }}\left(f_{\text {right }}-f_{\text {left }}\right) $ | (14) |
式中:δt为第t次迭代时的步长因子;fsign(·)为符号函数。
2.3 BAS-BP分类器模型(1) 确定网络拓扑结构。由于一共有9个特征指标和5种电压暂降类型,因此输入层节点个数为9,输出层节点个数为5,隐含层的节点个数根据式(15)计算可得。
| $ l=\sqrt{m+n}+a $ | (15) |
式中:a为1~10的常数;m为输出层节点个数;n为输入层节点个数。故隐含层节点个数范围为[4, 13]。
(2) 构建一个随机向量代表天牛须朝向,定义空间维度:
| $ k=n l+m l+l+m $ | (16) |
(3) 设置步长因子δ。步长可分为固定步长和可变步长,为避免搜索过程陷入局部最优,设置步长为可变步长,且初始步长应尽可能大,将其设置为:
| $ \delta_{t}=\delta_{t-1} e $ | (17) |
式中:e为区间[0, 1]之间靠近1的数字,取0.95。
(4) 以均方根误差M为适应度函数。
| $ M=\frac{1}{N} \sum\limits_{j=1}^{N}\left(y_{\mathrm{sim}, j}-y_{j}\right) $ | (18) |
式中:ysim,j为第j个样本的网络模型输出值;yj为第j个样本的实际数值;N为样本个数。
(5) 初始化天牛的空间位置作为BAS算法的初始解集,保存在Xbest中。
(6) 根据适应度函数计算天牛在初始位置时的初始适应度函数值,保存在fbest中。
(7) 迭代更新天牛左右长触角的位置,并分别求解当下位置左右两须的适应度函数值。若当前函数值优于初始适应度函数值,则更新Xbest和fbest。
(8) 若达到迭代次数则停止迭代,转步骤(9),否则返回步骤(7)继续迭代。
(9) 得到BP神经网络的最优初始权值和阈值。
BAS-BP分类器模型的构建过程具体如图 4所示。
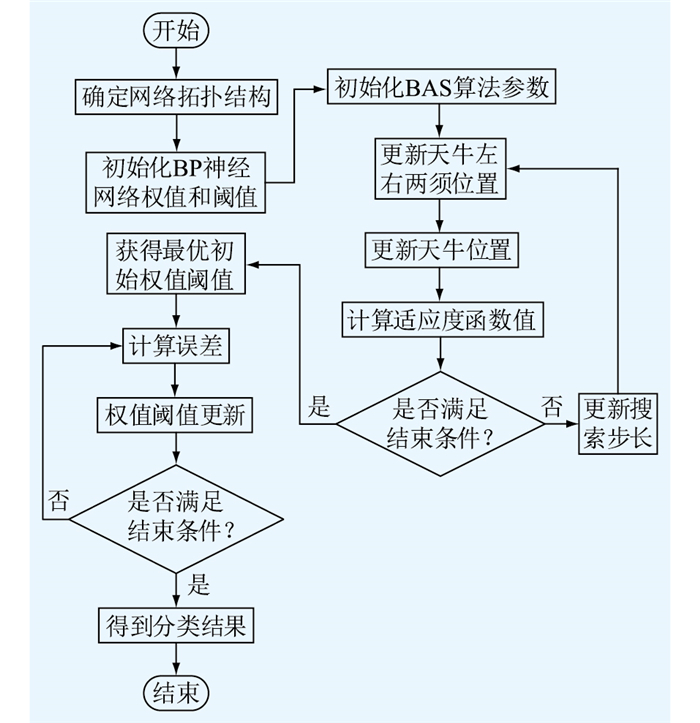
|
图 4 BAS-BP分类器分类流程 Fig. 4 Classificatior process of BAS-BP classifier |
基于Matlab/Simulink软件平台分别建立5种电压暂降的仿真模型并进行仿真实验。仿真模型中电源电压为11 kV,容量为30 MV·A,变压器的高压侧电压11 kV,低压侧电压0.4 kV,仿真时采样频率设定为1 600 Hz,采样点数设定为512点,基频频率取工频50 Hz。对于短路故障,改变断路器的开断时间、故障点距离母线的距离以及线路负荷;对于感应电动机启动,改变电动机的容量和电动机的启动时间;对于变压器投运,改变其变压器的容量、联接方式、投切时间以及线路负荷,共得到5种电压暂降类型各100组样本数据。
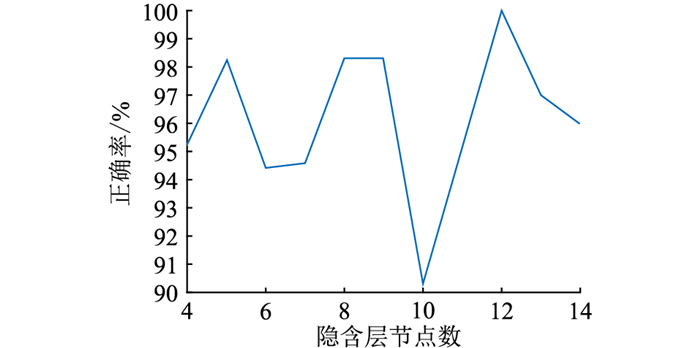
BP神经网络选择的隐含层节点数不同,对分类结果正确率有一定的影响,当隐含层节点个数分别取4~13时,得到的最终分类正确率如图 5所示。
|
图 5 分类识别正确率 Fig. 5 Classification recognition accuracy |
由图可知,当隐含层节点个数为12时,识别正确率达到100%,因此设置隐含层节点个数为12。
3.1 训练样本量对分类结果的影响为研究训练样本数量对分类识别结果的影响,从5种不同类型的电压暂降样本数据中分别选取100,200,300,400组样本作为BAS-BP分类器模型的训练数据。将100组测试样本数据输入已训练好的分类器,观察各自的识别效果,其结果如表 2所示。由此可以得出:BAS-BP分类器的训练样本数量越多,其最终的分类识别正确率也越高。
|
|
表 2 不同训练样本数的BAS-BP识别正确率 Table 2 Recognition accuracy of BAS-BP with different training samples |
由于实际环境通常含有一定量的噪声,为了测试BAS-BP分类器的抗干扰能力,在原来的仿真环境中分别添加20 dB,30 dB,40 dB,50 dB的信噪比,测试该分类器的抗噪能力,可得信噪比分别为20 dB,30 dB,40 dB,50 dB时,正确识别率分别为94%,95%,97%,98%。
由此可见,文中方法在含噪声情况下仍具有一定的识别正确率。随着噪声的减少,BAS-BP分类器的识别正确率升高。当信噪比为20 dB时,其识别正确率为94%,依然保持了良好的识别能力,具有一定的鲁棒性。因此该分类器在无噪声环境和含噪环境中均具有一定的适用性。
3.3 不同分类器的识别比较为了横向验证BAS-BP分类器模型的识别性能,将其识别正确率与传统的BP神经网络、粒子群优化(particle swarm optimization, PSO)-BP神经网络和遗传算法(genetic algorithm,GA)-BP神经网络相比较,其结果如表 3所示。可以看出,BAS-BP分类器对电压暂降源的识别正确率比其他传统分类器高,具有有效的识别能力,但BAS-BP分类器识别耗时相对BP神经网络和PSO-BP分类器更长,因此采用该分类器得到高识别正确率的同时,也需要更多的识别时间。
|
|
表 3 不同分类器的识别性能 Table 3 Recognition performance of different classifiers |
由于在提取特征指标数据时采用了改进S变换,为验证改进S变换与标准S变换对分类结果的影响,设置对比试验,分别测试4个分类器在标准S变换下的识别性能,其结果如表 4所示。
|
|
表 4 基于标准S变换的识别性能 Table 4 Recognition performance based on standard S-transform |
将表 4与表 3相对比,发现基于标准S变换下的识别正确率普遍低于基于改进S变换下的识别正确率。由此可以验证改进S变换可以克服标准S变换的部分缺点,能更好地控制窗口的形状,达到更好的时频分辨率,更加精确地提取电压暂降的相关指标数据,因而具有更好的分类识别效果。
3.5 标准模型分析应用IEEE 5节点系统标准模型为例验证文中算法,由于IEEE 5节点系统中无感应电动机接入,因此分别选取单相短路故障、两相短路故障、三相短路故障和变压器投运共400组数据。
在该标准模型下分别利用传统BP神经网络、PSO-BP、GA-BP和BAS-BP模型对暂降源进行识别,其结果如表 5所示。
|
|
表 5 不同分类器的识别性能(标准模型) Table 5 Recognition performance of different classifiers (standard model) |
同时测试4个分类器在标准S变换下的识别性能,其结果如表 6所示。
|
|
表 6 基于标准S变换的识别性能(标准模型) Table 6 Recognition performance based on standard S-transform (standard model) |
由表 5和表 6可以看出,利用BAS算法构建的BAS-BP分类器模型同样适用于IEEE 5节点系统标准模型,对不同电压暂降源有更高的识别正确率,并且改进S变换相比标准S变换,能更加精确地提取电压暂降特征指标,更有利于暂降源的识别工作。
4 结语文中选取均值、标准差、RMS值、暂降深度、能量、峰度、突变点个数、香农熵、对数能量熵、基频幅值上升和下降斜率、二次谐波含有率、偏度、波形系数、波峰系数和暂降时间比共16个指标构建电压暂降源识别特征指标体系,利用结合层次分析法和熵值法的组合赋权法筛选出其中特征指标权重较高的9个电压暂降特征指标。针对标准S变换特征指标提取中精确度不足的问题,采用改进S变换提取指标数据,有效提高了特征指标提取精确度。
利用BAS算法对BP神经网络的初始权值和阈值寻优,构建BAS-BP分类器模型。将BAS-BP分类器模型与传统的BP神经网络、PSO-BP分类器模型、GA-BP分类器模型相比,虽然该分类器进行暂降源识别所需的时间较BP神经网络和PSO-BP分类器长,但其不仅在无噪声环境中具有良好的识别性能,在加入噪声后,依然具有较高的识别能力,具有良好的鲁棒性和适用性,可以有效提高配电网不同电压暂降源的识别正确率。
但利用BAS算法对BP神经网络的初始权值和阈值寻优时,由于在BAS算法中步长因子的设置目前还没有行之有效的指导理论和方法,需要采用反复试验的方法确定初始步长,因此可能需要耗费一定的时间和精力,在实际工程中无法得到高效的应用。如何将该分类模型投入实际工程应用,将在后续进行研究。
本文得到国网江苏省电力有限公司科技项目(J2020097),2020江苏省研究生科研与实践创新计划项目(SJCX20_0721)资助,谨此致谢!
| [1] |
Recommended practice for monitoring electric power quality: IEEE Std. 1159—1995[S]. 1995.
(  0) 0) |
| [2] |
何娟, 刘晓波, 袁旭峰, 等. 含微网的配电网电压暂降检测算法[J]. 智慧电力, 2019, 47(2): 15-21, 74. HE Juan, LIU Xiaobo, YUAN Xufeng, et al. Simulation of voltage sag detection algorithms for distribution network with microgrid[J]. Smart Power, 2019, 47(2): 15-21, 74. (  0) 0) |
| [3] |
汪颖, 王欢, 李琼林, 等. 基于距离判别分析的电压暂降源识别方法[J]. 电力系统保护与控制, 2020, 48(19): 9-16. WANG Ying, WANG Huan, LI Qionglin, et al. Identification method of voltage sag source based on distance discriminant analysis[J]. Power System Protection and Control, 2020, 48(19): 9-16. (  0) 0) |
| [4] |
徐佳雄, 张明, 王阳, 等. 基于改进希尔伯特黄变换的电能质量扰动定位与分类[J/OL]. 现代电力: 1-8[2021-8-18]. https://doi.org/10.19725/j.cnki.1007-2322.2020.0179. XU Jiaxiong, ZHANG Ming, WANG Yang, et al. Location and classification of power quality disturbances based on improved Hilbert-Huang transform[J/OL]. Modern Electric Power: 1-8[2021-8-18]. https://doi.org/10.19725/j.cnki.1007-2322.2020.0179. (  0) 0) |
| [5] |
吴建章, 梅飞, 潘益, 等. 基于改进经验小波变换的电能质量扰动检测新方法[J]. 电力自动化设备, 2020, 40(6): 142-151. WU Jianzhang, MEI Fei, PAN Yi, et al. Novel detection method of power quality disturbance based on IEWT[J]. Electric Power Automation Equipment, 2020, 40(6): 142-151. (  0) 0) |
| [6] |
罗雪莲, 刘桂英, 刘香银. 基于小波变换与希尔伯特-黄变换的微电网暂态电能质量扰动检测及辨识研究[J]. 电力电容器与无功补偿, 2020, 41(3): 182-188. LUO Xuelian, LIU Guiying, LIU Xiangyin. Study on detection and identification of transient power quality disturbances of microgrid based on wavelet transform and Hilbert-Huang transform[J]. Power Capacitor & Reactive Power Compensation, 2020, 41(3): 182-188. (  0) 0) |
| [7] |
吴建章, 梅飞, 陈畅, 等. 基于经验小波变换的电力系统谐波检测方法[J]. 电力系统保护与控制, 2020, 48(6): 136-143. WU Jianzhang, MEI Fei, CHEN Chang, et al. Harmonic detection method in power system based on empirical wavelet transform[J]. Power System Protection and Control, 2020, 48(6): 136-143. (  0) 0) |
| [8] |
吴言, 李建闽. 基于改进S变换的电压骤降自适应检测方法[J]. 电测与仪表, 2019, 56(3): 111-115. WU Yan, LI Jianmin. Adaptive detection method for voltage sags based on improved S-transform[J]. Electrical Measurement & Instrumentation, 2019, 56(3): 111-115. (  0) 0) |
| [9] |
吴禹, 唐求, 滕召胜, 等. 基于改进S变换的电能质量扰动信号特征提取方法[J]. 中国电机工程学报, 2016, 36(10): 2682-2689. WU Yu, TANG Qiu, TENG Zhaosheng, et al. Feature extraction method of power quality disturbance signals based on modified S-transform[J]. Proceedings of the CSEE, 2016, 36(10): 2682-2689. (  0) 0) |
| [10] |
杨秀, 张彤瑶, 潘爱强, 等. 基于S变换与多维分形的电压暂降源特征识别[J]. 电网技术, 2021, 45(2): 672-679. YANG Xiu, ZHANG Tongyao, PAN Aiqiang, et al. Voltage sag source feature identification with S transform and multidimensional fractal[J]. Power System Technology, 2021, 45(2): 672-679. (  0) 0) |
| [11] |
甄超, 康健, 白天宇, 等. 基于BP神经网络的暂降域识别方法[J]. 科学技术与工程, 2020, 20(13): 5161-5166. ZHEN Chao, KANG Jian, BAI Tianyu, et al. Method to identify voltage sag exposed area based on back propagation neural network[J]. Science Technology and Engineering, 2020, 20(13): 5161-5166. DOI:10.3969/j.issn.1671-1815.2020.13.022 (  0) 0) |
| [12] |
赵洛印, 李忠诚, 王丹, 等. 基于GWO-SVM的电压暂降扰动源识别[J]. 电测与仪表, 2019, 56(23): 76-85. ZHAO Luoyin, LI Zhongcheng, WANG Dan, et al. Identification of voltage sag disturbance sources based on GWO-SVM[J]. Electrical Measurement & Instrumentation, 2019, 56(23): 76-85. (  0) 0) |
| [13] |
李夏林, 刘雅娟, 朱武. 基于配电网的复合电压暂降源分类与识别新方法[J]. 电力系统保护与控制, 2017, 45(2): 131-139. LI Xialin, LIU Yajuan, ZHU Wu. A new method to classify and identify composite voltage sag sources in distribution network[J]. Power System Protection and Control, 2017, 45(2): 131-139. (  0) 0) |
| [14] |
翁国庆, 王强, 黄飞腾, 等. 配电网络电压暂降源自动定位与智能识别[J]. 浙江工业大学学报, 2016, 44(1): 45-51. WENG Guoqing, WANG Qiang, HUANG Feiteng, et al. Automatic location and intelligent recognition of voltage sag source in distribution network[J]. Journal of Zhejiang University of Technology, 2016, 44(1): 45-51. (  0) 0) |
| [15] |
郑智聪, 王红, 齐林海. 基于深度学习模型融合的电压暂降源识别方法[J]. 中国电机工程学报, 2019, 39(1): 97-104, 324. ZHENG Zhicong, WANG Hong, QI Linhai. Recognition method of voltage sag sources based on deep learning models fusion[J]. Proceedings of the CSEE, 2019, 39(1): 97-104, 324. (  0) 0) |
| [16] |
李晨懿, 杨家莉, 徐永海, 等. 模糊综合评价在电压暂降源识别中的应用[J]. 电网技术, 2017, 41(3): 1022-1028. LI Chenyi, YANG Jiali, XU Yonghai, et al. Application of comprehensive fuzzy evaluation method on recognition of voltage sag disturbance sources[J]. Power System Technology, 2017, 41(3): 1022-1028. (  0) 0) |
| [17] |
刘佳翰, 陈克绪, 马建, 等. 基于卷积神经网络和随机森林的三相电压暂降分类[J]. 电力系统保护与控制, 2019, 47(20): 112-118. LIU Jiahan, CHEN Kexu, MA Jian, et al. Classification of three-phase voltage dips based on CNN and random forest[J]. Power System Protection and Control, 2019, 47(20): 112-118. (  0) 0) |
| [18] |
POLAJZER B, STUMBERGER G, DOLINAR D. Instantaneous positive-sequence current applied for detecting voltage sag sources[J]. IET Generation, Transmission & Distribution, 2015, 9(4): 319-327. (  0) 0) |
| [19] |
陈丽, 王硕, 孔维功. 基于改进S变换的复合电压暂降源识别特征分析[J]. 电力系统保护与控制, 2014, 42(4): 27-33. CHEN Li, WANG Shuo, KONG Weigong. Method to identify composite voltage sag disturbance sources based on generalized S-transform[J]. Power System Protection and Control, 2014, 42(4): 27-33. (  0) 0) |
| [20] |
卢彩霞, 王新环, 刘志超, 等. 基于改进S变换-TT变换的电压暂降特性研究[J]. 电子测量技术, 2019, 42(4): 58-64. LU Caixia, WANG Xinhuan, LIU Zhichao, et al. Research of voltage sag based on improved S-transform-TT transform[J]. Electronic Measurement Technology, 2019, 42(4): 58-64. (  0) 0) |
| [21] |
李冉. 基于改进S变换与支持向量机的电能质量扰动识别[D]. 北京: 华北电力大学, 2017. LI Ran. Power quality disturbance identification based on improved S transform and support vector machine[D]. Beijing: North China Electric Power University, 2017. (  0) 0) |
| [22] |
OSOWSKI S. Signal flow graphs and neural networks[J]. Biological Cybernetics, 1994, 70(4): 387-395. (  0) 0) |
| [23] |
JIANG X Y, LI S. BAS: beetle antennae search algorithm for optimization problems[J]. International Journal of Robotics and Control, 2018, 1(1): 1. (  0) 0) |
| [24] |
JIANG X Y, LI S. Beetle antennae search without parameter tuning (BAS-WPT) for multi-objective optimization[J]. Filomat, 2020, 34(15): 5113-5119. (  0) 0) |
2. Jiangsu Collaborative Innovation Center of Smart Distribution Network, Nanjing 211167, China
 2022, Vol. 41
2022, Vol. 41


 叶筱怡(1996), 女, 硕士在读, 研究方向为新能源接入下的配电网电能质量分析(Email:
叶筱怡(1996), 女, 硕士在读, 研究方向为新能源接入下的配电网电能质量分析(Email: