文章编号: 2096-3203(2021)04-0123-07 中图分类号: TM715
准确的母线负荷预测对电网的安全稳定运行具有重要意义。相较于系统负荷,母线负荷量级低,各母线的负荷成分也不同,不确定性更明显,因此预测难度更大[1]。
母线负荷的传统日前预测大多采用点预测方法[2-3],其预测结果为确定的预测点值,无法提供预测的不确定性信息。点预测方法对于趋势相近且波动性较弱的母线负荷,例如商业居民类负荷的日前预测可达到较高的精度。但如母线负荷成分中包含一定比例波动性强的工业负荷,点预测结果可能难以满足精度需求。区间预测方法可以提供某一置信区间下未来时刻负荷功率的波动范围(上、下限),对于波动性较强的母线负荷预测更具有实用性[4]。
国内外学者已提出多种区间预测的方法,常见的方法如基于误差统计的区间预测[5]、基于人工智能等方法的直接区间预测[6-7]和概率密度预测[8-9]等。文献[5]计及负荷的不确定性,将点预测值与预测误差值进行叠加获得预测区间的上、下限,该方法对预测模型的点预测精度要求较高。文献[6-7]利用神经网络建立区间预测模型,并将区间覆盖率、区间宽度等多个评价指标的综合函数作为目标,优化网络参数。但在构造目标函数的过程中,各项指标之间权重及参数的设置尚无统一方法。文献[8-9]采用将机器学习或深度学习与分位数回归相结合的方法获得不同分位点的概率密度预测结果,从而得到给定置信区间下预测负荷的变化区间。
文中针对具有较强波动性的母线负荷,提出了一种基于卷积神经网络(convolutional neural network, CNN)与长短期记忆网络分位数回归(quantile regression long short-term memory,QRLSTM)组合的日前负荷区间预测模型。采用基于时间分布层(time distributed layer, TDL)封装的一维CNN对输入的历史负荷特征进行提取和压缩,建立基于注意力(attention)机制的QRLSTM模型进行特征学习,从而获得给定置信区间内的负荷变化区间,并从区间覆盖率、区间宽度等方面对区间预测的效果进行评估以验证文中方法的有效性。
1 母线负荷日前区间预测原理与步骤 1.1 母线负荷日前区间预测原理文中采用分位数回归方法进行区间预测,其误差指标一般采用pinball损失函数,可表示为[10-11]:
| $ \begin{gathered} L_{\text {pinball }}^{\tau}=\frac{1}{M T} \sum\limits_{i=1}^{M} \sum\limits_{t=1}^{T}\left[(1-\tau)\left(\hat{y}_{i, t}^{\tau}-y_{i, t}\right) I_{\left\{\hat{y}_{i, t}^{\tau}-y_{i, t}\ge0\right\}}+\right. \\ \left.\tau\left(y_{i, t}-\hat{y}_{i, t}^{\tau}\right) I_{\left\{y_{i, t}-\hat{y}_{i, t}^{\tau}<0\right\}}\right] \end{gathered} $ | (1) |
式中:τ为分位点对应的概率;I为指示函数;T为模型日前预测的输出长度;M为样本数量;t为模型预测日前预测的第t个输出序号,t∈[1, T];i为样本序号,i∈[1, M];
分位数回归预测模型可获得不同分位点的预测结果,从而得到给定置信区间下待预测量的变化区间。其中,当τ=0.5时,Lpinball0.5等价为平均绝对误差(mean absolute error,MAE)。据此可将0.5分位数点的预测结果近似为点预测值。
1.2 母线负荷日前区间预测步骤母线负荷日前区间预测步骤如图 1所示。
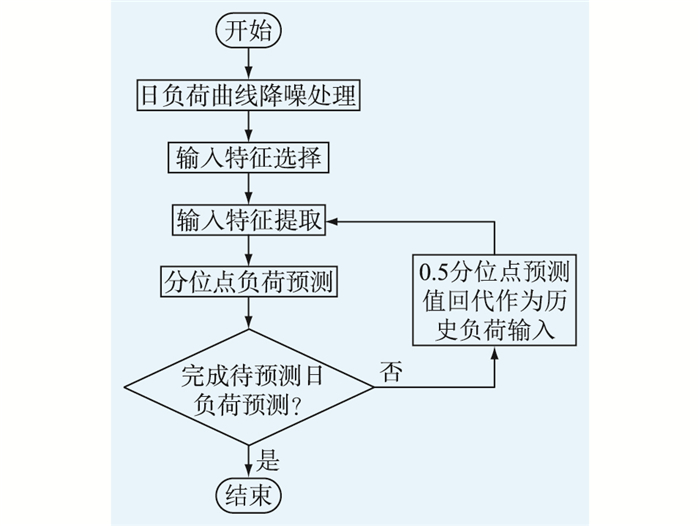
|
图 1 负荷区间预测流程 Fig. 1 Flow chart of day ahead load interval forecasting |
由图 1可知,预测首先进行降噪处理,其次进行特征选择,然后进行特征提取,最后进行分位点预测。由于第2步基于文献[12]所述方法进行特征选择,确定模型输入的历史特征为待预测时刻前2天的历史负荷,不做详细介绍。文中将重点介绍降噪处理、特征提取、分位点预测3个步骤的具体方法。
2 母线负荷日前区间预测方法 2.1 基于去噪自编码器的负荷数据降噪方法对于含工业类负荷的母线,其日负荷曲线中往往包含一些“毛刺”类高频波动,会增加模型的学习负担,影响负荷预测的精度。因此,文中采用去噪自编码器(denoising auto-encoder,DAE)进行数据平滑处理。DAE是自编码器(auto-encoder,AE)的一种变体,其在AE的基础上引入了噪声(通常使用高斯噪声),模型的鲁棒性更强。AE由编码器和解码器两部分组成。编码器可将原始输入数据编码转换成另一种表示,该表示蕴含了输入数据的信息。而解码器则是对该表示进行解码。DAE使用添加了噪声的数据进行编码和解码,并通过最小化网络输出与原始数据间的损失函数进行训练[13]。文中采用的DAE的结构如下。
(1) 编码器:由1个一维卷积层和1个最大池化层构成。
(2) 解码器:通过在2个一维卷积层之间添加1个一维上采样层来构成。
文中在DAE的输入端叠加高斯噪声,并使得其在训练过程中设法去除引入的噪声。训练数据以一天96点负荷为单位,训练目标为最小化重构误差,误差的损失函数取均方误差(mean squared error, MSE)。
2.2 基于TDL封装一维CNN网络的特征提取方法文中采用了基于TDL封装的一维CNN网络来进行特征提取。CNN简化结构主要包括输入层、卷积层和池化层等。
卷积层将输入的一维历史负荷数据先与一维卷积核进行卷积运算,再使用激活函数对经卷积运算后的数据进行非线性化处理,可表示为[14-15]:
| $ \boldsymbol{C}=f_{\mathrm{r}}\left(\boldsymbol{X} \otimes \boldsymbol{W}+\boldsymbol{b}_{1}\right) $ | (2) |
| $ f_{\mathrm{r}}(z)=\max (z, 0) $ | (3) |
式中:X=[x1 x2 … xn]T为长度为n的历史负荷数据;W为权重矩阵;b1为偏置;C为卷积层的输出;fr(z)为激活函数,文中采用的激活函数为Relu函数。
池化层的主要作用是能在保持特征不变性的前提下去除一些冗余信息,把重要的特征抽取出来,即特征的再提取,同时实现数据降维。目前常见的池化方法分为均值池化、最大池化等,由于均值池化性能不如最大池化而更少被使用[16-17]。文中选择的是最大池化,可表示为:
| $ \boldsymbol{S}=\max \boldsymbol{C}+\boldsymbol{b}_{2} $ | (4) |
式中:S为池化层的输出;b2为偏置。
由于网络的输入特征为前2天的历史负荷,即192点(日负荷曲线96点),如果直接使用一维CNN进行特征提取,会增加网络规模增加训练难度。因此,文中采用TDL对一维CNN的各层进行封装,从而将过长的时间序列数据切分成几个稍短的时间序列数据同时进行特征提取,提高模型训练效率。此外,考虑后续LSTM网络输入维度限制,在池化层后增加1个TDL封装的扁平层,用于数据维度的压缩。
文中将待预测目标时刻前192个时刻点的历史负荷数据均匀切分成8个较短的时间序列数据。经过特征压缩后,输出的数据维度则为(n, 8, 32)。其中,n为样本数,8为时间步长,32为变量维数[18-19],有利于后续LSTM网络的学习。整个特征提取与压缩的结构见图 2。
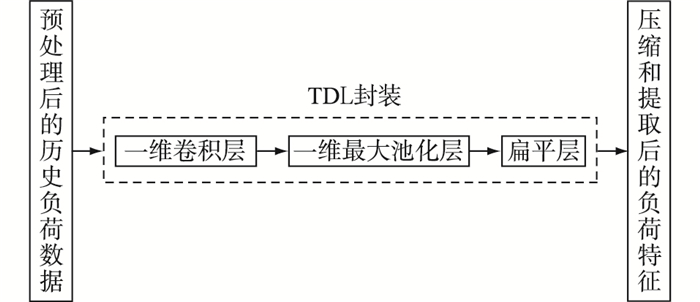
|
图 2 特征提取与压缩结构 Fig. 2 The structure of feature extraction and compression |
LSTM主要由输入门(it)、遗忘门(ft)、输出门(ot)和内部记忆单元(Ct)组成,通过对细胞状态中的信息进行有选择地“遗忘”和“记忆”,使得对后续时刻计算有用的信息得以传递,无用的信息被丢弃,并在每个时间步输出隐层状态(ht)。输入门控制接受新信息的程度,遗忘门控制历史信息被遗忘的程度,而输出门决定着最终输出的信息。通过这3种特殊的门结构LSTM可实现对较长的时间序列数据进行学习[20-21]。
为使LSTM模型在训练过程中更容易获取序列中长距离相互关联的特征,提高模型训练的效率与效果,文中引入了attention机制,其主要思路是通过对模型输入特征分配不同的概率权重,从而突出某些重要的特征。attention机制层的权重系数计算公式可表示为[21]:
| $ \boldsymbol{e}_{t}=\boldsymbol{u} \tanh \left(\boldsymbol{\omega} \boldsymbol{h}_{t}+\boldsymbol{b}\right) $ | (5) |
| $ \boldsymbol{a}_{t}=\mathrm{e}^{\boldsymbol{e}_{t}} / \sum\limits_{j=1}^{T} \boldsymbol{e}_{j} $ | (6) |
| $ \boldsymbol{s}_{t}=\sum\limits_{t=1}^{i} \boldsymbol{a}_{t} \boldsymbol{h}_{t} $ | (7) |
式中:tanh为激活函数;et为第t时刻由LSTM网络层输出向量ht所决定的注意力概率分布值;u和ω为权重系数;b为偏置系数; st为attention机制层在t时刻的输出。
综上可知,文中采用的QRLSTM网络总体结构如图 3所示。输入为经过压缩、提取的负荷特征,输出为待预测日负荷的不同分位点,训练的误差指标参考pinball损失函数。

|
图 3 分位数回归模型结构 Fig. 3 Structure of quantile regression model |
由于区间预测的结果是一个区间值,因此需要指标对模型的性能进行评价。文中采用文献[22]和文献[23]中的评价指标。
(1) 预测区间覆盖率(prediction interval coverage probability, PICP)。
| $ \left\{\begin{array}{l} J_{\mathrm{PICP}}=\frac{1}{s} \sum\limits_{i=1}^{s} \varepsilon_{i} \\ \varepsilon_{i}=\left\{\begin{array}{ll} 0 & d_{i} \in\left[L_{i}, U_{i}\right] \\ 1 & d_{i} \notin\left[L_{i}, U_{i}\right. \end{array}\right] \end{array}\right. $ | (8) |
式中:s为待预测的数据个数;di为第i个真实负荷值;Ui,Li分别为预测区间的上、下限。JPICP的值越大,说明越多的实际负荷落在预测出的区间内,即预测出的区间覆盖性更好。
(2) 预测区间平均宽度(prediction intervals normalized average width, PINAW)。
| $ J_{\text {PINAW }}=\frac{1}{s R} \sum\limits_{i=1}^{s}\left(U_{i}-L_{i}\right) $ | (9) |
式中:R为预测目标的最大、最小值之差。JPICP越大、JPINAW越小,则区间预测效果越好。
(3) 预测区间累计偏差(prediction intervals accumulative deviation, PIAD)。
| $ m_{i}=\left\{\begin{array}{lr} L_{i}-d_{i} \quad d_{i}<L_{i} \\ 0 \quad L_{i} \leqslant d_{i} \leqslant U_{i} \\ U_{i}-d_{i} \quad d_{i}>U_{i} \end{array}\right. $ | (10) |
式中:mi为第i个负荷实际值与对应预测区间的偏差。则预测区间累计偏差为:
| $ J_{\text {PIAD }}=\sum\limits_{i=1}^{s} m_{i} $ | (11) |
JPIAD用于衡量实际负荷与预测区间的偏离情况。在JPICP和JPINAW满足一定要求时,PIAD值越小,表明未落入预测区间的负荷值离预测区间的边界越近,区间预测效果更好。
4 实例分析 4.1 实例数据以2类典型负荷为例,一是工业与非工业混合的负荷,工业负荷占比大约2/3左右,后面简称为工业为主负荷;二是居民与商业混合的负荷,后面简称为居民商业负荷。数据是220 kV母线负荷,时间跨度为2017-01-01至2018-10-23,数据采样间隔为15 min,也即96点日负荷数据。
采用DAE对日负荷曲线进行降噪处理,高斯噪声系数根据经验选择为0.005。以工业为主负荷某日的曲线为例,其数据处理结果如图 4所示。由图 4可知,降噪后的负荷曲线既保留了原负荷曲线的变化趋势,又滤除了随机高频波动。
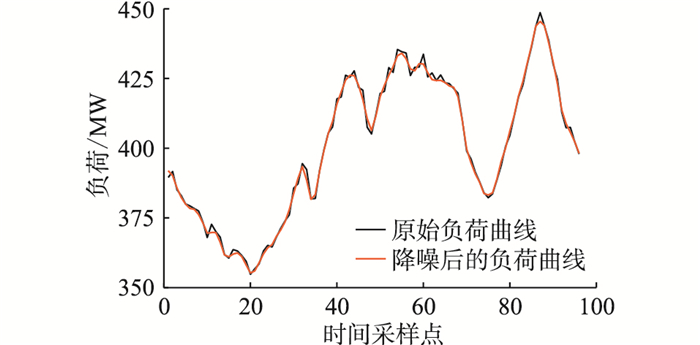
|
图 4 日负荷曲线降噪前后对比 Fig. 4 Daily load curve before and after noise filtering |
负荷曲线的波动性可采用负荷曲线各点与负荷均值之间的偏差程度来衡量,指标类似于均方根误差(root mean square error, RMSE),即:
| $ \left\{\begin{array}{l} \sigma_{1}=\sqrt{\frac{1}{N} \sum\limits_{k=1}^{N}[P(k)-\bar{P}]^{2}} \\ \bar{P}=\frac{1}{N} \sum\limits_{k=1}^{N} P(k) \end{array}\right. $ | (12) |
式中:N为总的负荷采样点数;P(k)为第k个采样点的负荷功率值;
考虑到不同负荷曲线的平均值大小不一样,所以采用百分比可能更加直观:
| $ \sigma_{2}=\sigma_{1} / \bar{P} \times 100 \% $ | (13) |
2类典型负荷的曲线如图 5所示,波动指标列于表 1。由此可见,工业为主负荷的偏差均方根大但均值也大,所以相对偏差均方根反而小。
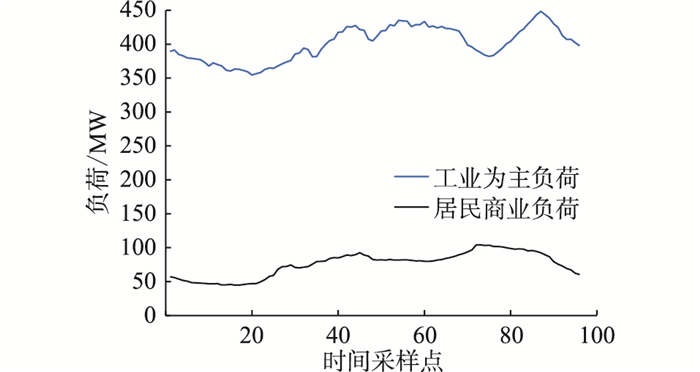
|
图 5 不同类型负荷的波动性对比 Fig. 5 Fluctuation of different loads |
|
|
表 1 2类负荷的波动性对比 Table 1 Fluctuation indexes of two types of loads |
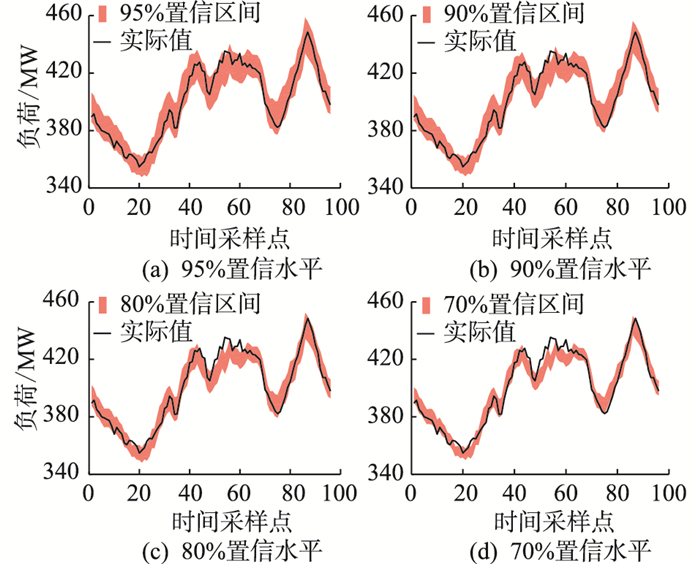
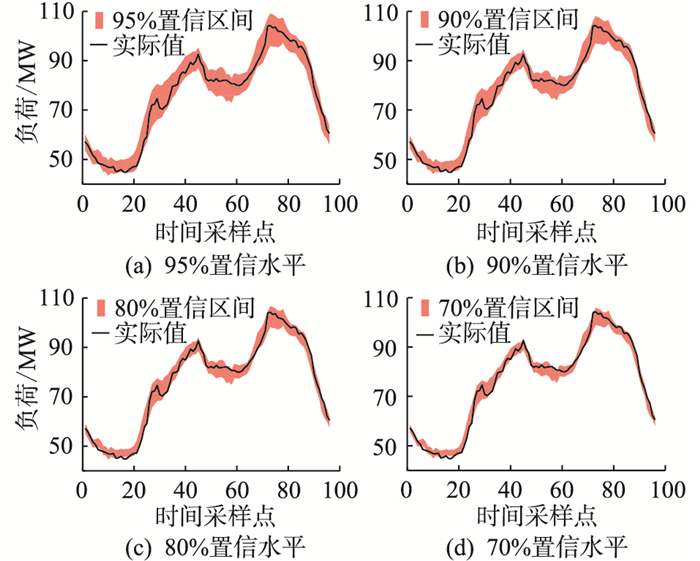
为检验文中提出的模型的区间预测效果,分别将工业为主负荷和居民商业类负荷中的某一日作为待预测日,并选取95%,90%,80%,70% 4个置信水平建立负荷日前预测区间,如图 6和图 7所示。
|
图 6 工业为主负荷不同置信水平下的区间预测 Fig. 6 Interval prediction chart of the industrial load at different confidence levels |
|
图 7 居民商业负荷不同置信水平下的区间预测 Fig. 7 Interval prediction chart of the residential and commercial load under different confidence levels |
由图 6和图 7可知:(1) 文中方法所预测出区间的变化趋势与负荷实际值的变化情况基本一致。(2) 随着置信水平的增加,模型的预测区间也逐渐变宽,这是由于越宽的预测区间越容易覆盖住实际负荷。(3) 对于2类不同负荷,文中方法在95%置信水平下均较好地覆盖了实际负荷。
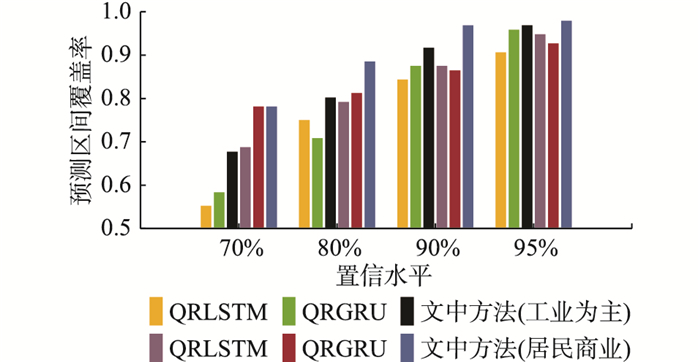
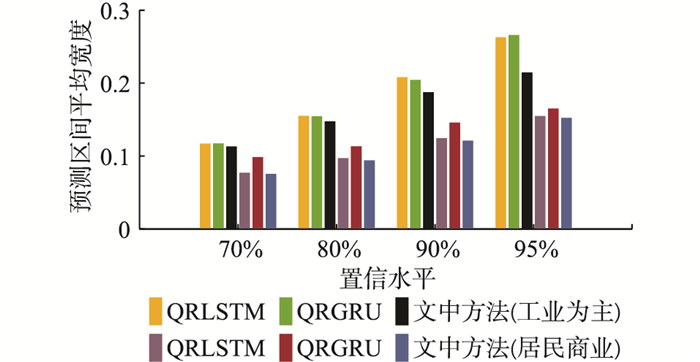
为了进一步验证文中方法的优势,分别采用文中方法、QRLSTM和门控循环单元分位数回归[24](quantile regression gated recurrent unit, QRGRU)进行区间预测对比。其中,QRLSTM中LSTM的神经元个数及QRGRU中GRU的神经元个数保持一致。不同方法的区间预测指标如图 8-图 10所示。
|
图 8 2类负荷不同置信水平下的预测区间覆盖率 Fig. 8 Prediction interval coverage probability of two types of loads at different confidence levels |
|
图 9 2类负荷不同置信水平下的预测区间平均宽度 Fig. 9 Prediction intervals normalized average width of two types of loads at different confidence levels |
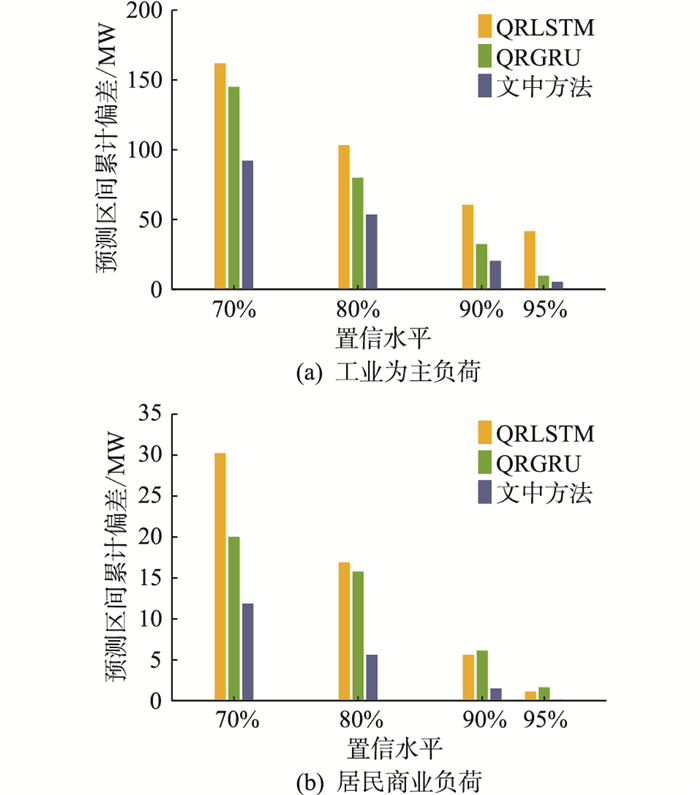
|
图 10 2类负荷不同置信水平下的预测区间累计偏差 Fig. 10 Prediction intervals accumulative deviation of two types of loads at different confidence levels |
(1) 在2类不同负荷中,文中方法的预测区间覆盖率JPICP基本满足或接近各个置信水平的期望。
(2) 对于2类不同负荷,文中方法相比其他2种方法而言,总体上区间覆盖率JPICP更大,区间平均宽度JPINAW和区间累计偏差JPIAD更小,因此具有更好的区间预测性能。以工业负荷90%置信水平为例,文中方法得到的预测区间的JPICP指标较QRLSTM和QRGRU增加了8.64%和4.77%,而JPINAW指标却减少了9.86%和8.27%,JPIAD指标则减少了66.48%和37.48%。
5 结语针对具有较强波动性的母线负荷,文中提出了一种基于CNN与QRLSTM组合的负荷区间预测模型。采用TDL对CNN进行封装,可将较长的时间序列数据切分成几个稍短的时间序列数据,实现特征提取与压缩,有利于后续LSTM网络的特征学习,同时在QRLSTM中引入attention机制,使模型更易学习特征序列中长距离相互依赖的关系。实例结果表明,相比于QRLSTM和QRGRU等以往模型,文中方法得到的预测区间总体上具有更高的区间覆盖率,同时区间宽度更窄,区间累计偏差更小,具有更好的区间预测性能。
| [1] |
刘波, 秦川, 鞠平, 等. 基于XGBoost与Stacking模型融合的短期母线负荷预测[J]. 电力自动化设备, 2020, 40(3): 147-153. LIU Bo, QIN Chuan, JU Ping, et al. Short-term bus load forecasting based on XGBoost and Stacking model fusion[J]. Electric Power Automation Equipment, 2020, 40(3): 147-153. (  0) 0) |
| [2] |
吴迪, 王正风. 基于逐日分段气象算法的日前负荷预测[J]. 电气应用, 2020, 39(6): 61-67. WU Di, WANG Zhengfeng. Day-ahead whether sensitive power load forecasting based on daily segmentation meteorological algorithm[J]. Electrotechnical Application, 2020, 39(6): 61-67. (  0) 0) |
| [3] |
臧海祥, 刘冲冲, 滕俊, 等. 基于CNN-GRU分位数回归的短期母线负荷概率密度预测[J]. 智慧电力, 2020, 48(8): 24-30, 69. ZANG Haixiang, LIU Chongchong, TENG Jun, et al. Short-term bus load probability density forecasting based on CNN-GRU quantile regression[J]. Smart Power, 2020, 48(8): 24-30, 69. (  0) 0) |
| [4] |
方仍存. 电力系统负荷区间预测[D]. 武汉: 华中科技大学, 2008. FANG Rengcun. Power system load interval forecasting[D]. Wuhan: Huazhong University of Science and Technology, 2008. (  0) 0) |
| [5] |
郝双. 基于B-ELM模型的风电场短期功率区间预测方法研究[D]. 沈阳: 沈阳工业大学, 2019. HAO Shuang. Research on short-term power interval prediction method of wind farm based on B-ELM model[D]. Shenyang: Shenyang University of Technology, 2019. (  0) 0) |
| [6] |
徐诗鸿, 张宏志, 林湘宁, 等. 基于改进评价指标的波动性负荷短期区间预测[J]. 电力系统自动化, 2020, 44(2): 156-163. XU Shihong, ZHANG Hongzhi, LIN Xiangning, et al. Improved evaluation index based short-term interval prediction of fluctuation load[J]. Automation of Electric Power Systems, 2020, 44(2): 156-163. (  0) 0) |
| [7] |
王若恒. 基于LSTM的风电功率区间预测研究[D]. 武汉: 华中科技大学, 2018. WANG Ruoheng. The research of interval prediction for wind power based on LSTM network[D]. Wuhan: Huazhong University of Science and Technology, 2018. (  0) 0) |
| [8] |
杨斌, 杨世海, 曹晓冬, 等. 基于EMD-QRF的用户负荷概率密度预测[J]. 电力系统保护与控制, 2019, 47(16): 1-7. YANG Bin, YANG Shihai, CAO Xiaodong, et al. Short-term consumer load probability density forecasting based on EMD-QRF[J]. Power System Protection and Control, 2019, 47(16): 1-7. (  0) 0) |
| [9] |
庞昊, 高金峰, 杜耀恒. 基于时间卷积网络分位数回归的短期负荷概率密度预测方法[J]. 电网技术, 2020, 44(4): 1343-1350. PANG Hao, GAO Jinfeng, DU Yaoheng. A short-term load probability density prediction based on quantile regression of time convolution network[J]. Power System Technology, 2020, 44(4): 1343-1350. (  0) 0) |
| [10] |
王玥, 张宇帆, 李昭昱, 等. 即插即用能量组织日前负荷概率预测方法[J]. 电网技术, 2019, 43(9): 3055-3060. WANG Yue, ZHANG Yufan, LI Zhaoyu, et al. Day-ahead probability load forecasting of energy tissues with plug-and-play function[J]. Power System Technology, 2019, 43(9): 3055-3060. (  0) 0) |
| [11] |
ZHANG Z D, QIN H, LIU Y Q, et al. Wind speed forecasting based on quantile regression minimal gated memory network and kernel density estimation[J]. Energy Conversion and Management, 2019, 196: 1395-1409. DOI:10.1016/j.enconman.2019.06.024 (  0) 0) |
| [12] |
严雪颖, 秦川, 鞠平, 等. 负荷功率模型的最优特征选择研究[J]. 电力工程技术, 2021, 40(3): 84-91. YAN Xueying, QIN Chuan, JU Ping, et al. Optimal feature selection of load power models[J]. Electric Power Engineering Technology, 2021, 40(3): 84-91. (  0) 0) |
| [13] |
姚添和. 基于自编码器和循环神经网络的短期风电功率预测研究[D]. 泉州: 华侨大学, 2019. YAO Tianhe. Research on short-term wind power prediction based on auto-encoder and recurrent neural network[D]. Quanzhou: Huaqiao University, 2019. (  0) 0) |
| [14] |
高昆仑, 杨帅, 刘思言, 等. 基于一维卷积神经网络的电力系统暂态稳定评估[J]. 电力系统自动化, 2019, 43(12): 18-26. GAO Kunlun, YANG Shuai, LIU Siyan, et al. Transient stability assessment for power system based on one-dimensional convolutional neural network[J]. Automation of Electric Power Systems, 2019, 43(12): 18-26. DOI:10.7500/AEPS20180911006 (  0) 0) |
| [15] |
赵兵, 王增平, 纪维佳, 等. 基于注意力机制的CNN-GRU短期电力负荷预测方法[J]. 电网技术, 2019, 43(12): 4370-4376. ZHAO Bing, WANG Zengping, JI Weijia, et al. A short-term power load forecasting method based on attention mechanism of CNN-GRU[J]. Power System Technology, 2019, 43(12): 4370-4376. (  0) 0) |
| [16] |
李道全, 王雪, 于波, 等. 基于一维卷积神经网络的网络流量分类方法[J]. 计算机工程与应用, 2020, 56(3): 94-99. LI Daoquan, WANG Xue, YU Bo, et al. Network traffic classification method based on one-dimensional convolution neural network[J]. Computer Engineering and Applications, 2020, 56(3): 94-99. (  0) 0) |
| [17] |
蒙亮, 于超, 张希翔, 等. 基于一维卷积神经网络和自注意力机制的非侵入式负荷分解[J]. 电力大数据, 2020, 23(10): 1-8. MENG Liang, YU Chao, ZHANG Xixiang, et al. Non-intrusive load disaggregation based on 1D convolutional neural network and self-attention mechanism[J]. Power Systems and Big Data, 2020, 23(10): 1-8. (  0) 0) |
| [18] |
刘建华, 李锦程, 杨龙月, 等. 基于EMD-SLSTM的家庭短期负荷预测[J]. 电力系统保护与控制, 2019, 47(6): 40-47. LIU Jianhua, LI Jincheng, YANG Longyue, et al. Short-term household load forecasting based on EMD-SLSTM[J]. Power System Protection and Control, 2019, 47(6): 40-47. (  0) 0) |
| [19] |
马梦冬, 彭道刚, 王丹豪. 基于EEMD-LSTM的区域能源短期负荷预测[J]. 浙江电力, 2020, 39(4): 29-35. MA Mengdong, PENG Daogang, WANG Danhao. Short-term load forecasting based on EEMD-LSTM for regional energy[J]. Zhejiang Electric Power, 2020, 39(4): 29-35. (  0) 0) |
| [20] |
李丹, 张远航, 杨保华, 等. 基于约束并行LSTM分位数回归的短期电力负荷概率预测方法[J]. 电网技术, 2021, 45(4): 1356-1364. LI Dan, ZHANG Yuanhang, YANG Baohua, et al. Short time power load probabilistic forecasting based on constrained parallel-LSTM neural network quantile regression mode[J]. Power System Technology, 2021, 45(4): 1356-1364. (  0) 0) |
| [21] |
谢小瑜, 周俊煌, 张勇军, 等. 基于W-BiLSTM的可再生能源超短期发电功率预测方法[J]. 电力系统自动化, 2021, 45(8): 175-184. XIE Xiaoyu, ZHOU Junhuang, ZHANG Yongjun, et al. W-BiLSTM based ultra-short-term generation power prediction method of renewable energy[J]. Automation of Electric Power Systems, 2021, 45(8): 175-184. (  0) 0) |
| [22] |
韦善阳, 黎静华, 黄乾. 基于改进权值优化模型的光伏功率区间预测[J]. 电力建设, 2019, 40(7): 26-33. WEI Shanyang, LI Jinghua, HUANG Qian. Interval prediction of photovoltaic power applying improved weight optimization model[J]. Electric Power Construction, 2019, 40(7): 26-33. (  0) 0) |
| [23] |
刘升伟, 王星华, 鲁迪, 等. 基于改进高斯过程回归的短期负荷概率区间预测方法[J]. 电力系统保护与控制, 2020, 48(1): 18-25. LIU Shengwei, WANG Xinghua, LU Di, et al. Electric load probabilistic interval prediction method based on improved Gaussian process regression[J]. Power System Protection and Control, 2020, 48(1): 18-25. (  0) 0) |
| [24] |
李锦程. 基于门控循环单元的短期风电功率预测研究[D]. 徐州: 中国矿业大学, 2019. LI Jincheng. Research on short-term wind power forecasting based on gated recurrent unit[D]. Xuzhou: China University of Mining and Technology, 2019. (  0) 0) |
 2021, Vol. 40
2021, Vol. 40


 唐戈(1996), 男, 硕士在读, 研究方向为负荷的区间分析(E-mail:
唐戈(1996), 男, 硕士在读, 研究方向为负荷的区间分析(E-mail: