文章编号: 2096-3203(2021)03-0060-06 中图分类号: TM743
2. 国网江苏省电力有限公司电力科学研究院,江苏 南京 211103
有载调压变压器能在带负荷情况下操作分接开关[1],具有灵活的在线控制特性,可实现分布式电源控制[2]、电压调节[3-4]、无功优化控制[5]、经济运行[6]、最优潮流控制[7-8]等功能,广泛应用于现代输配电系统。变压器分接开关档位变化会改变变压器的实际变比,同时也会影响变压器的等效串联阻抗和并联励磁导纳参数[9-11]。
现有非标准变比变压器的等值电路模型可分为三类。第一类模型完全忽略分接开关实际档位,始终认为变压器工作在额定变比条件下,如文献[1]中三相变压器T型等值电路模型和文献[12]中根据变压器两侧序分量相移关系建立的简化变压器支路模型。该类模型无法准确表达变压器实际变比对系统的影响。
第二类为两侧是理想变压器、中间部分采用T型等值电路的精确T型变压器模型[10, 13-14]。该模型既能准确反映变压器两侧分接头档位调整带来的变化,又将励磁支路的等效并联导纳计算在内,是目前最为精确的非标准变比变压器模型。该模型有1个额外的电路节点,导致系统导纳矩阵增大,程序对内存的需求增加,计算效率降低。
第三类为考虑了非标准变比因素,但进行不同程度近似的模型。BPA软件采用Π型模型,相对于精确T型模型,该模型无虚拟节点,但将励磁导纳取半并分别并联在两端节点的设定,不能准确表征两侧分接头档位变化对参数的影响[15]。PSS/E软件采用Γ型模型[16],相当于将精确T型模型中的并联导纳由虚拟节点移至原边节点,励磁导纳取值固定,故不能有效反映两侧分接头变化。PSASP软件和文献[17]均采用更为简化的Γ型等值电路模型,仍存在励磁导纳取值固定的问题。文献[9, 18-20]在BPA软件Π型模型基础上省略励磁导纳支路,模型精度进一步降低。文献[3, 21-26]则进一步省略,只保留单个理想变压器,故只能表达单侧绕组分接开关档位变化带来的影响,缺乏通用性。
综上所述,现有非标准变比变压器模型还存在精度或计算效率方面的不足。文中基于非标准变比的精确T型等值模型,有效利用Y-△阻抗网络等值变换建立改进Π-1型等值电路,并进一步提出适用于前推回代的改进Π-2型模型及其前推回代的计算方法。文中提出的改进Π-1和Π-2型等值电路模型在保证模型精度与精确T型模型完全等价的前提下,消除了额外电路节点,提升了计算效率,有效解决了现有非标准变比变压器模型难以兼顾精度与计算效率的问题。
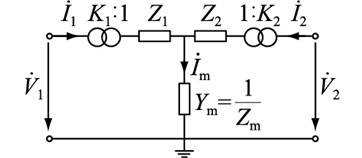
1 现有非标准变比变压器等值电路模型非标准变比变压器的精确T型等值电路模型如图 1所示。其中
|
图 1 精确T型非标准变比变压器等值电路 Fig. 1 Accurate T-type equivalent circuit of non-standard ratio transformer |
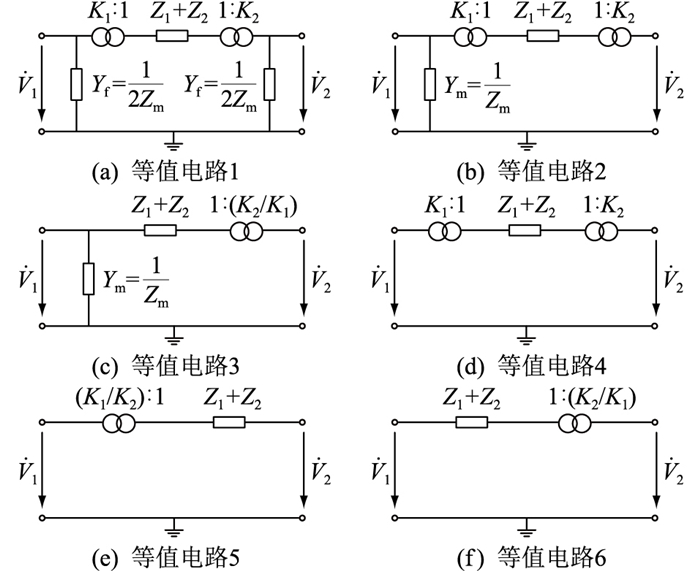
图 2(a)-(f)分别为现有常见非标准变比变压器的近似等值电路。在图 1精确T型等值电路基础上将励磁导纳均分后移至两侧,即得到BPA软件采用的等值电路[15],如图 2(a)所示;将励磁导纳移至原边节点,可得到PSS/E软件采用的等值电路[16],如图 2(b)所示;将图 2(b)中2个理想变压器合并后放置到副边,即为PSASP软件采用的等值电路,如图 2(c)所示[15, 17];移除图 2(b)中的励磁支路,可得文献[9, 18-20]采用的等值电路,如图 2(d)所示;将图 2(d)中2个理想变压器合并后分别放置在原边或者副边,得到文献[3]或文献[21-26]采用的等值电路,分别如图 2(e)、(f)所示。相对于精确T型等值电路,图 2中的各个模型都进行了不同程度的近似,各自特点此处不再赘述。
|
图 2 现有非标准变比变压器近似等值电路 Fig. 2 Existing approximate equivalent circuits of non-standard ratio transformer |
基于图 1所示的精确T型等值电路,根据基尔霍夫和欧姆定律,可得:
| $ \left\{\begin{array}{l} \dot{I}_{1} K_{1}+\dot{I}_{2} K_{2}-\dot{I}_{\mathrm{m}}=0 \\ \dot{V}_{1} / K_{1}-\dot{I}_{1} K_{1} Z_{1}-\dot{I}_{\mathrm{m}} Z_{\mathrm{m}}=0 \\ \dot{V}_{1} / K_{1}-\dot{I}_{1} K_{1} Z_{1}+\dot{I}_{2} K_{2} Z_{2}-\dot{V}_{2} / K_{2}=0 \end{array}\right. $ | (1) |
将式(1)中的
| $ \left\{\begin{array}{c} \dot{I}_{1}=\frac{\left(Z_{2}+Z_{\mathrm{m}}\right) / K_{1}^{2}}{Z_{1} Z_{2}+Z_{1} Z_{\mathrm{m}}+Z_{2} Z_{\mathrm{m}}} \dot{V}_{1}- \\ \frac{Z_{\mathrm{m}} /\left(K_{1} K_{2}\right)}{Z_{1} Z_{2}+Z_{1} Z_{\mathrm{m}}+Z_{2} Z_{\mathrm{m}}} \dot{V}_{2} \\ \dot{I}_{2}=\frac{\left(Z_{1}+Z_{\mathrm{m}}\right) / K_{2}^{2}}{Z_{1} Z_{2}+Z_{1} Z_{\mathrm{m}}+Z_{2} Z_{\mathrm{m}}} \dot{V}_{2}- \\ \frac{Z_{\mathrm{m}} /\left(K_{1} K_{2}\right)}{Z_{1} Z_{2}+Z_{1} Z_{\mathrm{m}}+Z_{2} Z_{\mathrm{m}}} \dot{V}_{1} \end{array}\right. $ | (2) |
式(2)可进一步变换为:
| $ \left\{\begin{array}{c} \dot{I}_{1}=\frac{K_{2} Z_{2}+\left(K_{2}-K_{1}\right) Z_{\mathrm{m}}}{K_{1}^{2} K_{2}\left(Z_{1} Z_{2}+Z_{1} Z_{\mathrm{m}}+Z_{2} Z_{\mathrm{m}}\right)} \dot{V}_{1}+ \\ \frac{\left[Z_{\mathrm{m}} /\left(K_{1} K_{2}\right)\right]\left(\dot{V}_{1}-\dot{V}_{2}\right)}{Z_{1} Z_{2}+Z_{1} Z_{\mathrm{m}}+Z_{2} Z_{\mathrm{m}}} \\ \dot{I}_{2}=\frac{K_{1} Z_{1}+\left(K_{1}-K_{2}\right) Z_{\mathrm{m}}}{K_{1} K_{2}^{2}\left(Z_{1} Z_{2}+Z_{1} Z_{\mathrm{m}}+Z_{2} Z_{\mathrm{m}}\right)} \dot{V}_{2}+ \\ \frac{\left[Z_{\mathrm{m}} /\left(K_{1} K_{2}\right)\right]\left(\dot{V}_{2}-\dot{V}_{1}\right)}{Z_{1} Z_{2}+Z_{1} Z_{\mathrm{m}}+Z_{2} Z_{\mathrm{m}}} \end{array}\right. $ | (3) |
将式(3)改写为:
| $ \left\{\begin{array}{l} \dot{I}_{1}=Y_{1} \dot{V}_{1}+\left(\dot{V}_{1}-\dot{V}_{2}\right) / Z \\ \dot{I}_{2}=Y_{2} \dot{V}_{2}+\left(\dot{V}_{2}-\dot{V}_{1}\right) / Z \end{array}\right. $ | (4) |
其中:
| $ \left\{\begin{array}{l} Z=K_{1} K_{2}\left(Z_{1}+Z_{2}+Z_{1} Z_{2} / Z_{\mathrm{m}}\right) \\ Y_{1}=\frac{K_{2} Z_{2}+\left(K_{2}-K_{1}\right) Z_{\mathrm{m}}}{K_{1}^{2} K_{2}\left(Z_{1} Z_{2}+Z_{1} Z_{\mathrm{m}}+Z_{2} Z_{\mathrm{m}}\right)} \\ Y_{2}=\frac{K_{1} Z_{1}+\left(K_{1}-K_{2}\right) Z_{\mathrm{m}}}{K_{1} K_{2}^{2}\left(Z_{1} Z_{2}+Z_{1} Z_{\mathrm{m}}+Z_{2} Z_{\mathrm{m}}\right)} \end{array}\right. $ | (5) |
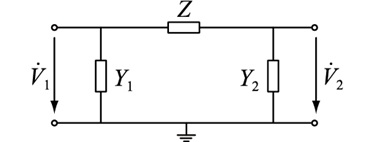
上述推导过程中,未采用任何假设,故所得模型与精确T型模型在数学上完全等价。该模型通过电路等值变换消除了额外的电路节点和理想变压器,保证了仿真计算效率。鉴于该模型为Π型结构且具备与精确T型模型完全相同的精度,文中称之为改进Π-1型非标准变比变压器精确等值电路模型,如图 3所示。
|
图 3 改进Π-1型非标准变比变压器精确等值电路 Fig. 3 Accurate improved Π-1 type equivalent circuit of non-standard ratio transformer |
经大量测试验证,改进Π-1型模型应用到机电暂态仿真以及基于非前推回代的潮流计算中,均能获得正确的仿真计算结果。然而,在基于前推回代的潮流计算中,采用图 3所示的改进Π-1型模型可能会出现不收敛现象。这是因为在变比K1,K2相差较大的特定情况下,式(5)中并联在变压器原副边节点上的等效导纳Y1和Y2取值较大,而前推回代潮流计算方法在处理取值较大的并联导纳时,可能会出现不收敛的情况[23]。为解决该问题,借鉴文献[23]中类似的处理方法,在对电路进行等值变换时,保留所有理想变压器,并在前推回代的计算过程中作相应变化。
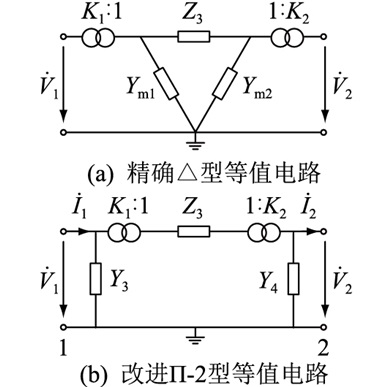
首先,基于图 1所示精确T型精确模型,利用Y-△阻抗网络等值变换原理,获得如图 4(a)所示的精确△型等值电路。其中Z3,Ym1,Ym2由图 1中的Z1,Z2,Ym经Y-△变换所得。
| $ \left\{\begin{array}{l} Z_{3}=Z_{1}+Z_{2}+Z_{1} Z_{2} / Z_{\mathrm{m}} \\ Y_{\mathrm{m1}}=Z_{2} /\left(Z_{1} Z_{2}+Z_{1} Z_{\mathrm{m}}+Z_{2} Z_{\mathrm{m}}\right) \\ Y_{\mathrm{m} 2}=Z_{1} /\left(Z_{1} Z_{2}+Z_{1} Z_{\mathrm{m}}+Z_{2} Z_{\mathrm{m}}\right) \end{array}\right. $ | (6) |
|
图 4 适用于前推回代的改进Π-2型非标准变比变压器等值电路 Fig. 4 Improved Π-2 type equivalent circuit of non-standard ratio transformer suitable for backward/forward sweep method |
其次,为便于前推回代计算,根据电路参数在理想变压器两侧的等效变换原理,可将并联导纳移至理想变压器外侧的原副边节点处,得到如图 4(b)所示的适用于前推回代的改进Π-2型非标准变比变压器等值电路。图中各参数取值为:
| $ \left\{\begin{array}{l} Y_{3}=Z_{2} /\left[K_{1}^{2}\left(Z_{1} Z_{2}+Z_{1} Z_{\mathrm{m}}+Z_{2} Z_{\mathrm{m}}\right)\right] \\ Y_{4}=Z_{1} /\left[K_{2}^{2}\left(Z_{1} Z_{2}+Z_{1} Z_{\mathrm{m}}+Z_{2} Z_{\mathrm{m}}\right)\right] \end{array}\right. $ | (7) |
由于模型中存在理想变压器,在前推回代过程中进行针对性处理。假设图 4(b)中的左侧为前端节点,即节点1;右侧为后向节点,即节点2。为了提升计算效率,并联在节点1和节点2的导纳Y3和Y4包含于系统导纳矩阵中,此时节点1和节点2之间相当于仅有阻抗Z3和2个理想变压器串联。
前推计算采用电流前推,每次电流前推过程中处理该变压器支路时,需要通过已知的注入节点2的电流
| $ \dot{I}_{1}=\dot{I}_{2} K_{2} / K_{1} $ | (8) |
每次电压回代过程中处理该支路时,利用已知节点1的电压
| $ \dot{V}_{2}=\left(\dot{V}_{1} / K_{1}-\dot{I}_{2} K_{2} Z\right) K_{2} $ | (9) |
相对于改进Π-1模型,改进Π-2模型保留了两侧的理想变压器,避免产生较大的并联导纳,保证了式(7)中Y3和Y4的取值始终在合理范围内,解决了计算不收敛的问题。
3 算例对比分析基于文中所提改进Π-1和Π-2型非标准变比变压器等值电路模型,分别从仿真精度、计算效率和收敛性能三方面,与BPA、PSASP软件采用的模型进行对比分析。
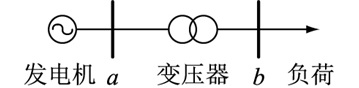
3.1 仿真精度对比为方便对比不同变压器模型在仿真精度上的差异,文中设计了如图 5所示的简化两节点测试算例。其中节点a,b分别为平衡节点和PQ节点,两节点由一变压器支路连接。该算例参数见表 1、表 2。
|
图 5 简化两节点测试算例 Fig. 5 The simplified 2-bus test case |
|
|
表 1 简化两节点测试算例节点参数 Table 1 Node parameters of the simplified 2-bus test case |
|
|
表 2 简化两节点测试算例支路参数 Table 2 Branch parameters of the simplified 2-bus test case |
分别采用精确T型、BPA-Π型、PSASP-Γ型和文中所提改进Π-1型变压器等值电路模型,对简化两节点测试算例进行潮流计算。以精确T型模型的计算结果为基准,其余方法所得结果的绝对误差如表 3所示。其中α为原边绕组阻抗在总串联阻抗中的占比;潮流计算的收敛精度ε取10-6;V2和θ2分别为节点2的电压幅值和相位;P1,Q1分别为节点1的注入有功和无功功率。
|
|
表 3 简化两节点测试算例潮流绝对误差对比 Table 3 Comparison of power flow absolute errors for 2-bus test case |
由表 3可知,随着α的变化,BPA-Π型和PSASP-Γ型模型的绝对误差也随之发生变化,文中所提改进Π-1型模型在收敛精度范围内与精确T型模型精度始终完全一致,与理论分析相符。BPA-Π和PSASP-Γ型模型均只考虑了总串联阻抗,而未区分原副边绕组的阻抗占比,因此随着α的变化呈现不同的计算误差。相对于忽略了原边分接头变化的Γ型模型,Π型模型考虑了原副边分接头变化,计算结果更加精确。
3.2 仿真计算效率对比为对比不同模型的计算效率,基于IEEE 300标准测试算例进行对比分析。由于潮流计算程序每次运行时间均不同,为减少随机性对计算效率分析带来的不良影响,采用各模型分别执行100次潮流计算,对比总运行时间。参与对比的模型为精确T型、BPA-Π型、PSASP-Γ型和文中所提改进Π-1型变压器模型,各模型计算时间如表 4所示。
|
|
表 4 IEEE 300测试算例潮流计算时间对比 Table 4 Time comparison of power flow calculation for the IEEE 300 test case |
由表 4可知,BPA-Π、PSASP-Γ和文中所提改进Π-1型模型的计算时间基本一致。基于3种变压器模型的IEEE 300测试算例等效节点数目均为300,采用同样的潮流计算方法,计算时间自然非常接近。而采用精确T型模型会使测试算例的等效节点数增加至407,计算时间更长。且精确T型模型的计算时间增幅较大,这是因为采用了稠密矩阵计算方式,若改为稀疏矩阵计算方式,则计算时间增幅会相应减小。
3.3 收敛性能对比为测试适用于前推回代的Π-2型模型与改进Π-1型模型在收敛性能方面的提升效果,分别基于图 5和修正IEEE 9测试算例进行对比验证。潮流计算方法均采用前推回代法,ε均取10-6。修正IEEE 9测试算例在标准IEEE 9算例基础上修改所有变压器原副边绕组的分接头档位,其余参数都不变。
简化两节点测试算例的收敛性能对比如表 5所示。由表 5可知,非标准变比情形下无论α如何取值,改进Π-1型模型的前推回代潮流计算均需约21次迭代才能达到收敛条件。保持其他参数和条件不变,采用改进Π-2型模型的前推回代计算只需4次迭代即可达到收敛条件。
|
|
表 5 简化两节点测试算例的迭代次数对比 Table 5 Comparison of iteration times for the simplified 2-bus test case |
修正IEEE 9测试算例的收敛性能对比如表 6所示。由表 6可知,在各种变比参数情形下,改进Π-2型模型的收敛性能均优于改进Π-1型模型。在原副边绕组分接头都为非标准位置时,采用改进Π-1型模型的潮流计算出现了不收敛现象。且变压器在标准变比时收敛性能最好、偏离标准变比越远则收敛性能越差。修正IEEE 9测试算例既有PV节点还有回环,故进入收敛条件的前推回代迭代计算次数整体偏高,这是由前推回代方法自身特点决定的。至于如何提升前推回代对PV节点和环状拓扑的适应能力,不在此处深入讨论。
|
|
表 6 基于修正IEEE 9测试算例的迭代次数对比 Table 6 Comparison of iteration times for the modified IEEE 9 test case |
由上述收敛性能仿真对比可知,在前推回代潮流计算中,改进Π-2型模型能够获得较改进Π-1型模型更好的收敛性能。
4 结语文中旨在解决现有非标准变比变压器模型在精度和计算效率方面难以兼顾的问题。对精确T型非标准变比变压器模型进行电路网络等值变换,构建了改进Π-1型变压器等值电路模型。该模型既实现了与精确T型模型一致的高精度,又无需增加额外节点,保证了高计算效率。同时,文中利用阻抗Y-△变换原理,提出了改进Π-2型模型,提升了模型应用于前推回代潮流计算的收敛性能,进一步增加了模型的实用性。基于自定义两节点、IEEE 9和IEEE 300测试算例,分别对改进Π-1、Π-2模型和现有常见模型进行了对比测试,结果表明文中所提模型在精度、计算速度和收敛性能方面具有明显综合优势。
本文得到南京工程学院人才启动基金项目(YKJ201714),江苏省主动配电网协同创新中心开放基金项目(XTCX201808)资助,谨此致谢!
| [1] |
韩祯祥. 电力系统分析[M]. 5版. 杭州: 浙江大学出版社, 2011. HAN Zhenxiang. Power system analysis[M]. 5th ed. Hangzhou: Zhejiang University Press, 2011. (  0) 0) |
| [2] |
REZVANI M M, MEHRAEEN S, RAMAMURTHY J, et al. Interaction of the substation load tap changer with the high penetration of distributed energy resources[C]//2020 IEEE Texas Power and Energy Conference (TPEC). College Station, TX, USA. IEEE, 2020: 1-5.
(  0) 0) |
| [3] |
郑涛, 陆格野, 黄婷, 等. 特高压有载调压变压器差动保护自适应算法[J]. 电工技术学报, 2017, 32(20): 271-280. ZHENG Tao, LU Geye, HUANG Ting, et al. An adaptive algorithm for the differential protection of the UHV voltage-regulating transformer with on-load tap changer[J]. Transactions of China Electrotechnical Society, 2017, 32(20): 271-280. (  0) 0) |
| [4] |
HASHEMIPOUR N, AGHAEI J, LOTFI M, et al. Multi-objective optimization method for coordinating battery storage systems, photovoltaic inverters and tap changers[J]. IET Renewable Power Generation, 2020, 14(3): 475-483. DOI:10.1049/iet-rpg.2019.0644 (  0) 0) |
| [5] |
KRAICZY M, STETZ T, BRAUN M. Parallel operation of transformers with on load tap changer and photovoltaic systems with reactive power control[J]. IEEE Transactions on Smart Grid, 2018, 9(6): 6419-6428. DOI:10.1109/TSG.2017.2712633 (  0) 0) |
| [6] |
高慧颐. 变压器经济运行及优化控制策略的研究[D]. 锦州: 辽宁工业大学, 2019. GAO Huiyi. Study on economic operation and optimal control strategy of transformer[D]. Jinzhou: Liaoning University of Technology, 2019. (  0) 0) |
| [7] |
WU W C, TIAN Z, ZHANG B M. An exact linearization method for OLTC of transformer in branch flow model[J]. IEEE Transactions on Power Systems, 2017, 32(3): 2475-2476. DOI:10.1109/TPWRS.2016.2603438 (  0) 0) |
| [8] |
李斌, 刘建坤, 李群, 等. 考虑决策风险的含UPFC多目标最优潮流计算[J]. 电力工程技术, 2018, 37(1): 19-25. LI Bin, LIU Jiankun, LI Qun, et al. Multi-objective optimal power flow calculation incorporating UPFC considering decision risk[J]. Electric Power Engineering Technology, 2018, 37(1): 19-25. DOI:10.3969/j.issn.1009-0665.2018.01.004 (  0) 0) |
| [9] |
徐树文, 李亚楼, 李文臣, 等. 基于ADPSS电磁暂态模型库的三相潮流建模与计算方法[J]. 电网技术, 2018, 42(2): 571-577. XU Shuwen, LI Yalou, LI Wenchen, et al. Research of three-phase load flow modeling and method based on ADPSS electromagnetic transient model library[J]. Power System Technology, 2018, 42(2): 571-577. (  0) 0) |
| [10] |
AHMAD A, FANG W L, LIU J, et al. Power transformer transient modeling considering the effects of on-load tap changer[C]//2017 4th International Conference on Electric Power Equipment-Switching Technology(ICEPE-ST). IEEE, 2017: 766-770.
(  0) 0) |
| [11] |
JUN L, ASAD A, NIE K J, et al. Research of transformer modeling considering the influence of tap positions on original parameters[C]//2016 IEEE PES Asia-Pacific Power and Energy Engineering Conference(APPEEC). IEEE, 2016: 2209-2214.
(  0) 0) |
| [12] |
杨雄, 卫志农, 孙国强, 等. 变压器支路处理新方法与配电网三相潮流计算[J]. 电力系统自动化, 2014, 38(18): 58-64. YANG Xiong, WEI Zhinong, SUN Guoqiang, et al. A novel method for transformer branch processing and three-phase power flow calculation in distribution networks[J]. Automation of Electric Power Systems, 2014, 38(18): 58-64. DOI:10.7500/AEPS20131107001 (  0) 0) |
| [13] |
COPPO M, BIGNUCOLO F, TURRI R. Generalised transformer modelling for power flow calculation in multi-phase unbalanced networks[J]. IET Generation, Transmission & Distribution, 2017, 11(15): 3843-3852. (  0) 0) |
| [14] |
中国电力科学研究院. ADPSS电力系统全数字仿真装置电磁暂态元件库用户手册(2.2版本)[R]. 2020. China Electric Power Research Institute. ADPSS (advanced digital power system simulator) electromagnetic transient simulation element library user′s manual (ver 2.2)[R]. 2020. (  0) 0) |
| [15] |
汤涌, 印永华. 电力系统多尺度仿真与试验技术[M]. 北京: 中国电力出版社, 2013. TANG Yong, YIN Yonghua. Multi scale simulation and test technology of power system[M]. Beijing: China Electric Power Press, 2013. (  0) 0) |
| [16] |
Siemens Power Technologies International. PSS/E 34 program application guide volume 1[Z]. 2020.
(  0) 0) |
| [17] |
汤涌, 田芳, 黄彦浩. 电力系统短路电流计算[M]. 北京: 中国电力出版社, 2015. TANG Yong, TIAN Fang, HUANG Yanhao. Short circuit calculation of power system[M]. Beijing: China Electric Power Press, 2015. (  0) 0) |
| [18] |
王帅兵, 李琳, 谢裕清, 等. 统一潮流控制器中串联耦合变压器特性及仿真模型研究[J]. 电网技术, 2017, 41(2): 551-557. WANG Shuaibing, LI Lin, XIE Yuqing, et al. Research on SCT characteristics and simulation model in UPFC system[J]. Power System Technology, 2017, 41(2): 551-557. (  0) 0) |
| [19] |
陈珩. 电力系统稳态分析[M]. 第2版. 北京: 中国电力出版社, 1995. CHEN Heng. Electric power system static analysis[M]. 2nd ed. Beijing: China Electric Power Press, 1995. (  0) 0) |
| [20] |
张伯明, 陈寿孙, 严正. 高等电力网络分析[M]. 2版. 北京: 清华大学出版社, 2007. ZHANG Boming, CHEN Shousun, YAN Zheng. Advanced electric power network analysis[M]. 2nd ed. Beijing: Tsinghua University Press, 2007. (  0) 0) |
| [21] |
王锡凡. 现代电力系统分析[M]. 北京: 科学出版社, 2003. WANG Xifan. Modern power system analysis[M]. Beijing: Science Press, 2003. (  0) 0) |
| [22] |
郭志忠. 电力网络解析论[M]. 北京: 科学出版社, 2008. GUO Zhizhong. Analytic theory of electric power network[M]. Beijing: Science Press, 2008. (  0) 0) |
| [23] |
颜伟, 刘方, 王官洁, 等. 辐射型网络潮流的分层前推回代算法[J]. 中国电机工程学报, 2003, 23(8): 76-80. YAN Wei, LIU Fang, WANG Guanjie, et al. Layer-by-layer back/forward sweep method for radial distribution load flow[J]. Proceedings of the CSEE, 2003, 23(8): 76-80. DOI:10.3321/j.issn:0258-8013.2003.08.015 (  0) 0) |
| [24] |
ALKAABI S S, ZEINELDIN H H, KHADKIKAR V. Simplified power flow modeling approach considering on-load tap changers[C]//2017 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT). Washington, DC, USA. IEEE, 2017: 1-5.
(  0) 0) |
| [25] |
JABR R A, D AFI I, KARAKI S. Tracking transformer tap position in real-time distribution network power flow applications[J]. IEEE Transactions on Smart Grid, 2016, 9(4): 2442-2452. (  0) 0) |
| [26] |
FAN J, BO Z. Modelling of on-load tap-changer with variable impedance and its applications[C]//Proceedings of International Conference on Energy Management and Power Delivery. 1998: 491-494.
(  0) 0) |
2. State Grid Jiangsu Electric Power Co., Ltd. Research Institute, Nanjing 211103, China
 2021, Vol. 40
2021, Vol. 40


 董亮(1981),男,博士,高级工程师,研究方向为电力及综合能源系统建模仿真技术(E-mail:
董亮(1981),男,博士,高级工程师,研究方向为电力及综合能源系统建模仿真技术(E-mail: