文章编号: 2096-3203(2021)03-0066-06 中图分类号: TM715
2. 东南大学电气工程学院,江苏 南京 210096
短期负荷预测是能源管理系统的重要组成部分,是市场机制下制定供电计划、电力调度计划和电力交易计划的重要基础,也为电力系统的经济、安全、稳定运行提供了有力保障[1-2]。传统的短期负荷预测方法主要有以自回归移动均值(auto regressive moving average, ARMA)[3-4]、线性回归方法(linear regression, LR)[5]和卡尔曼滤波法[6]为代表的统计学方法和以支持向量回归方法[7-8]、贝叶斯方法[9]和随机森林方法[10]为代表的机器学习方法。统计学方法具有模型简单、训练速度快的优点,但是对于非线性的负荷预测问题,该方法拟合能力不足,预测精度较低。传统机器学习方法虽然具有较强的非线性拟合能力,但是大多数模型参数寻优困难,容易陷入局部最优的困境。近年来随着深度学习的不断发展,很多学者也开展了利用深度学习模型进行短期负荷预测的研究,主要有基于反馈神经网络(back propagation, BP)[11]、基于循环神经网络(recurrent neural networks,RNN)[12-13]和基于卷积神经网络(convolutional neural network, CNN)的负荷预测方法[14]。文献[15]中利用BP神经网络的特征提取和非线性拟合能力,实现了短期负荷的有效预测,但该模型未考虑负荷特征之间的时序关系,预测精度不高。RNN模型具有记忆单元,可以实现对电力负荷数据时序关系提取,但在训练过程中容易产生梯度消失或爆炸的问题。基于RNN模型改进的长短期记忆网络[13, 16](long short-term memory,LSTM)模型引入门控制单元,解决了RNN模型训练过程中梯度消失或爆炸的问题。文献[17]中采用了基于LSTM模型改进的门限循环单元(gated recurrent unit, GRU)模型,能以更快的收敛速度取得与LSTM模型相近的预测效果。CNN模型具有可并行计算的优点,但是无法很好提取时间序列数据的时序依赖特征。针对此问题,文献[18]中提出了时间卷积网络(temporal convolutional network, TCN),并在多种数据集上验证了其预测性能。
为了进一步提高短期负荷预测精度,文中基于负荷预测影响因素时序特征的分析,提出了一种基于TCN-GRU的短期负荷预测方法。利用时间卷积网络对时序数据的特征提取能力和GRU神经网络的非线性拟合能力,搭建TCN-GRU模型,并基于我国广东省佛山市某工业负荷数据进行短期负荷预测。预测结果表明,TCN-GRU模型的负荷预测能力明显优于其他单预测模型。
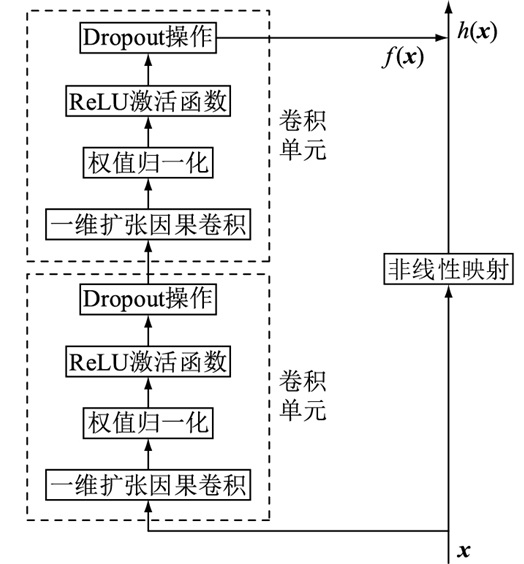
1 深度学习模型 1.1 TCN神经网络结构TCN模型是一种简单通用的解决时间序列问题的卷积神经网络架构[18]。TCN模型由一组残差单元组成,每个残差单元是一个具有残差连接[19]的小型神经网络,通过残差连接可以加快深层网络的反馈与收敛,解决随着网络层次增加造成的“退化现象”。TCN的残差单元如图 1所示。
|
图 1 TCN残差单元 Fig. 1 Residual unit of TCN |
残差连接是将残差单元的输入x添加到输出f(x),网络被强制模型化为:
| $ f(\boldsymbol{x})=h(\boldsymbol{x})-\boldsymbol{x} $ | (1) |
残差单元中包含2个卷积单元和非线性映射。卷积单元中首先进行一维扩张因果卷积,通过扩张系数调整采样间隔,实现更大的感受野(receptive field,RF),即卷积层上的特征能看到的区域范围,让网络可以记忆足够长的历史信息,并且只对t时刻之前的输入进行卷积以得到t时刻的输出,保证不会泄露未来的信息;然后对权重进行归一化处理,使用ReLU函数作为激活函数;最后采用Dropout操作,按照一定的概率随机丢弃神经元,达到防止过拟合和加速模型训练速度的目的。非线性映射是在残差单元的输入和输出具有不同的维度时,对高维度的数据进行降维。一维扩张因果卷积的运算式为:
| $ \boldsymbol{F}(s)=\sum\limits_{i=0}^{k-1} f(i) \boldsymbol{x}_{s-d i} $ | (2) |
式中:x为输入序列;f为过滤器;d为扩张系数;k为卷积核大小;s-di确保只能对过去的输入做卷积操作。
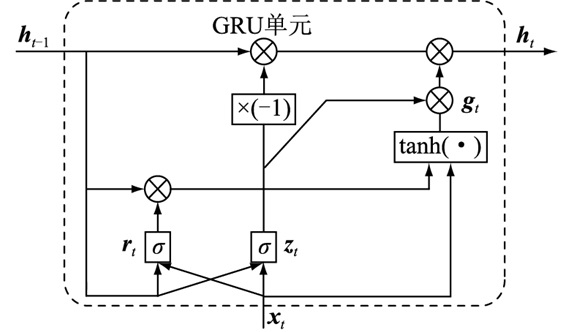
1.2 GRU神经网络结构GRU是LSTM的一个简化版本,其将LSTM的输入门和遗忘门整合为一个更新门,没有输出门,但增加了一个重置门。更新门控制前一时刻状态信息的保留程度,更新门的值越大说明前一时刻状态信息对当前状态的影响就越大[20]。重置门控制当前状态与先前信息的结合程度,值越小说明忽略的信息越多[21]。GRU单元结构如图 2所示。
|
图 2 GRU单元结构 Fig. 2 GRU structure |
GRU单元中h(t)的计算公式为:
| $ \boldsymbol{z}_{t}=\sigma\left(\boldsymbol{w}_{(\boldsymbol{x}, \boldsymbol{z})}^{\mathrm{T}} \boldsymbol{x}_{t}+\boldsymbol{w}_{(\boldsymbol{h}, \boldsymbol{z})}^{\mathrm{T}} \boldsymbol{h}_{t-1}\right) $ | (3) |
| $ \boldsymbol{r}_{t}=\sigma\left(\boldsymbol{w}_{(\boldsymbol{x}, \boldsymbol{r})}^{\mathrm{T}} \boldsymbol{x}_{t}+\boldsymbol{w}_{(\boldsymbol{h}, \boldsymbol{r})}^{\mathrm{T}} \boldsymbol{h}_{t-1}\right) $ | (4) |
| $ \boldsymbol{g}_{t}=\tanh \left[\boldsymbol{w}_{(\boldsymbol{x}, \boldsymbol{g})}^{\mathrm{T}} \boldsymbol{x}_{t}+\boldsymbol{w}_{(\boldsymbol{h}, \boldsymbol{g})}^{\mathrm{T}}\left(\boldsymbol{r} \otimes \boldsymbol{h}_{t-1}\right)\right] $ | (5) |
| $ \boldsymbol{h}_{t}=\left(-\boldsymbol{z}_{t}\right) \otimes \boldsymbol{h}_{t-1}+\boldsymbol{z}_{t} \otimes \boldsymbol{g}_{t} $ | (6) |
式中:x t为t时刻的输入;h t为t时刻的输出或状态;h t-1为t-1时刻的状态;w为权重;σ为激活函数sigmoid(·);tanh(·)为激活函数。
2 基于TCN-GRU的负荷预测模型电力负荷预测是一个非线性的时间序列预测问题[22]。时间序列数据是指随时间变化的数据,而影响电力负荷的因素不单单有电力负荷数据等时序序列数据, 也有温度、日期等非时间序列数据。如果将所有数据无差别的输入到单模型中进行训练,不能有效提取出原始数据内部蕴含的时序关系和非时序关系。
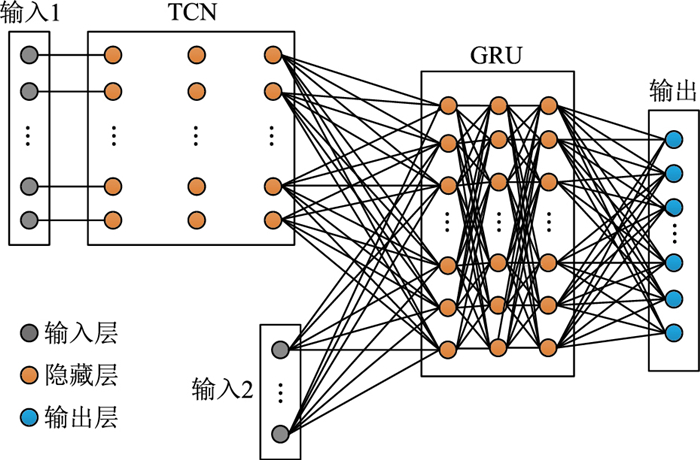
2.1 TCN-GRU模型结构TCN模型通过一维因果卷积对过去的数据进行提取,保证时序性,残差连接加快收敛速度,扩张卷积实现时序特征提取。GRU模型作为循环神经网络的变种,具有非线性拟合能力,能够有效提取数据特征,且在保障得到与LSTM相近预测效果的同时获得更快的收敛速度[23]。文中将两者结合搭建了TCN-GRU模型,如图 3所示。
|
图 3 TCN-GRU模型结构 Fig. 3 TCN-GRU model structure |
图 3中,TCN-GRU模型结构包括:
(1) 输入1。输入为连续7 d的电力负荷数据样本。每日的电力负荷数据是按照24 h设置96个采样点,时间间隔为15 min,获取得到96维电力负荷数据。
(2) 时间卷积网络层。设置2层的残差单元。每层残差单元包含2个卷积单元和1个非线性映射。其中卷积单元使用ReLU函数作为激活函数,对卷积核的权重进行归一化操作。卷积核大小为2;并设置Dropout系数为0.4,Dropout设置可以随机选取部分神经元失活,防止训练过拟合,同时加快模型的收敛速度;设置扩张系数为(1, 2, 4, 8, 16, 32);过滤器为128。残差单元的输入和输出具有不同的维度,不能直接做加和操作,将残差映射中增加了一个1×1的卷积层进行降维。
(3) 输入2。输入为连续7 d的非时序数据。每日的非时序数据包含日平均温度、日平均电价和日期类型经过one-hot编码后产生的7维的数据,一共9维数据。
(4) 门限循环单元层。设置3层的GRU单元。首先将TCN模型的输出g与输入2的输出x2进行连接,需要保证数据的维度和样本个数相同,得到数据c t。
| $ \boldsymbol{c}_{t}=f\left(\boldsymbol{x}_{(2, t)}, \boldsymbol{g}_{t}\right) $ | (7) |
式中:f表示连接操作,利用keras模型的concatenate函数实现,将时间卷积网络和输入2连接起来,作为门限循环单元的输入。
(5) 输出层。输出为预测日一天96个时间点的电力负荷预测结果y。输出层神经元个数设定为96。该层网络以Sigmoid函数作为激活函数。t时刻的输出式为:
| $ y_{t}=\sigma\left(\boldsymbol{w} \boldsymbol{h}_{t}+\boldsymbol{b}\right) $ | (8) |
式中:b为偏差向量。
2.2 优化器文中提出的TCN-GRU模型中采用Adam[24]优化器对模型的参数进行优化以减小损失。Adam是一种对随机目标函数执行一阶梯度优化的自适应优化算法,结合了AdaGrad优化器和RMSProp优化器的优点。损失函数L选取了平均绝对误差(mean absolute error,MAE)。
| $ L=\frac{1}{n} \sum\limits_{i=1}^{n}\left|\boldsymbol{y}_{i}-\hat{\boldsymbol{y}}_{i}\right| $ | (9) |
式中:n为预测日的采样点总数;yi为预测日第i个采样点的实际负荷;ŷi为预测日第i个采样点的预测负荷值。
2.3 实验评估标准实验选取平均绝对百分误差(mean absolute percentage error,MAPE)、均方误差(root mean square error,RMSE)、测试时间和决定系数R2作为模型衡量指标。MAPE可以衡量预测模型的精确度,RMSE可以体现预测平均误差的大小,R2可以表征预测模型的拟合程度。在进行负荷预测中,MAPE和RMSE的值越小,R2的值越接近于1表示模型的拟合效果越好。
| $ E_{\text {MAPE }}=\frac{1}{n} \sum\limits_{i=1}^{n} \frac{\left|\boldsymbol{y}_{i}-\hat{\boldsymbol{y}}_{i}\right|}{\boldsymbol{y}_{i}} \times 100 \% $ | (10) |
| $ E_{\mathrm{RMSE}}=\sqrt{\frac{1}{n} \sum\limits_{i=1}^{n}\left(\boldsymbol{y}_{i}-\hat{\boldsymbol{y}}_{i}\right)^{2}} $ | (11) |
| $ E_{R^{2}}=1-\frac{\sum\limits_{i=1}^{n}\left(\boldsymbol{y}_{i}-\hat{\boldsymbol{y}}_{i}\right)^{2}}{\sum\limits_{i=1}^{n}\left(\boldsymbol{y}_{i}-\overline{\boldsymbol{y}}\right)^{2}} $ | (12) |
| $ \overline{\boldsymbol{y}}=\frac{1}{n} \sum\limits_{i=1}^{n} \boldsymbol{y}_{i} $ | (13) |
式中:n为预测日的采样点总数;y i为预测日第i个采样点的实际负荷;ŷi为预测日第i个采样点的预测负荷值;y为预测日所有采样点的实际负荷平均值。
3 算例分析 3.1 实验环境文中运算使用的计算机配置为Window10系统,16 G运行内存,GTX1650显卡;采用的编程环境为PyCharm2017.1;搭建的神经网络模型为深度学习框架TensorFlow和Keras框架。
3.2 数据的选择文中选取广东省佛山市某行业2017年12个月的真实历史负荷数据作为数据集。每日设置了96个采样点,时间间隔为15 min,数据集获取96维电力负荷数据。考虑到工业用户用电情况受天气,工作日和非工作日以及电价的影响较大[14],选取了每日平均温度、日期类型、电价[25]作为其他输入。根据时序特征的特点,认定电力负荷为时序特征,每日平均温度、日期类型、电价作为非时序特征[22]。
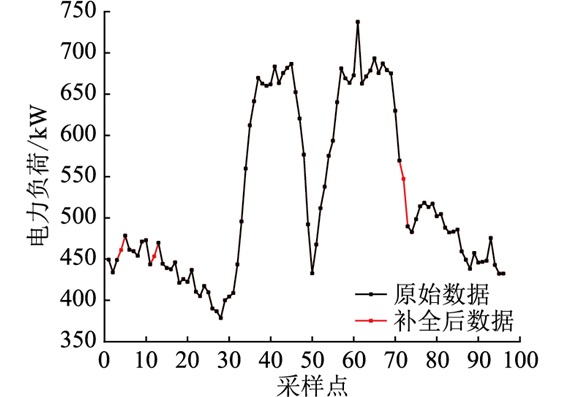
3.3 数据预处理 3.3.1 数据补全对于数据集中的数据缺失情况,文中采用均值填充的方式进行缺值填充,补全效果如图 4所示。
|
图 4 数据补全示例 Fig. 4 Example ofdata completion |
数据集中的样本数据衡量的是不同尺度的数据特征,如果直接放入模型中进行训练操作,会使模型偏向于数值较高的指标,而降低数值水平较低的指标在模型中的作用。因此,将历史负荷数据和温度数据进行归一化处理,归一化后的数据处于[0, 1]范围内。归一化xi, j′可表示为:
| $ \boldsymbol{x}_{i, j}^{\prime}=\frac{\boldsymbol{x}_{i, j}-\boldsymbol{x}_{(i, j) \min }}{\boldsymbol{x}_{(i, j) \max }-\boldsymbol{x}_{(i, j) \min }} $ | (14) |
式中:x i, j为矩量阵x的i行,j列元素值;x (i, j)min为输入数据x的最小元素值;x (i, j)max为输入数据x的最大元素值。
对于离散型数据,采用one-hot编码的方式进行预处理。比如日期类型中的周一类型可以表示为0000001。
3.3.3 数据集划分将数据集划分为训练集、测试集和验证集,其中训练集和验证集以9 ∶1比例分配,并选取2017-12-30的数据作为测试集。
3.4 TCN-GRU模型参数首先通过对比实验确定TCN-GRU模型中TCN残差单元的个数和GRU神经网络的网络层数。设定模型迭代次数均为500次,GRU模型中每层神经元个数为256个,TCN中扩张系数以2的倍数叠加。在设置不同残差单元的个数和GRU神经网络的网络层数时,模型的预测效果如表 1所示。
|
|
表 1 TCN-GRU参数比较 Table 1 Comparison of TCN-GRU model |
由表 1中数据可以得出:当残差单元的个数设置为2,GRU神经网络的网络层数设置为3时,预测效果最好。
3.5 预测结果对比为了验证模型的性能,实验将TCN-GRU模型与GRU模型、LSTM模型、TCN模型、深度神经网络(deep neural networks, DNN)模型进行了对比训练,其中GRU模型、LSTM模型、TCN模型、DNN模型的网络层数统一设置为3层。利用广东省佛山市的电力负荷数据集对模型进行训练,并利用训练好的模型对2017-12-30广东省佛山市某行业的电力负荷进行预测,预测效果如表 2所示。
|
|
表 2 模型对比 Table 2 Comparison of five models |
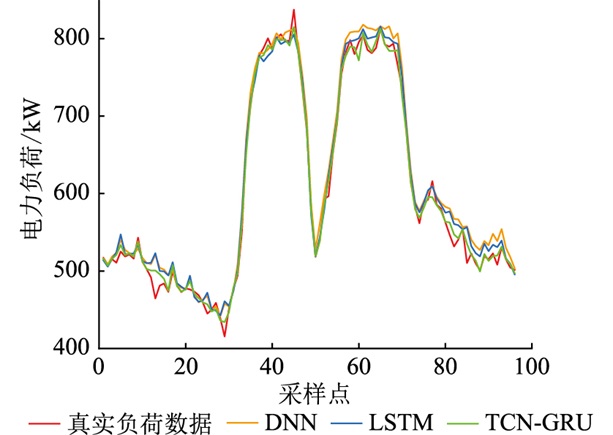
由表 2可知,TCN-GRU模型的MAPE值为1.75%,和现有的常用于负荷预测的深度学习模型相比,取得了更好的预测精度,对比单模型TCN模型和GRU模型,准确度也得到了提升。DNN模型和LSTM模型的预测效果与文中模型进行对比,如图 5所示。
|
图 5 预测结果对比 Fig. 5 Comparison of load forecasting results |
由图 5可以发现,文中预测曲线更加贴近真实负荷数据曲线,特别是几个高峰点和低谷点拟合效果更佳。
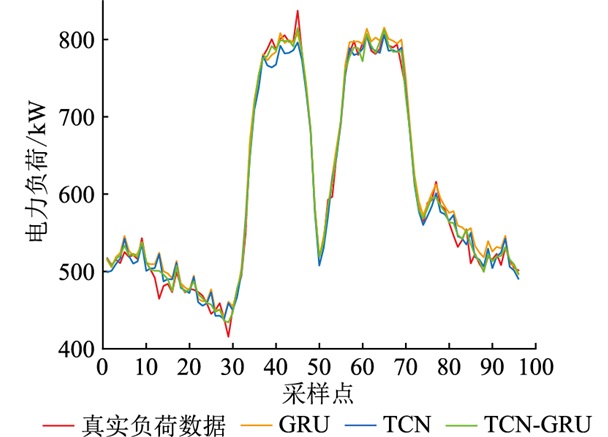
图 6对比了文中TCN-GRU预测模型和单模型之间的预测曲线。从图中可以得出文中提出的TCN-GRU模型预测效果要优于单模型TCN和GRU。
|
图 6 预测结果对比 Fig. 6 Comparison of load forecasting results |
对电力负荷的短期预测往往只考虑输入数据的时序特性或者不考虑输入数据之间的时序关系。文中提出的基于TCN-GRU模型的短期负荷预测方法兼顾数据的时序特性和非时序特征。首先该方法通过TCN模型提取时序数据的时间序列特征;然后结合非时序特征以组成新的数据集;最后利用GRU模型的非线性拟合能力以及深度学习能力对电力负荷进行预测。相较于经典的深度学习模型GRU、LSTM等模型,文中提出的TCN-GRU模型取得了更高的预测准确率,为电网系统提供了更加精确的预测结果,也为电网系统灵活调节供电量提供了更加可靠的依据。
未来将在以下几个方面进行深入研究:(1) 文中研究目标为单一的电力负荷数据,考虑将该模型应用于综合能源的负荷预测之中;(2) 文中研究输入数据为单一的负荷数据,考虑将空间特征引入短期负荷预测。
| [1] |
孙庆凯, 王小君, 张义志, 等. 基于LSTM和多任务学习的综合能源系统多元负荷预测[J]. 电力系统自动化, 2021, 45(5): 63-70. SUN Qingkai, WANG Xiaojun, ZHANG Yizhi, et al. Multiple load prediction of integrated energy system based on long short-term memory and multi-task learning[J]. Automation of Electric Power Systems, 2021, 45(5): 63-70. (  0) 0) |
| [2] |
何忠华, 张涛, 胡娱欧, 等. 考虑大气污染防治措施影响的短期电力负荷预测模型研究[J]. 智慧电力, 2019, 47(5): 1-9. HE Zhonghua, ZHANG Tao, HU Yuou, et al. Short-term electric load forecasting model considering the influence of air pollution prevention and control policy[J]. Smart Power, 2019, 47(5): 1-9. DOI:10.3969/j.issn.1673-7598.2019.05.001 (  0) 0) |
| [3] |
HUANG S J, SHIH K R. Short-term load forecasting via ARMA model identification including non-Gaussian process considerations[J]. IEEE Transactions on Power Systems, 2003, 18(2): 673-679. DOI:10.1109/TPWRS.2003.811010 (  0) 0) |
| [4] |
PAPPAS S S, EKONOMOU L, KARAMPELASP, et al. Electricity demand load forecasting of the Hellenic power system using an ARMA model[J]. Electric Power Systems Research, 2010, 80(3): 256-264. DOI:10.1016/j.epsr.2009.09.006 (  0) 0) |
| [5] |
KAWASHIMA M, DORGAN C E, MITCHELL J W. Hourly thermal load prediction for the next 24 hours by Arima, Ewma, LR, and an artificial neural network[J]. ASHRAE Transactions, 1995(1): 186-200. (  0) 0) |
| [6] |
赵峰, 孙波, 张承慧. 基于多变量相空间重构和卡尔曼滤波的冷热电联供系统负荷预测方法[J]. 中国电机工程学报, 2016, 36(2): 399-406. ZHAO Feng, SUN Bo, ZHANG Chenghui. Cooling, heating and electrical load forecasting method for CCHP system based on multivariate phase space reconstruction and Kalman filter[J]. Proceedings of the CSEE, 2016, 36(2): 399-406. (  0) 0) |
| [7] |
赵倩, 黄景涛. 基于EMD-SA-SVR的超短期风电功率预测研究[J]. 电力系统保护与控制, 2020, 48(4): 89-96. ZHAO Qian, HUANG Jingtao. On ultra-short-term wind power prediction based on EMD-SA-SVR[J]. Power System Protection and Control, 2020, 48(4): 89-96. (  0) 0) |
| [8] |
王义军, 李殿文, 高超, 等. 基于改进的PSO-SVM的短期电力负荷预测[J]. 电测与仪表, 2015, 52(3): 22-25. WANG Yijun, LI Dianwen, GAO Chao, et al. Short-term power load forecasting based on improved PSO-SVM[J]. Electrical Measurement & Instrumentation, 2015, 52(3): 22-25. DOI:10.3969/j.issn.1001-1390.2015.03.005 (  0) 0) |
| [9] |
王文秀, 田世明, 王泽忠, 等. 一种基于贝叶斯网络的电力负荷峰值预测方法[J]. 供用电, 2019, 36(7): 57-64. WANG Wenxiu, TIAN Shiming, WANG Zezhong, et al. A power peak load forecasting method based on Bayesian network[J]. Distribution & Utilization, 2019, 36(7): 57-64. (  0) 0) |
| [10] |
李焱, 贾雅君, 李磊, 等. 基于随机森林算法的短期电力负荷预测[J]. 电力系统保护与控制, 2020, 48(21): 117-124. LI Yan, JIA Yajun, LI Lei, et al. Short term power load forecasting based on a stochastic forest algorithm[J]. Power System Protection and Control, 2020, 48(21): 117-124. (  0) 0) |
| [11] |
张刚, 刘福潮, 王维洲, 等. 电网短期负荷预测的BP-ANN方法及应用[J]. 电力建设, 2014, 35(3): 54-58. ZHANG Gang, LIU Fuchao, WANG Weizhou, et al. BP-ANN method for power grid short-term load forecasting and its application[J]. Electric Power Construction, 2014, 35(3): 54-58. (  0) 0) |
| [12] |
ZHENG J, XU C C, ZHANG ZA, et al. Electric load forecasting in smart grids using Long-Short-Term-Memory based Recurrent Neural Network[C]//2017 51st Annual Conference on Information Sciences and Systems (CISS). Baltimore, MD. IEEE, 2017: 1-6.
(  0) 0) |
| [13] |
MUZAFFAR S, AFSHARI A. Short-term load forecasts using LSTM networks[J]. Energy Procedia, 2019, 158: 2922-2927. DOI:10.1016/j.egypro.2019.01.952 (  0) 0) |
| [14] |
陆继翔, 张琪培, 杨志宏, 等. 基于CNN-LSTM混合神经网络模型的短期负荷预测方法[J]. 电力系统自动化, 2019, 43(8): 131-137. LU Jixiang, ZHANG Qipei, YANG Zhihong, et al. Short-term load forecasting method based on CNN-LSTM hybrid neural network model[J]. Automation of Electric Power Systems, 2019, 43(8): 131-137. (  0) 0) |
| [15] |
王克杰, 张瑞. 基于改进BP神经网络的短期电力负荷预测方法研究[J]. 电测与仪表, 2019, 56(24): 115-121. WANG Kejie, ZHANG Rui. Research on short-term power load forecasting method based on improved BP neural network[J]. Electrical Measurement & Instrumentation, 2019, 56(24): 115-121. (  0) 0) |
| [16] |
汪欣, 蔡旭, 李征. 结合交叉局部异常因子和注意力机制的超短期风电功率预测方法[J]. 电力系统保护与控制, 2020, 48(23): 92-99. WANG Xin, CAI Xu, LI Zheng. Ultra-short-term wind power forecasting method based on a cross LOF preprocessing algorithm and an attention mechanism[J]. Power System Protection and Control, 2020, 48(23): 92-99. (  0) 0) |
| [17] |
GAO X Y, WANG Y, GAOY, et al. Short-term load forecasting model of GRU network based on deep learning framework[C]//2018 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2). Beijing, China. IEEE, 2018: 1-4.
(  0) 0) |
| [18] |
WAN R Z, MEI S P, WANGJ, et al. Multivariate temporal convolutional network: a deep neural networks approach for multivariate time series forecasting[J]. Electronics, 2019, 8(8): 876. DOI:10.3390/electronics8080876 (  0) 0) |
| [19] |
HE K M, ZHANG X Y, REN SQ, et al. Deep residual learning for image recognition[C]//2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Las Vegas, NV, USA. IEEE, 2016: 770-778.
(  0) 0) |
| [20] |
邓带雨, 李坚, 张真源, 等. 基于EEMD-GRU-MLR的短期电力负荷预测[J]. 电网技术, 2020, 44(2): 593-602. DENG Daiyu, LI Jian, ZHANG Zhenyuan, et al. Short-term electric load forecasting based on EEMD-GRU-MLR[J]. Power System Technology, 2020, 44(2): 593-602. (  0) 0) |
| [21] |
CHO K, VAN MERRIENBOER B, BAHDANAUD, et al. On the properties of neural machine translation: encoder-decoder approaches[C]//Proceedings of SSST-8, Eighth Workshop on Syntax, Semantics and Structure in Statistical Translation. Doha, Qatar. Stroudsburg, PA, USA: Association for Computational Linguistics, 2014: 103-111.
(  0) 0) |
| [22] |
王增平, 赵兵, 纪维佳, 等. 基于GRU-NN模型的短期负荷预测方法[J]. 电力系统自动化, 2019, 43(5): 53-58. WANG Zengping, ZHAO Bing, JI Weijia, et al. Short-term load forecasting method based on GRU-NN model[J]. Automation of Electric Power Systems, 2019, 43(5): 53-58. (  0) 0) |
| [23] |
WANG Y S, LIAO W L, CHANG Y Q. Gated recurrent unit network-based short-term photovoltaic forecasting[J]. Energies, 2018, 11(8): 2163. (  0) 0) |
| [24] |
YU A W, DOHAN D, LUONG MT, et al. QANet: combining local convolution with global self-attention for reading comprehension[EB/OL]. 2018.
(  0) 0) |
| [25] |
李鹏, 何帅, 韩鹏飞, 等. 基于长短期记忆的实时电价条件下智能电网短期负荷预测[J]. 电网技术, 2018, 42(12): 4045-4052. LI Peng, HE Shuai, HAN Pengfei, et al. Short-term load forecasting of smart grid based on long-short-term memory recurrent neural networks in condition of real-time electricity price[J]. Power System Technology, 2018, 42(12): 4045-4052. (  0) 0) |
2. School of Electrical Engineering, Southeast University, Nanjing 210096, China
 2021, Vol. 40
2021, Vol. 40


 郭玲(1996),女,硕士在读,研究方向为深度学习和智能电网技术(E-mail:
郭玲(1996),女,硕士在读,研究方向为深度学习和智能电网技术(E-mail: