文章编号: 2096-3203(2021)03-0007-08 中图分类号: TM912.6
2. 国网江苏省电力有限公司电力科学研究院,江苏 南京 211103
近年来,随着锂离子电池技术的不断发展,追求高能量密度、高功率密度、长续航能力电池的脚步从未停歇,而随着大规模储能系统广泛应用于输电、发电、配电、用电等电力服务领域,其安全性越来越受到各界的关注[1—5]。电池管理系统(battery management system,BMS)是电池储能系统必不可少的组成部分,承担电池运行状态监控、故障诊断、故障预警、安全保护、能量管理及均衡等任务[6—7]。储能系统BMS一般采用主从结构,从机为固定数量的单体串联构成的模组(一般12个单体),根据单体电压及电流计算各单体的荷电状态(state of charge,SOC);主机将各个从机信息汇总后计算得到电池堆或者电池簇的SOC(一般由SOC最高和SOC最低单体限定)[8—9]。BMS性能优劣一定程度上决定了电池储能系统的安全性和可靠性[10—11]。
BMS相互测试研究吸引了众多学者的关注。文献[12—13]采用基于Labview的集成开发,硬件采用基于面向仪器系统的PCI扩展(peripheral component interconnection extensions for instrumentation,PXI)的构架平台,形成了一套大功率电池管理自动测试平台;文献[14]运用现场可编程逻辑门阵列(field programmable gate array,FPGA)和ARM(Advanced RISC Machine)构建BMS测试装置,提出BMS的集约化、智能化和低功耗测试方案;文献[15—16]针对电动汽车用BMS产品出厂检测需求,开发了一套模块化集成电动汽车BMS自动检测平台,推进了行业标准化的进程。
综合上述研究成果,对于BMS的测试标准大多局限于电动汽车BMS,暂时还没有针对电池储能系统BMS准入规范与测试标准,且SOC估计方法的准确性尤其重要。现有的SOC估计方法有开路电压法、安时积分法、卡尔曼滤波法(Kalman filtering,KF)和扩展卡尔曼滤波法[17—19](extended Kalman filtering,EKF)。其中,开路电压法需要电池长时间静置;安时积分法需要准确的初始值;KF和EKF都需要离线获取电池模型的参数。文献[20—21]提出基于数据模型融合的SOC估计方法,通过结合EKF和在线数据驱动的参数辨识方法可以实现电池状态和模型参数的在线估计,提高了估计的精度。现有的SOC估计方法研究大多应用于电动汽车BMS中,关注电池参数的在线获取, 在有限的处理器运算条件下以简化计算量的方式实现信息采集和SOC状态估计。储能电站BMS入网测试平台更倾向于在上位机利用高精度测量数据实现精确SOC估计,从而校准被测BMS的SOC估计精度。因此,文中以应用于储能系统BMS的测试平台为基础,对SOC估计方法进行研究。
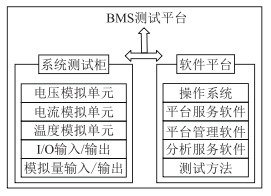
1 储能用BMS测试平台构成BMS测试平台构建主要包括硬件平台和软件平台两部分,其系统结构示意如图 1所示。其中硬件平台主要包含工控机、系统测试机柜以及通信接口等;软件平台包含人机交互界面、测试逻辑流程、测试数据处理与分析以及报表生成等。
|
图 1 BMS测试平台结构示意 Fig. 1 Schematic diagram of structure of BMS test system |
为了准确掌握电池当前状态,防止电池过充、过放,BMS需要对锂电池SOC进行准确估计,因此电池测试平台需要更高的SOC估计精度。考虑到电池模型参数会影响电池状态估计的精度问题,文中拟利用双扩展卡尔曼滤波(dual extended Kalman filter,DEKF)算法在线估计模型参数,提高SOC估计精度。
2 基于DEKF的SOC估计方法 2.1 储能电池系统模型的建立电池模型的建立是估计SOC的基础,等效电路模型是根据电池的外部特性,通过受控电压源、电阻、电容等电气元件建立的电池模型。等效电路模型具有结构简单、参数获取方便和易于实现锂电池模拟等优点,得到了广泛应用。
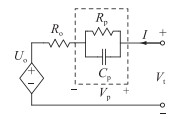
在考虑模型效果和模型复杂程度等因素后,选择现在使用最为广泛的Thevenin等效电路模型作为文中使用的锂电池模型,如图 2所示。
|
图 2 Thevenin模型示意 Fig. 2 Schematic diagram of the Thevenin model |
Thevenin等效电路模型的数学表达式如下:
| $ \left\{\begin{array}{l} C_{\mathrm{p}} \frac{\mathrm{d} V_{\mathrm{p}}}{\mathrm{d} t}+\frac{V_{\mathrm{p}}}{R_{\mathrm{p}}}=I \\ V_{\mathrm{t}}=U_{\mathrm{o}}+V_{\mathrm{p}}+I R_{\mathrm{o}} \end{array}\right. $ | (1) |
式中:Uo为电池的开路电压,可以表示为SOC的函数(详见3.2模型参数辨识部分);Ro为电池欧姆内阻;Rp为电池极化内阻;Cp为电池极化电容;Vp为极化电压;I为电池工作电流,充电为正;Vt为电池端电压。
对式(1)进行离散化可得式(2)和式(3)。
| $ V_{\mathrm{p}}(k+1)=V_{\mathrm{p}}(k) \mathrm{e}^{-\frac{t_{\mathrm{s}}}{R_{\mathrm{p}} C_{\mathrm{p}}}}+I(k-1) R_{\mathrm{p}}\left(1-\mathrm{e}^{-\frac{t_{\mathrm{s}}}{R_{\mathrm{p}} C_{\mathrm{p}}}}\right) $ | (2) |
| $ V_{\mathrm{t}}(k+1)=U_{\mathrm{o}}(k)+V_{\mathrm{p}}(k)+I(k) R_{\mathrm{o}} $ | (3) |
式中:ts为采样时间。
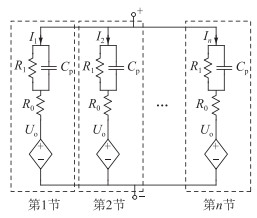
为获得储能电池系统模型,假定单体电池间具有相同参数,即单体完全相同,那么n节电池并联模型示意见图 3,Ii为第i节电池的端电流。根据假设单体完全一致,因此流过每节电池的电流相等,n节电池并联可以看作是容量为n倍的单体电池。
|
图 3 n节电池并联模型示意 Fig. 3 Schematic diagram of n cells in parallel connection model |
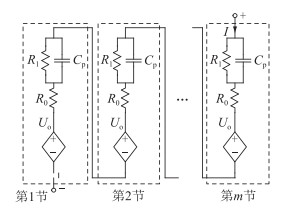
基于同样假设,m节电池串联模型示意如图 4所示。串联情况下流过电池的电流相同,由于电池单体完全一致,因此串联成组后的电压可以看作是电压m倍的单体电池电压。
|
图 4 m节电池串联模型示意 Fig. 4 Schematic diagram of m cells in series connection model |
由此可见,文中通过单体的串联和并联构建了电池储能系统模型,对于一个n×m的电池储能系统(n为并联数,m为串联数),可以将储能系统看作容量为单体容量的n倍、最大电流为单体最大电流的n倍、总电压为单体电压的m倍的储能系统。
2.2 DEKF算法步骤KF是一种高效率的递归滤波器,能根据一系列含有噪声的测量信号估计出动态线性系统的状态。为能将KF运用到非线性系统中,对非线性系统进行线性化,然后进行KF,形成了EKF。由于KF的基本方程是时间域内的递推形式,其计算过程是一个不断“预测-修正”的过程,在求解时不要求存储大量数据,并且一旦观测到新的数据,随即可以计算新的滤波值,因此这种滤波方法非常适用于数据实时处理和计算机编程。DEKF是运用2个EKF对系统的状态以及模型的参数同时进行估计。
假定非线性离散状态空间模型:
| $ \left\{\begin{array}{l} \boldsymbol{x}_{k}=f\left(\boldsymbol{x}_{k-1}, \boldsymbol{\theta}_{k-1}, \boldsymbol{u}_{k-1}\right)+\boldsymbol{\omega}_{k-1} \\ \boldsymbol{z}_{k}=h\left(\boldsymbol{x}_{k-1}, \boldsymbol{\theta}_{k-1}, \boldsymbol{u}_{k-1}\right)+\boldsymbol{v}_{k-1} \end{array}\right. $ | (4) |
式中:xk为状态向量;f(xk-1, θk-1, uk-1)为过程方程;θk-1为模型参数向量;uk-1为输入向量;ωk-1为过程激励噪声;zk为观测向量;h(xk-1, θk-1, uk-1)为观测方程;vk-1为观测噪声。
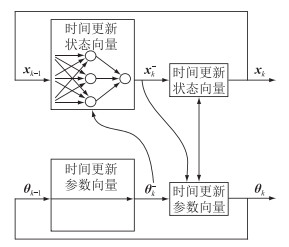
DEKF的结构框图如图 5所示。
|
图 5 DEKF的结构 Fig. 5 Block diagram of DEKF |
由图 5可知,DEKF具有2个EKF,一个用于估计状态向量,另一个用于估计模型参数向量,2个EKF同时运行。在每个时间步长内,EKF状态滤波器都会使用当前模型参数估计值估计状态,而EKF参数滤波器会使用当前状态估计值估计模型参数。
DEKF的具体步骤如下:
(1) 向前推算参数向量:
| $ \boldsymbol{\theta}_{k}^{-}=\boldsymbol{\theta}_{k-1} $ | (5) |
(2) 向前推算参数向量误差协方差:
| $ \boldsymbol{P}_{\theta, k}^{-}=\boldsymbol{P}_{\theta, k-1}+\boldsymbol{Q}_{\theta} $ | (6) |
(3) 向前推算状态向量:
| $ \boldsymbol{x}_{k}^{-}=f\left(\boldsymbol{x}_{k-1}, \boldsymbol{\theta}_{k-1}, \boldsymbol{u}_{k-1}\right) $ | (7) |
(4) 向前推算状态向量误差协方差:
| $ \boldsymbol{P}_{x, k}^{-}=\boldsymbol{A}_{x} \boldsymbol{P}_{x, k-1} \boldsymbol{A}_{x}^{\mathrm{T}}+\boldsymbol{Q}_{x} $ | (8) |
(5) 计算状态向量的卡尔曼增益:
| $ \boldsymbol{K}_{x, k}=\boldsymbol{P}_{x, k}^{-} \boldsymbol{H}_{x}^{\mathrm{T}}\left(\boldsymbol{H}_{x} \boldsymbol{P}_{x, k}^{-} \boldsymbol{H}_{x}^{\mathrm{T}}+\boldsymbol{R}_{x}\right)^{-1} $ | (9) |
(6) 由观测变量更新状态向量估计:
| $ \boldsymbol{x}_{k}=\boldsymbol{x}_{k}^{-}+\boldsymbol{K}_{x, k}\left(\boldsymbol{Z}_{k}-\boldsymbol{H}_{x} \boldsymbol{x}_{-{ }_{k}}\right) $ | (10) |
(7) 更新状态向量误差协方差:
| $ \boldsymbol{P}_{x, k}=\left(\boldsymbol{E}-\boldsymbol{K}_{x, k} \boldsymbol{H}_{x}\right) \boldsymbol{P}_{x, k}^{-} $ | (11) |
(8) 计算参数向量的卡尔曼增益:
| $ \boldsymbol{K}_{\theta, k}=\boldsymbol{P}_{\theta, k}^{-} \boldsymbol{H}_{\theta}^{\mathrm{T}}\left(\boldsymbol{H}_{\theta} \boldsymbol{P}_{\theta, k}^{-} \boldsymbol{H}_{\theta}^{\mathrm{T}}+\boldsymbol{R}_{\theta}\right)^{-1} $ | (12) |
(9) 由观测变量更新参数向量估计:
| $ \boldsymbol{\theta}_{k}=\boldsymbol{\theta}_{k}^{-}+\boldsymbol{K}_{\theta, k}\left(\boldsymbol{Z}_{k}-\boldsymbol{H}_{x} \boldsymbol{x}_{-_{k}}\right) $ | (13) |
(10) 更新参数向量误差协方差:
| $ \boldsymbol{P}_{\theta, k}=\left(\boldsymbol{E}-\boldsymbol{K}_{\theta, k} \boldsymbol{H}_{\theta}\right) \boldsymbol{P}_{\theta, k}^{-} $ | (14) |
式中:Qθ为参数向量的过程激励噪声协方差矩阵;Qx为状态向量的过程激励噪声协方差矩阵;Rx为状态向量的观测噪声协方差矩阵;Rθ为参数向量的观测噪声协方差矩阵;θ-,θ分别为参数向量先验估计和后验估计;x-,x分别为状态向量先验估计和后验估计;Pθ-,Pθ分别为参数向量先验协方差矩阵和后验协方差矩阵;Px-,Px分别为状态向量先验协方差矩阵和后验协方差矩阵;Kθ,Kx分别为参数向量卡尔曼增益和状态向量卡尔曼增益;E为单位矩阵;Ax,Hx,Hθ为系数矩阵,表达式见式(15)—式(19)。
| $ \boldsymbol{A}_{x}=\frac{\partial f\left(\boldsymbol{x}_{k-1}, \boldsymbol{\theta}_{k-1}, \boldsymbol{u}_{k-1}\right)}{\partial \boldsymbol{x}} $ | (15) |
| $ \boldsymbol{H}_{x}=\frac{\partial h\left(\boldsymbol{x}_{k}^{-}, \boldsymbol{\theta}_{k-1}, \boldsymbol{u}_{k-1}\right)}{\partial \boldsymbol{x}} $ | (16) |
| $ \begin{gathered} \boldsymbol{H}_{\theta}=\frac{\mathrm{d} h\left(\boldsymbol{x}_{k}^{-}, \boldsymbol{\theta}_{k}^{-}, \boldsymbol{u}_{k-1}\right)}{\mathrm{d} \boldsymbol{\theta}}= \\ \frac{\partial h\left(\boldsymbol{x}_{k}^{-}, \boldsymbol{\theta}_{k}^{-}, \boldsymbol{u}_{k-1}\right)}{\partial \boldsymbol{\theta}}+\frac{\partial h\left(\boldsymbol{x}_{k}^{-}, \boldsymbol{\theta}_{k}^{-}, \boldsymbol{u}_{k-1}\right)}{\partial \boldsymbol{x}_{k}^{-}} \frac{\mathrm{d} \boldsymbol{x}_{k}^{-}}{\mathrm{d} \boldsymbol{\theta}} \end{gathered} $ | (17) |
| $ \begin{gathered} \frac{\mathrm{d} \boldsymbol{x}_{k}^{-}}{\mathrm{d} \boldsymbol{\theta}}=\frac{\mathrm{d} f\left(\boldsymbol{x}_{k-1}, \boldsymbol{\theta}_{k}^{-}, \boldsymbol{u}_{k-1}\right)}{\mathrm{d} \boldsymbol{\theta}}= \\ \frac{\partial f\left(\boldsymbol{x}_{k-1}, \boldsymbol{\theta}_{k}^{-}, \boldsymbol{u}_{k-1}\right)}{\partial \boldsymbol{\theta}}+\frac{\partial f\left(\boldsymbol{x}_{k-1}, \boldsymbol{\theta}_{k}^{-}, \boldsymbol{u}_{k-1}\right)}{\partial \boldsymbol{x}_{k-1}} \frac{\mathrm{d} \boldsymbol{x}_{k-1}}{\mathrm{~d} \boldsymbol{\theta}} \end{gathered} $ | (18) |
| $ \frac{\mathrm{d} \boldsymbol{x}_{k-1}}{\mathrm{~d} \boldsymbol{\theta}}=\frac{\mathrm{d} \boldsymbol{x}_{k-1}^{-}}{\mathrm{d} \boldsymbol{\theta}}-\boldsymbol{K}_{x, k-1} \frac{\mathrm{d} h\left(\boldsymbol{x}_{k-1}^{-}, \boldsymbol{\theta}_{k}^{-}, \boldsymbol{u}_{k-1}\right)}{\mathrm{d} \boldsymbol{\theta}} $ | (19) |
安时积分法计算SOC会受到初始误差和计算过程中的累计误差影响。KF算法能够准确估计SOC的原理是:KF在安时积分法的基础上对SOC进行预测的同时,还通过电池模型的输出电压与实际测得的电压值进行比较,将比较的误差乘以卡尔曼增益作为SOC的修正部分,因此可以在存在初始SOC误差和累计误差的情况下修正SOC,减小误差,以保证准确估计SOC。
根据2.1节的假设,单体之间完全一致,即通过串并联组合就可以实现储能电站系统的扩展。为了能够利用DEKF算法估计储能电站SOC,需要选取状态向量和参数向量,获取对应的过程方程。以单体电池为例观测量为电池的端电压,DEKF算法的观测方程如式(20)所示。
| $ V_{\mathrm{t}}(k)=U_{\mathrm{o}}+V_{\mathrm{p}}(k)+I(k) R_{\mathrm{o}} $ | (20) |
可以看出,式(20)中还存在极化电压这一项,极化电压会随着电流的变化快速变化。为了得到准确的端电压,极化电压选为状态变量,单体SOC作为需要估计的值,也选为状态变量。
由安时积分法可得出单体SOC表达式:
| $ Z=Z_{0}+\int \frac{\eta I t}{C_{\mathrm{N}}} \mathrm{d} t $ | (21) |
式中:Z为当前单体电池SOC的值;Z0为电池SOC的初始值;η为库伦效率;I为流过单体的电流值;t为采样时间;CN为额定容量。
而对于n×m的电池储能系统而言,电流为n倍的I,额定容量为n倍的CN,在安时积分法中等式的右侧的第二项与单体电池相等,电池储能系统和单体电池SOC的初始值也是相等的。因此,在单体一致性相同假设前提下,整个电池储能系统与单体电池的SOC也是相等的。
根据式(2)和式(21)可以得到状态向量的过程方程,如式(22)所示。
| $ \begin{array}{c} {\left[\begin{array}{l} V_{\mathrm{p}}(k) \\ Z(k) \end{array}\right]=\left[\begin{array}{cc} \mathrm{e}^{-\frac{t_{\mathrm{s}}}{R_{\mathrm{p}}{C}_{\mathrm{p}}}} & 0 \\ 0 & 1 \end{array}\right]\left[\begin{array}{l} V_{\mathrm{p}}(k-1) \\ Z(k-1) \end{array}\right]+} \\ {\left[\begin{array}{c} \left(1-\mathrm{e}^{-\frac{t_{\mathrm{s}}}{R_{\mathrm{p}}{C}_{\mathrm{p}}}}\right) R_{\mathrm{P}} \\ -\frac{\eta t_{\mathrm{s}}}{Q_{\mathrm{N}}} \end{array}\right] I(k-1)} \end{array} $ | (22) |
根据2.1中的电池模型,将剩余的参数Ro、Rp和Cp选作模型参数向量,由于模型参数变化缓慢的特性,参数向量可以认定为在一个采样周期前后数值不发生变化。理论上,该方法同样适用于其他类型电池,只要构建相应的电池模型、观测方程和系统过程方程就可以运用该方法实现SOC估计。
3 实验验证 3.1 实验对象和实验设备根据2.1节对电池串并联的分析,储能电池系统为n×m的电池单体阵列,可将其看作是容量为n倍、电流为n倍和电压为m倍的单体电池。文中以单体电池为研究对象,根据2.3节推导实现储能电池系统的SOC估计。文中选取单体电池为三元锂电池,型号为ISR18650-2.2 A ·h,标称电压为3.6 V,额定容量为2.2 A ·h,电压范围为2.75~4.2 V。
实验设备选用Arbin电池测试系统,通道电压范围为2~60 V,电流量程为10 A。该设备电压和电流精度可达到0.2‰,将其测得的值作为实验的真值。
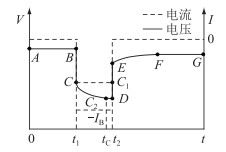
3.2 电池模型离线参数辨识Thevenin等效电路模型包含了4个参数,其中Ro、Rp和Cp在文中提出的方法中是在线估计,这里离线估计主要用于为算法实现提供必要的数据支撑。参数离线辨识采用使用最为广泛的混合动力脉冲能力特性(hybrid power pulse characterization,HPPC)测试实验。对电池施加脉冲电流,根据电池端电压的响应来获取电池当前状态下的参数,电压、电流示意曲线如图 6所示。
|
图 6 脉冲电流和电压曲线 Fig. 6 The curve of pulse current and voltage |
在0-t1时刻,电池处于长时间静置,内部处于平衡状态;在t1-t2时刻,在电池的两端施加一个负的电流脉冲,幅值为IB;在t2-t时刻电池处于静置状态。根据Thevenin等效电路模型可以得出,在施加电流的瞬间,电池端电压的降落是由欧姆内阻引起的,则可以得出Ro如式(23)所示。
| $ R_{\mathrm{o}}=\left|\frac{U_{\mathrm{AB}}}{I_{\mathrm{B}}}\right| $ | (23) |
式中:UAB为A、B两点的电压差。C、D两点的电压差是由极化电阻引起,因此可以得出Rp为:
| $ R_{\mathrm{p}}=\left|\frac{U_{\mathrm{CD}}}{I_{\mathrm{B}}}\right| $ | (24) |
其中,UCD为C、D两点的电压差。根据式(2)可以得出,在零状态响应下,极化电压在3τ时刻达到最大值的95%,τ为RP和CP的乘积。因此可以得出CP如式(25)所示。
| $ C_{\mathrm{p}}=\frac{\tau}{R_{\mathrm{p}}} $ | (25) |
式中:C、C2点之间的电压差是C、D点电压差的95%;3τ为tC和t1的时刻差。
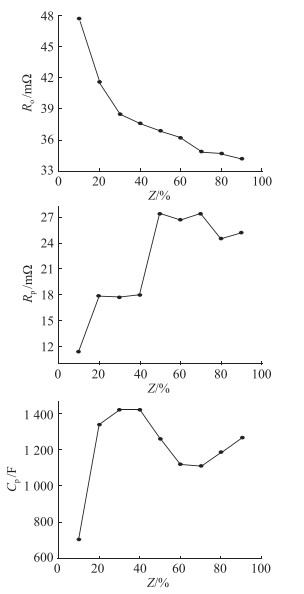
以10%的电量作为间隔点,依次进行HPPC测试实验可以得到模型参数和SOC的对照点,实验结果如图 7所示。
|
图 7 电池模型参数 Fig. 7 Battery model parameters |
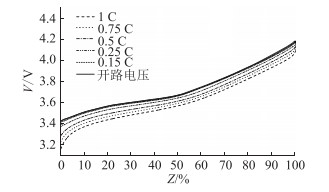
根据开路电压法可知,长时间静置下得到的开路电压(open circuit voltage,OCV)与SOC之间存在一一对应的关系。OCV和SOC的对应关系可以通过HPPC测试实验获得,但获取的只有某些点的对应关系,想要获得准确的关系就需要减小SOC的间隔点,这会需要很长的实验时间。文中采用1 C,0.75 C,0.5 C,0.25 C,0.1 C倍率的放电曲线,通过外推法[22]得出开路电压放电曲线,也就是电池的SOC-OCV曲线,如图 8所示。
|
图 8 SOC-OCV曲线 Fig. 8 The curve of SOC-OCV |
通过取1 C,0.75 C,0.5 C,0.25 C,0.1 C倍率曲线上相同SOC值的电压值,利用最小二乘法对放电倍率和电压值进行直线拟合,直线与电压轴交点的电压值为无电流时对应的电压值,即为开路电压。
多项式拟合SOC-OCV曲线需要较高阶次的多项式才能达到较好的拟合效果,且在某些点处的误差会比较大。因此,文中选择以0.5%的电量间隔大小设计SOC-OCV表格,以查表的方式获得OCV。查表过程中,中间值通过线性插值的方法获得。
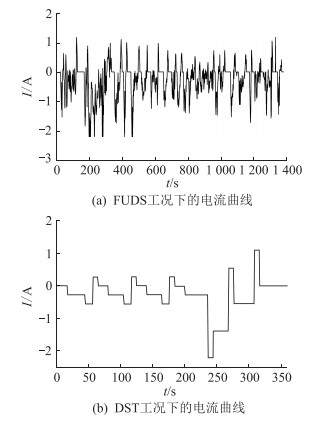
3.3 工况验证实验文中采用美国联邦城市运行工况(federal urban driving schedule,FUDS)和动态应力测试工况(dynamic stress test,DST)测试数据,一个周期内的电流值如图 9所示。
|
图 9 测试工况电流曲线 Fig. 9 Test current curves under two working conditions |
实验在25 ℃条件下进行,电池在充满后,以0.5 C放电,放出10%的电量,再以工况电流运行,放出90%的电量,最后静置30 min,电压采样时间为1 s。
3.4 实验结果分析为了验证所提出SOC估计方法的实际效果,文中的算法程序由Matlab语言编写,处理器为i5-4200H@2.80 GHz,内存为6 GB。在电池端电压已知的情况下,平均每个SOC点的计算时间为5.6×10-5 s。对于需要频繁调用的储能电站,SOC的计算速度也可以满足要求。
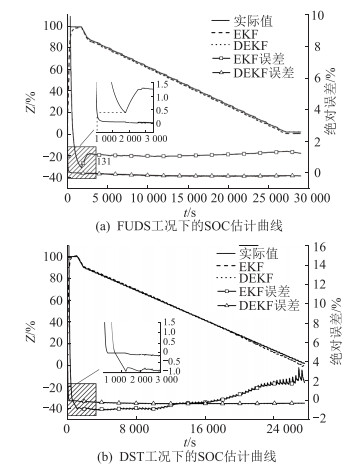
为了验证DEKF估计SOC的效果,文中增加了EKF算法估计SOC,EKF算法选取的状态变量为SOC和极化电压,模型的参数来自表2。DEKF和EKF的初始SOC设定为0,此时SOC估计的绝对误差为最大值100%。DEKF和EKF估计SOC的结果见图 10,DEKF估计的端电压曲线见图 11。
|
图 10 SOC估计曲线 Fig. 10 The curves of SOC estimation |
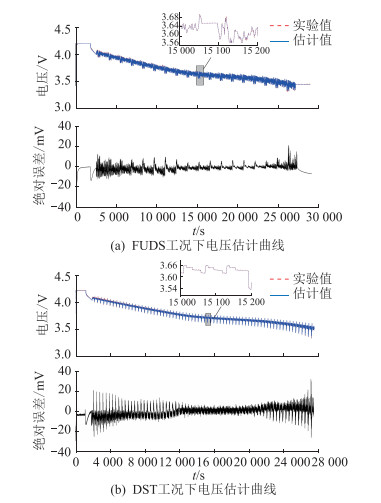
|
图 11 不同工况下电池端电压实验对比曲线 Fig. 11 The curves of battery SOC estimation under different conditions |
由图 10可以看出,DEKF和EKF估计的SOC曲线与实际曲线都很贴近,在FDUS工况实验下,EKF估计的SOC在稳定后的绝对误差在2%以内,DEKF在1%以内。在DST工况实验下,EKF估计的SOC在稳定后的绝对误差在4%以内,DEKF在1%以内。从图 10(a)和图 10(b)中的放大区域可以看出,在初始的一段时间内,EKF和DEKF的绝对误差都迅速减小,但DEKF误差收敛速度要远大于EKF。
由图 11可以看出,端电压的估计值与实际值基本一致。在FUDS工况实验下,绝对误差范围基本都在±10 mV以内,平均绝对误差为2.7 mV;在DST工况实验下,绝对误差范围基本都在在±20 mV以内,平均绝对误差为3.8 mV。绝对误差较大的地方出现在刚开始放电区域和最后结束放电区域,前者误差大是因为模型参数的初始值选择与实际值有所偏差,造成较大误差,但随着实验的继续,模型参数的误差渐渐减小,端电压的误差也逐渐减小;后者一方面是因为模型参数在SOC处于较低区域内的变化速度加快,参数估计的精度下降,另一方面是因为端电压变化较快,采样时间的略微偏差会使采样的电压值与实际值相差加大。
4 结论电池储能系统广泛应用于电网运行中,BMS准确估计SOC是电力调度安全可靠运行的前提。为了对储能用BMS的SOC功能进行测试,文中提出了一种基于DEKF的储能用BMS测试平台的SOC估计方法,通过电池建模、算法分析和实验验证得出以下结论:
(1) 提出一种基于DEKF算法的在线SOC估计方法,并与传统EKF估计方法进行比较,体现了其在在线参数辨识与SOC状态估计方面的优势。
(2) 在离线OCV-SOC曲线获取方面采用外推法实现曲线的快速获取,与传统的静置法和小电流放电法相比,保证精度的同时节约了测试时间。
(3) 分别在FUDS和DST工况下对基于DEKF和EKF的2种SOC状态估计方法进行了比较,证明了DEKF方法在收敛速度和SOC估计精度上的优势,在2种测试工况下2种方法的SOC估计误差都低于1%,电池端电压误差分别在±10 mV和±20 mV以内,平均绝对误差分别为2.7 mV和3.8 mV。
后续将主要针对不同受温度影响的SOC估计方法进行进一步研究。
本文得到江苏省研究生科研创新计划项目(储能电池功率状态估计方法研究,SJKY19_0323),江苏省研究生科研创新计划项目(梯次利用动力电池状态检测分选方法研究,SJCX19_0114)资助,谨此致谢!
| [1] |
LU L G, HAN X B, LI J Q, et al. A review on the key issues for lithium-ion battery management in electric vehicles[J]. Journal of Power Sources, 2013, 226: 272-288. DOI:10.1016/j.jpowsour.2012.10.060 (  0) 0) |
| [2] |
YAN L, BAEK M K, PARK J B, et al. Anoptimal energy storage operation scheduling algorithm for a smart home considering life cost of energy storage system[J]. Journal of Electrical Engineering and Technology, 2017, 12(4): 1369-1375. (  0) 0) |
| [3] |
ZHANG Z L, CHENG X, LU Z Y, et al. SOC estimation of lithium-ion battery pack considering balancing current[J]. IEEE Transactions on Power Electronics, 2018, 33(3): 2216-2226. DOI:10.1109/TPEL.2017.2700324 (  0) 0) |
| [4] |
刘大贺, 韩晓娟, 李建林. 基于光伏电站场景下的梯次电池储能经济性分析[J]. 电力工程技术, 2017, 36(6): 27-31, 77. LIU Dahe, HAN Xiaojuan, LI Jianlin. Economic analysis of echelon battery energy storage based on artificial fish swarm algorithm[J]. Electric Power Engineering Technology, 2017, 36(6): 27-31, 77. (  0) 0) |
| [5] |
张国玉, 洪超, 陈杜琳, 等. 面向储能电站调度的光储发电系统运行优化策略研究[J]. 电力工程技术, 2017, 36(3): 50-56. ZHANG Guoyu, HONG Chao, CHEN Dulin, et al. Operation optimization of photovoltaic-energy storage hybrid system based on scheduling of battery energy storage system[J]. Electric Power Engineering Technology, 2017, 36(3): 50-56. (  0) 0) |
| [6] |
LIU M J, LI W Y, WANG C S, et al. Reliability evaluation of large scale battery energy storage systems[J]. IEEE Transactions on Smart Grid, 2017, 8(6): 2733-2743. DOI:10.1109/TSG.2016.2536688 (  0) 0) |
| [7] |
FENG F, HU X S, HU L, et al. Propagation mechanisms and diagnosis of parameter inconsistency within Li-Ion battery packs[J]. Renewable and Sustainable Energy Reviews, 2019, 112: 102-113. DOI:10.1016/j.rser.2019.05.042 (  0) 0) |
| [8] |
彭鹏, 陈满, 梁靓, 等. 相内快速SOC均衡时MMC-BESS运行边界研究[J]. 供用电, 2020, 37(9): 78-84. PENG Peng, CHEN Man, LIANG Liang, et al. Analysis of operation boundary for modular multi-level converter energy storage system with inner phase rapid state of charge balancing[J]. Distribution & Utilization, 2020, 37(9): 78-84. (  0) 0) |
| [9] |
周喜超, 洪育金, 夏岩, 等. 基于多智能体的电池储能系统SOC均衡控制策略[J]. 浙江电力, 2020, 39(5): 35-40. ZHOU Xichao, HONG Yujin, XIA Yan, et al. SOC balanced control strategy for battery energy storage system based on multiple-agent[J]. Zhejiang Electric Power, 2020, 39(5): 35-40. (  0) 0) |
| [10] |
于昌海, 吴继平, 杨海晶, 等. 规模化储能系统参与电网调频的控制策略研究[J]. 电力工程技术, 2019, 38(4): 68-73, 105. YU Changhai, WU Jiping, YANG Haijing, et al. Frequency regulation strategy for power grid incorporating large-scale energy storage[J]. Electric Power Engineering Technology, 2019, 38(4): 68-73, 105. (  0) 0) |
| [11] |
ALLAFI W, ZHANG C, UDDIN K, et al. A lumped thermal model of lithium-ion battery cells considering radiative heat transfer[J]. Applied Thermal Engineering, 2018, 143: 472-481. (  0) 0) |
| [12] |
黄瑞, 赵春莲, 明鑫, 等. 电池管理系统测试平台设计与实现[J]. 自动化与仪表, 2017, 32(1): 62-67. HUANG Rui, ZHAO Chunlian, MING Xin, et al. Design and application of the battery management system test platform[J]. Automation & Instrumentation, 2017, 32(1): 62-67. (  0) 0) |
| [13] |
陈雨飞, 李志扬, 朱建新, 等. 基于LabVIEW的电池管理系统测试平台设计[J]. 电源技术, 2019, 43(7): 1205-1207, 1229. CHEN Yufei, LI Zhiyang, ZHU Jianxin, et al. Design of test platform for battery management system based on LabVIEW[J]. Chinese Journal of Power Sources, 2019, 43(7): 1205-1207, 1229. (  0) 0) |
| [14] |
郭敏, 庄信武, 高飞. 电池管理系统BMS性能测试装置方案设计[J]. 电子测量技术, 2019, 42(11): 43-46. GUO Min, ZHUANG Xinwu, GAO Fei. Scheme design of BMS performance test device[J]. Electronic Measurement Technology, 2019, 42(11): 43-46. (  0) 0) |
| [15] |
程浩, 蒋立琴, 何志辉, 等. 电动汽车用电池管理系统测试平台的设计与实现[J]. 自动化与仪表, 2019, 34(8): 55-59. CHENG Hao, JIANG Liqin, HE Zhihui, et al. Design and application of battery management system test platform for electric vehicle[J]. Automation & Instrumentation, 2019, 34(8): 55-59. (  0) 0) |
| [16] |
邢建旭, 王友旭, 张文杰, 等. 一种基于SOC的电动汽车充电过程等效电阻模型[J]. 供用电, 2019, 36(8): 61-66. XING Jianxu, WANG Youxu, ZHANG Wenjie, et al. An equivalent resistance model of electric vehicle charging process based on SOC[J]. Distibution & Utilization, 2019, 36(8): 61-66. (  0) 0) |
| [17] |
刘振华, 陈国平, 朱强. 基于扩展卡尔曼滤波的锂电池SOC估计[J]. 农业装备与车辆工程, 2017, 55(8): 45-48. LIU Zhenhua, CHEN Guoping, ZHU Qiang. Li-ion battery SOC estimation based on EKF[J]. Agricultural Equipment & Vehicle Engineering, 2017, 55(8): 45-48. (  0) 0) |
| [18] |
PLETTG L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: part 3. State and parameter estimation[J]. Journal of Power Sources, 2004, 134(2): 277-292. (  0) 0) |
| [19] |
刘子幸, 王子赟, 纪志成. 基于逆向卡尔曼滤波的电力变换器故障诊断方法[J]. 电力系统保护与控制, 2019, 47(9): 19-26. LIU Zixing, WANG Ziyun, JI Zhicheng. Inverse Kalman filtering based converter fault diagnosis method[J]. Power System Protection and Control, 2019, 47(9): 19-26. (  0) 0) |
| [20] |
熊瑞. 基于数据模型融合的电动车辆动力电池组状态估计研究[D]. 北京: 北京理工大学, 2014. XIONG Rui. Estimation of battery pack state for electric vehicles using model-data fusion approach[D]. Beijing: Beijing Institute of Technology, 2014. (  0) 0) |
| [21] |
张博文, 孙永辉, 张世达. 基于SOCP的综合能源系统日前调度概率最优能量流[J]. 电力系统自动化, 2019, 43(6): 25-33. ZHANG Bowen, SUN Yonghui, ZHANG Shida. Second-order cone programming based probabilistic optimal energy flow of day-ahead dispatch for integrated energy system[J]. Automation of Electric Power Systems, 2019, 43(6): 25-33. (  0) 0) |
| [22] |
DANILOV D, LYEDOVSKIKH A, NOTTEN P H L. Voltage and temperature dynamic simulations for advanced battery management systems[C]//2011 IEEE Vehicle Power and Propulsion Conference. Chicago, IL, USA. IEEE, 2011: 1-6.
(  0) 0) |
2. State Grid Jiangsu Electric Power Co., Ltd. Research Institute, Nanjing 211103, China
 2021, Vol. 40
2021, Vol. 40


 唐传雨(1995),男,硕士在读,研究方向为电池状态估计技术和电池均衡技术(E-mail:
唐传雨(1995),男,硕士在读,研究方向为电池状态估计技术和电池均衡技术(E-mail: